Anisotropic Fractional Cosmology: K-Essence Theory
Abstract
1. Introduction
2. Brief Review on Fractional Calculus and K-Essence Theory
2.1. Brief Review on Fractional Calculus
2.2. K-Essence Fractional in the Bianchi Type I Scenario
3. Lagrange and Hamilton Formalism
3.1. Exact Solution in the Gauge
3.2. Exact Solution without Gauge N in the Time
3.3. Case for
- Dust Scenario,
4. Quantum Regime
Solution to FDE Associated with the Different State Evolutions
5. Conclusions
- Using the k-essence formalism in a general way, applied to the anisotropic Bianchi type I cosmological model, we found the Hamiltonian density in the scalar field momenta raised to powers of non-integers, which produces in the quantum scheme a fractional differential equation in a natural way. We include the factor-ordering problem in both variables and its momenta , with the order , where , and it was solved in a general way, we include two particular scenarios of our universe.
- We found the solution in the classical scheme employing two gauges, , for two forms of the function in the time t; however, when we let the Lagrange multiplier N, we need to employ a transformed time for solving the classical equation and, only in the dust era, we recover the gauge time .
- In the quantum regime, when we include the factor-ordering problem, the fractional differential equation in the scalar field appears with variable coefficients, and it was necessary to use the fractional series expansion to solve it in a general way.
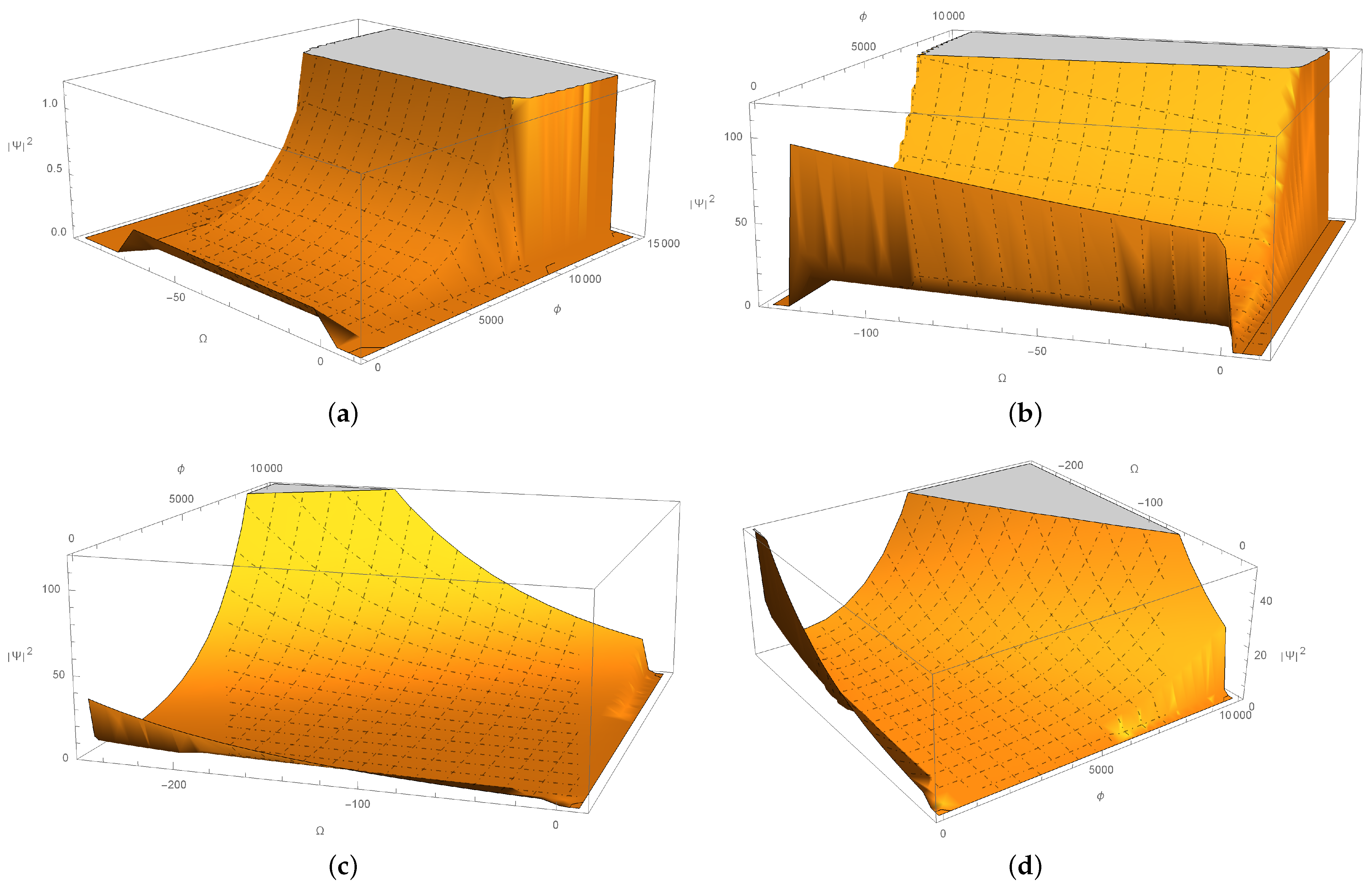
- In one of our analyses presented on the probability density, we consider the values of the scalar field as significant in the quantum regime, appearing in various scenarios in the behavior of the universe, mainly in those where the universe has a huge behavior; for example, in the actual epoch, where the scalar field appears as a background, the quantum regime appears with big values, but it presents a moderate development in other scenarios with different ordering parameters Q and s.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Uchaikin, V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction For Physicists; World Scientific Publishing Co., Pte., Ltd.: Singapore, 2011. [Google Scholar]
- Caputo, M.; Mainarde, F.A. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–137. [Google Scholar] [CrossRef]
- Wyss, W. Fractional diffusion equation. J. Math. Phys. 1986, 27, 2782–2785. [Google Scholar] [CrossRef]
- Westerlund, S. Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Rosu, H.C.; Madueno, A.L.; Socorro, J. Transform of Riccati equation of constant coefficients through fractional procedure. J. Phys. A Math. Gen. 2003, 36, 1087–1093. [Google Scholar] [CrossRef][Green Version]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publisher: Rodding, Denmark, 2006. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Duarte Ortigueira, M.; Martynyuk, V.; Kosenkov, V.; Batista, G.A. A new look at the capacitor theory. Fractal Fract. 2023, 7, 86. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Quantum Mechnics; World Scientific Publishing Co., Pte., Ltd.: Singapore, 2018. [Google Scholar]
- Moniz, P.V.; Jalalzadeh, S. From Fractional Quantum Mechanics to Quantum Cosmology: An Overture. Mathematics 2020, 8, 313. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; da Silva, F.R.; Moniz, P.V. Prospecting black hole thermodynamics with fractional quantum mechanics. Eur. Phys. J. C 2021, 81, 632. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Moniz, P.V. Challenging Routes in Quantum Cosmology; World Scientific Publiching Company: Singapore, 2023. [Google Scholar]
- Valério, D.; Ortigueira, M.D.; Lopes, A.M. How Many Fractional Derivatives are There? Mathematics 2022, 10, 737. [Google Scholar] [CrossRef]
- Ortigueira, M.D. A New Look at the Initial Condition Problem. Mathematics 2022, 10, 1771. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Bohannan, G.W. Fractional Scale Calculus: Hadamard vs.Liouville. Fractal Fract. 2023, 7, 296. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Bengochea, G. A Simple Solution for the General Fractional Ambartsumian Equation. Appl. Sci. 2023, 13, 871. [Google Scholar] [CrossRef]
- Godínez, F.A.; Rosales, J.J.; Esparza-Posadas, M.F. Newton’s Law of Cooling with Caputo Derivative: Consistent Dimensionality to Compare with Experiments. Fractals 2022, 30, 2250187. [Google Scholar] [CrossRef]
- Rosales-García, J.; Andrade-Lucio, J.A.; Shulika, O. Conformable derivative applied to experimental Newton law of cooling. Rev. Mex. FÍsica 2020, 66, 224–227. [Google Scholar] [CrossRef]
- El-Nabulsi, A.R. Fractional Unstable Euclidean Universe. EJTP 2005, 8, 1–11. [Google Scholar]
- El-Nabulsi, R.A. Gravitons in fractional action cosmology. Int. J. Theor. Phys. 2012, 51, 3978–3992. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Non-minimal coupling in fractional action cosmology. Indian J. Phys. 2013, 87, 835–840. [Google Scholar] [CrossRef]
- Rami, E.N.A. Fractional action oscillating phantom cosmology with conformal coupling. Eur. Phys. J. Plus 2015, 130, 102. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. A Cosmology Governed by a Fractional Differential Equation and the Generalized Kilbas-Saigo-Mittag-Leffler Function. Int. J. Theor. Phys. 2016, 55, 625–635. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Implications of the Ornstein-Uhlenbeck-like fractional differential equation in cosmology. Rev. Mex. Fis. 2016, 62, 240. [Google Scholar]
- El-Nabulsi, R.A. Fractional Action Cosmology with Variable Order Parameter. Int. J. Theor. Phys. 2017, 56, 1159–1182. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Wormholes in fractional action cosmology. Can. J. Phys. 2017, 95, 605–609. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Jalalzadeh, S.; Moniz, P.V. Broadening quantum cosmology with a fractional whirl. Mod. Phys. Lett. A 2021, 36, 2140005. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Costa, E.W.O.; Moniz, P.V. de Sitter fractional quantum cosmology. Phys. Rev. D 2022, 105, L121901. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Costa, E.W.O.; Moniz, P.V.; Jalalzadeh, S. Inflation and fractional quantum cosmology. Fractal Fract. 2022, 6, 655. [Google Scholar] [CrossRef]
- El-Nabulsi, A.R. Cosmology with Fractional Action Principle. Rom. Rep. Phys. 2007, 39, 763–771. [Google Scholar]
- García-Aspeitia, M.A.; Anaya, G.F.; Almada, A.H.; León, G.; Magaña, J. Cosmology under the fractional calculus approach. Mon. Not. 2022, 517, 4813–4826. [Google Scholar] [CrossRef]
- Leon, G.; García-Aspeitia, M.A.; Fernández-Anaya, G.; Hernández-Almada, A.; Magaña, J.; González, E. Cosmology under the fractional calculus approach: A possible H0 tension resolution. Mon. Not. R. Astron. Soc. 2022, 517, 4813–4826. [Google Scholar]
- Socorro, J.; Pimentel, L.O.; Espinoza-García, A. Classical Bianchi type I cosmology in K-essence theory. Adv. High Energy Phys. 2014, 2014, 805164. [Google Scholar] [CrossRef]
- Socorro, J.; Rosales, J.J. Quantum fraccionary cosmology: K-essence theory. Universe 2023, 9, 185. [Google Scholar] [CrossRef]
- El-Ajou, A.; Arqub, O.A.; Zhour, Z.A.; Momani, S. New Results on Fractional Power Series: Theories and Applications. Entropy 2013, 15, 5305–5323. [Google Scholar] [CrossRef]
- Rida, S.Z.; Arafa, A.A.M. New Method for Solving Linear Fractional Differential Equations. Int. J. Differ. Equations 2011, 2011, 814132. [Google Scholar] [CrossRef]
- Tarasov, V.E. No violation of the Leibniz rule. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2945–2948. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Tenreiro Machado, J.A. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Teodoro, G.S.; Machado, J.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A. Special Functions of Fractional Calculus: Applications to Diffusion and Random Search Processes; World Scientific Publishing Co., Pte., Ltd.: Singapore, 2023. [Google Scholar]
- Erdelyi, A.; Magnus, W.; Oberthettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef]
- García, A.E.; Socorro, J.; Pimentel, L.O. Quantum Bianchi type IX cosmology in K-essence theory. Int. J. Theor. Phys. 2014, 53, 3066–3077. [Google Scholar] [CrossRef]
- de Putter, R.; Linder, E.V. Kinetic k-essence and Quintessence. Astropart. Phys. 2007, 28, 263. [Google Scholar] [CrossRef]
- Chiba, T.; Dutta, S.; Scherrer, R.J. Slow-roll k-essence. Phys. Rev. D 2009, 80, 043517. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. A k-essence model of inflation, dark matter and dark energy. Phys. Rev. D 2009, 79, 103517. [Google Scholar] [CrossRef]
- Arroja, F.; Sasaki, M. Note on the equivalence of a barotropic perfect fluid with a k-essence scalar field. Phys. Rev. D 2010, 81, 107301. [Google Scholar] [CrossRef]
- García, L.A.; Tejeiro, J.M.; Castaneda, L. K-essence scalar field as dynamical dark energy. arXiv 2012, arXiv:1210.5259. [Google Scholar]
- Bilic, N.; Tupper, G.; Viollier, R. Unification of dark matter and dark energy: The inhomogeneous Chaplygin gas. Phys. Lett. B 2002, 535, 17. [Google Scholar] [CrossRef]
- Bento, M.; Bertolami, O.; Sen, A. Dynamics of dark energy. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Polyanin, A.C.; Zaitsev, V.F. Handbook of Exact Solutions for Ordinary Differential Equations, 2nd ed.; Chapman Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Micolta-Riascos, B.; Millano, A.D.; Genly, L.; Erices, C.; Paliathanasis, A. Revisiting Fractional Cosmology. Fractal Fract. 2023, 7, 149. [Google Scholar] [CrossRef]
- Socorro, J.; Rodríguez, P.A.; Nunez, O.E.; Hernández, R.; Espinoza-García, A. Quintom Potential from Quantum Anisotropic Cosmological Models. In Open Questions in Cosmology; Gonzalo, J.O., Ed.; Chapter 9; InTech Open: London, UK, 2012; pp. 219–240. ISBN 978-953-51-0880-1. [Google Scholar]
- Socorro, J.; Romero, P.; Pimentel, L.O.; Aguero, A. Quintom potentials from quantum cosmology using the FRW cosmological model. Int. J. Theor. Phys. 2013, 52, 2722–2734. [Google Scholar] [CrossRef]
- Zampeli, A.; Pailas, T.; Terzis, P.A.; Christodoulakis, T. Conditional symmetries in axisymmetric quantum cosmologies with scalar fields and the fate of the classical singularities. JCAP 2016, 2016, 66. [Google Scholar] [CrossRef]
- Socorro, J.; Nuñez, O.E. Scalar potentials with multi-scalar fields from quantum cosmology and supersymetric quantum mechanics. Eur. Phys. J. Plus 2017, 132, 168. [Google Scholar] [CrossRef]
- Paliathanasis, A. Dust fluid component from Lie symmetries in Scalar field Cosmology. Mod. Phys. Lett. A 2017, 32, 1750206. [Google Scholar] [CrossRef]
- Zampeli, A.; Paliathanasis, A. Quantization of inhomogeneous spacetimes with cosmological constant term. Class. Quantum Grav. 2021, 38, 165012. [Google Scholar] [CrossRef]
- Paliathanasis, A. Quantum potentiality in Inhomogeneous Cosmology. Universe 2021, 7, 52. [Google Scholar] [CrossRef]
- Oliveira Costa, E.W.; da Silva, P.F., Jr.; Rasouli, S.M.M.; Jalalzadeh, S. The estimation of the universe’s age as per fractional cosmology. arXiv 2023, arXiv:2310.09464. [Google Scholar]
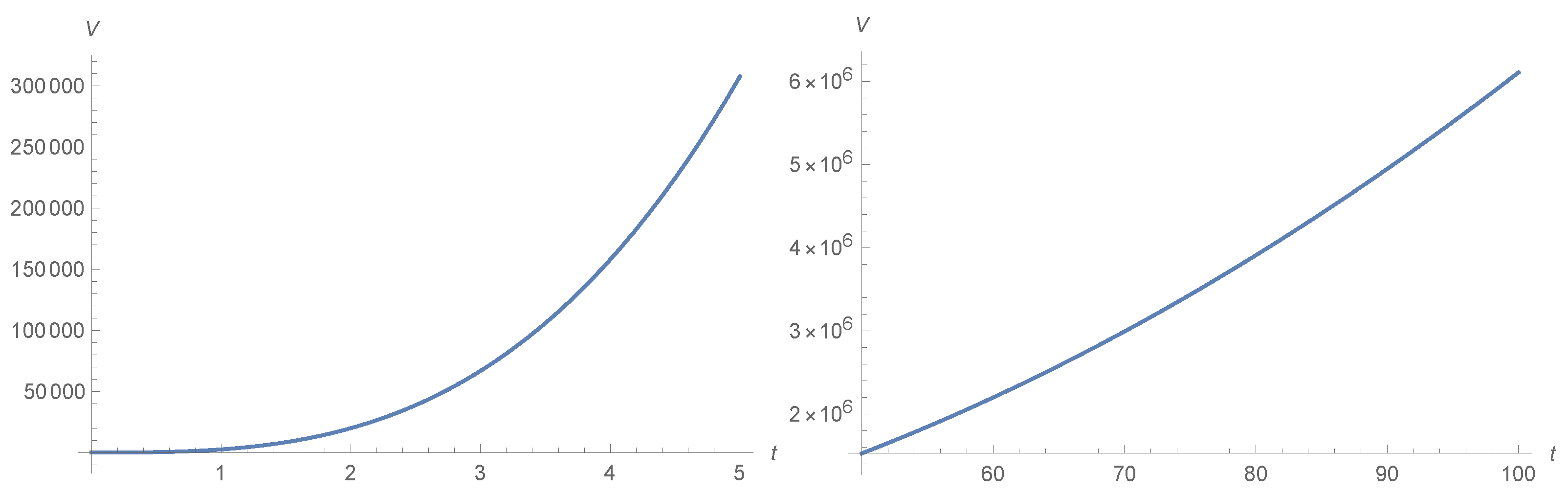

| State of Evolution | |||
|---|---|---|---|
| 1 | 1 | X | Stiff matter |
| 2 | Radiation | ||
| , | Dust-like | ||
| 0 | 1, | Inflation | |
| −1 | Inflation-like | ||
| Inflation-like |
| Fractionary Equation | |||
|---|---|---|---|
| 1 | 1 | 1 | |
| 2 | |||
| 0 | 0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Socorro, J.; Rosales, J.J.; Toledo-Sesma, L. Anisotropic Fractional Cosmology: K-Essence Theory. Fractal Fract. 2023, 7, 814. https://doi.org/10.3390/fractalfract7110814
Socorro J, Rosales JJ, Toledo-Sesma L. Anisotropic Fractional Cosmology: K-Essence Theory. Fractal and Fractional. 2023; 7(11):814. https://doi.org/10.3390/fractalfract7110814
Chicago/Turabian StyleSocorro, José, J. Juan Rosales, and Leonel Toledo-Sesma. 2023. "Anisotropic Fractional Cosmology: K-Essence Theory" Fractal and Fractional 7, no. 11: 814. https://doi.org/10.3390/fractalfract7110814
APA StyleSocorro, J., Rosales, J. J., & Toledo-Sesma, L. (2023). Anisotropic Fractional Cosmology: K-Essence Theory. Fractal and Fractional, 7(11), 814. https://doi.org/10.3390/fractalfract7110814






