Abstract
This paper investigates exact solutions of cosmological interest in fractional cosmology. Given , the order of Caputo’s fractional derivative, and w, the matter equation of state, we present specific exact power-law solutions. We discuss the exact general solution of the Riccati Equation, where the solution for the scale factor is a combination of power laws. Using cosmological data, we estimate the free parameters. An analysis of type Ia supernovae (SNe Ia) data and the observational Hubble parameter data (OHD), also known as cosmic chronometers, and a joint analysis with data from SNe Ia + OHD leads to best-fit values for the free parameters calculated at , and confidence levels (CLs). On the other hand, these best-fit values are used to calculate the age of the Universe, the current deceleration parameter (both at CL) and the current matter density parameter at CL. Finding a Universe roughly twice as old as the one of CDM is a distinction of fractional cosmology. Focusing our analysis on these results, we can conclude that the region in which is not ruled out by observations. This parameter region is relevant because fractional cosmology gives a power-law solution without matter, which is accelerated for . We present a fractional origin model that leads to an accelerated state without appealing to or dark energy.
1. Introduction
In fractional calculus, the classical derivatives and integrals of integer order are generalized to derivatives and integrals of arbitrary (real or complex) order [1,2,3,4,5,6,7,8,9]. Fractional derivatives have attracted increasing attention because they universally appear as empirical descriptions of complex social and physical phenomena. Fractional calculus applications have grown enormously in recent years because these operators have memory and are more flexible in describing the dynamic behavior of phenomena and systems using fractional differential equations, while the description with integer order differential equations uses local operators and they are limited in the order of differentiation to a constant. Consequently, the resulting models must be sufficiently precise in many cases [10]. Research into fractional differentiation is inherently multi-disciplinary and has applications across various disciplines, for example, fractional quantum mechanics and gravity for fractional spacetime [11,12] and fractional quantum field theory [13,14,15,16,17,18]. Such frameworks have been essential in understanding complex systems in classical and quantum regimes [19,20,21,22,23,24,25,26,27,28,29].
Regarding the classical regime, fractional derivative cosmology has been established by two methods: (i) The last-step modification method is the simplest one, in which the corresponding fractional field equations replace the given cosmological field equations for a specific model. (ii) The first-step modification method can be considered a more fundamental methodology. In this method, one starts by establishing a fractional derivative geometry. More concretely, the variational principle for fractional action is applied to establish a modified cosmological model.
Fractional calculus has recently been explored to address problems related to cosmology in [27,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. For example, in [30,34], the Riemann curvature and the Einstein tensor are defined as usual, but now with dependence on the fractional parameter. Then, it is possible to write a fractional analogous to the Einstein field equation through the expression , where is the Einstein tensor in fractional calculus and G is the Newton gravitational constant. These studies correspond to the last-step modification method, as mentioned above. Modifications to several astrophysical and cosmological events can be studied based on the last equation. For example, a fractional theory of gravitation for fractional spacetime has been developed in [31,32]. Non-holonomic deformations to cosmology lead to new classes of cosmological models, which have been studied in [33,57].
In reference [61], a joint analysis using data from cosmic chronometers and type Ia supernovae was performed. This comparison with observational tests was used to find best-fit values for the fractional order of the derivative. These methods are a robust scheme for investigating the physical behavior of cosmological models [61,63,64,65,66] and can be used in new contexts, such as in [62], where dynamical systems and phase spaces were used to analyze fractional cosmology for different matter contents, obtaining a late-time accelerating cosmology.
Undeniably, the late-time acceleration in the Universe expansion is one of the most challenging topics in modern cosmology.
Since 1998, when the independent projects High-z Supernova Search Team [67] and Supernova Cosmology Project [68] obtained results that suggested this behavior in the Universe, the type Ia supernovae (SNe Ia) data have become a definitive proof to study this era of the Universe and the transition between the decelerated expansion phase and the accelerated one. However, the latter is usually model dependent [69]. In this sense, the observational Hubble parameter data (OHD), also known as cosmic chronometers, have become a fundamental data test, complementary to the SNe Ia data, to study the Universe’s expansion rate in a model-independent way. Finally, using these cosmological data, we estimate the free parameters .
This research’s main objective is to investigate open problems in gravity and cosmology. Therefore, we estimate the free parameters using cosmological data. The analysis of the type Ia supernovae (SNe Ia) data and the observational Hubble parameter data (OHD), also known as cosmic chronometers, and the joint analysis of SNe Ia data + OHD lead to best-fit values for the free parameters calculated at the , and confidence levels (CLs). On the other hand, these best-fit values are used to calculate the age of the Universe, the current deceleration parameter (both at the CL) and the current matter density parameter at CL. Finding that the Universe is roughly twice as old as the one of CDM is a distinction of fractional cosmology; apart from that, it leads to an accelerated state without appealing to or dark energy. We confirm that this result, which is in disagreement with the value obtained with globular clusters with a value of [70], is a distinction of fractional cosmology. This result also agrees with the analysis performed in ([61], Section 5, page 4817). Despite the discrepancy between the age of the Universe and that determined by globular clusters, it is essential to highlight that fractional cosmology contributes to the solutions to other problems associated with the CDM model, for example, late-time acceleration without dark energy, as we explained before. In this sense, the non-inclusion of a cosmological constant (CC) or some DE can alleviate some other problems related to these components. One of these problems is the so-called CC problem, in which the observational value of the CC differs between 60 and 120 orders of magnitude compared with the value anticipated by particle physics [71,72,73,74,75]. Another problem related to the DE is the coincidence problem, which stipulates that, currently, we are living in an extraordinary epoch in the cosmic evolution, in which DM and DE densities are of the same order of magnitude, with a fine-tuning problem associated with the context of the CDM model [76,77,78].
Another issue that fractional cosmology can possibly alleviate is the Hubble tension. Measurements of the Hubble parameter at the current time, , exhibit a discrepancy of between the observational value obtained from the Hubble Space Telescope (HST) [79] and the one inferred from Planck CMB [80]. The first corresponds to model-independent measurements, while the second depends on the CDM model. According to Riess et al. [81], observational issues such as the tension are strong evidence that physics beyond the CDM model is required. Therefore, and following this line, a possible alternative to solve this tension considers extensions beyond CDM (see Di Valentino et al. [82] for a review). In [61], some results were discussed related to the tension in the context of fractional cosmology, and a trend of to the value obtained by SH0ES [81] at current times was observed, in agreement with Planck’s value [80] for . However, the tension is not fully resolved in the region .
Moreover, prospects for the density perturbation growth and cosmological structure formation could be described in this context. For example, in [83], it was shown that in the CDM cosmology, the perturbations do not change the stability of the late-time attractor of the background equations and the system still results in the dark-energy-dominated de Sitter solution, with a dark matter era transition and a growth index of . Here, is defined through the relation , where is the matter contrast and is the fractional energy density of matter. This result for the linear growth rate, , was corrected to in [84]. In fractional cosmology, the dimensionless energy density of dust matter depends on t through ; thus, the growth index in the matter-dominated solution should be different to . In addition, it could be exciting to investigate and try fractional cosmology within a very early universe, fitting data and determining the impact of the fractional derivative term on primordial nucleosynthesis. Fractional cosmology ingredients may enhance inflation, raising the question whether it is possible that issues such as the cosmic no-hair conjecture, isotropization, etc., could be solved [85,86,87,88,89,90,91].
According to previous statements, it is essential to see if fractional calculus or fractional cosmology can well-describe the observational data. Then, we can perform more sophisticated calculations to describe the late-time Universe or the very early Universe. Therefore, one can argue that the Universe can be better described with a fractional derivative, not just to fit the data but also to describe the fundamental dynamics, highlighting the demand for new physics. These approaches can help to understand the Universe’s acceleration with the mathematical background of fractional calculus. The mathematical richness generated by the corrections due to the fractional index of the fractional derivative can resolve the previous problems in future studies. Indeed, we can examine these topics in a forthcoming series of manuscripts with applications in inflation and dark energy models, investigating the physical implications and producing observational constraints.
In this paper, we investigate exact solutions of cosmological interest in fractional cosmology. In particular, we study the cosmological applications of power-law solutions of the type , where is the current age parameter. Additionally, given , the order of Caputo’s fractional derivative, and w, the equation of state (EoS) of matter, one must impose two compatibility conditions which allow particular solutions to . Moreover, we are interested in an exact solution that gives the general solution of the system. For this purpose, one can solve the Riccati equation independent of the EoS, where the solution for the scale factor is a combination of power-law solutions. Additionally, we investigate if the solutions take account of the current late-time acceleration.
The paper is organized as follows. Section 2 discusses the basics of the fractional variational approach to cosmology and presents the cosmological equations for a perfect fluid. In Section 2.3, we comment on the crucial difference between fractional and standard cosmology; that is, we obtain late-time acceleration without adding a cosmological constant, quintessence scalar field or other exotic fluids as compared to standard cosmology. In Section 2.5, we consider a model with cold dark matter to present a specific realization of these possibilities and we interpret the fractional modification as dark energy in Section 2.6. Section 3 is devoted to finding exact solutions for the Hubble factor in this scenario. They correspond mainly to power-law solutions for the scale factor and a combination of power-law functions. In Section 3.4, we provide a precise scheme to find approximated analytical solutions to aid in the asymptotic analysis. A discussion is presented in Section 3.5. We solve Bernoulli’s equation using differential inequalities and asymptotic expansions to estimate in redshift. A physical discussion of the results is presented in Section 3.6. In Section 4, a joint analysis using OHD and type Ia supernovae data is performed. This comparison with observational tests was used to find best-fit values for the fractional order of the derivative and the current age parameter . Section 5 is the conclusion.
2. Fractional Action Integral
Recently, a wide range of definitions of fractional derivatives [92], such as the Riemann–Liouville derivative (RLD) and the Caputo derivative (CD), among others, have been used in many applications.
2.1. Some Fractional Derivatives
The RLD with for is defined by
where and .
Note that the main parameter of fractional calculus is given by , recovering standard calculus when .
The Caputo left derivative is defined as
where . In fractional calculus, we now have the following relation (see [92]) for the case of more than one derivative:
or in other words , if not all derivatives are equal to zero at c. Additionally, the fractional derivative of the Leibniz rule [92] reads as
having the usual when .
2.2. Frational Action-like Variational Problems
Within the first-step modification method, one procedure uses the fractional variational approach developed in [30,93,94,95,96,97] with the following fractional action integral,
where is the Gamma function, is the Lagrangian, is the constant fractional parameter and and are the observers and intrinsic time, respectively, and the action integral depends on second order derivatives of the generalized coordinates .
2.3. Applications to Cosmology
In cosmology, it is assumed that the flat Friedmann provides the geometry of spacetime Lemaître–Robertson–Walker (FLRW) metric:
where denotes the scale factor and is the lapse function. This result is based on Planck’s observations [80].
For the metric (7), the Ricci’ scalar depends on the second derivatives of a and first derivatives of N and reads
Consider the point-like action integral
where is the Ricci scalar (8). In cosmology, the Einstein–Hilbert Lagrangian density is related to the Ricci scalar. Generically, one takes integration by parts, such that a total derivative is removed for the action, and the derivatives and are eliminated. We will use a fractional version of the Lagrangian (9); thus, we do not follow the standard procedure and keep the higher order derivatives and use formulation (5) leading to the Euler–Poisson Equation (6). We use fractional variational calculus with classical and Caputo derivatives.
For simplicity, we consider units in which and assume a perfect fluid for the matter content of the Universe, where for is the usual matter Lagrangian of a perfect fluid as in [98,99,100] and contains integer-order derivatives in the Lagrangian. We consider the transition to the effective fractional action used in [61], i.e.,
where is the Gamma function, , which recovers the usual matter Lagrangian of a perfect fluid as [98,99,100], is the constant fractional parameter and and are the observers and intrinsic time, respectively [34]. is a constant EoS for matter.
For a fixed , the expressions
and
define the energy density and the isotropic pressure of the matter fields. Then,
Defining in (5) for a fixed , we have the Lagrangian
The Euler–Poisson Equations (6) obtained after varying the action (10) for lead to the field equations
Here, we have substituted the lapse function after the variation.
To designate the temporary independent variables, the rule is applied, where new cosmological time t [34] is used, where the dots denote these derivatives. Furthermore, the Hubble parameter is . Hence, Equations (15) and (16) and the conservation Equation (13) can be written as
where expressions (11) and (12) are transformed to
which defines the energy density and the isotropic pressure of the matter fields in cosmological time.
2.4. Some Cosmological Solutions
From (18) and assuming , the Hubble parameter is
We have considered the positive root because we are interested in expanding universes.
To understand the self-accelerating behavior of H, let us assume that there is no matter, i.e., and . Then, from (18),
Henceforth,
and the deceleration parameter can be expressed as . Therefore,
and
where the usual case , corresponding to a cosmological constant , is excluded.
The case can also be interpreted as a fluid whose energy density quickly vanishes with evolution. The asymptotic solution (22) was examined in detail using a dynamical systems analysis in reference [61], and its properties are summarized in Table 1. The table summarizes the asymptotic behavior for when the energy density of matter tends to zero. Hence, even in the absence of matter, fractional cosmology gives a power-law solution , which is accelerated for . This is a crucial difference to standard cosmology, where we must add a cosmological constant, quintessence scalar field, or other exotic fluids to accelerate the expansion.

Table 1.
Asymptotic solution , examined in reference [61].
In General Relativity (GR), we have the flat Friedmann–Lemaître–Robertson–Walker metric; the main equations are the Friedmann constraint and conservation equation,
Using (29) and (30), we obtain
Now, using (29) and (31) we re-obtain (30). That is, we have three equations, two of them independent. However, as we discussed before, [62] studied Equations (17)–(19), and using a similar procedure as in GR, we obtain a new equation (see Equation (34)) instead of showing that two out of three equations are independent.
By demanding that (18) is conserved in time, i.e.,
we calculate the corresponding derivatives and substitute them into (26)–(28) to obtain
This equation is an identity for as expected in standard cosmology. However, for , we acquire the new relation for the pressure of the fluid:
Using a similar procedure as in GR, we obtain a new Equation (34) instead of showing that two out of three equations are independent. This characteristic of fractional cosmology leads to some restrictions of the matter fields in the Universe that were explored in [62] for different matter fields.
The previous results are valid for any ideal gas source.
Moreover, following references [61,62], the system can be extended by including several matter sources in Equations (15) and (16). After performing algebra, and using , the following Raychaudhuri equation (with ) is obtained:
along with the Friedmann equation
Furthermore, the continuity equation leads to
where and are the density and pressure of the ith matter component, respectively, and the sum is over all species, e.g., matter, radiation, etc. Note that when in Formula (38) and Formula (39), the standard cosmology without is recovered, which by itself does not produce an accelerated expanding universe.
Using the equation of state , where and are constants, we have
Assuming separate conservation equations for each species and integrating for each , we have the following solution:
where , is the age of the universe and is the current value of the energy density of the ith species. Therefore, by substituting (41) into (38), we have
Note that for , the modified continuity Equation (39) provides the condition
Combining these results with (37) and (38), we have the Riccati equation (35). This equation generically appears in fractional cosmology, independent of the matter content. Therefore, in the following, we consider only one matter source.
Comparing with other fractional formulations, according to [42,44], and assuming and using for simplicity, we obtain the field equations
where and P are the bare dark matter energy density and pressure, respectively. Equations (44)–(46) are equivalent to (17)–(19) under the scaling
Now, we consider a constant EoS,
Then, one obtains,
Then, for we have
and
Furthermore, we recover GR.
From Equations (45) and (44) and , it follows that
Replacing (45), we recover (49).
Setting , from (49) we obtain
That is, a “correction” to the usual CDM (, , ).
For , we recover the usual CDM (, ),
For , the solution of (55) is
We will search for solutions considering relativistic matter/radiation. Setting , from (49), we obtain
For , we recover the usual radiation (, ),
Another case of interest is when (quasi-vacuum matter, according to [42,44]).
The equation for H becomes
The solution to turns out to be
According to (64),
For , we have
Hence, we obtain a late-time de Sitter solution without including a cosmological constant.
In summary, fractional cosmology allows for an accelerated expansion without adding exotic fluids to the model. Therefore, we now consider a model with cold dark matter to present a specific realization of these possibilities.
2.5. Model with Cold Dark Matter
Assume
where is a constant and . If , we recover Equation (22).
The conservation equation for matter (19), for cold dark matter ( and ), takes the form
when then reduces to
Hence, we have for the matter energy density,
Choosing
we obtain
Then, from Equation (28), we obtain
Using the redshift parameter , we obtain
and
then,
where is defined by (71). Comparing with GR, where the EoS is defined through
we have
Similarly to GR, we have the usual relation . Therefore, in fractional cosmology, we have an acceleration () as is present in GR when the effective fluid has . Hence,
and
Finally, we have an accelerated expansion if , caused by the fractional derivative correction and not by the matter content. That is the powerful advantage of fractional cosmology over GR. This is consistent as with the asymptotic solution , where , which is a power-law solution . It is accelerated if and decelerated if , as proven in [61].
2.6. Interpretation of the Fractional Term as a Dark Energy Source
We write (18) as
where
where
and
Using and , we obtain
3. Exact Solutions
3.1. First Exact Solution
From Equations (28) and (34) and defining the effective equation of state , we have
Hence, in the intervals , both are non-negative. For , is negative and is positive. For , is zero.
The deceleration parameter for each algebraic solution is a constant
such that the solutions for the scale factor are power laws.
Therefore, upon physical consideration, we select the one that gives an accelerated Universe. The deceleration parameter is negative in the parameter region , and we have an accelerated expansion when and . If we choose the range , the solution becomes nonphysical, and the one that gives accelerated expansion is because is negative in the parameter region .
Substituting (94), (28) and (34) into (26) and (27), we obtain the compatibility conditions
where is defined by (95) for the existence of an exact solution. We define the current value of through , and is interpreted as the age parameter evaluated at (the current time).
Therefore, to obtain solutions, we solve (97) and (98) simultaneously for and w. Upon physical consideration, we remove the cases with and , and we assume .
From (94), the definition of q and Equations (28), (34) and (93), we have
and
where we set the conditions and fix the current value of the scale factor to .
For simplicity, let us assume that the source is dust, with (). Then, we have , where , which makes (99) an identity.
Hence, we have
For , the two conditions are simultaneously satisfied only for .
For , the two conditions are simultaneously satisfied only for . Since we are interested in the case where and an expanding Universe (), the parameter that gives the physical solution is . Substituting these values for w and , we obtain
That means if we fix the equation of state w, there are specific values that has to satisfy to obtain an exact solution.
3.2. Second Exact Solution
One can also solve a Riccati equation for :
which follows from substituting into (26) and removing using (28). We obtain the exact solution
where
is an integration constant, is the current value of H at and
These compatibility conditions have to be satisfied for all t, such that . Then, (106) becomes
and the compatibility conditions are
Therefore, to obtain solutions, we solve (112) and (113) simultaneously for and w. Upon physical consideration, we remove the cases with and , and we assume .
As before, we choose dust matter (). Then,
As before, two compatibility conditions are satisfied only for and .
For and , we have the physical solution
For and , we have the nonphysical solution
As in the previous section, if we impose the equation of the state of the fluid as dust, this fixes the values of to .
3.3. General Solution
In this section, we are interested in an exact solution that gives the general solution of the system. For this purpose, one can solve the Riccati Equation (35) independent of the EoS. That has the solution defined by
where
and for the current time , where is the value of t today. is the current value of the Hubble factor, , for which we obtain the best-fit values.
That is the exact solution for studied in [62] (see an analogous case in [36], Equation (36), and in [61], Equation (24)). In this case, expressions (28) and (34) are used to calculate and . Substituting all the expressions in the system (26)–(28) leads to identities. There is an arbitrary constant of integration and the equations are identically satisfied (no compatibility equations are required); thus, this is the general solution of the system. This result is generic since it does not require specifying the EoS. Hence, Equation (117) gives a one-parameter family of solutions that gives a complete solution and is independent of the matter content.
Defining the dimensionless time variable such that and , by definition, the current value of is and the expressions become
Taking the limit , we have
and
where is the age parameter.
The main difficulty of this approach is the need to invert (120) to obtain as a function of z because the data are in terms of redshift, which is impossible using analytical tools. After all, the equation is a rational one. However, the variable can be used as a parameter instead of z in the parametric representation.
3.4. Asymptotic Analysis
The following is a precise scheme which does not require inverting (120).
By introducing the logarithmic independent variable , with as , as and as , and defining the age parameter as , we obtain the initial value problem
Equation (128) gives a one-dimensional dynamical system. The equilibrium points are , that satisfies for , and , that satisfies for .
The eigenvalue of is for . Hence, is a source whenever it exists.
The eigenvalue of is for . Hence, is always a sink. It has asymptotic behavior for large s, which is consistent with [62], in which the attractor solution has an asymptotic age parameter
We introduce the parameter such that
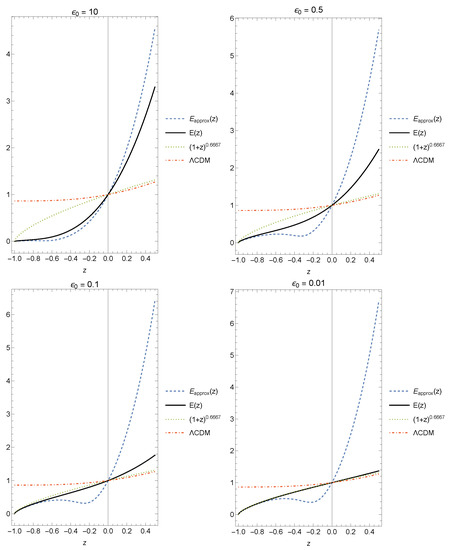
where is a measure of the limiting value of the relative error in the age parameter when it is approximated by . When , , which implies in (120) and (121). Thus, we obtain the leading term
We obtain the exact value of by integrating the initial value problem numerically
3.5. Approximated Analytical Solution
Substituting into (128), it is transformed into the following equation:
Let m be the solution of the following Bernoulli equation
The solutions of Bernoulli’s Equation (137) are three:
Assuming , where is the remainder in the approximation of y by m, and considering the following inequality
for and , from (139), we then obtain the differential inequality
The equality occurs at A values of
which are the values of the equilibrium points and of the one-dimensional dynamical system (128).
We choose the third solution of Bernoulli’s equation in (138). Hence, we obtain an approximation of y, given by
Then, we obtain an approximation of , given by
Calculating the limit
and imposing the equality with (131), we have
which is non-negative and satisfies inequality (142) for . Moreover, for or .
To calculate , we use the condition . Hence, .
For Equation (129), we obtain
with the solution given by
Now, considering an asymptotic expansion of the integral for large values of s, where and A is defined by (147), we obtain
Consequently,
We have substituted an asymptotic expansion of the integral for large s given by (151).
3.6. Discussion
Our analysis shows differences between standard CDM cosmology-based GR and the fractional version. Given the energy density expression in GR, one can calculate the Hubble parameter through the Friedmann equation. Therefore, we deduce H and we investigate the cosmological history. Finally, we consider the existence of dark matter (), as for and for quintessence, as suggested from the observations.
If we proceed as before, to give w, we use and then use the equations for and p, i.e., Equations (28) and (34). With these expressions, one can calculate and . In fractional cosmology, the asymptotic behavior is a characteristic due to the fractional parameter .
We related the possible matter scenarios, and according to the relevant discussion on the EoS w, we have two regimes of interest.
First, consider -like dark matter with the behavior of dark energy, , i.e., quintessence. This case was investigated and the relevant results are summarized in the following.
In the first approach, we solve (93) for H, obtaining two solutions , where the parameter is defined by (95) and takes the values .
Therefore, to obtain solutions, we solved (97) and (98) simultaneously for and w. For , we have the following solutions for Equations (97) and (98):
- .
- .
- .
- .
- if .
In this case, the equation of state for radiation is not recovered.
For , Equations (97) and (98) lead to
- . In this case, the equation of state for radiation is recovered for .
- .
- .
- if .
- if .
The second approach consisted of solving the Riccati equation (105) for following substitution of in (26) and removing using (28). The exact solution is (106), where is the current value of H at . From (26) and (27), we found that compatibility conditions have to be satisfied for all t. It is necessary that . Therefore, to obtain solutions, we solved (112) and (113) simultaneously for and w. We have the following solutions:
- .
- .
- .
- .
- .
- if .
- if .
- if .
Upon physical consideration, we remove the cases with and and we assume .
Using the two previous approaches, one obtains power-law solutions of the type . Additionally, one has to impose two compatibility conditions which allow particular solutions to . That means that any solution of the power law type is indeed a particular exact solution of the system, but not the general solution. To obtain an exact solution that gives the general solution of the system (for any value of the free parameters that have an integration constant), we solved the Riccati Equation (35) independent of the EoS. This gave us solution (117). This result is generic since it does not require specifying the EoS. That led to given by (119), given by (121), given by (122), given by (123), given by (124), given by (125) and given by (126), where we defined the new time variable , such that , , and .
We have
such that for and for . For large t, we have the asymptotic solution
and
where is the age parameter.
Finally, combining the solution of Bernoulli’s Equation (137) and inequality (140) and then solving the differential inequality (141) and approximating the different quadrature, we have
and
as , where is defined by (132), A is defined by (147), satisfying inequality (142) and . This is an accurate approximation of as provided . Moreover, for or .
4. Cosmological Constraints
In this section, to study the capability of the models obtained in fractional cosmology to describe the late-time accelerated Universe expansion, we shall constrain the free parameters with the SNe Ia data and OHD. In particular, for the first one, we consider the Pantheon sample [101], which consists of 1048 supernovae data points in the redshift range . On the other hand, we consider the OHD compiled by Magaña et al. [102], which consists of 51 data points in the redshift range .
For the constraints, we compute the best-fit parameters and their respective confidence regions at , and confidence levels (CLs) with the affine-invariant Markov chain Monte Carlo (MCMC) method [103], implemented in the pure-Python code emcee [104] by setting 35 chains or “walkers”. As a convergence test, we computed the autocorrelation time of the chains provided by the emcee module at every 50th step. Hence, if the current step is larger than and the values of changed by less than , then we will consider that the chains are converged and the constraint is stopped. The first steps are thus discarded as “burn-in” steps. This convergence test was complemented with the calculation of the mean acceptance fraction, which must have a value between and [104] and can be modified by the stretch move provided by the emcee module.
For this Bayesian statistical analysis, we need to construct the following Gaussian likelihood:
where is a normalization constant, which does not influence the MCMC analysis, and is the merit function of each dataset considered, i.e., I stands for SNe Ia, OHD and their joint analysis. In the following subsections, we will briefly describe the construction of the merit function of each dataset, and we will present the main results and discussions.
4.1. Observational Hubble Parameter Data
The merit function for the OHD is constructed as
where is the observational Hubble parameter at redshift with an associated error , all of them provided by the OHD sample, is the theoretical Hubble parameter at the same redshift and encompasses the free parameters of the model under study. It is important to mention that the current value of the Hubble parameter, , is a free parameter of the model, which for the constraint is written as , where h is dimensionless. Considering that we expect a value of between the value obtained from Planck CMB of [80] for the CDM model and the value obtained by A. G. Riess et al. of [81] in a model-independent way, then we consider for h the flat prior .
4.2. Type Ia Supernovae Data
Similarly to the OHD, the merit function for the SNe Ia data is constructed as
where is the observational distance modulus of each SNe Ia at redshift with an associated error , is the theoretical distance modulus for each SNe Ia at the same redshift and encompasses the free parameters of the model under study. Following this line, for a spatially flat FLRW spacetime, the theoretical distance modulus is given by
where and where c is the speed of light given in units of km/s. The above expression relates the merit function with the theoretical Hubble parameter through the luminosity distance, , as follows
On the other hand, the distance estimator used in the Pantheon sample is obtained by a modified version of Tripp’s formula [105], with two of the three nuisance parameters calibrated to zero with the BEAMS with bias correction (BBC) method [106]. Hence, the observational distance modulus for each SNe Ia reads
where is the corrected apparent B-band magnitude of a fiducial SNe Ia at redshift with an associated error , all of them provided by the Pantheon sample (currently available online in the GitHub repository https://github.com/dscolnic/Pantheon (accessed on 28 April 2023). The corrected apparent B-band magnitude for each SNe Ia with their respective redshifts and errors are available in the document lcparam_full_long.txt), and is a nuisance parameter which must be jointly estimated with the free parameters of the theoretical model. Furthermore, the Pantheon sample provides the systematic uncertainties in the BBC approach, (currently available online in the GitHub repository https://github.com/dscolnic/Pantheon (accessed on 28 April 2023) in the document sys_full_long.txt). Therefore, we can rewrite the merit function (160) in matrix notation (denoted by bold symbols as)
where and is the total uncertainty covariance matrix, where is the statistical uncertainty of .
Finally, one can marginalize over the nuisance parameters and by defining . Then, the merit function (164) can be expanded as [107]
where
Therefore, by minimizing the expanded merit function (165) with respect to , is obtained and the expanded merit is function reduced to
which depends only on the free parameters of the theoretical model.
It is essential to mention that the expanded and minimized merit function (169) provides the same information as the merit function (164). This is a consequence of the fact that the best-fit parameters minimize the merit function. Therefore, the evaluation of the best-fit parameters in the merit function can be used as an indicator of the goodness of the fit independently of the dataset used; the smaller the value of , the better the fit.
4.3. Joint Analysis and Theoretical Hubble Parameter Integration
The merit function for the joint analysis is constructed directly as
with and given by Equations (159) and (169), respectively. Following this line, note how in the merit function of the two datasets, the respective model is considered through the (theoretical) Hubble parameter as a function of the redshift (see Equations (159) and (162)). Hence, for the constraint, we numerically integrate the system given by Equations (128) and (129), which represents a system for the variables as a function of , and for which we consider the initial conditions and . Then, the Hubble parameter is obtained numerically by . For this integration, we consider the NumbaLSODA code, a python wrapper of the LSODA method in ODEPACK to C+ (currently available online in the GitHub repository https://github.com/Nicholaswogan/numbalsoda (accessed on 28 April 2023)). Furthermore, for further comparison, we also constrain the free parameters of the CDM model, whose respective Hubble parameter as a function of the redshift is given by
Finally, based on the analysis made in Section 3.5, we consider the parameterization given by Equation (132) for the free parameter . Therefore, the free parameters of the fractional cosmological model are and the free parameters of the CDM model are . For the free parameters , and , we consider the following flat priors: , and . It is important to mention that due to a degeneracy between and , the SNe Ia data are not able to constrain the free parameter h (as a reminder, ), contrary to the case for the OHD and, consequently, in the joint analysis. Thus, the posterior distribution of h for the SNe Ia data is expected to cover all the prior distributions. On the other hand, the prior is chosen as because is a measure of the limiting value of the relative error in the age parameter when it is approximated by as given by Equation (132). For the mean value , we acquire , which implies . Then, we have the leading term for defined by (133). The lower prior of is because the Hubble parameter (22) becomes negative when in the absence of matter, as we can see from Section 2.3.
4.4. Results and Discussion
In Table 2, we present the total steps, the mean acceptance fraction and the autocorrelation time, , of each free parameter obtained when the convergence test is fulfilled during our MCMC analysis for both the fractional cosmological model and the CDM model. The values of the mean acceptance fraction are obtained for a value of the stretch move of for the CDM model and for the fractional cosmological model.

Table 2.
The total number of steps, means acceptance fraction (MAF) and autocorrelation time, , for the free parameters of the fractional cosmological model and the CDM model. These values are obtained when the convergence test described in Section 4 is fulfilled for an MCMC analysis with 35 chains, a value of the stretch move of for the CDM model and for the fractional cosmological model and for the flat priors , , and .
The best-fit values of the free parameters space for the CDM model and the fractional cosmological model, obtained for the SNe Ia data, OHD and in their joint analysis, with their corresponding criteria, are presented in Table 3. The uncertainties correspond to , and CL. In Figure 2 and Figure 3, we depict the posterior distribution and joint admissible regions of the free parameter space of the CDM model and the fractional cosmological model, respectively. The joint admissible regions correspond to , and CL. Due to the degeneracy between and , the distribution of h for the SNe Ia data was not represented in its full parameter space.

Table 3.
Best-fit values and criteria for the fractional cosmological model with free parameters h, and and for the CDM model with free parameters h and . The values were obtained by the MCMC analysis described in Section 4 for the SNe Ia data, OHD and their joint analysis. The uncertainties presented correspond to , and confidence levels (CLs), respectively. The CDM model is used as a reference model.
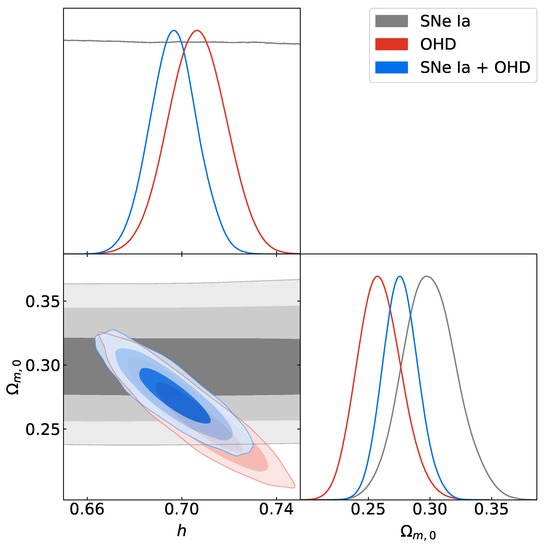
Figure 2.
Posterior distribution and joint admissible regions of the free parameters h and for the CDM model, obtained by the MCMC analysis described in Section 4. The admissible joint regions correspond to , and of confidence level (CL), respectively. The best-fit values for each model free parameter are shown in Table 3.
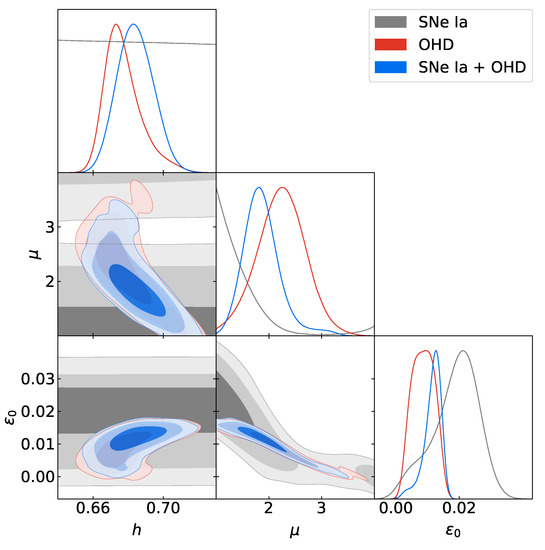
Figure 3.
Posterior distribution and joint admissible regions of the free parameters h, and for the fractional cosmological model, obtained by the MCMC analysis described in Section 4. The admissible joint regions correspond to , and confidence levels (CLs), respectively. The best-fit values for each model free parameter are shown in Table 3.
From the values for the criteria presented in Table 3, it is possible to see that the CDM model is the best model to constrain the SNe Ia data, OHD and SNe Ia + OHD data. Nevertheless, the fractional cosmological model studied in this paper exhibits values of the criteria close to the values of the CDM model, with differences of for the SNe Ia data, for the OHD data and for their joint analysis. Thus, this fractional cosmological model is suitable for describing the SNe Ia and OHD data, as can be seen from Figure 4 and Figure 5, which are characterized by accounting for a universe that experiences a transition between a deceleration expansion phase and an accelerated one. Therefore, fractional cosmology can be considered an alternative valid cosmological model to describe the late-time Universe. It is essential to mention that the core of this work is to probe this possibility by studying a particular model; the CDM model is used only as a reference model for this aim.
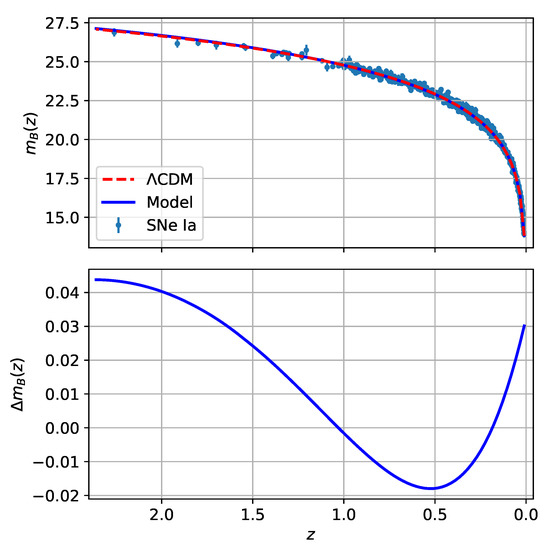
Figure 4.
(Top panel) Theoretical apparent B-band magnitude for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z, contrasted with the pantheon dataset. (Bottom panel) Variation in the theoretical apparent B-band magnitude of the fractional cosmological model compared to the CDM model as a function of the redshift z. The curve is obtained through the expression . The figures were obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3.
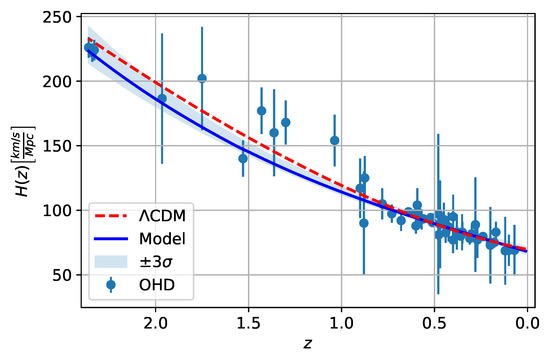
Figure 5.
Theoretical Hubble parameter for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z, contrasted with the OHD sample. The shaded curve represents the confidence region of the Hubble parameter for the fractional cosmological model at a confidence level (CL). The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3.
The analysis of the SNe Ia data leads to , and , which are the best-fit values at CL. In this case, the value obtained for h cannot be considered as a best fit due to the degeneracy between and . On the other hand, the lower limit of the best fit for is very close to 1. That is because the posterior distribution for this parameter is close to this value, as seen from Figure 3. This indicates that a value of the SNe Ia data prefers , but, as a reminder, this value leads to a negative Hubble parameter in the absence of matter. However, as can be seen from the same Figure 3, the posterior distribution for these parameters is multi-modal (this explains the large value of presented in Table 2) and, therefore, it is possible to obtain a best-fit value that satisfies . It is important to mention that the OHD and the joint analysis do not experience this issue, which allows us to maintain the validity of the prior used for .
On the other hand, the analysis from OHD leads to , and , which are the best-fit values at CL. In this case, note how the OHD can properly constrain the free parameters h, and , i.e., we obtain the best fit for the priors considered in our MCMC analysis. Furthermore, note how the posterior distribution of includes the value of 1, as seen from Figure 3, but for a CL greater than .
Finally, the joint analysis with data from SNe Ia + OHD leads to , and , which are the best-fit values at CL. Focusing our analysis on these results, we can conclude that the region in which is not ruled out by observations. On the other hand, these best-fit values lead to an age of the Universe with a value of at CL. Universe age is roughly double the one of the CDM models, and is also in disagreement with the value obtained with globular clusters, with a value of [70]. This discrepancy is a distinction of fractional cosmology. This result also agrees with the analysis made in Section 8 of [61], where the best-fit -value was obtained from the reconstruction of for different priors of . The results are summarized in Table 4. In [61], a set of 31 points obtained by differential age tools was considered, namely cosmic chronometers (CC), to represent the measurements of the Hubble parameter, which is cosmologically independent [69] (in the present research we consider the datasets from [102], which consists of 51 data points in the redshift range , 20 more points as compared with [69]). The 1048 luminosity modulus measurements, known as the Pantheon sample, from Type Ia Supernovae cover the region [101]. In [61], it is unclear if the different priors used for lead to properly constraining . Their analysis is inconclusive because of their present different values of for the different priors used.

Table 4.
The best-fit values for different priors of derived in [61].
In order to establish that this fractional cosmological model can describe a universe that experiences a transition from a decelerated expansion phase to an accelerated one, we computed the deceleration parameter , using the Riccati Equation (35), which leads to
Following this line, in Figure 6, we depict the deceleration parameter for the fractional cosmological model as a function of the redshift z obtained from the best-fit values for the SNe Ia+OHD data presented in Table 3, with an error band at CL. We also depict the deceleration parameter for the CDM model as a reference model. From this figure, we can conclude that the fractional cosmological model effectively experiences this transition at , with the characteristic that , where is the transition redshift of the CDM model. Furthermore, the current deceleration parameter of the fractional cosmological model is at CL. On the other hand, in Figure 7 and Figure 8, we depict the matter density and fractional density parameters for the fractional cosmological model (the last one interpreted as dark energy), respectively, as a function of the redshift z for the best-fit values for the SNe Ia+OHD data presented in Table 3, with an error band at CL. We depict the matter density and dark energy density parameters in both figures for the CDM model. From Figure 7, we can see that the matter density parameter for the fractional cosmological model, obtained from Equation (126), presents significant uncertainties, which could be a consequence of their reconstruction from a Hubble parameter that does not take into account any EoS. In this sense, the current value of this matter density parameter at CL is , a value that is in agreement with the asymptotic value obtained from Equation (155) of , computed at CL for the best-fit values for the SNe Ia+OHD data presented in Table 3. Therefore, this larger value of for the fractional cosmological model can, in principle, explain the lower value of the current deceleration parameter and the excess of matter in the effective term with (see Section 2.6). Note that the current value can be interpreted as the dark energy density parameter for the fractional cosmological model as , which satisfies the condition .
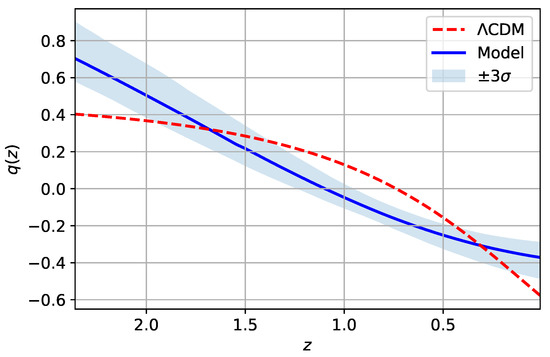
Figure 6.
Deceleration parameters for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z. The shaded curve represents the confidence region of the deceleration parameter for the fractional cosmological model at a confidence level (CL). The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3.
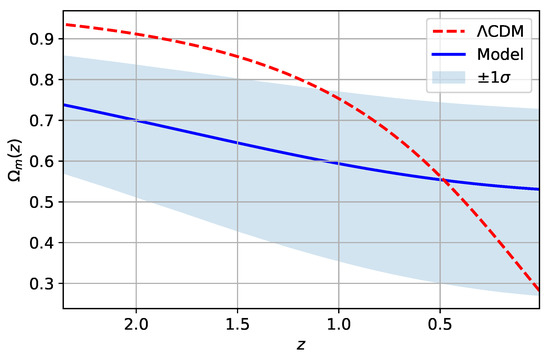
Figure 7.
Matter density parameters for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z. The shaded curve represents the confidence region of the matter density parameter for the fractional cosmological model at a confidence level (CL). The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3.
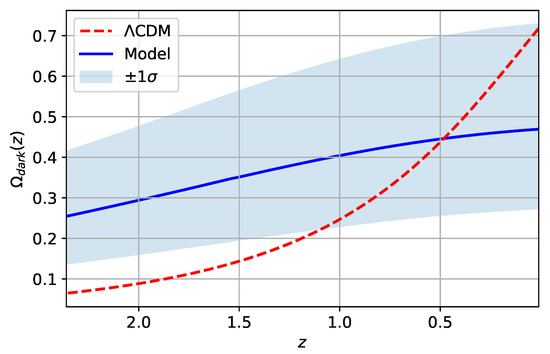
Figure 8.
Dark energy density parameters for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z. The shaded curve represents the confidence region of the dark energy density parameter for the fractional cosmological model at a confidence level (CL). The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3.
Finally, we compute the cosmographic parameter known as the jerk, which quantifies if the fractional cosmological model tends to or if it another kind of DE, which can be written as
where q is given by Equation (172). Hence,
Figure 9 represents the jerks for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z. The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3 with an error band at CL, represented by a shaded region. A departure of more than a CL for the current value for CDM shows an alternative cosmology with an effective dynamical equation of state for the Universe for late times in contrast to CDM.
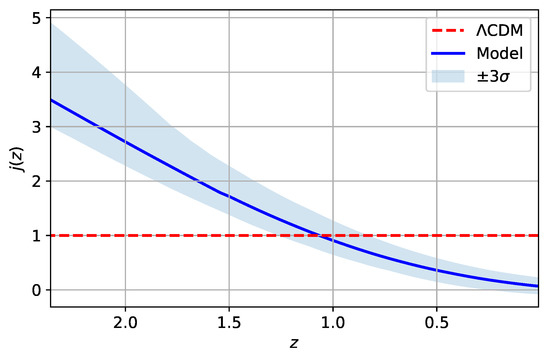
Figure 9.
Jerks for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z. The shaded curve represents the confidence region of the jerk for the fractional cosmological model at a confidence level (CL). The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3.
On the other hand, for the reconstruction of the diagnostic [108] for the fractional cosmology, we define
where the Hubble parameter is obtained numerically by as we explained before. Therefore, in Figure 10, we depict diagnostic for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z. The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3, with an error band at CL, represented by a shaded region. As a reminder, in both Figure 9 and Figure 10, we also depict the jerk and the diagnostic for the CDM model as a reference model.
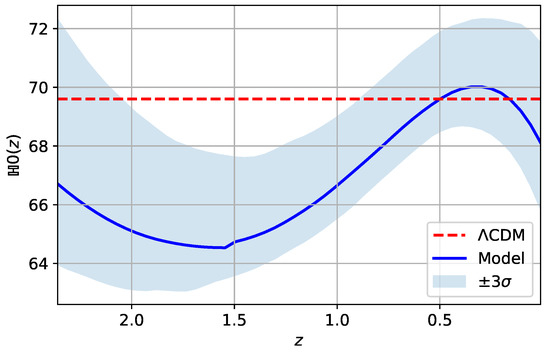
Figure 10.
diagnostics for the CDM model (red dashed line) and the fractional cosmological model (solid blue line) as a function of the redshift z. The shaded curve represents the confidence region of the diagnostic for the fractional cosmological model at a confidence level (CL). The figure was obtained using the best-fit values for the SNe Ia+OHD data presented in Table 3.
5. Conclusions
In this paper, we investigated the cosmological applications of power-law solutions of the type in fractional cosmology, where is the current age parameter. Additionally, given , the order of the fractional derivative, and w, the matter equation of state, we have imposed compatibility conditions which allow particular solutions to . That means that any solution of power law type is indeed a particular exact solution of the system, e.g., solution (22) for ; solution (74) for dust matter where is defined by (71); solutions defined by (94), with defined by (95) and where the compatibility conditions (97) and (98) are satisfied simultaneously for and w; and the solution (111) such that and w satisfy (112) and (113), respectively. However, they are not the general solution. Moreover, we are interested in an exact solution that gives the general solution of the system. For this purpose, we solved the Riccati equation (35) independent of the EoS, where the solution for the scale factor is a combination of power laws, i.e., (117). This solution is analyzed in Section 3.3.
Finally, combining the solution of Bernoulli’s Equation (137) and the inequality (140), solving the differential inequality (141) and approximating the different quadrature, we have obtained the approximate analytical solution given by (153), and given by (154) as , where is defined by (132), A is defined by (147) and satisfies (142) and . This is an accurate approximation of as provided .
Finally, we estimated the free parameters using cosmological data and the re-parameterization , .
Separate analyses of the SNe Ia data and OHD, and the joint analysis with SNe Ia data + OHD, led, respectively, to , and ; , and ; and , and , where the best-fit values were calculated at CL. On the other hand, these best-fit values led to an age of the Universe with a value of , a current deceleration parameter of (both at CL) and a current matter density parameter of at CL. Finding a Universe roughly twice as old as the one of CDM is a distinction of fractional cosmology. Focusing our analysis on these results, we can conclude that the region in which is not ruled out by observations. This region of a parameter is relevant because, in the absence of matter, fractional cosmology gives a power-law solution , which is accelerated for . We presented a fractional origin model that leads to an accelerated state without appealing to or dark energy.
Author Contributions
Conceptualization, E.G. and G.L.; methodology, E.G., G.L. and G.F.-A.; software, E.G. and G.L.; validation, E.G., G.L. and G.F.-A.; formal analysis, E.G., G.L. and G.F.-A.; investigation, E.G., G.L. and G.F.-A.; resources, G.L.; writing—original draft preparation, G.L.; writing—review and editing, E.G., G.L. and G.F.-A.; visualization, E.G. and G.L.; supervision, G.L.; project administration, G.L.; funding acquisition, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
G.L. was funded by Vicerrectoría de Investigación y Desarrollo Tecnológico (VRIDT) at Universidad Católica del Norte through Concurso De Pasantías De Investigación Año 2022, Resolución VRIDT No. 040/2022 and Resolución VRIDT No. 054/2022.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting this article can be found in Section 4.
Acknowledgments
The authors are thankful for the support of Núcleo de Investigación Geometría Diferencial y Aplicaciones, Resolución VRIDT No. 096/2022. The authors thank Samuel Lepe for initial discussions. E.G. acknowledges the support of Dirección de Investigación y Postgrado at Universidad de Aconcagua. GFA acknowledges support from DINVP and Universidad Iberoamericana.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Advances in Industrial Control; Springer: London, UK, 2010. [Google Scholar]
- Tarasov, V.E. Review of Some Promising Fractional Physical Models. Int. J. Mod. Phys. B 2013, 27, 13300053. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Kamal, S. Stabilization and Control of Fractional Order Systems: A Sliding Mode Approach; Lecture Notes in Electrical Engineering; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar]
- Padula, F.; Visioli, A. Advances in Robust Fractional Control; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction For Physicists, 2nd ed.; World Scientific Publishing Company: Singapore, 2014. [Google Scholar]
- Tarasov, V.E. Applications in Physics, Part A; De Gruyter Reference; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Klafter, J.; Lim, S.C.; Metzler, R. Fractional Dynamics: Recent Advances; World Scientific: Singapore, 2012. [Google Scholar]
- Malinowska, A.B.; Odzijewicz, T.; Torres, D.F.M. Advanced Methods in the Fractional Calculus of Variations; Springer Briefs in Applied Sciences and Technology; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar]
- Lorenzo, C.F.; Hartley, T.T. The Fractional Trigonometry: With Applications to Fractional Differential Equations and Science; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- West, B.J. Fractional Calculus and the Future of Science. Entropy 2021, 23, 1566. [Google Scholar] [CrossRef] [PubMed]
- Calcagni, G. Quantum field theory, gravity and cosmology in a fractal universe. JHEP 2010, 03, 120. [Google Scholar] [CrossRef]
- Calcagni, G. Fractal universe and quantum gravity. Phys. Rev. Lett. 2010, 104, 251301. [Google Scholar] [CrossRef]
- Lim, S.C. Fractional derivative quantum fields at positive temperature. Phys. A 2006, 363, 269–281. [Google Scholar] [CrossRef]
- Lim, S.C.; Eab, C.H. Fractional quantum fields. In Volume 5 Applications in Physics, Part B; Tarasov, V.E., Ed.; De Gruyter: Berlin, Germany, 2019; pp. 237–256. [Google Scholar] [CrossRef]
- Moniz, P.V.; Jalalzadeh, S. Challenging Routes in Quantum Cosmology; World Scientific Publishing: Singapore, 2020. [Google Scholar] [CrossRef]
- Moniz, P.V.; Jalalzadeh, S. From Fractional Quantum Mechanics to Quantum Cosmology: An Overture. Mathematics 2020, 8, 313. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Jalalzadeh, S.; Moniz, P.V. Broadening quantum cosmology with a fractional whirl. Mod. Phys. Lett. A 2021, 36, 2140005. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; da Silva, F.R.; Moniz, P.V. Prospecting black hole thermodynamics with fractional quantum mechanics. Eur. Phys. J. C 2021, 81, 632. [Google Scholar] [CrossRef]
- Rami, E.N.A. Fractional dynamics, fractional weak bosons masses and physics beyond the standard model. Chaos Solitons Fractals 2009, 41, 2262–2270. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractional Lagrangian Formulation of General Relativity and Emergence of Complex, Spinorial and Noncommutative Gravity. Int. J. Geom. Methods Mod. Phys. 2009, 6, 25–76. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Modifications at Large Distances From Fractional and Fractal Arguments. Fractals 2010, 18, 185–190. [Google Scholar] [CrossRef]
- El-Nabulsi, A.R. The fractional white dwarf hydrodynamical nonlinear differential equation and emergence of quark stars. Appl. Math. Comput. 2011, 218, 2837–2849. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Glaeske-Kilbas-Saigo fractional integration and fractional Dixmier trace. Acta Math. Vietnam. 2012, 37, 149–160. [Google Scholar]
- El-Nabulsi, R.A.; Wu, C.G. Fractional Complexified Field Theory from Saxena-Kumbhat Fractional Integral, Fractional Derivative of Order (α,β) and Dynamical Fractional Integral Exponent. Afr. Diaspora J. Math. New Ser. 2012, 13, 45–61. [Google Scholar]
- El-Nabulsi, R.A. Fractional derivatives generalization of Einstein`s field equations. Indian J. Phys. 2013, 87, 195–200. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractional elliptic operator of order 2/3 from Glaeske-Kilbas-Saigo fractional integral transform. Funct. Anal. Approx. Comput 2015, 7, 29–33. [Google Scholar]
- El-Nabulsi, R.A. A Cosmology Governed by a Fractional Differential Equation and the Generalized Kilbas-Saigo-Mittag–Leffler Function. Int. J. Theor. Phys. 2016, 55, 625–635. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Finite two-point space without quantization on noncommutative space from a generalized fractional integral operator. Complex Anal. Oper. Theory 2018, 12, 1609–1616. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. On generalized fractional spin, fractional angular momentum, fractional momentum operators in quantum mechanics. Few-Body Syst. 2020, 61, 25. [Google Scholar] [CrossRef]
- Roberts, M.D. Fractional Derivative Cosmology. SOP Trans. Theor. Phys. 2014, 1, 310. [Google Scholar] [CrossRef]
- Vacaru, S.I. New Classes of Off-Diagonal Cosmological Solutions in Einstein Gravity. Int. J. Theor. Phys. 2010, 49, 2753–2776. [Google Scholar] [CrossRef]
- Vacaru, S.I. Fractional Nonholonomic Ricci Flows. Chaos Solitons Fractals 2012, 45, 1266–1276. [Google Scholar] [CrossRef]
- Vacaru, S.I. Fractional Dynamics from Einstein Gravity, General Solutions, and Black Holes. Int. J. Theor. Phys. 2012, 51, 1338–1359. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Cosmological Models with Fractional Derivatives and Fractional Action Functional. Commun. Theor. Phys. 2011, 56, 389–396. [Google Scholar] [CrossRef]
- Jamil, M.; Momeni, D.; Rashid, M.A. Fractional Action Cosmology with Power Law Weight Function. J. Phys. Conf. Ser. 2012, 354, 012008. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Cosmic Evolution in Fractional Action Cosmology. Discontinuity Nonlinearity Complex 2013, 2, 115–123. [Google Scholar] [CrossRef]
- Debnath, U.; Jamil, M.; Chattopadhyay, S. Fractional Action Cosmology: Emergent, Logamediate, Intermediate, Power Law Scenarios of the Universe and Generalized Second Law of Thermodynamics. Int. J. Theor. Phys. 2012, 51, 812–837. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Gravitons in fractional action cosmology. Int. J. Theor. Phys. 2012, 51, 3978–3992. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Non-minimal coupling in fractional action cosmology. Indian J. Phys. 2013, 87, 835–840. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Nonstandard fractional exponential Lagrangians, fractional geodesic equation, complex general relativity, and discrete gravity. Can. J. Phys. 2013, 91, 618–622. [Google Scholar] [CrossRef]
- Debnath, U.; Chattopadhyay, S.; Jamil, M. Fractional action cosmology: Some dark energy models in emergent, logamediate, and intermediate scenarios of the universe. J. Theor. Appl. Phys. 2013, 7, 25. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Fractional Einstein–Hilbert Action Cosmology. Mod. Phys. Lett. A 2013, 28, 1350056. [Google Scholar] [CrossRef]
- Calcagni, G. Multi-scale gravity and cosmology. J. Cosmol. Astropart. Phys. 2013, 12, 041. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Testing Fractional Action Cosmology. Eur. Phys. J. Plus 2016, 131, 256. [Google Scholar] [CrossRef]
- Rami, E.N.A. Fractional action oscillating phantom cosmology with conformal coupling. Eur. Phys. J. Plus 2015, 130, 102. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Implications of the Ornstein-Uhlenbeck-like fractional differential equation in cosmology. Rev. Mex. Fis. 2016, 62, 240. [Google Scholar]
- Calcagni, G.; Kuroyanagi, S.; Tsujikawa, S. Cosmic microwave background and inflation in multi-fractional spacetimes. J. Cosmol. Astropart. Phys. 2016, 8, 39. [Google Scholar] [CrossRef]
- Calcagni, G. Multifractional theories: An unconventional review. J. High Energy Phys. 2017, 3, 138, Erratum in J. High Energy Phys. 2017, 6, 20. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractional Action Cosmology with Variable Order Parameter. Int. J. Theor. Phys. 2017, 56, 1159–1182. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Wormholes in fractional action cosmology. Can. J. Phys. 2017, 95, 605–609. [Google Scholar] [CrossRef]
- Calcagni, G. Complex dimensions and their observability. Phys. Rev. D 2017, 96, 046001. [Google Scholar] [CrossRef]
- Calcagni, G.; Kuroyanagi, S.; Marsat, S.; Sakellariadou, M.; Tamanini, N.; Tasinato, G. Quantum gravity and gravitational-wave astronomy. J. Cosmol. Astropart. Phys. 2019, 10, 012. [Google Scholar] [CrossRef]
- Calcagni, G.; Kuroyanagi, S. Stochastic gravitational-wave background in quantum gravity. J. Cosmol. Astropart. Phys. 2021, 3, 19. [Google Scholar] [CrossRef]
- Calcagni, G.; De Felice, A. Dark energy in multifractional spacetimes. Phys. Rev. D 2020, 102, 103529. [Google Scholar] [CrossRef]
- Calcagni, G. Multifractional theories: An updated review. Mod. Phys. Lett. A 2021, 36, 2140006. [Google Scholar] [CrossRef]
- Calcagni, G. Classical and quantum gravity with fractional operators. Class. Quant. Grav. 2021, 38, 165005, Erratum in Class. Quant. Grav. 2021, 38, 169601. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Fractional-order derivatives in cosmological models of accelerated expansion. Mod. Phys. Lett. A 2021, 36, 2130014. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Costa, E.W.O.; Moniz, P.V. de Sitter fractional quantum cosmology. Phys. Rev. D 2022, 105, L121901. [Google Scholar] [CrossRef]
- Landim, R.G. Fractional dark energy: Phantom behavior and negative absolute temperature. Phys. Rev. D 2021, 104, 103508. [Google Scholar] [CrossRef]
- Landim, R.G. Fractional dark energy. Phys. Rev. D 2021, 103, 083511. [Google Scholar] [CrossRef]
- García-Aspeitia, M.A.; Fernandez-Anaya, G.; Hernández-Almada, A.; Leon, G.; Magaña, J. Cosmology under the fractional calculus approach. Mon. Not. R. Astron. Soc. 2022, 517, 4813–4826. [Google Scholar] [CrossRef]
- Micolta-Riascos, B.; Millano, A.D.; Leon, G.; Erices, C.; Paliathanasis, A. Revisiting Fractional Cosmology. Fractal Fract. 2023, 7, 149. [Google Scholar] [CrossRef]
- Hernández-Almada, A.; Leon, G.; Magaña, J.; García-Aspeitia, M.A.; Motta, V. Generalized Emergent Dark Energy: Observational Hubble data constraints and stability analysis. Mon. Not. R. Astron. Soc. 2020, 497, 1590–1602. [Google Scholar] [CrossRef]
- Leon, G.; Magaña, J.; Hernández-Almada, A.; García-Aspeitia, M.A.; Verdugo, T.; Motta, V. Barrow Entropy Cosmology: An observational approach with a hint of stability analysis. J. Cosmol. Astropart. Phys. 2021, 12, 032. [Google Scholar] [CrossRef]
- Hernández-Almada, A.; Leon, G.; Magaña, J.; García-Aspeitia, M.A.; Motta, V.; Saridakis, E.N.; Yesmakhanova, K.; Millano, A.D. Observational constraints and dynamical analysis of Kaniadakis horizon-entropy cosmology. Mon. Not. R. Astron. Soc. 2022, 512, 5122–5134. [Google Scholar] [CrossRef]
- Hernández-Almada, A.; Leon, G.; Magaña, J.; García-Aspeitia, M.A.; Motta, V.; Saridakis, E.N.; Yesmakhanova, K. Kaniadakis-holographic dark energy: Observational constraints and global dynamics. Mon. Not. R. Astron. Soc. 2022, 511, 4147–4158. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 5, 14. [Google Scholar] [CrossRef]
- Valcin, D.; Jimenez, R.; Verde, L.; Bernal, J.L.; Wandelt, B.D. The age of the Universe with globular clusters: Reducing systematic uncertainties. J. Cosmol. Astropart. Phys. 2021, 2021, 17. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The Cosmological constant. Ann. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rept. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Sadjadi, H.M.; Alimohammadi, M. Cosmological coincidence problem in interactive dark energy models. Phys. Rev. D 2006, 74, 103007. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.M.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; An, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Basilakos, S.; Leon, G.; Papagiannopoulos, G.; Saridakis, E.N. Dynamical system analysis at background and perturbation levels: Quintessence in severe disadvantage comparing to ΛCDM. Phys. Rev. D 2019, 100, 043524. [Google Scholar] [CrossRef]
- Alho, A.; Uggla, C.; Wainwright, J. Perturbations of the Lambda-CDM model in a dynamical systems perspective. J. Cosmol. Astropart. Phys. 2019, 9, 45. [Google Scholar] [CrossRef]
- Wald, R.M. Asymptotic behavior of homogeneous cosmological models in the presence of a positive cosmological constant. Phys. Rev. D 1983, 28, 2118. [Google Scholar] [CrossRef]
- Kitada, Y.; Maeda, K.I. Cosmic no-hair theorem in homogeneous spacetimes. Vistas Astron. 1993, 37, 461–464. [Google Scholar] [CrossRef]
- Barrow, J.D.; Stein-Schabes, J. Inhomogeneous cosmologies with cosmological constant. Phys. Lett. A 1984, 103, 315–317. [Google Scholar] [CrossRef]
- Maeda, K.I. Recent topics on the inflationary universe: Cosmic no hair conjecture. In Proceedings of the 2nd Workshop on Elementary Particle Picture of the Universe, Tsukuba, Japan, 4–6 February 1988; pp. 51–64. [Google Scholar]
- Cotsakis, S.; Flessas, G. Generalized cosmic no hair theorems. Phys. Lett. B 1993, 319, 69–73. [Google Scholar] [CrossRef]
- Capozziello, S.; De Ritis, R. Cosmic no-hair theorem in anisotropic, nonminimally coupled cosmologies. Int. J. Mod. Phys. D 1996, 5, 209–215. [Google Scholar] [CrossRef]
- Bruni, M.; Mena, F.C.; Tavakol, R.K. Cosmic no hair: Nonlinear asymptotic stability of de Sitter universe. Class. Quant. Grav. 2002, 19, L23–L29. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Higher Education Press: Beijing, China, 2013. [Google Scholar]
- El-Nabulsi, R.A. Fractional unstable Euclidean universe. Electron. J. Theor. Phys. 2005, 2, 1–11. [Google Scholar]
- El-Nabulsi, R.A. Accelerated universe dominated by holographic dark energy, supergravity inflationary potential. Rom. J. Phys. 2007, 52, 163–170. [Google Scholar]
- El-Nabulsi, R.A. Cosmology with a fractional action principle. Rom. Rep. Phys. 2007, 59, 763–771. [Google Scholar]
- El-Nabulsi, R.A. Increasing effective gravitational constant in fractional ADD brane cosmology. Electron. J. Theor. Phys. 2008, 5, 103–106. [Google Scholar]
- Frederico, G.S.; Torres, D. Necessary Optimality Conditions for Fractional Action-like Problems with Intrinsic and Observer Times. WSEAS Trans. Math. 2008, 7, 6–11. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 2010. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Carroll, S.; Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Addison Wesley: Boston, MA, USA, 2004. [Google Scholar]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Magaña, J.; Amante, M.H.; Garcia-Aspeitia, M.A.; Motta, V. The Cardassian expansion revisited: Constraints from updated Hubble parameter measurements and type Ia supernova data. Mon. Not. R. Astron. Soc. 2018, 476, 1036. [Google Scholar] [CrossRef]
- Goodman, J.; Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Conley, A.; Meierjurgen Farr, W.; Hogg, D.W.; Lang, D.; Marshall, P.; Price-Whelan, A.; Sanders, J.; Zuntz, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Tripp, R. A two-parameter luminosity correction for Type IA supernovae. Astron. Astrophys. 1998, 331, 815. [Google Scholar]
- Kessler, R.; Scolnic, D. Correcting Type Ia Supernova Distances for Selection Biases and Contamination in Photometrically Identified Samples. Astrophys. J. 2017, 836, 56. [Google Scholar] [CrossRef]
- Lazkoz, R.; Nesseris, S.; Perivolaropoulos, L. Exploring cosmological expansion parametrizations with the gold SnIa data set. J. Cosmol. Astropart. Phys. 2005, 2005, 010. [Google Scholar] [CrossRef]
- Krishnan, C.; Ó Colgáin, E.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble tension and a H0 diagnostic. Phys. Rev. D 2021, 103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).