A Quicker Iteration Method for Approximating the Fixed Point of Generalized α-Reich-Suzuki Nonexpansive Mappings with Applications
Abstract
:1. Introduction
2. A Short Survey on the Applications of Fixed Point Theory
- Economics: Kenneth Arrow utilized fixed point theorems to argue that there is no perfect voting system, which is a foundational conclusion in social choice theory [41].
- Computer Science: the halting problem: Alan Turing’s fixed point theorem proved the undecidability of the halting problem, which is a key notion in computer science [42].
- Topology: the Brouwer fixed point theorem is a key conclusion in topology that has implications in domains such as game theory and economics [43].
- Physics: fixed point theory is utilized in the study of quantum mechanics, specifically in understanding the behavior of quantum systems in regard to fixed points [44].
- Image Processing: image registration: image registration, a technique that aligns two or more pictures for diverse applications such as medical imaging, uses fixed point algorithms [45].
- Game Theory: Nash equilibrium: fixed point theorems were used by John Nash to demonstrate the existence of Nash equilibria in non-co-operative games [46].
- Finance: fixed point approaches are used in the formulation of the Black–Scholes equation, which is a key model in financial mathematics [47].
- Social Sciences: sociology and network theory: fixed point theory is used to investigate network architecture, social dynamics, and social system stability [47].
- Optimization: fixed point iterations are often employed in optimization methods such as the Gauss–Seidel method for solving linear equations [48].
3. Preliminaries
4. Comparison Analysis and Stability
- Conversely, let . Therefore,
5. Convergence Analysis
- is bounded. Let . Now, by combining the above inequality and Theorem 6, =q. Additionally,
6. Application to Fractional 1-Fredholm Integro Differential Equation
- If we take , then (15) can be written as
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Browder, F.E. Fixed-point theorems for noncompact mappings in Hilbert space. Proc. Natl. Acad. Sci. USA 1965, 53, 1272–1276. [Google Scholar] [CrossRef]
- Browder, F.E. Nonexpansive nonlinear operators in Banach spaces. Proc. Natl. Acad. Sci. USA 1965, 54, 1041–1044. [Google Scholar] [CrossRef] [PubMed]
- Göhde, D. Zum Prinzip def Kontraktiven Abbilding. Math. Nachr. 1965, 30, 251–258. [Google Scholar] [CrossRef]
- Goebel, K.; Kirk, W.A. Iteration processes for nonexpansive mappings. In Topological Methods in Nonlinear Functional Analysis; Singh, S.P., Thomeier, S., Watson, B., Eds.; Contemporary Mathematics; American Mathematical Society: Providence, RI, USA, 1983; Volume 21, pp. 115–123. [Google Scholar]
- Goebel, K.; Kirk, W.A. Topics in Metric Fixed Point Theory; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Suzuki, T. Fixed point theorems and convergence theorems for some generalized nonexpansive mappings. J. Math. Anal. Appl. 2008, 340, 1088–1095. [Google Scholar] [CrossRef]
- Aoyama, K.; Kohsaka, F. Fixed point theorem for a-nonexpansive mappings in Banach spaces. Nonlinear Anal. 2011, 74, 4387–4391. [Google Scholar] [CrossRef]
- Pant, D.; Shukla, R. Approximating fixed points of generalized a-nonexpansive mappings in Banach spaces. Numer. Funct. Anal. Optim. 2017, 38, 248–266. [Google Scholar] [CrossRef]
- Pant, R.; Pandey, R. Existence and convergence results for a class of non-expansive type mappings in hyperbolic spaces. Appl. Gen. Topol. 2019, 20, 281–295. [Google Scholar] [CrossRef]
- Pandey, R.; Pant, R.; Rakocevic, V.; Shukla, R. Approximating Fixed Points of a General Class of Nonexpansive Mappings in Banach Spaces with Applications. Results Math 2019, 74, 7. [Google Scholar] [CrossRef]
- Park, S. Extensions of ordered fixed point theorems. Nonlinear Funct. Anal. Appl. 2023, 28, 831–850. [Google Scholar]
- Abou, Bakr, A.; Mohamed, S. On various types of cone metric spaces and some applications in fixed point theory. Int. J. Nonlinear Anal. Appl. 2023, 14, 163–184. [Google Scholar]
- Liu, X.; Chen, L.; Zhao, Y. Existence Theoremsfor Solutions of a Nonlinear Fractional-Order Coupled Delayed System via Fixed Point Theory. Mathematics 2023, 11, 1634. [Google Scholar] [CrossRef]
- Azmi, F.M.; Haque, S. Fixed Point Theory on Triple Controlled Metric-like Spaces with a Numerical Iteration. Symmetry 2023, 15, 1403. [Google Scholar] [CrossRef]
- Suwais, K.; Tas, N.; Özgür, N.; Mlaiki, N. Fixed Point Theorems in Symmetric Controlled M-Metric Type Spaces. Symmetry 2023, 15, 1665. [Google Scholar] [CrossRef]
- Omran, S.; Masmali, I.; Alhamzi, G. Banach Fixed Point Theorems in Generalized Metric Space Endowed with the Hadamard Product. Symmetry 2023, 15, 1325. [Google Scholar] [CrossRef]
- Ravichandran, C.; Munusamy, K.; Nisar, K.S.; Valliammal, N. Results on neutral partial integrodifferential equations using Monch-Krasnosel’Skii fixed point theorem with nonlocal conditions. Fractal Fract. 2022, 6, 75. [Google Scholar] [CrossRef]
- Faraji, H.; Savic, D.; Radenovic, S. Fixed point theorems for Geraghty contraction type mappings in b-metric spaces and applications. Axioms 2019, 8, 34. [Google Scholar] [CrossRef]
- Sahin, M.; Kargin, A.; Çoban, M.A. Fixed point theorem for neutrosophic triplet partial metric space. Symmetry 2018, 10, 240. [Google Scholar] [CrossRef]
- Das, A.; Hazarika, B.; Kumam, P. Some new generalizations of Darbo’s fixed point theorem and its application on integral equations. Mathematics 2019, 7, 214. [Google Scholar] [CrossRef]
- Petrov, E. Fixed point theorem for mappings contracting perimeters of triangles. J. Fixed Point Theory Appl. 2023, 25, 74. [Google Scholar] [CrossRef]
- Sanatee, A.G.; Rathour, L.; Mishra, V.N.; Dewangan, V. Some fixed point theorems in regular modular metric spaces and application to Caratheodory’s type anti-periodic boundary value problem. J. Anal. 2023, 31, 619–632. [Google Scholar] [CrossRef]
- de Cabral-García, G.J.; Baquero-Mariaca, K.; Villa-Morales, J. A fixed point theorem in the space of integrable functions and applications. Rend. Circ. Mat. Palermo Ser. 2023, 72, 655–672. [Google Scholar] [CrossRef]
- Benzarouala, C.; Brzdek, J.; Oubbi, L. A fixed point theorem and Ulam stability of a general linear functional equation in random normed spaces. J. Fixed Point Theory Appl. 2023, 25, 33. [Google Scholar] [CrossRef]
- Liu, J.B.; Butt, A.R.; Nadeem, S.; Ali, S.; Shoaib, M. Higher order of convergence with multivalued contraction mappings. J. Math. 2020, 2020, 8867897. [Google Scholar] [CrossRef]
- Banach, S. Sur les opérations dans les ensembles abstraits et leurs application aux équations intégrales. Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Hussain, A.; Hussain, N.; Ali, D. Estimation of Newly Established Iterative Scheme for Generalized Nonexpansive Mappings. J. Funct. Space 2021, 2021, 6675979. [Google Scholar] [CrossRef]
- Hussain, A.; Ali, D.; Karapinar, E. Stability data dependency and errors estimation for a general iteration method. Alex. Eng. J. 2021, 60, 703–710. [Google Scholar] [CrossRef]
- Ishikawa, S. Fixed points and iteration of a nonexpansive mapping in a Banach space. Proc. Am. Math. Soc. 1976, 59, 65–71. [Google Scholar] [CrossRef]
- Khan, H.S. A Picard-Man hybrid iterative process. Fixed Point Theory Appl. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Noor, M.A. New approximation schemes for general variational inequalities. J. Math. Anal. Appl. 2000, 251, 217–229. [Google Scholar] [CrossRef]
- Ofem, A.E.; Igbokwe, D.I. A new faster four-step iterative algorithm for Suzuki generalized nonexpansive mappings with an application. Adv. Theory Nonlinear Anal. Appl. 2021, 5, 482–506. [Google Scholar]
- Ofem, A.E.; I¸sik, H.; Ali, F.; Ahmad, J. A new iterative approximation scheme for Reich–Suzuki type nonexpansive operators with an application. J. Inequal. Appl. 2022, 2022, 28. [Google Scholar] [CrossRef]
- Ofem, A.E.; Udofia, U.E.; Igbokwe, D.I. A robust iterative approach for solving nonlinear Volterra Delay integro-differential equations. Ural. Math. J. 2021, 7, 59–85. [Google Scholar] [CrossRef]
- Güsoy, F. A Picard-S iterative Method for Approximating Fixed Point of Weak-Contraction Mappings. Filomat 2016, 30, 2829–2845. [Google Scholar]
- Abbas, M.; Nazir, T. A new faster iteration process applied to constrained minimization and feasibility problems. Mat. Vesnik. 2014, 66, 223–234. [Google Scholar]
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex Anal. 2007, 8, 61–79. [Google Scholar]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Ullah, K.; Arshad, M. Numerical Reckoning Fixed Points for Suzuki’s Generalized Nonexpansive Mappings via New Iteration Process. Filomat 2018, 32, 187–196. [Google Scholar] [CrossRef]
- Ali, J.; Ali, F. A new iterative scheme to approximating fixed points and the solution of a delay differential equation. J. Nonlinear Convex Anal. 2020, 21, 2151–2163. [Google Scholar]
- Arrow, K.J. Social Choice and Individual Values; Yale University Press: New Haven, CT, USA, 2012; Volume 12. [Google Scholar]
- Turing, A.M. On Computable Numbers, with an Application to the Entscheidungsproblem. J. Math. 1936, 58, 345–363. [Google Scholar]
- Brouwer, L.E.J. Über Abbildung von Mannigfaltigkeiten. Math. Ann. 1911, 71, 97–115. [Google Scholar] [CrossRef]
- Witten, E. Dynamical breaking of supersymmetry. Nucl. Phys. B 1981, 188, 513–554. [Google Scholar] [CrossRef]
- Zitova, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Nash, J.F., Jr. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Bertsekas, D.P.; Hager, W.; Mangasarian, O. Nonlinear Programming; Athena Scientific: Belmont, MA, USA, 1999. [Google Scholar]
- Berinde, V. Iterative Approximation of Fixed Points; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Harder, A.M. Fixed Point Theory and Stability Results for Fixed Point Iteration Procedures. Ph.D. Thesis, University of Missouri, Rolla, MO, USA, 1987. [Google Scholar]
- Schu, J. Weak and strong convergence to fixed points of asymptotically nonexpansive mappings. Bull. Aust. Math. Soc. 1991, 43, 153–159. [Google Scholar] [CrossRef]
- Marcdanov, M.J.; Sharifov, Y.A.; Aliyev, H.N. Existence and Uniqueness of Solution for Nonlinear Fractional Integro-Differential Equations with Nonlocal Boundary Conditions. Eur. J. Pure Appl. Math. 2022, 15, 726–735. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Partohaghighi, M.; Saifullah, S.; Akgul, A.; Jarad, F. Oscillatory and complex behaviour of Caputo-Fabrizio fractional order HIV-1 infection mode. Aims Math. 2022, 7, 4778–4792. [Google Scholar] [CrossRef]
- Rahman, M.; Arfan, M.; Shah, Z.; Alzahran, E. Evolution of fractional mathematical model for drinking under Atangana-Baleanu Caputo derivatives. Phys. Scr. 2021, 96, 115203. [Google Scholar] [CrossRef]
- Rahman, M.; Ahmad, S.; Arfan, M.; Akgul, A.; Jarad, F. Fractional Order Mathematical Model of Serial Killing with Different Choices of Control Strategy. Fractal Fract. 2022, 6, 162. [Google Scholar] [CrossRef]
- Mamoud, A.; Ghadle, K.P.; Isa, M.S.B.; Giniswamy, G. Existence and Uniqueness Theorems for Fractional Volterra-Fredholm Integro-Differential Equations. Int. J. Appl. Math. 2018, 31, 33–348. [Google Scholar]
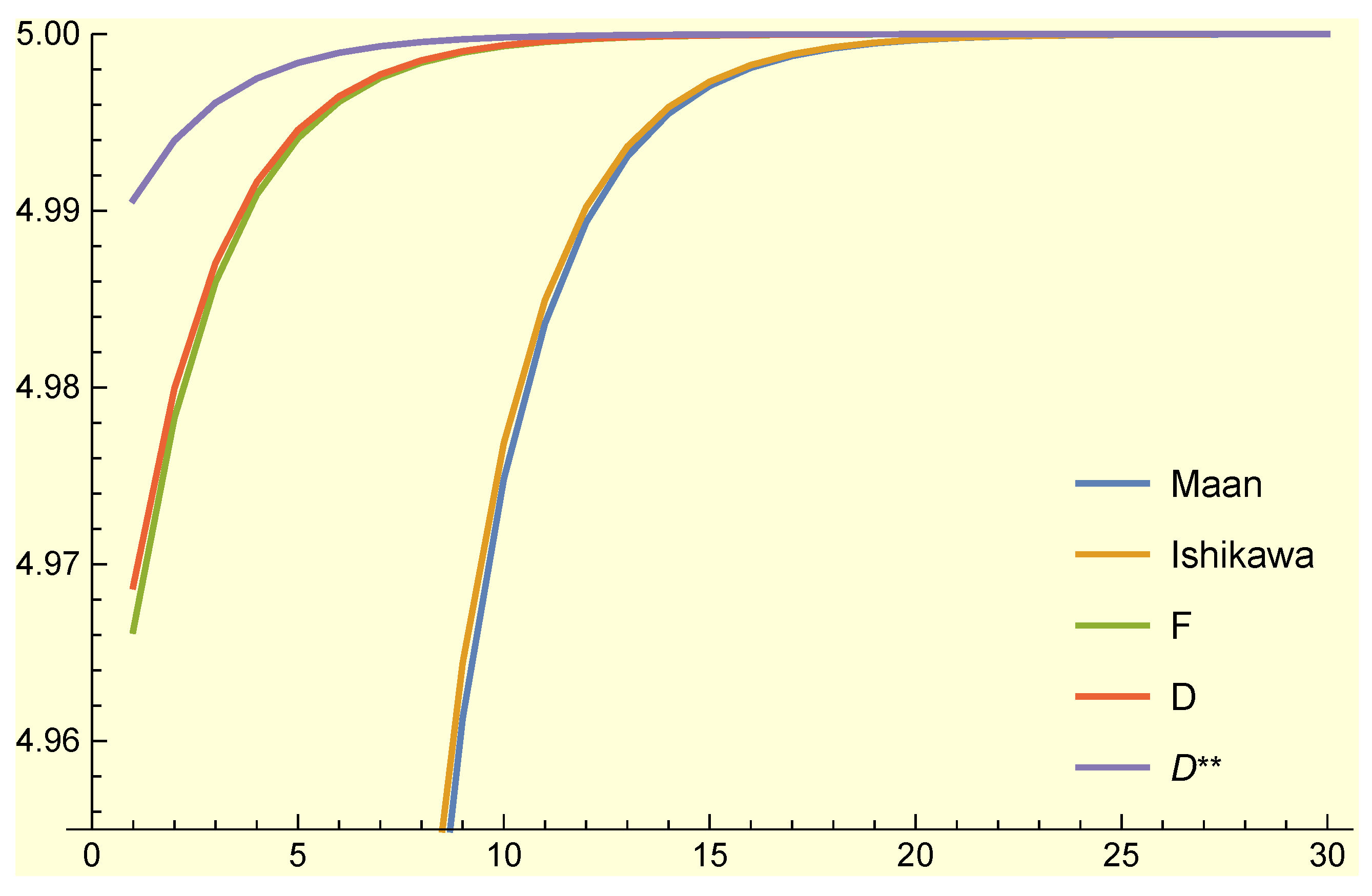
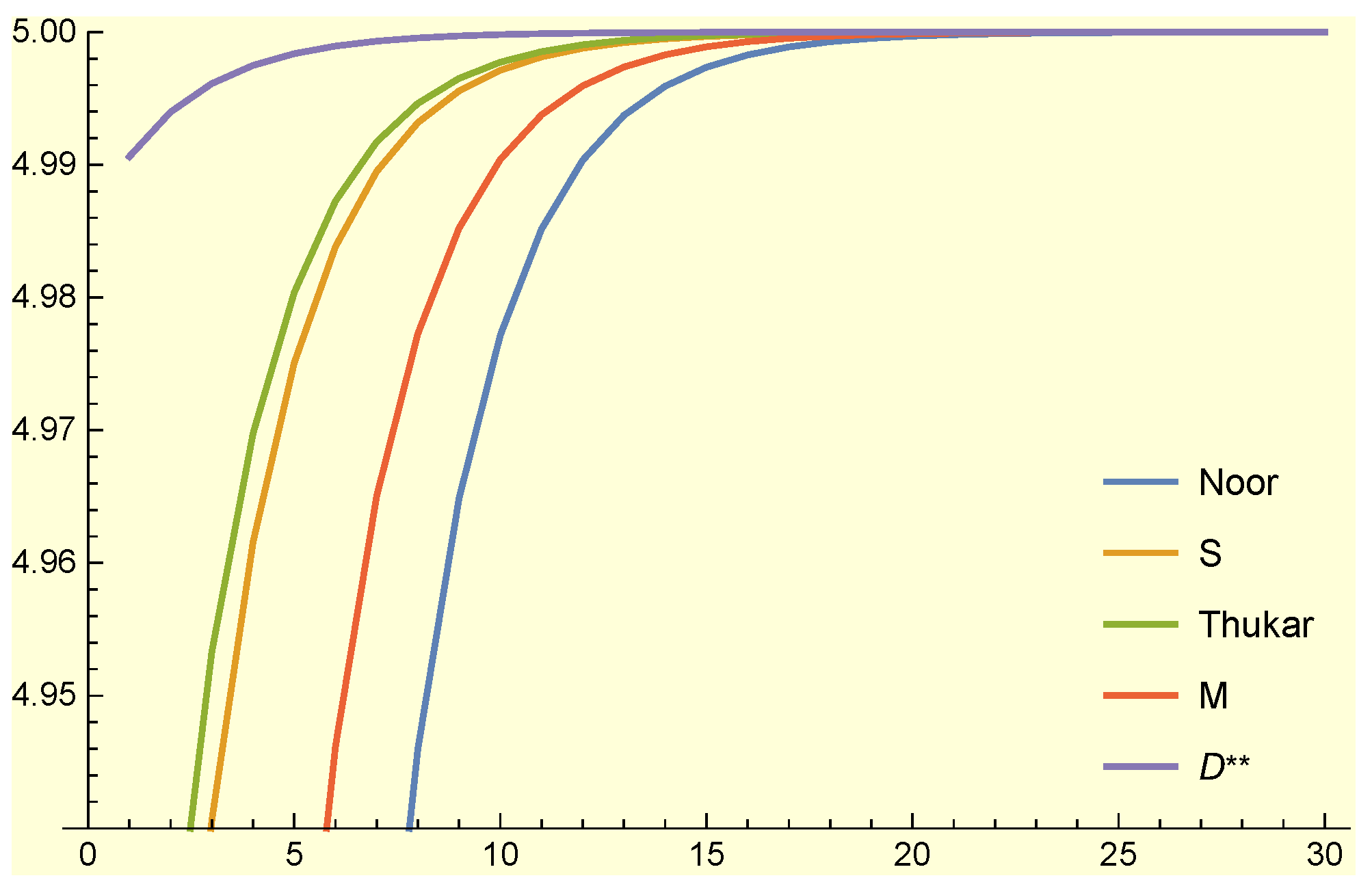
| Iteration | Maan | Ishikawa | F | D | |
|---|---|---|---|---|---|
| 1 | 3.81359 | 3.91521 | 4.96625 | 4.96876 | 4.99062 |
| 2 | 4.22201 | 4.28724 | 4.97828 | 4.97994 | 4.99398 |
| 3 | 4.49145 | 4.53352 | 4.98597 | 4.98707 | 4.99612 |
| 4 | 4.66824 | 4.69545 | 4.99092 | 4.99163 | 4.99749 |
| 5 | 4.78385 | 4.80148 | 4.99411 | 4.99458 | 4.99837 |
| 6 | 4.85929 | 4.87073 | 4.99618 | 4.99648 | 4.99895 |
| 7 | 4.90845 | 4.91587 | 4.99752 | 4.99772 | 4.99932 |
| 8 | 4.94045 | 4.94528 | 4.99839 | 4.99852 | 4.99956 |
| 9 | 4.96128 | 4.96441 | 4.99895 | 4.99904 | 4.99971 |
| 10 | 4.97482 | 4.97686 | 4.99932 | 4.99937 | 4.99981 |
| 11 | 4.98363 | 4.98496 | 4.99956 | 4.99959 | 4.99988 |
| 12 | 4.98936 | 4.99022 | 4.99971 | 4.99974 | 4.99992 |
| 13 | 4.99308 | 4.99364 | 4.99981 | 4.99983 | 4.99995 |
| 14 | 4.99550 | 4.99587 | 4.99988 | 4.99989 | 4.99997 |
| 15 | 4.99708 | 4.99731 | 4.99992 | 4.99993 | 4.99998 |
| 16 | 4.99810 | 4.99825 | 4.99995 | 4.99995 | 4.99999 |
| 17 | 4.99877 | 4.99886 | 4.99997 | 4.99997 | 4.99999 |
| 18 | 4.99920 | 4.99926 | 4.99998 | 4.99998 | 4.99999 |
| 19 | 4.99948 | 4.99952 | 4.99999 | 4.99999 | 5.00000 |
| 20 | 4.99966 | 4.99969 | 4.99999 | 4.99999 | 5.00000 |
| 21 | 4.99978 | 4.99980 | 4.99999 | 4.99999 | 5.00000 |
| 22 | 4.99986 | 4.99987 | 5.00000 | 5.00000 | 5.00000 |
| 23 | 4.99991 | 4.99991 | 5.00000 | 5.00000 | 5.00000 |
| 24 | 4.99994 | 4.99994 | 5.00000 | 5.00000 | 5.00000 |
| 25 | 4.99996 | 4.99996 | 5.00000 | 5.00000 | 5.00000 |
| 26 | 4.99997 | 4.99998 | 5.00000 | 5.00000 | 5.00000 |
| 27 | 4.99998 | 4.99998 | 5.00000 | 5.00000 | 5.00000 |
| 28 | 4.99999 | 4.99999 | 5.00000 | 5.00000 | 5.00000 |
| 29 | 4.99999 | 4.99999 | 5.00000 | 5.00000 | 5.00000 |
| 30 | 5.00000 | 5.00000 | 5.00000 | 5.00000 | 5.00000 |
| Iteration | Noor | S | Thukar | M | |
|---|---|---|---|---|---|
| 1 | 3.93161 | 4.85694 | 4.88787 | 4.52880 | 4.99062 |
| 2 | 4.29749 | 4.90798 | 4.92774 | 4.69565 | 4.99398 |
| 3 | 4.54002 | 4.94059 | 4.95329 | 4.80296 | 4.99612 |
| 4 | 4.69962 | 4.96155 | 4.96975 | 4.87225 | 4.99749 |
| 5 | 4.80416 | 4.97508 | 4.98038 | 4.91709 | 4.99837 |
| 6 | 4.87246 | 4.98383 | 4.98727 | 4.94617 | 4.99895 |
| 7 | 4.91699 | 4.9895 | 4.99173 | 4.96503 | 4.99932 |
| 8 | 4.94600 | 4.99318 | 4.99463 | 4.97728 | 4.99956 |
| 9 | 4.96488 | 4.99557 | 4.99651 | 4.98524 | 4.99971 |
| 10 | 4.97717 | 4.99712 | 4.99773 | 4.99041 | 4.99981 |
| 11 | 4.98515 | 4.99813 | 4.99853 | 4.99376 | 4.99988 |
| 12 | 4.99035 | 4.99878 | 4.99904 | 4.99595 | 4.99992 |
| 13 | 4.99373 | 4.99921 | 4.99938 | 4.99737 | 4.99995 |
| 14 | 4.99592 | 4.99949 | 4.99960 | 4.99829 | 4.99997 |
| 15 | 4.99735 | 4.99967 | 4.99974 | 4.99889 | 4.99998 |
| 16 | 4.99828 | 4.99978 | 4.99983 | 4.99928 | 4.99999 |
| 17 | 4.99888 | 4.99986 | 4.99989 | 4.99953 | 4.99999 |
| 18 | 4.99927 | 4.99991 | 4.99993 | 4.99969 | 4.99999 |
| 19 | 4.99953 | 4.99994 | 4.99995 | 4.99980 | 5.00000 |
| 20 | 4.99969 | 4.99996 | 4.99997 | 4.99987 | 5.00000 |
| 21 | 4.99980 | 4.99997 | 4.99998 | 4.99992 | 5.00000 |
| 22 | 4.99987 | 4.99998 | 4.99999 | 4.99995 | 5.00000 |
| 23 | 4.99992 | 4.99999 | 4.99999 | 4.99996 | 5.00000 |
| 24 | 4.99995 | 4.99999 | 4.99999 | 4.99998 | 5.00000 |
| 25 | 4.99996 | 5.00000 | 5.00000 | 4.99999 | 5.00000 |
| 26 | 4.99998 | 5.00000 | 5.00000 | 4.99999 | 5.00000 |
| 27 | 4.99998 | 5.00000 | 5.00000 | 4.99999 | 5.00000 |
| 28 | 4.99999 | 5.00000 | 5.00000 | 5.00000 | 5.00000 |
| 29 | 4.99999 | 5.00000 | 5.00000 | 5.00000 | 5.00000 |
| 30 | 5.00000 | 5.00000 | 5.00000 | 5.00000 | 5.00000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, D.; Ali, S.; Pompei-Cosmin, D.; Antoniu, T.; Zaagan, A.A.; Mahnashi, A.M. A Quicker Iteration Method for Approximating the Fixed Point of Generalized α-Reich-Suzuki Nonexpansive Mappings with Applications. Fractal Fract. 2023, 7, 790. https://doi.org/10.3390/fractalfract7110790
Ali D, Ali S, Pompei-Cosmin D, Antoniu T, Zaagan AA, Mahnashi AM. A Quicker Iteration Method for Approximating the Fixed Point of Generalized α-Reich-Suzuki Nonexpansive Mappings with Applications. Fractal and Fractional. 2023; 7(11):790. https://doi.org/10.3390/fractalfract7110790
Chicago/Turabian StyleAli, Danish, Shahbaz Ali, Darab Pompei-Cosmin, Turcu Antoniu, Abdullah A. Zaagan, and Ali M. Mahnashi. 2023. "A Quicker Iteration Method for Approximating the Fixed Point of Generalized α-Reich-Suzuki Nonexpansive Mappings with Applications" Fractal and Fractional 7, no. 11: 790. https://doi.org/10.3390/fractalfract7110790
APA StyleAli, D., Ali, S., Pompei-Cosmin, D., Antoniu, T., Zaagan, A. A., & Mahnashi, A. M. (2023). A Quicker Iteration Method for Approximating the Fixed Point of Generalized α-Reich-Suzuki Nonexpansive Mappings with Applications. Fractal and Fractional, 7(11), 790. https://doi.org/10.3390/fractalfract7110790









