Abstract
The advent of quantum computers could enable the resolution of complex computational problems that conventional cryptographic protocols find challenging. As a result, the formidable computing capabilities of quantum computers may render all present-day cryptographic schemes that rely on computational complexity ineffectual. Inspired by these possibilities, the primary purpose of this paper is to suggest a quantum image encryption scheme based on quantum cellular automata with mixed multi-chaos hybrid maps and a hyperchaotic system with quantum operations. To achieve desirable encryption outcomes, we designed an encryption scheme involving two main operations: (1) pixel-level diffusion and (2) pixel-level permutation. Initially, the secret keys generated using the hyperchaotic system were closely tied to the original image. During the first phase, the establishment of correlations among the image pixels, in addition to the three chaotic sequences obtained from the hyperchaotic system, was achieved with the application of a quantum-state superposition and measurement principle, wherein the color information of a pixel is described using a single qubit. Therefore, the three channels of the plain image were subjected to quantum operations, which involve Hadamard transformation and the quantum-controlled NOT gate, before the diffusion of each color channel with the hyperchaotic system. Subsequently, a quantum ternary Toffoli gate was used to perform the diffusion operation. Next, the appropriate measurement was performed on the three diffused channels. To attain the confusion phase, a blend of mixed multi-chaos hybrid maps and a two-dimensional quantum cellular automaton was used to produce random and chaotic sequence keys. Subsequently, the circular shift was utilized to additionally shuffle the rows and columns of the three diffused components, in order to alter the positions of their pixel values, which significantly contributes to the permutation process. Lastly, the three encoding channels, R, G, and B, were merged to acquire the encrypted image. The experimental findings and security analyses established that the designed quantum image encryption scheme possesses excellent encryption efficiency, a high degree of security, and the ability to effectively withstand a diverse variety of statistical attacks.
1. Introduction
With the acceleration of cybercrimes due to the rapid growth of the Internet and recent technologies [1], multimedia information, such as digital images, audio data, and video, is increasingly transmitted online, where people can obtain various types of data at any time and in any location, as well as sharing resources and exchanging information [2,3].
In addition, with the birth and development of fifth-generation mobile communication technology and with recent advancements in social media platforms [3,4,5,6,7], the transmission of digital images has become normalized since digital images are highly visual and informative. In addition, various digital images are transmitted over the web daily, which is considered an insecure line of communication. Since some of these transmitted digital images may contain individual secret information, military secrets, and even national strategies, the illegal sharing of these digital images through any digital medium causes serious damage to any organization. Hence, transmitted digital images pose high levels of risk once they are lost and intercepted (i.e., copied and distributed illegally), and they can be altered maliciously.
Securing such digital images against unwanted disclosure and other malicious behavior is considerably more critical for users in various fields that involve unique security issues [5]. Therefore, information security has consistently commanded extensive attention from academia and industry, especially image information security, which has been a major focus of research [8]. To meet the above needs in practice, with regard to guaranteeing the security and protection of digital images, researchers have developed many techniques, including image encryption, watermarking, and steganography. Of these techniques [9], image encryption is considered the most direct and effective method since, in this method, information is encoded in such a way that the intended receiver is the only user who can retrieve its contents.
Digital images [10,11] are different from textual information due to their vivid and intuitive characteristics, such as bulk data capacity, high redundancy, and strong correlations between adjacent pixels. All these defects make conventional encryption algorithms [12,13], such as DES, AES, RSA, ECC, and IDEA, appear to be inappropriate for digital-image encryption due to their inefficiency and computational expenses. Therefore, image-information encryption [14] has become a major focus of research in the field of information security. To satisfy the emerging demand, a significant number of useful image-encryption algorithms based on optical transformation, DNA-sequence operations, wave motion, Brownian motion, cellular automata, compressive sensing, and chaotic theory were developed in the literature to secure these digital images [15]. One very promising direction is the application of chaotic maps and systems to image encryption. This is because cryptography places a particular emphasis on the introduction of nonlinear transformations, which is a distinctive feature of chaotic systems [16].
Chaos is a complex physical phenomenon, which can be represented in many dynamical systems [17,18]. It therefore penetrates various scientific fields, such as physics, biology, economics, sociology, stochastic computing, cryptography, etc. Chaotic systems have many inherent characteristics, such as ergodicity, extreme sensitivity to initial conditions and control parameters, unpredictability, good pseudorandom behavior, non-periodicity, and highly complex nonlinearity, which are very similar to the properties required by cryptography [19]. Thus, the research direction of cryptography based on chaos was born. Accordingly, image encryption based on chaos has become one of the most important image protection methods [12,20]. Some examples of typical image encryption algorithms are the following. In [13], a fast image encryption algorithm based on logistics–sine–cosine mapping was proposed, in which the algorithm first generates five sets of encrypted sequences from the logistics–sine–cosine mapping, and then uses the order of the encryption sequence to scramble the image pixels and designs a new pixel-diffusion network to further improve the key sensitivity and plain-image sensitivity of the encryption algorithm. Nehal Abd El-Salam Mohamed et al. [15] proposed an image encryption algorithm based on combining a hyperchaotic system and quantum 3D logistic map, which have the advantage of excellent random sequence to expand the key space, stronger randomness, and enhance the performance of resisting common attacks. The authors [21] presented a meaningful data encryption scheme by combining a P-tensor product compressive sensing model, a newly designed chaotic map, and data embedding technology, which ensures sufficient security and improves the proposed encryption scheme in terms of visual security, compressibility, and encryption efficiency greatly. On the other hand, a 1D sinusoidal polynomial composite chaotic system (SPCCS) combining the sine function with some special polynomial functions was proposed and proved that SPCCS satisfies Devaney’s definition of chaos in Ref. [22], wherein its detailed simulation results verify superiority and effectiveness of the proposed image encryption algorithm.
In the literature, some authors used cellular automata in collaboration with different chaotic maps to enhance the security of image encryption schemes. Mondal et al. [23] present a highly secure image encryption scheme for secure image communication and storage. The scheme is based on a chaotic skew tent map and cellular automata (CA), where the combination of both a chaotic map and CA gives a system with higher key space and a faster PRNS generator and is capable of resisting any kind of known attacks. In 2022, the authors [24] used the Lorenz system as the first encryption stage in a three-stage encryption process. The other two stages involve an S-box and Rule 30 cellular automaton. The authors apply different scan patterns to each of the RGB color channels of the image to be encrypted. Next, they separate the Lorenz equations and apply the use of each equation on a different color channel.
Meanwhile, despite the significant role of chaotic maps in designing modern cryptographic mechanisms, and as the traditional computer approaches its physical limits [25,26,27,28,29], researchers are beginning to study a new computing model, and quantum computers have produced a series of satisfactory encryption results. Given the quantum outstanding advantages of entanglement, superposition, and parallelism, quantum computing is widely used in all aspects of information science. With quantum computation’s rapid development, studies on image processing have been developed from classical image processing to quantum image processing (QIP), which has triggered researchers’ interest and is considered a new interdisciplinary subject that integrates quantum computing and digital image processing. Since one of the merits of quantum computers and quantum algorithms is that qubits obey the no-cloning theorem [30,31], which means no qubit can be cloned, quantum mapping theory has been introduced in image encryption schemes, aiming to improve the security level and practical value of image cryptography in the quantum era. Furthermore [32], quantum encryption protocols also include scrambling the pixel positions and/or changing the pixel value using chaos theory or any other quantum transformations.
For example, the authors [33] presented an encryption scheme based on discrete cosine transform (DCT) and alternate quantum walks (AQW) which explores the integration of quantum walks into an optical image encryption framework and uses different encryption matrices to encrypt images in the spatial domain and DCT domain. Ref. [34] introduced a self-adaptive encryption scheme to protect quantum images efficiently with minimal storage requirements which uses two rounds of encryption with two different pseudorandom number sequences which are obtained from a newly designed pseudorandom number generator (PRNG) and achieves less time complexity than many recently published quantum image encryption schemes. Zhang and Wang [35] proposed an image encryption scheme based on controlled zigzag transform and bit-level encryption under the quantum walk environment, which has good key security to resist attacks effectively such as statistical analysis, brute force search, and noise influence, as well as having better key sensitivity and dislocation effect.
Motivated by the better dynamics of hyperchaotic systems, the benefits of using many chaotic systems, and based on the physical properties of quantum computing, this study investigates a simple but further secure and efficient quantum image encryption algorithm. The principal contributions of this presented research work can be recapped as given below:
- (1)
- From the perspectives of cryptography and information theory, quantum transformation theory is applied as a new tool to quantum image encryption technology. Hence, based on Hadamard transformation theory and CNOT gate (entangle qubits procedure), we design a safe and efficient quantum image encryption with a new algorithm.
- (2)
- The proposed quantum image encryption scheme uses both confusion and diffusion to achieve a higher level of security, which is developed in accordance with Shannon’s theories.
- (3)
- Two different types of chaos, namely, a Lü system as a hyperchaotic system or a quantum logistic map as a multi-dimensional chaotic map (pixel-level diffusion), are utilized in designing a new visually meaningful quantum image cryptosystem.
- (4)
- The proposed scheme uses a secret key generated dependent on the original image to determine the number of cycles for both chaotic systems. Hence, it verifies that the proposed scheme has a strong resistance to chosen-plaintext attacks.
- (5)
- Concretely, this study investigates the integration of quantum cellular automata (QCA) as a quantum-inspired model and mixed multi-chaos maps as hybrid chaotic maps (pixel-level permutation).
- (6)
- To accomplish the permutation process, a circular shift is utilized to additionally shuffle the rows and columns of the diffused R, G, and B channels.
- (7)
- The key size of the proposed algorithm is sufficiently large to withstand brute-force attacks.
- (8)
- Statistical analysis, differential analysis, key analysis, and robustness analysis confirm that the designed scheme achieves a high level of security against most various attacks.
- (9)
- The proposed quantum scheme attains a reduced time complexity, leading to faster encryption and decryption processes. Additionally, a lower time complexity can make the proposed scheme more resistant to attacks that rely on brute-force methods as there are fewer possible combinations to test within a given amount of time.
- (10)
- The efficacy of the proposed method in safeguarding quantum image information is validated using numerical simulation and performance comparison.
The remainder of this article is structured as follows. Section 2 outlines the fundamental concepts utilized in the proposed scheme and analyses their dynamic characteristics. Section 3 provides a detailed explanation of the presented quantum image encryption and decryption scheme. Section 4 showcases the experimental and numerical outcomes of the proposed encryption scheme concerning diverse visual, statistical, differential, and brute-force analyses. In conclusion, Section 5 summarizes the main findings of this paper.
2. Preliminary Knowledge
2.1. Hyperchaotic Systems
Hyperchaotic systems are a valuable tool for exploring the behavior of nonlinear systems and developing new techniques for their analysis and control [36,37,38,39,40,41]. These systems are characterized by having more than one chaotic attractor, which means that they exhibit more complex and unpredictable behavior than chaotic systems. In addition, hyperchaotic systems have several advantages over lower-dimensional chaotic systems that make them useful for a wide range of applications in science, technology, and engineering, which can be summarized as follows: (1) increased complexity; (2) more sensitivity to small changes in initial conditions; (3) richer mathematical properties, where these systems also exhibit a rich variety of bifurcations and strange attractors; and (4) better performance in certain applications where hyperchaotic systems can be used to generate multiple secure encryption keys.
Hence, researchers continue to study hyperchaotic systems because of their intrinsic properties and their potential for applications in a wide range of fields, including secure communication, random number generation, cryptography, and control theory.
In addition, most existing encryption algorithms are still using a single chaotic system for encryption operation. These schemes cannot resist brute-force attacks efficiently as their key space is small. Moreover, a single chaotic system only has a few chaotic sequences that can be applied. The use of multi-chaotic systems has many benefits, which can be listed as follows: (1) multi-chaotic sequences; (2) expanded key space; (3) increased level of security; and (4) resisting brute-force attack.
In this section, we briefly present the two hyperchaotic systems considered in this work. One example of a hyperchaotic system is the Lü system, which has three nonlinear differential equations that describe the evolution of its state variables. Another example is the quantum logistic map, which has three nonlinear differential equations that describe the evolution of its state variables. Both systems have been extensively studied, and their properties are well-understood.
2.1.1. Hyperchaotic Lü System
In 2002 [42,43], Lü et al. found a new three-dimensional autonomous chaotic system, namely–Lü system which is given by Lü and Chen in the chaotic anti-control method. This system is considered an extension of the well-known Lü system.
The hyperchaotic Lü system has been studied extensively in recent years and has been found to have important applications in cryptography, chaos-based communications, and other fields. For example, the system can be used to generate random numbers, which are essential for many cryptographic applications.
It governs the evolution of its state variables x, y, and z. These equations contain various nonlinear terms, such as cubic and quadratic terms, that give rise to the system’s hyperchaotic behavior. This system is described by three-dimensional nonlinear differential equations that exhibit hyperchaotic behavior as follows [44]:
where are system control parameters. The Lü system is in a chaotic state [42] when the parameter set is fixed while parameter varies and, likewise, it may not be chaotic for any other parameter. This system is hyperchaotic with four positive Lyapunov exponents , and Lyapunov dimension which indicates that it has multiple unstable directions in phase space [45], as displayed in Figure 1. The hyper-chaos attractors and the bifurcation diagram of this hyperchaotic system are illustrated in Figure 2a,b, respectively.
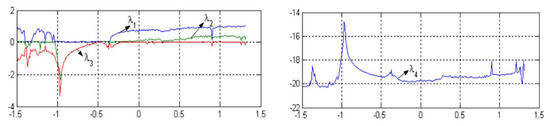
Figure 1.
Lyapunov exponents spectrum of a hyperchaotic Lü system.
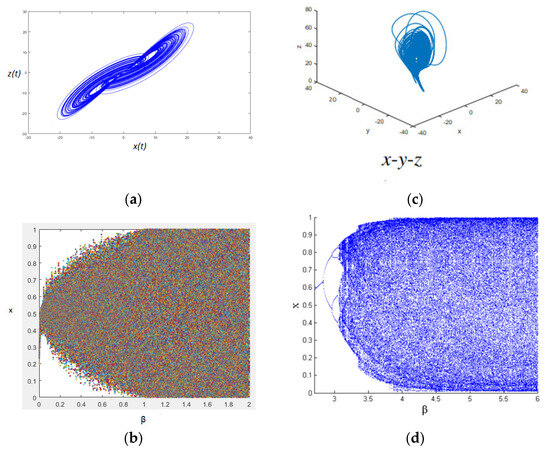
Figure 2.
Chaotic behavior analysis result: (a) phase diagram of a Lü hyperchaotic system, (b) bifurcation diagram of a Lü hyperchaotic system, (c) phase diagram of a quantum logistic map, and (d) bifurcation diagram of a quantum logistic map.
2.1.2. Hyperchaotic Quantum Logistic Map
The quantum 3D logistic map [46,47] was first proposed by Muthuswamy and Lakshmanan in 2005 to explore the behavior of quantum systems that exhibit classical chaotic behavior. It exhibits complex behavior that is similar to that of the classical 3D logistic map, including bifurcations and chaos. However, the quantum version of the system also exhibits unique quantum properties, such as quantum interference and entanglement, which arise from the system’s quantum nature. Researchers continue to explore its properties and applications to develop new insights and techniques. One promising direction of research is the use of the system for quantum chaos-based cryptography, which relies on the chaotic behavior of the system to generate secure cryptographic keys.
The quantum 3D logistic map [15] is described as a three-dimensional quantum map that is derived from the classical 3D logistic map. The map can be expressed as follows:
where β is the dissipation parameter, represents the control parameter, and are the complex conjugates of , respectively. However, the initial conditions are set as real numbers to meet the requirement of communication.
The quantum 3D logistic map is analyzed in terms of hyper-chaos attractors of the quantum logistic map and its bifurcation diagram, respectively, as shown in Figure 2c,d. Whereas Figure 3 depicts the Lyapunov exponents spectrum.
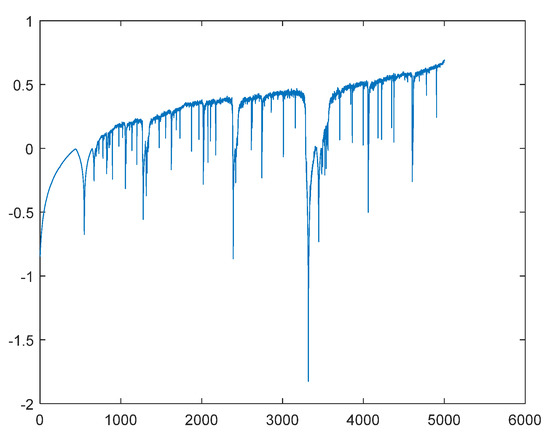
Figure 3.
Lyapunov exponents spectrum of a quantum logistic map.
2.2. Hadamard Gate
In quantum mechanics [48], a particle can exist in a superposition state, which means that it is in multiple states simultaneously. For example, an electron can exist in a superposition of two energy levels, or a photon can be in a superposition of two polarization states. In contrast, bringing a qubit into a superposition state is a relatively simple task for quantum computing developers. The process simply requires applying a specific gate to the qubit. The Hadamard gate, for example, is a fundamental single-qubit gate in quantum computing that plays an important role in creating superposition states and other quantum algorithms and protocols. The quantum circuit of the Hadamard gate is shown in Figure 4, and its matrix representation is given by [49]:

Figure 4.
Quantum circuit of the Hadamard gate.
The Hadamard gate has the following action on both the computational basis states |0⟩ and |1⟩:
Finally, as depicted in Figure 5 [50], when a qubit initially in the state |0⟩ undergoes the Hadamard gate operation, it enters a superposition state, where the chances of measuring 0 and 1 are equal amplitudes. The Hadamard gate is also important because it has its own inverse. That is, applying the Hadamard gate twice returns the qubit to its original state. This property is useful in quantum algorithms that require the ability to create and undo superposition states.
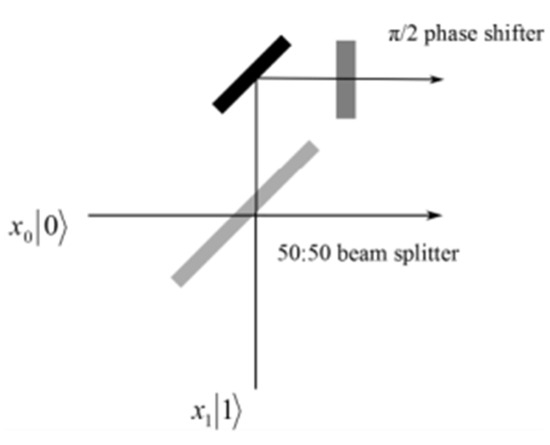
Figure 5.
Optical implementation of the Hadamard gate.
2.3. Quantum Cellular Automata
Quantum cellular automata (QCA) is the quantum version of cellular [51,52,53]. It is a theoretical model of computation that combines principles of quantum mechanics and cellular automata. In QCA, the state of each cell is a quantum superposition of two or more states, and the evolution of the system is governed by quantum mechanical laws. The evolution of the system is typically described using a unitary operator, which represents a quantum gate that acts on the state of each cell, and the evolutionary pattern of quantum cellular automata is displayed in Figure 6.
Figure 6.
Evolutionary pattern of quantum cellular automata.
The basic idea behind QCA is to use the principles of quantum mechanics to perform certain computations more efficiently than classical methods. Quantum cellular automata (QCA) has several potential advantages over classical cellular automata (CA), including (1) increased speed, where QCA has the potential to provide a significant speedup over classical CA for certain computations that are inherently quantum in nature; (2) increased capacity, where QCA has the potential to store and process more information than classical CA; (3) increased security, where QCA has the potential to provide enhanced security for communication and data storage; and (4) novel applications, where QCA has the potential to provide new insights into physical and biological systems that are difficult to study using classical methods. However, the design and implementation of QCA circuits can be complex and require specialized knowledge of quantum mechanics and circuit design.
2.4. Hybrid Chaotic Maps
Hybrid chaotic maps [54,55] are mathematical models that combine multiple chaotic maps or systems to create intricate and versatile dynamical behaviors. By interconnecting individual chaotic maps with techniques like sequential coupling, parallel coupling, or feedback coupling, hybrid chaotic maps exhibit enhanced complexity and unpredictability compared with their constituent maps. In essence, the purpose of combining these maps is to generate more intricate dynamics, increase randomness, or improve certain characteristics of chaotic behavior.
Three hybrid chaotic systems are utilized in this work. Each chaotic system comprises a nonlinear mixture of two different one-dimensional chaotic maps, i.e., the logistic map, tent map, and sine map, which are supposed to be seed maps. These hybrid chaotic maps are the logistic–tent system, logistic–sine system, and tent–sine system, which are defined, respectively, as:
These maps find applications in various fields such as cryptography, secure communications, random number generation, image encryption, and chaotic control systems. With their diverse and dynamic behaviors, hybrid chaotic maps provide a powerful tool for generating secure encryption algorithms, optimizing complex functions, and exploring the fascinating realm of chaotic dynamics.
3. Proposed Quantum Image Encryption and Decryption Scheme
This section provides a detailed presentation of the proposed quantum image encryption scheme, which utilizes quantum cellular automata (QCA) and mixed multi-chaos hybrid systems to safeguard both grayscale and color images.
3.1. Encryption Procedure
The fundamental C. E. Shannon’s permutation–diffusion model [56] serves as the basis for the entire scheme, which comprises two primary operations, namely, pixel-level diffusion and pixel-level permutation. The detailed steps of these operations can be listed as follows, and the framework of the designed encryption scheme is shown in Figure 7.
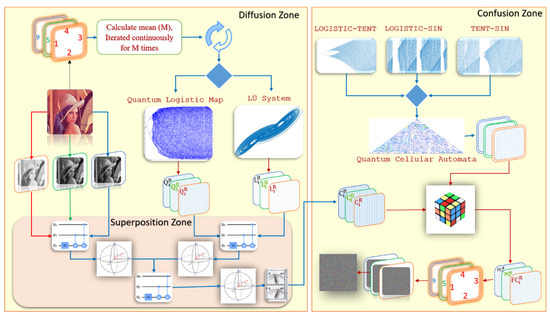
Figure 7.
Block diagram of the designed encryption procedure.
3.1.1. Pixel Plane Diffusion
Step 1. Import the color plain image , then acquire the dimensions and of the input color plain image .
Step 2. From the input plain image of size , crop the first row and first column from each component.
Step 3. Meanwhile, while carrying out Step 2, extract the R, G, and B components of the color image, which has dimensions .
Step 4. Preceding the process of image encryption, a parameter is generated based on a plain image by determining the mean pixel values of any cropped row or column in any of the three components of the plain image.
Step 5. The user can choose to apply one of the hyperchaotic systems, either a quantum logistic map or Lü system at the level of pixel diffusion. Afterward, the calculated mean value is taken to pre-iterate the chosen hyperchaotic system times, with the aim of eliminating any transient effects and ensuring that the system enters a fully chaotic state.
Step 6. Set the initial values and control parameters of the chosen hyperchaotic system by applying calculation Formula (1) for the Lü system or calculation Formula (2) for the quantum logistic map as outlined in Section 2.1.1 and Section 2.1.2, respectively.
Step 7. If the selected hyperchaotic system is the quantum logistic map, it will undergo iterations to produce three chaotic matrices of length . These matrices act as the diffusion keys and can be determined using the provided formula.
where ) are two large prime numbers and are random sequences, which are generated using 3D quantum logistic map Equation (2).
Step 7.1. Whereas, if the chosen hyperchaotic system is the Lü system, iterations will be performed to generate three chaotic matrices of length . These matrices serve as the diffusion keys and can be calculated using the given formula.
where and are random sequences that are generated using Lü system Equation (1).
Step 8. The generated three different diffusion keys either with a quantum logistic map or Lü system as well as the original separated R, G, and B components of the color image are subjected to Hadamard transformation and the CNOT gate together in one quantum circuit to produce entangled qubits. Using a Hadamard gate followed by a CNOT gate will bring all values in all the resulted matrices into the zone of the superposition state and create entanglement. Hadamard gate H can be defined using Equation (3) in Section 2.2 and the action of the CNOT gate can be represented by its truth table alongside its quantum circuit, as shown in Figure 8 [57]:
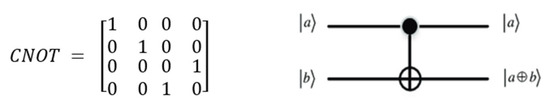
Figure 8.
Matrix representation and quantum circuit of CNOT gate.
Step 9. Once all values of the three channels of the plain image and the three chaotic matrices obtained from either mathematical Formula (4) or mathematical Formula (5) are brought into a superposition state zone, a ternary Toffoli quantum gate is executed to modify the value of each pixel qubit. To effectively accomplish pixel-level diffusion, an XOR operation with the corresponding qubits of the three chaotic matrices obtained from either mathematical Formula (4), or mathematical Formula (5) must be performed. The quantum gate form of the Toffoli gate is often called CCNOT. Its quantum circuit diagram and its matrix can be illustrated as follows in Figure 9 [57].
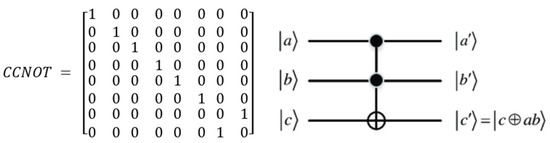
Figure 9.
Matrix representation and quantum circuit of Toffoli gate.
Step 10. Perform the quantum measurement process, which collapses the quantum state of the diffused red, green, and blue components of the image into a classical state their classical versions .
3.1.2. Pixel Plane Confusion
The objective of pixel plane confusion is to disrupt the positions of image pixels. To achieve this, a combination of quantum cellular automata and mixed multi-chaos hybrid maps is utilized to generate chaotic sequences. The detail of each step of the pixel plane confusion is given below.
Step 1. Multiple hybrid chaotic maps are generated, namely, the Logistic–Tent chaotic map, the Logistic–Sine chaotic map, and the Tent–Sine chaotic map. Each uses a mix of one-dimensional chaotic maps, as outlined in Section 2.4.
Step 2. Initialize the control parameter and the original variable for both Logistic–Tent Equation (4) and Logistic–Sine Equation (5) hybrid chaotic maps, whereas set parameter coefficient µ and the original variable for Tent–Sine Equation (6) hybrid chaotic map, to acquire two chaotic sequences. The calculation procedure for obtaining these sequences is as follows.
where is the chaotic sequence generated from each of the hybrid chaotic maps.
Step 3. By selecting two resulting chaotic sequences of one of the hybrid chaotic maps to use as the parameters for the two-dimensional cellular automata (2D-CA), one chaotic sequence is generated using the 2D-CA. This can be expressed as follows.
where are the chosen chaotic sequences generated from one of the hybrid chaotic maps and n_states refer to the number of possible values that each pixel in the image can take on.
Step 4. Reshape the generated chaotic sequence into a matrix with size .
Where represents the column numbers in the image.
Step 5. For the diffused R, G, and B components, select one of the hybrid chaotic maps to be applied on each one of them in the permutation process.
Step 6. The chaotic sequence produced by the cellular automaton has a size of , indicating that it comprises three chaotic sequences, each with a length of . This also allows the user to choose which sequence from the to utilize in the permutation process.
Step 7. Using the selected sequence from the chaotic sequence generated by the cellular automaton in the former step, the pixels positions in each row of the diffused channels are shuffled. The confusion operation is achieved by using the circular shift operation in the subsequent manner.
where refers to the selected vector from the chaotic sequence generated by the .
Step 8. Transpose the red, green, and blue components of the scrambled image to randomly permute their rows and columns as represented as follows.
Step 9. To obtain the desired final versions of the three confused channels , execute steps 7 and 8 one more time.
Step 10. The first cropped original row and column are added to each of the three encoding components. Afterward, at the last, recompose the three cipher layers into one RGB image.
3.2. Decryption Procedure
Due to the quantum operations being invertible, the decryption process involves executing the steps of the encryption process in reverse order and utilizing the identical set of keys generated earlier. This means that the encryption and decryption are reciprocal processes in the presented scheme.
The process of decryption comprises two stages: (1) reversing the pixel plane confusion and (2) reversing the pixel plane diffusion. Figure 10 depicts a diagram of the designed decryption process, which demonstrates that the proposed scheme enables the retrieval of the original image precisely from the encoded cipher image.
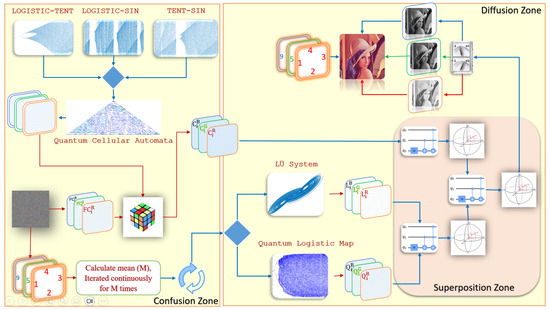
Figure 10.
Block diagram of the designed decryption procedure.
4. Experimental Results and Numerical Analysis
4.1. Experiment Platform
The efficiency of the proposed scheme is assessed by conducting simulations and comparing the results against security parameters. Quantum computing is a relatively new field, and while there have been significant advances in recent years, a practical and fully functional quantum computer is not yet available. As a result, all the experimental results of the proposed quantum image encryption scheme are tested using the MATLAB R2017b platform on a classical computer to authenticate the security and efficacy of the quantum image encryption algorithm that is presented.
The numerical simulation of the proposed encryption scheme is run in a Windows 11 Home Single-Language environment. The specification of the utilized computer system includes 11th Gen Intel(R) Core (TM) i7-11800H applied as the central processing unit (CPU) @ 2.30 GHz and the random-access memory (RAM) is 16 GB.
4.2. Experiment Results
Numerous experiments were conducted to evaluate the efficiency of the proposed image encryption algorithm and demonstrate its capability and effectiveness in the encryption and decryption process. In these experiments, six diverse images (including grayscale and colored images) are selected from the CVG-UGR-Image Database [58] and from the USC-SIPI (University of Southern California Signal and Image Processing Institute) Image Database [59] as standard test images for this method. Table 1 contains a comprehensive list of their detailed information.

Table 1.
Selected test images.
Figure 11 illustrates the simulation results of the proposed image encryption and decryption approach. It showcases the plain images (PI), namely, “Male”, “Baboon”, “Airport”, “Lena”, “Splash”, and “Airplane” in Figure 11a–f. Their corresponding cipher images (CIs) are presented in Figure 11g–l, whereas the decryption images (DIs) are shown in Figure 11m–r, which are consistent with the original images before encryption.

Figure 11.
Encryption and decryption results: (a–f) plain images of “Male”, “Baboon”, “Airport”, “Lena”, “Splash”, and “Airplane”; (g–l) the corresponding encrypted images; and (m–r) decrypted images, respectively.
As illustrated in Figure 11, the proposed encryption scheme is not limited by the number and size of the images, it is implemented on multiple images with different sizes and different numbers of images. In addition, the proposed scheme obfuscates the clear patterns in the plain image and generates a ciphered image that appears to have a random noise-like pattern, thereby making it difficult for an intruder to discern any meaningful information. There is no correlation between the encrypted and decrypted images, and the decryption algorithm effectively produces a visually indistinguishable decrypted image from the original image. As a result, the proposed encryption algorithm achieves a high level of encryption and decryption effectiveness, ensuring both the security and visual integrity of the image data.
4.3. Security Analysis
Cryptography is vulnerable to various types of attacks, such as entropy attacks, chosen-plaintext/ciphertext attacks, and brute-force attacks. Therefore, an image encryption method must possess sufficient strength to withstand such attacks. It is important to note that no encryption algorithm can provide perfect security, but a robust algorithm should provide a high level of security against a wide range of attacks.
Several well-known encryption evaluation metrics are commonly used to assess the security and the quantitative performance of the proposed image encryption algorithm. Some of these metrics are (1) key security analysis; (2) statistical attack analysis; and (3) differential attack analysis. In addition to the measures mentioned, there are other techniques used to gauge the algorithm’s ability to determine its effectiveness in protecting image data including robustness to noise and robustness to attacks. A detailed discussion of each of these measures is provided in the accompanying subsections. The last subsection also includes a discussion on the speed of the proposed algorithm.
4.3.1. Key Security Analysis
Key Space Analysis
In modern cryptography [60,61], the size of the key space is a crucial factor in determining the cryptosystem’s effectiveness against brute-force attacks. To protect against brute-force attacks, it is important to use strong passwords or passphrases and to use encryption algorithms with sufficiently large key spaces. While there is no universal standard for an ideal key space, it is generally recommended that the key space should be at least to withstand a brute-force attack, which is approximately . Generally, the larger the key space, the more difficult it is to guess the correct key using brute force, and the more secure the scheme is. The key space is computed based on the number of distinct keys used in both the diffusion and confusion stages [62]. The private key for the proposed quantum image encryption scheme consists of a number of initial conditions and control parameters in total, listed as follows: (1) The parameters of Lü’s hyperchaotic system are a, b, and c, and each of the original variables has two decimal places; there exist possible values for each value. This applies to as well. Thus, there are possible values for each value. (2) The Lü system has the capacity to produce numerous distinct values, estimated at , for all of its generated keys as they can be represented up to 14 decimal places. Overall, the Lü’s hyperchaotic system has a key space of . (3) Parameters β and r are used in the quantum logistic chaotic map, where β consists of four decimal places; there exist possible values for β and r consists of two decimal places, and there exist possible guesses of its value. Thus, there are possible values of β and r. (4) Each initial value of quantum logistic map consists of 12 decimal places with a range between 0 and 1; there exist possible values for each value. Thus, there are possible values of . (5) Two large prime numbers consist of eight decimal places; there exist possible values for each value. Thus, there are possible values of . Overall, the quantum logistic chaotic map possesses a key space that is equivalent to . (6) The cellular automata Logistic–Sine hybrid map has one control parameter r, and an original variable , wherein r consists of four decimal places; there exist possible values for r, while has two decimal places; there exist possible values for its value. Thus, there are possible values of r and . (7) Likewise, the cellular automata Logistic–Tent hybrid map possesses a total of potential values for its parameter and initial value r and , respectively. (8) The initial condition and control parameter of the cellular automata Logistic–Tent hybrid map are , wherein µ consists of three decimal places; there exist possible values for µ, while has two decimal places; there exist possible values for its value. Thus, there are possible values of . (9) Each hybrid chaotic map produces two chaotic sequences, , which can be represented with up to 14 and 16 decimal places, respectively. As a result, this provides for a total of feasible value guesses for each map. (10) The key value utilized for circular shift is derived from any of the former-mentioned cellular automata hybrid maps, which has a size of or approximately .
As a result, the estimated overall key space for the suggested quantum image encryption scheme comes out as follows:
, which is greater than Consequently, the proposed cryptosystem has a key space that is adequately large to withstand all possible types of brute-force attacks and even potential attacks from quantum computers, and hence, it is able to ensure a high degree of security.
Table 2 highlights the key space comparison of the proposed quantum image encryption scheme with other recently presented schemes [2,10,20,60,63]. Based on the comparison results, it can be concluded that the proposed scheme provides better security than its competitors when transmitting images through unsecured communication channels.

Table 2.
Security key space comparison of proposed and recent encryption schemes.
Key Sensitivity Analysis
In an ideal image encryption scheme [27,64,65,66], the encryption and decryption processes are dependent on a secret key. Each bit of the key plays a crucial role in determining the output of the encryption and decryption process. The sensitivity of the key refers to the degree of protection required for the key to prevent unauthorized access to the encrypted data. If any bit of the key is changed, even slightly, the result for both the encryption and decryption output would be drastically different, making it impossible to access the original data without the correct key. The more sensitive the encryption algorithm is to the key, the more robust and secure it is. To test the sensitivity of the proposed quantum image encryption scheme, the color image “Lena” with dimensions of is used as an example, as shown in Figure 12a. A minor modification was made to one of the original secret keys, which is used to encrypt the original image using the same encryption algorithm during the testing phase, while the rest of the keys remained unchanged. In the proposed cryptosystem, using the initial set of the control parameters and original variables of Lü’s system which are denoted as , produces the encrypted image , as shown in Figure 12b. Here, the values of serve as the private key, and are the public key. Assuming a minor modification is made only to the value of in can be represented as Utilizing the same encryption algorithm, the plain image is then encrypted with the algorithm to produce another encrypted image , as depicted in Figure 12c. From the results, there is a considerable difference between the image encrypted with and the image encrypted with , as illustrated in Figure 12d. In addition, Figure 12e displays the decryption outcome when the incorrect decryption key, , is used to decrypt the image in Figure 12b. The correct decrypted image is presented in Figure 12f. It is apparent that the process of decrypting the encrypted image is feasible only when the same key is used. In conclusion, the proposed encryption and decryption scheme is extremely sensitive to the secret key. This contributes to achieving superior levels of security and performance. Moreover, it ensures that the cryptosystem can withstand attacks and maintain its robustness against various threats.

Figure 12.
Key sensitivity analysis.
4.3.2. Statistical Attack Analysis
The assessment of an image encryption scheme’s security using statistical attack analysis involves analyzing its susceptibility to statistical attacks by focusing on analyzing the statistical characteristics of the encrypted image to gather insights about the encryption key or the original image. Various metrics are available to assess an image encryption scheme’s resistance to statistical attacks. These metrics comprise the correlation coefficient, pixel distribution, and entropy of the encrypted image, which aid in measuring the level of randomness and complexity in the encrypted image. The succeeding subsections provide a detailed description of these metrics.
Histogram Analysis
Histogram analysis is a statistical metric in image processing and analysis, which is also widely used in image encryption. In image encryption [67], histogram analysis is one of the fundamental indicators for evaluating the security of an encryption scheme against statistical attacks. A histogram [68,69,70] is a visual depiction that illustrates the frequency distribution of the pixel values in an image, and it displays the number of pixels that have a particular intensity level. The horizontal axis of the histogram represents the intensity levels of the pixels, while the vertical axis represents their frequency or count. A histogram can be created for each color channel of an image, such as red, green, and blue. Histogram analysis uncovers that the original images have non-uniform histograms, making them more susceptible to attacks. In the case of cipher images, the histogram should be as consistently uniform and flat as possible to achieve maximum security.
Figure 13a,c illustrates the histogram analysis of the standard test grayscale image “Baboon” and color image “Splash” for red (R), green (G), and blue (B) channels before the encryption process, both of dimensions 512 × 512, and Figure 13b,d presents their corresponding encrypted versions, respectively. As shown in these figures, the histogram distribution is more uniform in the cipher image, which means a stronger resistance against various statistical analysis attacks, such as known-plaintext attacks and chosen-plaintext attacks.
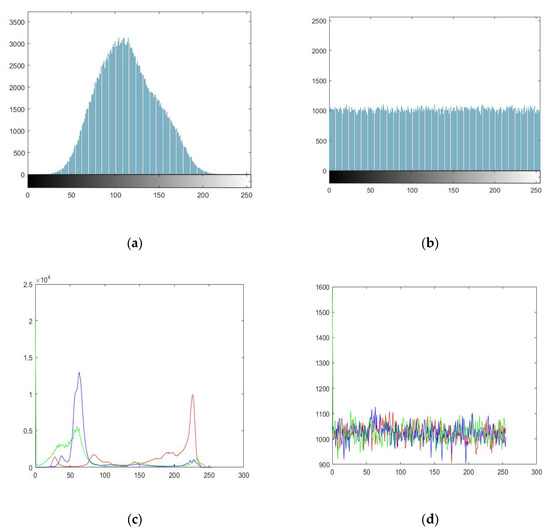
Figure 13.
Histogram analysis: (a) histogram of “Baboon” grayscale plain image, (b) histogram of “Baboon” grayscale cipher image, (c) histogram of “Splash” color plain image (red, green, and blue channels), and (d) histogram of “Splash” color cipher image (red, green, and blue channels).
In quantitative analysis of the image histogram [71,72], another important metric called the histogram variance (var) is used to demonstrate the degree of variation or diversity in the pixel intensity distribution of the encrypted image’s histogram. A higher histogram variance indicates a greater diversity of pixel values in the image, while a lower variance indicates a more uniform pixel distribution. The variance in the histogram can be computed as follows [15]:
where is a one-dimensional array of the histogram values, with pixel values recorded as , respectively. Table 3 and Table 4 display the intensity channels of the experimented grayscale and color plaint and cipher images, respectively, and illustrate that the variance in the images after encryption is greatly reduced when compared with the variance in those images before encryption.

Table 3.
Histogram variance analysis for greyscale images.

Table 4.
Histogram variance analysis for color images.
By observing the former figures and tables of the current test, it is apparent that the distribution of grayscale and RGB components in plain images contains numerous peaks and valleys, whereas the distribution of grayscale and RGB components in cipher images is highly uniform, and their histogram is entirely dissimilar to that of the plain images. This establishes the arduousness of extracting meaningful information from the encrypted image; thereby, the proposed quantum image encryption scheme is secure enough to overcome statistical attacks.
Information Entropy Analysis
In image encryption, entropy analysis is used to evaluate the effectiveness of an encryption algorithm in producing encrypted images that are resistant to attacks. Information entropy analysis [73,74] is a fundamental metric in image encryption that assesses the degree of randomness and unpredictability in the distribution of pixel values within an image. It is based on the concept of entropy, which is a measure of the amount of uncertainty or randomness in a system.
The entropy of an image is computed before and after the encryption process. As the level of disorder in a cipher image increases, so does its information entropy, while the amount of information conveyed decreases. This correlation leads to an improved encryption outcome making it more difficult for unauthorized parties to access the information. The entropy (E) of an image can be calculated using the mathematical formula given below [75]:
where is the probability of having the ith gray level in the image. Due to the uniform distribution of values in grayscale images, which have identical values among the 256 possible values, an ideal entropy value suitable for grayscale images is equal to 8 bits. To verify the effectiveness of the presented image encryption scheme, the entropy values for each component in the cipher image ought to be very close to 8.
Nevertheless [76], the overall entropy may not accurately capture the distribution of entropy within encrypted images. Therefore, local Shannon entropy is used to enhance the security and randomness of the encrypted image. It is derived by computing the global entropy for K non-overlapping blocks, each comprising a fixed number of pixels. Table 5 displays the results for both global entropy and local Shannon entropy of several standard test images alongside their encrypted versions. From the stated data in Table 5, the information entropy values of the cipher images generated with the proposed approach are actually very near to the ideal value of 8. This proves that the proposed approach provides a high level of security against various types of attacks, including statistical analysis and brute-force attacks.

Table 5.
Information entropy of both plain and cipher images.
In addition, Table 6 exposes a comparison of the information entropy values resulting from the proposed scheme with those obtained from other recent schemes. It can be seen that its overall performance is thus the same as that of the approach proposed in [15], and better than that of the other tested methods, which indicates the superiority of the proposed quantum image encryption scheme over existing schemes implies that it provides better protection against statistical attacks of any kind.

Table 6.
Information entropy comparative analysis.
Correlation Distribution Analysis
Due to the nature of digital images [80,81], the pixels within the image are not independent entities, resulting in a significant degree of correlation between adjacent pixels. In image encryption, a high correlation between adjacent pixels can make the encrypted image susceptible to various attacks, such as differential attacks and linear attacks. Whereas a low correlation coefficient indicates that the encryption algorithm has successfully randomized the pixel values in the image and reduced the correlation between adjacent pixels, making it more challenging for an attacker to extract information from the encrypted image. Therefore, correlation coefficient analysis is a vital metric for evaluating the effectiveness of image encryption algorithms in reducing the correlation between adjacent pixels and improving the security of the encrypted image.
Correlation coefficient analysis provides a quantitative measure of the degree of correlation between adjacent pixels in an encrypted image. It ranges from −1 to 1, where −1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation [82]. Thus, a low correlation coefficient is desirable in image encryption to enhance the security and resistance of the encryption scheme against various attacks.
The correlation coefficient among adjacent pixels can be represented mathematically as [12]:
where and are randomly chosen pixels values of two adjacent pixels, N represents the total number of selected samples in each direction, is the covariance of x and y, and and denote the mean value and the variance of pixel value x, respectively.
Moreover, correlation coefficient analysis can be performed in different directions, such as horizontal, vertical, and diagonal, to evaluate the degree of correlation between adjacent pixels in different directions. Thus, 2500 pairs of two adjacent pixels in both the plain and cipher images in each direction were randomly selected to evaluate the effectiveness of the proposed quantum image encryption scheme in reducing the correlation between adjacent pixels. Compared with the histogram and data entropy, the correlation coefficient provides a more discernible visual representation of the dissimilarity between the plain and cipher images. To figure out this differentiation, the grayscale “Baboon” image and color “Splash” image, with dimensions of , were used before and after applying the image encryption technique, as shown in Figure 14 and Figure 15, respectively. From these figures and Table 7, you can clearly notice that the correlation among adjacent pixel pairs in the plain image is highly concentrated, whereas in the cipher image, it appears to be randomly dispersed, resulting in a more uniform distribution and a significant reduction in the correlation. In addition, the correlation coefficient between adjacent pixels is close to 0.
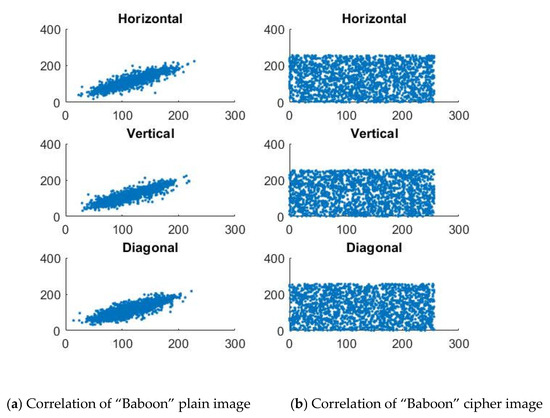
Figure 14.
Correlation distribution analysis of grayscale image in the horizontal, vertical, and diagonal directions.
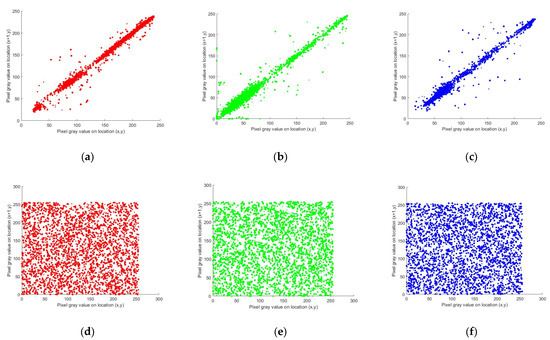
Figure 15.
Correlation distribution of “Splash” color image: (a–c) show RGB channels of plain image; (d–f) show RGB channels of cipher image in the vertical, horizontal, and diagonal directions, respectively.

Table 7.
Correlation coefficients results.
4.3.3. Differential Attack Analysis
Differential attack analysis [83,84,85] is considered another type of widely used cryptanalysis technique for evaluating the security of image encryption schemes. It is based on the idea that small changes in the plaintext should result in large changes in the ciphertext. In this analysis, an attacker studies the differences between two images that are similar, such as an original image and a slightly modified version of that image. The attacker then compares the two images pixel-by-pixel to determine the differences in pixel values between the two images. By examining these differences, the attacker can attempt to identify patterns or relationships that could be exploited to break the encryption and hence, successfully recover the original image or the encryption key.
Assuming an original image with dimension is available, along with a set of encryption keys, the encrypted images and can be generated either with a slight modification to one of the encryption keys in the set or a single pixel in one of the intensity channels in the same original image . A bipolar array , with sizes similar to those of and resulting from this modification can be defined as follows:
To protect against differential attacks, encryption schemes must be designed so that small changes in the plaintext result in significant changes in the ciphertext, and this can be achieved using techniques such as confusion and diffusion. The plain image sensitivity of the proposed quantum image encryption scheme can be evaluated by utilizing differential attack test metrics, such as the number of pixels changing rate (NPCR) and unified average changing intensity (UACI). The proposal of these metrics aims to improve the evaluation of the diffusion and confusion properties of the encryption scheme by providing more accurate measurements for each property.
NPCR measures the diffusivity of the encryption scheme. It calculates the percentage of pixels that change between two encrypted images generated from two plain images that differ by only one pixel. Meanwhile, UACI measures the confusion property of the encryption scheme. It calculates the average difference between the pixel values of the two encrypted images generated from two plain images that differ by only one pixel. The NPCR and UACI are defined as follows:
A secure encryption scheme should produce a high NPCR and a low UACI, indicating that even small changes in the plaintext image result in significant changes in the encrypted image, and the pixel values in the encrypted image are more random and less correlated with the pixel values in the original image. For a grayscale image, the NPCR and UACI have theoretical ideal values of 99.6094% and 33.4635%, respectively. Table 8 and Table 9 present the results of differential attack analysis on grayscale and color images of various sizes, respectively.

Table 8.
NPCR and UACI results of cipher grayscale images.

Table 9.
NPCR and UACI of cipher color images.
Table 8 and Table 9 demonstrate that the NPCR and UACI simulation outcomes for all components on the testing images are near their ideal values. These results indicate that the proposed quantum image encryption scheme is highly immune to differential attacks and provides a high level of security, as it exhibits a high degree of sensitivity even to slight pixel variations in the intensity channels of the plaintext images.
4.3.4. Robustness to Attacks Analysis
Chosen/Known-Plaintext Attacks Analysis
The chosen-plaintext attack and the known-plaintext attack [86,87] are two of the most common types of attacks used in cryptanalysis to break encryption algorithms, including those used for image encryption. In the context of image encryption, these attacks can be particularly challenging, as images often contain large amounts of data that can be difficult to protect against attack. By utilizing these attacks, assailants attempt to uncover the connection between plain and cipher images, with the intention of extracting recurring patterns that aid in deducing the private encryption key or recovering the original image.
Since the attacker has more control over the data being encrypted, the chosen-plaintext attack is considered more potent than the known-plaintext attack. Consequently, an image encryption algorithm that is capable successfully of withstanding a chosen-plaintext attack is also able to resist a known-plaintext attack [60]. To defend against chosen/known-plaintext attacks in image encryption, multiple plain images including “Black”, “White”, and “Gray Bars” are chosen as test images to undergo encryption using the proposed quantum image encryption scheme, to break the scheme, as shown in Figure 16.

Figure 16.
Encryption results of chosen- and known-plaintext attacks.
From Figure 16, it is evident that the cipher images generated using the proposed quantum image encryption scheme exhibit a noise-like pattern and possess uniformly distributed pixel values, thus providing the proposed scheme with the ability to effectively resist both chosen-plaintext and known-plaintext attacks.
Noise Attack Analysis
The conveying of cipher images via physical communication channels is prone to noise or interference, making it necessary for the image decryption scheme to possess the strength to decrypt the cipher images even if noise accumulates during transmission [88]. A noise attack is a type of attack in which an attacker introduces random noise into the encrypted image, with the hope of discovering information about the original image. To evaluate the security of an image encryption scheme against noise attacks, an attacker may use various types of noise attacks to try to retrieve the original image.
For the current test, salt-and-pepper noise is utilized to assess the effectiveness of the image’s anti-noise capabilities. The noise gets its name from the fact that it randomly changes some pixels in the original image to either black or white, simulating the effect of random errors in the transmission. The mean square error (MSE) and the peak signal-to-noise ratio (PSNR) are widely used metrics for evaluating the robustness of an image encryption scheme against salt-and-pepper noise. The MSE measures the average squared difference between the original image and the decrypted image, while the PSNR measures the ratio of the maximum possible power of a signal to the power of the noise that corrupts the signal.
A lower MSE value indicates that the decrypted image is closer to the original image, whereas a higher PSNR value indicates that the decrypted image has less noise and is closer in quality to the original image. Therefore, these metrics are important indicators for measuring the ability of an encryption system to resist noise and maintain the quality of the image. These metrics are defined below [64]:
In this experiment, to evaluate the resilience of this algorithm over its ability to withstand noise, the “Lena” color image of dimension is subjected to different levels of added noise, specifically 0.001, 0.005, 0.01, and 0.05, as shown in Figure 17. Figure 17 illustrates that the proposed quantum image encryption scheme maintains the decrypted image’s clarity and recognizability, even when the image is affected by noise data. This finding indicates that the encryption scheme provides a high level of security and is capable of effectively resisting noise attacks.

Figure 17.
Decryption results from salt and pepper noise attack with densities of (a) 0.001, (b) 0.005, (c) 0.01, and (d) 0.05.
Moreover, Table 10 presents the experimental findings, which demonstrate that despite a decrease in the PSNR of the encrypted image following decryption in the presence of an attack, the decrypted image remains visually distinguishable. These results confirm the efficacy of the proposed scheme in effectively combating salt-and-pepper noise.

Table 10.
Noise attack analysis.
Occlusion Attack Analysis
In image encryption, occlusion attacks are used to compromise the integrity of an encrypted image, with the intention of impeding the decryption process or revealing its content [89]. The idea behind occlusion attacks is that by obscuring parts of the encrypted image, an adversary tries to decrypt an encrypted image by partially or completely obscuring some parts of the encrypted image. The adversary may perform this by covering parts of the image with opaque objects, adding random pixels or patterns, or using other techniques to mask parts of the image.
To counteract occlusion attacks, the proposed approach encrypts and decrypts the image of “Lena” subsequent to the loss of 1/16, 1/8, 1/4, and 1/2 of its information, respectively, as depicted in Figure 18.

Figure 18.
Occlusion attacks analysis results.
The findings presented in Figure 15 reveal that, despite considerable data loss from the encrypted image due to occlusion attacks, the decryption process can recover a substantial amount of the original information. These outcomes suggest that the designed quantum image encryption scheme is highly resistant to occlusion attacks.
4.3.5. Time Complexity Analysis
Time complexity plays a crucial role in determining the efficiency and performance of image encryption schemes. In image encryption schemes, time complexity refers to the measure of the computational time required to encrypt or decrypt an image and is typically expressed as a function of the size of the input image, which is represented by the number of pixels in the image [90,91].
The time consumption of the proposed quantum image encryption scheme primarily can be divided into two components: the time required for pixel-level substitution operations and the time needed for pixel-level permutation operations.
In the pixel-level substitution stage, the mean operation on any cropped row or column in the R, G, and B channels of the original image has a complexity of O(1); the complexity of the pre-iterate process, which is performed M times for the chosen hyperchaotic system, is O(n); the application of either the quantum logistic map or Lü system hyperchaotic systems requires a complexity of O(n2); the computational complexity associated with utilizing a Hadamard gate, followed by a CNOT gate, and then applying a ternary Toffoli quantum gate is O(n2); executing the quantum measurement operation incurs a time cost of O(n2). In the pixel-level permutation stage, using a hybrid of mixed multi-chaos hybrid maps and a two-dimensional quantum cellular automaton has a computational complexity of O(n2); a circular shift operation has a computational complexity of O(n). Based on this analysis, the computational complexity of the proposed quantum scheme is O(n2).
In addition, Table 11 showcases the performance of the proposed quantum encryption scheme in terms of execution time on a variety of standard images with different sizes. Table 12 compares the execution time of the proposed quantum encryption scheme with other relevant schemes considering the “Lena” image with dimensions of as an instance. According to the results listed in Table 12, the proposed scheme takes less time than the others, which means that the proposed scheme exhibits the highest encryption speed, which makes it a suitable candidate for deployment in encryption systems that require both fast communication and high security.

Table 11.
Execution time analysis.

Table 12.
Encryption speed comparison of proposed and recent encryption.
5. Conclusions
The efficiency and security of the quantum image encryption algorithm are enhanced by leveraging the properties of dynamics of hyperchaotic systems and quantum computation. This study introduces an efficacious and safe quantum image encryption scheme that is grounded on the utilization of quantum operations with hyper-chaos systems and a fusion of quantum cellular automata and mixed multi-chaos maps.
A stronger correlation between the plain image and the secret key can be achieved by computing the average of the first row/column of the original image. The presented scheme is essentially made up of two phases, which are pixel-level diffusion and pixel-level permutation. In this work, the emphasis of the diffusion process is on generating and encrypting superposition states using hyper-chaos systems and quantum operations. On the other hand, the confusion phase is conducted following the application of suitable measurements on the three diffused channels. Subsequently, a chaos row/column cyclic shift is applied to further modify the positions of the pixel values in the three diffused components of the image. These phases are explored in detail throughout this paper.
The scheme was implemented and analyzed with various parameters, such as key sensitivity and key space analyses. In addition, various statistical and differential analyses covering histograms, histogram variance, global entropy, Shannon entropy, correlation coefficients, NPCR and UACI, chosen/known-plaintext attacks, MSE, and PSNR are performed in this work.
Using these several tests and experiments, the security and robustness evaluation of the designed quantum image encryption scheme demonstrated its high sensitivity to even minor modifications in either the plain image or the secret key, and its resilience against various common attacks. It is characterized by computationally low cost. Moreover, the results of such analysis are compared with those of the existing scheme, which demonstrates that the proposed scheme works more effectively than the existing schemes.
Although the proposed scheme offers several advantages, there is still room for potential improvements in the future. It may be beneficial to provide a further combination of a novel enhanced quantum representation (NEQR) model for digital images with hyperchaotic systems. Another limitation of this study is that it may not be suitable for real-time applications due to it consuming long encryption and decryption time for the digital images with dimensions . In upcoming research, we aim to address these limitations and further improve the encryption scheme.
Author Contributions
Conceptualization, N.A.E.-S.M.; methodology, N.A.E.-S.M.; software, N.A.E.-S.M.; validation, N.A.E.-S.M.; formal analysis, N.A.E.-S.M.; investigation, N.A.E.-S.M.; resources, N.A.E.-S.M.; data curation, N.A.E.-S.M.; writing—original draft preparation, N.A.E.-S.M.; writing—review and editing, N.A.E.-S.M.; supervision, H.E.-S. and A.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- AbdElHaleem, S.H.; Abd-El-Hafiz, S.K.; Radwan, A.G. A generalized framework for elliptic curves based PRNG and its utilization in image encryption. Sci. Rep. 2022, 12, 13278. [Google Scholar] [CrossRef] [PubMed]
- Khalid, I.; Shah, T.; Eldin, S.; Shah, D.; Asif, M.; Saddique, I. An Integrated Image Encryption Scheme Based on Elliptic Curve. IEEE Access 2023, 11, 5483–5501. [Google Scholar] [CrossRef]
- Liu, Y.; Cen, G.; Xu, B.; Wang, X. Color Image Encryption Based on Deep Learning and Block Embedding. Secur. Commun. Netw. 2022, 2022, 6047349. [Google Scholar] [CrossRef]
- Liu, G.; Li, W.; Fan, X.; Li, Z.; Wang, Y.; Ma, H. An Image Encryption Algorithm Based on Discrete-Time Alternating Quantum Walk and Advanced Encryption Standard. Entropy 2022, 24, 608. [Google Scholar] [CrossRef]
- Rezai, A.; Aliakbari, D.; Karimi, A. Novel multiplexer circuit design in quantum-dot cellular automata technology. Nano Commun. Netw. 2023, 35, 100435. [Google Scholar] [CrossRef]
- Chen, X.; Gong, M.; Gan, Z.; Lu, Y.; Chai, X.; He, X. CIE-LSCP: Color image encryption scheme based on the lifting scheme and cross-component permutation. Complex Intell. Syst. 2023, 9, 927–950. [Google Scholar] [CrossRef]
- Wang, J.; Song, X.; El-Latif, A. Single-Objective Particle Swarm Optimization-Based Chaotic Image Encryption Scheme. Electronics 2022, 11, 2628. [Google Scholar] [CrossRef]
- Hua, W.; Dong, Y. Quantum color image encryption based on a novel 3D chaotic system. Appl. Phys. 2022, 131, 114402. [Google Scholar] [CrossRef]
- Tian, P.; Su, R. A Novel Virtual Optical Image Encryption Scheme Created by Combining Chaotic S-Box with Double Random Phase Encoding. Sensors 2022, 22, 5325. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Xu, M.; Li, X. A novel content-selected image encryption algorithm based on the LS chaotic model. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 8245–8259. [Google Scholar] [CrossRef]
- Abd-El-Atty, B.; Abd El-Latif, A.; Venegas-Andraca, S. An encryption protocol for NEQR images based on one-particle quantum walks on a circle. Quantum Inf. Process. 2019, 18, 272. [Google Scholar] [CrossRef]
- Mohamed, N.; El-Azeim, M.; Zaghloul, A. Improving Image Encryption Using 3D Cat Map and Turing Machine. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2016, 7, 208–215. [Google Scholar]
- Wang, P.; Wang, Y.; Xiang, J.; Xiao, X. Fast Image Encryption Algorithm for Logistics-Sine-Cosine Mapping. Sensors 2022, 22, 9929. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, N.; Zaghloul, A.; El-Azeim, M. Color Block Image Encryption Scheme based on Confusion—Diffusion Architecture. J. Inf. Assur. Secur. 2015, 10, 250–259. [Google Scholar]
- Mohamed, N.; Youssif, A.; El-Sayed, H. Fast and Robust Image Encryption Scheme Based on Quantum Logistic Map and Hyperchaotic System. Complexity 2022, 2022, 3676265. [Google Scholar] [CrossRef]
- Ullah, A.; Shah, A.; Khan, J.; Sajjad, M.; Boulila, W.; Akgul, A.; Masood, J.; Ghaleb, F.; Shah, S.; Ahmad, J. An Efficient Lightweight Image Encryption Scheme Using Multichaos. Secur. Commun. Netw. 2022, 2022, 5680357. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L.; Xiang, H. A Novel Plain-Text Related Image Encryption Algorithm Based on LB Compound Chaotic Map. Mathematics 2021, 9, 2778. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J. A cluster of 1D quadratic chaotic map and its applications in image encryption. Math. Comput. Simul. 2023, 204, 89–114. [Google Scholar] [CrossRef]
- Zang, H.; Tai, M.; Wei, X. Image Encryption Schemes Based on a Class of Uniformly Distributed Chaotic Systems. Mathematics 2022, 10, 1027. [Google Scholar] [CrossRef]
- Zhu, S.; Deng, X.; Zhang, W.; Zhu, C. Image Encryption Scheme Based on Newly Designed Chaotic Map and Parallel DNA Coding. Mathematics 2022, 11, 231. [Google Scholar] [CrossRef]
- Rong, X.; Jiang, D.; Zheng, M.; Yu, X.; Wang, X. Meaningful data encryption scheme based on newly designed chaotic map and P-tensor product compressive sensing in WBANs. Nonlinear Dyn. 2022, 110, 2831–2847. [Google Scholar] [CrossRef]
- Zhua, H.; Gea, J.; Qia, W.; Zhanga, X.; Lu, X. Dynamic analysis and image encryption application of a sinusoidal-polynomial composite chaotic system. Math. Comput. Simul. 2022, 198, 188–210. [Google Scholar] [CrossRef]
- Mondal, B.; Singh, S.; Kumar, P. A secure image encryption scheme based on cellular automata and chaotic skew tent map. J. Inf. Secur. Appl. 2019, 45, 117–130. [Google Scholar] [CrossRef]
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. Lightweight Image Encryption: Cellular Automata and the Lorenz System. In Proceedings of the 2021 International Conference on Microelectronics (ICM), IEEE, New Cairo City, Egypt, 19–22 December 2021. [Google Scholar]
- Wang, X.; Guan, N.; Zhao, H.; Wang, S.; Zhang, Y. A new image encryption scheme based on coupling map lattices with mixed multi-chaos. Sci. Rep. 2020, 10, 9784. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S. A Quantum Image Encryption Method Based on DNACNot. IEEE Access 2020, 8, 178336–178344. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D.; Liu, C. Three-level quantum image encryption based on Arnold transform and logistic map. Quantum Inf. Process. 2021, 20, 23. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, J.; Lei, H.; Zhou, Y.; Shi, W. Novel quantum image encryption using one-dimensional quantum cellular automata. Inf. Sci. 2016, 345, 257–270. [Google Scholar] [CrossRef]
- Khan, M.; Waseem, H. A novel image encryption scheme based on quantum dynamical spinning and Rotations. PLoS ONE 2018, 13, e0206460. [Google Scholar] [CrossRef]
- Khan, M.; Rasheed, A. A fast quantum image encryption algorithm based on affine transform and fractional-order Lorenz-like chaotic dynamical system. Quantum Inf. Process. 2022, 21, 134. [Google Scholar] [CrossRef]
- Wang, H.-K.; Xu, G.-B.; Jiang, D.-H. Quantum grayscale image encryption and secret sharing schemes based on Rubik’s Cube. Phys. A Stat. Mech. Its Appl. 2023, 612, 128482. [Google Scholar] [CrossRef]
- Sedik, A.; Abd El-Latif, A.; Wani, M.; Abd El-Samie, F.; Bauomy, N.; Hashad, F. Efficient Multi-Biometric Secure-Storage Scheme Based on Deep Learning and Crypto-Mapping Techniques. Mathematics 2023, 11, 703. [Google Scholar] [CrossRef]
- Ma, Y.; Li, N.; Zhang, W.; Wang, S.; Ma, H. Image encryption scheme based on alternate quantum walks and discrete cosine transform. Opt. Express 2021, 29, 28338–28351. [Google Scholar] [CrossRef] [PubMed]
- Abdelfatah, R. Quantum Image Encryption Using a Self-Adaptive Hash Function-Controlled Chaotic Map (SAHF-CCM). IEEE Access 2022, 10, 107152–107169. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, S. Image encryption scheme based on a controlled zigzag transform and bit-level encryption under the quantum walk. Front. Phys. 2023, 10, 1097754. [Google Scholar] [CrossRef]
- Hyperchaos. Available online: http://www.scholarpedia.org/article/Hyperchaos (accessed on 20 May 2023).
- Yadav, N.P.; Handa, H. Projective synchronization for a new class of chaotic/hyperchaotic systems with and without parametric uncertainty. Trans. Inst. Meas. Control. 2023, 45, 1975–1985. [Google Scholar] [CrossRef]
- Singh, J.; Roy, B. 5-D Hyperchaotic and Chaotic Systems with Non-hyperbolic Equilibria and Many Equilibria. In Nonlinear Dynamical Systems with Self-Excited and Hidden Attractors, Studies in Systems, Decision and Control, 1st ed.; Pham, V.-T., Volos, C.S., Kapitaniak, T., Eds.; Springer: Warsaw, Poland, 2018; Volume 133, pp. 465–497. [Google Scholar]
- Zhang, J.; Xu, L. A novel asymmetrical double-wing hyperchaotic system with multiple different attractors: Application to finite-time synchronization and image encryption. Multimed. Tools Appl. 2023, 82, 37503–37527. [Google Scholar] [CrossRef]
- Zhong, M.; Yan, Z. Data-driven forward and inverse problems for chaotic and hyperchaotic dynamic systems based on two machine learning architectures. Phys. D Nonlinear Phenom. 2023, 446, 133656. [Google Scholar] [CrossRef]
- Yang, J.; Feng, Z.; Liu, Z. A New Five-Dimensional Hyperchaotic System with Six Coexisting Attractors. Qual. Theory Dyn. Syst. 2021, 20, 18. [Google Scholar] [CrossRef]
- Lu, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Lai, Q.; Norouzi, B.; Liu, F. Dynamic analysis, circuit realization, control design and image encryption application of an extended Lü system with coexisting attractors. Chaos Solitons Fractals 2018, 114, 230–245. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N. On differences and similarities in the analysis of Lorenz, Chen, and Lu systems. Appl. Math. Comput. 2015, 256, 334–343. [Google Scholar] [CrossRef]
- Chena, A.; Lua, J.; Lü, J.; Yu, S. Generating hyperchaotic Lu¨ attractor via state feedback control. Phys. A Stat. Mech. Its Appl. 2006, 364, 103–110. [Google Scholar] [CrossRef]
- Ye, G.; Jiao, K.; Huang, X. Quantum logistic image encryption algorithm based on SHA-3 and RSA. Nonlinear Dyn. 2021, 104, 2807–2827. [Google Scholar] [CrossRef]
- Ye, G.; Jiao, K.; Huang, X.; Goi, B.-M.; Yap, W.-S. An image encryption scheme based on public key cryptosystem and quantum logistic map. Sci. Rep. 2020, 10, 21044. [Google Scholar] [CrossRef] [PubMed]
- All about Hadamard Gates. Available online: https://freecontent.manning.com/all-about-hadamard-gates/ (accessed on 26 May 2023).
- Hadamard Gate. Available online: https://www.sciencedirect.com/topics/engineering/hadamard-gate (accessed on 26 May 2023).
- Young, R.; Birch, P.; Chatwin, C. Coherent optical implementations of the fast Fourier transform and their comparison to the optical implementation of the quantum Fourier transform. In Proceedings of the SPIE—The International Society for Optical Engineering, Baltimore, MD, USA, 29 April–3 May 2013. [Google Scholar]
- Miranda, E.; Miller-Bakewell, H. Cellular Automata Music Composition: From Classical to Quantum. In Quantum Computer Music, 1st ed.; Miranda, E.R., Ed.; Springer: Plymouth, UK, 2022; pp. 105–130. [Google Scholar]
- A Review of Quantum Cellular Automata. Available online: https://quantum-journal.org/papers/q-2020-11-30-368/ (accessed on 26 May 2023).
- Wiesner, K. Quantum Cellular Automata. In Encyclopedia of Complexity and Systems Science, 1st ed.; Meyers, R., Ed.; Springer: New York, NY, USA, 2009; Volume 18, pp. 7154–7164. [Google Scholar]
- Mfungo, D.; Fu, X.; Xian, Y.; Wang, X. A Novel Image Encryption Scheme Using Chaotic Maps and Fuzzy Numbers for Secure Transmission of Information. Appl. Sci. 2023, 13, 7113. [Google Scholar] [CrossRef]
- Kari, A.; Navin, A.; Bidgoli, A.; Mirnia, M. A new image encryption scheme based on hybrid chaotic maps. Multimed. Tools Appl. 2020, 80, 2753–2772. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Cryptography Bell System Technical Memo MM; Alcatel-Lucent: Paris, France, 1945. [Google Scholar]
- Liu, W.; Xu, Y.; Liu, W.; Wang, H.; Lei, Z. Quantum Searchable Encryption for Cloud Data Based on Full-Blind Quantum Computation. IEEE Access 2019, 7, 186284–186295. [Google Scholar] [CrossRef]
- CVG-UGR-Image Database. Available online: https://ccia.ugr.es/cvg/dbimagenes/ (accessed on 14 February 2023).
- The USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/ (accessed on 14 February 2023).
- Li, N.; Xie, S.; Zhang, J. A Color Image Encryption Algorithm Based on Double Fractional Order Chaotic Neural Network and Convolution Operation. Entropy 2022, 24, 933. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Enginoğlu, S.; Akbacak, E.; Thanh, D. An image encryption scheme based on chaotic logarithmic map and key generation using deep CNN. Multimed. Tools Appl. 2022, 81, 7365–7391. [Google Scholar] [CrossRef]
- Sun, M.; Cui, W.; Tao, Y.; Shi, T. Chaotic Color Image Encryption Algorithm Based on RNA Operations and Heart Shape Chunking. IAENG Int. J. Comput. Sci. 2023, 50, 1–14. [Google Scholar]
- Shen, Y.; Huang, J.; Chen, L.; Wen, T.; Li, T.; Zhang, G. Fast and Secure Image Encryption Algorithm with Simultaneous Shuffling and Diffusion Based on a Time-Delayed Combinatorial Hyperchaos Map. Entropy 2023, 25, 753. [Google Scholar] [CrossRef]
- Hua, N.; Liu, H.-Y.; Xiong, X.-Y.; Wang, J.-L.; Lian, J.-Q. A Dynamic Image Encryption Scheme Based on Quantum Walk and Chaos-Induced DNA. Quantum Eng. 2023, 2023, 3431107. [Google Scholar] [CrossRef]
- Aouissaoui, I.; Bakir, T.; Sakly, A. Robustly correlated key-medical image for DNA-chaos based encryption. IET Image Process. 2021, 15, 122770–122786. [Google Scholar] [CrossRef]
- Zhuang, Z.; Wang, J.; Liu, J.; Yang, D.; Chen, S. A New Digital Image Encryption Algorithm Based on Improved Logistic Mapping and Josephus Circle. J. Comput. Commun. 2018, 6, 31–44. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Chen, L.; Yu, K.; Gao, Y.; Ma, Y. An Image Encryption Scheme Based on Logistic Quantum Chaos. Entropy 2022, 24, 251. [Google Scholar] [CrossRef] [PubMed]
- Alexan, W.; Elkandoz, M.; Mashaly, M.; Azab, E.; Aboshousha, A. Color Image Encryption Through Chaos and KAA Map. IEEE Access 2023, 11, 11541–11554. [Google Scholar] [CrossRef]
- Jirjees, S.; Alkalid, F.; Shareef, W. Image Encryption Using Dynamic Image as a Key Based on Multilayers of Chaotic Permutation. Symmetry 2023, 15, 409. [Google Scholar] [CrossRef]
- Daoui, A.; Yamni, M.; Chelloug, S.; Wani, M.; Abd El-Latif, A. Efficient Image Encryption Scheme Using Novel 1D Multiparametric Dynamical Tent Map and Parallel Computing. Mathematics 2023, 11, 1589. [Google Scholar] [CrossRef]
- Kitio, G.; Fanda, A.; Feulefack, I.; Pone, J.; Kengne, R.; Tiedeu, A. Biomedical Image Encryption with a Novel Memristive Chua Oscillator Embedded in a Microcontroller. Braz. J. Phys. 2023, 53, 56. [Google Scholar] [CrossRef]
- Shafique, A.; Mehmood, A.; Elhadef, M.; Khan, K. A lightweight noise-tolerant encryption scheme for secure communication: An unmanned aerial vehicle application. PLoS ONE 2022, 17, e0273661. [Google Scholar] [CrossRef]
- Lu, Q.; Yu, L.; Zhu, C. Symmetric Image Encryption Algorithm Based on a New Product Trigonometric Chaotic Map. Symmetry 2022, 14, 373. [Google Scholar] [CrossRef]
- Abd El-Latif, A.; Ramadoss, J.; Abd-El-Atty, B.; Khalifa, H.; Nazarimehr, F. A Novel Chaos-Based Cryptography Algorithm and Its Performance Analysis. Mathematics 2022, 10, 2434. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C.; Yan, H. Cryptanalyzing and Improving an Image Encryption Algorithm Based on Chaotic Dual Scrambling of Pixel Position and Bit. Entropy 2023, 25, 400. [Google Scholar] [CrossRef]
- Abd-El-Atty, B.; ElAffendi, M.; Abd El-Latif, A. A novel image cryptosystem using gray code, quantum walks, and Henon map for cloud applications. Complex Intell. Syst. 2022, 9, 609–624. [Google Scholar] [CrossRef]
- Shraida, G.; Younis, H.; Al-Amiedy, T.; Anbar, M.; Younis, H.; Hasbullah, I. An Efficient Color-Image Encryption Method Using DNA Sequence and Chaos Cipher. Comput. Mater. Contin. 2023, 75, 2641–2654. [Google Scholar] [CrossRef]
- Alli, P.; Peter, J. Three Tier Framework Iris Authentication for Secure Image Storage and Communication. Theor. Appl. Inf. Technol. 2023, 101, 2498–2516. [Google Scholar]
- Song, X.; Chen, G.; Abd El-Latif, A. Quantum Color Image Encryption Scheme Based on Geometric Transformation and Intensity Channel Diffusion. Mathematics 2022, 10, 3038. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Li, B.; Banerje, S.; Sun, B. Multi-Image Hybrid Encryption Algorithm Based on Pixel Substitution and Gene Theory. Fractals 2023, 31, 2340111. [Google Scholar] [CrossRef]
- Zheng, J.; Bao, T. An Image Encryption Algorithm Using Cascade Chaotic Map and S-Box. Entropy 2022, 24, 1827. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Du, H.; Huang, D. A Quantum Image Encryption Algorithm Based on The Feistel Structure. Quantum Inf. Process. 2022, 21, 20. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Q.; Fan, L.; Yu, S. A Novel Chaotic Image Encryption Scheme Armed with Global Dynamic Selection. Entropy 2023, 25, 476. [Google Scholar] [CrossRef] [PubMed]
- Man, X.; Song, Y. Encryption of Color Images with an Evolutionary Framework Controlled by Chaotic Systems. Entropy 2023, 25, 631. [Google Scholar] [CrossRef]
- Gao, X.; Miao, M.; Chen, X. Multi-Image Encryption Algorithm for 2D and 3D Images Based on Chaotic System. Front. Phys. 2022, 10, 901800. [Google Scholar] [CrossRef]
- Alawida, M.; Teh, J.S.; Alshoura, W.H. A New Image Encryption Algorithm Based on DNA State Machine for UAV Data Encryption. Drones 2023, 7, 38. [Google Scholar] [CrossRef]
- Huo, D.; Zhu, Z.; Zhou, X.; Wei, L.; Bai, X.; Bai, Y.; Han, C. A flexible and visually meaningful multi-image compression, encryption and hiding scheme based on 2D compressive sensing. Heliyon 2023, 9, e14072. [Google Scholar] [CrossRef]
- Neamah, A. An image encryption scheme based on a seven-dimensional hyperchaotic system and Pascal’s matrix. J. King Saud Univ.—Comput. Inf. Sci. 2023, 35, 3238–3248. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, S.; Zhang, L. Block Image Encryption Algorithm Based on Novel Chaos and DNA Encoding. Information 2023, 14, 150. [Google Scholar] [CrossRef]
- Liang, J.; Song, Z.; Sun, Z.; Lv, M.; Ma, H. Coupling Quantum Random Walks with Long- and Short-Term Memory for High Pixel Image Encryption Schemes. Entropy 2023, 25, 353. [Google Scholar] [CrossRef]
- Ma, Y.; Yu, F.-F.; Gong, L.-H.; Zou, W.-P. Fast quantum image encryption scheme based on multilayer short memory fractional order Lotka-Volterra system and dual-scale triangular map. Front. Phys. 2022, 10, 1001. [Google Scholar] [CrossRef]
- Khan, S.; Han, L.; Mudassir, G.; Guehguih, B.; Ullah, H. 3C3R, an Image Encryption Algorithm Based on BBI, 2D-CA, and SM-DNA. Entropy 2019, 21, 1075. [Google Scholar] [CrossRef]
- Iqbal, N.; Hanif, M.; Abbas, S.; Khan, M.; Almotiri, S.; Al Ghamd, M. DNA Strands Level Scrambling Based Color Image Encryption Scheme. IEEE Access 2020, 8, 178167–178182. [Google Scholar] [CrossRef]
- Yang, C.; Taralova, I.; El Assad, S.; Loiseau, J.-J. Image encryption based on fractional chaotic pseudo-random number generator and DNA encryption method. Nonlinear Dyn. 2022, 109, 2103–2127. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).