Unsupervised Deep Learning Approach for Characterizing Fractality in Dried Drop Patterns of Differently Mixed Viscum album Preparations

Abstract

This paper presents a novel unsupervised deep learning methodology for the analysis of self-assembled structures formed in evaporating droplets. The proposed approach focuses on clustering these structures based on their texture similarity to characterize three different mixing procedures (turbulent, laminar, and diffusion-based) applied to produce Viscum album Quercus ${10}^{-3}$ according to the European Pharmacopoeia guidelines for the production of homeopathic remedies. Texture clustering departs from obtaining a comprehensive texture representation of the full texture patch database using a convolutional neural network. This representation is then dimensionally reduced to facilitate clustering through advanced machine learning techniques. Following this methodology, 13 clusters were found and their degree of fractality determined by means of Local Connected Fractal Dimension histograms, which allowed for characterization of the different production modalities. As a consequence, each image was represented as a vector in ${\mathbb{R}}^{13}$, enabling classification of mixing procedures via support vectors. As a main result, our study highlights the clear differences between turbulent and laminar mixing procedures based on their fractal characteristics, while also revealing the nuanced nature of the diffusion process, which incorporates aspects from both mixing types. Furthermore, our unsupervised clustering approach offers a scalable and automated solution for analyzing the databases of evaporated droplets.

1. Introduction

Computerized microscopy image analysis is crucial in various fields, including materials science, pathology, drug discovery, and biomedical research [1]. However, this field faces challenges due to data complexity, as microscopic images contain intricate structures that require advanced analysis methods [2]. Traditional approaches, such as manual annotation [3], morphological operations [4], segmentation techniques [5], and feature extraction using descriptors [6], heavily rely on human intervention, leading to subjectivity and limited adaptability [7,8,9]. Nevertheless, recent advances in computer vision and deep learning have significantly impacted microscopic image analysis, providing more automated and accurate approaches for processing and interpretation [1,10]. In pharmaceutical research, microscopic image analysis is essential for examining pharmaceutical extracts and understanding their properties and quality [11]. The Droplet Evaporation Method (DEM) is a notable method used for this purpose, involving the deposition of a liquid sample onto a surface and studying patterns formed in the droplet residues dried under controlled conditions [12,13]. Recent work [14] revealed significant differences in DEM patterns of pharmaceutical preparations with varying mixing procedures, emphasizing the importance of precise mixing control to ensure product quality and stability [15]. In many studies, DEM images were analyzed exclusively through visual evaluation [16]. To improve this, researchers have introduced the use of fractal descriptors [17,18,19,20], GLCM properties [21], Gabor filters [22], and Fourier transform (FT) [23] for texture feature extraction. Notably, deep learning models, especially convolutional neural networks (CNNs), have shown remarkable capabilities in capturing and learning complex patterns and features from microscopic images, including textures [24].

In a previous study [25], we proposed a semi-supervised deep learning-based methodology for analyzing three different mixing procedures (turbulent, laminar, and diffusion-based) used to produce Viscum album Quercus ${10}^{-3}$ according to the European Pharmacopoeia guidelines for homeopathic remedies [26]. This approach was based on the clustering of full texture patches with a texture similarity criterion. The mixing procedure characterization was restricted to three clusters since each procedure was used as an input to the Dense Convolutional Neural Network (DenseNet) architecture. An approach to overcome this restriction is unsupervised deep learning clustering [27], one of which implements clustering algorithms on coded texture representations obtained as a result of the hierarchical processing of a CNN model [28]. To create these deep texture representations, a pre-trained CNN model, such as VGGNet, ResNet, or InceptionNet, is trained on a large-scale dataset (e.g., ImageNet). Although the CNN model is initially trained for a classification task, it can be reused for other purposes, such as texture representation [29].

In this paper, we propose a novel unsupervised deep learning methodology for clustering DEM patterns obtained from differently produced Viscum album Quercus ${10}^{-3}$ dilution variants [14]. With the aim of characterizing the mixing modalities used to produce pharmaceutical extracts, we propose a method based on Regions of Interest (ROI) analysis through four stages. The first stage consists of the automatic selection of patches that present a rich texture along the database. In the second stage, a Deep Texture Representation (DTR) of each patch is obtained through the processing of the convolutional neural network architecture VGG-19. During the third stage, the deep texture representations undergo dimensionality reduction through Principal Component Analysis (PCA) to cluster similar textures using hierarchical clustering. Finally, outliers are re-clustered by the Dense Convolutional Neural Network (DenseNet) in the fourth stage. This scheme allowed us to automatically identify and discriminate thirteen clusters of patches that share texture similarity in the DEM image database. Once the patches were clustered, we verified their fractal degree using Local Connected Fractal Dimension (LCFD) histograms. In addition, with this clustering methodology we were able to determine image patch composition for the purposes of classifying the three mixing procedures via support vector machines.

2. Materials and Methods

The utilization of plants in this study adheres to international institutional guidelines. The Viscum album Quercus extract used for DEM experimentation was obtained from ISCADOR AG in Arlesheim, Switzerland. Viscum album L. was collected from Quercus robur plants growing in their natural habitats in Switzerland, which belonged to ISCADOR AG; hence, no harvesting permission was required. The plants were identified by Mirio Grazi from the Society for Cancer Research in Arlesheim, Switzerland. A voucher specimen (C.H. Quaresma 18.329) was deposited at the Herbarium of the Faculdade de Formação de Professores, Universidade Estadual do Rio de Janeiro, Brazil. Viscum album preparations are used in medicine, including as supportive treatment for cancer [30,31,32].

The DEM image database analyzed here was generously provided by the Society for Cancer Research, Arlesheim, Switzerland under a data-sharing agreement. This valuable database, as detailed in reference [25], consists of 606 images in resolution of 960 × 720 pixels. These images were obtained using the droplet evaporation method applied to analyze three Viscum album Quercus ${10}^{-3}$ (VAQ) dilution variants produced using the following different mixing procedures:

1

Turbulent Flow (Variant T): The mixing process involves using a machine to apply vertical strokes. This set comprises a total of 206 images.

2

Laminar Flow (Variant L): The mixing process is carried out manually, inducing a sequence of vortex-like flows. This set comprises a total of 196 images.

3

Diffusion Control (Variant D): This set, consisting of 204 images, represents the control variant where the mixture remains as undisturbed as possible, relying on diffusion processes for dilution.

The Rolling Ball and Sliding Paraboloid technique was employed for background removal in all the images. This involved calculating a local background value for each pixel by averaging it over a large surrounding ball. Subsequently, this calculated value was subtracted from the original image, effectively eliminating significant spatial variations in background intensities [33]. This approach successfully reduced glare effects commonly observed in microscopic images due to their physical characteristics. It is worth noting that the database used for this process did not include images with saturated or blurred conditions, as these conditions could potentially reduce the model’s ability to distinguish textures.

The proposed DEM image texture analysis method is shown in the flowchart of Figure 1. The next sections of this paper are organized in accordance with the flowchart as follows: first, we explain our method for automatic full texture patch selection; the codified texture information obtained by CNN is described later; then, the clustering process is detailed in the last two stages; in the last sections, we provide characterization and classification results, as well as a discussion and concluding remarks.

2.1. Automatic Full Texture Patch Selection

When encoding texture information through a CNN for a specific dataset, such as the VAQ database, it is important to consider regions of interest that exhibit full texture. This ensures that the network learns from all relevant image information and prevents biased learning, resulting in a more balanced and complete understanding of the data. To this end, we use the full texture patch selection method previously developed in [25], which consists of selecting patches of size 128 × 128 pixels that correspond to 108.4 × 108.4 μm to then undergo skewness analysis and PCA outlier removal to define patches observing full texture. Automatic selection of full texture patches (Stage 1) led to the formation of the patch database, containing 705 patches from each mixing procedure (D, diffusion control; T, turbulent flow; L, laminar flow), being used as inputs for the proposed unsupervised methodology in this paper. It is important to mention that our technique is not restricted to 128 × 128 size patches. Depending on hardware capabilities, larger sizes such as 256 × 256 and 512 × 512 could also be used.

2.2. Deep Texture Representation Using Convolutional Neural Network

The deep texture representation (DTR) used in this paper borrows ideas from [34], in which the texture encoding of the patch database was obtained through the sequential processing of the VGG-19 architecture, exhibiting advantages over other architectures. As VGG-19 was previously trained on large-scale Imagenet datasets for object recognition, it provides a wide variety of convolutional primitives for generalizing texture patterns. It is important to note that we did not train or fine-tune VGG-19 using the Viscum album dataset, as our aim was to obtain DTR from every image patch using the already-computed parameters and weights of VGG-19.

A linearly rectified convolution, with filters of size 3 × 3 and a maximum pooling in non-overlapping regions of 2 × 2, was used for the two fundamental computations of the used architecture. The deep texture representation was obtained by applying these computations in an alternating manner throughout five convolutions. Since the number of feature maps is doubled after the third pooling layer, the dimension of the DRT is 512 × 512. A schematic overview of the network process for obtaining the DRT is provided in Figure 2.

As the deep texture representation is obtained using the VGG-19 CNN architecture, the generated model provides a stationary description that fully specifies the texture of the input patches. This DTR matrix is the representation used for texture clustering purposes.

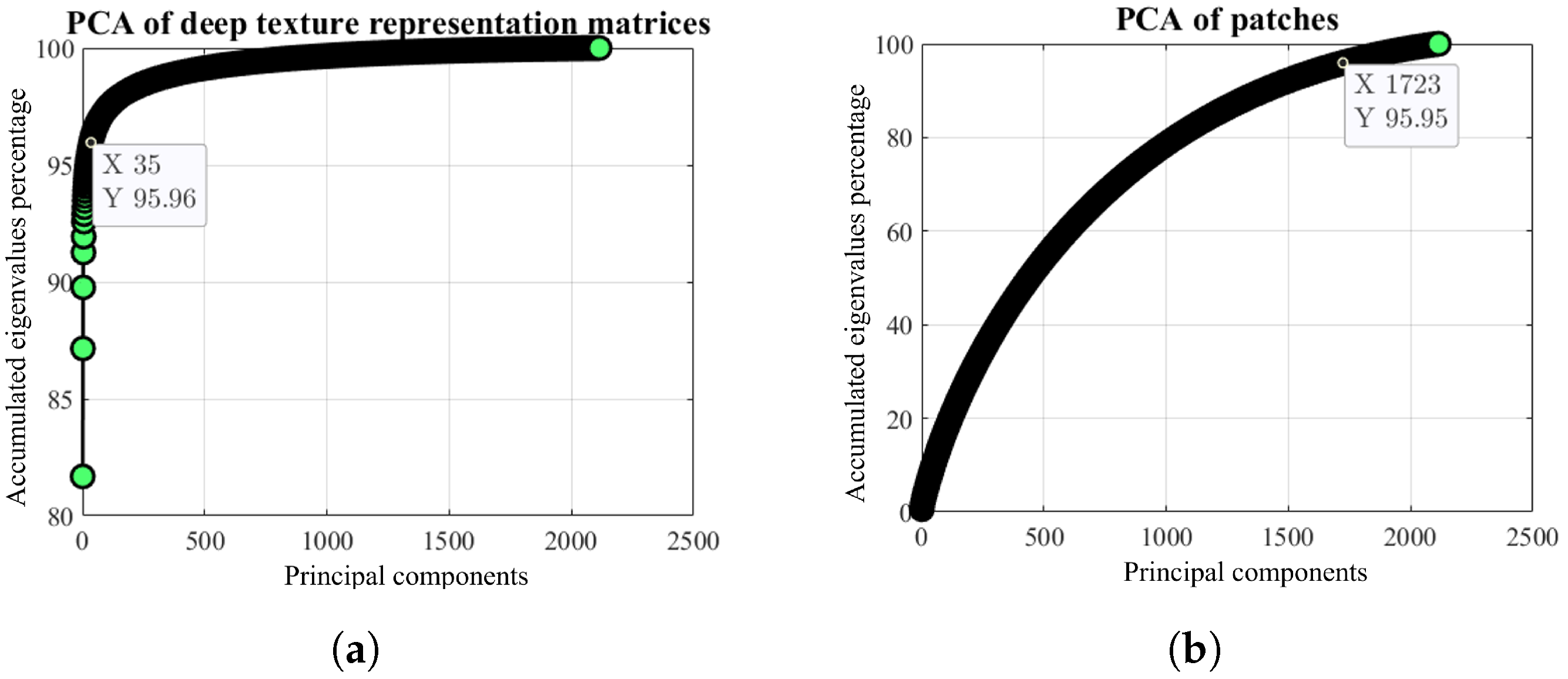
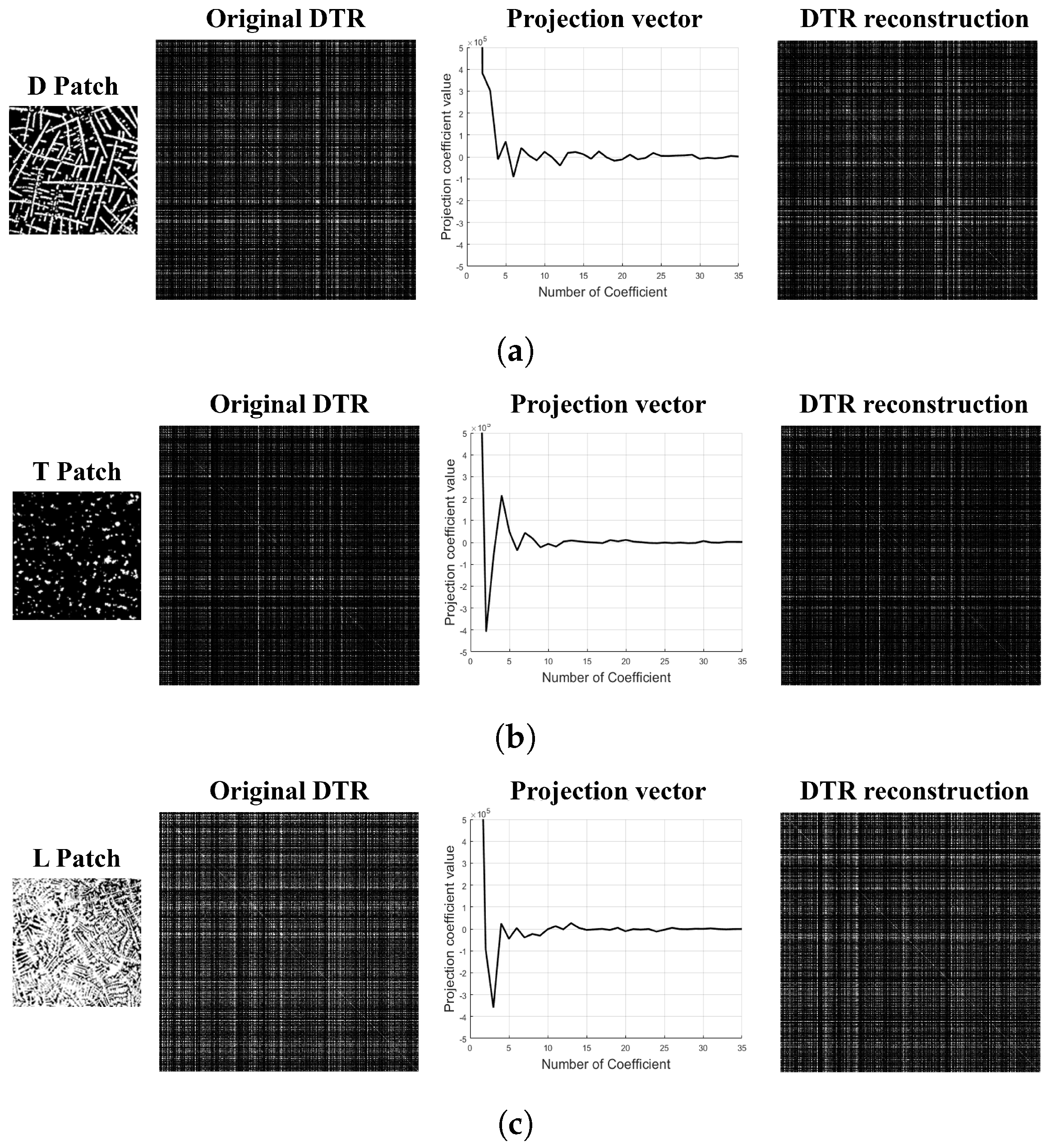
2.3. Dimensionality Reduction of the Deep Texture Representation

Since the dimension of the deep texture representation ($512\times 512$) is not tractable for clustering algorithms, dimensionality reduction is required. To this end, we performed a principal component analysis (PCA) of the DTR matrices database. Subsequently, we used DTR matrices to construct the training set data matrix, ${\mathbf{T}}_{k\times n}=[{\mathbf{t}}_{k,1}\mid {\mathbf{t}}_{k,2}\mid \cdots \mid {\mathbf{t}}_{k,n}]$, where $n=2115$ (705 patches for each mixing procedure) is the number of patches and $k=512\times 512=262,144$ is the number of texture values encoded in each DTR matrix. The differences from the average $\overline{\mathbf{t}}$ are used to build the centered training data matrix ${\overline{\mathbf{T}}}_{k\times n}=[({\mathbf{t}}_1-\overline{\mathbf{t}})\mid ({\mathbf{t}}_2-\overline{\mathbf{t}})\mid \cdots \mid ({\mathbf{t}}_n-\overline{\mathbf{t}})]$. The covariance matrix is calculated as ${\mathbf{\Sigma }}_{n\times n}={\overline{\mathbf{T}}}^T\overline{\mathbf{T}}$. Given that $\mathbf{\Sigma }$ is symmetric, there always exists an orthogonal basis ${\mathbf{U}}_{n\times n}$ and a diagonal matrix ${\mathbf{\Lambda }}_{n\times n}$ that satisfies the relationship $\mathbf{\Sigma }=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^T$, where ${\mathbf{U}}_{n\times n}$ is the eigenvector matrix and the eigenvalues of $\mathbf{\Sigma }$ are the diagonal elements of matrix $\mathbf{\Lambda }$.

Figure 3a shows that, with 35 components, the PCA model constructed from the DRT matrices achieves 95.96% variability. In contrast, Figure 3b shows that the PCA constructed directly from the pixel information of the patches (i.e., $k=128\times 128$ = 16,384) requires 1723 components to achieve 95.95% of the variability. This indicates that the variables in the DTR matrices are highly correlated and, therefore, can be effectively represented by a few principal components. We selected $l=35$ principal components based on the variability achieved by the DTR model (see Figure 3a). The texture encoded information of the DTR matrices in the column space of U is given by ${\mathbf{A}}_{k\times l}={\mathbf{T}}_{k\times n}{\widehat{\mathbf{U}}}_{n\times l}{\mathbf{\Lambda }}_{l\times l}^{-1}$. The dimensionality reduction is defined by the orthogonal projection of the centered matrix $\overline{\mathbf{T}}$ in the column space of $\mathbf{A}$ by the expression ${\widehat{\mathbf{T}}}_{l\times n}={\mathbf{A}}_{k\times l}^T{\overline{\mathbf{T}}}_{k\times n}$. This expression allows movement from a dimension k = 262,144 $(512\times 512)$ to a reduced-dimension space $l=35$, which will facilitate, in the context of computational efficiency, the grouping of textures by means of hierarchical clustering.

Figure 4 shows the DTR matrices from representative patches of DEM images from differently mixed VAQ variants, as well as their respective reconstructions through the 35-dimensional PCA model.

It is possible to notice that the coded information is denser in patch L (see Figure 4c) compared to patch T (see Figure 4b), which is in agreement with the visual information of each patch.

2.4. DTR Clusterization in the Reduced-Dimension Space

In order to cluster projections of DTR matrices on the reduced space, we used the hierarchical clustering algorithm [35] since it provides reproducible results and is not limited to the spheroidal shape of the data [36]. However, because the algorithm is sensitive to outliers [37], PCA outlier removal was performed before clustering.

By analyzing the first 35 principal components, 369 outliers were extracted considering a standard deviation of 2, and the remaining 1746 patches (textures) were clustered. In other words, we used the matrix ${\widehat{\mathbf{T}}}_{l\times n-m}$ as input to the hierarchical clustering, where m corresponds to the 369 outliers and $l=35$ is the encoded texture information represented in the reduced-dimension space.

The number of clusters was determined through the elbow method [38] which iterates over the number of clusters and obtains the intra-cluster variance of each iteration. The optimal number of clusters for our database was 13, i.e., beyond that point (see Figure 5a), increasing the number of clusters did not lead to a significant reduction in the distortion score. Clustering results are presented in Figure 5b as a distribution of patches along the 13 clusters. The orange portion of the bars indicates the number of patches that are considered outliers based on the analysis of their principal components. In total, 925 outliers were extracted, 369 before hierarchical clustering and 556 after; the latter can be attributed to the inherent limitations of the hierarchical clustering algorithm, primarily due to its reliance on the Euclidean distance metric and its proximity-based clustering approach. In certain cases, if an outlier is in close proximity to a cluster, it may be merged with that cluster, even if it does not exhibit significant similarity with the majority of data points [39].

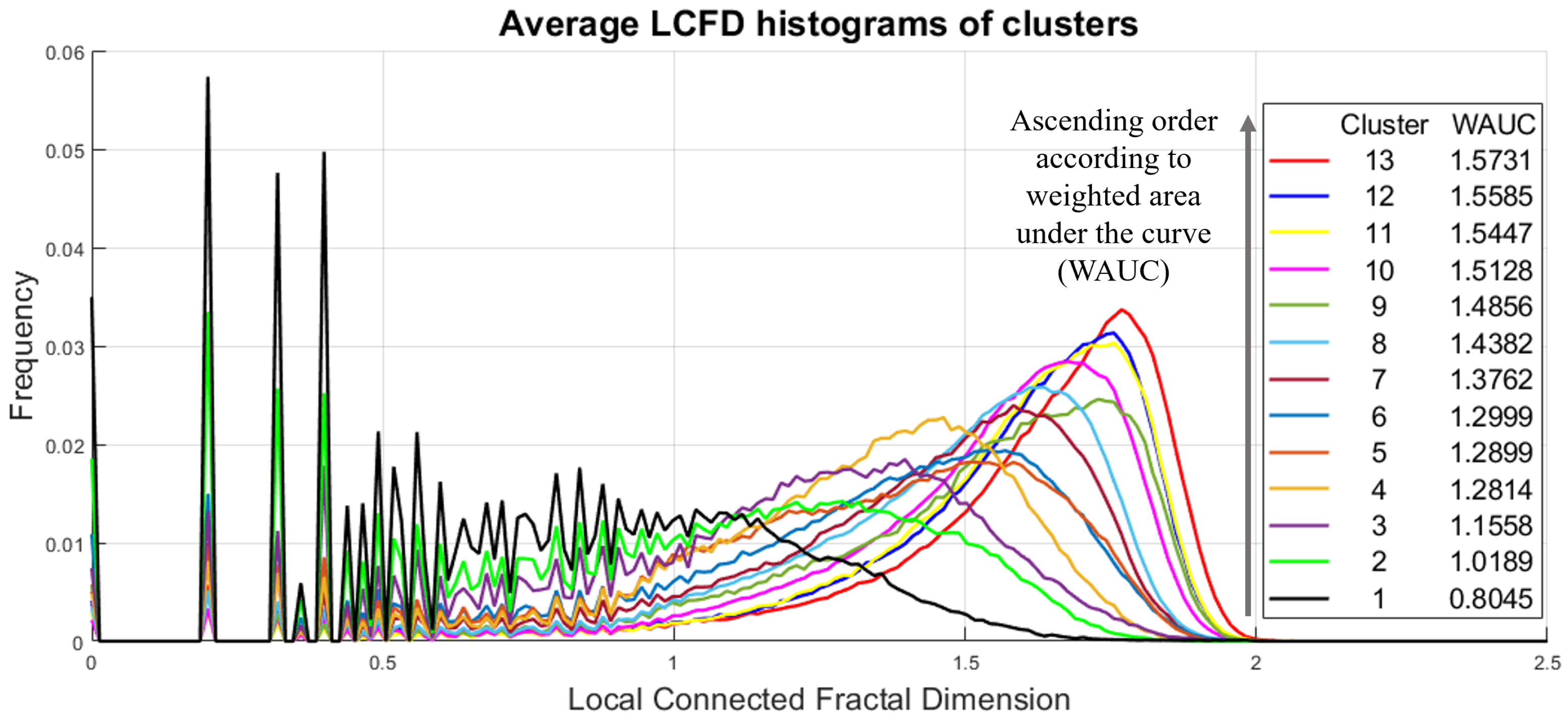
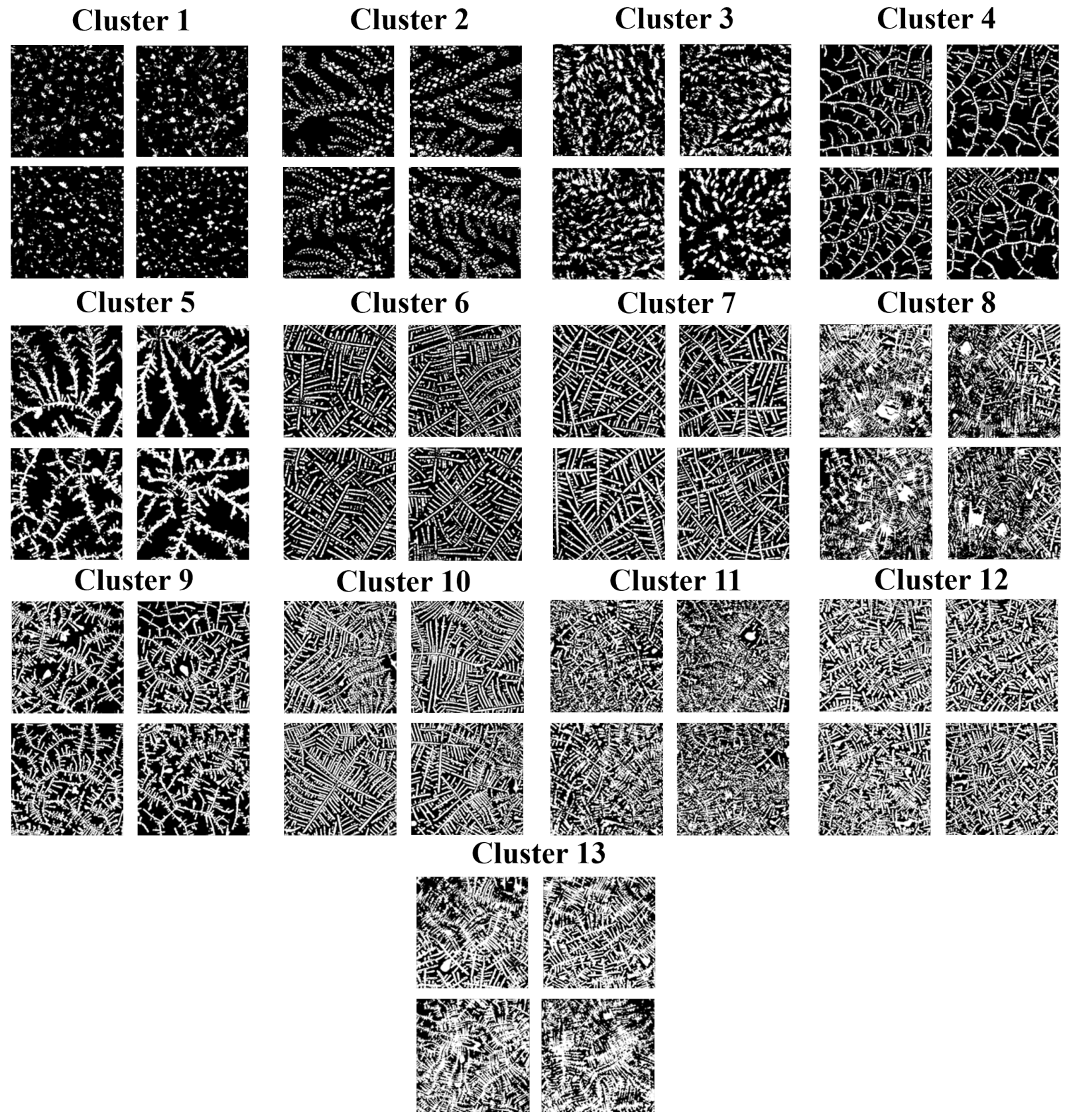
2.5. Clustering Refinement

To finally determine the cluster each outlier belonged to, we proposed a clustering refinement stage based on a Dense Convolutional Network architecture DenseNet121 [40]. The training dataset consisted of patches of the 13 outlier-free clusters (black bars in Figure 5b). With the aim of reducing learning bias, we trained DenseNet121 with the same number of samples per cluster by increasing the training database through 5 rotations: 30°, 60°, 90°, 120°, and 150°. Since cluster 7 was the one with the lowest number of patches, it limited data augmentation for the rest of clusters, which were randomly selected until the same number of patches as (augmented) cluster 7 was achieved.

Testing data consisted of the outliers, which were reorganized into the 13 clusters using the DenseNet121 architecture. The results presented in Figure 6 show that, after clustering refinement, there was a significant reduction in the number of final outliers, having only 31, representing 1.46% of the total patch database, revealing increased cluster cohesiveness after clustering refinement.

To assess the fractality of each cluster, we calculated the weighted area under the curve (WAUC) of the average LCFD histogram for each cluster, as illustrated in Figure 7. In other words, WAUC was obtained as a result of the inner product of the frequency and the Local Connected Fractal Dimension for each of the 13 average LCFD histograms. This enabled us to arrange the clusters in ascending order based on their fractality degree.

In Figure 8 we present patch samples of each cluster, in ascending order according to their degree of fractality. It is noteworthy that each cluster can be visually differentiated. In the samples of cluster 1, there is a great dispersion of the particles; in clusters 6 and 7, the particles are joining to generate structures that determine a greater fractality; and in the last clusters, complex patterns with intricate details are observed.

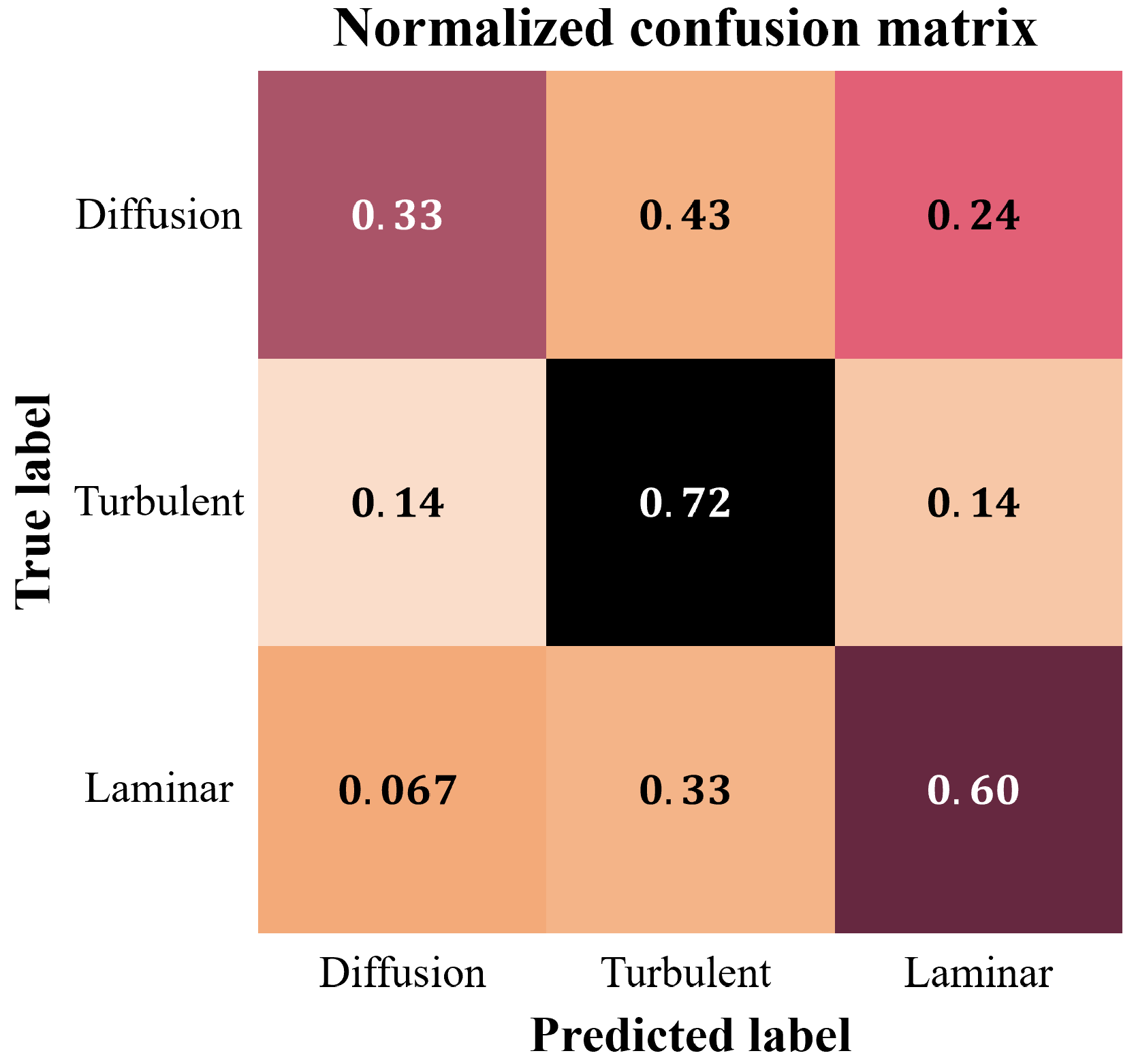
3. Results at the Image Level

Figure 9 exhibits the distribution of patches with respect to the DEM image of each mixing procedure. The x-axis corresponds to the image number, while the y-axis corresponds to the number of clusters, ordered from least to most fractal. The cells, represented in grayscale, refer to the number of patches in each cluster, where white pixels indicate the highest number of patches and black pixels the absence of patches. Note how the distribution of patches in the turbulent mixing procedure shows a bias toward the bottom part (Figure 9b), revealing that this procedure tends to simplify fractal composition, reducing the complexity and intricacy that are often associated with fractal patterns. This may be attributed to the turbulent nature of the mixing process, which may lead to a more chaotic and disordered distribution of elements within the image. On the other hand, Figure 9c shows that the patches of the laminar mixing procedure accumulate towards the top, revealing that inducing a vortex-like flow results in a higher degree of fractality. Finally, the distribution of patches in the diffusion mixing procedure (Figure 9a), presents a uniform behavior, that is, the images of this mixing procedure tend to exhibit patches along the whole fractal spectrum.

As a result of clustering refinement, each image can be represented as a vector in ${\mathbb{R}}^{13}$, which characterizes the patch composition of the image. These vectors were used for classification purposes by means of a support vector machine (SVM). To this end, 60% of the vectors were considered for training and the remaining 40% for testing. Results are shown as a confusion matrix in Figure 10, where it is revealed that the best classification was obtained in turbulent flow with 72% accuracy, followed by 60% for laminar flow, and the lowest accuracy corresponded to the diffusion mixing procedure with 33%. These results are congruent with the patch distribution shown in Figure 9 since the distributions of mixing procedures T and L exhibit a particular footprint that allows for separability. However, mixing procedure D presents a uniform distribution, resulting in 43% confusion regarding turbulent flow and 24% regarding laminar flow. These results suggest that mixing procedure D holds the base fractal footprint of the pharmaceutical extract, with a greater similarity to procedure T than to procedure L.

4. Discussion

The analysis of DEM patterns obtained from differently mixed variants of Viscum album Quercus ${10}^{-3}$ (turbulent, laminar, and diffusion-based mixing) present several challenges due to the complexity and variability of the micrographs. As the DEM patterns of the three VAQ variants originate from the same plant extract, a diverse range of textures is observed, making their differentiation a challenging task. Traditional techniques applied directly such as Gabor filters, Gray Level Co-occurrence Matrix (GLCM), and fractal-based measures do not succeed in determining the imprint of each mixing procedure. In a previous study [25], we introduced an analysis using a semi-supervised deep learning framework, leveraging a Dense Convolutional Network architecture to characterize the mixing procedures. Through this approach, we successfully identified three distinct groups of textures. However, one area of improvement worth considering is the restriction of categorizing the patterns only using three texture groups. This constraint restricts missing subtle variations or additional patterns that could be relevant to understand and differentiate plant extract’s behavior under different mixing conditions.

Motivated by this, the present study explores an unsupervised learning solution. By employing the proposed methodology, we successfully identified and defined thirteen distinct texture groups found within the VAQ database. These texture groups were organized based on their fractality degree, determined by calculating the weighted area under the curve of the average Local Connected Fractal Dimension histograms. The results obtained through this approach provided a much more detailed characterization of the patterns, enabling us to gain valuable insights into the fractal distribution across the DEM images of VAQ variants obtained by different mixing procedures. This deeper understanding of the fractal composition sheds light on the underlying structures and variations present in the microscopic textures of dried droplets. Moreover, we leveraged the ${\mathbb{R}}^{13}$ vectors, which describe the fractal composition of each image, to perform classification using a support vector machine (SVM). By adopting an unsupervised learning strategy, we overcame the limitations of relying on predefined labels and allowed the data to reveal the inherent structures naturally. This data-driven approach not only provided a more comprehensive characterization, but also facilitated the discovery of previously unnoticed patterns and relationships within the VAQ database.

5. Conclusions

Through this paper we have shown that it is possible to characterize the DEM images of the VAQ dataset as vectors of 13 values, thus assessing classification attributes, per image, at the level of mixing procedures. We found that turbulent and laminar mixing modalities are more separable between them than they are with diffusion, i.e., diffusion exhibits features that are characteristic of both laminar and turbulence motions. These findings provide more detailed evidence that there may be an original DEM imprint in the diffusion state, which either becomes stronger (more fractal) with laminar motion or debilitates its fractality (is destructed—becomes less fractal) with turbulent motion. Our study suggests that the proposed unsupervised methodology for texture clustering provides a systematic and efficient approach to identify distinct DEM texture patterns within a set of pharmaceutical extract micrographs. This approach improves how succussions can be understood and interpreted in the context of solution preparations, which is relevant for homeopathy basic research as well as the manufacturing and distribution of pharmaceutical preparations.

Finally, we must note that clustering through deep learning techniques has gained much attention in the community. An example of a major clustering work is [41], which applies generative adversarial networks to generate deep representations. Compared to ours, such representations would demand a higher computational cost and more specialized hardware. Additionally, our work is the first to consider a refinement module such as the one based on DenseNet proposed in this paper. For a recent review in clustering methods see [42].