The Importance of Non-Systemically Important Banks—A Network-Based Analysis for China’s Banking System
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. GCoVaR Model
- The risk spillover between bank i and j
- 2.
- The risk contribution of bank i to the financial system
- 3.
- The risk spillover of bank i suffered from financial system
3.2. To Measure GCoVaR Based on Copula Model
4. Empirical Analysis
4.1. Sample Selection
4.2. Risk Spillover Effect Analysis
4.2.1. The Risk Spillover Effect between Banks
4.2.2. The Risk Spillover Effect from Bank to Banking System
4.2.3. The Risk Spillover Effect from Banking System to Individual Banks
4.3. A Robustness Test
5. Conclusions
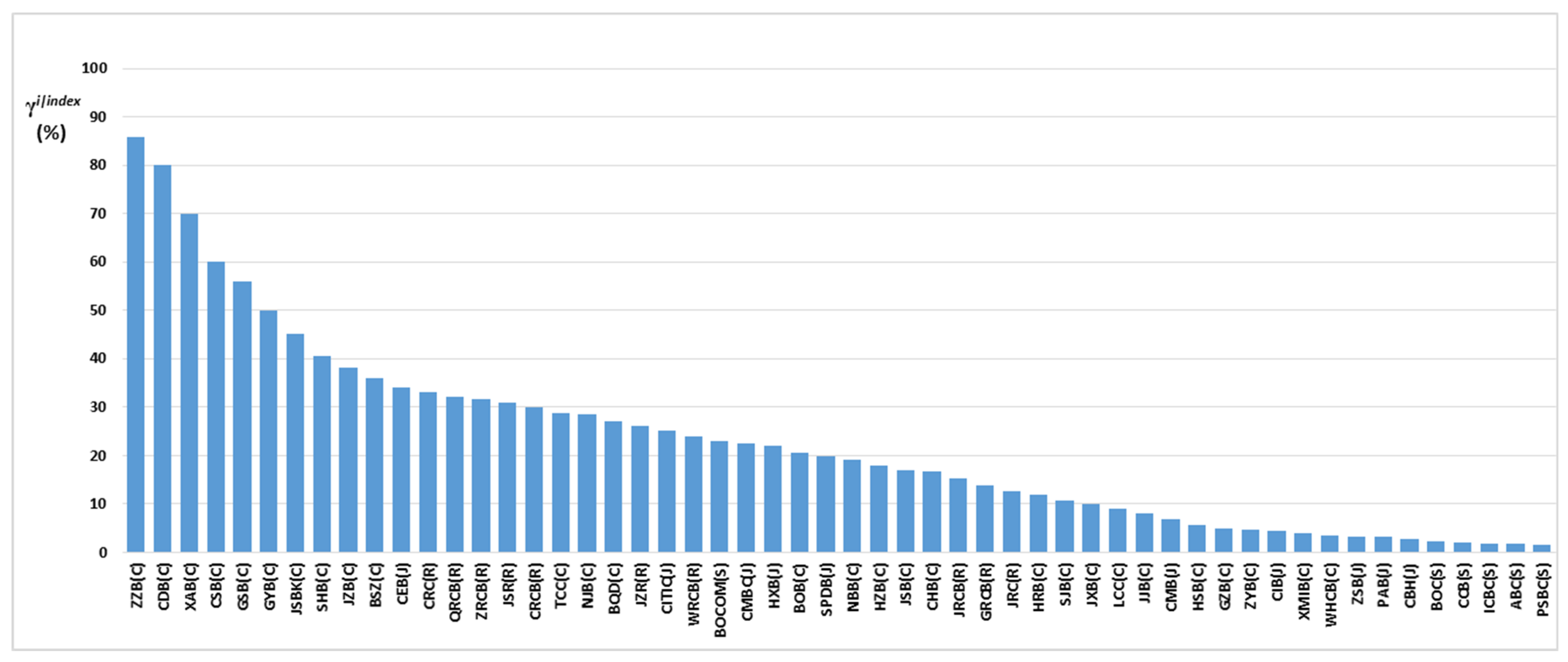
- Compared with SIBs, the non-SIBs are weaker to resist systemic risk impact. Figure 3 ranks the individual banks based on the intensity of systemic risk impact in descending order. Most of the SIBs have a stronger ability to withstand the impact of systemic risks in the banking sector, especially the state-owned SIBs are almost unaffected by systemic risk in terms of γi|index. On the contrary, non-SIBs are mostly severely affected by systemic risks.
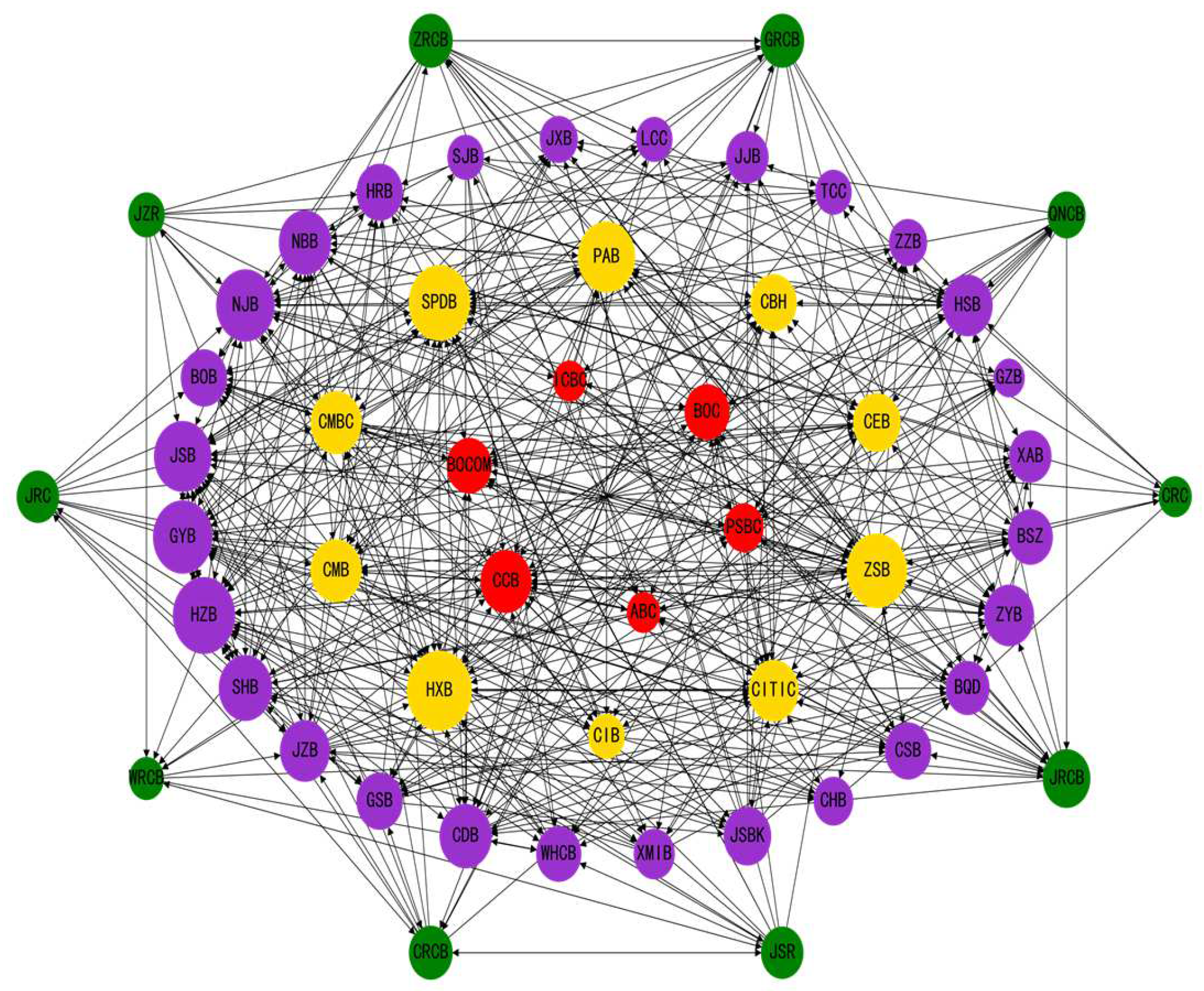
- China’s banking risk spillover has characteristics of hierarchical diffusion from rural commercial banks to city commercial banks to joint-stock commercial banks and state-owned commercial banks. It is mainly from non- SIBs that SIBs receive large risk impacts. It can be seen that in China’s banking system, some non-SIBs, especially some city commercial banks, are more vulnerable to the shocks of systemic risk than SIBs, and they are more likely to act as key intermediaries to transmit risk to SIBs, in turn to trigger systemic risk. So, if the risk prevention and control efforts for the key intermediary are insufficient, the seemingly small risk shocks are likely to be transmitted from non-SIBs to SIBs, thus generating the ‘butterfly effect’ of risk shocks and inducing systemic risks in the banking sector.
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Institution Code | Short Name | Total Assets (Billion Yuan) | Attributes of Banks | |
|---|---|---|---|---|
| 1 | Bank of China | BOC | 24,402.66 | Six state-owned banks |
| 2 | Industrial and Commercial Bank of China | ICBC | 33,345.06 | |
| 3 | Bank of Communications | BOCOM | 10,697.62 | |
| 4 | China Construction Bank | CCB | 28,132.25 | |
| 5 | Agricultural Bank of China | ABC | 27,205.05 | |
| 6 | Postal Savings Bank of China | PSBC | 11,353.26 | |
| 7 | Ping An Bank | PAB | 4468.51 | Ten joint-stock commercial banks |
| 8 | Shanghai Pudong Development Bank | SPDB | 7950.22 | |
| 9 | China Minsheng Banking | CMBC | 6950.23 | |
| 10 | China Merchants Bank | CMB | 8361.45 | |
| 11 | Hua Xia Bank | HXB | 3399.82 | |
| 12 | Industrial Bank | CIB | 7894.00 | |
| 13 | China CITIC Bank | CITIC | 7511.16 | |
| 14 | China Zheshang Bank | ZSB | 2048.23 | |
| 15 | China Everbright Bank | CEB | 5368.11 | |
| 16 | China Bohai Bank Co., Ltd. | CBH | 1393.52 | |
| 17 | Bank of Ningbo | NBN | 1626.75 | Twenty-eight city commercial banks |
| 18 | Bank of Nanjing | NJB | 1517.08 | |
| 19 | Bank of Beijing | BOB | 2900.01 | |
| 20 | Bank of Jiangsu | JSB | 2337.89 | |
| 21 | Bank of Guiyang | GYB | 590.68 | |
| 22 | Bank of Hangzhou | HZB | 1169.26 | |
| 23 | Bank of Shanghai | SHB | 2462.14 | |
| 24 | Bank of Jinzhou | JZB | 777.99 | |
| 25 | Bank of Gansu | GSB | 342.36 | |
| 26 | Bank of Chendu | CDB | 652.43 | |
| 27 | Weihai City Commercial Bank | WHCB | 267.60 | |
| 28 | Xiamen International Bank | XMIB | 285.15 | |
| 29 | Jin Shang Bank | JSBk | 270.94 | |
| 30 | Bank of Chongqing | CHB | 561.64 | |
| 31 | Bank of Changsha | CSB | 704.24 | |
| 32 | Bank of Qingdao | BQD | 459.83 | |
| 33 | Zhongyuan Bank | ZYB | 757.48 | |
| 34 | Bank of Suzhou | BSZ | 388.07 | |
| 35 | Bank of Xi’an | XAB | 306.39 | |
| 36 | Bank of Guizhou | GZB | 456.40 | |
| 37 | Huishang Bank | HSB | 1271.70 | |
| 38 | Bank of Zhengzhou | ZZB | 547.81 | |
| 39 | Tianjin City CommercialBank | TCC | 687.76 | |
| 40 | Bank of Jiujiang | JJB | 415.79 | |
| 41 | Luzhou City Commercial Bank | LCC | 118.89 | |
| 42 | Jiangxi Bank | JXB | 458.69 | |
| 43 | Shengjing Bank | SJB | 1037.96 | |
| 44 | Harbin Bank | HRB | 598.60 | |
| 45 | Jiangyin Rural Commercial Bank | JRC | 142.77 | Ten rural commercial banks |
| 46 | Wuxi Rural Commercial Bank | WRCB | 180.02 | |
| 47 | Changshu Rural Commercial Bank | CRCB | 208.69 | |
| 48 | Jiangsu Suzhou Rural Commercial Bank | JSR | 139.44 | |
| 49 | Jiutai Rural Commercial Bank | JRCB | 200.36 | |
| 50 | Chongqing Rural Commercial Bank | CRC | 1135.93 | |
| 51 | Qingdao Rural Commercial Bank | QRCB | 406.81 | |
| 52 | Guangzhou Rural commercial Bank | GRCB | 1027.87 | |
| 53 | Rural Commercial Bank of Zhangjiagang | ZRCB | 143.82 | |
| 54 | Jiangsu Zijin Rural Commercial Bank | JZR | 217.66 |
Appendix B. Edge Distribution, Time Varying Copula Model and Its Parameter Estimation
| library(copula) library(psych) library(VineCopula) X_1 <- runif(100, 0, 100) X_2 <-X_1+ runif(100, 0, 50) plot(X_1,X_2) abline(lm(X_2~X_1),col=‘red’,lwd=1) cor(X_1,X_2,method=‘spearman’) #u <- pobs(as.matrix(cbind(X_1,X_2)))[,1] #v <- pobs(as.matrix(cbind(X_1,X_2)))[,2] #selectedCopula <- BiCopSelect(u,v,familyset=NA) #selectedCopula gaussian.cop <- normalCopula(dim=2) set.seed(500) m <- pobs(as.matrix(cbind(X_1,X_2))) fit <- fitCopula(gaussian.cop,m,method=‘ml’) coef(fit) rho <- coef(fit)[1] cor(u,method=‘spearman’) X_1_mu <- mean(X_1) X_1_sd <- sd(X_1) X_2_mu <- mean(X_2) X_2_sd <- sd(X_2) copula_dist <- mvdc(copula=normalCopula(rho,dim=2), margins=c(“norm”,”norm”), paramMargins=list(list(mean=X_1_mu, sd=X_1_sd), list(mean=X_2_mu, sd=X_2_sd))) sim <- rMvdc(3965,copula_dist) plot(X_1,X_2,main=‘relation’) points(sim[,1],sim[,2],col=‘red’,pch=‘.’) legend(‘bottomright’,c(‘Observed’,’Simulated’),col=c(‘black’,’red’),pch=21) ################################################# t.cop <- tCopula(dim=2) set.seed(500) m <- pobs(as.matrix(cbind(X_1,X_2))) fit <- fitCopula(t.cop,m,method=‘ml’) coef(fit) rho <- coef(fit)[1] df <- coef(fit)[2] persp(tCopula(dim=2,rho,df=df),dCopula) u <- rCopula(3965,tCopula(dim=2,rho,df=df)) plot(u[,1],u[,2],pch=‘.’,col=‘blue’) cor(u,method=‘spearman’) X_1_mu <- mean(X_1) X_1_sd <- sd(X_1) X_2_mu <- mean(X_2) X_2_sd <- sd(X_2) copula_dist <- mvdc(copula=tCopula(rho,dim=2,df=df), margins=c(“norm”,”norm”), paramMargins=list(list(mean=X_1_mu, sd=X_1_sd), list(mean=X_2_mu, sd=X_2_sd))) sim <- rMvdc(3965,copula_dist) plot(X_1,X_2,main=‘relation’) points(sim[,1],sim[,2],col=‘red’,pch=‘.’) legend(‘bottomright’,c(‘Observed’,’Simulated’),col=c(‘black’,’red’),pch=21) ############################################################## clayton.cop <- claytonCopula(dim=2) set.seed(500) m <- pobs(as.matrix(cbind(X_1,X_2))) fit <- fitCopula(clayton.cop,m,method=‘ml’) coef(fit) alpha <- coef(fit)[1] persp(claytonCopula(dim=2,alpha),dCopula) u <- rCopula(3965,claytonCopula(dim=2,alpha)) plot(u[,1],u[,2],pch=‘.’,col=‘blue’) cor(u,method=‘spearman’) X_1_mu <- mean(X_1) X_1_sd <- sd(X_1) X_2_mu <- mean(X_2) X_2_sd <- sd(X_2) copula_dist <- mvdc(copula=claytonCopula(dim=2,alpha), margins=c(“norm”,”norm”), paramMargins=list(list(mean=X_1_mu, sd=X_1_sd), list(mean=X_2_mu, sd=X_2_sd))) sim <- rMvdc(3965,copula_dist) plot(X_1,X_2,main=‘relation’) points(sim[,1],sim[,2],col=‘red’,pch=‘.’) legend(‘bottomright’,c(‘Observed’,’Simulated’),col=c(‘black’,’red’),pch=21) ############################################################# gumbel.cop <- gumbelCopula(dim=2) set.seed(500) m <- pobs(as.matrix(cbind(X_1,X_2))) fit <- fitCopula(gumbel.cop,m,method=‘ml’) coef(fit) alpha <- coef(fit)[1] persp(gumbelCopula(dim=2,alpha),dCopula) u <- rCopula(3965,gumbelCopula(dim=2,alpha)) plot(u[,1],u[,2],pch=‘.’,col=‘blue’) cor(u,method=‘spearman’) X_1_mu <- mean(X_1) X_1_sd <- sd(X_1) X_2_mu <- mean(X_2) X_2_sd <- sd(X_2) copula_dist <- mvdc(copula=gumbelCopula(dim=2,alpha), margins=c(“norm”,”norm”), paramMargins=list(list(mean=X_1_mu, sd=X_1_sd), list(mean=X_2_mu, sd=X_2_sd))) sim <- rMvdc(3965,copula_dist) plot(X_1,X_2,main=‘relation’) points(sim[,1],sim[,2],col=‘red’,pch=‘.’) legend(‘bottomright’,c(‘Observed’,’Simulated’),col=c(‘black’,’red’),pch=21) |
Appendix C. Algorithm for the Adjacency Information Entropy of the Bank
- calculate the weight (Eji) of effect on bank j by bank i.where eji denotes the extent of the risk connection effect by bank i on bank j, can be obtained by Granger causality test between the return rate offered by banks’ stocks.
- calculate the in-degree of bank j (), which denotes the risk spillover received by bank j,where is the set of banks connected with bank j.
- calculate the out-degree of bank j (), which denotes the risk spillover transmitted by bank j,
- calculate the total risk spillover of bank j (),where λ is the relative importance effect coefficient.
- calculate the adjacency degree (),
- calculate the adjacency information entropy of bank j (),
References
- BCBS. Global Systemically Important Banks, Assessment Methodology and the Additional Loss Absorbency Requirement; BCBS: Basel, Switzerland, 2011. [Google Scholar]
- Acharya, V.; Santos, J.; Yorulmazer, T. Systemic Risk and Deposit Insurance Premiums. Econ. Policy Rev. Fed. Reserve Bank N. Y. 2010, 16, 89–99. [Google Scholar] [CrossRef]
- Brownlees, C.; Engle, R. Volatility, Correlation and Tails for Systemic Risk Measurement; Working Paper; New York University: New York, NY, USA, 2011. [Google Scholar]
- Drehmann, M.; Tarashev, N. Systemic importance, some simple indicators. BIS Q. Rev. 2011, 25–37. [Google Scholar]
- Adrian, T.; Brunnermeier, M.K. CoVaR. Am. Econ. Rev. 2016, 106, 1705–1741. [Google Scholar] [CrossRef]
- Zhou, C. Are Banks Too Big to Fail? Measuring Systemic Importance of Financial Institutions. Int. J. Cent. Bank. 2010, 6, 205–250. [Google Scholar]
- Aldasoro, I.; Alves, I. Multiplex interbank networks and systemic importance—An application to European data. J. Financ. Stab. 2018, 35, 17–37. [Google Scholar] [CrossRef]
- Corsi, F.; Lillo, F.; Pirino, D.; Trapin, L. Measuring the propagation of financial distress with Granger-causality tail risk networks. J. Financ. Stab. 2018, 38, 18–36. [Google Scholar] [CrossRef]
- Poledna, S.; Hinteregger, A.; Thurner, S. Identifying Systemically Important Companies by Using the Credit Network of an Entire Nation. Entropy 2018, 20, 792. [Google Scholar] [CrossRef] [PubMed]
- Pablo, R.K.; Alessandro, S. Identifying systemically important financial institutions, a network approach. Comput. Manag. Sci. 2019, 16, 155–185. [Google Scholar]
- Diebold, F.X.; Yilmaz, K. On the network topology of variance decompositions, Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef]
- Demirer, M.; Diebold, F.X.; Liu, L.; Yilmaz, K. Estimating global bank network connectedness. J. Appl. Econom. 2018, 33, 1–15. [Google Scholar] [CrossRef]
- Baumöhl, E.; Bouri, E.; Hoang, T.-H.-V.; Shahzad, S.J.H.; Výrost, T. From Physical to Financial Contagion, the COVID-19 Pandemic and Increasing Systemic Risk among Banks; ZBW—Leibniz Information Centre for Economics: Hamburg, Germany, 2020. [Google Scholar]
- Guo, Y.; Li, P.; Li, A. Tail risk contagion between international financial markets during COVID-19 pandemic. Int. Rev. Financ. Anal. 2021, 73, 101649. [Google Scholar] [CrossRef]
- Naifar, N.; Shahzad, S.J.H. Tail event-based sovereign credit risk transmission network during COVID-19 pandemic. Financ. Res. Lett. 2022, 45, 102182. [Google Scholar] [CrossRef]
- King, M.; Wadhwani, S. Transmission of Volatility between Stock Markets. Rev. Financ. Stud. 1990, 3, 5–33. [Google Scholar] [CrossRef]
- Eichengreen, B.; Rose, A.; Wyplosz, C. Contagious Currency Crises, First Tests. Scand. J. Econ. 1996, 98, 463–484. [Google Scholar] [CrossRef]
- Arize, A. Foreign trade and exchange-rate risk in the G-7 countries, co-integration and error—Correction models. Rev. Finan. Econ. 1997, 6, 95–112. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Ugolini, A. Systemic risk in European sovereign debt markets, A CoVaR—Copula approach. J. Int. Money Financ. 2015, 51, 214–244. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Rivera-Castro, M.A.; Ugolini, A. Downside and Upside Risk Spillovers Between Exchange Rates and Stock Prices. J. Bank. Financ. 2016, 62, 76–96. [Google Scholar]
- Warshaw, E. Extreme dependence and risk spillovers across North American equity markets. N. Am. J. Econ. Financ. 2019, 47, 237–251. [Google Scholar] [CrossRef]
- Lopez-Espinosa, G.; Moreno, A.; Rubia, A.; Valderrama, L.; Moreno, A. Systemic risk and asymmetric responses in the financial industry. IMF Work. Pap. 2012, 58, 471–485. [Google Scholar] [CrossRef]
- Girardi, G.; Erguen, A.T. Systemic risk measurement, Multivariate GARCH estimation of CoVaR. J. Bank. Financ. 2013, 37, 3169–3180. [Google Scholar] [CrossRef]
- Torri, G.; Giacometti, R.; Tichý, T. Network tail risk estimation in the European banking system. J. Econ. Dyn. Control. 2021, 127, 104125. [Google Scholar] [CrossRef]
- Lai, Y.; Hu, Y. A study of systemic risk of global stock markets under COVID-19 based on complex financial networks. Phys. A Stat. Mech. Its Appl. 2021, 566, 125613. [Google Scholar] [CrossRef]
- Barigozzi, M.; Hallin, M.; Soccorsi, S.; von Sachs, R. Time-varying feneral dynamic factor models and the measurement of financial connectedness. J. Econom. 2021, 222, 324–343. [Google Scholar] [CrossRef]
- Mistrulli, P.E. Assessing Financial Contagion in the Interbank Market, Maximum Entropy versus Observed Interbank Lending Patterns. J. Bank. Financ. 2011, 35, 1114–1127. [Google Scholar] [CrossRef]
- Peltonen, T.A.; Scheicher, M.; Vuillemey, G. The Network Structure of the CDS Market and its Determinants. J. Financ. Stab. 2014, 13, 118–133. [Google Scholar] [CrossRef]
- Georg, C.P. The Effect of the Interbank Network Structure on Contagion and Common Shocks. J. Bank. Financ. 2013, 37, 2216–2228. [Google Scholar] [CrossRef]
- Yang, G.A.; Yl, A.; Yw, B. Risk spillover and network connectedness analysis of China’s green bond and financial markets, Evidence from financial events of 2015–2020. N. Am. J. Econ. Financ. 2021, 57, 101386. [Google Scholar]
- Berger, A.N.; Cai, J.; Roman, R.A.; Sedunov, J. Supervisory enforcement actions against banks and systemic risk. J. Bank. Financ. 2022, 140, 106222. [Google Scholar] [CrossRef]
- Jamil, S.; Yukongdi, V. Information Systems Workforce and Innovative Work Behavior, The Role of Participatory Management, Affective Trust and Guanxi. Int. J. Semant. Web Inf. Syst. 2020, 16, 146–165. [Google Scholar] [CrossRef]
- Allen, F.; Gale, D. Financial Contagion. J. Political Econ. 2000, 108, 1–33. [Google Scholar] [CrossRef]
- Hu, G.; Xu, X.; Gao, H.; Guo, X. Node importance recognition algorithm based on adjacency information entropy in networks. Syst. Eng.—Theory Pract. 2020, 40, 714–725. [Google Scholar]
- Zhao, L.; Li, Y.; Wu, Y.J. An Identification Algorithm of Systemically Important Financial Institutions Based on Adjacency Information Entropy. Comput. Econ. 2022, 59, 1735–1753. [Google Scholar] [CrossRef]


| Bank i | Bank j | MCoVaRj|i | GCoVaRj|i | ΔGCoVaRj|i | γj|i (%) | |||
|---|---|---|---|---|---|---|---|---|
| Bank Code | Total Assets (Billion Yuan) | Bank Code | Total Assets (Billion Yuan) | |||||
| 1 | CDB | 652.43 | CMBC | 6950.23 | 8.14 | 12.36 | 4.22 | 51.84 |
| 2 | BSZ | 388.07 | NJB | 1517.08 | 7.45 | 11.26 | 3.81 | 51.14 |
| 3 | ZYB | 757.48 | ZZB | 561.64 | 9.4 | 13.19 | 3.79 | 40.32 |
| 4 | CRC | 1135.93 | CHB | 547.81 | 7.73 | 10.66 | 2.93 | 37.90 |
| 5 | NJB | 1517.08 | CEB | 5368.11 | 8.13 | 11.04 | 2.91 | 35.79 |
| 6 | CSB | 704.24 | CIB | 7894.00 | 9.72 | 13.16 | 3.44 | 35.39 |
| 7 | CRCB | 208.69 | HZB | 1169.26 | 8.11 | 10.8 | 2.69 | 33.17 |
| 8 | JZB | 777.99 | HRB | 598.60 | 7.45 | 9.70 | 2.25 | 30.20 |
| 9 | CHB | 561.64 | SJB | 1037.96 | 7.48 | 9.66 | 2.18 | 29.14 |
| 10 | JRCB | 200.36 | JZB | 777.99 | 8.17 | 10.51 | 2.34 | 28.64 |
| 11 | QRCB | 406.81 | BQD | 459.83 | 8.2 | 10.52 | 2.32 | 28.29 |
| 12 | SPDB | 7950.22 | GYB | 590.68 | 8.73 | 11.18 | 2.45 | 28.06 |
| 13 | SJB | 1037.96 | PAB | 4468.51 | 8.87 | 11.26 | 2.39 | 26.94 |
| 14 | ZRCB | 143.82 | JSB | 2337.89 | 7.64 | 9.66 | 2.02 | 26.44 |
| 15 | CRCB | 208.69 | JSR | 139.44 | 9.26 | 11.59 | 2.33 | 25.16 |
| 16 | JJB | 415.79 | JXB | 458.69 | 8.51 | 10.54 | 2.03 | 23.85 |
| 17 | JSB | 2337.89 | ZSB | 2048.23 | 9.15 | 11.33 | 2.18 | 23.83 |
| 18 | GZB | 456.40 | HXB | 6950.23 | 8.87 | 10.95 | 2.08 | 23.45 |
| 19 | HSB | 1271.70 | CBH | 3399.82 | 9.26 | 11.39 | 2.13 | 23.00 |
| 20 | GYB | 590.68 | CITIC | 1393.52 | 9.86 | 12.11 | 2.25 | 22.82 |
| 21 | ZRCB | 143.82 | NJB | 7511.16 | 9.83 | 12.00 | 2.17 | 22.08 |
| 22 | JRCB | 142.77 | WRCB | 547.81 | 9.14 | 11.13 | 1.99 | 21.77 |
| 23 | JZR | 217.66 | JJB | 415.79 | 9.78 | 11.81 | 2.03 | 20.76 |
| 24 | CMBC | 6950.23 | GSB | 342.36 | 9.36 | 11.29 | 1.93 | 20.62 |
| 25 | TCC | 687.76 | BOB | 2900.00 | 9.81 | 11.83 | 2.02 | 20.59 |
| 26 | NBB | 1626.75 | JSR | 139.44 | 10.76 | 12.97 | 2.21 | 20.54 |
| 27 | NJB | 1517.08 | BSZ | 388.07 | 9.72 | 11.71 | 1.99 | 20.47 |
| 28 | CMBC | 6950.23 | CDB | 415,79 | 9.56 | 11.51 | 1.95 | 20.40 |
| 29 | WRCB | 547.81 | JRCB | 757.48 | 9.86 | 11.87 | 2.01 | 20.39 |
| 30 | ABC | 28,132.25 | CCB | 27,205.05 | 9.62 | 11.57 | 1.95 | 20.27 |
| No. | CDB Transmits Risk Spillover to | No. | CDB Receives Risk Spillover from | ||||
|---|---|---|---|---|---|---|---|
| Bank Code | Total Assets (Billion Yuan) | γi|CDB (%) | Bank Code | Total Assets (Billion Yuan) | γCDB|i (%) | ||
| 1 | CMBC | 6950.23 | 51.84 | 1 | CMBC | 6950.23 | 20.40 |
| 2 | CIB | 7894.00 | 18.19 | 2 | SHB | 2462.14 | 19.91 |
| 3 | CBH | 1393.52 | 18.12 | 3 | CRC | 1135.93 | 18.79 |
| 4 | BOC | 24,402.66 | 14.49 | 4 | JSB | 143.82 | 13.69 |
| 5 | PAB | 4468.514 | 14.34 | 5 | WHCB | 267.602 | 11.45 |
| 6 | CRC | 1135.93 | 12.45 | 6 | JSR | 2337.89 | 8.28 |
| 7 | BOCOM | 10,697.62 | 12.05 | 7 | CHB | 561.64 | 7.64 |
| 8 | HXB | 3399.82 | 11.77 | 8 | JZB | 1169.26 | 7.32 |
| 9 | CHB | 561.64 | 7.57 | 9 | JJB | 2462.14 | 6.16 |
| 10 | GZB | 456.40 | 5.23 | 10 | JRC | 200.363 | 5.09 |
| 11 | WHCB | 267.60 | 1.56 | 11 | HSB | 1271.70 | 3.37 |
| 12 | BQD | 459.83 | 1.32 | 12 | SJB | 1037.96 | 1.57 |
| 13 | JZR | 139.44 | 0.44 | ||||
| 14 | JRCB | 142.77 | 0.23 | ||||
| No. | CRC Transmits Risk Spillover to | No. | CRC Receives Risk Spillover from | ||||
|---|---|---|---|---|---|---|---|
| Bank Code | Total Assets (Billion Yuan) | γi|CRC (%) | Bank Code | Total Assets (Billion Yuan) | γCRC|i (%) | ||
| 1 | CHB | 561.64 | 40.32 | 1 | JSR | 139.44 | 18.79 |
| 2 | CDB | 652.43 | 19.91 | 2 | GRCB | 1027.87 | 15.22 |
| 3 | JSR | 217.66 | 13.69 | 3 | JZR | 217.66 | 12.16 |
| 4 | ZRCB | 143.82 | 7.32 | 4 | JRC | 142.77 | 12.04 |
| 5 | WHCB | 267.60 | 19.91 | 5 | CHB | 561.64 | 9.25 |
| 6 | JZB | 777.99 | 4.49 | 6 | CDB | 652.43 | 8.12 |
| 7 | JZR | 217.66 | 4.34 | ||||
| 8 | JSB | 2337.89 | 2.45 | ||||
| 9 | GSB | 342.36 | 1.77 | ||||
| 10 | GRCB | 1027.87 | 1.52 | ||||
| 11 | NBB | 1626.75 | 0.22 | ||||
| No. | CCB Transmits Risk Spillover to | No. | CCB Receives Risk Spillover from | ||||
|---|---|---|---|---|---|---|---|
| Bank Code | Total Assets (Billion Yuan) | γi|ABC (%) | Bank Code | Total Assets (Billion Yuan) | γABC|i (%) | ||
| 1 | ABC | 28,132.25 | 20.27 | 1 | BOB | 2900.01 | 18.86 |
| 2 | HXB | 3399.82 | 9.98 | 2 | JSB | 2337.89 | 8.04 |
| 3 | CIB | 7894.00 | 4.27 | 3 | SJB | 1037.96 | 7.80 |
| 4 | SHB | 2462.14 | 3.72 | 4 | JJB | 415.79 | 5.99 |
| 5 | CMBC | 6950.23 | 1.11 | 5 | CHB | 561.64 | 5.45 |
| 6 | HRB | 598.60 | 0.95 | 6 | SHB | 2462.14 | 5.00 |
| 7 | CBH | 1393.52 | 0.92 | 7 | JZB | 777.99 | 1.52 |
| 8 | BOB | 2900.01 | 0.83 | 8 | WHCB | 267.60 | 1.16 |
| 9 | JSB | 2337.89 | 0.44 | 9 | JSBK | 270.94 | 0.46 |
| 10 | SJB | 1037.96 | 0.27 | 10 | ZYB | 757.48 | 0.33 |
| 11 | BSZ | 388.07 | 0.21 | ||||
| 12 | ABC | 28,132.25 | 0.18 | ||||
| 13 | HSB | 1271.70 | 0.15 | ||||
| 14 | XMIB | 285.15 | 0.14 | ||||
| 15 | XAB | 306.39 | 0.11 | ||||
| No. | CMBC Transmits Risk Spillover to | No. | CMBC Receives Risk Spillover from | ||||
|---|---|---|---|---|---|---|---|
| Bank Code | Total Assets (Billion Yuan) | γi|CMBC (%) | Bank Code | Total Assets (Billion Yuan) | γCMBC|i (%) | ||
| 1 | GSB | 342.36 | 20.62 | 1 | CDB | 415,79 | 51.84 |
| 2 | CDB | 415.79 | 20.40 | 2 | JSB | 2337.89 | 18.04 |
| 3 | ZSB | 2048.23 | 14.27 | 3 | SHB | 1037.96 | 17.80 |
| 4 | SHB | 2462.14 | 3.72 | 4 | XAB | 415.79 | 15.29 |
| 5 | NJB | 1517.08 | 2.44 | 5 | CHB | 561.64 | 11.45 |
| 6 | CBH | 1393.52 | 0.95 | 6 | SPDB | 7950.22 | 9.20 |
| 7 | CIB | 7894.00 | 0.92 | 7 | GYB | 590.68 | 7.52 |
| 8 | CCB | 28,132.25 | 0.83 | 8 | JSBK | 270.94 | 3.16 |
| 9 | ABC | 27,205.05 | 0.55 | 9 | ZYB | 757.48 | 1.46 |
| 10 | BSZ | 388.07 | 1.33 | ||||
| 11 | HRB | 598.60 | 1.18 | ||||
| 12 | HSB | 1271.70 | 1.15 | ||||
| 13 | CIB | 7894.00 | 0.78 | ||||
| 14 | XMIB | 285.15 | 0.51 | ||||
| 15 | CSB | 7042.35 | 0.48 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y. The Importance of Non-Systemically Important Banks—A Network-Based Analysis for China’s Banking System. Fractal Fract. 2023, 7, 735. https://doi.org/10.3390/fractalfract7100735
Li Y. The Importance of Non-Systemically Important Banks—A Network-Based Analysis for China’s Banking System. Fractal and Fractional. 2023; 7(10):735. https://doi.org/10.3390/fractalfract7100735
Chicago/Turabian StyleLi, Yong. 2023. "The Importance of Non-Systemically Important Banks—A Network-Based Analysis for China’s Banking System" Fractal and Fractional 7, no. 10: 735. https://doi.org/10.3390/fractalfract7100735
APA StyleLi, Y. (2023). The Importance of Non-Systemically Important Banks—A Network-Based Analysis for China’s Banking System. Fractal and Fractional, 7(10), 735. https://doi.org/10.3390/fractalfract7100735






