On Stability of a Fractional Discrete Reaction–Diffusion Epidemic Model
Abstract
:1. Introduction
- At the core of our investigation is the introduction of a new discrete fractional epidemic model. This model is created by skillfully combining the L1 scheme and the second-order central difference scheme, which effectively transforms the continuous model into its discrete form. This transformation results in a carefully crafted discrete model, laying the foundation for our subsequent analyses.
- Central to our study is a thorough examination of both the local and global asymptotic stability within the proposed fractional discrete reaction–diffusion epidemic model. We employ a powerful linearization technique to analyze the complex stability characteristics near equilibrium points. To establish global stability, we utilize a Lyapunov function that effectively captures historical data, strengthening the reliability of our findings.
- The theoretical framework resulting from our analyses strongly aligns with real-world dynamics. This alignment is robustly confirmed through a series of simulations, where the practical significance of our theoretical discoveries becomes evident. The simulations clearly validate the substantial influence of our findings on the complex network of disease transmission dynamics.
2. A Novel Fractional Discrete-Time Reaction–Diffusion Epidemic Model
3. Fixed Points and Basic Reproduction Number
3.1. Fixed Points
3.2. Basic Reproduction Number
4. Local Stability
4.1. Local Stability of the Free Diffusion Epidemic Model
- •
- If the epidemic equilibrium point is asymptotically stable.
- The Jacobian matrix at the free disease pointThe Jacobian matrix’s eigenvalues associated with areSystem (19) is asymptotically stable if . Clearly, the eigenvalues are reel and if . This implies . Hence,
- The Jacobian matrix at the free disease pointandClearly, and .Now, we have the following discriminantThe eigenvalues of the Jacobian matrix are obviously dependent on the sing of ; therefore, we may analyze the stability in the following situations:
- -
- If and since . As a consequence, the negativity of the eigenvalues is determined by the sign of , and as , the eigenvalues and are real, and we haveAs a consequence of this, . It is self-evident that As a result, according to Theorem 1, the equilibrium is asymptotically stable.
- -
- If , thenBecause , System (19) is then asymptotically stable, based on the identical situation studied before.
- -
- If , cannot have a value of zero. The sign of the eigenvalues corresponds to the sign of . Consequently, is asymptotically stable for all .
We can conclude that if is locally asymptotically stable regardless of the sign of
4.2. Local Stability of the Diffusion Epidemic Model
- •
- If we suppose thatSystem (9) is asymptotically stable at the steady state if the following hold:
- -
- If and
- -
- If and , in addition the eigenvaluessatisfy
- -
- If , then the two solutions of the equation are both negative. Thus, , and the roots of (34) areNote that the solutions are real, and In addition, This leads towhich ensures is asymptotic stability.
- -
- If , we have This returns us to the previous scenario Again, for and hence, and are negative and must meet the conditions of Theorem 1.
5. Global Stability
5.1. Global Stability of
5.2. Global Stability of
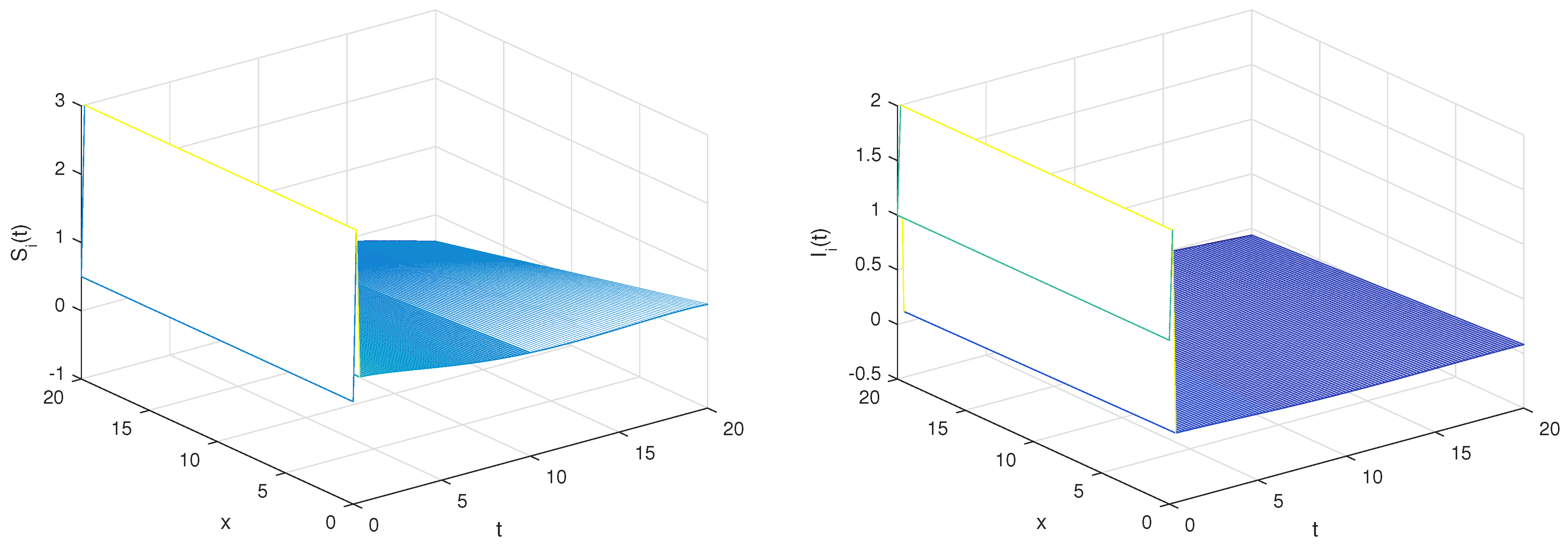
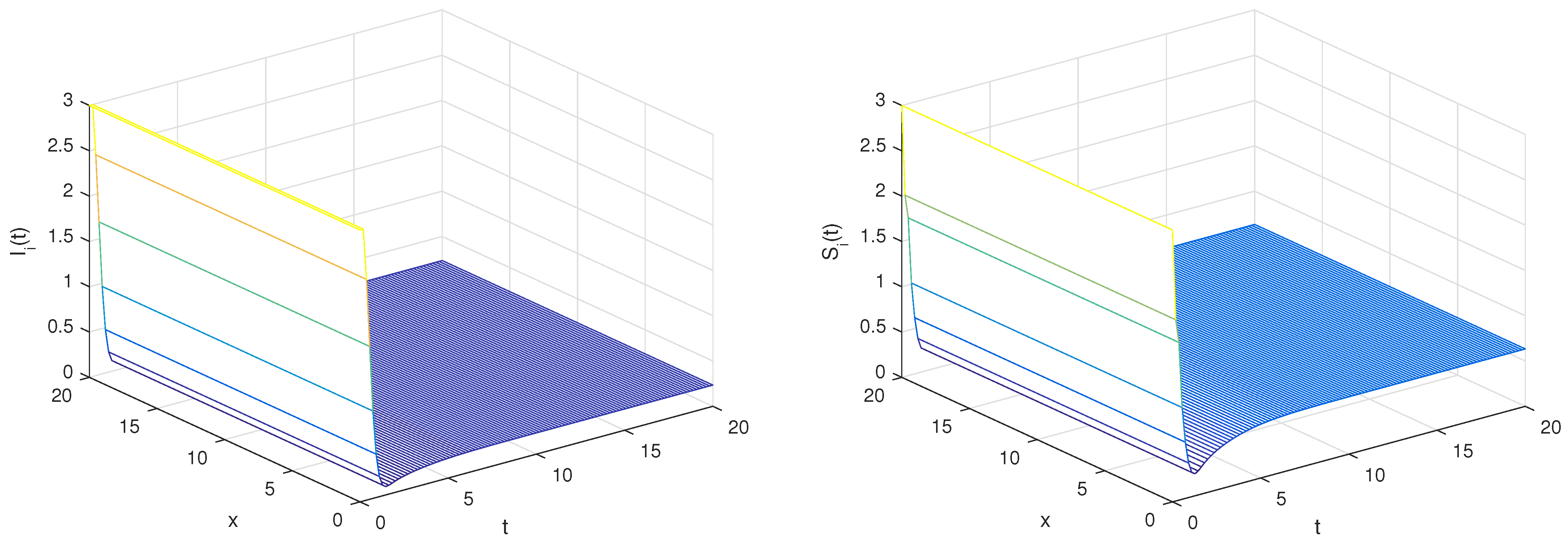
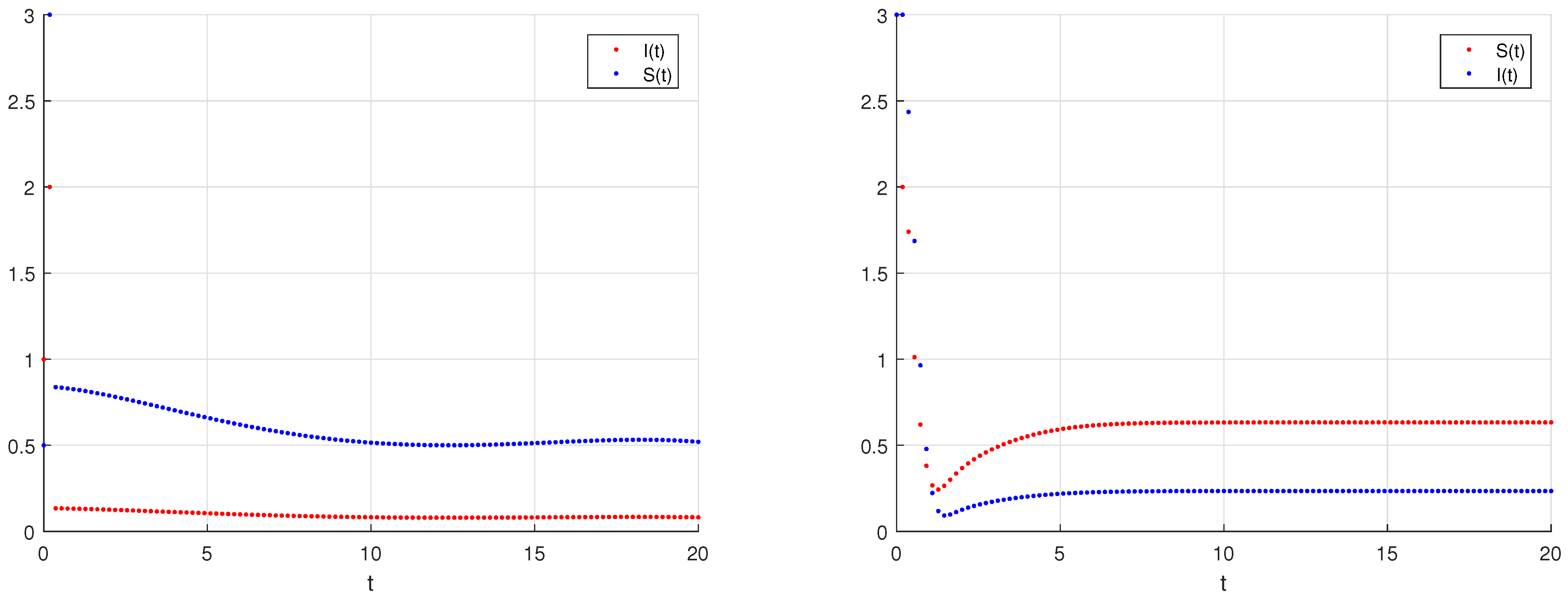
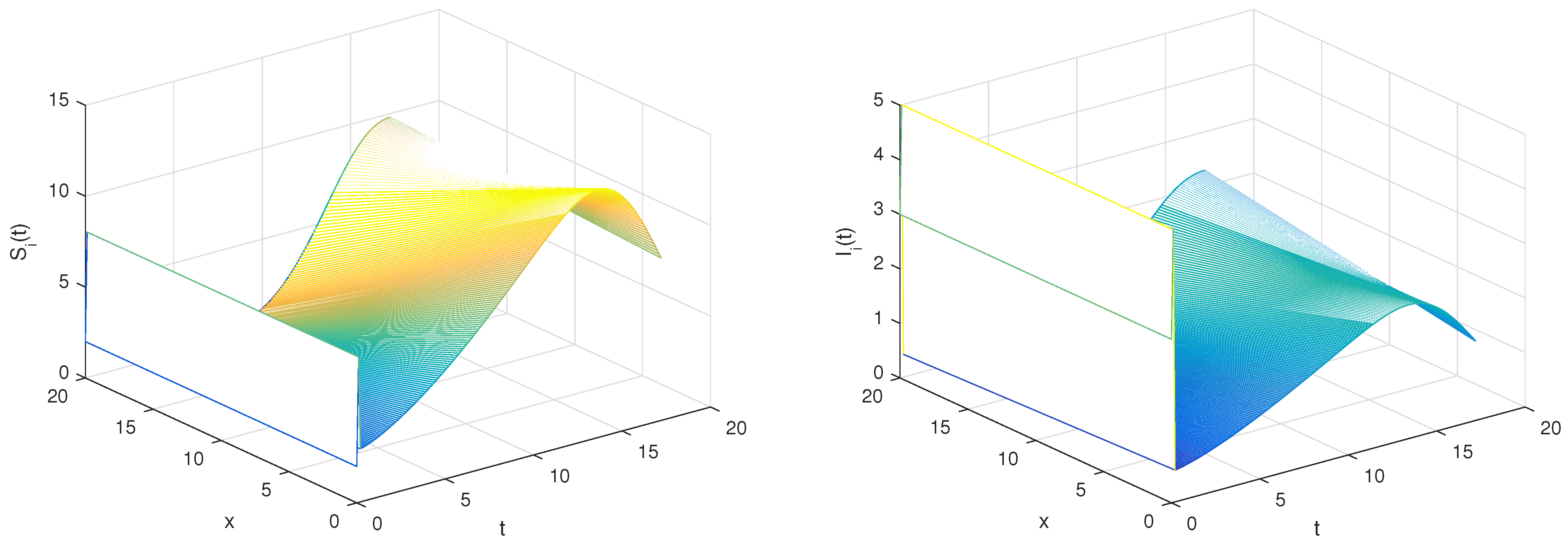
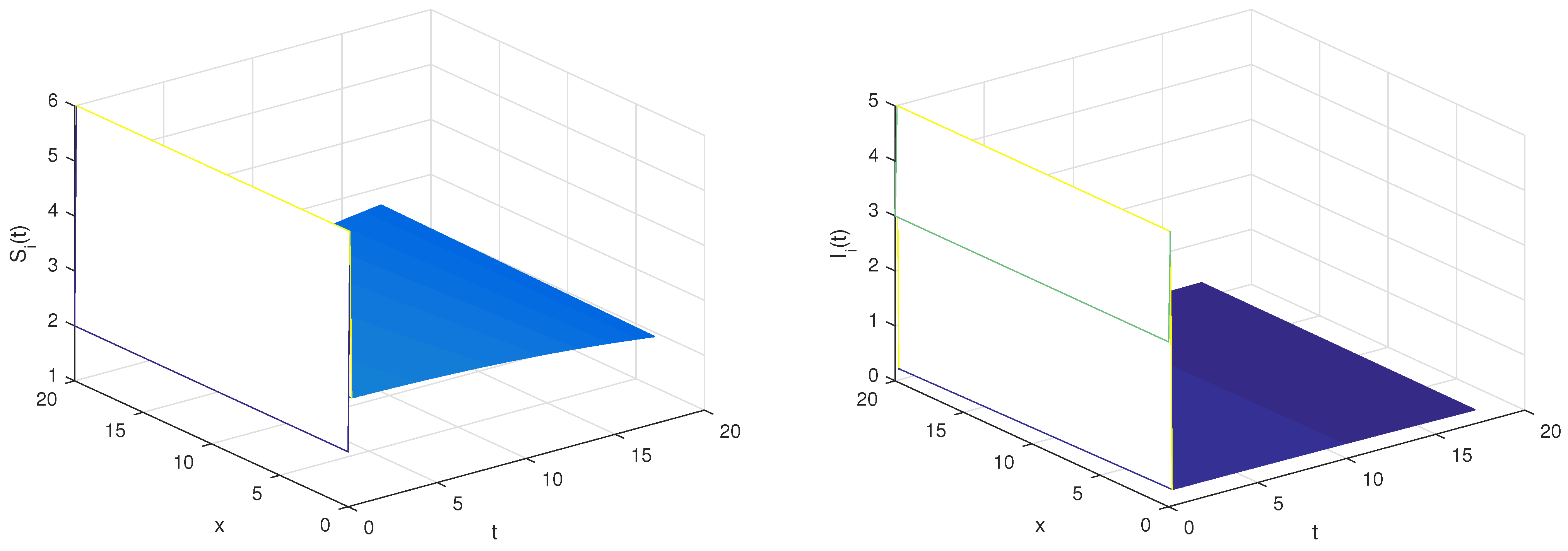
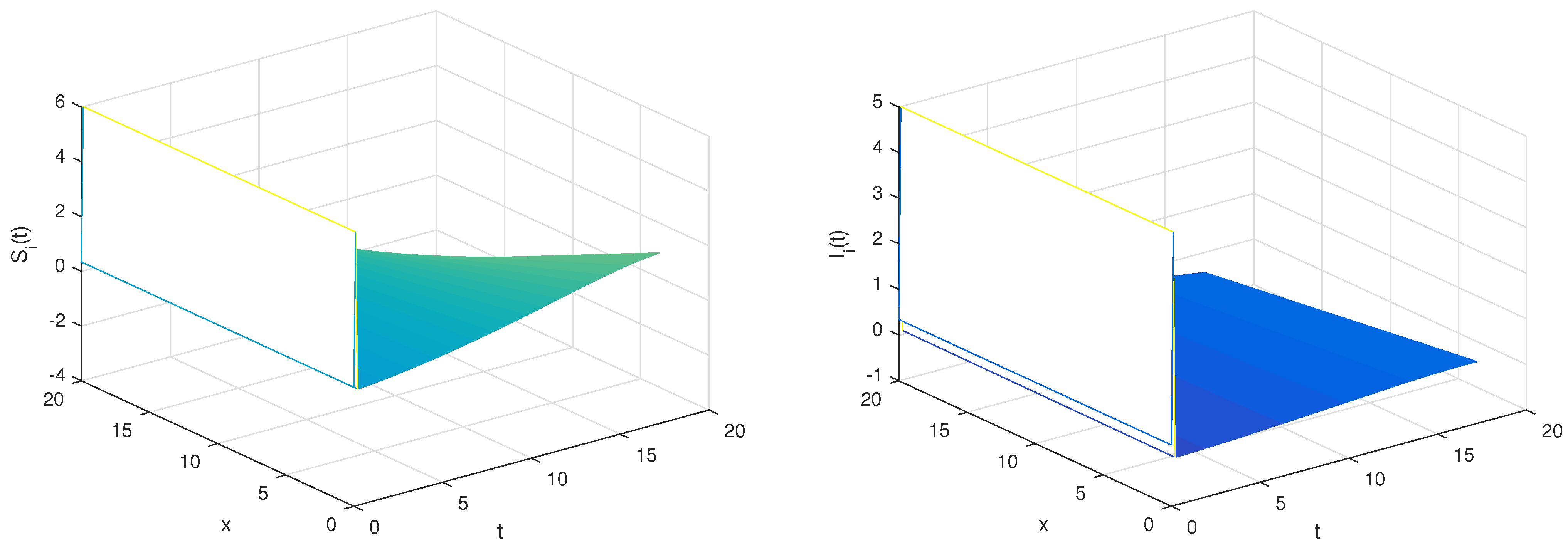
6. Numerical Simulations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El-Saka, H.A.A. The fractional-order SIS epidemic model with variable population size. J. Egypt. Math. Soc. 2014, 22, 50–54. [Google Scholar] [CrossRef]
- Vargas-De-León, C. Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 75–85. [Google Scholar] [CrossRef]
- Ahmed, E.; Elgazzar, A.S. On fractional order differential equations model for nonlocal epidemics. Phys. A Stat. Mech. Its Appl. 2007, 379, 607–614. [Google Scholar] [CrossRef]
- Rihan, F.A.; Al-Mdallal, Q.M.; AlSakaji, H.J.; Hashish, A. A fractional-order epidemic model with time-delay and nonlinear incidence rate. Chaos Solitons Fractals 2019, 126, 97–105. [Google Scholar] [CrossRef]
- He, Z.Y.; Abbes, A.; Jahanshahi, H.; Alotaibi, N.D.; Wang, Y. Fractional-order discrete-time SIR epidemic model with vaccination: Chaos and complexity. Mathematics 2022, 10, 165. [Google Scholar] [CrossRef]
- Can, N.H.; Nikan, O.; Rasoulizadeh, M.N.; Jafari, H.; Gasimov, Y.S. Numerical computation of the time non-linear fractional generalized equal width model arising in shallow water channel. Therm. Sci. 2020, 24, 49–58. [Google Scholar] [CrossRef]
- Asaduzzaman, M.; Kilicman, A.; Ali, M.Z. Presence and diversity of positive solutions for a Caputo-type fractional order nonlinear differential equation with an advanced argument. J. Math. Comput. Sci 2021, 23, 230–244. [Google Scholar] [CrossRef]
- AlAhmad, R.; AlAhmad, Q.; Abdelhadi, A. Solution of fractional autonomous ordinary differential equations. J. Math. Comput. Sci. 2022, 27, 59–64. [Google Scholar] [CrossRef]
- Henry, B.I.; Wearne, S.L. Fractional reaction–diffusion. Phys. A Stat. Mech. Its Appl. 2000, 276, 448–455. [Google Scholar] [CrossRef]
- Seki, K.; Wojcik, M.; Tachiya, M. Fractional reaction-diffusion equation. J. Chem. Phys. 2003, 119, 2165–2170. [Google Scholar] [CrossRef]
- Gafiychuk, V.; Datsko, B.; Meleshko, V. Mathematical modeling of time fractional reaction–diffusion systems. J. Comput. Appl. Math. 2008, 220, 215–225. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A.; Akgul, A. Modelling and analysis of fractal-fractional partial differential equations: Application to reaction-diffusion model. Alex. Eng. J. 2020, 59, 2477–2490. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ali, A. A numerical study on time fractional Fisher equation using an extended cubic B-spline approximation. J. Math. Comput. Sci. 2021, 22, 85–96. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, J.; Tang, J. Clarify the physical process for fractional dynamical systems. Nonlinear Dyn. 2020, 100, 2353–2364. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A fractional-order infectivity SIR model. Phys. A Stat. Mech. Appl. 2016, 452, 86–93. [Google Scholar] [CrossRef]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Almeida, R. Analysis of a fractional SEIR model with treatment. Appl. Math. Lett. 2018, 84, 56–62. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Donnelly, I.C.; Henry, B.I.; Jacobs, B.A.; Langlands, T.A.M.; Nichols, J.A. From stochastic processes to numerical methods: A new scheme for solving reaction subdiffusion fractional partial differential equations. J. Comput. Phys. 2016, 307, 508–534. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Donnelly, I.C.; Henry, B.I.; Nichols, J.A. A discrete time random walk model for anomalous diffusion. J. Comput. Phys. 2015, 293, 53–69. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A fractional order recovery SIR model from a stochastic process. Bull. Math. Biol. 2016, 78, 468–499. [Google Scholar] [CrossRef]
- Dababneh, A.; Djenina, N.; Ouannas, A.; Grassi, G.; Batiha, I.M.; Jebril, I.H. A new incommensurate fractional-order discrete COVID-19 model with vaccinated individuals compartment. Fractal Fract. 2022, 6, 456. [Google Scholar] [CrossRef]
- Saadeh, R.; Abbes, A.; Al-Husban, A.; Ouannas, A.; Grassi, G. The Fractional Discrete Predator–Prey Model: Chaos, Control and Synchronization. Fractal Fract. 2023, 7, 120. [Google Scholar] [CrossRef]
- Yi, N.; Liu, P.; Zhang, Q. Bifurcations analysis and tracking control of an epidemic model with nonlinear incidence rate. Appl. Math. Model. 2012, 36, 1678–1693. [Google Scholar] [CrossRef]
- Chen-Charpentier, B.M.; Dimitrov, D.T.; Kojouharov, H.V. Numerical simulation of multi-species biofilms in porous media for different kinetics. Math. Comput. Simul. 2009, 79, 1846–1861. [Google Scholar] [CrossRef]
- Jang, S.; Elaydi, S. Difference equations from discretization of a continuous epidemic model with immigration of infectives. Math. Fac. Res. 2003, 11, 93–105. [Google Scholar]
- Sekiguchi, M.; Ishiwata, E. Global dynamics of a discretized SIRS epidemic model with time delay. J. Math. Anal. Appl. 2010, 371, 195–202. [Google Scholar] [CrossRef]
- Almatroud, O.A.; Hioual, A.; Ouannas, A.; Grassi, G. On Fractional-Order Discrete-Time Reaction Diffusion Systems. Mathematics 2023, 11, 2447. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Zeng, S.D.; Deng, Z.G. Discrete fractional diffusion equation. Nonlinear Dyn. 2015, 80, 281–286. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Xie, H.P.; Zeng, S.D. Discrete fractional diffusion equation of chaotic order. Int. J. Bifurc. Chaos 2016, 26, 1650013. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, Y.; Xu, W.; Ren, G.; Meng, X. Global dynamics for a class of discrete fractional epidemic model with reaction-diffusion. arXiv 2022, arXiv:2208.06548. [Google Scholar]
- Abu Falahah, I.; Hioual, A.; Al-Qadri, M.O.; AL-Khassawneh, Y.A.; Al-Husban, A.; Hamadneh, T.; Ouannas, A. Synchronization of Fractional Partial Difference Equations via Linear Methods. Axioms 2023, 12, 728. [Google Scholar] [CrossRef]
- Hamadneh, T.; Hioual, A.; Alsayyed, O.; AL-Khassawneh, Y.A.; Al-Husban, A.; Ouannas, A. Local Stability, Global Stability, and Simulations in a Fractional Discrete Glycolysis Reaction–Diffusion Model. Fractal Fract. 2023, 7, 587. [Google Scholar] [CrossRef]
- Hamadneh, T.; Hioual, A.; Alsayyed, O.; Al-Khassawneh, Y.A.; Al-Husban, A.; Ouannas, A. The FitzHugh–Nagumo Model Described by Fractional Difference Equations: Stability and Numerical Simulation. Axioms 2023, 12, 806. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, Y.; Ren, G.; Xu, C.; Meng, X. Global dynamics for a class of reaction–diffusion multigroup SIR epidemic models with time fractional-order derivatives. Nonlinear Anal. Model. Control. 2022, 27, 142–162. [Google Scholar] [CrossRef]
- Kelley, W.G.; Peterson, A.C. Difference Equations: An Introduction with Applications; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Sharkovsky, A.N.; Maistrenko, Y.L.T.; Romanenko, E.Y. Difference Equations and Their Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 250. [Google Scholar]
- Baleanu, D.; Wu, G.C.; Bai, Y.R.; Chen, F.L. Stability analysis of Caputo–like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 520–530. [Google Scholar] [CrossRef]
- Hioual, A.; Ouannas, A.; Oussaeif, T.E.; Grassi, G.; Batiha, I.M.; Momani, S. On variable-order fractional discrete neural networks: Solvability and stability. Fractal Fract. 2022, 6, 119. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Čermák, J.; Nechvátal, L. On a problem of linearized stability for fractional difference equations. Nonlinear Dyn. 2021, 104, 1253–1267. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, L.J.; Chang, Z.X.; Feng, J.T.; Zhang, G. Turing instability and pattern formation in a semi-discrete Brusselator model. Mod. Phys. Lett. B 2013, 27, 1350006. [Google Scholar] [CrossRef]
- Franco-Perez, L.; Fernandez-Anaya, G.; Quezada-Téllez, L.A. On stability of nonlinear nonautonomous discrete fractional Caputo systems. J. Math. Anal. Appl. 2020, 487, 124021. [Google Scholar] [CrossRef]
- Elaydi, S. An Introduction to Difference Equations; Springer: San Antonio, TX, USA, 2015. [Google Scholar]
- Anakira, N.; Hioual, A.; Ouannas, A.; Oussaeif, T.E.; Batiha, I.M. Global Asymptotic Stability for Discrete-Time SEI Reaction-Diffusion Model. In International Conference on Mathematics and Computations; Springer Nature: Singapore, 2022; pp. 345–357. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsayyed, O.; Hioual, A.; Gharib, G.M.; Abualhomos, M.; Al-Tarawneh, H.; Alsauodi, M.S.; Abu-Alkishik, N.; Al-Husban, A.; Ouannas, A. On Stability of a Fractional Discrete Reaction–Diffusion Epidemic Model. Fractal Fract. 2023, 7, 729. https://doi.org/10.3390/fractalfract7100729
Alsayyed O, Hioual A, Gharib GM, Abualhomos M, Al-Tarawneh H, Alsauodi MS, Abu-Alkishik N, Al-Husban A, Ouannas A. On Stability of a Fractional Discrete Reaction–Diffusion Epidemic Model. Fractal and Fractional. 2023; 7(10):729. https://doi.org/10.3390/fractalfract7100729
Chicago/Turabian StyleAlsayyed, Omar, Amel Hioual, Gharib M. Gharib, Mayada Abualhomos, Hassan Al-Tarawneh, Maha S. Alsauodi, Nabeela Abu-Alkishik, Abdallah Al-Husban, and Adel Ouannas. 2023. "On Stability of a Fractional Discrete Reaction–Diffusion Epidemic Model" Fractal and Fractional 7, no. 10: 729. https://doi.org/10.3390/fractalfract7100729
APA StyleAlsayyed, O., Hioual, A., Gharib, G. M., Abualhomos, M., Al-Tarawneh, H., Alsauodi, M. S., Abu-Alkishik, N., Al-Husban, A., & Ouannas, A. (2023). On Stability of a Fractional Discrete Reaction–Diffusion Epidemic Model. Fractal and Fractional, 7(10), 729. https://doi.org/10.3390/fractalfract7100729









