An Algorithm for the Solution of Nonlinear Volterra–Fredholm Integral Equations with a Singular Kernel

Abstract

The nonlinear Volterra–Fredholm integral Equation (NVFIE) with a singular kernel is discussed such that the kernel of position can take the Hilbert kernel form, Carleman function, logarithmic form, or Cauchy kernel. Using the quadrature method, the NVFIE with a singular kernel leads to a system of nonlinear integral equations. The existence and unique numerical solution of this system is discussed, as is the truncation error of the numerical solution. The solution of the nonlinear integral equation system is obtained using the spectral relations and techniques of the Chebyshev polynomial method. Finally, we will discuss examples of when the kernel takes various forms to demonstrate this technique’s high accuracy and simplicity. Some numerical results and estimating errors are calculated and plotted using the program Wolfram Mathematica 10.

1. Introduction

Integral equations often appear in mathematical modeling, which has engineering, life sciences, and physics applications. Specific fields include, for instance, telecommunications, biology, heat transfer, the dynamics of population, elasticity, epidemiology, genetics, hydrodynamics, and viscoelasticity [1,2,3]. Integral equations (IEs) have different names based on their shape. In other words, depending on the limits of integration, an IE could have fixed limits (Fredholm IE), variable limits (Volterra IE), or both in the same equation (Fredholm–Volterra IE), with the unknown function only showing up inside the integration (the first type of IE), outside the integration (the second type of IE), or both inside and outside the integration (the third type of IE). The integral equations of the Fredholm–Volterra type appear in two forms: the first is the Fredholm–Volterra disjoint integral [4], and the other form is mixed, so that these two integrals are in one term multiple integrals (for more details, see [5,6,7]).

Due to the difficulty in obtaining an exact solution for the integral equations of the Volterra–Fredholm type, we tend to use numerical methods [8]. Recently, different computational techniques have been developed to obtain the approximate solution of the nonlinear and linear integral equations of the Volterra–Fredholm type. In [9], the Taylor series expansion is an important method that has been developed. Two powerful methods can often provide the exact solution in some cases: the modified decomposition method [10] and the Adomian decomposition method [11]. Collocation methods have become very popular and have attracted the attention of many researchers. They are based on general approximate functions, Bernstein polynomials, Chelyshkov polynomials, Fibonacci polynomials, Boubaker polynomials, Bell polynomials, Lucas polynomials, Muntz–Legendre polynomials, Jacobi polynomials, Bernoulli polynomials, and block-pulse functions. Galerkin methods are also one of the methods that attracted the attention of researchers and are widely used with general approximate functions, Bernstein polynomials [12], Legendre polynomials [13], Alpert’s multiwavelet bases [14], and conflict-type wavelets [15]. Furthermore, among the numerical methods that have been developed are the Quadrature methods [16], Homotopy analysis methods [17], Modified homotopy perturbation methods [18], and least squares approximation methods [19]. Several typical examples of iterative approximation methods are the block-by-block method and Runge–Kutta method [20], optimal perturbation iteration method [21], and Picard iteration method [22]. Fixed point methods are some of the methods that have been used successfully, especially those based on rationalized Haar wavelets [23], fixed point methods in extended b-metric space [24], Schauder bases in an adequate Banach space [25], and Schauder bases [26]. Among the numerical methods that were also introduced using Hosoya polynomials [27], there are Haar wavelets [1], Bernstein polynomials [28], hyperbolic basis functions [29], and block-pulse functions [30]. Some of the methods that have been reported to be successful include a neural network approach [31], Tau methods [32], and parameter continuation methods [33]. Finally, we considered the results of uniqueness and existence in [34,35].

In this present study, we consider the NVFIE with a singular kernel of the second type. The kernel of the position can take the Hilbert kernel, Carleman form, logarithmic form, or Cauchy kernel. The continuity and boundedness of the integral operator are studied and proved in Section 2. The stability and rate of convergence of the proposed scheme are introduced in Section 3. In Section 4, we use the quadrature method to reduce the solution of Equation (1) to the system of nonlinear Fredholm integral equations. The techniques of the Chebyshev polynomial method and some spectral relations used to find a solution of the system of the algebraic integral are presented in Section 5. The existence and unique numerical solution of this system are discussed, and the truncation error of the numerical solution is presented in Section 6, while Section 7 solves various illustrative examples using the program Wolfram Mathematica 10 to show the efficiency of the method. Finally, some conclusions and remarks are given in Section 8.

Now, we will study the solvability of the following NVFIE with the singular kernel:

$$\mu \mathrm{\Psi }(u,t)-\lambda {\int }_0^t{\int }_{-1}^{1}f(t,\tau )k(w\left(u\right)-w\left(v\right))\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau ))\mathrm{d}v\mathrm{d}\tau =F(u,t).$$

(1)

Here, $F(u,t)$ and $\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau \left)\right)$ are two given functions, while the function $\mathrm{\Psi }(u,t)$ is unknown in the Banach space $L_2[-1,1]\times C[0,T]$, where the time $t\in [0,T],T<1$. The kernel of position for $u,v\in [-1,1],k\left(w\right(u)-w(v\left)\right)$ has a singularity at $w\left(u\right)=w\left(v\right)$, where the two functions $w\left(u\right),w\left(v\right)$ are continuous functions. The kernel of time $f(t,\tau ),t,$$\tau \in [0,T],$$T<1$ is continuous in class $C[0,T]$. The constant $\mu$ determines the type of the integral equation, whereas $\lambda$ is a complex constant with a distinct physical meaning.

2. The Existence and Unique Solution of Equation (1)

The Banach fixed point theorem will be used in this section as a source of the existence and uniqueness of the solution of Equation (1). To discuss its existence and unique solution, Equation (1) can be expressed in the integral operator form as follows:

$$\overline{V}\mathrm{\Psi }(u,t)=\frac{1}{\mu }F(u,t)+\frac{1}{\mu }V\mathrm{\Psi }(u,t);\mu \ne 0,$$

(2)

where

$$V\mathrm{\Psi }(u,t)=\lambda {\int }_0^t{\int }_{-1}^{1}f(t,\tau )k(w\left(u\right)-w\left(v\right))\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau ))\mathrm{d}v\mathrm{d}\tau .$$

(3)

We assume the following:

(i)

The kernel of position $k\left(w\right(u)-w(v\left)\right)$ satisfies the discontinuity condition

$${\left[{\int }_{-1}^1{\int }_{-1}^1{\left|k(w\left(u\right)-w\left(v\right))\right|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}=\varkappa ;\forall u,v\in [-1,1];\varkappa \mathrm{is}\mathrm{a}\mathrm{constant}.$$

(ii)

The kernel of time $f(t,\tau )$ is continuous and satisfies

$$\left|f\right(t,\tau \left)\right|\le \varsigma ;\forall t,\tau \in [0,T],0\le \tau \le t\le T<1;\varsigma \mathrm{is}\mathrm{a}\mathrm{constant}.$$

(iii)

The norm of the continuous given function $F(u,t)$ is defined as

$${\parallel F(u,t)\parallel }_{L_2[-1,1]\times C[0,T]}=\underset{0\le t\le T}{max}\left|{\int }_0^t{\left[{\int }_{-1}^1{F}^2(u,\tau )du\right]}^{\frac{1}{2}}\mathrm{d}\tau \right|=\varpi ;\varpi \mathrm{is}\mathrm{a}\mathrm{constant}.$$

(iv)

The known function $\gamma (u,v,t,\tau ,\mathrm{\Psi }(u,t\left)\right)$ for the constants $\epsilon$ and $\vartheta$ satisfies:

$$\begin{array}{cc}\hfill \left(a\right)& \left|\gamma (u,v,t,\tau ,\mathrm{\Psi }(u,t))\right|\le L_1(u,v;t,\tau )\left|\mathrm{\Psi }(u,t)\right|\hfill \\ \hfill \left(b\right)& |\gamma (u,v,t,\tau ,{\mathrm{\Psi }}_1(u,t))-\gamma (u,v,t,\tau ,{\mathrm{\Psi }}_2(u,t))|\le L_2(u,v;t,\tau )|{\psi }_1(u,t)-{\psi }_2(u,t)|,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \parallel L_1(u,v;t,\tau )\parallel =& \underset{0\le \tau \le t\le T<1}{max}{\int }_0^t{\left[{\int }_{-1}^1{\int }_{-1}^1{\left|L_1(u,v;t,\tau )\right|}^{2}dudv\right]}^{\frac{1}{2}}\mathrm{d}\tau =\epsilon \hfill \\ \hfill \parallel L_2(u,v;t,\tau )\parallel =& \underset{0\le \tau \le t\le T<1}{max}{\int }_0^t{\left[{\int }_{-1}^1{\int }_{-1}^1{\left|L_2(u,v;t,\tau )\right|}^{2}dudv\right]}^{\frac{1}{2}}\mathrm{d}\tau =\vartheta .\hfill \end{array}$$

We must note that the normality of the unknown function $\mathrm{\Psi }(u,t)$ in the space of integration $L_2[-1,1]\times C[0,T]$ is ${\parallel \mathrm{\Psi }(u,t)\parallel }_{L_2[-1,1]\times C[0,T]}={max}_{0\le t\le T}{\int }_0^t{\left[{\int }_{-1}^1{\mathrm{\Psi }}^2(u,\tau )du\right]}^{\frac{1}{2}}\mathrm{d}\tau .$

Theorem 1. 

If the conditions (i)–(iv) are satisfied, then Equation (1) has a unique solution in the Banach space $L_2[-1,1]\times C[0,T]$.

We have to consider the following lemmas in order to prove the previous theorem:

Lemma 1. 

Under the conditions (i)–(iv-a), the operator $\overline{V}$ maps the space $L_2(-1,1)\times C[0,T]$ into itself.

Proof. 

From the two Formulas (2) and (3), we have

$$\parallel \overline{V}\mathrm{\Psi }(u,t)\parallel \le \frac{1}{\left|\mu \right|}\parallel F(u,t)\parallel +\frac{\left|\lambda \right|}{\left|\mu \right|}∥{\int }_0^t{\int }_{-1}^1\left|f(t,\tau )\right|\left|k(w\left(u\right)-w\left(v\right))\right|\left|\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau ))\right|\mathrm{d}v\mathrm{d}\tau ∥.$$

Using the conditions (ii) and (iii), then applying Cauchy–Schwarz inequality, we obtain

$$\begin{array}{cc}\hfill \parallel \overline{V}\mathrm{\Psi }(u,t)\parallel & \le \frac{\varpi }{\left|\mu \right|}+\frac{\left|\lambda \right|}{\left|\mu \right|}\varsigma ∥{\left[{\int }_{-1}^1{\int }_{-1}^1{\left|k(w\left(u\right)-w\left(v\right))\right|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}\hfill \\ \hfill & \times \underset{0\le \tau \le t\le T}{max}{\int }_0^t{\left[{\int }_{-1}^1{\int }_{-1}^1{\left|\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau ))\right|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}\mathrm{d}\tau ∥.\hfill \end{array}$$

From the conditions (i) and (iv-a), the above inequality takes the form of

$$\parallel \overline{V}\psi (u,t)\parallel \le \frac{\varpi }{\left|\mu \right|}+\beta \parallel \psi (u,t)\parallel ,\beta =\frac{\left|\lambda \right|}{\left|\mu \right|}\varsigma \varkappa \sigma ,\sigma =max\{\epsilon ,\vartheta \}.$$

(4)

As provided by inequality (4), the operator $\overline{V}$ maps the ball $S_r$ into itself, where

$$r=\frac{\varpi }{\left(\right|\mu |-|\lambda \left|\varsigma \varkappa \sigma \right)}.$$

(5)

Since $r>0,\varpi >0$, we, therefore, have $\beta <1$. Additionally, inequality (5) includes the boundedness of the operator V of Equation (3), where

$$\parallel V\psi (u,t)\parallel \le \beta \parallel \psi (u,t)\parallel .$$

(6)

Moreover, inequalities (4) and (6) define the boundedness of the operator $\overline{V}$. □

Lemma 2. 

Assume that the conditions (i), (ii), and (iv-b) are verified; then, $\overline{V}$ is a contraction operator in the space $L_2[-1,1]\times C[0,T]$.

Proof. 

For the functions ${\psi }_1(u,t),{\psi }_2(u,t)$ in $L_2[-1,1]\times C[0,T]$, and from Equations (2) and (3), we find

$$\begin{array}{cc}\hfill \parallel \overline{V}& {\mathrm{\Psi }}_1(u,t)-\overline{V}{\mathrm{\Psi }}_2(u,t)\parallel \hfill \\ & \le \frac{\left|\lambda \right|}{\left|\mu \right|}∥{\int }_0^t{\int }_{-1}^1\left|f(t,\tau )\right|\left|k(w\left(u\right)-w\left(v\right))\right||\gamma (u,v,t,\tau ,{\mathrm{\Psi }}_1(v,\tau ))-\gamma (u,v,t,\tau ,{\mathrm{\Psi }}_2(v,\tau ))|\mathrm{d}v\mathrm{d}\tau ∥.\hfill \end{array}$$

The above inequality becomes, via conditions (ii) and (iv-b) in the following:

$$\begin{array}{cc}\hfill \parallel \overline{V}& {\mathrm{\Psi }}_1(u,t)-\overline{V}{\mathrm{\Psi }}_2(u,t)\parallel \hfill \\ & \le \frac{\left|\lambda \right|}{\left|\mu \right|}\varsigma ∥{\int }_0^t{\int }_{-1}^1\left|k(w\left(u\right)-w\left(v\right))\right|L(u,v,t,\tau )\parallel {\psi }_1(u,t)-{\psi }_2(u,t)\parallel \mathrm{d}v\mathrm{d}\tau ∥.\hfill \end{array}$$

Applying the Cauchy–Schwarz inequality to the integral term, and then using (i), we finally obtain

$$\parallel \overline{V}{\mathrm{\Psi }}_1(u,t)-\overline{V}{\mathrm{\Psi }}_2(u,t)\parallel \le \beta \parallel {\mathrm{\Psi }}_1(u,t)-{\psi }_2(u,t)\parallel .$$

(7)

With the aid of inequality (7), the operator $\overline{V}$ is continuous in $L_2[-1,1]\times C[0,T]$, and then $\overline{V}$ is a contraction operator under the condition $\beta <1$. □

Proof of Theorem 1. 

From the above Lemmas 1 and 3, we deduced that the operator $\overline{V}$ of Equation (2) is contractive in the Banach space $L_2[-1,1]\times C[0,T]$. Thus, $\overline{V}$ has a unique fixed point, which is the unique solution of Equation (1). □

3. The Stability and Rate of Convergence

Here, we introduced the stability and rate of convergence of the proposed scheme.

Lemma 3. 

Besides the conditions (i)–(iv), the infinite series ${\sum }_{i=0}^{\infty }{\mathrm{\Phi }}_i(u,t)$ is uniformly convergent to a continuous solution function $\mathrm{\Psi }(u,t)$.

Proof. 

We construct the sequence of functions ${\mathrm{\Psi }}_n(u,t)$ as

$$\begin{array}{cc}\hfill \mu {\mathrm{\Psi }}_n(u,t)=& F(u,t)+\lambda {\int }_0^t{\int }_{-1}^{1}f(t,\tau )k(w\left(u\right)-w\left(v\right))\gamma (u,v,t,\tau ,{\mathrm{\Psi }}_{n-1}(v,\tau ))\mathrm{d}v\mathrm{d}\tau \hfill \\ \hfill F(u,t)=& {\mathrm{\Psi }}_0(u,t).\hfill \end{array}$$

Then, we introduce

$${\mathrm{\Phi }}_n(u,t)={\mathrm{\Psi }}_n(u,t)-{\mathrm{\Psi }}_{n-1}(u,t),{\mathrm{\Phi }}_0(u,t)=F(u,t),$$

(8)

where

$${\mathrm{\Psi }}_n(u,t)=\sum _{i=0}^n{\mathrm{\Phi }}_n(u,t),n=1,2,\dots .$$

Using the properties of the modulus, and then with the aid of Formula (8), we have

$$\begin{array}{cc}\hfill \parallel {\mathrm{\Phi }}_n(u,t)\parallel & \le \frac{\left|\lambda \right|}{\left|\mu \right|}\varsigma \sigma .∥{\left[{\int }_{-1}^1{\int }_{-1}^1{\left|k(w\left(u\right)-w\left(v\right))\right|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}∥\hfill \\ \hfill & \times \underset{0\le t\le T}{max}{\int }_0^t{\left[{\int }_{-1}^1|{\mathrm{\Phi }}_{n-1}(v,\tau ){\left)\right|}^2\mathrm{d}v\right]}^{\frac{1}{2}}\mathrm{d}\tau .\hfill \end{array}$$

Hence, we obtain

$$\parallel {\mathrm{\Phi }}_n{(u,t)\parallel }_{L_2[-1,1]\times C[0,T]}\le \beta \parallel {\mathrm{\Phi }}_{n-1}(u,t)\parallel ;\beta =\left|\frac{\lambda }{\mu }\right|\varsigma \varkappa \sigma .$$

Using the conditions (i) and (ii) and the mathematical induction method, we obtain

$$\parallel {\mathrm{\Phi }}_n{(u,t)\parallel }_{L_2[-1,1]\times C[0,T]}\le {\beta }^n\parallel {\mathrm{\Phi }}_{n-1}(u,t)\parallel ;\beta =\left|\frac{\lambda }{\mu }\right|\varsigma \varkappa \sigma .$$

This bound makes the sequence $\left\{{\mathrm{\Phi }}_n(u,t)\right\}$ converge, and then, the sequence $\left\{{\mathrm{\Psi }}_n(u,t)\right\}$ converges. Hence, the infinite series

$$\mathrm{\Psi }(u,t)=\sum _{i=0}^{\infty }{\mathrm{\Phi }}_i(u,t),\forall t\in [0,T],$$

is uniformly convergent since the terms $\left\{{\mathrm{\Phi }}_i(u,t)\right\}$ are dominated by ${\beta }^i$. □

4. The System of Fredholm Integral Equations

The solution of Equation (1) is often reduced to a system of Fredholm integral equations using the quadrature method [36]. We divide the interval $[0,T],0\le t\le T,$ as $0=t_0<t_1<\cdots <t_m<\cdots <t_M=T,$ where $t=t_m,m=0,1,\dots ,M$ to obtain

$$\mu \mathrm{\Psi }(u,t_m)-\lambda {\int }_0^{t_m}{\int }_{-1}^{1}f(t_m,\tau )k(w\left(u\right)-w\left(v\right))\gamma (u,v,t_m,\tau ,\mathrm{\Psi }(v,\tau ))\mathrm{d}v\mathrm{d}\tau =F(u,t_m).$$

(9)

The term for the Volterra integral is as follows:

$$\begin{array}{cc}\hfill {\int }_0^{t_m}{\int }_{-1}^1& f(t_m,\tau )k(w\left(u\right)-w\left(v\right))\gamma (u,v,t_m,\tau ,\mathrm{\Psi }(v,\tau ))\mathrm{d}v\mathrm{d}\tau \hfill \\ \hfill & =\sum _{l=0}^m{\nu }_{l}f(t_m,t_l){\int }_{-1}^{1}k(w\left(u\right)-w\left(v\right))\gamma (u,v,t_m,t_l,\mathrm{\Psi }(v,t_l))\mathrm{d}v+O\left({\hslash }_m^{\ell +1}\right),\hfill \end{array}$$

(10)

where

$${\hslash }_m^{\ell +1}⟶0,\ell >0,{\hslash }_m=\underset{0\le l\le m}{max}{\Delta }_l\mathrm{and}{\Delta }_l=t_{l+1}-t_l.$$

The constant ℓ and the values of the weight formula ${\nu }_l$ depend on the number of derivatives $f(t,\tau )$, $\forall \tau \in [0,T],$ with respect to t.

• Using Equation (10) in Equation (9), we obtain

$$\mu \mathrm{\Psi }(u,t_m)-\lambda \sum _{l=0}^m{\nu }_{l}f(t_m,t_l){\int }_{-1}^{1}k(w\left(u\right)-w\left(v\right))\gamma (u,v,t_m,t_l,\mathrm{\Psi }(v,t_l))\mathrm{d}v=F(u,t_m),$$

(11)

using the notations below:

$$\mathrm{\Psi }(u,t_m)={\mathrm{\Psi }}_m\left(u\right),F(u,t_m)=F_m\left(u\right),f(t_m,t_l)=f_{m,l}.$$

Equation (11) can be rewritten in the following form:

$$\mu {\mathrm{\Psi }}_m\left(u\right)-\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^{1}k(w\left(u\right)-w\left(v\right)){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l\left(v\right))\mathrm{d}v=F_m\left(u\right).$$

(12)

When $\mu =0,$ we obtain a system of Fredholm integral equations of the first-type, whereas Equation (12) represents a system of Fredholm integral equations of the second-type when $\mu \ne 0$.

5. Chebyshev Polynomials

In this section, we resort to the use of techniques and spectral relations of the method of Chebyshev polynomials [37] to obtain a solution of the algebraic integral system (12). Let $T_i\left(u\right)=cos\left(i{cos}^{-1}u\right);u\in [-1,1];i\ge 0$ represent the first type of Chebyshev polynomials, while $U_i\left(u\right)=sin\left[(i+1){cos}^{-1}u\right]/sin\left({cos}^{-1}u\right),i\ge 0$ represents the second type of Chebyshev polynomials. It is well known that $T_i\left(u\right)$ forms an orthogonal sequence of functions concerning the weight function ${(1-u^2)}^{-1/2}$, while $U_i\left(u\right)$ forms an orthogonal sequence of functions concerning the weight function ${(1-u^2)}^{1/2}$.

We can apply the following well-known relations if the singular kernel of the integral equation is in the form of Carleman, ${|u-v|}^{-\alpha },0<\alpha <1$ (see Aleksandrovsk and Covalence [38]):

$${|u-v|}^{-\alpha }=\frac{ln|u-v|}{G(u,v)};G(u,v)={|u-v|}^{\alpha }ln|u-v|,$$

(13)

where $G(u,v)$ is a continuous function, where $u=v$; one of the important relations that can be used is the following well-known relation of Chebyshev polynomials (Gradstein and Ryzhik [39]).

$$\frac{\mathrm{d}}{\mathrm{d}u}{T}_i\left(u\right)=i{U}_{i-1}\left(u\right).$$

(14)

Here, we can use the Chebyshev polynomials [40] to solve the algebraic integral system (12), which naturally leads one to consider replacing the given $k\left(w\right(u)-w(v\left)\right)$ approximately with a kernel $k_n(w\left(u\right)-w\left(v\right))$ that should satisfy the condition:

$${\left\{{\int }_{-1}^1{\int }_{-1}^1{|k(w\left(u\right)-w\left(v\right))-k_n(w\left(u\right)-w\left(v\right))|}^2\mathrm{d}u\mathrm{d}v\right\}}^{\frac{1}{2}}\to 0,\mathrm{as}n\to \infty .$$

(15)

As a result, Equation (12) can be expressed in the following form of an algebraic system:

$$\mu {\mathrm{\Psi }}_m^n\left(u\right)-\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^1{k}_n(w\left(u\right)-w\left(v\right)){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))\mathrm{d}v+R_n=F_m\left(u\right).$$

(16)

Consequently, the estimated error can be calculated using the following equation:

$$R_n=|{\mathrm{\Psi }}_m\left(u\right)-{\mathrm{\Psi }}_m^n\left(u\right)|\to 0asn\to \infty .$$

(17)

Write the kernel of (16) in the following form for using the spectral relationships:

$$k_n(w\left(u\right)-w\left(v\right))=\sum _{j=0}^n{T}_j\left(u\right)T_j\left(v\right),$$

(18)

where $T_j\left(x\right)$ is the Chybeshev polynomials of the first kind and degree j.

• Using (18) in (16), we have

$$\mu {\mathrm{\Psi }}_m^n\left(u\right)-\lambda \sum _{l=0}^m\sum _{j=0}^n{\nu }_l{f}_{m,l}{T}_j\left(u\right){\int }_{-1}^1{T}_j\left(v\right){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))\mathrm{d}v+R_n=F_m\left(u\right).$$

(19)

Formula (19) is an algebraic integral system that may be solved numerically. We put $m=0$ in the system (19), and we first obtain the value of ${\mathrm{\Psi }}_0^n\left(u\right)$.

$$\mu {\mathrm{\Psi }}_0^n\left(u\right)-\lambda \sum _{j=0}^n{\nu }_0{f}_{0,0}{T}_j\left(u\right){\int }_{-1}^1{T}_j\left(v\right){\gamma }_{0,0}(u,v,{\mathrm{\Psi }}_0^n\left(v\right))\mathrm{d}v+R_n=F_0\left(u\right).$$

(20)

After obtaining the solution of Equation (20), we will enable the utilization of the mathematical induction to obtain the general solution of (19).

In a special case of the original form, namely

$$\mu {\mathrm{\Psi }}_m^n\left(u\right)-\lambda \sum _{l=0}^m\sum _{j=0}^n{\nu }_l{f}_{m,l}{T}_j\left(u\right){\int }_{-1}^1{T}_j\left(v\right){\xi }_{m,l}(u,v){\mathrm{\Psi }}_l^n\left(v\right)\mathrm{d}v+R_n=F_m\left(u\right),$$

(21)

it attracted the interest of many researchers. The unknown function ${\mathrm{\Psi }}_m^n\left(u\right)$ is considered to have the following form:

$${\mathrm{\Psi }}_m^n\left(u\right)=A\left(u\right)B\left(u\right);A\left(u\right)={(1-u^2)}^{-\frac{1}{2}},$$

(22)

where $A\left(u\right)$ represents the weight function of $T_i\left(u\right)$, and $B\left(u\right)$ is the unknown function. Therefore, we obtain

$${\mathrm{\Psi }}_{m,\wp }^n\left(u\right)=\sum _{i=0}^{\wp }{\Lambda }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}},$$

(23)

where $T_i\left(u\right)$ are the first-kind of Chebyshev polynomials, and ${\Lambda }_{i,m}$ are constants. Additionally, the well-known function $F_m\left(u\right)$ can be approximated in the following form:

$$F_{m,\wp }\left(u\right)=\sum _{i=0}^{\wp }{\aleph }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}},$$

(24)

where the coefficients ${\aleph }_{i,m};i\ge 0,$ are constants, which can be found from

$$\begin{array}{c}\hfill {\aleph }_{i,m}=\left\{\begin{array}{cc}\frac{2}{\pi }{\int }_{-1}^1{F}_m\left(u\right)T_i\left(u\right)du;\hfill & i\ne 0,\hfill \\ \frac{1}{\pi }{\int }_{-1}^1{F}_m\left(u\right)\mathrm{d}u;\hfill & i=0.\hfill \end{array}\right.\end{array}$$

(25)

Using Equations (23) and (24) in Equation (21), we obtain

$$\begin{array}{cc}\hfill \mu \sum _{i=0}^{\wp }{\Lambda }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}}-& \lambda \sum _{l=0}^m\sum _{j=0}^n\sum _{i=0}^{\wp }{\nu }_l{f}_{m,l}{T}_j\left(u\right){\Lambda }_{i,l}{\int }_{-1}^1{T}_j\left(v\right){\xi }_{m,l}(u,v)\frac{T_i\left(v\right)}{\sqrt{1-v^2}}\mathrm{d}v\hfill \\ \hfill & =\sum _{i=0}^{\wp }{\aleph }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}},\hfill \end{array}$$

(26)

which satisfies the orthogonal relation as follows:

$$\begin{array}{c}\hfill {\int }_{-1}^1\frac{T_i\left(u\right)T_j\left(u\right)}{\sqrt{1-u^2}}\mathrm{d}u=\left\{\begin{array}{cc}0,\hfill & i\ne j\hfill \\ \pi ,\hfill & i=j=0\hfill \\ \frac{\pi }{2},\hfill & i=j\ne 0.\hfill \end{array}\right.\end{array}$$

(27)

$$T_i\left(u\right)T_j\left(u\right)=\frac{1}{2}[T_{i+j}\left(u\right)+T_{|i-j|}\left(u\right)],(i,j\ge 0).$$

(28)

$$\begin{array}{c}\hfill {\int }_{-1}^1{T}_i\left(u\right)\mathrm{d}u=\left\{\begin{array}{cc}\frac{2}{1-i^2},\hfill & i=0,2,4,...\hfill \\ 0,\hfill & i=1,3,5,....\hfill \end{array}\right.\end{array}$$

(29)

If ${\xi }_{m,l}(u,v)=1$ in Equation (26), then the solution of this equation can be obtained after discussing the following:

• Case (i): For $i=0,j=0$, we obtain

  $$\mu {\Lambda }_{0,m}\frac{T_0\left(u\right)}{\sqrt{1-u^2}}-\lambda \pi \sum _{l=0}^m{\nu }_l{f}_{m,l}{T}_0\left(u\right){\Lambda }_{0,l}={\aleph }_{0,m}\frac{T_0\left(u\right)}{\sqrt{1-u^2}},$$

  (30)

  multiplying both sides of (30) by the term $T_j\left(u\right)\mathrm{d}u$, then integrating the result from $-1$ to 1, yield the following result:

  $$\mu {\Lambda }_{0,m}-\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\Lambda }_{0,l}={\aleph }_{0,m}.$$

  (31)
• Case (ii): Let $i=0,j\ne 0$; after using the orthogonal relation, Equation (26) tends to

  $$\begin{array}{cc}\hfill \mu {\Lambda }_{0,m}\frac{T_0\left(u\right)}{\sqrt{1-u^2}}& ={\aleph }_{0,m}\frac{T_0\left(u\right)}{\sqrt{1-u^2}};j\ge 1,\hfill \\ \hfill \mu {\Lambda }_{0,m}& ={\aleph }_{0,m},\hfill \end{array}$$

  (32)

  where

  $${\aleph }_{0,m}=\frac{1}{\pi }{\int }_{-1}^1{F}_m\left(u\right)du.$$
• Case (iii): For $i\ne 0,j=0$, we deduce

  $$\begin{array}{cc}\hfill \mu {\Lambda }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}}& ={\aleph }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}};i\ge 1,\hfill \\ \hfill \mu {\Lambda }_{i,m}& ={\aleph }_{i,m},\hfill \end{array}$$

  (33)

  where

  $${\aleph }_{i,m}=\frac{2}{\pi }{\int }_{-1}^1{F}_m\left(u\right)T_i\left(u\right)du.$$
• Case (iv): For $i=j\ne 0;i,j\ge 1$, we can confirm

  $$\begin{array}{c}\hfill \mu {\Lambda }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}}-\frac{\lambda \pi }{2}\sum _{l=0}^m{\nu }_l{f}_{m,l}{T}_i\left(u\right){\Lambda }_{i,l}={\aleph }_{i,m}\frac{T_i\left(u\right)}{\sqrt{1-u^2}};i\ge 1.\end{array}$$

  (34)

  Multiplying both sides of (34) by the term $T_j\left(u\right)du$, then integrating the result from $-1$ to 1, we yield the following result:

  $$\mu {\Lambda }_{i,m}-\frac{2\lambda (8i^2-1)}{(4i-1)(4i+1)}\sum _{l=0}^m{\nu }_l{f}_{m,l}{\Lambda }_{i,l}={\aleph }_{i,m};i\ge 1.$$

  (35)

6. Convergence Analysis

In this section, under some conditions, we will provide proof of the existence of the unique numerical solution of the system and obtain the truncation error of the numerical solution. These aims will be achieved using the outlined theorems.

6.1. The Existence and Unique Numerical Solution

Lemma 4. 

Let $k_n(w\left(u\right)-w\left(v\right))\in L_2([-1,1]\times [-1,1])$ with the condition (15); then, the following condition is satisfied:

$${\left[{\int }_{-1}^1{\int }_{-1}^1{\left|k_n(w\left(u\right)-w\left(v\right))\right|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}\le \varkappa ;\forall n>n_0,n_0\in N,\varkappa \mathit{is}a\mathit{constant}.$$

(36)

Proof. 

We apply the following formula to prove this lemma:

$$\begin{array}{cc}\hfill {\int }_{-1}^1{\int }_{-1}^1& |k_n{(w\left(u\right)-w\left(v\right))|}^{2}du\mathrm{d}v\le \hfill \\ \hfill & {\int }_{-1}^1{\int }_{-1}^1{|k_n(w\left(u\right)-w\left(v\right))-k(w\left(u\right)-w\left(v\right))+k(w\left(u\right)-w\left(v\right))|}^{2}du\mathrm{d}v,\hfill \end{array}$$

then

$$\begin{array}{cc}\hfill {\left[{\int }_{-1}^1{\int }_{-1}^1{\left|k_n(w\left(u\right)-w\left(v\right))\right|}^{2}du\mathrm{d}v\right]}^{\frac{1}{2}}\le & \left[{\int }_{-1}^1{\int }_{-1}^1\left[\right|k(w\left(u\right)-w\left(v\right))-k_n(w\left(u\right)-w\left(v\right))|\right.\hfill \\ \hfill & +{\left.{\left|k(w\left(u\right)-w\left(v\right))\right|]}^{2}du\mathrm{d}v\right]}^{\frac{1}{2}},\hfill \end{array}$$

and using condition (15), we obtain

$$\forall \alpha >0,\exists n_0\in N:{\left[{\int }_{-1}^1{\int }_{-1}^1{|k(w\left(u\right)-w\left(v\right))-k_n(w\left(u\right)-w\left(v\right))|}^{2}du\mathrm{d}v\right]}^{\frac{1}{2}}<\alpha ,\forall n>n_0.$$

Applying Minkowski’s inequality and using condition $\left(i\right)$, we obtain

$$\forall \alpha >0,\exists n_0\in N:{\left[{\int }_{-1}^1{\int }_{-1}^1{\left|k_n(w\left(u\right)-w\left(v\right))\right|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}\le \varkappa ,\forall n>n_0.$$

□

Theorem 2. 

Assume that the Lemma 4 and conditions of Theorem 1 are verified; then, the sequence of operators ${\overline{V}}_n$ defined using

$${\overline{V}}_n\mathrm{\Psi }(u,t)=\frac{1}{\mu }F(u,t)+\frac{\lambda }{\mu }{\int }_0^t{\int }_{-1}^{1}f(t,\tau )k_n(w\left(u\right)-w\left(v\right))\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau ))\mathrm{d}v\mathrm{d}\tau$$

(37)

maps the set $S_r$ continuously into itself for each $n>n_0.$

Proof. 

Firstly, for the normality, we use formula (37) to obtain

$$\parallel {\overline{V}}_n\mathrm{\Psi }(u,t)\parallel \le \frac{1}{\left|\mu \right|}\parallel F(u,t)\parallel +\frac{\left|\lambda \right|}{\left|\mu \right|}∥{\int }_0^t{\int }_{-1}^1\left|f(t,\tau )\right||k_n(w\left(u\right)-w\left(v\right))\left|\right|\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau ))|\mathrm{d}v\mathrm{d}\tau ∥.$$

Using the conditions (i)–(iv-a) and (15), the above inequality takes the following form

$$\parallel {\overline{V}}_n\psi (u,t)\parallel \le \frac{\varpi }{\left|\mu \right|}+\beta \parallel \psi (u,t)\parallel ;\beta =\frac{\left|\lambda \right|}{\left|\mu \right|}\varsigma \varkappa \sigma .$$

(38)

According to inequality (38), the operator $\overline{V}$ transforms the ball $S_r$ into itself.

Secondly, for the continuity, we suppose that the functions ${\psi }_1(u,t),{\psi }_2(u,t)$ satisfy formula (37); then,

$$\begin{array}{c}\parallel {\overline{V}}_n{\mathrm{\Psi }}_1(u,t)-{\overline{V}}_n{\mathrm{\Psi }}_2(u,t)\parallel \hfill \\ \le \frac{\left|\lambda \right|}{\left|\mu \right|}∥{\int }_0^t{\int }_{-1}^1\left|f(t,\tau )\right||k_n(w\left(u\right)-w\left(v\right))\left|\right|\gamma (u,v,t,\tau ,{\mathrm{\Psi }}_1(v,\tau ))-\gamma (u,v,t,\tau ,{\mathrm{\Psi }}_2(v,\tau ))|\mathrm{d}v\mathrm{d}\tau ∥.\hfill \end{array}$$

Using the conditions (i)-(iv-a) and (15), the last inequality becomes

$$\parallel {\overline{V}}_n{\mathrm{\Psi }}_1(u,t)-{\overline{V}}_n{\mathrm{\Psi }}_2(u,t)\parallel \le \frac{\left|\lambda \right|}{\left|\mu \right|}\varsigma \varkappa \sigma \parallel {\mathrm{\Psi }}_1(u,t)-{\psi }_2(u,t)\parallel ,\forall n>n_0.$$

□

6.2. Error Analysis of the Numerical Solution

Consider the approximate solution to satisfy the integral equation:

$$\mu {\mathrm{\Psi }}_m^n\left(u\right)-\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^1{k}_n(w\left(u\right)-w\left(v\right)){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))\mathrm{d}v=F_m\left(u\right).$$

(39)

Then, the error is

$$\begin{array}{cc}\hfill R_n& =\mu [{\mathrm{\Psi }}_m\left(u\right)-{\mathrm{\Psi }}_m^n\left(u\right)]\hfill \\ \hfill & =\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^1[k(w\left(u\right)-w\left(v\right)){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l\left(v\right))-k_n(w\left(u\right)-w\left(v\right)){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))]\mathrm{d}v.\hfill \end{array}$$

We assume the following conditions in order to discuss the error:

a.

The kernel of position satisfies a condition:

$$\begin{array}{cc}\hfill & {\left[{\int }_{-1}^1{\int }_{-1}^1{|k(w\left(u\right)-w\left(v\right))-k_n(w\left(u\right)-w\left(v\right))|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}\hfill \\ \hfill & ={\left[{\int }_{-1}^1{\int }_{-1}^1{\left|k_{n+1}(w\left(u\right)-w\left(v\right))\right|}^2\mathrm{d}u\mathrm{d}v\right]}^{\frac{1}{2}}\le {\varkappa }^{*}.\hfill \end{array}$$

b.

The kernel of time satisfies a condition:

$${\left[\sum _{l=0}^m{\nu }_l^2{f}_{m,l}^2\right]}^{\frac{1}{2}}\le {\varsigma }^{*}.$$

c.

The nonlinear continuous function $\gamma (u,v,t,\tau ,\mathrm{\Psi }(v,\tau \left)\right)$ satisfies a condition:

$$\begin{array}{cc}\hfill \underset{m}{max}{\int }_{-1}^1\left|{\gamma }_{m,m}(u,v,{\mathrm{\Psi }}_m\left(v\right))-{\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_m^n\left(v\right))\right|dv& \le \underset{m}{max}{\int }_{-1}^1\left|{\mathrm{\Psi }}_m\left(v\right)-{\mathrm{\Psi }}_m^n\left(v\right)\right|dv\hfill \\ \hfill & =\underset{m}{max}{\int }_{-1}^1\left|{\mathrm{\Psi }}_m^{n+1}\left(v\right)\right|dv={\sigma }^{*}.\hfill \end{array}$$

Theorem 3. 

The error of Equation (1) is stable under the conditions (a)–(c) and estimated to be

$$\parallel R_n\parallel \le |\lambda {\varsigma }^{*}|(\varkappa +{\varkappa }^{*}){\sigma }^{*}.$$

(40)

Proof. 

After assuming the approximate solution $\mathrm{\Psi }(u,v)=\mathrm{\Psi }(u,t_m)={\mathrm{\Psi }}_m\left(u\right)$, the error takes the form

$$\begin{array}{cc}\hfill R_n& =\mu [{\mathrm{\Psi }}_m\left(u\right)-{\mathrm{\Psi }}_m^n\left(u\right)]\hfill \\ \hfill & =\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^1[k(w\left(u\right)-w\left(v\right)){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l\left(v\right))-k_n(w\left(u\right)-w\left(v\right)){\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))]\mathrm{d}v.\hfill \end{array}$$

We adapt the above equation to take the following form:

$$\begin{array}{cc}\hfill R_n& =\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^1[k(w\left(u\right)-w\left(v\right))\{{\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l\left(v\right))-{\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))\}\hfill \\ \hfill & +\{k(w\left(u\right)-w\left(v\right))-k_n(w\left(u\right)-w\left(v\right))\}{\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))]\mathrm{d}v.\hfill \end{array}$$

Using the properties of the norm, we obtain

$$\begin{array}{cc}\hfill \parallel R_n\parallel & \le ∥\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^{1}k(w\left(u\right)-w\left(v\right))\{{\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l\left(v\right))-{\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))\}∥\hfill \\ \hfill & +∥\lambda \sum _{l=0}^m{\nu }_l{f}_{m,l}{\int }_{-1}^1\{k(w\left(u\right)-w\left(v\right))-k_n(w\left(u\right)-w\left(v\right))\}{\gamma }_{m,l}(u,v,{\mathrm{\Psi }}_l^n\left(v\right))\mathrm{d}v∥.\hfill \end{array}$$

Using the above conditions,

$$\parallel R_n\parallel \le |\lambda {\varsigma }^{*}|(\varkappa +{\varkappa }^{*}){\sigma }^{*}.$$

□

7. Numerical Applications

In this section, we illustrate the Chebyshev polynomials that are explained in Section 2 and Section 4 considering the following three examples. We solve these examples using the program Wolfram Mathematica 10.

Example 1. 

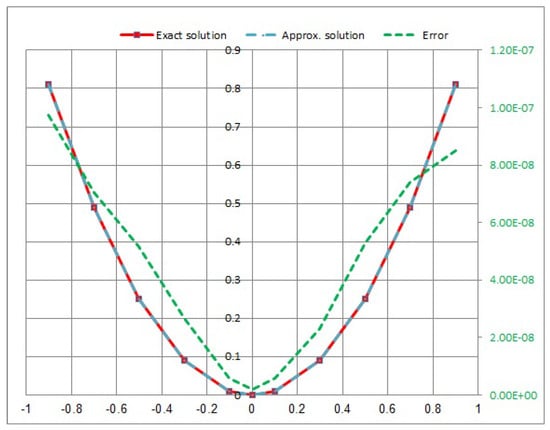
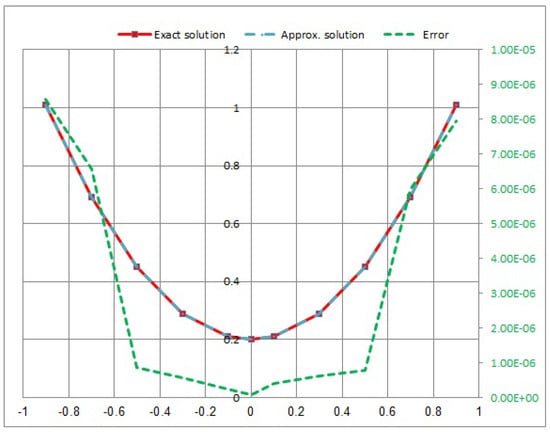
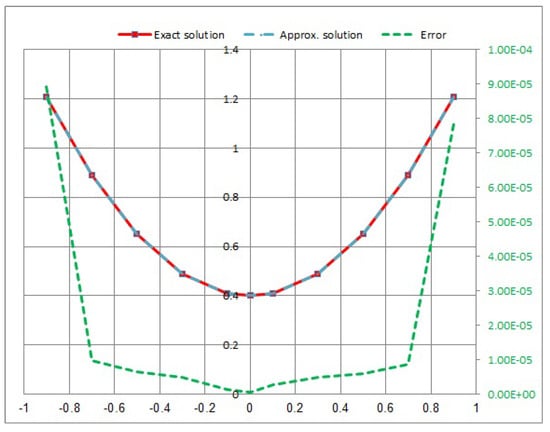
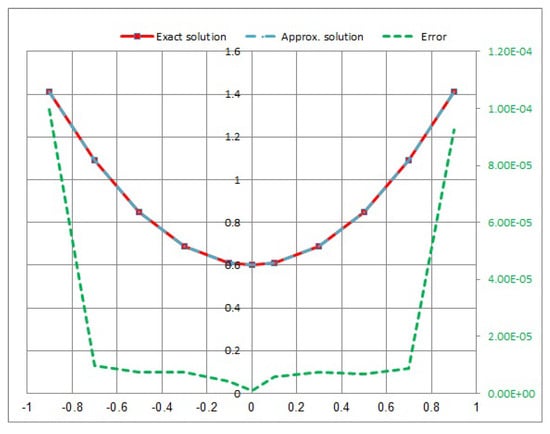
Consider the following NVFIE:

$$30\mathrm{\Psi }(u,t)-2{\int }_0^t{\int }_{-1}^{1}t{\tau }^2(e^{u^2}-e^{v^2})\left(uvs\text{.}t\tau {\mathrm{\Psi }}^2(v,\tau )\right)\mathrm{d}v\mathrm{d}\tau =F(u,t),$$

(41)

where the function $F(u,t)$ has presented by letting $\mathrm{\Psi }(u,t)=u^2+t$ as an exact solution and $\lambda =2$. The constant $\mu =30$, describing Equation (41). The function of time is $f(t,\tau )=t{\tau }^2$, while the kernel of position is $k(w\left(u\right)-w\left(v\right))=(e^{u^2}-e^{v^2})$. The fundamental surface of the material is represented by the given function $F(u,t)$, whereas the unknown function is $\mathrm{\Psi }(u,t)$. Equation (41) will be computed at time $t\in [0,0.6]$. The proposed numerical method is used with $M=3$ and $T=0.6$.

In

Table 1. Error results of the quadrature method with $0\le t\le 0.6$.

u	|Exact-Approx.|${}_{{\mathit{t}}_0}$	|Exact-Approx.|${}_{{\mathit{t}}_1}$	|Exact-Approx.|${}_{{\mathit{t}}_2}$	|Exact-Approx.|${}_{{\mathit{t}}_3}$
−0.9	9.75485 $\times {10}^{-8}$	8.57458 $\times {10}^{-6}$	8.92185 $\times {10}^{-5}$	9.96543 $\times {10}^{-5}$
−0.7	7.03693 $\times {10}^{-8}$	6.58423 $\times {10}^{-6}$	9.63241 $\times {10}^{-6}$	9.86545 $\times {10}^{-6}$
−0.5	5.61475 $\times {10}^{-8}$	8.52387 $\times {10}^{-7}$	6.39556 $\times {10}^{-6}$	7.51273 $\times {10}^{-6}$
−0.3	2.46587 $\times {10}^{-8}$	5.26217 $\times {10}^{-7}$	4.78569 $\times {10}^{-6}$	7.42428 $\times {10}^{-6}$
−0.1	5.75813 $\times {10}^{-9}$	2.93561 $\times {10}^{-7}$	1.25865 $\times {10}^{-6}$	4.23171 $\times {10}^{-6}$
0	1.75434 $\times {10}^{-9}$	8.56468 $\times {10}^{-8}$	5.64758 $\times {10}^{-7}$	8.47585 $\times {10}^{-7}$
0.1	5.89767 $\times {10}^{-9}$	3.89657 $\times {10}^{-7}$	2.58769 $\times {10}^{-6}$	5.87418 $\times {10}^{-6}$
0.3	2.53144 $\times {10}^{-8}$	6.03217 $\times {10}^{-7}$	4.78557 $\times {10}^{-6}$	7.52431 $\times {10}^{-6}$
0.5	5.22873 $\times {10}^{-8}$	7.84574 $\times {10}^{-7}$	5.63264 $\times {10}^{-6}$	6.85768 $\times {10}^{-6}$
0.7	7.41562 $\times {10}^{-8}$	5.98784 $\times {10}^{-6}$	8.54282 $\times {10}^{-6}$	8.85441 $\times {10}^{-6}$
0.9	8.52129 $\times {10}^{-8}$	7.96546 $\times {10}^{-6}$	7.85668 $\times {10}^{-5}$	9.24574 $\times {10}^{-5}$

, we illustrate the changes that occur in the absolute error ${|Exact-Approx.|}_{t_m},m=0,$$1,2,3$ for various values of u using the quadrature method with $M=3$ in the interval $[0,0.6]$.

In Figure 1, Figure 2, Figure 3 and Figure 4, we provided a comparison between the approximate solution, the exact solution, and the absolute error of the solution using the quadrature with different values of t.

Example 2. 

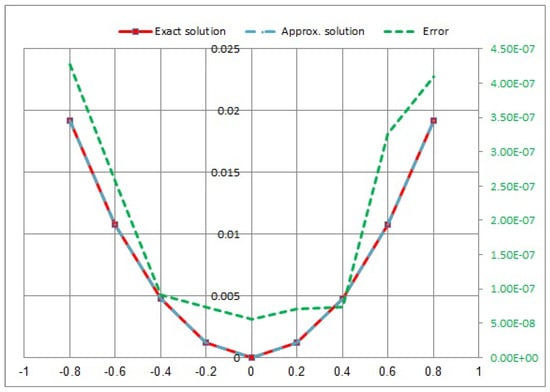
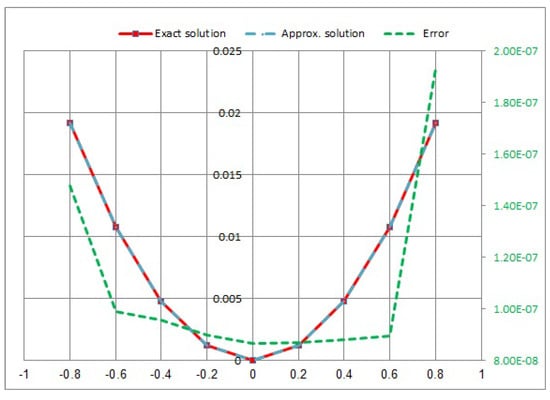
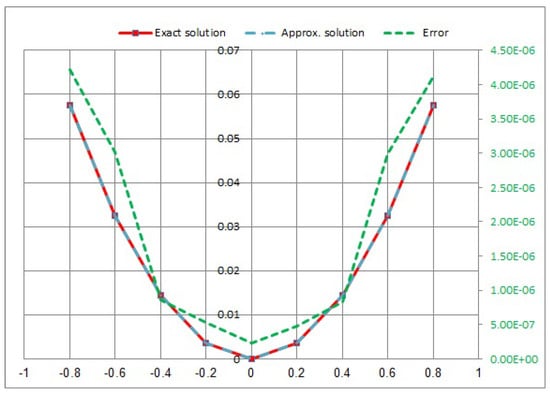
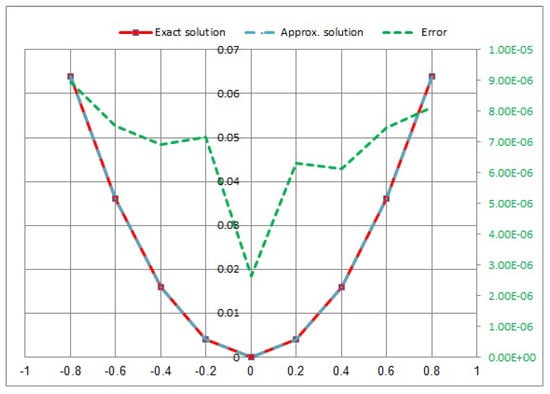
Consider the NVFIE when $\mu =10$ and $\lambda =4$:

$$10\mathrm{\Psi }(u,t)-4{\int }_0^t{\int }_{-1}^1{t}^2\tau \left(\frac{uv}{u-v}\right)(u^2-v^2)\mathrm{\Psi }(v,\tau )\mathrm{d}v\mathrm{d}\tau =F(u,t),$$

(42)

where the function $F(u,t)$ is specified by laying $\mathrm{\Psi }(u,t)=u^{2}t$ as an exact solution. The kernel of position is $k(w\left(u\right)-w\left(v\right))=\left(\frac{uv}{u-v}\right)$, while the kernel of time is $f(t,\tau )=t^2\tau$. Equation (42) will be computed for $n=20,\wp =20$.

Table 2. Numerical and error results of the Chebyshev polynomials with $0\le t\le 0.1$.

u	Error of $\mathit{t}=0.03$	Error of $\mathit{t}=0.06$	Error of $\mathit{t}=0.09$	Error of $\mathit{t}=0.1$
−0.8	4.26831 $\times {10}^{-7}$	1.47857 $\times {10}^{-7}$	4.21364 $\times {10}^{-6}$	8.96321 $\times {10}^{-6}$
−0.6	2.58214 $\times {10}^{-7}$	9.89765 $\times {10}^{-8}$	3.02146 $\times {10}^{-6}$	7.52301 $\times {10}^{-6}$
−0.4	9.20135 $\times {10}^{-8}$	9.56212 $\times {10}^{-8}$	8.63254 $\times {10}^{-7}$	6.92541 $\times {10}^{-6}$
−0.2	7.41234 $\times {10}^{-8}$	8.96326 $\times {10}^{-8}$	5.32874 $\times {10}^{-7}$	7.15246 $\times {10}^{-6}$
0	5.64123 $\times {10}^{-8}$	8.64129 $\times {10}^{-8}$	2.36581 $\times {10}^{-7}$	2.63214 $\times {10}^{-7}$
0.2	7.08745 $\times {10}^{-8}$	8.69546 $\times {10}^{-8}$	4.82031 $\times {10}^{-7}$	6.30254 $\times {10}^{-6}$
0.4	7.41233 $\times {10}^{-8}$	8.80231 $\times {10}^{-8}$	8.36521 $\times {10}^{-7}$	6.12543 $\times {10}^{-6}$
0.6	3.25647 $\times {10}^{-7}$	8.93541 $\times {10}^{-8}$	2.98652 $\times {10}^{-6}$	7.45213 $\times {10}^{-6}$
0.8	4.10258 $\times {10}^{-7}$	1.93254 $\times {10}^{-7}$	4.12984 $\times {10}^{-5}$	8.12984 $\times {10}^{-6}$

presents the absolute error of Chebyshev polynomials for the different values of u with $0\le t\le 0.1$.

In Figure 5, Figure 6, Figure 7 and Figure 8, we showed a comparison between the approximate solution, the exact solution, and the absolute error of the solution using the presented numerical approaches with different values of t.

Example 3. 

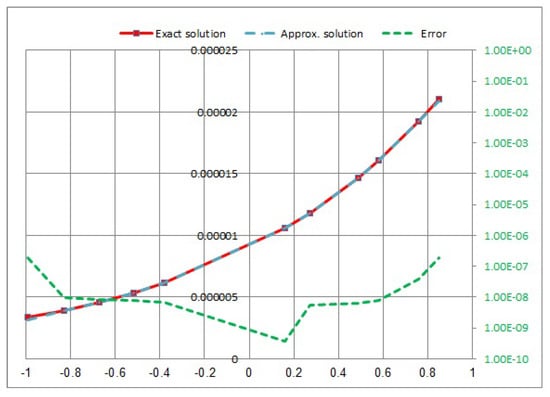
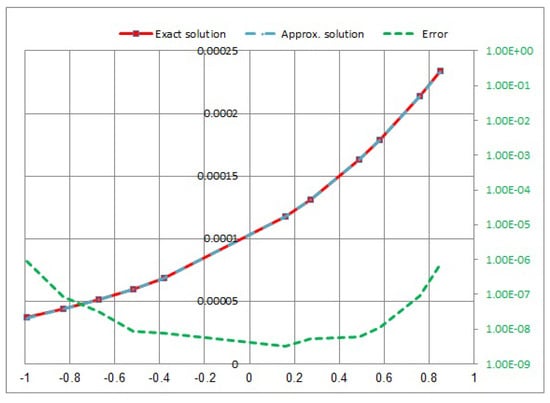
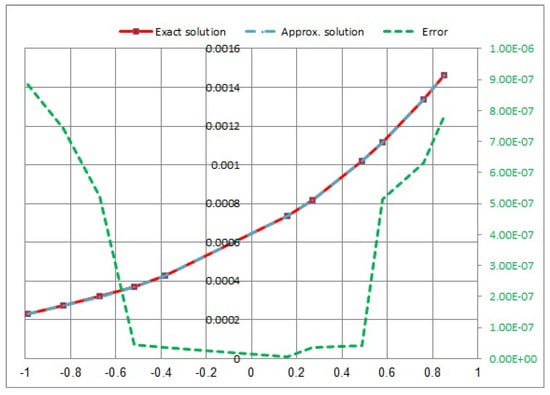
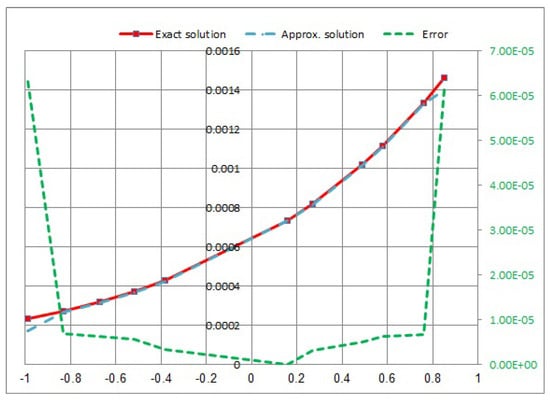
Consider the following NVFIE with the logarithmic kernel:

$$0.5152\mathrm{\Psi }(u,t)-0.001{\int }_0^t{\int }_{-1}^1{t}^2{\tau }^2(ln|u-v\left|\right)\mathrm{\Psi }(v,\tau )\mathrm{d}v\mathrm{d}\tau =F(u,t),$$

(43)

where the function $F(u,t)$ has presented by letting $\mathrm{\Psi }(u,t)=t^2+e^u$ as an accurate solution, the kernel of singular is $k\left(w\right(u)-w(v\left)\right)=\left(\ln \right|u-v\left|\right)$, and the kernel of time is $f(t,\tau )=t^2{\tau }^2$. Equation (43) will be computed four different times: $t_0\in [0,0.006],t_1\in [0,0.02],t_2\in [0,0.05]$, and $t_3\in [0,0.09]$ for $n=50,\wp =50$.

To obtain the solution of an integral Equation (43), we use the approximate kernel form (18).

Table 3. Numerical and error results of the Chebyshev polynomials with four different times: $t_0,t_1,t_2$, and $t_3$.

u	Error in ${\mathit{t}}_0$	Error in ${\mathit{t}}_1$	Error in ${\mathit{t}}_2$	Error in ${\mathit{t}}_3$
$-0.99$	1.85746 $\times {10}^{-7}$	8.76325 $\times {10}^{-7}$	8.83697 $\times {10}^{-7}$	6.32154 $\times {10}^{-5}$
−0.83	9.47854 $\times {10}^{-9}$	8.52365 $\times {10}^{-8}$	7.41235 $\times {10}^{-7}$	6.93254 $\times {10}^{-6}$
−0.67	8.61543 $\times {10}^{-9}$	3.25483 $\times {10}^{-8}$	5.23147 $\times {10}^{-7}$	6.32154 $\times {10}^{-6}$
−0.52	7.64423 $\times {10}^{-9}$	8.45821 $\times {10}^{-9}$	4.36258 $\times {10}^{-8}$	5.62147 $\times {10}^{-6}$
−0.38	6.58477 $\times {10}^{-9}$	7.52314 $\times {10}^{-9}$	3.56214 $\times {10}^{-8}$	3.26984 $\times {10}^{-6}$
0.16	3.65215 $\times {10}^{-10}$	3.12754 $\times {10}^{-9}$	6.12453 $\times {10}^{-9}$	5.63021 $\times {10}^{-8}$
0.27	5.69821 $\times {10}^{-9}$	5.29475 $\times {10}^{-9}$	3.56214 $\times {10}^{-8}$	3.14752 $\times {10}^{-6}$
0.49	6.32154 $\times {10}^{-9}$	5.96872 $\times {10}^{-9}$	4.21235 $\times {10}^{-8}$	4.96235 $\times {10}^{-6}$
0.58	7.92315 $\times {10}^{-9}$	1.12548 $\times {10}^{-8}$	5.14258 $\times {10}^{-7}$	6.23154 $\times {10}^{-6}$
0.76	3.95426 $\times {10}^{-8}$	9.15347 $\times {10}^{-8}$	6.32514 $\times {10}^{-7}$	6.63215 $\times {10}^{-6}$
0.85	1.85465 $\times {10}^{-7}$	7.58479 $\times {10}^{-7}$	7.81548 $\times {10}^{-7}$	6.14789 $\times {10}^{-5}$

presents the absolute error of the Chebyshev polynomials for different values of u with $n=50,\wp =50$.

In Figure 9, Figure 10, Figure 11 and Figure 12, we showed a comparison between the approximate solution, the exact solution, and the absolute error of the solution using the presented numerical approaches for $n=50,\wp =50$ with different values of t.

Example 4. 

Consider the following NVFIE:

$$\mathrm{\Psi }(u,t)=tu+0.26t^5{u}^3+0.7u{\int }_0^t{\int }_{-1}^{1}t\tau {(u-v)}^{3}v{\mathrm{\Psi }}^2(v,\tau )\mathrm{d}v\mathrm{d}\tau ,$$

(44)

The constant $\mu =1$, describing Equation (44). The function of time is $f(t,\tau )=t\tau$, while the kernel of position is $k(w\left(u\right)-w\left(v\right))={(u-v)}^3$. The fundamental surface of the material is represented as the given function $F(u,t)=tu+0.26t^5{u}^3$, whereas the unknown function is $\mathrm{\Psi }(u,t)$. Equation (44) will be computed at time $t\in [0,0.05]$. The proposed numerical method is used with $M=6,n=30,\wp =30$, and $T=0.0.05$.

In

Table 4. Numerical solution of Equation (44) with $0\le t\le 0.05$.

u	Approx.|${}_{\mathit{t}=0}$	Approx.|${}_{\mathit{t}=0.01}$	Approx.|${}_{\mathit{t}=0.02}$	Approx.|${}_{\mathit{t}=0.03}$	Approx.|${}_{\mathit{t}=0.04}$	Approx.|${}_{\mathit{t}=0.05}$
−1.00	0	0.01	0.02	0.03	0.0400001	0.0500002
−0.95	0	0.0095	0.019	0.0285	0.038	0.0475001
−0.71	0	0.0071	0.0142	0.0213	0.0284	0.0355001
−0.54	0	0.0054	0.0108	0.0162	0.0216	0.027
−0.38	0	0.0038	0.0076	0.0114	0.0152	0.019
0.00	0	0	0	0	0	0
0.26	0	0.0026	0.0052	0.0078	0.0104	0.013
0.43	0	0.0043	0.0086	0.0129	0.0172	0.0215
0.65	0	0.0065	0.013	0.0195	0.026	0.0325001
0.86	0	0.0086	0.0172	0.0258	0.0344	0.0430001
0.99	0	0.0099	0.0198	0.0297	0.0396001	0.0495002

, we illustrate the changes that occur in the numerical solution ${|}_{t_m},m=0,1,2,3,4,5$ for various values of u using the proposed numerical with $M=6,n=30,\wp =30$, and $T=0.0.05$ in the interval $[0,0.05]$.

Example 5. 

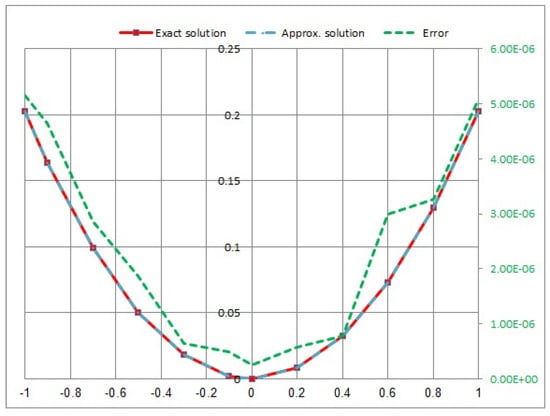
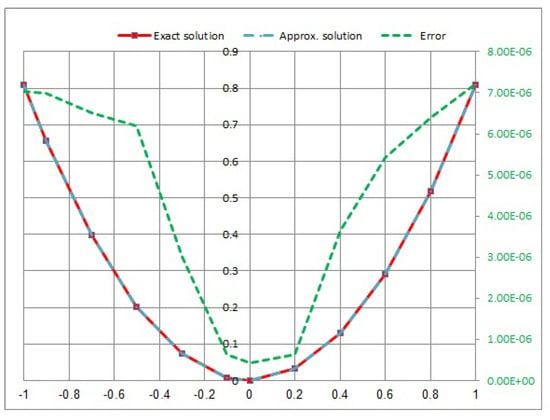
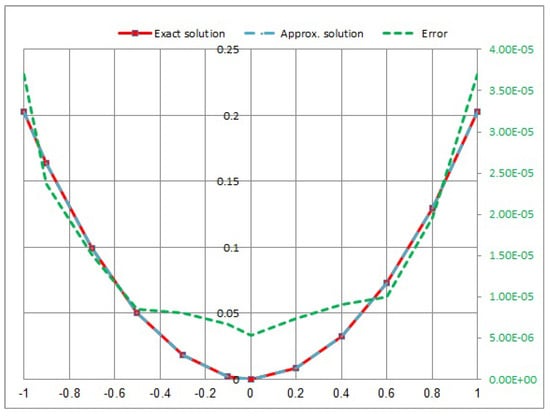
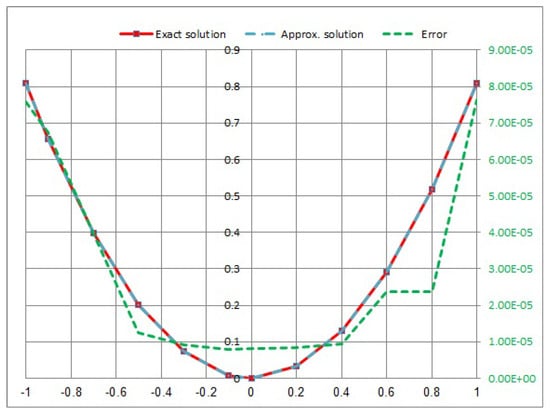
Consider the following NVFIE with the Carleman kernel:

$$0.8\mathrm{\Psi }(u,t)-0.021{\int }_0^t{\int }_{-1}^1{t}^2{\tau }^{2}k(w\left(u\right)-w\left(v\right))\mathrm{\Psi }(v,\tau )\mathrm{d}v\mathrm{d}\tau =F(u,t),$$

(45)

where the function $F(u,t)$ has presented by letting $\mathrm{\Psi }(u,t)=u^2{t}^2$ as an accurate solution.

The kernel of singular is taken in the Carleman form as follows:

$$k(w\left(u\right)-w\left(v\right))={|u-v|}^{-\alpha },0<\alpha <1,$$

where α is named the Poisson rate, and in this case, the kernel is called the weakly singular kernel. Applying the quadrature method by taking $M=2$, then using the proposed numerical with $n=25,\wp =25$ we obtain the convergent solution of Equation (45).

The numerical results of Example 5 are shown in

Table 5. Numerical results of Example 5 with different $\alpha$.

	$\mathit{\alpha }=0.15$		$\mathit{\alpha }=0.35$
$\mathit{u}$	Error in $\mathit{t}=\mathbf{0}.\mathbf{45}$	Error in $\mathit{t}=\mathbf{0}.\mathbf{9}$	Error in $\mathit{t}=\mathbf{0}.\mathbf{45}$	Error in $\mathit{t}=\mathbf{0}.\mathbf{9}$
−1.0	5.15478 $\times {10}^{-6}$	7.02587 $\times {10}^{-6}$	3.69851 $\times {10}^{-5}$	7.58742 $\times {10}^{-5}$
−0.9	4.63897 $\times {10}^{-6}$	6.98521 $\times {10}^{-6}$	2.36823 $\times {10}^{-5}$	6.74185 $\times {10}^{-5}$
−0.7	2.85217 $\times {10}^{-6}$	6.52147 $\times {10}^{-6}$	1.50698 $\times {10}^{-5}$	3.96587 $\times {10}^{-5}$
−0.5	1.87456 $\times {10}^{-6}$	5.19854 $\times {10}^{-6}$	0.85236 $\times {10}^{-5}$	1.25874 $\times {10}^{-5}$
−0.3	0.64423 $\times {10}^{-6}$	3.02587 $\times {10}^{-6}$	8.08574 $\times {10}^{-6}$	0.91114 $\times {10}^{-5}$
−0.1	4.85214 $\times {10}^{-7}$	6.32541 $\times {10}^{-7}$	6.63242 $\times {10}^{-6}$	7.98524 $\times {10}^{-6}$
0.0	2.58746 $\times {10}^{-7}$	4.36985 $\times {10}^{-7}$	5.36985 $\times {10}^{-6}$	8.21475 $\times {10}^{-6}$
0.2	5.68712 $\times {10}^{-7}$	6.39478 $\times {10}^{-7}$	7.36985 $\times {10}^{-6}$	8.52147 $\times {10}^{-6}$
0.4	0.77632 $\times {10}^{-6}$	3.65287 $\times {10}^{-6}$	9.02584 $\times {10}^{-6}$	9.51236 $\times {10}^{-6}$
0.6	2.98571 $\times {10}^{-6}$	5.41721 $\times {10}^{-6}$	9.98526 $\times {10}^{-6}$	2.36985 $\times {10}^{-5}$
0.8	3.25874 $\times {10}^{-6}$	6.39852 $\times {10}^{-6}$	1.96358 $\times {10}^{-5}$	5.36575 $\times {10}^{-5}$
1.0	5.08745 $\times {10}^{-6}$	7.21456 $\times {10}^{-6}$	3.69852 $\times {10}^{-5}$	7.63988 $\times {10}^{-5}$

and Figure 13, Figure 14, Figure 15 and Figure 16 for a range of different Poisson coefficient values α at time $t=0.45,0.9.$

8. General Conclusions

From the above tables and our numerical results, we can deduce the following:

• In comparison to the other approaches, the one provided in this study is the most effective numerical method for solving the NVFIE with a single kernel.
• The approach described in this study can be generalized to more general kernels.
• In Example 1, the quadratic integral Equation (41) after using the quadrature method leads to a system of nonlinear integral equations. It can be observed that the error increases with an increasing M. When we take the maximum value error, Figure 4 is $(8.47585\times {10}^{-7})$ at $t=0.6$. Furthermore, the minimum error value in Figure 1 is $(1.75434\times {10}^{-9})$ at $t=0$ (see Table 1).
• In Example 2, the quadratic integral Equation (42) after using the Chebyshev polynomials leads to a system of nonlinear integral equations. It can be observed that the error increases with an increase in time. When we take the maximum value error, Figure 8 is $(2.63214\times {10}^{-7})$ at $t=0.1$. Furthermore, the minimum error value in Figure 4 is $(5.64123\times {10}^{-8})$ at $t=0.03$ (see Table 2).
• In Example 3, when the kernel takes the logarithmic kernel $k\left(w\right(u)-w(v\left)\right)=(ln|u-v\left|\right)$, the results are computed at $t=0.003,0.01,0.025$, and $0.045$ for $n=50,\wp =50$ (see Table 3). As $n,\wp$ increases, and the errors decrease. The error takes the maximum value at $u=\pm 1$, where t is increasing, and vice versa.
• In Example 5, we consider the NVFIE with the kernel as the Carleman kernel $k(w\left(u\right)-w\left(v\right))={|u-v|}^{-\alpha }$. When we take the maximum value error, the ends of position is $(7.63988\times {10}^{-5})$ at $t=0.9,\alpha =0.35$. Furthermore, the minimum error value in the midpoint of the position is $(2.58746\times {10}^{-7})$ at $t=0.45,\alpha =0.15$ (see Table 5). The error takes the maximum value at $\alpha =1$, and vice versa.

9. Future Work

The authors will consider the solution of the principal equation of this paper in the two–dimensional problem with a phase-lag in time as follows:

$$\mu \mathrm{\Psi }(u,t+\delta t)-\lambda {\int }_0^{t+\delta t}{\int }_{-1}^{1}f(t+\delta t,\tau )k(w\left(u\right)-w\left(v\right))\gamma (u,v,t+\delta t,\tau ,\mathrm{\Psi }(v,\tau ))\mathrm{d}v\mathrm{d}\tau =F(u,t+\delta t).$$