On Some New AB-Fractional Inclusion Relations

Abstract

The theory of integral inequality has gained considerable attention due to its influential impact on several fields of mathematics and applied sciences. Over the years, numerous refinements, generalizations, and extensions of convexity have been explored to achieve more precise variants of already established results. The principal idea of this article is to establish some interval-valued integral inequalities of the Hermite–Hadamard type in the fractional domain. First, we propose the idea of generalized interval-valued convexity with respect to the continuous monotonic functions ⋎, bifunction $\zeta$, and based on the containment ordering relation, which is termed as $(⋎,\mathfrak{h})$ pre-invex functions. This class is innovative due to its generic characteristics. We generate numerous known and new classes of convexity by considering various values for ⋎ and $\mathfrak{h}$. Moreover, we use the notion of $(⋎,\mathfrak{h})$-pre-invexity and Atangana–Baleanu (AB) fractional operators to develop some fresh fractional variants of the Hermite–Hadamard (HH), Pachpatte, and Hermite–Hadamard–Fejer (HHF) types of inequalities. The outcomes obtained here are the most unified forms of existing results. We provide several specific cases, as well as a numerical and graphical study, to show the significance of the major results.

1. Introduction and Preliminaries

Convex analysis is regarded as the most fundamental branch of mathematical analysis. It has gained effective attention due to its major role in the development of both pure and applied mathematics. Convexity and its consequences provide both a geometrical and analytical approach to solving a problem. The role of convexity is unforgettable in linear algebra, topology, and functional analysis, especially separation axioms, fixed point theory, engineering, and economics as well. Firstly, in 1905, Jensen made the theory function much more interesting by introducing the concept of convex mappings on the basis of a convex set. One would like to characterize it by functions and their derivatives, as a positive second derivative indicates the convexity of functions. It is closely related to the theory of optimization, especially in linear programming. Convex mappings are often utilized to derive a feasible solution, and they provide unique minima.

The theory of inequalities is a broad discipline of research in mathematical analysis, and it has several applications in numerous areas of mathematics, physics, and engineering. Strong linkages between this theory and other disciplines, including functional analysis, approximation theory, probability theory, and information theory, have been found. As a consequence of its influence on applied mathematics, this field’s prominence will rise in the future. Theory convex functions have played a significant role in the development of the theory of inequalities. Many inequalities can be obtained directly by utilizing the notion of convexity such as Jensen’s inequality, HH inequality, Young’s inequality, etc. In this regard, we recall the well-known inequality due to Hermite and Hadamard separately. Let $\mathfrak{f}:[{}_{1}j,{}_{2}j]\subset \mathbb{R}\to \mathbb{R}$ be a convex function with ${}_{1}j<{}_{2}j$, then

$$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{{}_{1}j+{}_{2}j}{2}\right)\le \frac{1}{{}_{2}j-{}_{1}j}{\int }_{{}_{1}j}^{{}_{2}j}f\left({♭}_1\right)\mathrm{d}{♭}_1\le \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2}.\end{array}$$

Through the utilization of the above inequality, one can check the concavity of the different mappings. For more detail about this, see [1,2].

Recently, the concept of convexity has been refined and extended by using novel and innovative ideas, especially by making use of weighted means, for example, harmonic, geometric, and P convexity based on weighted harmonic mean, weighted geometric mean, and generalized weighted p mean, respectively. In 2019, Wu et al. [3] explored the new class of convexity by utilizing the quasi-arithmetic mean, which is described as:

Definition 1.

Let $⋎:K\to \mathbb{R}$ be a strictly continuous function. Then, $K\subset \mathbb{R}$ is said to be ⋎-convex set with respect to ⋎ if:

$$\begin{array}{c}\hfill {⋎}^{-1}((1-\mathfrak{z})⋎\left({♭}_1\right)+\mathfrak{z}⋎\left({♭}_2\right))\in K\forall {♭}_1,{♭}_2\in K\mathfrak{z}\in [0,1].\end{array}$$

Now, we revisit the class ⋎-convex function, which is studied in [3].

Definition 2.

A function $\mathfrak{f}:K\to \mathbb{R}$ is said to be a ⋎-convex function with respect to a strictly monotonic continuous function ⋎ if

$$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}((1-\mathfrak{z})⋎\left({♭}_1\right)+\mathfrak{z}⋎\left({♭}_2\right))\right)\le (1-\mathfrak{z})\mathfrak{f}\left({♭}_1\right)+\mathfrak{z}\mathfrak{f}\left({♭}_2\right)\forall {♭}_1,{♭}_2\in K\mathfrak{z}\in [0,1].\end{array}$$

In 2021, Kashuri et al. [4] discuss the ⋎ invex set and exponential preinvex functions, which are given by:

Definition 3.

Let $\zeta :K\times K\to \mathbb{R}$ be a bifunction and ⋎ be a strictly monotonic continuous function. Then, k is said to be K⋎-invex set, if

$$\begin{array}{c}\hfill {⋎}^{-1}(⋎\left({♭}_1\right)+\mathfrak{z}\zeta (⋎\left({♭}_2\right),⋎\left({♭}_1\right)))\forall {♭}_1,{♭}_2\in K\mathfrak{z}\in [0,1].\end{array}$$

Next, we have an exponential ⋎-exponential preinvex function.

Definition 4

([4]). Let $\zeta :K\times K\to \mathbb{R}$ be a bifunction, ⋎ be a strictly monotonic continuous function, and β be non-positive. Then, $\mathfrak{f}:K\subset \mathbb{R}\to \mathbb{R}$ is said to be ⋎-exponential preinvex function if

$$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}(⋎\left({♭}_1\right)+\mathfrak{z}\zeta (⋎\left({♭}_2\right),⋎\left({♭}_1\right)))\right)\le (1-\mathfrak{z})\frac{\mathfrak{f}\left({♭}_1\right)}{e^{\beta {♭}_1}}+\mathfrak{z}\frac{\mathfrak{f}\left({♭}_2\right)}{e^{\beta {♭}_2}}\forall {♭}_1,{♭}_2\in K\mathfrak{z}\in [0,1].\end{array}$$

Now, we present Condition C.

Let $K\subseteq \mathbb{R}$ be an invex set with respect to a bifunction $\zeta (.,.)$. Then, $\zeta$ satisfies the condition c for any ${♭}_1,{♭}_2\in K$ and $\mathfrak{z}\in [0,1]$ if

1.

$\zeta ({♭}_1,{♭}_1+\mathfrak{z}\zeta ({♭}_2,{♭}_1))=-\mathfrak{z}\zeta ({♭}_2,{♭}_1).$

2.

$\zeta ({♭}_2,{♭}_1+\mathfrak{z}\zeta ({♭}_2,{♭}_1))=-(1-\mathfrak{z})\zeta ({♭}_2,{♭}_1)$

In set-valued analysis, we deal with multi-valued functions, and I.V. analysis is a sub-discipline of this subject. Initially, interval analysis was used to calculate the error estimates of finite machines. As in daily life processes, if we assign a single value to any variable, then the chance of error increases; to overcome this deficiency, a numerical single number is replaced by interval numbers. Moore wrote some interesting books on interval analysis, which revealed new directions in executing this theory, and proposed some applications for computer programming and error analysis. After remarkable and applicable work due to Moore, many authors have shown their interest in the field and used it in different directions. I.V. techniques are used to investigate dynamic systems of differential equations, fluid mechanics, combinatorics, neural networking, and inequalities (see [5]). In the continuation, Breckner [6] purported the idea of convexity from the perspective of set-valued mappings, which are given as:

Definition 5.

Let $\mathfrak{f}:I=[{}_{1}j,{}_{2}j]\to {\mathbb{R}}_{+}$, which is said to be an I.V. convex function if

$$\begin{array}{c}\hfill \mathfrak{f}((1-\mathfrak{z}){}_{1}j+\mathfrak{z}{}_{2}j)\supseteq (1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)+t\mathfrak{z}\left({}_{2}j\right),\mathfrak{z}\in [0,1].\end{array}$$

The space of intervals is denoted by ${\mathbb{R}}_I$. Sadowska was the first who examined the classical HH-type inequality through convex set-valued mappings. This is stated as:

Let $\mathfrak{f}:\Lambda \subseteq \mathbb{R}\to {\mathbb{R}}_I$ be an interval-valued convex mapping defined over the interval $\Lambda$ and ${}_{1}j,{}_{2}j\in \Lambda$ together with ${}_{1}j\ne {}_{2}j$.

$$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{{}_{1}j+{}_{2}j}{2}\right)\supseteq \frac{1}{{}_{2}j-{}_{1}j}{\int }_{{}_{1}j}^{{}_{2}j}\mathfrak{f}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}\supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2}\end{array}$$

If $Z\left([{}_{1}j,{}_{2}j]\right)$ is set of all partitions of $[{}_{1}j,{}_{2}j]$ and $Z(\rho ,[{}_{1}j,{}_{2}j])$ is the set of all points P such that $mash\left(P\right)<\rho$, then $\mathfrak{f}:[{}_{1}j,{}_{2}j]\to {\mathbb{R}}_{\mathbb{I}}$ is called an interval Riemann integrable on $[{}_{1}j,{}_{2}j]$ if there exist $K\in {\mathbb{R}}_{\mathbb{I}}$ and for each $ϵ>0$ there exists $\rho >0$ such that

$$\begin{array}{c}\hfill d\left(S\right(\mathfrak{f},P,\rho ),k)<ϵ,\end{array}$$

(1)

where $S(\mathfrak{f},P,\rho )$ is the Riemann sum of $\mathfrak{f}$ with respect to $P\in Z(\rho ,[{}_{1}j,{}_{2}j])$. Relation (1) shows that K is the $\left(IR\right)$-integral of $\mathfrak{f}$ and given by

$$\begin{array}{c}\hfill K=\left(IR\right){\int }_{{}_{1}j}^{{}_{2}j}\mathfrak{f}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}.\end{array}$$

Definition 6.

Let $C\subset \mathbb{R}$, which is said to be a generalized invex set with respect to mapping $\zeta :C\times C\to \mathbb{R}$, and ⋎ be a monotonically continuous function if

$$\begin{array}{c}\hfill M_{\zeta ,⋎}({♭}_1,{♭}_2)={⋎}^{-1}(⋎\left({♭}_1\right)+\mathfrak{z}\zeta (⋎\left({♭}_2\right),⋎\left({♭}_1\right))),\forall {♭}_1,{♭}_2\in C.\end{array}$$

Theorem 1.

Let $\mathfrak{f}:[{}_{1}j,{}_{2}j]\to \mathbb{R}$ be an I.V. function such that $\mathfrak{f}\left(\mathfrak{z}\right)=[{\mathfrak{f}}_{*},{\mathfrak{f}}^{*}],\mathfrak{f}\in I{R}_{[{}_{1}j,{}_{2}j]}$ if and only if ${\mathfrak{f}}_{*},{\mathfrak{f}}^{*}\in R_{[{}_{1}j,{}_{2}j]}$ and

$$\begin{array}{c}\hfill \left(IR\right){\int }_{{}_{1}j}^{{}_{2}j}\mathfrak{f}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}=\left[\left(R\right){\int }_{{}_{1}j}^{{}_{2}j}{\mathfrak{f}}_{*}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},\left(R\right){\int }_{{}_{1}j}^{{}_{2}j}{\mathfrak{f}}^{*}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}\right].\end{array}$$

Next, we give the I.V. analog of AB-fractional operators.

Definition 7.

The fractional integral concerned with the new fractional derivative with the nonlocal kernel of a mapping $\mathfrak{f}\in L^1({}_{1}j,{}_{2}j)$ is described as:

$$\begin{array}{cc}\hfill & {}_{{}_{1}j}^{AB}{I}_{\vartheta }^{\alpha }\mathfrak{f}\left(\vartheta \right)=\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\mathfrak{f}\left(\vartheta \right)+\frac{\alpha }{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_{{}_{1}j}^{\vartheta }\mathfrak{f}\left({♭}_1\right){(\vartheta -{♭}_1)}^{\alpha -1}\mathrm{d}{♭}_1,\hfill \\ \hfill & where{}_{2}j>{}_{1}j,\alpha \in [0,1].\hfill \end{array}$$

Similarly, the right-sided AB-operator is stated as:

$$\begin{array}{c}\hfill {}^{AB}{I}_{{}_{2}j}^{\alpha }\mathfrak{f}\left(\vartheta \right)=\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\mathfrak{f}\left(\vartheta \right)+\frac{\alpha }{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_{\vartheta }^{{}_{2}j}\mathfrak{f}\left({♭}_1\right){({♭}_1-\vartheta )}^{\alpha -1}\mathrm{d}{♭}_1.\end{array}$$

Here, $\Gamma \left(\alpha \right)$ is the gamma function. $\mathcal{D}\left(\alpha \right)>0$ is called the normalization function.

For more detail about fractional calculus see [7].

Assume that $\mathfrak{f}:[{}_{1}j,{}_{2}j]\to {\mathbb{R}}_I$ is an I.V. mapping. Now, we revisit I.V. fractional $AB$-operators, which are defined as:

Definition 8.

$\mathfrak{f}\left({♭}_1\right)=[\underline{\mathfrak{f}}\left({♭}_1\right),\overline{\mathfrak{f}}\left({♭}_1\right)]$, and both mappings $\underline{\mathfrak{f}}\left({♭}_1\right)$ and $\overline{\mathfrak{f}}\left({♭}_1\right)$ are Riemann integrable defined on the interval $[{}_{1}j,{}_{2}j]$. Then,

$$\begin{array}{c}\hfill {}^{AB}{I}_{{{♭}_1}^{+}}^{\alpha }\left\{\mathfrak{f}\left({}_{2}j\right)\right\}=\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\mathfrak{f}\left({}_{2}j\right)+\frac{\alpha }{\mathcal{D}\left(\alpha \right)}{\int }_{{♭}_1}^{{}_{2}j}{({}_{2}j-\mathfrak{z})}^{\alpha -1}\mathfrak{f}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},{}_{2}j>{♭}_1\end{array}$$

and

$$\begin{array}{c}\hfill {}^{AB}{I}_{{{♭}_2}^{-},w,\rho }^{\alpha }\left\{\mathfrak{f}\left({}_{1}j\right)\right\}=\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\mathfrak{f}\left({}_{1}j\right)+\frac{\alpha }{\mathcal{D}\left(\alpha \right)}{\int }_{{}_{1}j}^{{♭}_2}{(\mathfrak{z}-{}_{1}j)}^{\alpha -1}\mathfrak{f}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},{}_{1}j<{♭}_2,\end{array}$$

with $\alpha \in [0,1]$ and $\mathcal{D}\left(\alpha \right)>0$ as the normalization function. We clearly see that

$$\begin{array}{c}\hfill {}^{AB}{I}_{{{♭}_1}^{+}}^{\alpha }\left\{\mathfrak{f}\left({}_{2}j\right)\right\}=\left[{}^{AB}{I}_{{{♭}_1}^{+}}^{\alpha }\left\{\underline{\mathfrak{f}}\left({}_{2}j\right)\right\},{}^{AB}{I}_{{{♭}_1}^{+}}^{\alpha }\left\{\overline{\mathfrak{f}}\left({}_{2}j\right)\right\}\right]\end{array}$$

and

$$\begin{array}{c}\hfill {}^{AB}{I}_{{{♭}_2}^{-}}^{\alpha }\left\{\mathfrak{f}\left({}_{1}j\right)\right\}=\left[{}^{AB}{I}_{{{♭}_2}^{-}}^{\alpha }\left\{\underline{\mathfrak{f}}\left({}_{1}j\right)\right\},{}^{AB}{I}_{{{♭}_2}^{-}}^{\alpha }\left\{\overline{\mathfrak{f}}\left({}_{1}j\right)\right\}\right].\end{array}$$

Recently, several inequalities have been extended and refined by implementing the I.V. mappings and ordering relations defined over interval numbers. In this regard, Chalco-Cano et al. [8,9] computed the familiar Ostrowski’s integral inequality via I.V. mappings and Hukuhara derivatives and concluded the applicable utility of the main outcomes in a numerical analysis, respectively. In 2017, Costa et al. [10] explored the novel integral inequalities by applying the mappings defined over fuzzy numbers. In the continuation, Flores et al. [11] computed the new variants of integral inequalities associated with I.V. mappings. In [12], the authors investigated the integral inequalities of HH involving preinvex I.V. mappings. Zhao et al. [13,14] established the Jensen’s and HH-type containment involving a general class of I.V. convexity, which is referred to as $\mathfrak{h}$-I.V. mapping and Chebyshev-type inequalities, respectively. Fractional calculus has contributed extraordinary impacts on the growth of integral inequalities. In 2012, Sarikaya et al. [15] made the first successful attempt to establish fractional counterparts of HH-type inequalities, essentially considering integral fractional operators. After this, several inequalities have been improved by using fractional tools, and this is still a very active field of research. In [16,17], Mohammad et al. examined the new tempered Hermite-Hadmard-like inequalities and presented some applications as well as fractional mid-point-like inequalities in the frame of fractional calculus. In [18], Akdemir et al. analyzed the Chebyshev-like inequalities through unified fractional operators. Set et al. [19] concluded with the inequalities involving AB-fractional integral operators and differentiability of convex mappings. In 2020, Budak et al. [20] studied the interval-valued fractional operators to explore the HH-type inequalities. Kara et al. [21] used the conception of interval-valued coordinated convexity and new double fractional operators to prove some HH-type inequalities. Recently, Bin-Mohsin et al. [22] introduced the notion of interval-valued coordinated harmonically convex mappings and double fractional operators involving the generalized Mittag-Leffler function introduced by Raina as a kernel to extract some novel fractional versions of HH-type inequalities. Zhou et al. [23] explored the trigonometric convex functions with exponential weight to formulate some new variants of HH-like inequalities. In [24], they discussed trigonometric convexity and related integral containment, implementing the fuzzy ordered relation. In [25], Kalsoom et al. used the idea of I.V. convexity and $(p,q)$ calculus to establish some new refinements of existing results. In [26], the authors introduced the concept of the fuzzy interval-valued bi-convex function to obtain some HH-like inequalities. In [27,28], the authors obtained fractional variants of Hermite–Hadamard-type inequalities for interval-coordinated convex functions and product inequalities of Hermite–Hadamard-type inequalities, respectively. In [29], they concluded with new Hermite–Hadamard-type inequalities involving interval-valued convexity and generalized quantum calculus. For more detail and recent developments see [30,31,32,33,34].

The main focus of the proceeding study is to obtain new generic inclusion relations of the HH-type by invoking AB-fractional concepts. First of all, we develop a novel class of convexity based on the bi-function $\zeta$ and monotonically continuous function ⋎ in interval analysis. The novelty of this study is that by applying different values of $\rho$ and $\zeta$, several existing and new fractional counterparts can be deduced. Additionally, we validated our theoretical outcomes via numerical simulations. To the best of our knowledge, these results are more beneficial for acquiring variants of I.V. HH-type inequalities for several classes of convexity. The structure of the paper consists of two sections: in the first segment of the study, we recall some facts relative to convexity and fractional calculus, and some history of the problem is explained. In the second section, we introduce the newly proposed class of convexity, and its consequences and applications in integral inequalities are provided. Later on, concluding remarks are added.

2. Main Results

Now, we define I.V. $(⋎,\mathfrak{h})$ pre-invex mappings.

Definition 9.

Let $\mathfrak{h}:[0,1]\to \mathbb{R}$ be a non-negative mapping with $\mathfrak{h}\ne 0$, then $\mathfrak{f}:[{}_{1}j,{}_{2}j]\to {\mathbb{R}}_i$ is called I.V. $(⋎,\mathfrak{h})$ pre-invex mappings, satisfying the condition $\mathfrak{f}\left({♭}_1\right)=[{\mathfrak{f}}_{*}\left({♭}_1\right),{\mathfrak{f}}^{*}\left({♭}_1\right)]$ if

$$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\supseteq \mathfrak{h}(1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)+\mathfrak{h}\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{2}j\right),\end{array}$$

(2)

$\forall {♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$ and $\mathfrak{z}\in [0,1]$.

Now, we discuss some special cases of Definition 2.

• Choosing $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$, we acquire a fresh class ⋎ I.V. pre-invex function:

  $$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\supseteq (1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)+\mathfrak{z}\mathfrak{f}\left({}_{2}j\right).\end{array}$$
• Choosing $⋎\left(\mathfrak{z}\right)=\frac{1}{\mathfrak{z}}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$, we then obtain a class of I.V. harmonically pre-invexity:

  $$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}{ta+(1-\mathfrak{z})\zeta ({}_{2}j,{}_{1}j)}\right)\supseteq (1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)+\mathfrak{z}\mathfrak{f}\left({}_{2}j\right).\end{array}$$
• Choosing $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$, we then obtain a class of I.V. P pre-invex functions:

  $$\begin{array}{c}\hfill \mathfrak{f}\left[{({{}_{1}j}^p+\zeta \mathfrak{z}({{}_{2}j}^p,{{}_{1}j}^p))}^{\frac{1}{p}}\right]\supseteq (1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)+\mathfrak{z}\mathfrak{f}\left({}_{2}j\right).\end{array}$$
• Choosing $⋎\left(\mathfrak{z}\right)=e^{\mathfrak{z}}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$, we then obtain a class of I.V. log-exponential pre-invex functions:

  $$\begin{array}{c}\hfill \mathfrak{f}\left(ln(e^{{}_{1}j}+\mathfrak{z}\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right)\supseteq (1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)+\mathfrak{z}\mathfrak{f}\left({}_{2}j\right).\end{array}$$

Remark 1.

Choosing $⋎\left(\mathfrak{z}\right)=\mathfrak{z}$, we then obtain the definition of classical I.V. pre-invex functions.

Definition 10.

Choosing $\mathfrak{h}\left(\mathfrak{z}\right)={\mathfrak{z}}^s$ in Definition 2, we acquire a fresh class $(⋎,s)$ I.V. -pre-invex function

$$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}(\mathfrak{z}⋎\left({}_{1}j\right)+(1-\mathfrak{z})⋎\left({}_{2}j\right))\right)\supseteq {(1-\mathfrak{z})}^{s}f\left({}_{1}j\right)+{\mathfrak{z}}^{s}f\left({}_{2}j\right).\end{array}$$

Now, we investigate some special cases of Definition 10.

• Setting $⋎\left(\mathfrak{z}\right)=\frac{1}{\mathfrak{z}}$, we then obtain I.V. harmonically s pre-invex functions, which follow as

  $$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{{}_{1}j\zeta ({}_{2}j,{}_{1}j)}{ta+(1-\mathfrak{z})\zeta ({}_{2}j,{}_{1}j)}\right)\supseteq {(1-\mathfrak{z})}^{s}f\left({}_{1}j\right)+{\mathfrak{z}}^{s}f\left({}_{2}j\right).\end{array}$$
• Setting $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$, $p\ge -1$, we then obtain I.V. $(P,s)$ pre-invex functions, which follow as

  $$\begin{array}{c}\hfill \mathfrak{f}\left[{({{}_{1}j}^p+\mathfrak{z}\zeta ({{}_{2}j}^p,{{}_{1}j}^p))}^{\frac{1}{p}}\right]\supseteq {(1-\mathfrak{z})}^{s}f\left({}_{1}j\right)+{\mathfrak{z}}^{s}f\left({}_{2}j\right).\end{array}$$
• Choosing $⋎\left(\mathfrak{z}\right)=e^{\mathfrak{z}}$ and $\mathfrak{h}\left(\mathfrak{z}\right)={\mathfrak{z}}^s$, we then obtain a class of I.V. log-exponential s pre-invex functions:

  $$\begin{array}{c}\hfill \mathfrak{f}\left(ln(e^{{}_{1}j}+\mathfrak{z}\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right)\supseteq {(1-\mathfrak{z})}^{s}f\left({}_{1}j\right)+{\mathfrak{z}}^{s}f\left({}_{2}j\right).\end{array}$$

Definition 11.

Choosing $\mathfrak{h}\left(\mathfrak{z}\right)={\mathfrak{z}}^{-s}$, we acquire a fresh class $(⋎,s)$ of the I.V. Godunova–Levin-type pre-invex function

$$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}(\mathfrak{z}⋎\left({}_{1}j\right)+(1-\mathfrak{z})⋎\left({}_{2}j\right))\right)\supseteq {\mathfrak{z}}^{-s}\mathfrak{f}\left({}_{1}j\right)+{(1-\mathfrak{z})}^{-s}\mathfrak{f}\left({}_{2}j\right).\end{array}$$

By taking different values of $⋎\left(\mathfrak{z}\right)$, we obtain some new and previously known classes of pre-invex functions.

For our convenience, we specify that the space of $(⋎,\mathfrak{h})$ I.V. preinvex mappings, $(⋎,\mathfrak{h})m$ interval-valued pre-concave functions, $(⋎,\mathfrak{h})$ preinvex mappings, and $(⋎,\mathfrak{h})$ pre-concave functions are denoted by $SIGPX\left([{}_{1}j,{}_{2}j],{\mathbb{R}}_I^{+}\right)$, $SIGPV\left([{}_{1}j,{}_{2}j],{\mathbb{R}}_I^{+}\right)$, $SGPX\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$, and $SGPV\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$, respectively.

Theorem 2.

Suppose $\mathfrak{f}:[{}_{1}j,{}_{2}j]\to {\mathbb{R}}_I^{+}$ is an interval-valued mapping such that $\mathfrak{f}=[{\mathfrak{f}}_{*},{\mathfrak{f}}^{*}]$ with ${\mathfrak{f}}_{*}\le {\mathfrak{f}}^{*}$. Then, $\mathfrak{f}\in SIGPX\left([{}_{1}j,{}_{2}j],{\mathbb{R}}_I^{+}\right)\iff {\mathfrak{f}}_{*}\in SGPX\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$ and ${\mathfrak{f}}^{*}\in SGPV\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$.

Proof. 

Assume that $\mathfrak{f}\in SIGPX\left([{}_{1}j,{}_{2}j],{\mathbb{R}}_I^{+}\right)$, ${♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$, and $\mathfrak{z}\in [0,1]$, then

$$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right)\supseteq \mathfrak{h}\left(\mathfrak{z}\right)\mathfrak{f}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z})\mathfrak{f}\left({♭}_2\right).\end{array}$$

This implies that

$$\begin{array}{cc}\hfill & \left[{\mathfrak{f}}_{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right),{\mathfrak{f}}^{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right)\right]\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \supseteq \left[\mathfrak{h}\left(\mathfrak{z}\right){\mathfrak{f}}_{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}_{*}\left({♭}_2\right),\mathfrak{h}\left(\mathfrak{z}\right){\mathfrak{f}}^{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}^{*}\left({♭}_2\right)\right]\hfill \end{array}$$

(4)

From (3), we have

$$\begin{array}{c}\hfill {\mathfrak{f}}_{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right)\le \mathfrak{h}\left(\mathfrak{z}\right){\mathfrak{f}}_{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}_{*}\left({♭}_2\right).\end{array}$$

(5)

Additionally,

$$\begin{array}{c}\hfill {\mathfrak{f}}^{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right)\ge \mathfrak{h}\left(\mathfrak{z}\right){\mathfrak{f}}^{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}^{*}\left({♭}_2\right).\end{array}$$

(6)

Inequalities (5) and (6) indicate that ${\mathfrak{f}}_{*}\in SGPX\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$ and ${\mathfrak{f}}^{*}\in SGPV\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$.

Conversely, suppose that ${\mathfrak{f}}_{*}\in SGPX\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$ and ${\mathfrak{f}}^{*}\in SGPV\left([{}_{1}j,{}_{2}j],\mathbb{R}\right)$, then

$$\begin{array}{c}\hfill {\mathfrak{f}}_{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right)\le \mathfrak{h}\left(\mathfrak{z}\right){\mathfrak{f}}_{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}_{*}\left({♭}_2\right).\end{array}$$

(7)

Additionally,

$$\begin{array}{c}\hfill {\mathfrak{f}}^{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right)\ge \mathfrak{h}\left(\mathfrak{z}\right){\mathfrak{f}}^{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}^{*}\left({♭}_2\right).\end{array}$$

(8)

From the fact that ${\mathfrak{f}}_{*}\le {\mathfrak{f}}^{*}$,

$$\begin{array}{cc}\hfill & \left[{\mathfrak{f}}_{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right),{\mathfrak{f}}^{*}\left({⋎}^{-1}(\mathfrak{z}⋎\left({♭}_1\right)+(1-\mathfrak{z})⋎\left({♭}_2\right))\right)\right]\hfill \\ \hfill & \supseteq \left[\mathfrak{h}\left(\mathfrak{z}\right){\mathfrak{f}}_{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}_{*}\left({♭}_2\right),\mathfrak{h}\left(\mathfrak{z}\right)\mathfrak{z}{\mathfrak{f}}^{*}\left({♭}_1\right)+\mathfrak{h}(1-\mathfrak{z}){\mathfrak{f}}^{*}\left({♭}_2\right)\right].\hfill \end{array}$$

In this way, we acquire our required result. □

Now, we aim to conclude a new fractional variant of the HH inequality when $\mathfrak{f}\in SIGPX([{}_{1}j,{}_{2}j],\mathbb{R})$.

Theorem 3.

Let $\mathfrak{f}:[{}_{1}j,{}_{2}j]\to {\mathfrak{R}}_{\mathfrak{I}}$ be a $(⋎,\mathfrak{h})$ I.V. pre-invex function with ${}_{1}j<{}_{2}j$ and $\mathfrak{h}:[0,1]\to (0,\infty )$ be a continuous function; then, we have

$$\begin{array}{cc}\hfill & \frac{1}{\mathfrak{h}\left(\frac{1}{2}\right)}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left({}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\circ {⋎}^{-1}\left(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\right)\hfill \\ \hfill & \supseteq \alpha [\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)]{\int }_0^1{\mathfrak{z}}^{\alpha -1}[\mathfrak{h}\left(\mathfrak{z}\right)+\mathfrak{h}(1-\mathfrak{z})]\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Proof. 

Since $\mathfrak{f}$ is a $(⋎,\mathfrak{h})$ I.V. pre-invex function, then

$$\begin{array}{c}\hfill \mathfrak{f}\left({⋎}^{-1}\left(⋎\left({♭}_1\right)+\frac{\zeta (⋎\left({♭}_2\right),⋎\left({♭}_1\right))}{2}\right)\right)\supseteq \mathfrak{h}\left(\frac{1}{2}\right)[\mathfrak{f}\left({♭}_1\right)+\mathfrak{f}\left({♭}_2\right)].\end{array}$$

Substituting ${♭}_1={⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))$ and ${♭}_2={⋎}^{-1}(⋎\left({}_{1}j\right)$+ $\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))$ in the above inequality, multiplying both sides by ${\mathfrak{z}}^{\alpha -1}$ and using Condition C, and then integrating with respect to $\mathfrak{z}$ over $[0,1]$

$$\begin{array}{cc}\hfill \frac{1}{\mathfrak{h}\left(\frac{1}{2}\right)}{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z}& \supseteq {\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

(9)

Now,

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & =\left[\left(R\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{f}}_{*}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z},\left(R\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{f}}^{*}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z}\right]\hfill \\ \hfill & =\left[\frac{1}{\alpha }{\mathfrak{f}}_{*}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)+\frac{1}{\alpha }{\mathfrak{f}}^{*}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\right]\hfill \\ \hfill & =\frac{1}{\alpha }\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right),\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right).\hfill \end{array}$$

(10)

Additionally,

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ & +\left(IR\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & =\left[\left(R\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{f}}_{*}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\right.\hfill \\ & +\left(R\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{f}}_{*}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z},\hfill \\ \hfill & \left(R\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{f}}^{*}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ & \left.+\left(R\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{f}}^{*}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\right]\hfill \\ \hfill & =\left[\frac{1}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))-u)}^{\alpha -1}{\mathfrak{f}}_{*}\circ {⋎}^{-1}\left(u\right)\mathrm{d}u\right.\hfill \\ & +\frac{1}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(u-⋎\left({}_{1}j\right))}^{\alpha -1}{\mathfrak{f}}_{*}\circ {⋎}^{-1}\left(u\right)\mathrm{d}u,\hfill \\ \hfill & \frac{1}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))-u)}^{\alpha -1}{\mathfrak{f}}^{*}\circ {⋎}^{-1}\left(u\right)\mathrm{d}u\hfill \\ & \left.+\frac{1}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(u-⋎\left({}_{1}j\right))}^{\alpha -1}{\mathfrak{f}}^{*}\circ {⋎}^{-1}\left(u\right)\mathrm{d}u\right].\hfill \end{array}$$

We obtain

$$\begin{array}{cc}\hfill & \frac{1}{\mathfrak{h}\left(\frac{1}{2}\right)\alpha }\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\hfill \\ \hfill & \supseteq \frac{1}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))-u)}^{\alpha -1}\mathfrak{f}\circ {⋎}^{-1}\left(u\right)\mathrm{d}u\right.\hfill \\ \hfill & \left.+{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(u-⋎\left({}_{1}j\right))}^{\alpha -1}\mathfrak{f}\circ {⋎}^{-1}\left(u\right)\mathrm{d}u\right].\hfill \end{array}$$

Multiplying both sides by $\frac{\alpha }{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}$ and then adding both sides $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)$, we obtain

$$\begin{array}{cc}\hfill & \frac{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\mathfrak{h}\left(\frac{1}{2}\right)\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}\mathfrak{f}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)+\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\hfill \\ \hfill & \supseteq {}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\circ {⋎}^{-1}\left(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\circ (⋎\left({}_{1}j\right)).\hfill \end{array}$$

(11)

Combining (9)–(11), we obtain the right-sided inclusion. To prove the second part, we use the $(⋎,\mathfrak{h})$ I.V. convexity of $\mathfrak{f}$,

$$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\supseteq \mathfrak{h}\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{1}j\right)+\mathfrak{h}(1-\mathfrak{z})\mathfrak{f}\left({}_{2}j\right).\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\supseteq \mathfrak{h}(1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)+\mathfrak{h}\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{2}j\right).\hfill \end{array}$$

(13)

Adding (12) and (13), and multiplying the resulting inequality by ${\mathfrak{z}}^{\alpha -1}$ and integrating with respect to $\mathfrak{z}$ on $[0,1]$, then we have

$$\begin{array}{cc}\hfill & {\int }_0^1{\mathfrak{z}}^{\alpha -1}\left(\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)+\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & \supseteq {\int }_0^1{\mathfrak{z}}^{\alpha -1}[\mathfrak{h}\left(\mathfrak{z}\right)+\mathfrak{h}(1-\mathfrak{z})][\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)]\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Multiplying both sides by $\frac{\alpha }{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}$ and then adding $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)$ to both sides, we obtain the second part of our required result. □

Now, we provide various consequences of Theorem 3.

• Choosing $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 3, we obtain

  $$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left({}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\circ {⋎}^{-1}\left(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\right)\hfill \\ \hfill & \supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2}.\hfill \end{array}$$
• Choosing $⋎\left({♭}_1\right)={♭}_1$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 3, we obtain

  $$\begin{array}{cc}\hfill \mathfrak{f}\left(\frac{2{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}{2}\right)& \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta ({}_{2}j,{}_{1}j)\right)}^{\alpha }}\left({}^{AB}{I}_{{{}_{1}j}^{+}}^{\alpha }\mathfrak{f}\left({}_{1}j+\zeta ({}_{2}j,{}_{1}j)\right)+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta ({}_{2}j,{}_{1}j)}^{-}}^{\alpha }\mathfrak{f}\left({}_{1}j\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}({}_{1}j+\zeta ({}_{2}j,{}_{1}j))\right)\supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2}.\hfill \end{array}$$
• Choosing $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$, $p\ge -1$ in Theorem 3, we obtain

  $$\begin{array}{cc}\hfill & \frac{1}{\mathfrak{h}\left(\frac{1}{2}\right)}\mathfrak{f}\left({\left(\frac{2{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}{2}\right)}^{\frac{1}{p}}\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{{\left(\zeta ({{}_{2}j}^p,{{}_{1}j}^p)\right)}^{\alpha }}\left({}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\mathfrak{f}\circ k\left({{}_{1}j}^p+\zeta ({{}_{2}j}^p+{{}_{1}j}^p)\right)+{}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}^{-}}^{\alpha }\mathfrak{f}\circ k\left({{}_{1}j}^p\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\circ k\left({{}_{1}j}^p\right)+\mathfrak{f}\circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right)\hfill \\ \hfill & \supseteq \alpha [\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)]{\int }_0^1{\mathfrak{z}}^{\alpha -1}[\mathfrak{h}\left(\mathfrak{z}\right)+\mathfrak{h}(1-\mathfrak{z})]\mathrm{d}\mathfrak{z}.\hfill \end{array}$$
• Choosing $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$, $p\ge -1$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 3, we obtain

  $$\begin{array}{cc}\hfill & \mathfrak{f}\left({\left(\frac{2{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}{2}\right)}^{\frac{1}{p}}\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta ({{}_{2}j}^p,{{}_{1}j}^p)\right)}^{\alpha }}\left({}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\mathfrak{f}\circ k\left({{}_{1}j}^p+\zeta ({{}_{2}j}^p+{{}_{1}j}^p)\right)+{}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}^{-}}^{\alpha }\mathfrak{f}\circ k\left({{}_{1}j}^p\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\circ k\left({{}_{1}j}^p\right)+\mathfrak{f}\circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right)\hfill \\ \hfill & \supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2},\hfill \end{array}$$

  where $k\left({♭}_1\right)={{♭}_1}^{\frac{1}{p}}$.
• Choosing $⋎\left(\mathfrak{z}\right)=e^{\mathfrak{z}}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 3, we obtain

  $$\begin{array}{cc}\hfill & \mathfrak{f}\left(ln\left(\frac{2e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})}{2}\right)\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta (e^{{}_{2}j},e^{{}_{1}j})\right)}^{\alpha }}\left({}^{AB}{I}_{{e^{{}_{1}j}}^{+}}^{\alpha }\mathfrak{f}\circ k\left(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})\right)+{}^{AB}{I}_{{e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})}^{-}}^{\alpha }\mathfrak{f}\circ k\left(e^{{}_{1}j}\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\circ k\left(e^{{}_{1}j}\right)+\mathfrak{f}\circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right)\right)\hfill \\ \hfill & \supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2},\hfill \end{array}$$

  where $k\left(\mathfrak{z}\right)=ln\left(\mathfrak{z}\right)$.

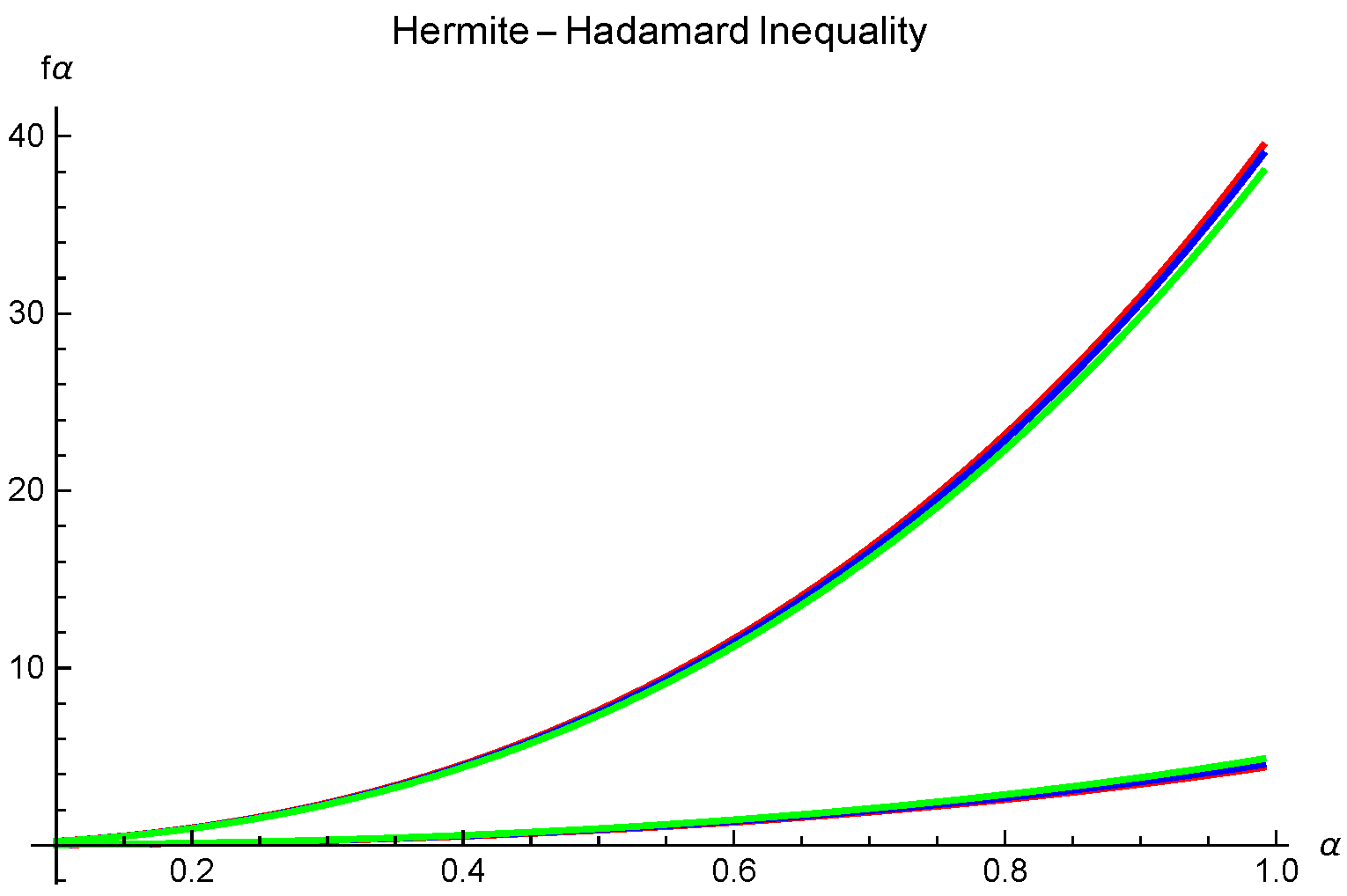
Example 1.

Assume that all the assumptions of Theorem 3 are fulfilled; we take $\mathfrak{f}\left(\mathfrak{z}\right)=[2{\mathfrak{z}}^2,-6{\mathfrak{z}}^2+20\mathfrak{z}+24]$ with $[{}_{1}j,{}_{2}j]=[1,2],⋎\left(\mathfrak{z}\right)=\mathfrak{z}$, $\zeta ({}_{2}j,{}_{1}j)={}_{2}j-{}_{1}j$ and $\mathcal{D}\left(\alpha \right)=\frac{2-\alpha }{\alpha }$ with $\alpha =\frac{1}{2}$, we have

$$\begin{array}{cc}\hfill & \frac{\alpha }{(2-\alpha )\Gamma \left(\alpha \right)}\mathfrak{f}\left(\frac{1}{2}\right)=[0.846284,7.61656]\hfill \\ \hfill & \frac{\alpha }{2(2-\alpha )\Gamma \left(\alpha \right)}\left[{\int }_1^2\left({(2-\mathfrak{z})}^{\alpha -1}+{(\mathfrak{z}-1)}^{\alpha -1}\right)\mathfrak{f}\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}\right]=[0.890166,7.48492]\hfill \\ \hfill & \frac{\alpha (\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right))}{2(2-\alpha )\Gamma \left(\alpha \right)}=[0.940316,7.33446].\hfill \end{array}$$

For graphical visualization, we vary $0<\alpha \le 1$ (see Figure 1).

Now, we provide the generalized fractional version of the Fejer-type HH’s-type inequality.

Theorem 4.

Let $\mathfrak{f}:[{}_{1}j,{}_{2}j]\to {\mathfrak{R}}_{\mathfrak{I}}$ be a $(⋎,\mathfrak{h})$ I.V. pre-invex function with ${}_{1}j<{}_{2}j$ and $\mathfrak{h}:[0,1]\to (0,\infty )$ be a continuous function; then, we have

$$\begin{array}{cc}\hfill & \frac{1}{2\mathfrak{h}\left(\frac{1}{2}\right)}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right.\hfill \\ \hfill & \left.+{}^{AB}{I}_{⋎{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))}^{-}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right]\hfill \\ \hfill & \supseteq \left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))\right]\hfill \\ \hfill & \supseteq \frac{\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}\left({\int }_0^1{\mathfrak{z}}^{\alpha -1}[\mathfrak{h}\left(\mathfrak{z}\right)+\mathfrak{h}(1-\mathfrak{z})]\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)[\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)]\mathrm{d}\mathfrak{z}\right)\hfill \end{array}$$

$\alpha >0$ and $\forall {♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$.

Proof. 

Since $\mathfrak{f}$ is a $(⋎,\mathfrak{h})$ I.V. pre-invex function, for $\mathfrak{z}=\frac{1}{2}$, we have

$$\begin{array}{cc}\hfill & \frac{1}{\mathfrak{h}\left(\frac{1}{2}\right)}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({♭}_1\right)+\zeta (⋎\left({♭}_2\right),⋎\left({♭}_1\right))}{2}\right)\right)\supseteq \mathfrak{f}\left({♭}_1\right)+\mathfrak{f}\left({♭}_2\right).\hfill \end{array}$$

Substituting ${♭}_1={⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))$ and ${♭}_2={⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))$ in the above inequality, multiplying both sides by ${\mathfrak{z}}^{\alpha -1}\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))$, we have

$$\begin{array}{cc}\hfill & \frac{1}{\mathfrak{h}\left(\frac{1}{2}\right)}{\int }_0^1{\mathfrak{z}}^{\alpha -1}\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & \supseteq {\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\mathrm{d}\mathfrak{z}\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

(14)

Now, we use fact that $\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)$= $\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)$

$$\begin{array}{cc}\hfill & {\int }_0^1{\mathfrak{z}}^{\alpha -1}\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & =\frac{1}{2}\left[{\int }_0^1{\mathfrak{z}}^{\alpha -1}\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z}\right.\hfill \\ \hfill & \left.+{\int }_0^1{\mathfrak{z}}^{\alpha -1}\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\mathrm{d}\mathfrak{z}\right]\hfill \\ \hfill & =\frac{1}{2{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))-u)}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\right.\hfill \\ \hfill & \left.\xi \circ {⋎}^{-1}\left(u\right)\mathrm{d}u+{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(u-⋎\left({}_{1}j\right))}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\xi \circ {⋎}^{-1}\left(u\right)\mathrm{d}u\right].\hfill \end{array}$$

Multiplying both sides by $\frac{\alpha }{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}$ and then adding $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))$+ $\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))$ to both sides, we obtain

$$\begin{array}{cc}\hfill & =\frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right.\hfill \\ \hfill & \left.+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))\right].\hfill \end{array}$$

(15)

Now,

$$\begin{array}{cc}\hfill & {\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\mathrm{d}\mathfrak{z}\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\mathrm{d}\mathfrak{z}\hfill \\ \hfill & =\frac{1}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))-u)}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(u\right)\right)\xi \left({⋎}^{-1}\left(u\right)\right)\mathrm{d}u\right.\hfill \\ \hfill & \left.+{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(u-⋎\left({}_{1}j\right))}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(u\right)\right)\xi \left({⋎}^{-1}\left(u\right)\right)\mathrm{d}u\right].\hfill \end{array}$$

Multiplying both sides by $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)$ and then adding $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))$ to both sides, we acquire

$$\begin{array}{cc}\hfill & =\frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right.\hfill \\ & \left.+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))\right].\hfill \end{array}$$

(16)

To prove our second inequality, we add (12) and (13), multiplying both sides by ${\mathfrak{z}}^{\alpha -1}\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))$ and integrating with respect to $\mathfrak{z}$ on $[0,1]$; then, we have

$$\begin{array}{cc}\hfill & {\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\mathrm{d}\mathfrak{z}\hfill \\ \hfill & \supseteq {\int }_0^1{\mathfrak{z}}^{\alpha -1}[\mathfrak{h}\left(\mathfrak{z}\right)+\mathfrak{h}(1-\mathfrak{z})]\xi ({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))[\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)]\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Multiplying both sides by $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}$ and then adding $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))$+ $\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))$ to both sides, we obtain our required second inclusion. □

Now, we deliver several consequences of Theorem 4.

• If we choose $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 4, we have

  $$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right.\hfill \\ \hfill & \left.+{}^{AB}{I}_{⋎{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))}^{-}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right]\hfill \\ \hfill & \supseteq \left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))+{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))\right]\hfill \\ \hfill & \supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2}\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))+{}^{AB}{I}_{⋎{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))}^{-}}^{\alpha }\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right],\hfill \end{array}$$

  where $\alpha >0$ and ${♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$.
• If we choose $⋎\left(\mathfrak{z}\right)=\mathfrak{z}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 4, then

  $$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{2{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}{2}\right)\left[{}^{AB}{I}_{{{}_{1}j}^{+}}^{\alpha }\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j)){+}^{AB}{I}_{{{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}^{-}}^{\alpha }\xi \left({}_{1}j\right)-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\xi \left({}_{1}j\right)+\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j)))\right]\hfill \\ \hfill & \supseteq \left[{}^{AB}{I}_{{{}_{1}j}^{+}}^{\alpha }\mathfrak{f}\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j))+{}^{AB}{I}_{{{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}^{-}}^{\alpha }\mathfrak{f}\xi \left({}_{1}j\right)-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \left({}_{1}j\right)+\mathfrak{f}\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j)))\right]\hfill \\ \hfill & \supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2}\left[{}^{AB}{I}_{{{}_{1}j}^{+}}^{\alpha }\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j)){+}^{AB}{I}_{{{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}^{-}}^{\alpha }\xi \left({}_{1}j\right)-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\xi \left({}_{1}j\right)+\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j)))\right],\hfill \end{array}$$

  where $\alpha >0$ and ${♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$.
• If we choose $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$ in Theorem 4, then

  $$\begin{array}{cc}\hfill & \frac{1}{2\mathfrak{h}\left(\frac{1}{2}\right)}\mathfrak{f}\left({\left(\frac{2{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}{2}\right)}^{\frac{1}{p}}\right)\left[{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)){+}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}^{-}}^{\alpha }\xi \circ k\left({{}_{1}j}^p\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\xi \circ k\left({{}_{1}j}^p\right)+\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right]\hfill \\ \hfill & \supseteq \left[{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))+{}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}^{-}}^{\alpha }\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)+\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right]\hfill \\ \hfill & \supseteq \frac{\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}\left({\int }_0^1{\mathfrak{z}}^{\alpha -1}[\mathfrak{h}\left(\mathfrak{z}\right)+\mathfrak{h}(1-\mathfrak{z})]\xi \circ k({{}_{1}j}^p+(1-\mathfrak{z})\zeta ({{}_{2}j}^p,{{}_{1}j}^p))[\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)]\mathrm{d}\mathfrak{z}\right),\hfill \end{array}$$

  where $\alpha >0$ and ${♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$.
• If we choose $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 4, then

  $$\begin{array}{cc}\hfill & \mathfrak{f}\left({\left(\frac{2{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}{2}\right)}^{\frac{1}{p}}\right)\left[{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)){+}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}^{-}}^{\alpha }\xi \circ k\left({{}_{1}j}^p\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\xi \circ k\left({{}_{1}j}^p\right)+\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right]\hfill \\ \hfill & \supseteq \left[{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))+{}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}^{-}}^{\alpha }\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)+\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right]\hfill \\ \hfill & \supseteq \frac{\mathfrak{f}\left({{}_{1}j}^p\right)+\mathfrak{f}\left({{}_{2}j}^p\right)}{2}\left[{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)){+}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{}_{1}j)}^{-}}^{\alpha }\xi \circ k\left({{}_{1}j}^p\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\xi \circ k\left({{}_{1}j}^p\right)+\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right],\hfill \end{array}$$

  where $\alpha >0$ and ${♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$.
• If we choose $⋎\left(\mathfrak{z}\right)=e^{\mathfrak{z}}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 4, then

  $$\begin{array}{cc}\hfill & \mathfrak{f}\left(ln\left(\frac{2e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})}{2}\right)\right)\left[{}^{AB}{I}_{{e^{{}_{1}j}}^{+}}^{\alpha }\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right.\hfill \\ \hfill & \left.+{}^{AB}{I}_{⋎{(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))}^{-}}^{\alpha }\xi \circ k\left(e^{{}_{1}j}\right)-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\xi \circ k\left(e^{{}_{1}j}\right)+\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right]\hfill \\ \hfill & \supseteq \left[{}^{AB}{I}_{{e^{{}_{1}j}}^{+}}^{\alpha }\mathfrak{f}\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))+{}^{AB}{I}_{{e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})}^{-}}^{\alpha }\mathfrak{f}\xi \circ k\left(e^{{}_{1}j}\right)\right.\hfill \\ & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ k\left(e^{{}_{1}j}\right)+\mathfrak{f}\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})))\right]\hfill \\ \hfill & \supseteq \frac{\mathfrak{f}\left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)}{2}\left[{}^{AB}{I}_{{e^{{}_{1}j}}^{+}}^{\alpha }\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right.\hfill \\ \hfill & \left.+{}^{AB}{I}_{⋎{(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))}^{-}}^{\alpha }\xi \circ k\left(e^{{}_{1}j}\right)-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\xi \circ k\left(e^{{}_{1}j}\right)+\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right],\hfill \end{array}$$

  where $k\left(\mathfrak{z}\right)=ln\left(\mathfrak{z}\right)$, $\alpha >0$ and ${♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$.

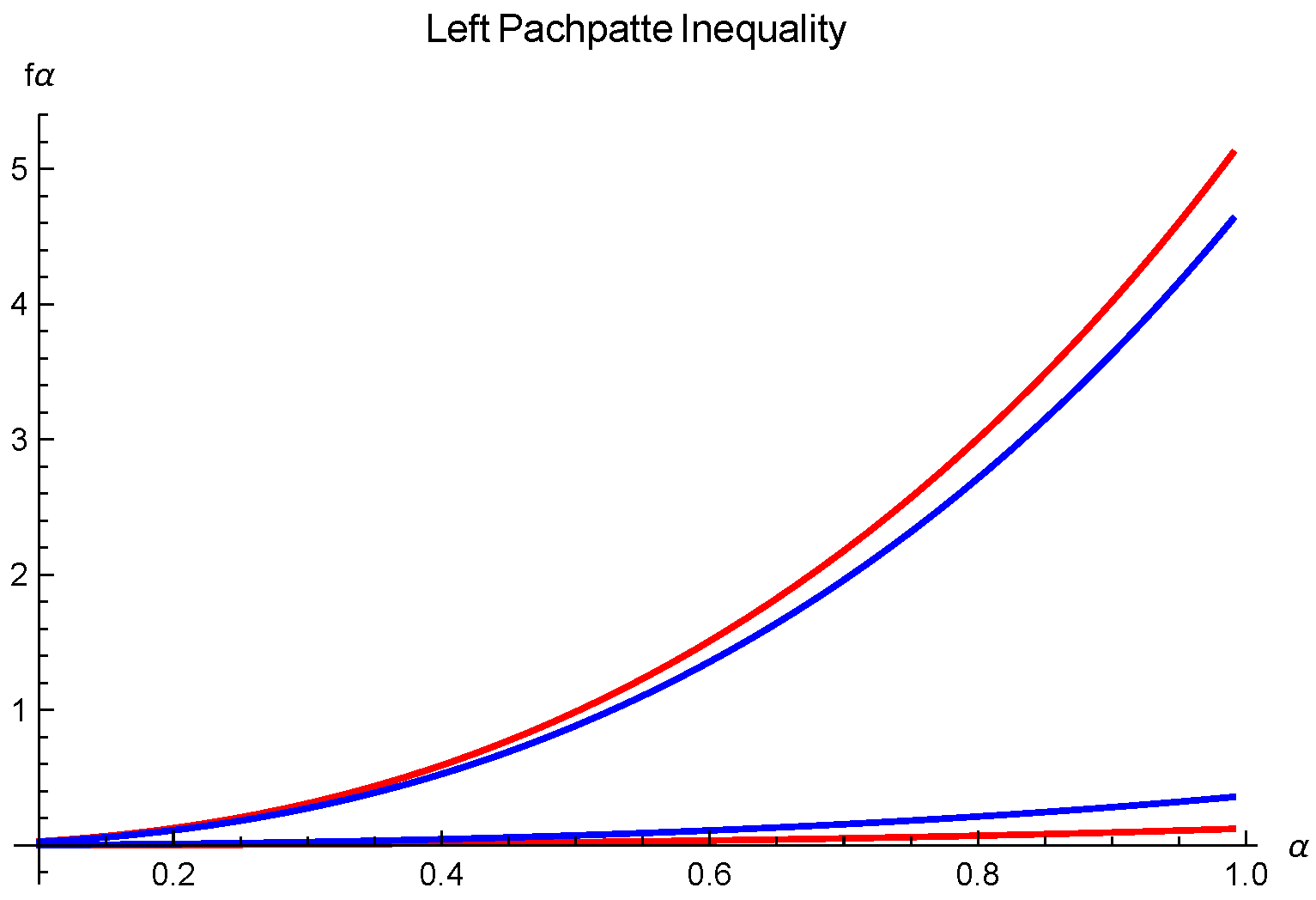
Example 2.

Assume that all the assumptions of Theorem 4 are fulfilled. If we take $\mathfrak{f}:[0,2]\to {\mathbb{R}}_I$, where $\mathfrak{f}\left(\mathfrak{z}\right)=[2e^{\mathfrak{z}},-6{\mathfrak{z}}^2+12\mathfrak{z}+24]$ with $⋎\left(\mathfrak{z}\right)=\mathfrak{z}$, $\zeta ({}_{2}j,{}_{1}j)={}_{2}j-{}_{1}j$, and $\mathcal{D}\left(\alpha \right)=\frac{2-\alpha }{\alpha }$ and symmetric function $\xi \left(\mathfrak{z}\right)$ with respect to $\frac{{}_{1}j+{}_{2}j}{2}$ such that $\xi ({}_{1}j+{}_{2}j-{♭}_1)=\xi \left({♭}_1\right),{♭}_1\in [0,2]$ and $\xi \left(\mathfrak{z}\right)$ are defined as:

$$\begin{array}{c}\hfill \xi \left(\mathfrak{z}\right)=\left\{\begin{array}{c}\mathfrak{z},\mathfrak{z}\in [0,1]\hfill \\ 2-\mathfrak{z},\mathfrak{z}\in [1,2].\hfill \end{array}\right.\end{array}$$

$$\begin{array}{cc}\hfill & \frac{{\alpha }^2\mathfrak{f}\left(1\right)}{(2-\alpha )\Gamma \left(\alpha \right)}\left[{\int }_0^2[{(2-\mathfrak{z})}^{\alpha -1}+{\mathfrak{z}}^{\alpha -1}]\xi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}\right]=[1.11343,6.23187]\hfill \\ \hfill & \frac{{\alpha }^2}{(2-\alpha )\Gamma \left(\alpha \right)}\left[{\int }_0^2[{(2-\mathfrak{z})}^{\alpha -1}+{\mathfrak{z}}^{\alpha -1}]\mathfrak{f}\xi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}\right]=[1.24544,5.98512]\hfill \\ \hfill & \frac{{\alpha }^2(\mathfrak{f}\left(0\right)+\mathfrak{f}\left(2\right))}{2(2-\alpha )\Gamma \left(\alpha \right)}\left[{\int }_0^2[{(2-\mathfrak{z})}^{\alpha -1}+{\mathfrak{z}}^{\alpha -1}]\xi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}\right]=[1.74077,4.98549].\hfill \end{array}$$

For a graphical visualization, we vary $0<\alpha \le 1$ (see Figure 2).

Theorem 5.

Let $\mathfrak{f},\xi :[{}_{1}j,{}_{2}j]\to {\mathfrak{R}}_{\mathfrak{I}}$ be $(⋎,\mathfrak{h})$ I.V. pre-invex functions with ${}_{1}j<{}_{2}j$ and $\mathfrak{h}:[0,1]\to (0,\infty )$ be a continuous function; then,

$$\begin{array}{cc}\hfill & \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))+{}^{AB}{I}_{{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))\right]\hfill \\ \hfill & \supseteq \mathcal{P}({}_{1}j,{}_{2}j){\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2\left(\mathfrak{z}\right)+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2(1-\mathfrak{z})]\mathrm{d}\mathfrak{z}+\mathcal{Q}({}_{1}j,{}_{2}j){\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2(1-\mathfrak{z})+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2\left(\mathfrak{z}\right)]\mathrm{d}\mathfrak{z},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & \mathcal{P}({}_{1}j,{}_{2}j)=\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{2}j\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \mathcal{Q}({}_{1}j,{}_{2}j)=\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{2}j\right)+\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{1}j\right),\hfill \end{array}$$

(18)

and $\alpha >0$, ${♭}_1,{♭}_2\in [{}_{1}j,{}_{2}j]$.

Proof. 

Since $\mathfrak{f}$ and $\xi$ are $(⋎,\mathfrak{h})$ I.V. pre-invex functions, then

$$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\supseteq {\mathfrak{h}}_1\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{1}j\right)+{\mathfrak{h}}_1(1-\mathfrak{z})\mathfrak{f}\left({}_{2}j\right).\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\supseteq {\mathfrak{h}}_2\left(\mathfrak{z}\right)\xi \left({}_{1}j\right)+{\mathfrak{h}}_2(1-\mathfrak{z})\xi \left({}_{2}j\right).\hfill \end{array}$$

(20)

Multiplying (19) and (20), we have

$$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\hfill \\ \hfill & \supseteq {\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{1}j\right)+{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2(1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{2}j\right)+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{1}j\right)+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2(1-\mathfrak{z})\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{2}j\right).\hfill \end{array}$$

(21)

Similarly, we have

$$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\hfill \\ \hfill & \supseteq {\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2(1-\mathfrak{z})\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{1}j\right)+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{2}j\right)+{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2(1-\mathfrak{z})\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{1}j\right)+{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2\left(\mathfrak{z}\right)\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{2}j\right).\hfill \end{array}$$

(22)

By adding (21) and (22), multiplying both sides by ${\mathfrak{z}}^{\alpha -1}$ and integrating with respect to $\mathfrak{z}$ on $[0,1]$, then we have

$$\begin{array}{cc}\hfill & {\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & \supseteq {\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2\left(\mathfrak{z}\right)+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2(1-\mathfrak{z})][\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{2}j\right)]\mathrm{d}\mathfrak{z}\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2(1-\mathfrak{z})+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2\left(\mathfrak{z}\right)][\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{2}j\right)+\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{1}j\right)]\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

(23)

Multiplying both sides by $\frac{\alpha }{\Gamma \left(\alpha \right)\mathcal{D}\left(\alpha \right)}$ and then adding $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))$+ $\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))$ to both sides, we obtain

$$\begin{array}{cc}\hfill & \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))+{}^{AB}{I}_{{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))\right]\hfill \\ \hfill & \supseteq [\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{1}j\right)+\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{2}j\right)]{\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2\left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}+[\mathfrak{f}\left({}_{1}j\right)\xi \left({}_{2}j\right)+\mathfrak{f}\left({}_{2}j\right)\xi \left({}_{1}j\right)]{\int }_0^1{\mathfrak{z}}^{\alpha -1}{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2(1-\mathfrak{z})\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

This completes the proof. □

Now, we extract a few important inclusions from Theorem 5 for the product of different kinds of convex functions.

• If we choose $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 5, then

  $$\begin{array}{cc}\hfill & \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))+{}^{AB}{I}_{{(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))))\right]\hfill \\ \hfill & \supseteq \mathcal{P}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{2}{(\alpha +1)(\alpha +2)}.\hfill \end{array}$$
• If we choose $⋎\left(\mathfrak{z}\right)=\mathfrak{z}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 5, then

  $$\begin{array}{cc}\hfill & \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2\alpha {({}_{2}j-{}_{1}j)}^{\alpha }}\left[{}^{AB}{I}_{{{}_{1}j}^{+}}^{\alpha }\mathfrak{f}\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j))+{}^{AB}{I}_{{({}_{1}j+\zeta ({}_{2}j,{}_{1}j))}^{-}}^{\alpha }\mathfrak{f}\xi \left({}_{1}j\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \left({}_{1}j\right)+\mathfrak{f}\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j)))\right]\hfill \\ \hfill & \supseteq \mathcal{P}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{2}{(\alpha +1)(\alpha +2)}.\hfill \end{array}$$
• If we choose $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$ in Theorem 5, then

  $$\begin{array}{cc}\hfill & \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2\alpha {({{}_{2}j}^p,{{}_{1}j}^p)}^{\alpha }}\left[{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))+{}^{AB}{I}_{{({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))}^{-}}^{\alpha }\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ \left({{}_{1}j}^p\right)+\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right]\hfill \\ \hfill & \supseteq \mathcal{P}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{2}{(\alpha +1)(\alpha +2)}.\hfill \end{array}$$
• If we choose $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 5, then

  $$\begin{array}{cc}\hfill & \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\alpha {\left(\zeta ({{}_{2}j}^p,{{}_{1}j}^p)\right)}^{\alpha }}\left[{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))+{}^{AB}{I}_{{({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))}^{-}}^{\alpha }\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ \left({{}_{1}j}^p\right)+\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)))\right]\hfill \\ \hfill & \supseteq \mathcal{P}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{2}{(\alpha +1)(\alpha +2)}.\hfill \end{array}$$
• If we choose $⋎\left(\mathfrak{z}\right)=e^{\mathfrak{z}}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 5, then

  $$\begin{array}{cc}\hfill & \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\alpha {\left(\zeta (e^{{}_{2}j},e^{{}_{1}j})\right)}^{\alpha }}\left[{}^{AB}{I}_{{e^{{}_{1}j}}^{+}}^{\alpha }\mathfrak{f}\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))+{}^{AB}{I}_{{(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))}^{-}}^{\alpha }\mathfrak{f}\xi \circ K\left(e^{{}_{1}j}\right)\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}(\mathfrak{f}\xi \circ k\left(e^{{}_{1}j}\right)+\mathfrak{f}\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})))\right]\hfill \\ \hfill & \supseteq \mathcal{P}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{2}{(\alpha +1)(\alpha +2)},\hfill \end{array}$$

  where $k\left(\mathfrak{z}\right)=e^{\mathfrak{z}}$.

Example 3.

Assume that all the assumptions of Theorem 5 are fulfilled. If we take $\mathfrak{f},\xi :[0,1]\to {\mathbb{R}}_I$ where $\mathfrak{f}\left(\mathfrak{z}\right)=[{\mathfrak{z}}^2,2-{\mathfrak{z}}^2]$ and $\xi \left(\mathfrak{z}\right)=[{\mathfrak{z}}^2,\mathfrak{z}+1]$ with $⋎\left(\mathfrak{z}\right)=\mathfrak{z}$, $\zeta ({}_{2}j,{}_{1}j)={}_{2}j-{}_{1}j$ and $\mathcal{D}\left(\alpha \right)=\frac{2-\alpha }{\alpha }$, then

$$\begin{array}{cc}\hfill & \frac{{\alpha }^2}{(2-\alpha )\Gamma \left(\alpha \right)}\left[{\int }_0^1\left({(1-\mathfrak{z})}^{\alpha -1}+{\mathfrak{z}}^{\alpha -1}\right)\mathfrak{f}\xi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}\right]=[0.0973152,0.877628]\hfill \\ \hfill & \frac{{\alpha }^2}{(2-\alpha )\Gamma \left(\alpha \right)}\left[\mathcal{P}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{2}{(\alpha +1)(\alpha +2)}\right]=[0.137913,0.802403].\hfill \end{array}$$

For visualization, please see Figure 3.

Theorem 6.

Let $\mathfrak{f},\xi :[{}_{1}j,{}_{2}j]\to {\mathfrak{R}}_{\mathfrak{I}}$ be $(⋎,\mathfrak{h})$ I.V. pre-invex functions with ${}_{1}j<{}_{2}j$ and $\mathfrak{h}:[0,1]\to (0,\infty )$ be a continuous function; then,

$$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\xi \left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\hfill \\ \hfill & \supseteq \frac{{\mathfrak{h}}_1\left(\frac{1}{2}\right){\mathfrak{h}}_2\left(\frac{1}{2}\right)\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ (⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\right]\hfill \\ \hfill & +\alpha {\mathfrak{h}}_1\left(\frac{1}{2}\right){\mathfrak{h}}_2\left(\frac{1}{2}\right)\left[\mathcal{P}({}_{1}j,{}_{2}j){\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2(1-\mathfrak{z})+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2\left(\mathfrak{z}\right)]\right.\hfill \\ \hfill & \left.+\mathcal{Q}({}_{1}j,{}_{2}j){\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2\left(\mathfrak{z}\right)+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2(1-\mathfrak{z})]\mathrm{d}\mathfrak{z}\right],\hfill \end{array}$$

where $\mathcal{P}({}_{1}j,{}_{2}j)$ and $\mathcal{Q}({}_{1}j,{}_{2}j)$ are given by (17) and (18), respectively.

Proof. 

Since $\mathfrak{f}$ and $\xi$ are I.V. $(⋎,\mathfrak{h})$ pre-invex functions, then we have

$$\begin{array}{cc}\hfill & \mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\xi \left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\hfill \\ \hfill & \supseteq {\mathfrak{h}}_1\left(\frac{1}{2}\right){\mathfrak{h}}_2\left(\frac{1}{2}\right)\left[\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\right.\hfill \\ \hfill & +\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\hfill \\ \hfill & +\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\hfill \\ \hfill & \left.+\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\right].\hfill \end{array}$$

Multiplying the proceeding inequality by ${\mathfrak{z}}^{\alpha -1}$ and integrating with respect to $\mathfrak{z}$ on $[0,1]$, we have

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(\frac{⋎\left({}_{1}j\right)+⋎({{}_{2}j}^{)}}{2}\right)\right)\xi \left({⋎}^{-1}\left(\frac{⋎\left({}_{1}j\right)+⋎({{}_{2}j}^{)}}{2}\right)\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & \supseteq {\mathfrak{h}}_1\left(\frac{1}{2}\right){\mathfrak{h}}_2\left(\frac{1}{2}\right)\left[{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\right.\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & \left.+{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\right].\hfill \end{array}$$

Applying the definition of interval-valued convexity, we acquire

$$\begin{array}{cc}\hfill & {\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}\left(\frac{⋎\left({}_{1}j\right)+⋎({{}_{2}j}^{)}}{2}\right)\right)\xi \left({⋎}^{-1}\left(\frac{⋎\left({}_{1}j\right)+⋎({{}_{2}j}^{)}}{2}\right)\mathrm{d}\mathfrak{z}\right)\hfill \\ \hfill & =\frac{1}{\alpha }\mathfrak{f}\left({⋎}^{-1}\left(\frac{⋎\left({}_{1}j\right)+⋎\left({}_{2}j\right)}{2}\right)\right)\xi \left({⋎}^{-1}\left(\frac{⋎\left({}_{1}j\right)+⋎\left({}_{2}j\right)}{2}\right)\right)\hfill \\ \hfill & \supseteq {\mathfrak{h}}_1\left(\frac{1}{2}\right){\mathfrak{h}}_2\left(\frac{1}{2}\right)\left[{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\right.\hfill \\ \hfill & +{\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & \left.+\mathcal{P}({}_{1}j,{}_{2}j){\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2(1-\mathfrak{z})+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2\left(\mathfrak{z}\right)]\mathrm{d}\mathfrak{z}+\mathcal{Q}({}_{1}j,{}_{2}j){\int }_0^1{\mathfrak{z}}^{\alpha -1}[{\mathfrak{h}}_1\left(\mathfrak{z}\right){\mathfrak{h}}_2\left(\mathfrak{z}\right)+{\mathfrak{h}}_1(1-\mathfrak{z}){\mathfrak{h}}_2(1-\mathfrak{z})]\mathrm{d}\mathfrak{z}\right].\hfill \end{array}$$

(24)

Additionally,

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+\mathfrak{z}\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & =\frac{1}{{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}{\int }_{⋎\left({}_{1}j\right)}^{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{(u-⋎\left({}_{1}j\right))}^{\alpha -1}\mathfrak{f}\xi \circ {⋎}^{-1}\left(u\right)\mathrm{d}u.\hfill \end{array}$$

Adding $\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))$ to both sides, we obtain

$$\begin{array}{cc}\hfill & =\frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))\right].\hfill \end{array}$$

(25)

Additionally,

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\mathfrak{z}}^{\alpha -1}\mathfrak{f}\left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\xi \left({⋎}^{-1}(⋎\left({}_{1}j\right)+(1-\mathfrak{z})\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\mathrm{d}\mathfrak{z}\hfill \\ \hfill & =\frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{\alpha {\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right].\hfill \end{array}$$

(26)

Comparing (15)–(26), we obtain our required result. □

Now, we extract a few important inclusions from Theorem 6, for the product of different kinds of convex functions.

• If we choose $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 6, then

  $$\begin{array}{cc}\hfill & 2\mathfrak{f}\left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\xi \left({⋎}^{-1}\left(\frac{2⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}{2}\right)\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))\right)}^{\alpha }}\left[{}^{AB}{I}_{{⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right))}^{-}}^{\alpha }\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+{}^{AB}{I}_{⋎{\left({}_{1}j\right)}^{+}}^{\alpha }\mathfrak{f}\xi \circ (⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right))+\mathfrak{f}\xi \circ {⋎}^{-1}(⋎\left({}_{1}j\right)+\zeta (⋎\left({}_{2}j\right),⋎\left({}_{1}j\right)))\right)\right]\hfill \\ \hfill & +\mathcal{P}({}_{1}j,{}_{2}j)\frac{\alpha }{(\alpha +1)(\alpha +2)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{2(\alpha +2)(\alpha +1)},\hfill \end{array}$$

  where $\mathcal{P}({}_{1}j,{}_{2}j)$ and $\mathcal{Q}({}_{1}j,{}_{2}j)$ are given by (17) and (18), respectively.
• If we choose $⋎\left(\mathfrak{z}\right)=\mathfrak{z}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 6, then

  $$\begin{array}{cc}\hfill & 2\mathfrak{f}\left(\frac{2{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}{2}\right)\xi \left(\frac{2{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}{2}\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta ({}_{2}j,{}_{1}j)\right)}^{\alpha }}\left[{}^{AB}{I}_{{{}_{1}j+\zeta ({}_{2}j,{}_{1}j)}^{-}}^{\alpha }\mathfrak{f}\xi \left({}_{1}j\right)+{}^{AB}{I}_{{{}_{1}j}^{+}}^{\alpha }\mathfrak{f}\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j))-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\xi \left({}_{1}j\right)+\mathfrak{f}\xi ({}_{1}j+\zeta ({}_{2}j,{}_{1}j))\right)\right]\hfill \\ \hfill & +\mathcal{P}({}_{1}j,{}_{2}j)\frac{\alpha }{(\alpha +1)(\alpha +2)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{2(\alpha +2)(\alpha +1)},\hfill \end{array}$$

  where $\mathcal{P}({}_{1}j,{}_{2}j)$ and $\mathcal{Q}({}_{1}j,{}_{2}j)$ are given by (17) and $\left(\right)$, respectively.
• If we choose $⋎\left(\mathfrak{z}\right)={\mathfrak{z}}^p$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 6, then

  $$\begin{array}{cc}\hfill & 2\mathfrak{f}\left({\left(\frac{2{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}{2}\right)}^{\frac{1}{p}}\right)\xi \left({\left(\frac{2{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}{2}\right)}^{\frac{1}{p}}\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta ({{}_{2}j}^p,{{}_{1}j}^p)\right)}^{\alpha }}\left[{}^{AB}{I}_{{{{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p)}^{-}}^{\alpha }\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)+{}^{AB}{I}_{{{{}_{1}j}^p}^{+}}^{\alpha }\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\xi \circ k\left({{}_{1}j}^p\right)+\mathfrak{f}\xi \circ k({{}_{1}j}^p+\zeta ({{}_{2}j}^p,{{}_{1}j}^p))\right)\right]+\mathcal{P}({}_{1}j,{}_{2}j)\frac{\alpha }{(\alpha +1)(\alpha +2)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{2(\alpha +2)(\alpha +1)},\hfill \end{array}$$

  where $\mathcal{P}({}_{1}j,{}_{2}j)$ and $\mathcal{Q}({}_{1}j,{}_{2}j)$ are given by (17) and (18), respectively.
• If we choose $⋎\left(\mathfrak{z}\right)=e^{\mathfrak{z}}$ and $\mathfrak{h}\left(\mathfrak{z}\right)=\mathfrak{z}$ in Theorem 6, then

  $$\begin{array}{cc}\hfill & 2\mathfrak{f}\left(ln\left(\frac{2e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})}{2}\right)\right)\xi \left(ln\left(\frac{2e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})}{2}\right)\right)\hfill \\ \hfill & \supseteq \frac{\mathcal{D}\left(\alpha \right)\Gamma \left(\alpha \right)}{2{\left(\zeta (e^{{}_{2}j},e^{{}_{1}j})\right)}^{\alpha }}\left[{}^{AB}{I}_{{e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j})}^{-}}^{\alpha }\mathfrak{f}\xi \circ k\left(e^{{}_{1}j}\right)+{}^{AB}{I}_{{e^{{}_{1}j}}^{+}}^{\alpha }\mathfrak{f}\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right.\hfill \\ \hfill & \left.-\frac{1-\alpha }{\mathcal{D}\left(\alpha \right)}\left(\mathfrak{f}\xi \circ k\left(e^{{}_{1}j}\right)+\mathfrak{f}\xi \circ k(e^{{}_{1}j}+\zeta (e^{{}_{2}j},e^{{}_{1}j}))\right)\right]\hfill \\ \hfill & +\mathcal{P}({}_{1}j,{}_{2}j)\frac{\alpha }{(\alpha +1)(\alpha +2)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{2(\alpha +2)(\alpha +1)},\hfill \end{array}$$

  where $k(\mathfrak{z}=e^{\mathfrak{z}}$, $\mathcal{P}({}_{1}j,{}_{2}j)$ and $\mathcal{Q}({}_{1}j,{}_{2}j)$ are given by (17) and (18), respectively.

Example 4.

Assume that all the assumptions of Theorem 6 are fulfilled. If we take $\mathfrak{f},\xi :[0,1]\to {\mathbb{R}}_I$ where $\mathfrak{f}\left(\mathfrak{z}\right)=[{\mathfrak{z}}^2,2-{\mathfrak{z}}^2]$ and $\xi \left(\mathfrak{z}\right)=[{\mathfrak{z}}^2,\mathfrak{z}+1]$ with $⋎\left(\mathfrak{z}\right)=\mathfrak{z}$, $\zeta ({}_{2}j,{}_{1}j)={}_{2}j-{}_{1}j$ and $\mathcal{D}\left(\alpha \right)=\frac{2-\alpha }{\alpha }$, then

$$\begin{array}{cc}\hfill & \frac{2{\alpha }^2}{(2-\alpha )\Gamma \left(\alpha \right)}\mathfrak{f}\left(\frac{1}{2}\right)\xi \left(\frac{1}{2}\right)=[0.0235079,0.987332]\hfill \\ \hfill & \frac{{\alpha }^2}{2(2-\alpha )\Gamma \left(\alpha \right)}\left[{\int }_0^1\left({(1-\mathfrak{z})}^{\alpha -1}+{\mathfrak{z}}^{\alpha -1}\right)\mathfrak{f}\xi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}+\mathcal{P}({}_{1}j,{}_{2}j)\frac{2}{(\alpha +1)(\alpha +2)}+\mathcal{Q}({}_{1}j,{}_{2}j)\frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}\right]\hfill \\ \hfill & =[0.0737327,0.883897].\hfill \end{array}$$

For visualization, please see Figure 4.

3. Conclusions

The theory of inequalities is investigated from various aspects in different domains. One of the rigorous perspectives is to establish new unified and refined forms of already-known results. In the current proceeding, we have introduced a new generalized notion of convex mappings, and some consequences of the proposed notion are discussed. Moreover, we have explored the HH, HH–Fejer, and Pachpatte’s-type containments, essentially implementing the newly established notion of convexity together with AB-fractional integral operators. The reliability of the findings is verified through examples and simulations. The advantage of this class is that it consolidates several other known classes of convexity. Consequently, the outcomes derived from this class also unify classical results. To the best of our knowledge, the results have no limitations, except ⋎ should be monotonically continuous functions. In the future, we will try to conclude fuzzy and quantum variants of these kinds of inequalities. Additionally, based on the idea of quasi-mean, numerous other classes such as $(⋎,log)$ and $(⋎,\eta )$, $(⋎,(h_1,h_2))$, $(⋎,n)$-polynomial convex functions and stronger versions of convexity can also be introduced in a classical and fuzzy sense as well. Moreover, based on other ordering relations, several new forms of convexity can also be established. Utilizing these classes, several other inequalities can be explored in quantum calculus and time scale calculus. We hope that the ideas and methodology of the current study will inspire interested readers.