A Fractional (q,q′) Non-Extensive Information Dimension for Complex Networks
Abstract
:Simple Summary
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Entropy
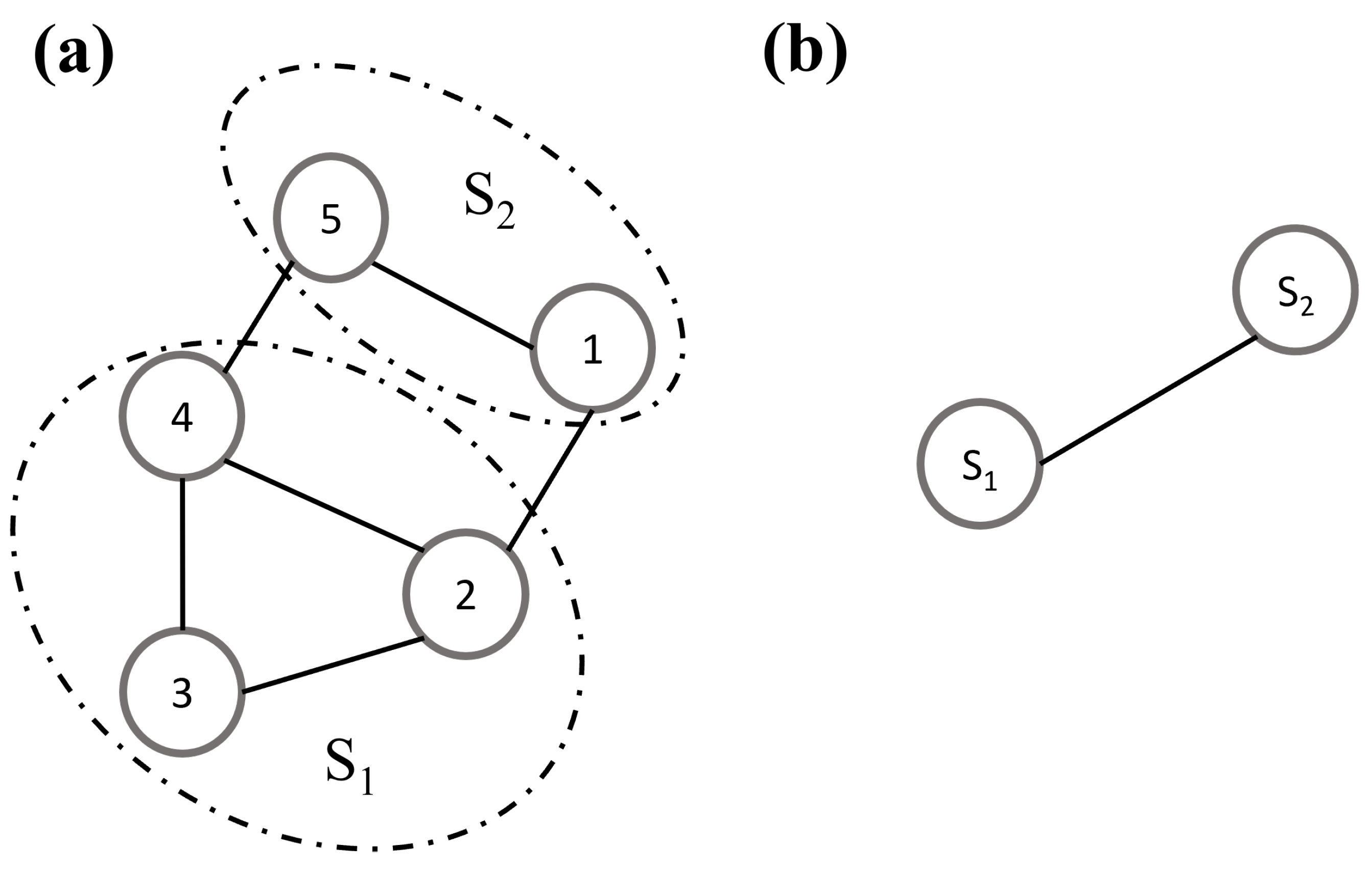
2.2. Information Dimension of Networks
3. Fractional Information Dimension of Complex
Computation of
4. Results
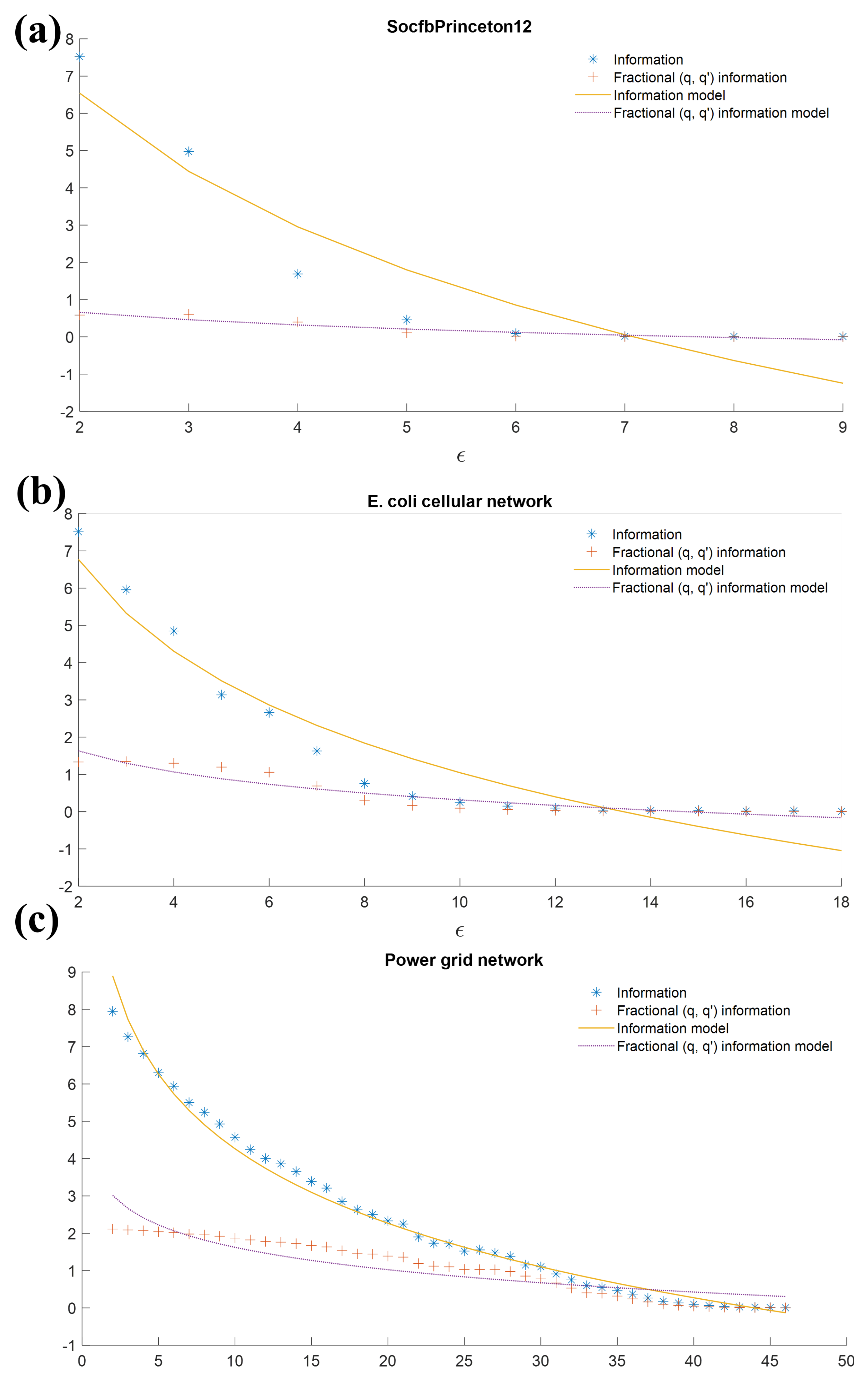
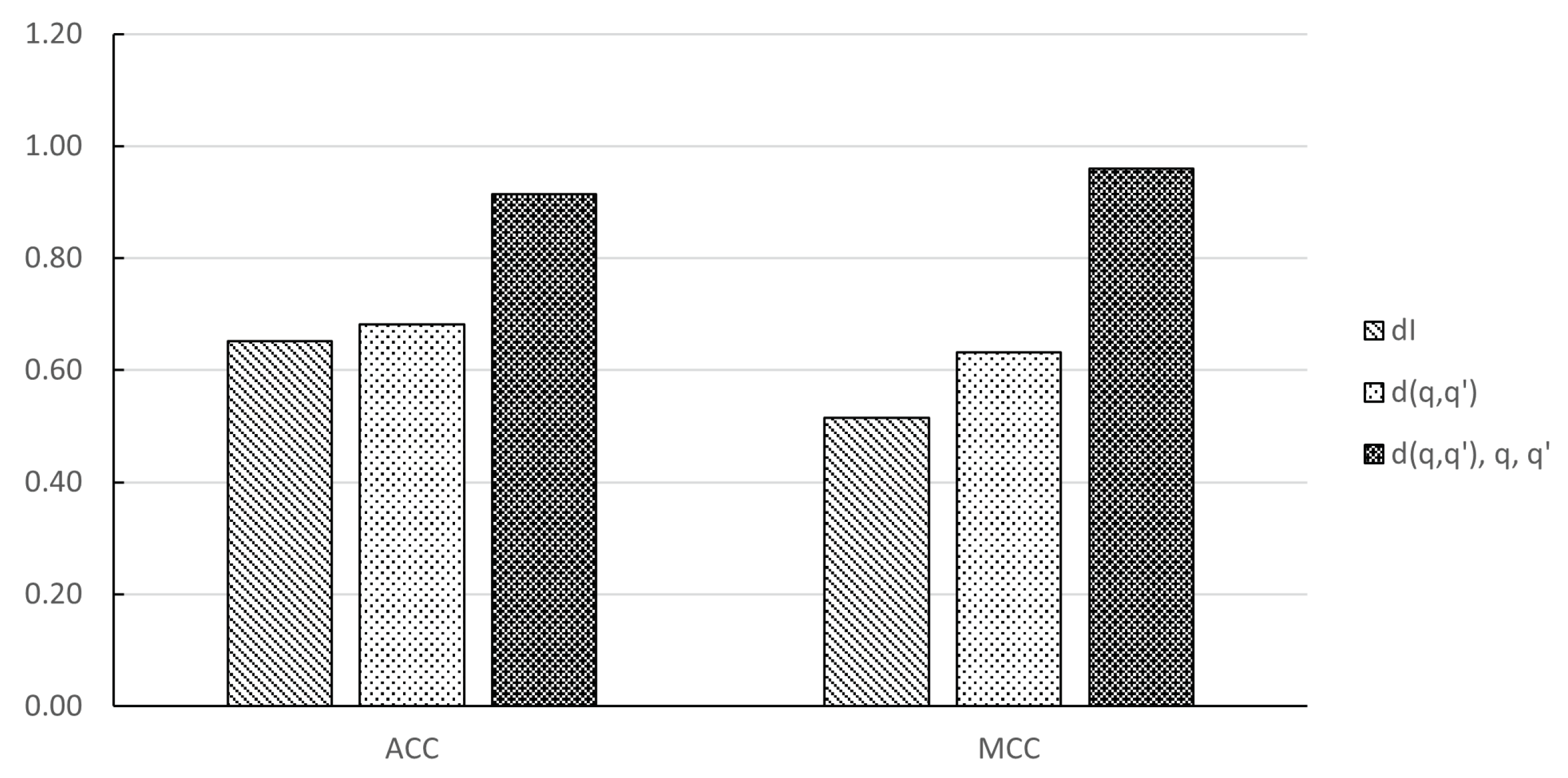
4.1. Real-World Networks
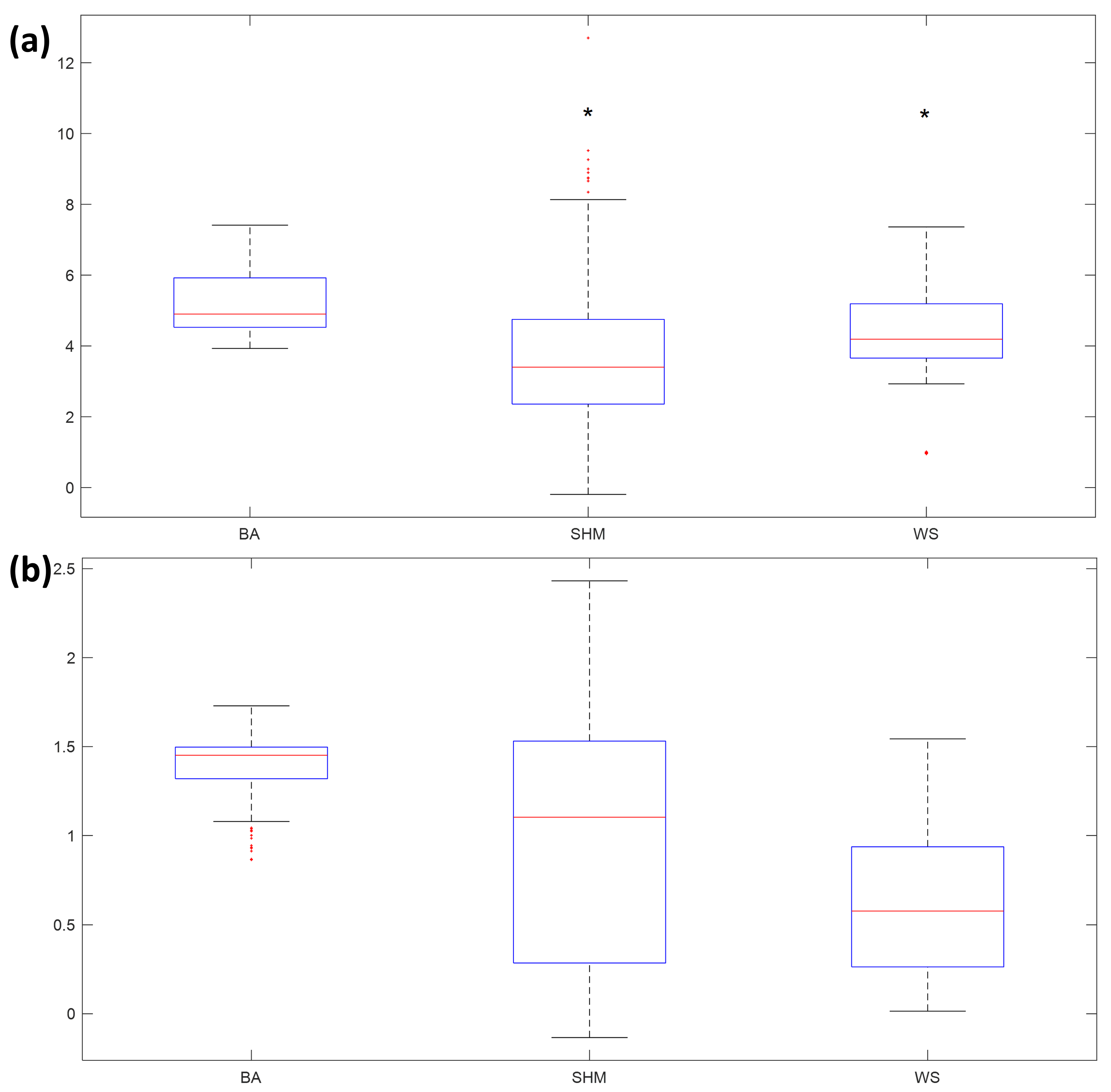
4.2. Synthetic Networks
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACC | Accuracy |
| MCC | Matthew’s Correlation Coefficient |
| MDPI | Multidisciplinary Digital Publishing Institute |
| SBICR | Bayesian Information Criterion with Bonuses |
| BA | Barabasi–Albert |
| SHM | Song, Havlin, and Makse |
| WS | Watts and Strogatz |
References
- Clausius, R. The Mechanical Theory of Heat: With Its Applications to the Steam-Engine and to the Physical Properties of Bodies; Creative Media Partners: Sacramento, CA, USA, 1867. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Beck, C. Generalized information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Esteban, M.D. A general class of entropy statistics. Appl. Math. 1997, 42, 161–169. [Google Scholar] [CrossRef]
- Esteban, M.D.; Morales, D. A summary on entropy statistics. Kybernetika 1995, 31, 337–346. [Google Scholar]
- Ribeiro, M.; Henriques, T.; Castro, L.; Souto, A.; Antunes, L.; Costa-Santos, C.; Teixeira, A. The entropy universe. Entropy 2021, 23, 222. [Google Scholar] [CrossRef] [PubMed]
- Lopes, A.M.; Tenreiro Machado, J.A. A review of fractional order entropies. Entropy 2020, 22, 1374. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Abe, S. A note on the q-deformation-theoretic aspect of the generalized entropies in nonextensive physics. Phys. Lett. A 1997, 224, 326–330. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Tirnakli, U. Non-additive entropy and nonextensive statistical mechanics—Some central concepts and recent applications. J. Phys. Conf. Ser. 2010, 201, 012001. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to non-extensive Statistical Mechanics: Approaching a Complex World. In Introduction to Non-Extensive Statistical Mechanics: Approaching a Complex World; Chapter Thermodynamical and Nonthermodynamical Applications; Springer: New York, NY, USA, 2009; pp. 221–301. [Google Scholar]
- Jackson, D.O.; Fukuda, T.; Dunn, O.; Majors, E. On q-definite integrals. Quart. J. Pure Appl. Math 1910, 41, 193–203. [Google Scholar]
- Johal, R.S. q calculus and entropy in nonextensive statistical physics. Phys. Rev. E 1998, 58, 4147. [Google Scholar] [CrossRef]
- Lavagno, A.; Swamy, P.N. q-Deformed structures and nonextensive-statistics: A comparative study. Phys. A Stat. Mech. Appl. 2002, 305, 310–315. [Google Scholar] [CrossRef]
- Shafee, F. Lambert function and a new non-extensive form of entropy. IMA J. Appl. Math. 2007, 72, 785–800. [Google Scholar] [CrossRef]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Ubriaco, M.R. A simple mathematical model for anomalous diffusion via Fisher’s information theory. Phys. Lett. A 2009, 373, 4017–4021. [Google Scholar] [CrossRef]
- Karci, A. Fractional order entropy: New perspectives. Optik 2016, 127, 9172–9177. [Google Scholar] [CrossRef]
- Karci, A. Notes on the published article “Fractional order entropy: New perspectives” by Ali KARCI, Optik-International Journal for Light and Electron Optics, Volume 127, Issue 20, October 2016, Pages 9172–9177. Optik 2018, 171, 107–108. [Google Scholar] [CrossRef]
- Radhakrishnan, C.; Chinnarasu, R.; Jambulingam, S. A Fractional Entropy in Fractal Phase Space: Properties and Characterization. Int. J. Stat. Mech. 2014, 2014, 460364. [Google Scholar] [CrossRef]
- Ferreira, R.A.C.; Tenreiro Machado, J. An Entropy Formulation Based on the Generalized Liouville Fractional Derivative. Entropy 2019, 21, 638. [Google Scholar] [CrossRef]
- Ferreira, R.A.C. An entropy based on a fractional difference operator. J. Differ. Equations Appl. 2021, 27, 218–222. [Google Scholar] [CrossRef]
- Lad, F.; Sanfilippo, G.; Agrò, G. Extropy: Complementary dual of entropy. Statist. Sci. 2015, 30, 40–58. [Google Scholar] [CrossRef]
- Xue, Y.; Deng, Y. Tsallis eXtropy. Comm. Statist. Theory Methods 2023, 52, 751–762. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, F. Renyi extropy. Comm. Statist. Theory Methods 2023, 52, 5836–5847. [Google Scholar] [CrossRef]
- Buono, F.; Longobardi, M. A dual measure of uncertainty: The Deng extropy. Entropy 2020, 22, 582. [Google Scholar] [CrossRef]
- González, S.H.; De La Mota, I.F. Applying complex network theory to the analysis of Mexico city metro network (1969–2018). Case Stud. Transp. Policy 2021, 9, 1344–1357. [Google Scholar] [CrossRef]
- Eguíluz, V.M.; Hernández-García, E.; Piro, O.; Klemm, K. Effective dimensions and percolation in hierarchically structured scale-free networks. Phys. Rev. E 2003, 68, 055102. [Google Scholar] [CrossRef]
- Ortiz-Vilchis, P.; Ramirez-Arellano, A. Learning Pathways and Students Performance: A Dynamic Complex System. Entropy 2023, 25, 291. [Google Scholar] [CrossRef]
- Ramirez-Arellano, A.; Ortiz-Vilchis, P.; Bory-Reyes, J. The role of D-summable information dimension in differentiating covid-19 disease. Fractals 2021, 29, 2150255. [Google Scholar] [CrossRef]
- Ramirez-Arellano, A. Students learning pathways in higher blended education: An analysis of complex networks perspective. Comput. Educ. 2019, 141, 103634. [Google Scholar] [CrossRef]
- Ortiz-Vilchis, P.; De-la Cruz-García, J.S.; Ramirez-Arellano, A. Identification of Relevant Protein Interactions with Partial Knowledge: A Complex Network and Deep Learning Approach. Biology 2023, 12, 140. [Google Scholar] [CrossRef]
- RamirezArellano, A. Classification of Literary Works: Fractality and Complexity of the Narrative, Essay, and Research Article. Entropy 2020, 22, 904. [Google Scholar] [CrossRef] [PubMed]
- Ortiz-Vilchis, P.; Ramirez-Arellano, A. An Entropy-Based Measure of Complexity: An Application in Lung-Damage. Entropy 2022, 24, 1119. [Google Scholar] [CrossRef] [PubMed]
- De la Cruz-García, J.S.; Bory-Reyes, J.; Ramirez-Arellano, A. A Two-Parameter Fractional Tsallis Decision Tree. Entropy 2022, 24, 572. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press, Inc.: New York, NY, USA, 2011. [Google Scholar]
- Rosenberg, E. A Survey of Fractal Dimensions of Networks; Springer Briefs in Computer Science; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Rosenberg, E. Fractal Dimensions of Networks; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Wen, T.; Cheong, K.H. The fractal dimension of complex networks: A review. Inf. Fusion 2021, 73, 87–102. [Google Scholar] [CrossRef]
- Xu, T.; Moore, I.D.; Gallant, J.C. Fractals, fractal dimensions and landscapes—A review. Geomorphology 1993, 8, 245–262. [Google Scholar] [CrossRef]
- Camacho, D.; Panizo-LLedot, Á.; Bello-Orgaz, G.; Gonzalez-Pardo, A.; Cambria, E. The four dimensions of social network analysis: An overview of research methods, applications, and software tools. Inf. Fusion 2020, 63, 88–120. [Google Scholar] [CrossRef]
- Peach, R.; Arnaudon, A.; Barahona, M. Relative, local and global dimension in complex networks. Nat. Commun. 2022, 13, 3088. [Google Scholar] [CrossRef]
- Ramirez-Arellano, A.; Sigarreta-Almira, J.M.; Bory-Reyes, J. Fractional information dimensions of complex networks. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 093125. [Google Scholar] [CrossRef]
- Ramirez-Arellano, A.; Hernández-Simón, L.M.; Bory-Reyes, J. Two-parameter fractional Tsallis information dimensions of complex networks. Chaos Solitons Fractals 2021, 150, 111113. [Google Scholar] [CrossRef]
- Borges, E.P.; Roditi, I. A family of nonextensive entropies. Phys. Lett. A 1998, 246, 399–402. [Google Scholar] [CrossRef]
- Chakrabarti, R.; Jagannathan, R. A (p, q)-oscillator realization of two-parameter quantum algebras. J. Phys. Math. Gen. 1991, 24, L711. [Google Scholar] [CrossRef]
- Wei, D.; Wei, B.; Hu, Y.; Zhang, H.; Deng, Y. A new information dimension of complex networks. Phys. Lett. A 2014, 378, 1091–1094. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-similarity of complex networks. Nature 2005, 433, 392. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Gallos, L.K.; Havlin, S.; Makse, H.A. How to calculate the fractal dimension of a complex network: The box covering algorithm. J. Stat. Mech. Theory Exp. 2007, 2007, P03006. [Google Scholar] [CrossRef]
- Rosenberg, E. Maximal entropy coverings and the information dimension of a complex network. Phys. Lett. A 2017, 381, 574–580. [Google Scholar] [CrossRef]
- Ramirez-Arellano, A.; Hernández-Simón, L.M.; Bory-Reyes, J. A box-covering Tsallis information dimension and non-extensive property of complex networks. Chaos Solitons Fractals 2020, 132, 109590. [Google Scholar] [CrossRef]
- Ramirez-Arellano, A.; Bermúdez-Gómez, S.; Hernández-Simón, L.M.; Bory-Reyes, J. d-summable fractal dimensions of complex networks. Chaos Solitons Fractals 2019, 119, 210–214. [Google Scholar] [CrossRef]
- Seber, G.; Wild, C. Nonlinear Regression; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Rossi, R.A.; Ahmed, N.K. The Network Data Repository with Interactive Graph Analytics and Visualization. In Proceedings of the AAAI, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Dudley, R.M.; Haughton, D. Information criteria for multiple data sets and restricted parameters. Stat. Sin. 1997, 7, 265–284. [Google Scholar]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Havlin, S.; Makse, H.A. Origins of fractality in the growth of complex networks. Nat. Phys. 2006, 2, 275. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Data Mining Software: An Update. SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
| Network | Full Name | Source | Diameter | Nodes | Edges |
|---|---|---|---|---|---|
| ACF | American college football | [46] | 4 | 115 | 613 |
| BCEPG | Bio-CE-PG | [46] | 8 | 1692 | 47,309 |
| BGP | Bio-grid-plant | [46] | 26 | 1272 | 2726 |
| BGW | Bio-grid-worm | [46] | 12 | 16,259 | 762,774 |
| CEN | C. elegans neural network | [46] | 5 | 297 | 2148 |
| CNC | Ca-netscience | [46] | 17 | 379 | 914 |
| COL | SocfbColgate88 | [56] | 6 | 3482 | 155,044 |
| DRO | Drosophilamedulla1 | [56] | 6 | 1770 | 33,635 |
| DS | Dolphins social network | [46] | 8 | 62 | 159 |
| ECC | E. coli cellular network | [46] | 18 | 2859 | 6890 |
| EM | [46] | 8 | 1133 | 5451 | |
| IOF | Infopenflights | [56] | 14 | 2905 | 30,442 |
| JM | Jazz-musician | [46] | 6 | 198 | 2742 |
| JUN | Jung2015 | [56] | 16 | 2989 | 31,548 |
| LAS | Lada Adamic’s network | [46] | 8 | 350 | 3492 |
| LDU | Labanderiadunne | [56] | 6 | 700 | 6444 |
| MAR | Marvel | [56] | 11 | 19,365 | 96,616 |
| MIT | SocfbMIT | [56] | 8 | 6402 | 251,230 |
| PAIR | Pairdoc | [56] | 14 | 8914 | 25,514 |
| PG | Power grid network | [46] | 46 | 4941 | 6594 |
| PGP | Techpgp | [56] | 24 | 10,680 | 24,340 |
| POW | Powerbcspwr10 | [56] | 49 | 5300 | 13,571 |
| PRI | SocfbPrinceton12 | [56] | 9 | 6575 | 293,307 |
| TC | Topology of communications | [46] | 7 | 174 | 557 |
| USAA | USA airport network | [46] | 7 | 500 | 2980 |
| WHO | TechWHOIS | [56] | 8 | 7476 | 56,943 |
| YEAST | Protein interaction | [46] | 11 | 2223 | 7046 |
| ZCK | Zachary’s karate club | [46] | 5 | 34 | 78 |
| Network | q | |||||
|---|---|---|---|---|---|---|
| ACF | −10.135 | −7.348 | 1.913 | 0.930 | 2.976 | 0.442 |
| BCEPG | −35.380 | −20.988 | 1.828 | 1.004 | 6.109 | 1.814 |
| BGP | −95.919 | −95.442 | 1.591 | 1.037 | 3.558 | 0.817 |
| BGW | −64.525 | −42.927 | 1.949 | 1.006 | 2.437 | 1.219 |
| CEN | −13.897 | −12.103 | 1.822 | 0.988 | 3.253 | 0.805 |
| CNC | −58.166 | −49.747 | 1.835 | 1.014 | 3.606 | 0.733 |
| COL | −25.187 | −18.343 | 2.679 | 1.001 | 3.655 | 1.364 |
| DRO | −23.34 | −18.202 | 1.443 | 0.998 | 5.856 | 0.662 |
| DS | −17.868 | −14.616 | 1.498 | 0.989 | 3.959 | 0.788 |
| ECC | −87.426 | −66.706 | 1.625 | 1.029 | 5.044 | 1.442 |
| EM | −34.459 | −31.15 | 1.547 | 1.001 | 4.663 | 0.915 |
| IOF | −65.328 | −51.656 | 1.736 | 1.028 | 4.846 | 1.112 |
| JM | −19.449 | −13.532 | 2.805 | 0.986 | 2.659 | 0.726 |
| JUN | −63.643 | −58.511 | 2.485 | 1.006 | 5.95 | 1.105 |
| LAS | −30.269 | −21.898 | 2.103 | 1.020 | 3.459 | 0.365 |
| LDU | −20.750 | −20.091 | 1.850 | 0.998 | 2.879 | 0.864 |
| MAR | −52.612 | −46.428 | 1.644 | 1.003 | 3.976 | 0.900 |
| MIT | −39.208 | −25.351 | 2.295 | 1.006 | 4.353 | 1.165 |
| PAIR | −68.947 | −57.065 | 1.582 | 1.004 | 2.726 | 0.670 |
| PG | −186.322 | −199.049 | 1.463 | 0.999 | 5.221 | 1.324 |
| PGP | −117.159 | −100.827 | 1.573 | 1.013 | 2.930 | 1.666 |
| POW | −186.721 | −206.691 | 1.589 | 0.994 | 5.176 | 0.489 |
| PRI | −45.866 | −27.325 | 2.533 | 1.016 | 6.338 | 1.234 |
| TC | −22.759 | −22.025 | 1.57 | 0.991 | 5.494 | 1.143 |
| USAA | −26.655 | −18.497 | 1.678 | 0.996 | 2.358 | 0.626 |
| WHO | −36.125 | −29.873 | 1.675 | 1.002 | 4.751 | 1.280 |
| YEAST | −48.576 | −43.622 | 1.533 | 1.006 | 6.500 | 0.594 |
| ZCK | −9.77 | −3.672 | 1.500 | 0.950 | 5.094 | 0.696 |
| Network Model | Nodes | Edges | Model | ||
|---|---|---|---|---|---|
| BA | 2000–4500 | 2685–40,455 | 3.930–7.412 | 0.864–1.729 | (100%) |
| SHM | 10–36,480 | 9–880,475 | 0.831–12.689 | 0.005–2.432 | (70.83%) |
| WS | 2000–4000 | 4000–40,000 | 0.955–7.363 | 0.015–1.540 | (100%) |
| G | M | |||
|---|---|---|---|---|
| 2 | 2 | 0 | 0.400 | 1 |
| 2 | 2 | 0.400 | 0.400 | 1 |
| 2 | 3 | 0 | 0.400 | 1 |
| 2 | 3 | 0.400 | 1 | |
| 2 | 4 | 0 | 0.800 | 1 |
| 3 | 2 | 0 | 1 | |
| 3 | 2 | 0.400 | 1 | |
| 3 | 3 | ≤0.800 | 1 | |
| 3 | 4 | 0 | 1 | 1 |
| 4 | 0 | 0.400 | 1 | |
| 2 | 2 | 0 | 2 | |
| 2 | 2 | 0.400 | 2 | |
| 2 | 2 | 1 | ≤0.800 | 2 |
| 2 | 3 | 0 | ≤0.400 | 2 |
| 2 | 3 | 0.400 | 0.200 | 2 |
| 3 | 2 | 0 | 2 | |
| 3 | 2 | 0.400 | 0.800 | 2 |
| 3 | 4 | 0 | 0.400 | 2 |
| 4 | 2 | 0 | ≤0.200 | 2 |
| 4 | 2 | 0.400 | 2 | |
| 4 | 3 | 0 | 0.800 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramirez-Arellano, A.; De-la-Cruz-Garcia, J.-S.; Bory-Reyes, J. A Fractional (q,q′) Non-Extensive Information Dimension for Complex Networks. Fractal Fract. 2023, 7, 702. https://doi.org/10.3390/fractalfract7100702
Ramirez-Arellano A, De-la-Cruz-Garcia J-S, Bory-Reyes J. A Fractional (q,q′) Non-Extensive Information Dimension for Complex Networks. Fractal and Fractional. 2023; 7(10):702. https://doi.org/10.3390/fractalfract7100702
Chicago/Turabian StyleRamirez-Arellano, Aldo, Jazmin-Susana De-la-Cruz-Garcia, and Juan Bory-Reyes. 2023. "A Fractional (q,q′) Non-Extensive Information Dimension for Complex Networks" Fractal and Fractional 7, no. 10: 702. https://doi.org/10.3390/fractalfract7100702
APA StyleRamirez-Arellano, A., De-la-Cruz-Garcia, J.-S., & Bory-Reyes, J. (2023). A Fractional (q,q′) Non-Extensive Information Dimension for Complex Networks. Fractal and Fractional, 7(10), 702. https://doi.org/10.3390/fractalfract7100702







