A Fractional-Order Telegraph Diffusion Model for Restoring Texture Images with Multiplicative Noise
Abstract
1. Introduction
2. Preliminaries
3. Some Related Works and Motivation
3.1. Review of Some Related Works
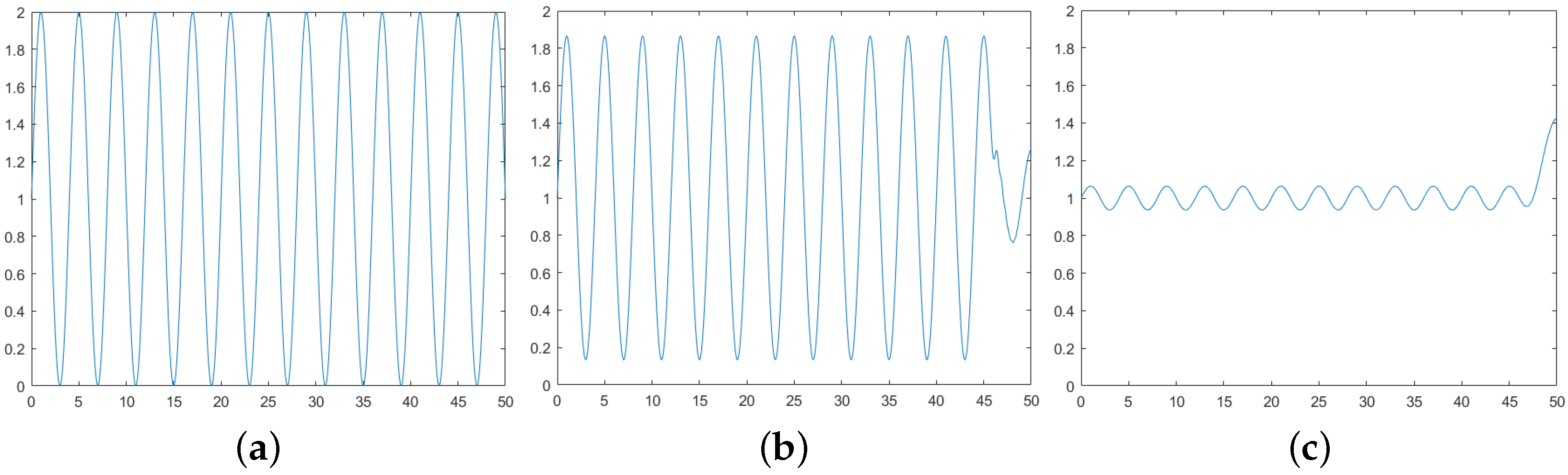
3.2. The Property of Telegraph Diffusion Based Methods
4. The FTDE Model and Its Theoretical Analysis
4.1. The Proposed FTDE Model
4.2. Existence and Uniqueness of the Solution
- (i)
- ,
- (ii)
- ,
5. Numerical Scheme and Experiments
5.1. Numerical Scheme
| Algorithm 1 DFT-based algorithm of the proposed model |
Input: Noisy level L, original image , Initialize:, Output: |
5.2. Numerical Experiments and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tur, M.; Chin, K.; Goodman, J. When is speckle noise multiplicative? Appl. Opt. 1982, 21, 1157–1159. [Google Scholar] [CrossRef] [PubMed]
- Wagner, R.; Smith, S.; Sandrik, J.; Lopez, H. Statistics of speckle in ultrasound B-scans. IEEE Trans. Son. Ultrason. 1983, 30, 156–163. [Google Scholar] [CrossRef]
- Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A tutorial on speckle reduction in synthetic aperture radar images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- Yao, W.; Guo, Z.; Sun, J.; Wu, B.; Gao, H. Multiplicative noise removal for texture images based on adaptive anisotropic fractional diffusion equations. SIAM J. Imaging Sci. 2019, 12, 839–873. [Google Scholar] [CrossRef]
- Majee, S.; Ray, R.; Majee, A. A gray level indicator-based regularized telegraph diffusion model: Application to image despeckling. SIAM J. Imaging Sci. 2020, 13, 844–870. [Google Scholar] [CrossRef]
- Bamler, R. Principles of synthetic aperture radar. Surv. Geophys. 2000, 21, 147–157. [Google Scholar] [CrossRef]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Images; SciTech Publishing: Raleigh, NC, USA, 2004. [Google Scholar]
- Aubert, G.; Aujol, J. A variational approach to removing multiplicative noise. SIAM J. Appl. Math. 2008, 68, 925–946. [Google Scholar] [CrossRef]
- Shi, J.; Osher, S. A nonlinear inverse scale space method for a convex multiplicative noise model. SIAM J. Imaging Sci. 2008, 1, 294–321. [Google Scholar] [CrossRef]
- Huang, Y.; Ng, M.; Wen, Y. A new total variation method for multiplicative noise removal. SIAM J. Imaging Sci. 2009, 2, 20–40. [Google Scholar] [CrossRef]
- Dong, Y.; Zeng, T. A convex variational model for restoring blurred images with multiplicative noise. SIAM J. Imaging Sci. 2013, 6, 1598–1625. [Google Scholar] [CrossRef]
- Abd-Elmoniem, K.; Youssef, A.; Kadah, Y. Real-time speckle reduction and coherence enhancement in ultrasound imaging via nonlinear anisotropic diffusion. IEEE Trans. Biomed. Eng. 2002, 49, 997–1014. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Guo, Z.; Dong, G.; Sun, J.; Zhang, D.; Wu, B. A doubly degenerate diffusion model based on the gray level indicator for multiplicative noise removal. IEEE Trans. Image Process. 2015, 24, 249–260. [Google Scholar] [CrossRef] [PubMed]
- Averbuch, A.; Epstein, B.; Rabin, N.; Turkel, E. Edge-enhancement postprocessing using artificial dissipation. IEEE Trans. Image Process. 2006, 15, 1486–1498. [Google Scholar] [CrossRef] [PubMed]
- Ratner, V.; Zeevi, Y. Image enhancement using elastic manifolds. In Proceedings of the 14th International Conference on Image Analysis and Processing, Modena, Italy, 10–14 September 2007; pp. 769–774. [Google Scholar]
- Zauderer, E. Partial Differential Equations of Applied Mathematics; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Cao, Y.; Yin, J.; Liu, Q.; Li, M. A class of nonlinear parabolic-hyperbolic equations applied to image restoration. Nonlinear Anal. Real World Appl. 2010, 11, 253–261. [Google Scholar] [CrossRef]
- You, Y.; Kaveh, M. Fourth-order partial differential equations for noise removal. IEEE Trans. Image Process. 2000, 9, 1723–1730. [Google Scholar] [CrossRef]
- Zeng, W.; Lu, X.; Tan, X. A class of fourth-order telegraph-diffusion equations for image restoration. J. Appl. Math. 2011, 2011, 240370. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Yang, Y. Spatial fractional telegraph equation for image structure preserving denoising. Signal Process. 2015, 107, 368–377. [Google Scholar] [CrossRef]
- Majee, S.; Jain, S.K.; Ray, R.K.; Majee, A.K. A Fuzzy Edge Detector Driven Telegraph Total Variation Model for Image Despeckling. arXiv 2019. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, Y. Variational Formulation of the Stress-Strain Problem in Capillary-Porous Materials with Fractal Structure. In Proceedings of the IEEE 15th International Conference on Computer Sciences and Information Technologies (CSIT), Zbarazh, Ukraine, 23–26 September 2020; pp. 1–4. [Google Scholar]
- Hendy, M.; Amin, M.; Ezzat, M. Two-dimensional problem for thermoviscoelastic materials with fractional order heat transfer. J. Therm. Stress. 2019, 42, 1298–1315. [Google Scholar] [CrossRef]
- Zhou, J.; Salahshour, S.; Ahmadian, A. Modeling the dynamics of COVID-19 using fractal-fractional operator with a case study. Results Phys. 2022, 33, 105103. [Google Scholar] [CrossRef]
- Bai, J.; Feng, X. Fractional-order anisotropic diffusion for image denoising. IEEE Trans. Image Process. 2007, 16, 2492–2502. [Google Scholar] [CrossRef]
- Cuesta, E.; Finat, J. Image Processing by means of linear integro-differential equation. In Proceedings of the Third IASTED International Conference on Visualization, Imaging and Image Processing, Benalmadena, Spain, 8–10 September 2003. [Google Scholar]
- Janev, M.; Pilipović, S.; Atanacković, T.; Obradović, R.; Ralević, N. Fully fractional anisotropic diffusion for image denoising. Math. Comput. Model. 2011, 54, 729–741. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, K. A total fractional-order variation model for image restoration with nonhomogeneous boundary conditions and its numerical solution. SIAM J. Imaging Sci. 2015, 8, 2487–2518. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Z.; Xiao, L. A fast adaptive reweighted residual-feedback iterative algorithm for fractional-order total variation regularized multiplicative noise removal of partly-textured images. Signal Process. 2014, 98, 381–395. [Google Scholar] [CrossRef]
- Chen, D.; Sun, S.; Zhang, C.; Chen, Y.; Xue, D. Fractional-order TV-L2 model for image denoising. Open Phys. 2013, 11, 1414–1422. [Google Scholar] [CrossRef]
- Dong, F.; Chen, Y. A fractional-order derivative based variational framework for image denoising. Inverse Probl. Imaging 2016, 10, 27–50. [Google Scholar] [CrossRef]
- Che, J.; Guan, Q.; Wang, X. Image denoising based on adaptive fractional partial differential equations. In Proceedings of the 2013 6th International Congress on Image and Signal Processing (CISP), Hangzhou, China, 16–18 December 2013; pp. 288–292. [Google Scholar]
- Pu, Y. Fractional calculus approach to texture of digital image. In Proceedings of the International Conference on Signal Processing, Guilin, China, 16–20 November 2006; pp. 1002–1006. [Google Scholar]
- Pu, Y.; Wang, W.; Zhou, J.; Wang, Y.; Jia, H. Fractional differential approach to detecting textural features of digital image and its fractional differential filter implementation. Sci. China 2008, 51, 1319–1339. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, R.; Ren, J.; Gui, Q. Adaptive Fractional Image Enhancement Algorithm Based on Rough Set and Particle Swarm Optimization. Fractal Fract. 2022, 6, 100. [Google Scholar] [CrossRef]
- Li, D.; Tian, X.; Jin, Q.; Hirasawa, K. Adaptive fractional-order total variation image restoration with split Bregman iteration. ISA Trans. 2017, 82, 210–222. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Sun, J.; Guo, Z.; Yao, W.; Zhou, Z. Fractional-order diffusion model for multiplicative noise removal in texture-rich images and its fast explicit diffusion solving. BIT Numer. Math. 2022, 62, 1319–1354. [Google Scholar] [CrossRef]
- Ju, N. The maximum principle and the global attractor for the dissipative 2D quasi-geostrophic equations. Commun. Math. Phys. 2005, 255, 161–181. [Google Scholar] [CrossRef]
- Burczak, J.; Granero-Belinchón, R. Suppression of blow up by a logistic source in 2D Keller–Segel system with fractional dissipation. J. Differ. Equ. 2017, 263, 6115–6142. [Google Scholar] [CrossRef]
- Schumer, R.; Benson, D.; Meerschaert, M.; Wheatcraft, S. Eulerian derivation of the fractional advection-dispersion equation. J. Contam. Hydrol. 2001, 48, 69–88. [Google Scholar] [CrossRef]
- He, J. Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng. 1998, 167, 57–68. [Google Scholar] [CrossRef]
- Chen, S.; Liu, F.; Jiang, X.; Turner, I.; Burrage, K. Fast finite difference approximation for identifying parameters in a two-dimensional space-fractional nonlocal model with variable diffusivity coefficients. SIAM J. Numer. Anal. 2017, 54, 606–624. [Google Scholar] [CrossRef]
- Pan, M.; Zheng, L.; Liu, F.; Liu, C.; Chen, X. A spatial-fractional thermal transport model for nanofluid in porous media. Appl. Math. Model. 2018, 53, 622–634. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, an Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering Process; Mag. Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Xu, W.; Tang, C.; Zhang, J.; Su, Y.; Su, R.K.L. Two parabolic–hyperbolic oriented partial differential equations for denoising in electronic speckle pattern interferometry fringes. Appl. Opt. 2015, 54, 4720–4726. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, Z.; Zhang, D.; Wu, B. A nonlinear diffusion equation-based model for ultrasound speckle noise removal. J. Nonlinear Sci. 2018, 28, 443–470. [Google Scholar] [CrossRef]
- Shan, X.; Sun, J.; Guo, Z. Multiplicative noise removal based on the smooth diffusion equation. J. Math. Imaging Vis. 2019, 61, 763–779. [Google Scholar] [CrossRef]
- Tychonoff, A. Ein fixpunktsatz. Math. Ann. 1935, 111, 767–776. [Google Scholar] [CrossRef]
- Adams, R.; Fournier, J. Sobolev Spaces; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Evans, L. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Lions, J.; Magenes, E. Non-Homogeneous Boundary Value Problems and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Roubíček, T. Nonlinear Partial Differential Equations with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Candan, C.; Kutay, M.; Ozaktas, H. The discrete fractional Fourier transform. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Phoenix, AZ, USA, 15–19 March 1999; pp. 1713–1716. [Google Scholar]
- Ozaktas, H.; Arikan, O.; Kutay, M.; Bozdagt, G. Digital computation of the fractional Fourier transform. IEEE Trans. Signal Process. 1996, 44, 2141–2150. [Google Scholar] [CrossRef]
- Taylor, M. Partial Differential Equations I; Basic Theory, Applied Mathematical Sciences; Springer: New York, NY, USA, 2011. [Google Scholar]
- LeVeque, R. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007. [Google Scholar]
- Do, M.; Vetterli, M. The finite ridgelet transform for image representation. IEEE Trans. Image Process. 2003, 12, 16–28. [Google Scholar] [CrossRef]
- Deledalle, C.; Denis, L.; Tabti, S.; Tupin, F.; Reigber, A.; Jager, M. Mulog, or how to apply Gaussian denoisers to multi-channel SAR speckle reduction? IEEE Trans. Image Process. 2017, 26, 4389–4403. [Google Scholar] [CrossRef]
- Durand, S.; Fadili, J.; Nikolova, M. Multiplicative noise removal using L1 fidelity on frame coefficients. J. Math. Imaging Vis. 2010, 36, 201–226. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Lu, L. Why is image quality assessment so difficult? In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, China, 6–10 April 2003. [Google Scholar]









| Image | Texture1 | Texture2 | Satellite1 | Satellite2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | 1 | 4 | 10 | 1 | 4 | 10 | 1 | 4 | 10 | 1 | 4 | 10 |
| b | 6 | 4 | 4 | 6 | 3 | 4 | 3 | 3 | 3 | 5 | 4 | |
| Parameters | |||
|---|---|---|---|
| Algorithm | |||
| AA () | 200 | 400 | 600 |
| SO () | |||
| CV () | |||
| TD () | |||
| NTV () | |||
| DD () | |||
| FDE () | |||
| Model | SO | CV | AA | TD | NTV | DD | FDE | BM3D-SAR | Ours |
|---|---|---|---|---|---|---|---|---|---|
| PSNR | 9.31 | 10.98 | 12.65 | 11.15 | 12.45 | 12.57 | 12.58 | 12.83 | 12.82 |
| MAE | 68.50 | 49.91 | 46.68 | 52.57 | 46.39 | 47.55 | 46.18 | 41.63 | 45.56 |
| SSIM | 0.15 | 0.31 | 0.25 | 0.21 | 0.31 | 0.25 | 0.40 | 0.36 | 0.40 |
| IICC | 0.52 | 0.43 | 0.54 | 0.38 | 0.53 | 0.46 | 0.58 | 0.59 | 0.55 |
| PSNR | 14.65 | 13.73 | 13.90 | 13.87 | 15.27 | 14.55 | 15.78 | 15.85 | 15.70 |
| MAE | 34.81 | 39.11 | 41.75 | 38.42 | 32.15 | 36.66 | 31.62 | 29.31 | 32.22 |
| SSIM | 0.57 | 0.45 | 0.37 | 0.40 | 0.63 | 0.56 | 0.69 | 0.67 | 0.68 |
| IICC | 0.76 | 0.65 | 0.76 | 0.64 | 0.79 | 0.71 | 0.80 | 0.81 | 0.79 |
| PSNR | 17.13 | 15.28 | 14.80 | 16.56 | 17.85 | 17.27 | 18.22 | 18.30 | 18.07 |
| MAE | 25.98 | 33.09 | 37.54 | 27.30 | 23.41 | 26.28 | 23.48 | 21.81 | 24.14 |
| SSIM | 0.73 | 0.59 | 0.48 | 0.63 | 0.80 | 0.77 | 0.82 | 0.82 | 0.81 |
| IICC | 0.86 | 0.75 | 0.84 | 0.80 | 0.88 | 0.86 | 0.89 | 0.89 | 0.88 |
| Model | SO | CV | AA | TD | NTV | DD | FDE | BM3D-SAR | Ours |
|---|---|---|---|---|---|---|---|---|---|
| PSNR | 10.96 | 12.56 | 14.35 | 13.92 | 14.92 | 15.30 | 15.01 | 14.19 | 15.52 |
| MAE | 50.46 | 37.44 | 33.56 | 34.81 | 30.41 | 30.97 | 32.30 | 29.02 | 30.96 |
| SSIM | 0.23 | 0.37 | 0.39 | 0.29 | 0.37 | 0.39 | 0.43 | 0.43 | 0.45 |
| IICC | 0.72 | 0.62 | 0.75 | 0.64 | 0.74 | 0.74 | 0.76 | 0.71 | 0.76 |
| PSNR | 17.66 | 16.55 | 15.38 | 16.61 | 17.99 | 17.56 | 18.06 | 17.47 | 18.17 |
| MAE | 22.10 | 25.84 | 31.45 | 24.85 | 20.91 | 23.18 | 22.58 | 21.14 | 22.53 |
| SSIM | 0.60 | 0.49 | 0.51 | 0.51 | 0.63 | 0.64 | 0.67 | 0.62 | 0.68 |
| IICC | 0.87 | 0.82 | 0.87 | 0.82 | 0.88 | 0.85 | 0.88 | 0.86 | 0.88 |
| PSNR | 19.80 | 18.28 | 15.74 | 19.07 | 20.45 | 20.04 | 20.62 | 20.22 | 20.48 |
| MAE | 16.97 | 20.76 | 30.43 | 18.52 | 15.62 | 17.23 | 16.56 | 15.64 | 16.87 |
| SSIM | 0.75 | 0.65 | 0.56 | 0.70 | 0.80 | 0.79 | 0.80 | 0.79 | 0.80 |
| IICC | 0.92 | 0.88 | 0.91 | 0.90 | 0.93 | 0.92 | 0.93 | 0.93 | 0.93 |
| Model | SO | CV | AA | TD | NTV | DD | FDE | BM3D-SAR | Ours |
|---|---|---|---|---|---|---|---|---|---|
| PSNR | 13.02 | 15.44 | 17.77 | 17.47 | 18.56 | 20.26 | 19.61 | 20.50 | 20.47 |
| MAE | 42.07 | 25.80 | 23.09 | 22.33 | 20.57 | 17.75 | 18.84 | 16.55 | 17.46 |
| SSIM | 0.28 | 0.36 | 0.64 | 0.46 | 0.46 | 0.73 | 0.73 | 0.74 | 0.76 |
| IICC | 0.82 | 0.67 | 0.79 | 0.68 | 0.81 | 0.85 | 0.85 | 0.86 | 0.86 |
| PSNR | 20.64 | 21.75 | 21.20 | 21.40 | 21.67 | 22.60 | 22.89 | 23.40 | 23.18 |
| MAE | 16.15 | 14.59 | 15.39 | 14.31 | 14.15 | 13.13 | 12.94 | 11.59 | 12.58 |
| SSIM | 0.78 | 0.60 | 0.86 | 0.80 | 0.66 | 0.86 | 0.88 | 0.88 | 0.88 |
| IICC | 0.90 | 0.90 | 0.90 | 0.88 | 0.90 | 0.92 | 0.92 | 0.93 | 0.93 |
| PSNR | 23.62 | 24.04 | 23.96 | 23.93 | 23.74 | 24.64 | 24.97 | 25.66 | 25.19 |
| MAE | 11.33 | 11.03 | 11.05 | 10.74 | 11.17 | 10.30 | 10.17 | 8.93 | 9.91 |
| SSIM | 0.89 | 0.90 | 0.92 | 0.92 | 0.93 | 0.93 | 0.93 | 0.94 | 0.93 |
| IICC | 0.94 | 0.94 | 0.95 | 0.94 | 0.94 | 0.95 | 0.95 | 0.96 | 0.95 |
| Model | SO | CV | AA | TD | NTV | DD | FDE | BM3D-SAR | Ours |
|---|---|---|---|---|---|---|---|---|---|
| PSNR | 11.03 | 13.74 | 16.32 | 15.38 | 16.52 | 17.74 | 16.33 | 17.90 | 17.77 |
| MAE | 56.07 | 34.88 | 29.43 | 29.66 | 27.68 | 24.94 | 29.29 | 23.77 | 24.97 |
| SSIM | 0.28 | 0.25 | 0.53 | 0.48 | 0.32 | 0.59 | 0.58 | 0.61 | 0.61 |
| IICC | 0.78 | 0.65 | 0.79 | 0.68 | 0.78 | 0.81 | 0.78 | 0.82 | 0.81 |
| PSNR | 18.68 | 18.90 | 17.43 | 18.76 | 19.18 | 19.53 | 19.67 | 20.07 | 19.90 |
| MAE | 21.80 | 21.23 | 26.48 | 20.93 | 20.20 | 29.71 | 19.85 | 18.33 | 19.42 |
| SSIM | 0.75 | 0.44 | 0.65 | 0.73 | 0.54 | 0.77 | 0.78 | 0.80 | 0.79 |
| IICC | 0.88 | 0.86 | 0.88 | 0.85 | 0.88 | 0.88 | 0.89 | 0.89 | 0.89 |
| PSNR | 21.07 | 20.65 | 17.86 | 20.88 | 21.10 | 21.34 | 21.60 | 21.92 | 21.72 |
| MAE | 16.32 | 17.17 | 25.37 | 16.59 | 16.13 | 16.04 | 15.85 | 14.80 | 15.68 |
| SSIM | 0.87 | 0.82 | 0.69 | 0.85 | 0.88 | 0.86 | 0.87 | 0.88 | 0.87 |
| IICC | 0.92 | 0.91 | 0.91 | 0.91 | 0.92 | 0.92 | 0.93 | 0.93 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, X.; Zhang, D.; Shi, S.; Yao, W.; Guo, Z.; Sun, J. A Fractional-Order Telegraph Diffusion Model for Restoring Texture Images with Multiplicative Noise. Fractal Fract. 2023, 7, 64. https://doi.org/10.3390/fractalfract7010064
Bai X, Zhang D, Shi S, Yao W, Guo Z, Sun J. A Fractional-Order Telegraph Diffusion Model for Restoring Texture Images with Multiplicative Noise. Fractal and Fractional. 2023; 7(1):64. https://doi.org/10.3390/fractalfract7010064
Chicago/Turabian StyleBai, Xiangyu, Dazhi Zhang, Shengzhu Shi, Wenjuan Yao, Zhichang Guo, and Jiebao Sun. 2023. "A Fractional-Order Telegraph Diffusion Model for Restoring Texture Images with Multiplicative Noise" Fractal and Fractional 7, no. 1: 64. https://doi.org/10.3390/fractalfract7010064
APA StyleBai, X., Zhang, D., Shi, S., Yao, W., Guo, Z., & Sun, J. (2023). A Fractional-Order Telegraph Diffusion Model for Restoring Texture Images with Multiplicative Noise. Fractal and Fractional, 7(1), 64. https://doi.org/10.3390/fractalfract7010064








