Quadratic Admissibility for a Class of LTI Uncertain Singular Fractional-Order Systems with 0 < α < 2
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
3. Main Results
3.1. Admissibility of Unforced Linear Singular FOS with Order
3.2. Stabilization of Singular FOS with Order
3.3. Quadratic Admissibility of Uncertain Linear Singular FOS with Order
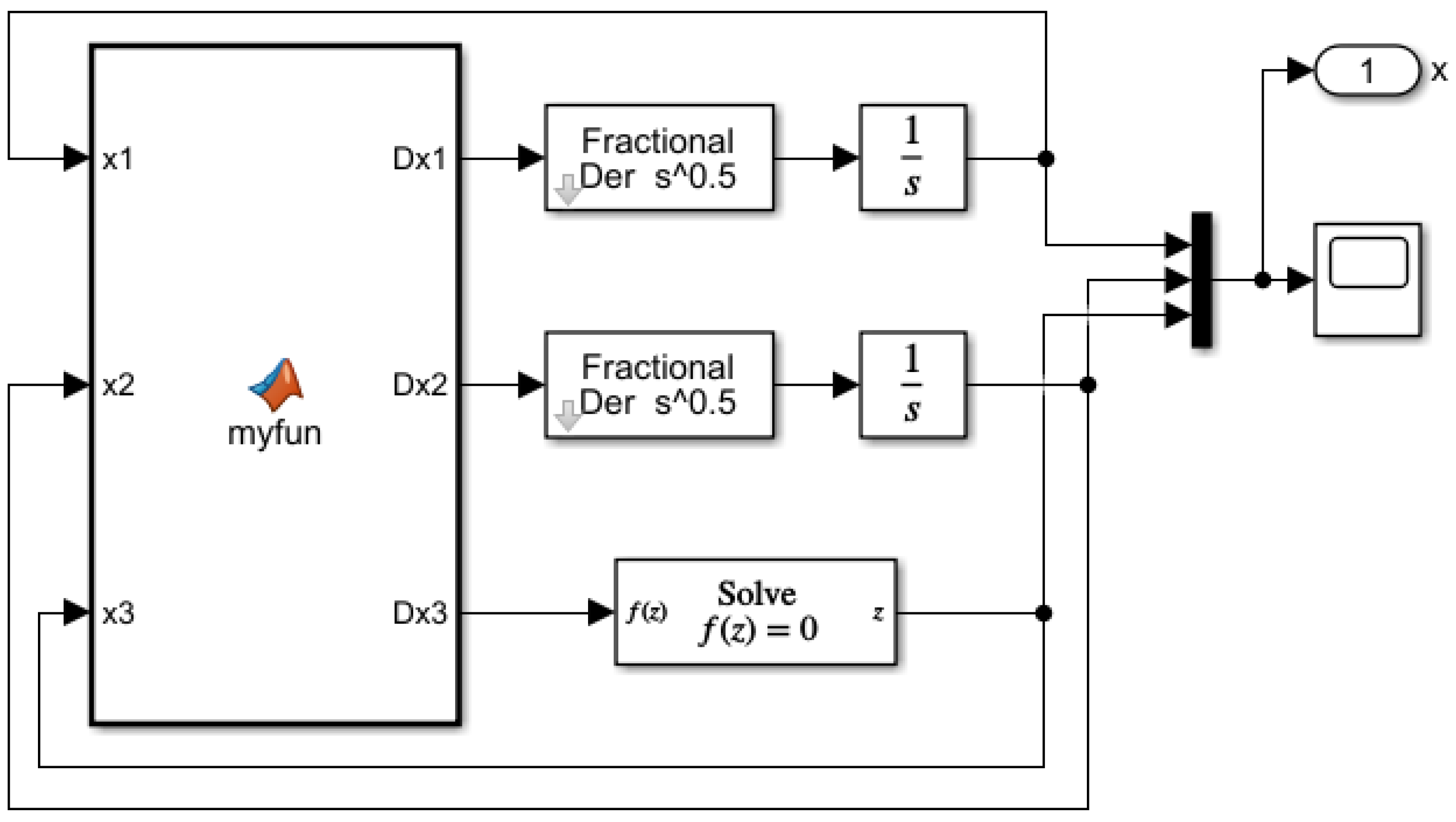
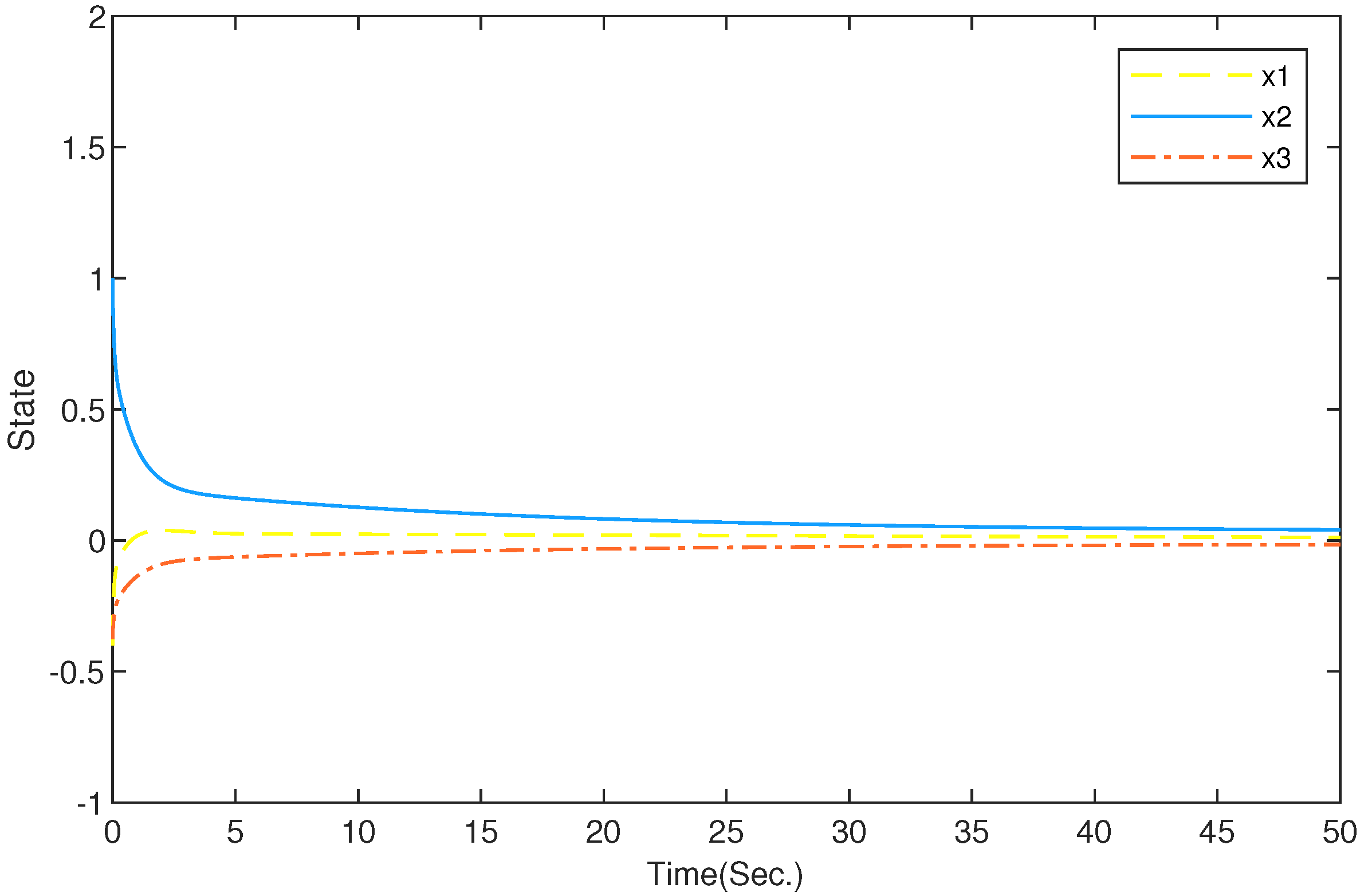
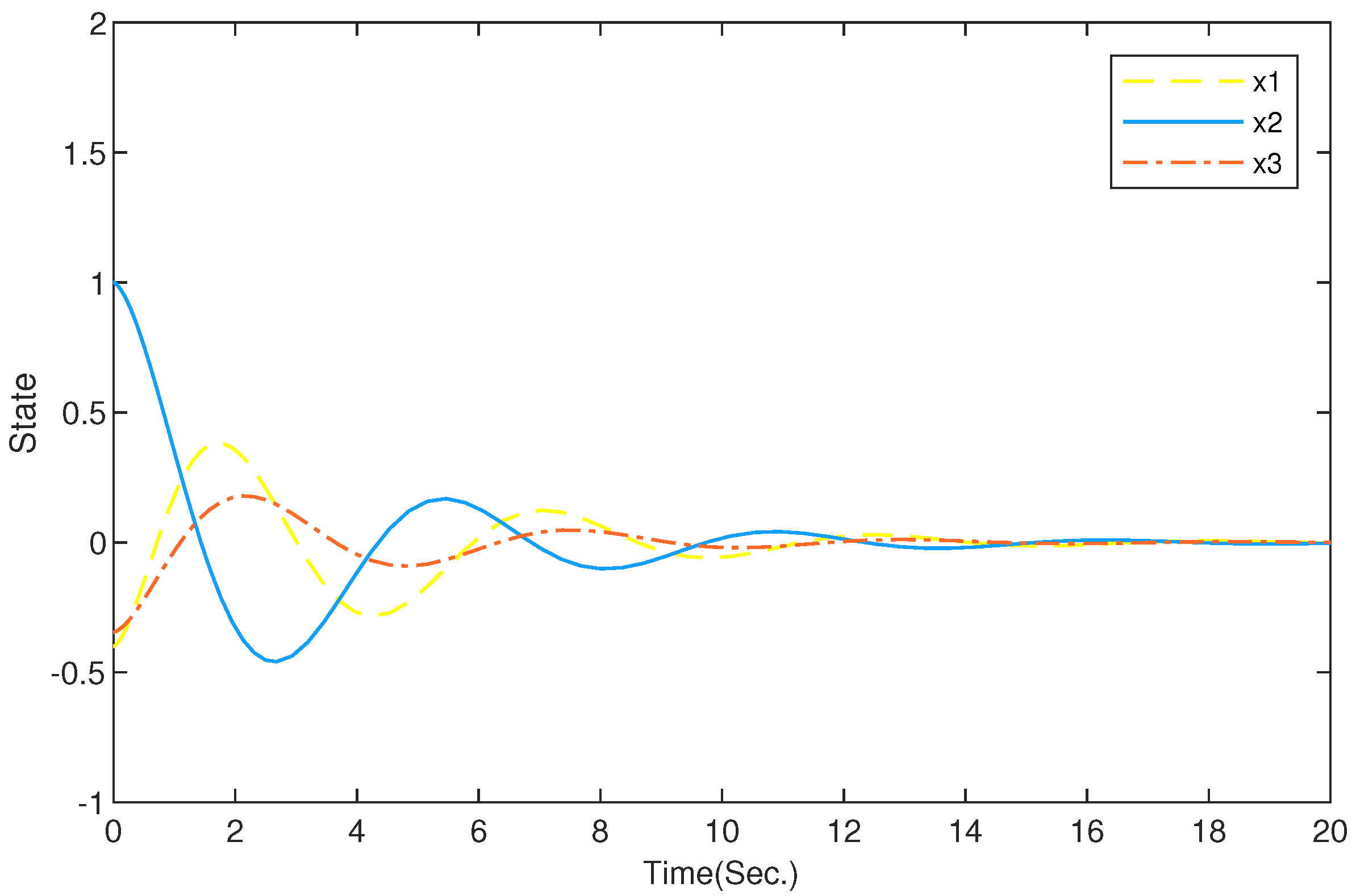
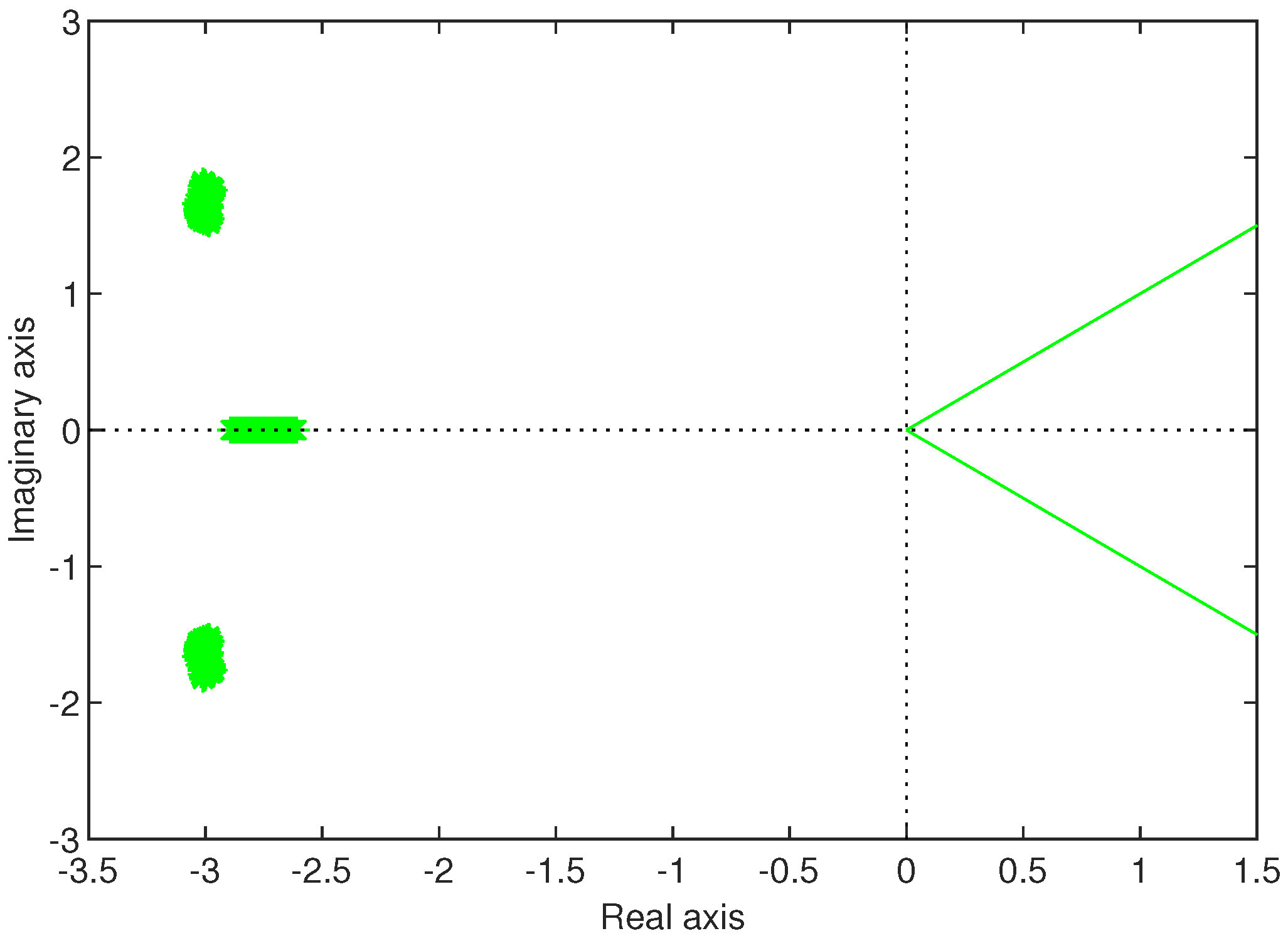
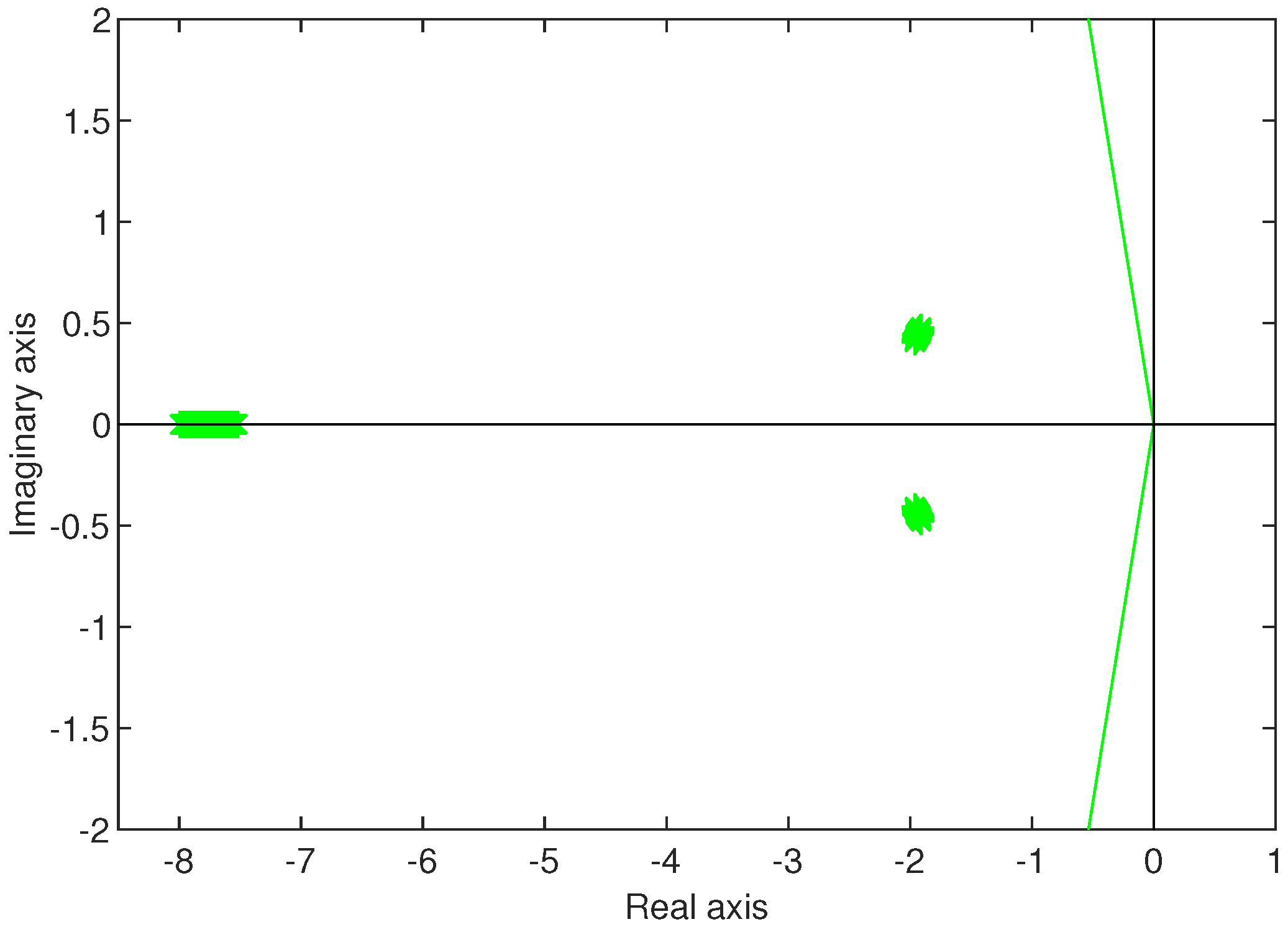
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm 1: The partial LMI algorithm for solving matrices X, Q and Z with Theorem 3 |
 |
References
- Tavazoei, M.; Haeri, M. Rational approximations in the simulation and implementation of fractional-order dynamics: A descriptor system approach. Automatica 2010, 46, 94–100. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.; Gallegos, J. Lyapunov functions for fractional order systems. Commun. Nonlin. Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Zhang, J.X.; Wang, Q.G.; Ding, W. Global output-feedback prescribed performance control of nonlinear systems with unknown virtual control coefficients. IEEE Trans. Automat. Contr. 2021, 99, 1. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fault-tolerant output-constrained control of unknown Euler-Lagrange systems with prescribed tracking accuracy. Automatica 2020, 111, 108606. [Google Scholar] [CrossRef]
- Zhang, X.F.; Huang, W.K.; Wang, Q.G. Robust H∞ adaptive sliding mode fault tolerant control for T-S fuzzy fractional order systems with mismatched disturbances. IEEE Trans. Circuits Syst. I Reg. Pap. 2021, 68, 1297–1307. [Google Scholar] [CrossRef]
- Zhan, T.; Liu, X.; Ma, S. A new singular system approach to output feedback sliding mode control for fractional order nonlinear systems. J. Franklin Inst. 2018, 355, 6746–6762. [Google Scholar] [CrossRef]
- Ahn, H.; Chen, Y. Necessary and sufficient stability condition of fractional-order interval linear systems. Automatica 2008, 44, 2985–2988. [Google Scholar] [CrossRef]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Khargonekar, P.; Petersen, I.; Zhou, K. Robust stabilization of uncertain linear systems: Quadratic stabilizability and H∞ control theory. IEEE Trans. Automat. Contr. 1990, 35, 356–361. [Google Scholar] [CrossRef]
- Kebria, P.M.; Khosravi, A.; Nahavandi, S.; Shi, P.; Alizadehsani, R. Robust adaptive control scheme for teleoperation systems with delay and uncertainties. IEEE Trans. Cybern. 2020, 50, 3243–3253. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Mittag–Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Yu, J.; Hu, H.; Zhou, S.; Lin, X. Generalized Mittag-Leffler stability of multi-variables fractional order nonlinear systems. Automatica 2013, 49, 1798–1803. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional order interval systems with the fractional order α: The 0 < α < 1 case. IEEE Trans. Automat. Contr. 2010, 55, 152–158. [Google Scholar]
- Semary, M.; Radwan, A.; Hassan, H. Fundamentals of fractional-order LTI circuits and systems: Number of poles, stability, time and frequency responses. Int. J. Circuit Theory Appl. 2016, 44, 2114–2133. [Google Scholar] [CrossRef]
- Alagoz, B. Hurwitz stability analysis of fractional order LTI systems according to principal characteristic equations. ISA Trans. 2017, 70, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Kharade, J.; Kucche, K. On the impulsive implicit Ψ-Hilfer fractional differential equations with delay. Math. Methods Appl. Sci. 2020, 43, 1938–1952. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhou, Y. Mittag-Leffler-Ulam stabilities of fractional evolution equations. Appl. Math. Lett. 2012, 25, 723–728. [Google Scholar] [CrossRef] [Green Version]
- Abu-Shady, M.; Kaabar, M. A generalized definition of the fractional derivative with applications. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Kaabar, M. A novel computational tool for the fractional-order special functions arising from modeling scientific phenomena via Abu-Shady-Kaabar fractional derivative. Comput. Math. Methods Med. 2022, 2022, 2138775. [Google Scholar] [CrossRef]
- Ibrir, S.; Bettayeb, M. New sufficient conditions for observer-based control of fractional-order uncertain systems. Automatica 2015, 59, 216–223. [Google Scholar] [CrossRef]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica 2010, 46, 1730–1734. [Google Scholar] [CrossRef]
- Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0 < α < 2. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3237–3241. [Google Scholar]
- Xu, S.Y.; Lam, J. Robust Control and Filtering of Singular Systems; Springer: Berlin, Germany, 2006; pp. 31–44. [Google Scholar]
- Lin, C.; Wang, J.L.; Yang, G.H.; Lam, J. Robust stabilization via state feedback for descriptor systems with uncertainties in the derivative matrix. Int. J. Control 1999, 32, 3319–3324. [Google Scholar] [CrossRef]
- Xu, S.Y.; Van Dooren, P.; Stefan, R.; Lam, J. Robust stability and stabilization for singular systems with state delay and parameter uncertainty. IEEE Trans. Automat. Contr. 2002, 47, 1122–1128. [Google Scholar]
- Yu, Y.; Jiao, Z.; Sun, C.Y. Sufficient and necessary condition of admissibility for fractional-order singular system. Acta Autom. Sin. 2013, 39, 2160–2164. [Google Scholar] [CrossRef]
- Wei, Y.H.; Tse, P.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Trans. 2017, 69, 1–9. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar]
- Marir, S.; Chadli, M.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. J. Franklin Inst. 2017, 354, 752–766. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Lu, J.G.; Ma, Y.D.; Chen, Y.Q. Time domain solution analysis and novel admissibility conditions of singular fractional-order systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 842–855. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Lu, J.G. Necessary and sufficient conditions for extended strictly positive realness of singular fractional-order systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1997–2001. [Google Scholar] [CrossRef]
- Ji, Y.; Qiu, J. Stabilization of fractional-order singular uncertain systems. ISA Trans. 2015, 56, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Marir, S.; Chadli, M. Robust admissibility and stabilization of uncertain singular fractional-order linear time-invariant systems. IEEE/CAA J. Autom. Sin. 2019, 6, 685–692. [Google Scholar] [CrossRef]
- Li, R.C.; Zhang, X.F. Adaptive sliding mode observer design for a class of T-S fuzzy descriptor fractional order systems. IEEE Trans. Fuzzy Syst. 2020, 28, 1951–1959. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhao, Z.L. Normalization and stabilization for rectangular singular fractional order T-S fuzzy systems. Fuzzy Sets Syst. 2020, 38, 140–153. [Google Scholar] [CrossRef]
- Yin, C.; Zhong, S.; Huang, X.; Cheng, Y. Robust stability analysis of fractional-order uncertain singular nonlinear system with external disturbance. Appl. Math. Comput. 2015, 269, 351–362. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.; Chen, Y.; Wang, Y. A universal framework of the generalized Kalman–Yakubovich–Popov lemma for singular fractional-order systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5209–5217. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Basin, M. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica 2022, 135, 109962. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, J.; Liu, T.; Wang, Y. Sufficient and necessary conditions for stabilizing singular fractional order systems with partially measurable state. J. Franklin Inst. 2019, 356, 1975–1990. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.F.; Huang, W.K. Adaptive neural network sliding mode control for nonlinear singular fractional order systems with mismatched uncertainties. Fractal Fract. 2020, 4, 50. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Automat. Contr. 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Wang, Y.; He, P.; Shi, P.; Zhang, H. Fault detection for systems with model uncertainty and disturbance via coprime factorization and gap metric. IEEE Trans. Cybern. 2022, 52, 7765–7775. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.X.; Yang, G.H. Robust adaptive fault-tolerant control for a class of unknown nonlinear systems. IEEE Trans. Ind. Electron. 2017, 64, 585–594. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fuzzy adaptive output feedback control of uncertain nonlinear systems with prescribed performance. IEEE Trans. Cybern. 2018, 48, 1342–1354. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, X.; Boutat, D.; Shi, P. Quadratic Admissibility for a Class of LTI Uncertain Singular Fractional-Order Systems with 0 < α < 2. Fractal Fract. 2023, 7, 1. https://doi.org/10.3390/fractalfract7010001
Wang Y, Zhang X, Boutat D, Shi P. Quadratic Admissibility for a Class of LTI Uncertain Singular Fractional-Order Systems with 0 < α < 2. Fractal and Fractional. 2023; 7(1):1. https://doi.org/10.3390/fractalfract7010001
Chicago/Turabian StyleWang, Yuying, Xuefeng Zhang, Driss Boutat, and Peng Shi. 2023. "Quadratic Admissibility for a Class of LTI Uncertain Singular Fractional-Order Systems with 0 < α < 2" Fractal and Fractional 7, no. 1: 1. https://doi.org/10.3390/fractalfract7010001





