Mechanical Behaviors and Acoustic Emission Fractal Characteristics of Bump-Prone Coal under Different Loading Rates
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
2.2. Experimental System
2.3. Experimental Procedure
3. Results and Discussions
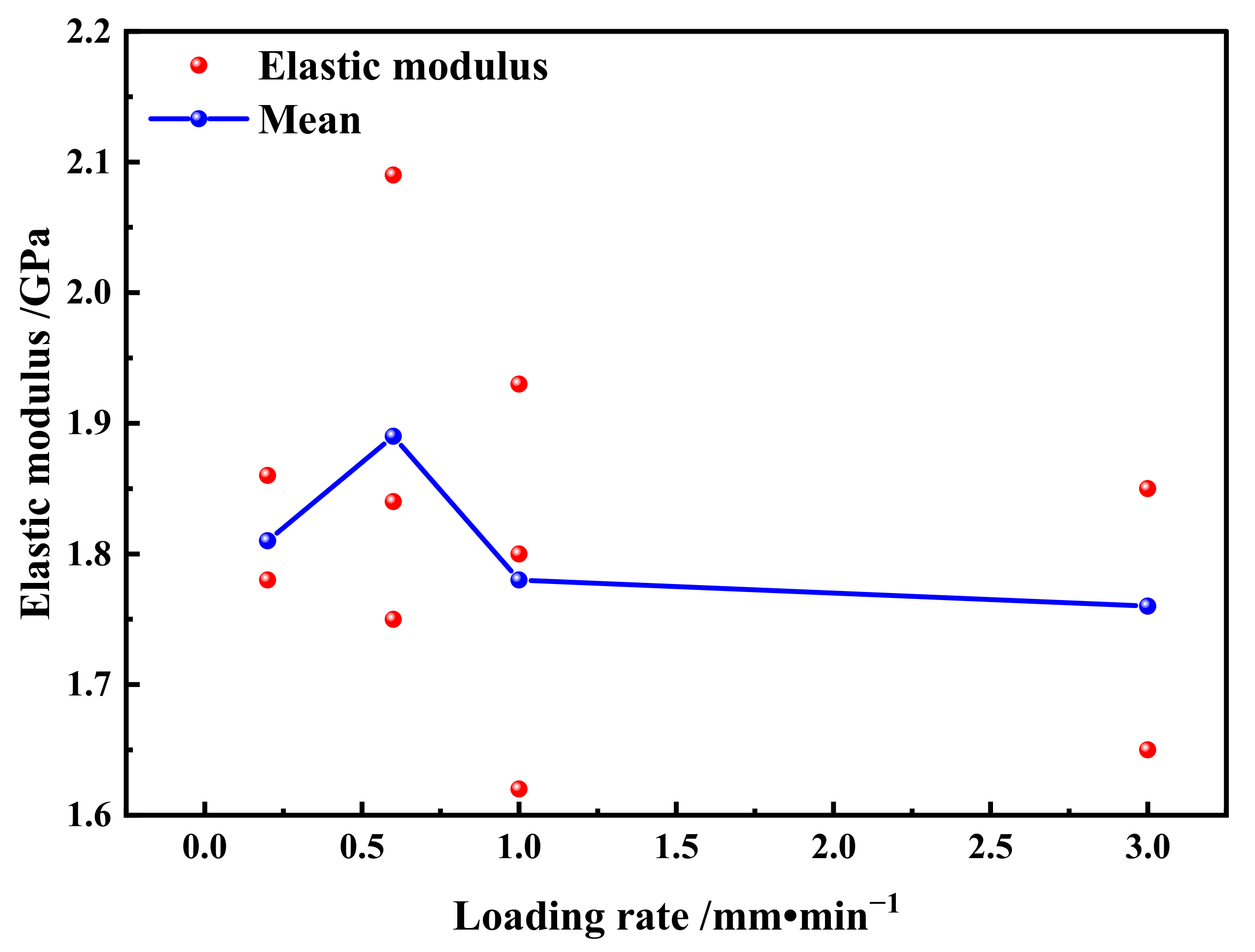
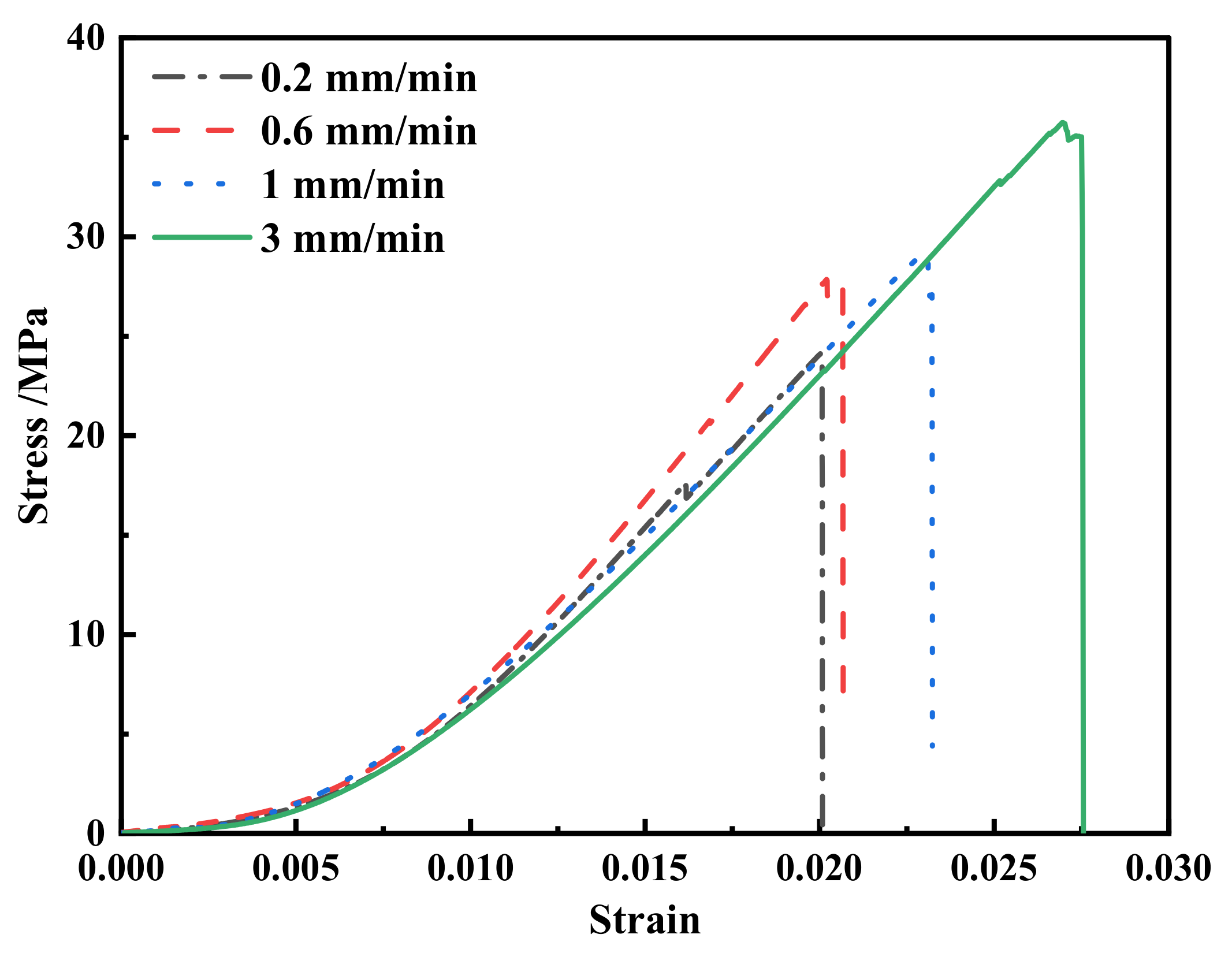
3.1. Mechanical Properties
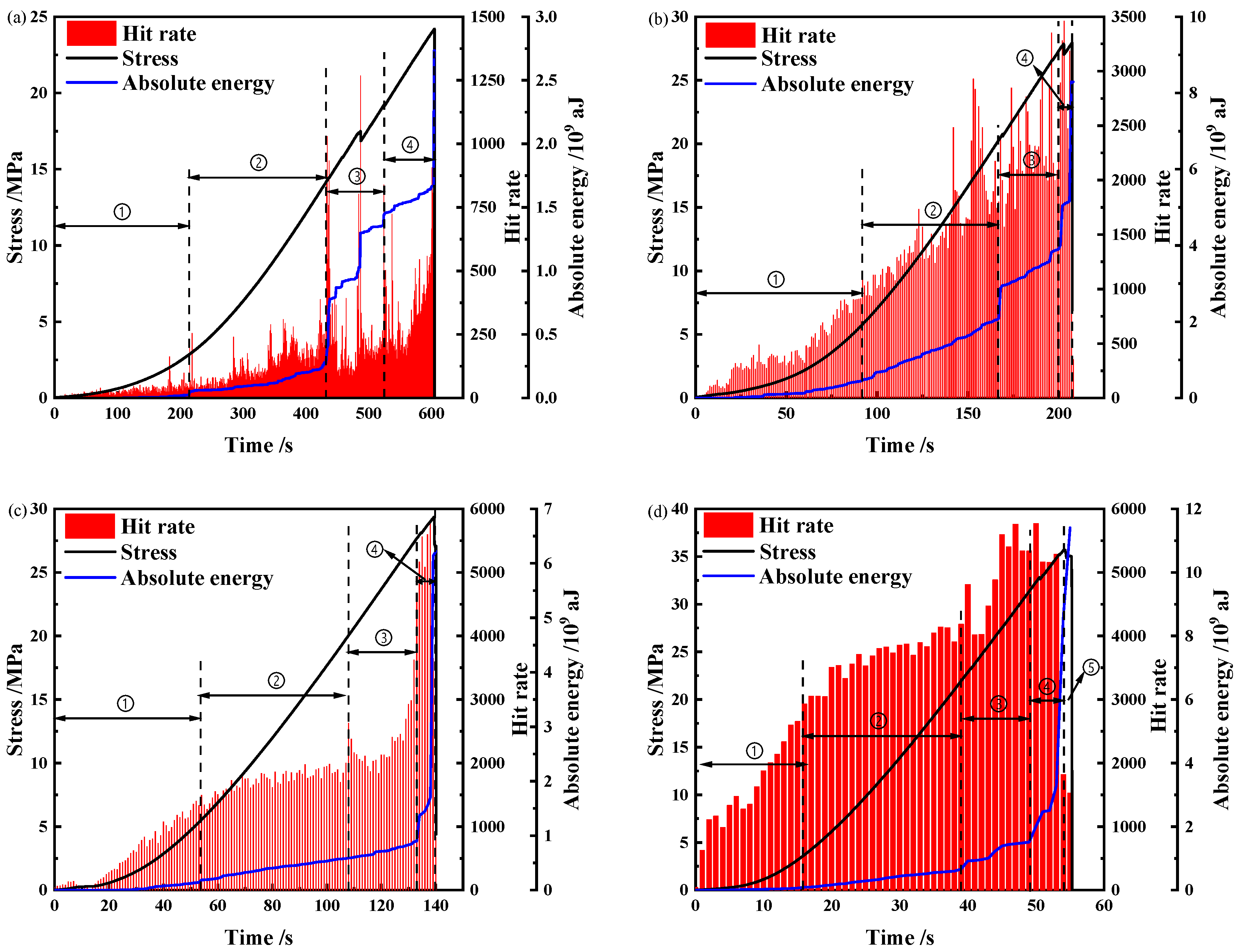
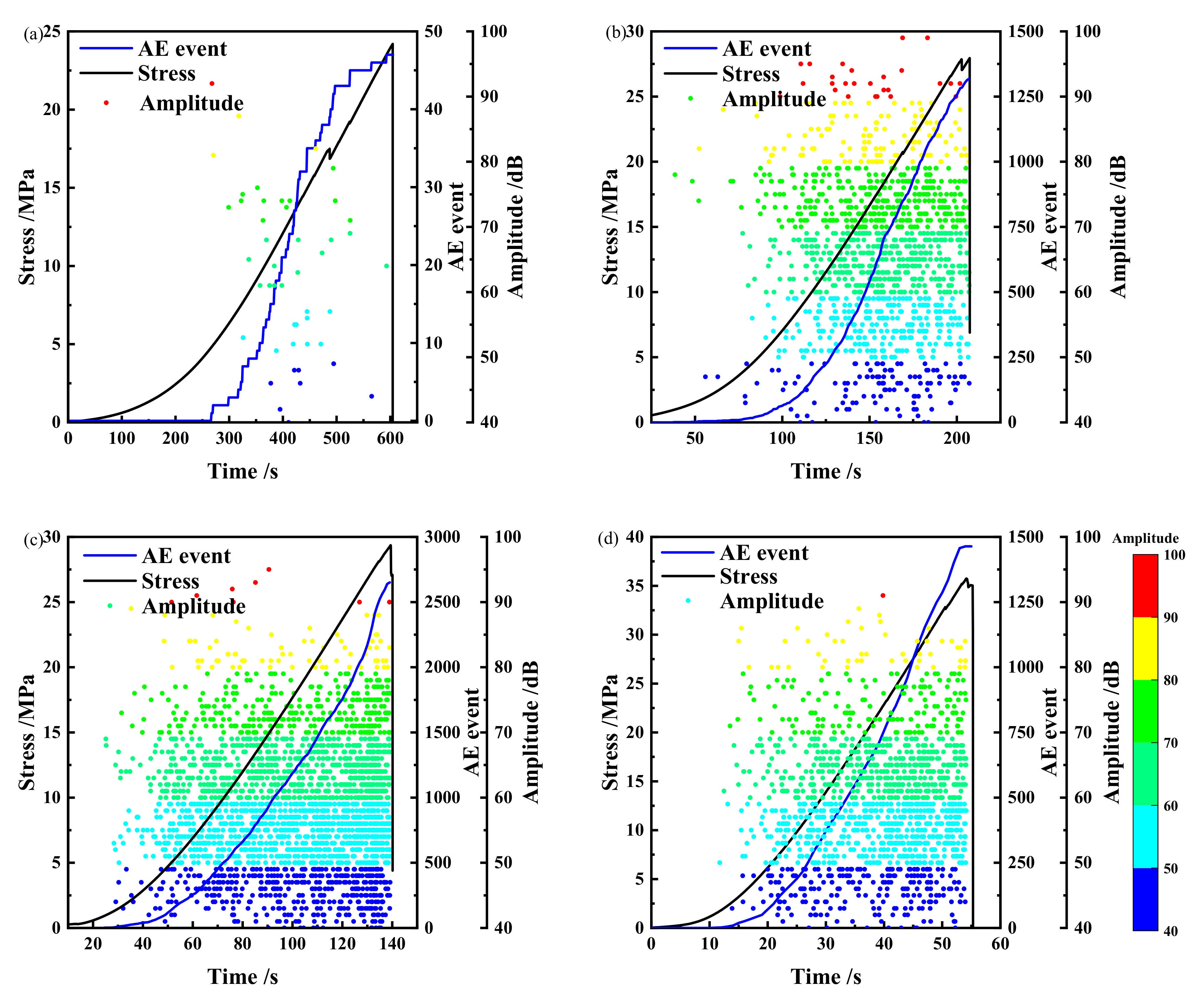
3.2. AE Temporal Characteristics
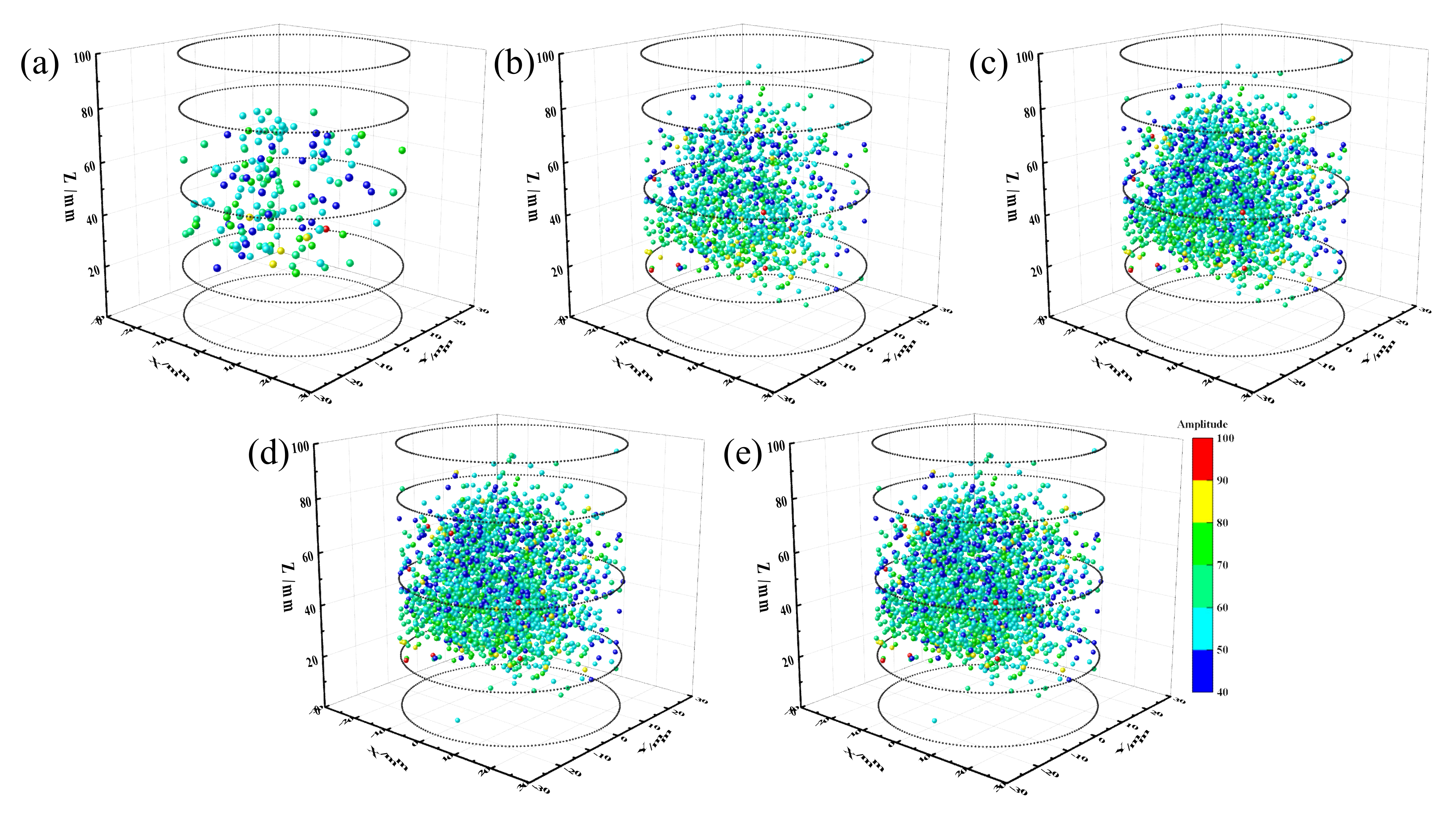
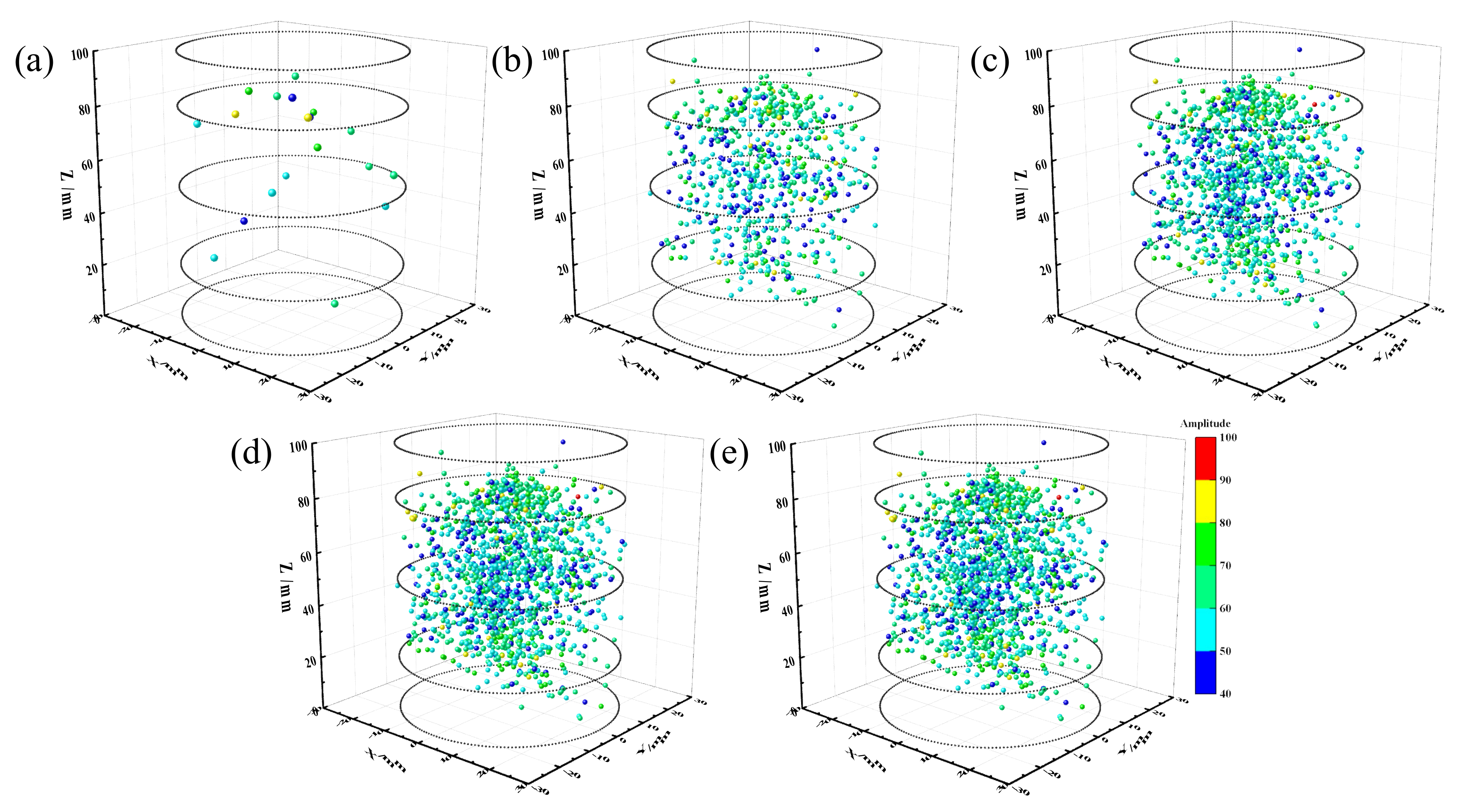
3.3. AE Spatial Characteristics
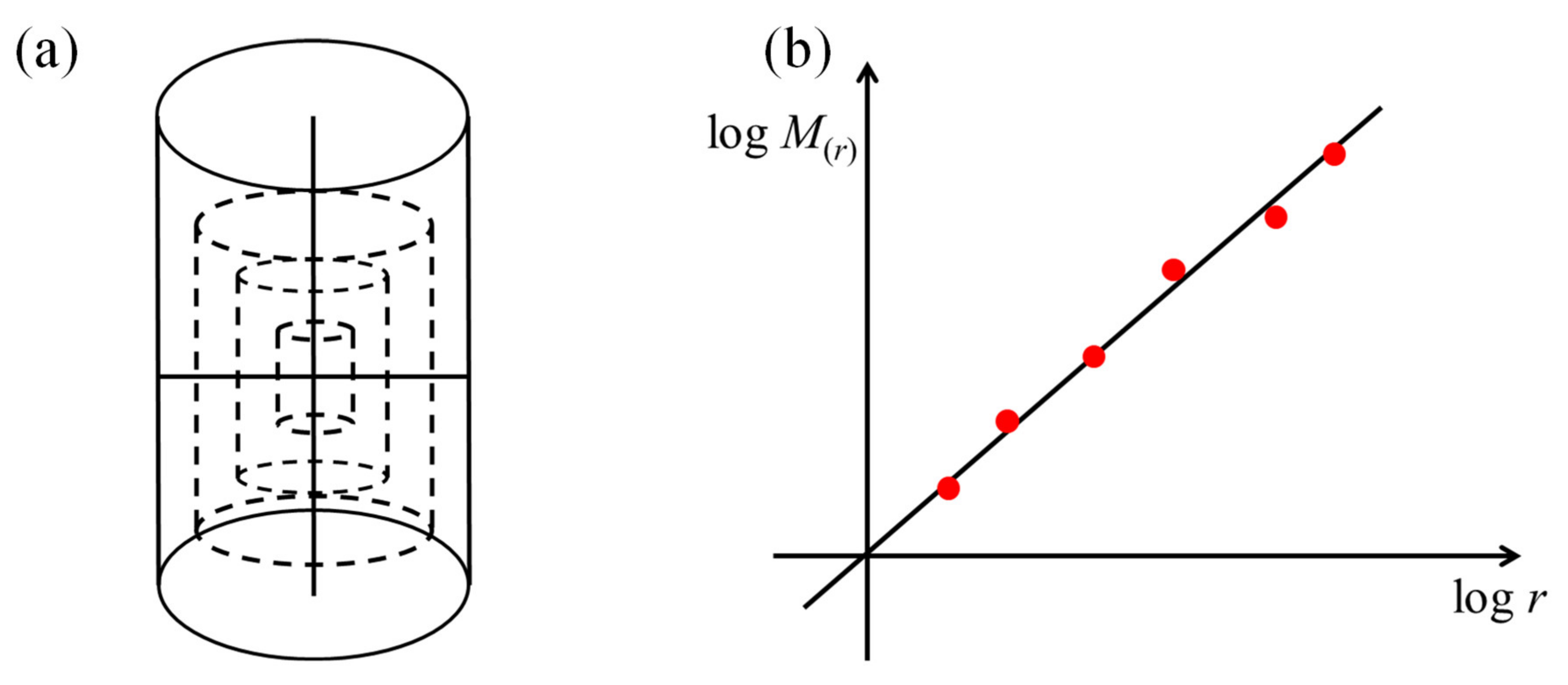
3.4. Column-Covering Fractal Model of AE Events
3.5. Spatial Fractal Characteristics
4. Conclusions
- (1)
- The UCS is positively related to the loading rate, and the elastic modulus increases before decreasing with the loading rate. The failure strain is positively related to the loading rate, and the percentage of the compaction phase relative to the pre-peak phase decreases with the loading rate.
- (2)
- The hit rate, absolute energy, AE events, and amplitude evolution of coal samples under various loading rates are consistent. The maximum hit rate and absolute energy of coal samples are positively related to the loading rate, and there are some differences in the distribution of AE amplitude.
- (3)
- The spatial evolution of AE events of coal samples under various loading rates is consistent, showing a “slow increase → slow increase → fast increase → rapid increase → slow increase” trend. AE events mainly occur in the middle of the coal sample during the whole loading process, with fewer events at both ends.
- (4)
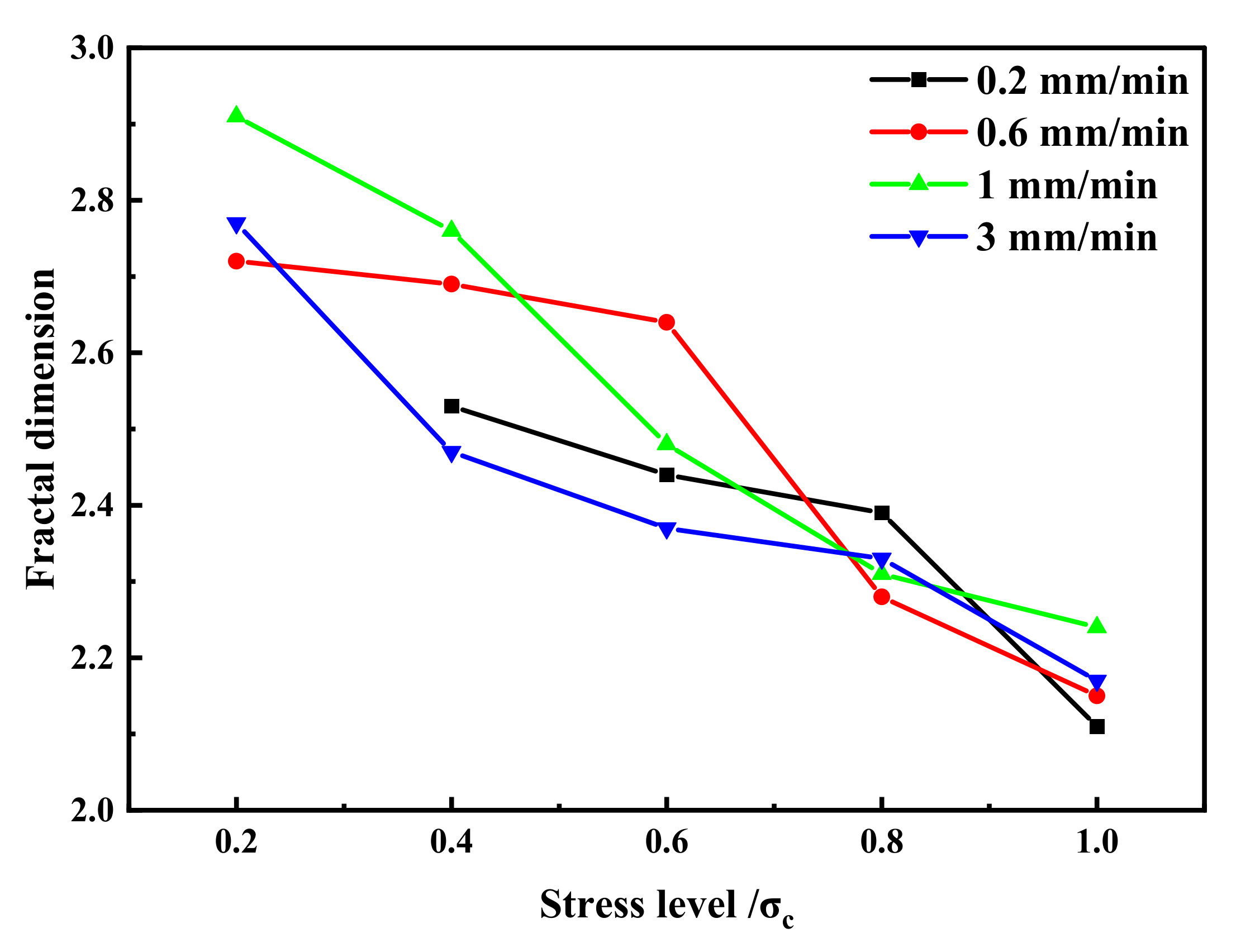
- The AE spatial fractal dimension ranges from 2.1 to 2.9, and the evolution of coal samples with various loading rates is consistent, showing a downward trend. There exist some differences in fractal dimension evolution at various loading rates.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, L. Research Progress of Mining Response and Disaster Prevention and Control in Deep Coal Mines. Meitan Xuebao = J. China Coal Soc. 2021, 46, 716–725. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Zhang, C.; Zhou, J.; Li, Y.; Sun, Z. Characteristic Strength and Acoustic Emission Properties of Weakly Cemented Sandstone at Different Depths under Uniaxial Compression. Int. J. Coal Sci. Technol. 2021, 8, 1288–1301. [Google Scholar] [CrossRef]
- Jia, Z.; Xie, H.; Zhang, R.; Li, C.; Wang, M.; Gao, M.; Zhang, Z.; Zhang, Z. Acoustic Emission Characteristics and Damage Evolution of Coal at Different Depths Under Triaxial Compression. Rock Mech. Rock Eng. 2020, 53, 2063–2076. [Google Scholar] [CrossRef]
- Xie, H.; Gao, M.; Zhang, R.; Peng, G.; Wang, W.; Li, A. Study on the Mechanical Properties and Mechanical Response of Coal Mining at 1000 m or Deeper. Rock Mech. Rock Eng. 2019, 52, 1475–1490. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, H.; Zhang, R.; Zhang, Z.; Gao, M.; Jia, Z.; Xie, J. Deformation Damage and Energy Evolution Characteristics of Coal at Different Depths. Rock Mech. Rock Eng. 2019, 52, 1491–1503. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Wang, H.; Gao, Y.; Sun, Z. Tensile Properties and Multiparameter Response Characteristics of Coal under Different Loading Rates. Nat. Resour. Res. 2022, 31, 2787–2803. [Google Scholar] [CrossRef]
- Wang, X.; Wang, E.; Liu, X.; Zhou, X. Failure Mechanism of Fractured Rock and Associated Acoustic Behaviors under Different Loading Rates. Eng. Fract. Mech. 2021, 247, 107674. [Google Scholar] [CrossRef]
- Cao, A.; Jing, G.; Ding, Y.; Liu, S. Mining-Induced Static and Dynamic Loading Rate Effect on Rock Damage and Acoustic Emission Characteristic under Uniaxial Compression. Saf. Sci. 2019, 116, 86–96. [Google Scholar] [CrossRef]
- Li, H.; Zhou, H.; Jiang, Y.; Wang, H. An Evaluation Method for the Bursting Characteristics of Coal Under the Effect of Loading Rate. Rock Mech. Rock Eng. 2016, 49, 3281–3291. [Google Scholar] [CrossRef]
- Wu, W.; Li, J.; Zhao, J. Loading Rate Dependency of Dynamic Responses of Rock Joints at Low Loading Rate. Rock Mech. Rock Eng. 2012, 45, 421–426. [Google Scholar] [CrossRef]
- Mirzaghorbanali, A.; Nemcik, J.; Aziz, N. Effects of Shear Rate on Cyclic Loading Shear Behaviour of Rock Joints under Constant Normal Stiffness Conditions. Rock Mech. Rock Eng. 2014, 47, 1931–1938. [Google Scholar] [CrossRef]
- Gong, F.; Zhao, G. Dynamic Indirect Tensile Strength of Sandstone Under Different Loading Rates. Rock Mech. Rock Eng. 2014, 47, 2271–2278. [Google Scholar] [CrossRef]
- Wasantha, P.L.P.; Ranjith, P.G.; Zhao, J.; Shao, S.; Permata, G. Strain Rate Effect on the Mechanical Behaviour of Sandstones with Different Grain Sizes. Rock Mech. Rock Eng. 2015, 48, 1883–1895. [Google Scholar] [CrossRef]
- Liu, X.; Hao, Q.; Wu, S.; Zhang, R.; Yu, J. Nonlinear Mechanical Properties of Coal Rock under Quasi-Static Strain Rate. Meitan Xuebao = J. China Coal Soc. 2019, 44, 1437–1445. [Google Scholar] [CrossRef]
- Hou, Z.; Gutierrez, M.; Ma, S.; Almrabat, A.; Yang, C. Mechanical Behavior of Shale at Different Strain Rates. Rock Mech. Rock Eng. 2019, 52, 3531–3544. [Google Scholar] [CrossRef]
- Zou, C.; Li, H. Combined Numerical and Experimental Studies on the Dynamic and Quasi-Static Failure Modes of Brittle Rock. Int. J. Rock Mech. Min. Sci. 2021, 148, 104957. [Google Scholar] [CrossRef]
- Zreihan, N.; Faran, E.; Vives, E.; Planes, A.; Shilo, D. Relations between Stress Drops and Acoustic Emission Measured during Mechanical Loading. Phys. Rev. Mater. 2019, 3, 1–8. [Google Scholar] [CrossRef]
- Li, D.; Wang, E.; Kong, X.; Ali, M.; Wang, D. Mechanical Behaviors and Acoustic Emission Fractal Characteristics of Coal Specimens with a Pre-Existing Flaw of Various Inclinations under Uniaxial Compression. Int. J. Rock Mech. Min. Sci. 2019, 116, 38–51. [Google Scholar] [CrossRef]
- Tan, J.; Hu, C.; Lyu, Q.; Dick, J.M.; Ranjith, P.G.; Li, L.; Wang, Z. Multi-Fractal Analysis for the AE Energy Dissipation of CO2 and CO2+ Brine/Water Treated Low-Clay Shales under Uniaxial Compressive Tests. Fuel 2019, 246, 330–339. [Google Scholar] [CrossRef]
- Lou, Q.; Song, D.; He, X.; Li, Z.; Qiu, L.; Wei, M.; He, S. Correlations between Acoustic and Electromagnetic Emissions and Stress Drop Induced by Burst-Prone Coal and Rock Fracture. Saf. Sci. 2019, 115, 310–319. [Google Scholar] [CrossRef]
- Deng, M.; Zhang, Z.; Xin, J.; Yu, W.; Yu, X. Acoustic Emission Fractal Characteristics of Different Prefabricated Fractured Sandstone under Uniaxial Compression Tests. Geotech. Geol. Eng. 2021, 39, 3161–3170. [Google Scholar] [CrossRef]
- Ge, Z.; Sun, Q. Acoustic Emission Characteristics of Gabbro after Microwave Heating. Int. J. Rock Mech. Min. Sci. 2021, 138. [Google Scholar] [CrossRef]
- Zha, E.; Zhang, Z.; Zhang, R.; Wu, S.; Li, C.; Ren, L.; Gao, M.; Zhou, J. Long-Term Mechanical and Acoustic Emission Characteristics of Creep in Deeply Buried Jinping Marble Considering Excavation Disturbance. Int. J. Rock Mech. Min. Sci. 2021, 139, 104603. [Google Scholar] [CrossRef]
- Dou, L.; Yang, K.; Chi, X. Fracture Behavior and Acoustic Emission Characteristics of Sandstone Samples with Inclined Precracks. Int. J. Coal Sci. Technol. 2021, 8, 77–87. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, B. Deformation Field and Acoustic Emission Characteristics of Weakly Cemented Rock under Brazilian Splitting Test. Nat. Resour. Res. 2021, 30, 1925–1939. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, Z.; Gao, Y.; Wang, X.; Song, H. Influence of Bedding Planes on Fracture Characteristics of Coal under Mode II Loading. Theor. Appl. Fract. Mech. 2022, 117, 103131. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, Z.; Teng, T.; Wang, W.; Noraei Danesh, N.; Zhang, C. Comparative Study on Modes I and II Fracture Characteristics of Bituminous Coal Using Asymmetric Semi-Circular Bend Specimen. Theor. Appl. Fract. Mech. 2022, 120, 103377. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Zhang, H.; Yuan, Y. Acoustic Emission Characteristics of Coal under Uniaxialcompression and Brazilian Splitting. Caikuang yu Anquan Gongcheng Xuebao = J. Min. Saf. Eng. 2020, 37, 613–621. [Google Scholar] [CrossRef]
- Yan, Z.; Dai, F.; Liu, Y.; Li, Y.; You, W. Experimental Investigation of Pre-Flawed Rocks under Combined Static-Dynamic Loading: Mechanical Responses and Fracturing Characteristics. Int. J. Mech. Sci. 2021, 211, 106755. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, T.; Zhang, H.; Yuan, Q. Mechanical Properties and Acoustic Emission Characteristics of Weakly Cemented Sandstone With Different Grain Sizes. Front. Earth Sci. 2022, 10, 939372. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, X.; Yang, H.; Lv, X.; Guo, F.; Shi, Y.; Hanif, A. Investigation and application of fractal theory in cement-based materials: A review. Fractal Fract. 2021, 5, 247. [Google Scholar] [CrossRef]
- Wang, L.; Lu, X.; Liu, L.; Xiao, J.; Zhang, G.; Guo, F.; Li, L. Influence of MgO on the hydration and shrinkage behavior of low heat Portland cement-based materials via pore structural and fractal analysis. Fractal Fract. 2022, 6, 40. [Google Scholar] [CrossRef]
- Peng, Y.; Tang, S.; Huang, J.; Tang, C.; Wang, L.; Liu, Y. Fractal analysis on pore structure and modeling of hydration of magnesium phosphate cement paste. Fractal Fract. 2022, 6, 337. [Google Scholar] [CrossRef]
- Xie, H.P.; Liu, J.F.; Ju, Y.; Li, J.; Xie, L.Z. Fractal Property of Spatial Distribution of Acoustic Emissions during the Failure Process of Bedded Rock Salt. Int. J. Rock Mech. Min. Sci. 2011, 48, 1344–1351. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, B.; Li, C.; Cao, C.; Sui, Q.; Zhao, G.; Yu, W.; Chen, Z.; Wang, Y.; Liu, B.; et al. Experimental Investigation on the Spatio-Temporal-Energy Evolution Pattern of Limestone Fracture Using Acoustic Emission Monitoring. J. Appl. Geophys. 2022, 206, 104787. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, J.; Sa, Z.; Wang, Z.; Lu, S.; Lv, Z. Fractal Characteristics of Acoustic Emission of Gas-Bearing Coal Subjected to True Triaxial Loading. Meas. J. Int. Meas. Confed. 2021, 169, 108349. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Shi, Y.; Xue, Z.; Cao, M. Surface Cracking and Fractal Characteristics of Cement Paste after Exposure to High Temperatures. Fractal Fract. 2022, 6, 465. [Google Scholar] [CrossRef]
- Pei, J.; Fei, W.P.; Liu, J.; Zhang, R. Fractal Study on Spatial Distribution of Acoustic Emission Events of Granite Specimens by Cylindrical Covering Method. Undergr. Storage CO 2010, 42, 121. [Google Scholar] [CrossRef]
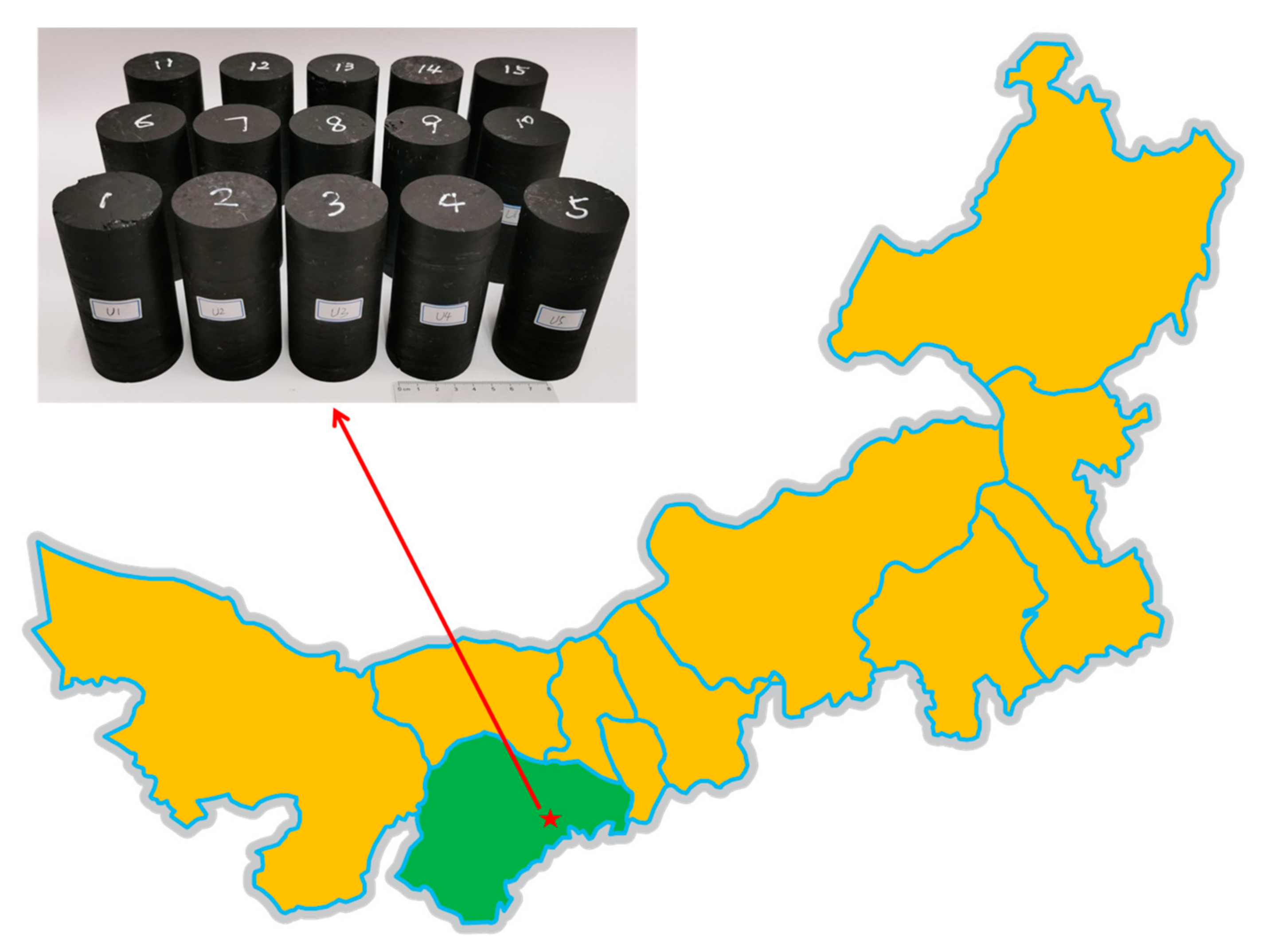
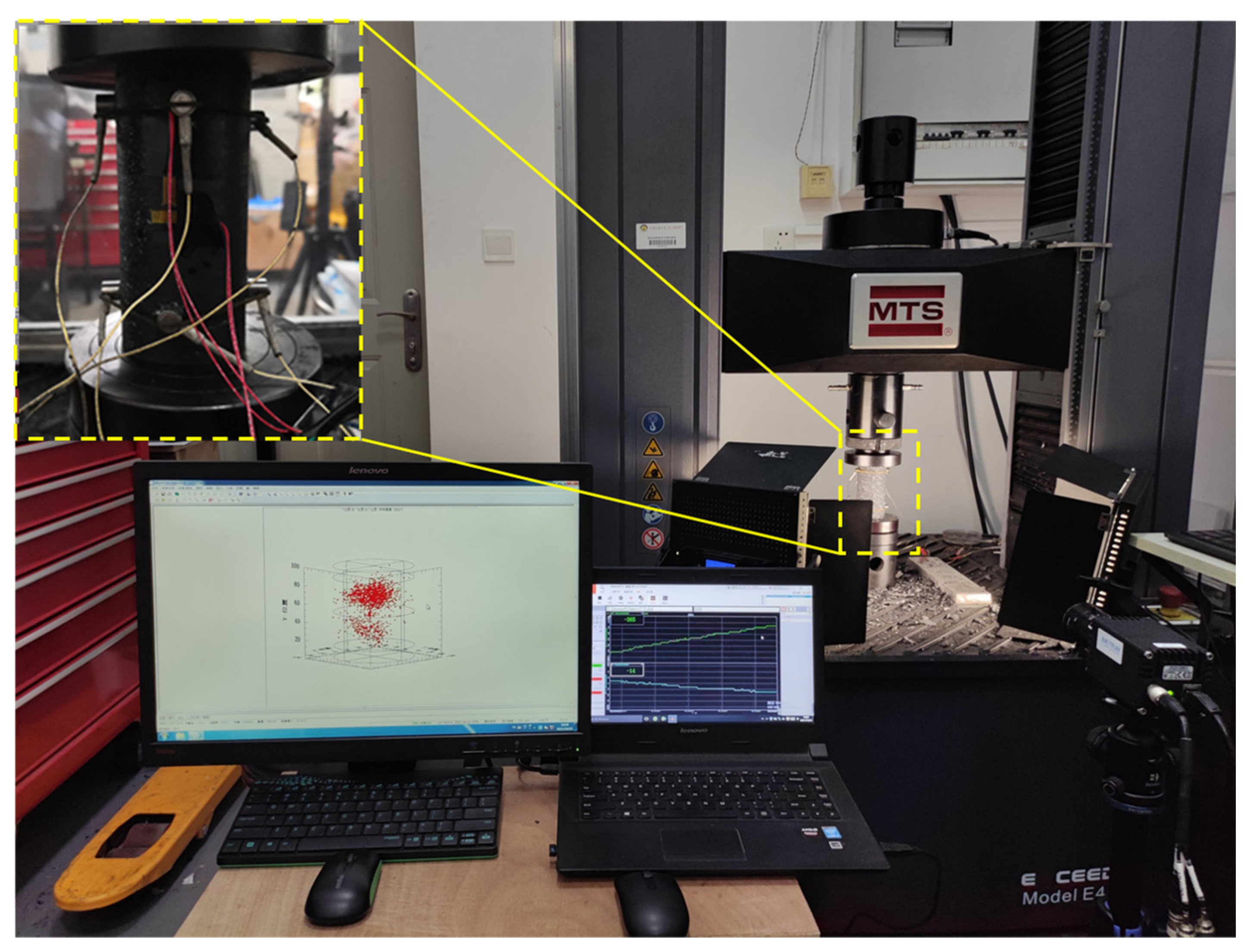



| Sample No. | Diameter (mm) | Height (mm) | Density (g/cm3) | Loading Rate (mm/min) |
|---|---|---|---|---|
| U1 | 49.50 | 100.40 | 1.25 | 0.20 |
| U2 | 49.65 | 100.30 | 1.26 | |
| U3 | 49.60 | 100.65 | 1.23 | |
| U4 | 49.60 | 100.42 | 1.23 | 0.60 |
| U5 | 49.50 | 100.40 | 1.31 | |
| U6 | 49.50 | 100.36 | 1.27 | |
| U7 | 49.41 | 100.30 | 1.26 | 1.00 |
| U8 | 49.63 | 100.50 | 1.26 | |
| U9 | 49.52 | 100.60 | 1.24 | |
| U10 | 49.60 | 100.41 | 1.26 | 3.00 |
| U11 | 49.73 | 99.88 | 1.27 | |
| U12 | 49.43 | 100.15 | 1.24 |
| Sample No. | Density (g/cm3) | Loading Rate (mm/min) | UCS (MPa) | Mean (MPa) | Elastic Modulus (GPa) | Mean (GPa) |
|---|---|---|---|---|---|---|
| U1 | 1.25 | 0.20 | 24.19 | 24.65 | 1.86 | 1.81 |
| U2 | 1.26 | 21.07 | 1.81 | |||
| U3 | 1.23 | 28.69 | 1.78 | |||
| U4 | 1.23 | 0.60 | 26.21 | 26.48 | 1.75 | 1.89 |
| U5 | 1.31 | 25.28 | 1.84 | |||
| U6 | 1.27 | 27.95 | 2.09 | |||
| U7 | 1.26 | 1.00 | 22.30 | 27.10 | 1.62 | 1.78 |
| U8 | 1.26 | 29.64 | 1.93 | |||
| U9 | 1.24 | 29.36 | 1.80 | |||
| U10 | 1.26 | 3.00 | 35.73 | 30.04 | 1.85 | 1.76 |
| U11 | 1.27 | 27.51 | 1.76 | |||
| U12 | 1.24 | 29.88 | 1.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Sun, X.; Ling, C.; Huang, Z.; Zhang, H. Mechanical Behaviors and Acoustic Emission Fractal Characteristics of Bump-Prone Coal under Different Loading Rates. Fractal Fract. 2023, 7, 45. https://doi.org/10.3390/fractalfract7010045
Liu B, Sun X, Ling C, Huang Z, Zhang H. Mechanical Behaviors and Acoustic Emission Fractal Characteristics of Bump-Prone Coal under Different Loading Rates. Fractal and Fractional. 2023; 7(1):45. https://doi.org/10.3390/fractalfract7010045
Chicago/Turabian StyleLiu, Bin, Xiang Sun, Chunwei Ling, Zujun Huang, and Hongwei Zhang. 2023. "Mechanical Behaviors and Acoustic Emission Fractal Characteristics of Bump-Prone Coal under Different Loading Rates" Fractal and Fractional 7, no. 1: 45. https://doi.org/10.3390/fractalfract7010045
APA StyleLiu, B., Sun, X., Ling, C., Huang, Z., & Zhang, H. (2023). Mechanical Behaviors and Acoustic Emission Fractal Characteristics of Bump-Prone Coal under Different Loading Rates. Fractal and Fractional, 7(1), 45. https://doi.org/10.3390/fractalfract7010045







