Adaptive Quantized Synchronization of Fractional-Order Output-Coupling Multiplex Networks
Abstract
1. Introduction
- (1)
- Different from the models of multiplex networks [35,36], the intra-layer coupling and the inter-layer coupling are described separately in the modelling of multiplex networks in this article. In addition, instead of the state coupling in [29,30,37], nodes communicate with each other by their output states, which is more realistic and valuable when the node states are unmeasured.
- (2)
- Quantized adaptive control is introduced to achieve the synchronization of fractional-order multiplex networks for the first time, which can reduce signal transmission frequency and improve the effective utilization rate of network resources compared with the traditional adaptive control utilized in [27,28,29,30].
- (3)
- The developed control schemes and the synchronization criteria are more generic, since they are also applicable when the factional-order system is reduced to the integer-order model. Thus, our results can be regarded as a valuable extension of the previous results on the integer-order multiplex networks [35,36,37].
2. Preliminaries and Model Description
2.1. Preliminaries
2.2. Model Description
3. Main Results
3.1. Adaptive Synchronization
3.2. Adaptive Quantized Synchronization
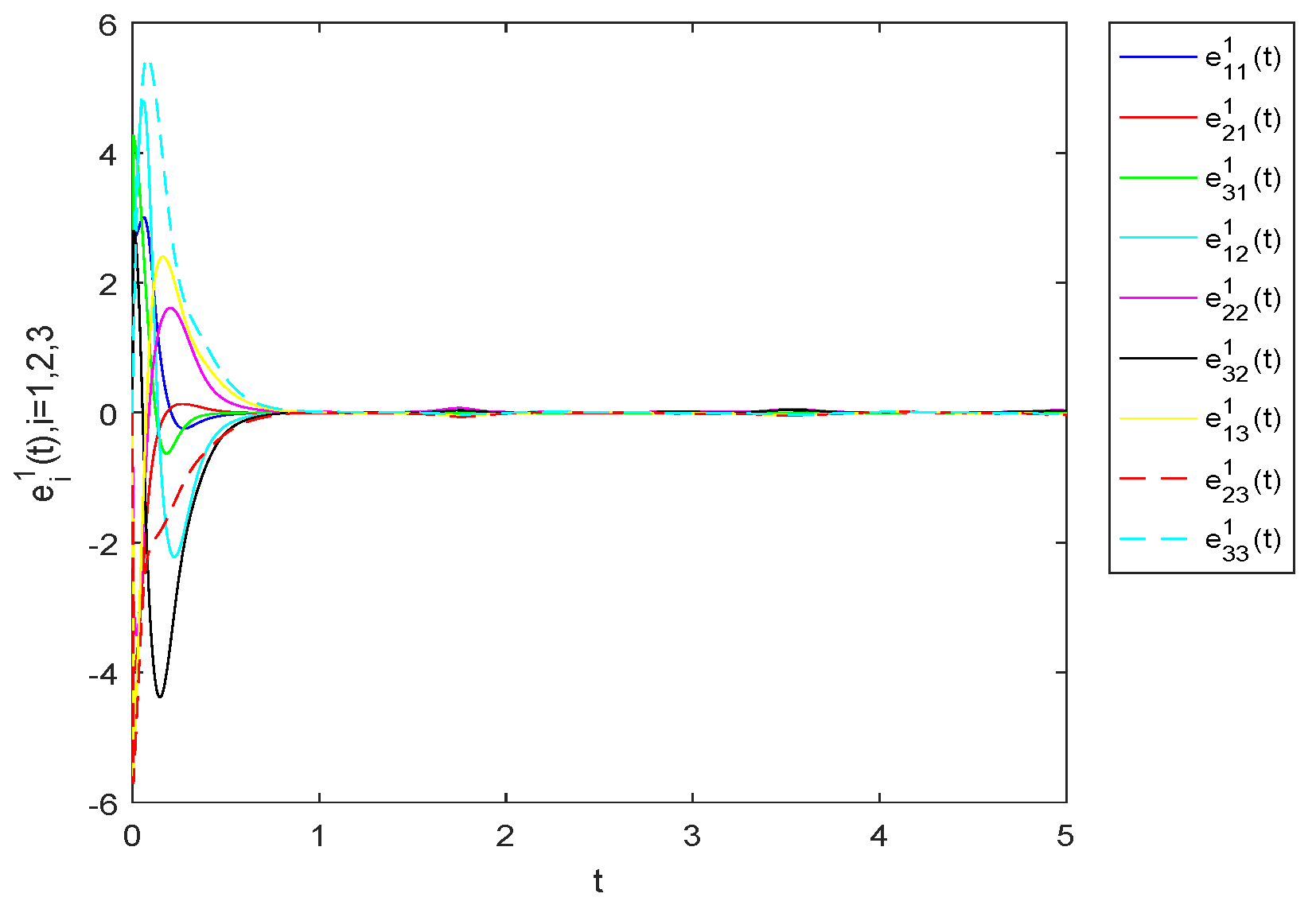
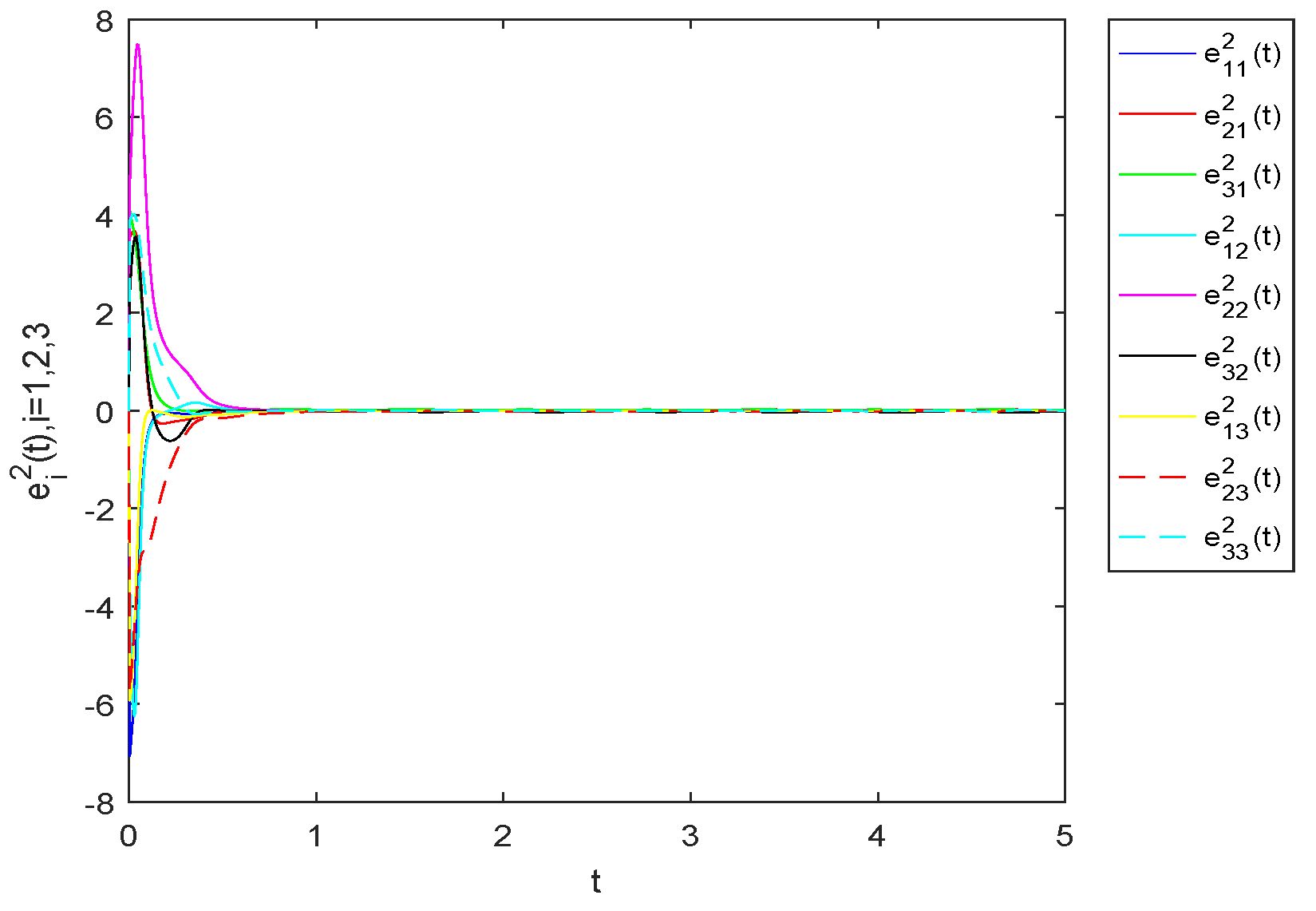
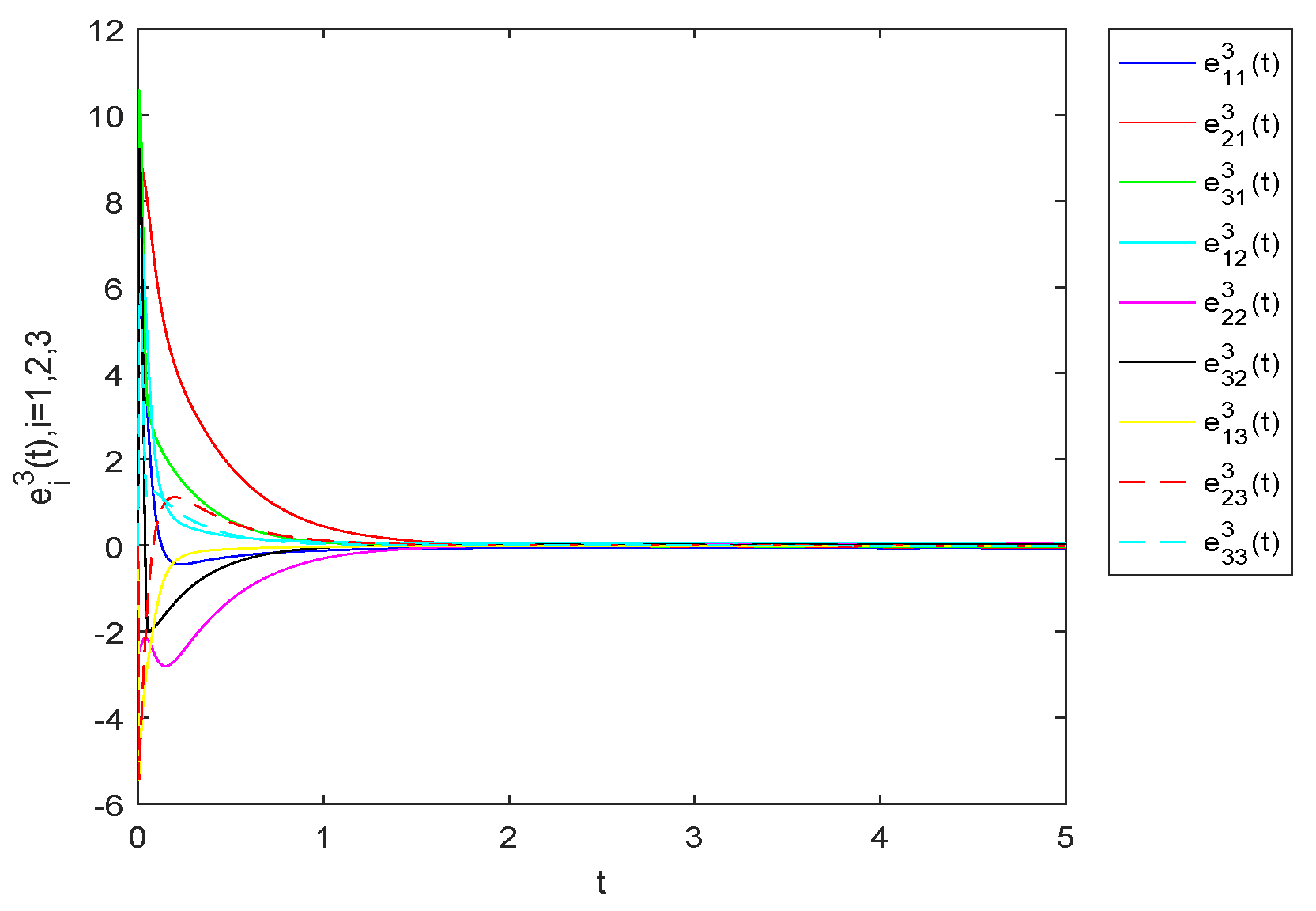
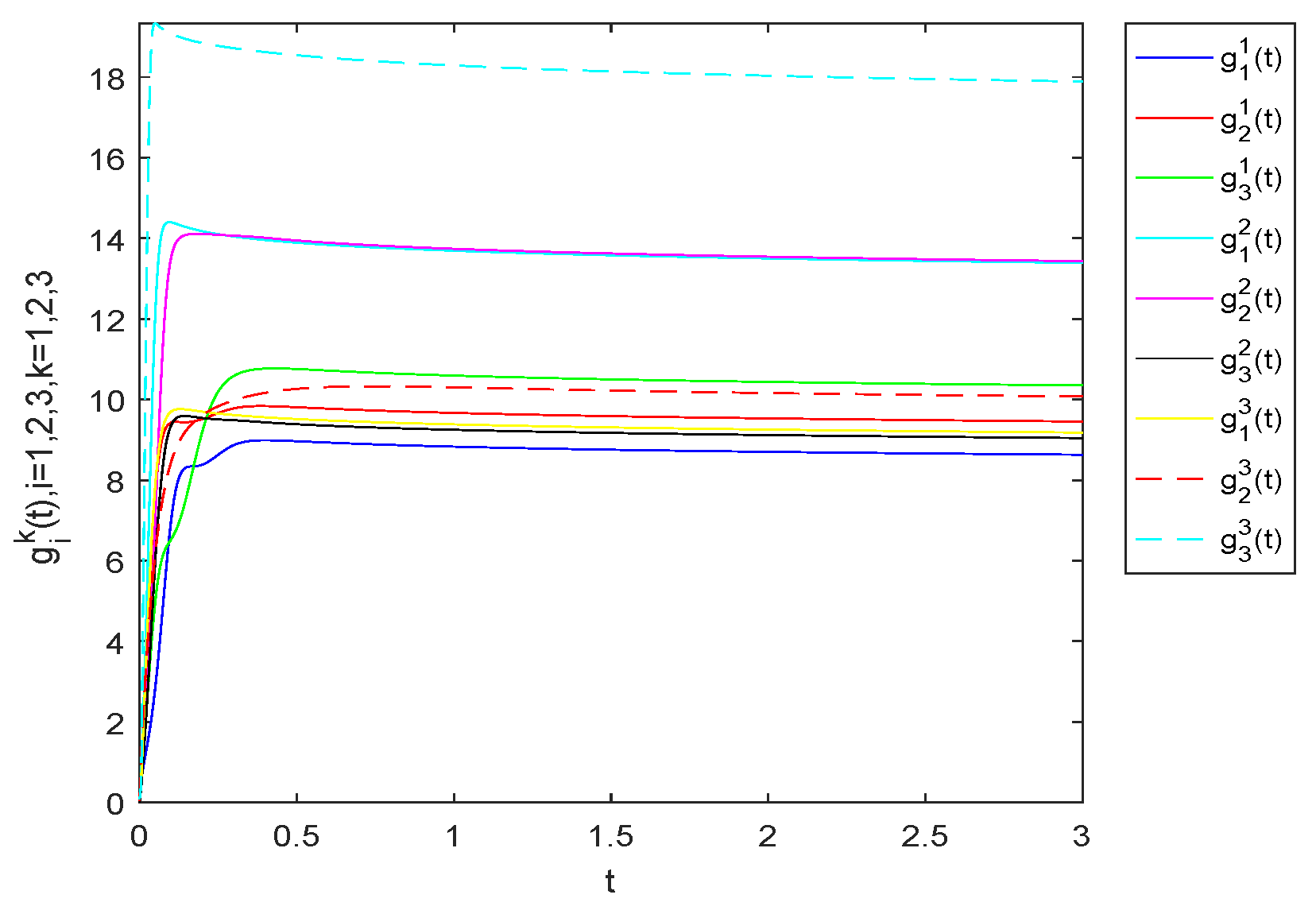
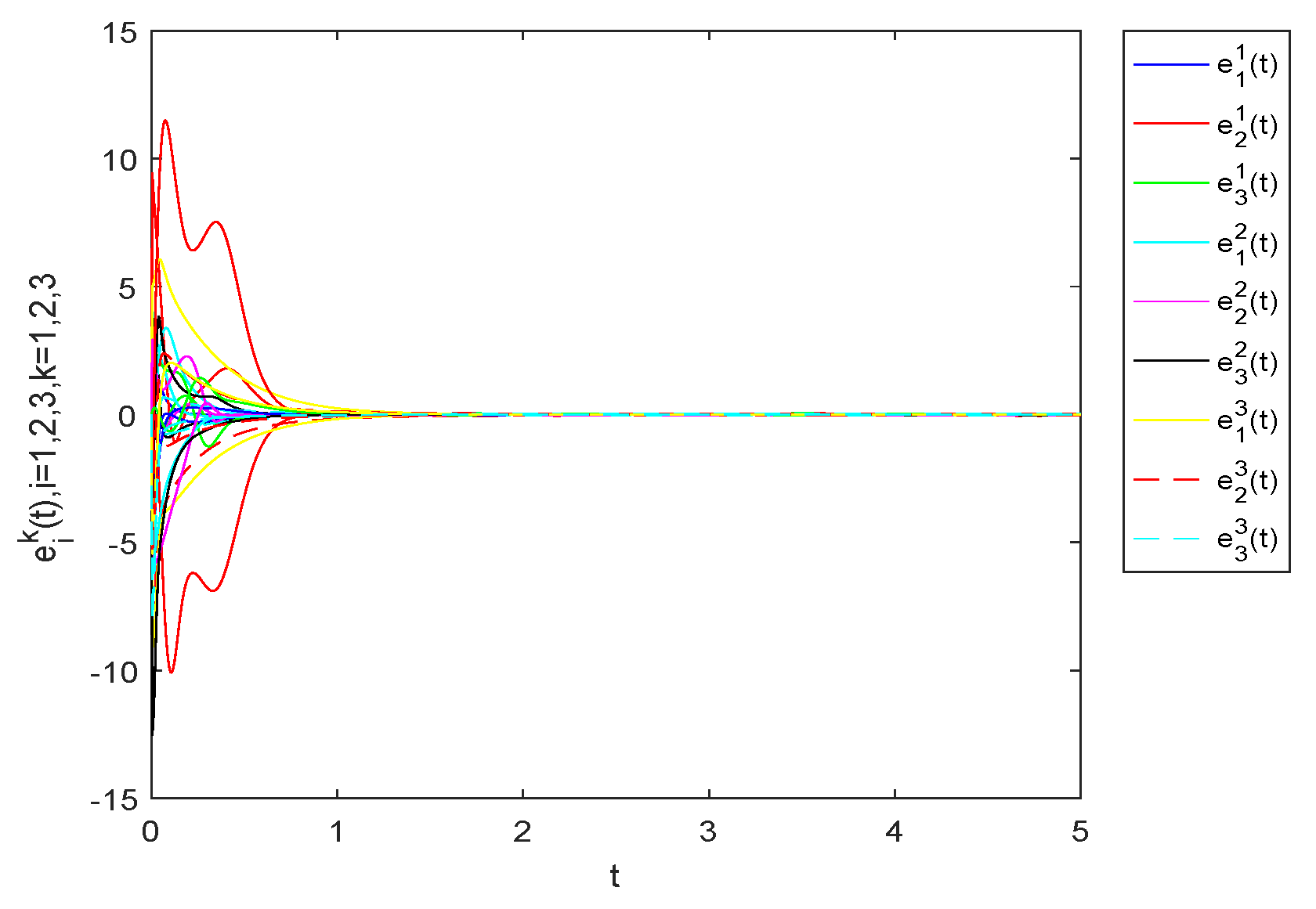
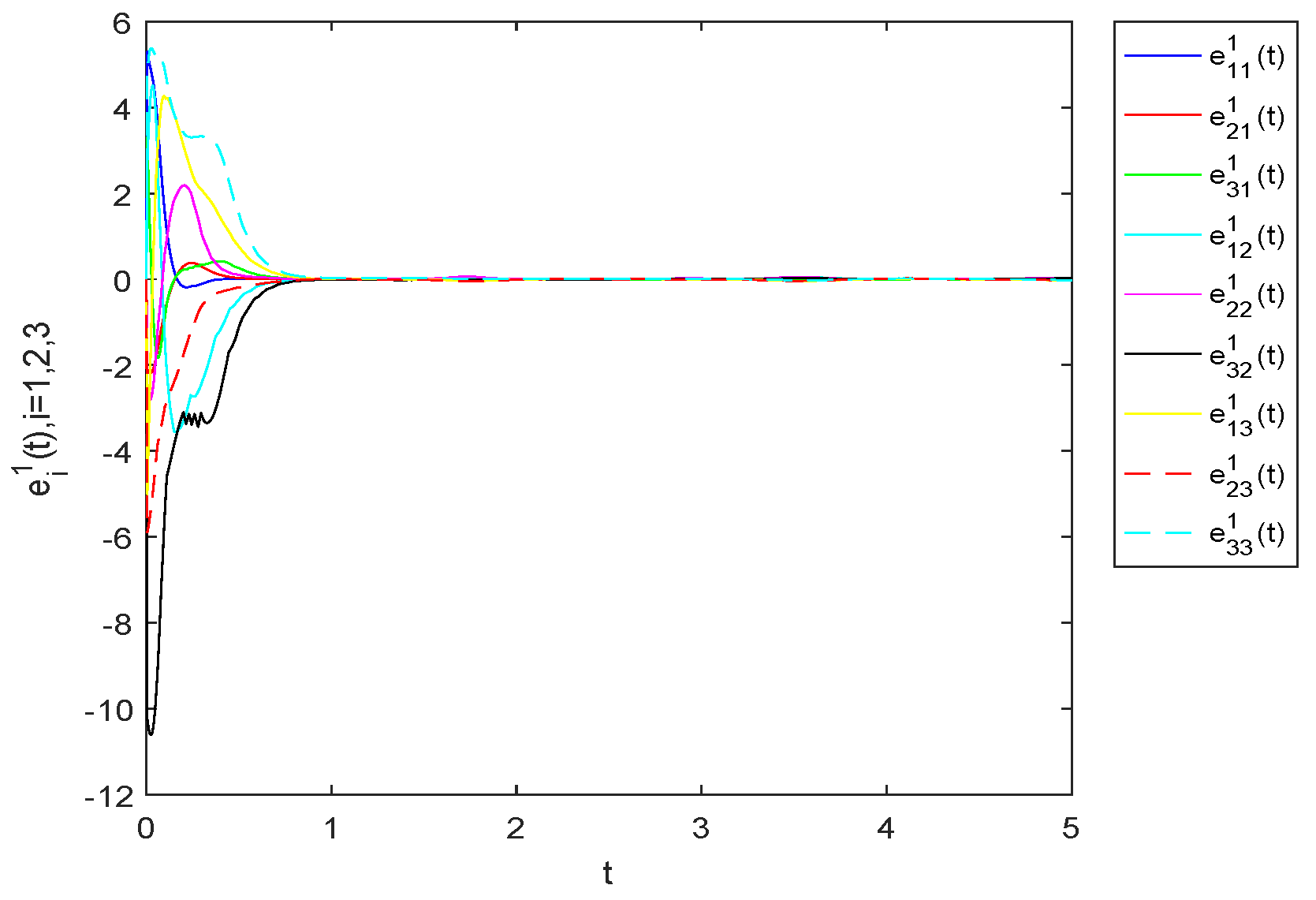
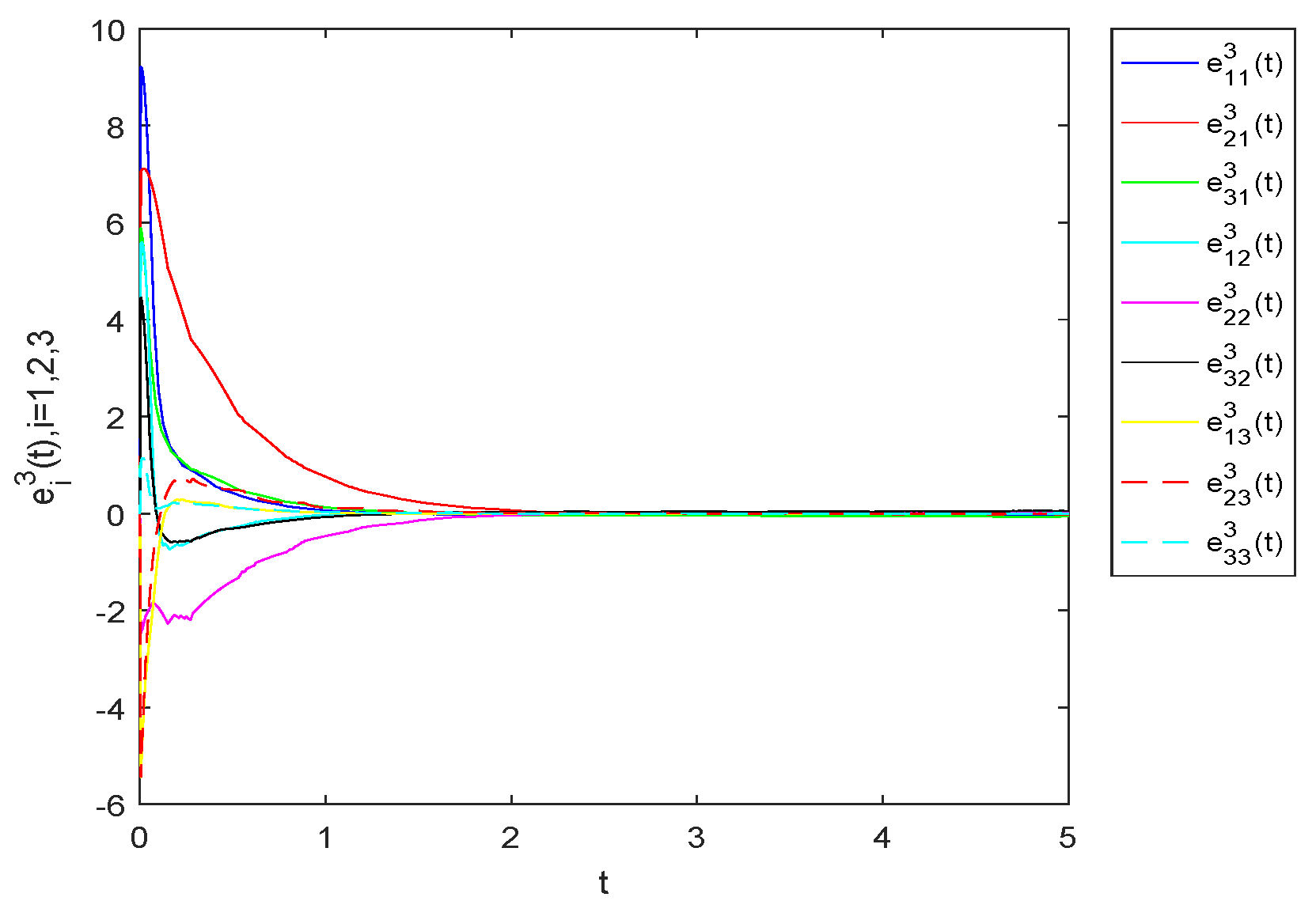
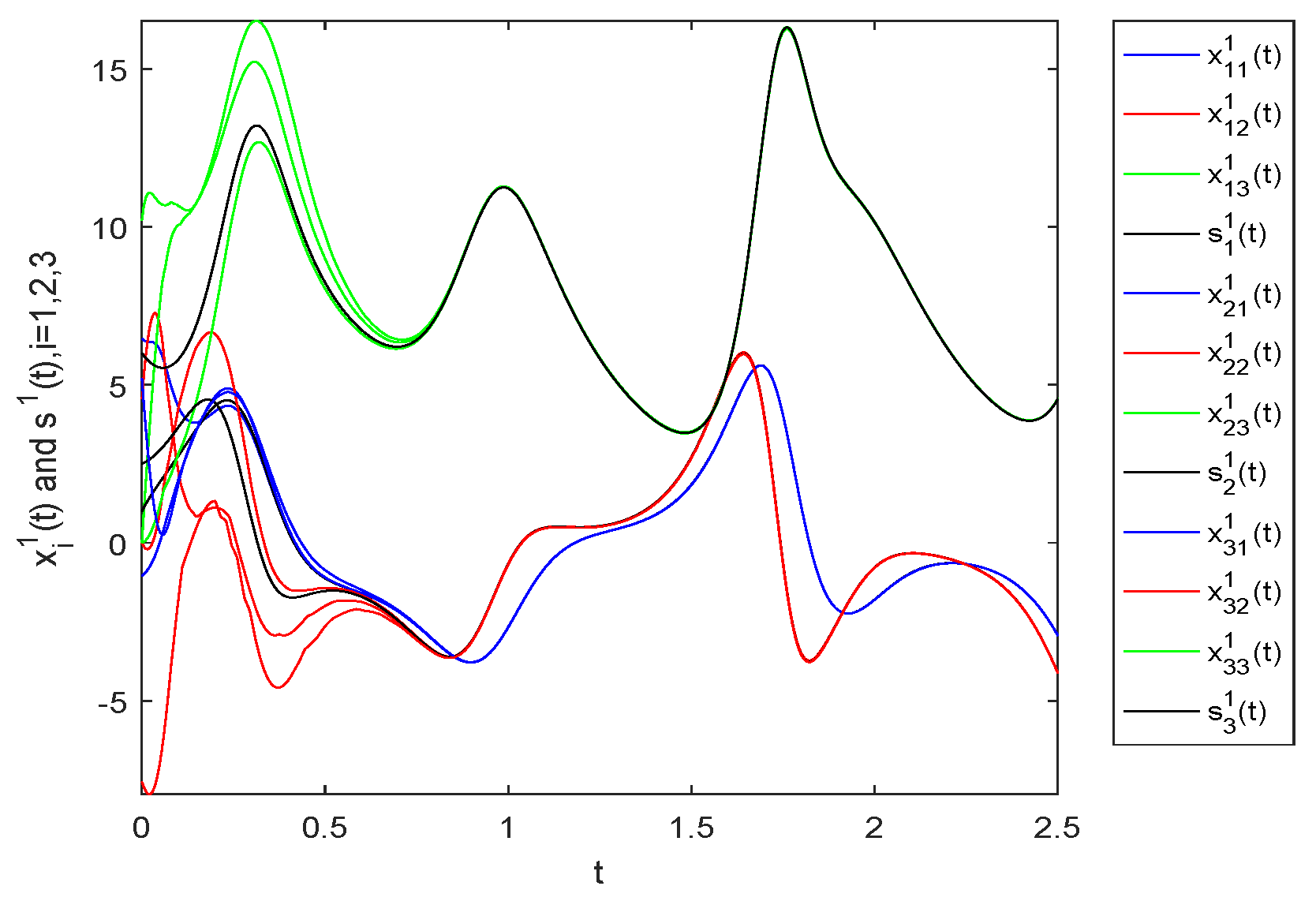
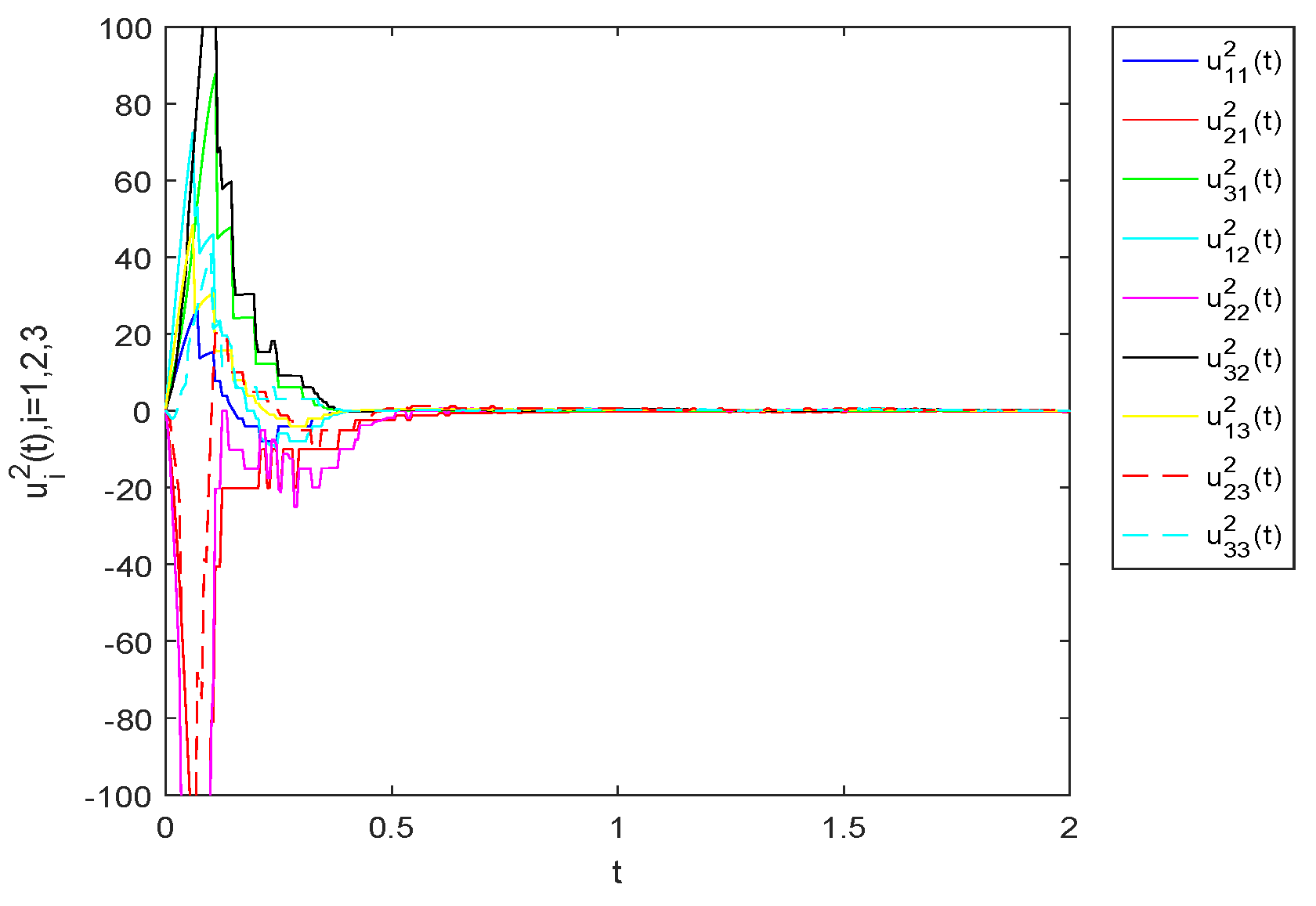
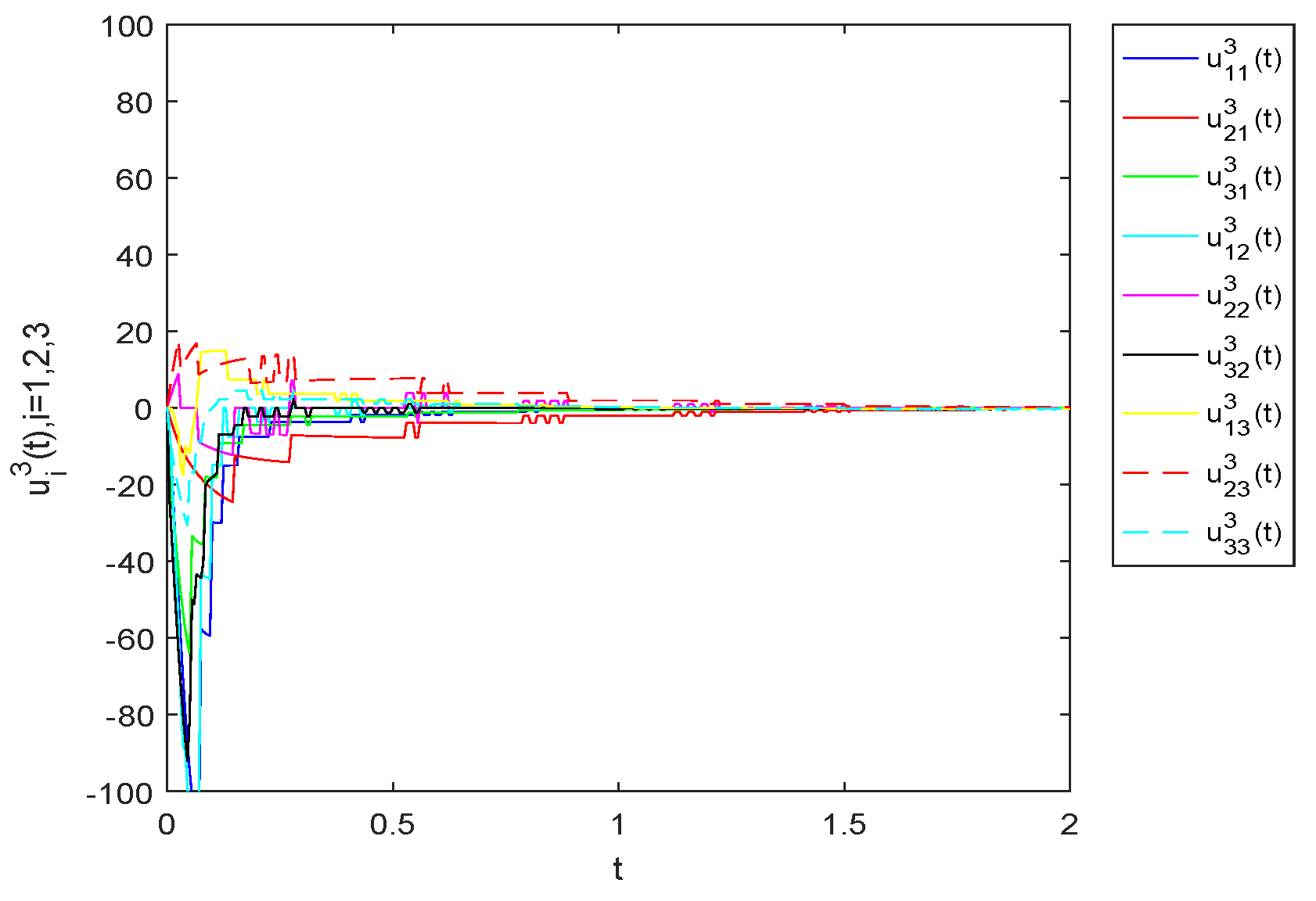
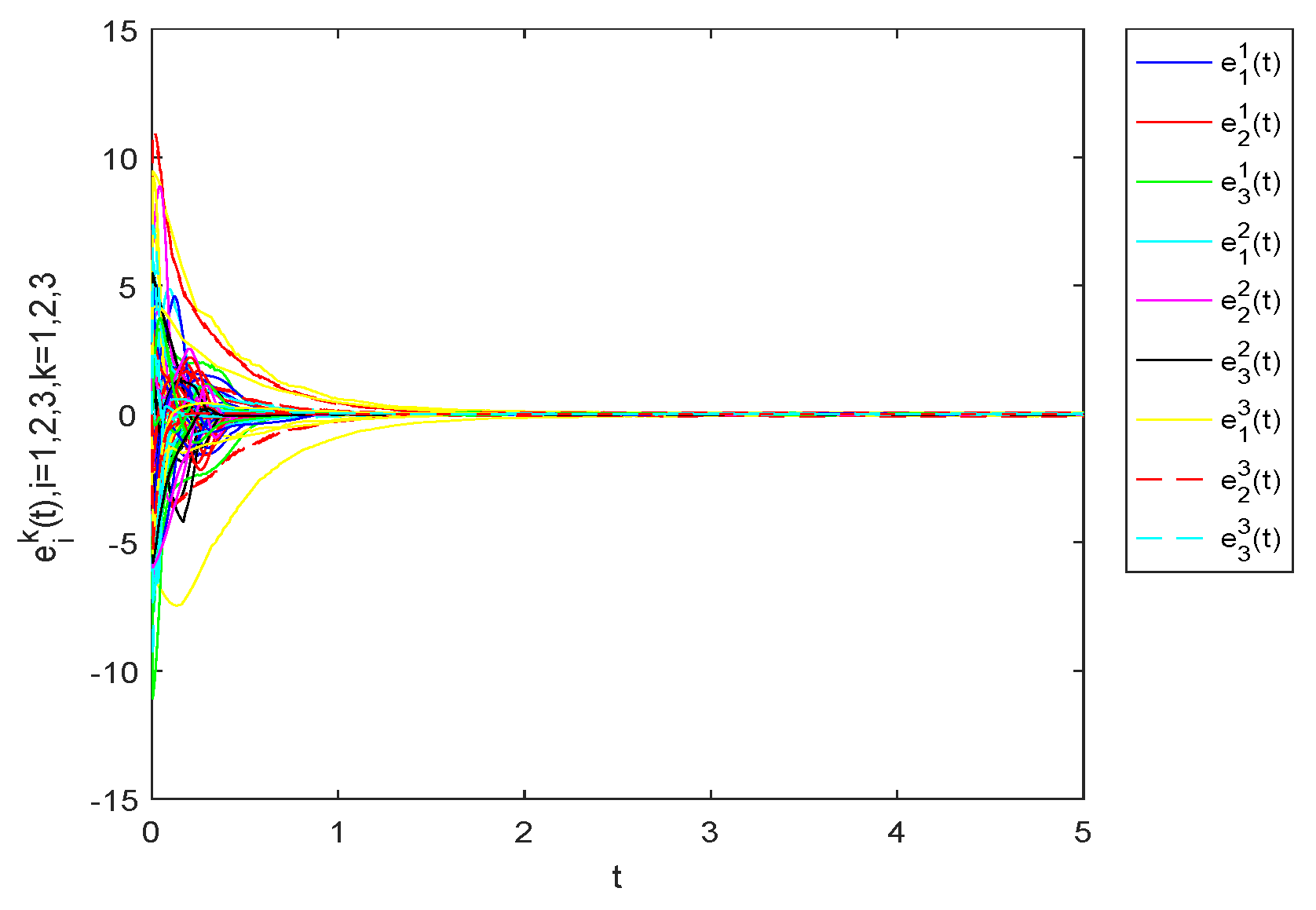
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gan, C.; Yang, X.; Liu, W. Propagation of computer virus both across the internet and external computers: A complex-network approach. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2785–2792. [Google Scholar] [CrossRef]
- Teeter, J.; Jacobs, A.; Werblin, F. How neural interactions form neural responses in the salamander retina. J. Comput. Neurosci. 1997, 4, 5–27. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Wang, Z.; Chen, X.; Cao, Y.; Jiang, G. Stochastic synchronization of multiplex networks with continuous and impulsive couplings. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2533–2544. [Google Scholar] [CrossRef]
- Saha, S. Resilience in multiplex networks by addition of cross-repulsive links. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1594–1603. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Mei, G.; Wu, X.; Wang, Y.; Hu, M.; Lu, J.; Chen, G. Compressive-sensing-based structure identification for multilayer networks. IEEE Trans. Cybern. 2018, 48, 754–764. [Google Scholar] [CrossRef]
- D’Agostino, G.; Scala, A. Networks of Networks: The Last Frontier of Complexity; Elsevier: Amsterdam, The Netherlands; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Chang, X.; Zhou, L.; Hu, F. Scale-free analysis of scientific collaboration hyper-networks. In Proceedings of the 2020 International Conference on Computer Science and Management Technology, Shanghai, China, 20–22 November 2020; pp. 85–90. [Google Scholar]
- Kumar, R.; Narayan, S.; Kumar, S.; Roy, S. Knowledge-based neural networks for fast design space exploration of hybrid copper-graphene on-chip interconnect networks. IEEE Trans. Electromagn. Compat. 2021, 99, 1–14. [Google Scholar] [CrossRef]
- Amato, R.; Diaz-Guilera, A.; Kleineberg, K. Interplay between social influence and competitive strategical games in multiplex networks. Sci. Rep. 2017, 7, 7087. [Google Scholar] [CrossRef]
- Nicosia, V.; Latora, V. Measuring and modeling correlations in multiplex networks. Phys. Rev. E 2015, 92, 032805. [Google Scholar] [CrossRef]
- Pocock, M.; Evans, D.; Memmott, J. The robustness and restoration of a network of ecological networks. Science 2012, 335, 973–977. [Google Scholar] [CrossRef]
- Chen, L.; Wu, R.; Cheng, Y.; Chen, Y. Delay-dependent and order-dependent stability and stabilization of fractional-order linear systems with time-varying delay. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1064–1068. [Google Scholar] [CrossRef]
- Fu, H.; Wu, G.; Yang, G.; Huang, L. Fractional calculus with exponential memory. Chaos, Solitons Fractals 2021, 31, 031103. [Google Scholar] [CrossRef]
- Hong, L.; Cao, J.; Jiang, H.; Alsaedi, A. Graph theory-based finite-time synchronization of fractional-order complex dynamical networks. J. Frankl. Inst. 2018, 355, 5771–5789. [Google Scholar]
- Yang, S.; Yu, J.; Hu, C.; Jiang, H. Finite-time synchronization of memristive neural networks with fractional-order. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 3739–3750. [Google Scholar] [CrossRef]
- Wu, G.; Abdeljawad, T.; Liu, J.; Baleanu, D.; Wu, K. Mittag-leffler stability analysis of fractional discrete-time neural networks via fixed point technique. Nonlinear Anal. Model. Control. 2019, 24, 919–936. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, S.; Wei, Y.; Chen, C. Finite-time stability of delayed memristor-based fractional-order neural networks. IEEE Trans. Cybern. 2020, 50, 1607–1616. [Google Scholar] [CrossRef]
- Yang, S.; Yu, J.; Hu, C.; Jiang, H. Exponential stability of fractional-order impulsive control systems with applications in synchronization. IEEE Trans. Cybern. 2020, 50, 3157–3168. [Google Scholar] [CrossRef]
- Wu, X.; Bao, H. Finite time complete synchronization for fractional-order multiplex networks. Appl. Math. Comput. 2020, 377, 125188. [Google Scholar] [CrossRef]
- Li, C.; Liao, X.; Wong, K. Lag synchronization of hyperchaos with application to secure communications. Chaos Solitons Fractals 2005, 23, 183–193. [Google Scholar] [CrossRef]
- Sun, K.; Liu, L.; Qiu, J.; Feng, G. Fuzzy adaptive finite-time fault-tolerant control for strict-feedback nonlinear systems. IEEE Trans. Fuzzy Syst. 2021, 29, 786–796. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, S.; Li, W. Exponential stability of fractional-order complex multi-links networks with aperiodically intermittent control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4063–4074. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Chen, H.; Li, W. Stability for multi-links stochastic delayed complex networks with semi-markov jump under hybrid multi-delay impulsive control. Neurocomputing 2021, 449, 214–228. [Google Scholar] [CrossRef]
- Wang, S.; Cao, Y.; Guo, Z.; Yan, Z.; Huang, T. Periodic event-triggered synchronization of multiple memristive neural networks with switching topologies and parameter mismatch. IEEE Trans. Cybern. 2021, 51, 427–437. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Hu, C.; Yu, J.; Jiang, H.; Huang, T. Edge-based fractional-order adaptive strategies for synchronization of fractional-order coupled networks with reaction-diffusion terms. IEEE Trans. Cybern. 2018, 50, 1582–1594. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, C.; Yu, J.; Jiang, H.; Wen, S. Synchronization of fractional-order spatiotemporal complex networks with boundary communication. Neurocomputing 2021, 450, 197–207. [Google Scholar] [CrossRef]
- Liu, P.; Xu, M.; Sun, J.; Zeng, Z. On pinning linear and adaptive synchronization of multiple fractional-order neural networks with unbounded time-varying delays. IEEE Trans. Cybern. 2022. [Google Scholar] [CrossRef]
- Luo, T.; Wang, Q.; Jia, Q.; Xu, Y. Asymptotic and finite-time synchronization of fractional-order multiplex networks with time delays by adaptive and impulsive control. Neurocomputing 2022, 493, 445–461. [Google Scholar] [CrossRef]
- Kalman, R. Nonlinear aspects of sampled-data control systems. Proc. 1956 Symp. Nonlinear Circuit Anal. 1956, 6, 273–313. [Google Scholar]
- Wu, Z.; Xu, Y.; Pan, Y.; Su, H.; Tang, Y. Event-triggered control for consensus problem in multi-agent systems with quantized relative state measurements and external disturbance. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 65, 2232–2242. [Google Scholar] [CrossRef]
- Sun, B.; Cao, Y.; Guo, Z.; Yan, Z.; Wen, S. Synchronization of discrete-time recurrent neural networks with time-varying delays via quantized sliding mode control. Appl. Math. Comput. 2020, 375, 125093. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.; Cao, J. Adaptive synchronization of fractional-order output-coupling neural networks via quantized output control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3230–3239. [Google Scholar] [CrossRef]
- Zhuang, J.; Cao, J.; Tang, L.; Xia, Y.; Perc, M. Synchronization analysis for stochastic delayed multilayer network with additive couplings. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 50, 4807–4816. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, X.; Pan, L.; Feng, Y.; Cao, J. Quasi-synchronization of delayed stochastic multiplex networks via impulsive pinning control. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 52, 5389–5397. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Z.; Yang, H.; Song, Q.; Xiao, M. Synchronization of multiplex networks with stochastic perturbations via pinning adaptive control. J. Frankl. Inst. 2021, 358, 3994–4012. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and applications of fractional differential equations. North-Holl. Math. Stud. 2006, 204, 1–523. [Google Scholar]
- Aguila, N.; Duarte, M.; Gallegos, J. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Li, W.; Zhou, J.; Li, J.; Xie, T.; Lu, J. Cluster synchronization of two-layer networks via aperiodically intermittent pinning control. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1338–1342. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, X.; Mao, B.; Lu, J.; Xie, C. Finite-time intra-layer and inter-layer quasi-synchronization of two-layer multi-weighted networks. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 1589–1598. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Li, Z.; Zeng, Z.; Lu, J. Intralayer synchronization of multiplex dynamical networks via pinning impulsive control. IEEE Trans. Cybern. 2022, 52, 2110–2122. [Google Scholar] [CrossRef]
- Pecora, L.; Sorrentino, F.; Hagerstrom, A.; Murphy, T.; Roy, R. Cluster synchronization and isolated desynchronization in complex networks with symmetries. Nat. Commun. 2014, 5, 4079. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Park, J.; Wang, Y.; Zheng, W. Synchronization on lur’e cluster networks with proportional delay: Impulsive effects method. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 4555–4565. [Google Scholar] [CrossRef]
- Hu, C.; Jiang, H. Pinning synchronization for directed networks with node balance via adaptive intermittent control. Nonlinear Dyn. 2015, 80, 295–307. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L.; Hu, J.; Feng, G. Adaptive antisynchronization of multilayer reaction-diffusion neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 807–818. [Google Scholar] [CrossRef]
- Liu, P.; Kong, M.; Zeng, Z. Projective synchronization analysis of fractional-order neural networks with mixed time delays. IEEE Trans. Cybern. 2020. [Google Scholar] [CrossRef]
- Liu, P.; Xu, M.; Sun, J.; Wen, S. Cluster synchronization of multiple fractional-order recurrent neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Yu, J.; Hu, C. Adaptive Quantized Synchronization of Fractional-Order Output-Coupling Multiplex Networks. Fractal Fract. 2023, 7, 22. https://doi.org/10.3390/fractalfract7010022
Bai Y, Yu J, Hu C. Adaptive Quantized Synchronization of Fractional-Order Output-Coupling Multiplex Networks. Fractal and Fractional. 2023; 7(1):22. https://doi.org/10.3390/fractalfract7010022
Chicago/Turabian StyleBai, Yunzhan, Juan Yu, and Cheng Hu. 2023. "Adaptive Quantized Synchronization of Fractional-Order Output-Coupling Multiplex Networks" Fractal and Fractional 7, no. 1: 22. https://doi.org/10.3390/fractalfract7010022
APA StyleBai, Y., Yu, J., & Hu, C. (2023). Adaptive Quantized Synchronization of Fractional-Order Output-Coupling Multiplex Networks. Fractal and Fractional, 7(1), 22. https://doi.org/10.3390/fractalfract7010022







