Further Midpoint Inequalities via Generalized Fractional Operators in Riemann–Liouville Sense
Abstract
:1. Introduction
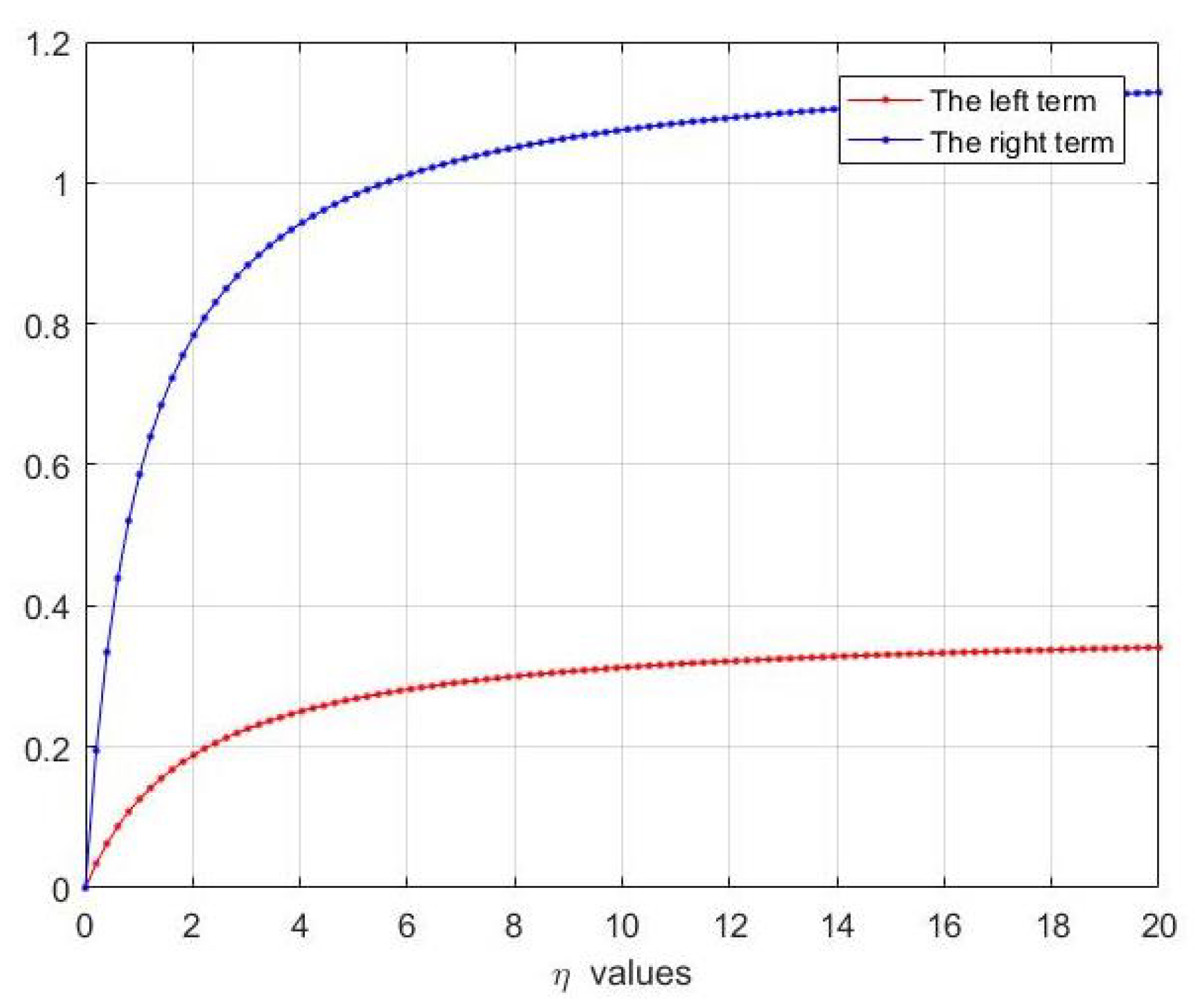
2. Main Results
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Anastassiou, G.A. Generalized Fractional Calculus: New Advancements and Pplications; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Wang, L.F.; Yang, X.J.; Baleanu, D.; Zhao, C.C.Y. Fractal Dynamical Model of Vehicular Traffic Flow within the Local Fractional Conservation Laws. Abstr. Appl. Anal. 2014, 2014, 635760. [Google Scholar] [CrossRef]
- Imran, M.A.; Sarwar, S.; Abdullah, M.; Khan, I. An analysis of the semi-analytic solutions of a viscous fluid with old and new definitions of fractional derivatives. Chin. J. Phys. 2018, 56, 1853–1871. [Google Scholar] [CrossRef]
- Iqbal, N.; Akgül, A.; Shah, R.; Bariq, A.; Al-Sawalha, M.M.; Ali, A. On Solutions of Fractional-Order Gas Dynamics Equation by Effective Techniques. J. Funct. Spaces 2022, 2022, 3341754. [Google Scholar] [CrossRef]
- Attia, N.; Akgül, A.; Seba, D.; Nour, A. An efficient numerical technique for a biological population model of fractional order. Chaos Solut. Fractals 2020, 141, 110349. [Google Scholar]
- Gabr, A.; Kader, A.H.A.; Latif, M.S.A. The Effect of the Parameters of the Generalized Fractional Derivatives On the Behavior of Linear Electrical Circuits. Int. J. Appl. Comput. Math. 2021, 7, 247. [Google Scholar] [CrossRef]
- Budak, H.; Yıldırım, S.K.; Sarıkaya, M.Z.; Yıldırım, H. Some parameterized Simpson-, midpoint- and trapezoid-type inequalities for generalized fractional integrals. J. Inequalities Appl. 2022, 2022, 40. [Google Scholar] [CrossRef]
- Barakat, M.A.; Soliman, A.H.; Hyder, A. Langevin Equations with Generalized Proportional Hadamard–Caputo Fractional Derivative. Comput. Intell. Neurosci. 2021, 2021, 6316477. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdelhakim, A.A. The flaw in the conformable calculus: It is conformable because it is not fractional. Fract. Calc. Appl. Anal. 2019, 22, 242–254. [Google Scholar] [CrossRef]
- Zhao, D.; Luo, M. General conformable fractional derivative and its physical interpretation. Calcolo 2017, 54, 903–917. [Google Scholar]
- Hyder, A.; Soliman, A.H. A new generalized θ-conformable calculus and its applications in mathematical physics. Phys. Scr. 2020, 96, 015208. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D. Monotonicity results for fractional difference operators with discrete exponential kernels. Adv. Differ. Equations 2017, 2017, 78. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Sci. B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Jarad, F.; Uğurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Hyder, A.; Barakat, M.A. Novel improved fractional operators and their scientific applications. Adv. Differ. Equ. 2021, 2021, 389. [Google Scholar] [CrossRef]
- Alomari, M.; Darus, M.; Kirmaci, U.S. Refinements of Hadamard-type inequalities for quasi-convex functions with applications to trapezoidal formula and to special means. Comput. Math. Appl. 2010, 59, 225–232. [Google Scholar] [CrossRef]
- Özdemir, M.E.; Avci, M.; Kavurmaci, H. Hermite–Hadamard-type inequalities via (α,m)-convexity. Comput. Math. Appl. 2011, 61, 2614–2620. [Google Scholar] [CrossRef]
- Özdemir, M.E.; Avcı, M.; Set, E. On some inequalities of Hermite–Hadamard type via m-convexity. Appl. Math. Lett. 2010, 23, 1065–1070. [Google Scholar] [CrossRef]
- Latif, M.A.; Rashid, S.; Dragomir, S.S.; Chu, Y.-M. Hermite–Hadamard type inequalities for co-ordinated convex and qausi-convex functions and their applications. J. Inequalities Appl. 2019, 2019, 317. [Google Scholar] [CrossRef]
- Valdés, J.E.N.; Rodríguez, J.M.; Sigarreta, J.M. New Hermite–Hadamard Type Inequalities Involving Non-Conformable Integral Operators. Symmetry 2019, 11, 1108. [Google Scholar] [CrossRef]
- Butt, S.I.; Kashuri, A.; Tariq, M.; Nasir, J.; Aslam, A.; Gao, W. Hermite–Hadamard-type inequalities via n-polynomial exponential-type convexity and their applications. Adv. Differ. Equ. 2020, 2020, 508. [Google Scholar] [CrossRef]
- Shuang-Shuang, Z.; Saima, R.; Aslam, N.M.; Inayat, N.K.; Farhat, S.; Yu-Ming, C. New Hermite-Hadamard type inequalities for exponentially convex functions and applications. AIMS Math. 2020, 5, 6874–6901. [Google Scholar]
- Sarikaya, M.Z.; Alp, N. On Hermite-Hadamard-Fejér type integral inequalities for generalized convex functions via local fractional integrals. Open J. Math. Sci. 2019, 3, 273–284. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Farid, G.; Nazeer, W.; Ullah, S.; Kang, S.M. Generalized Riemann–Liouville k -Fractional Integrals Associated With Ostrowski Type Inequalities and Error Bounds of Hadamard Inequalities. IEEE Access 2018, 6, 64946–64953. [Google Scholar] [CrossRef]
- Budak, H.; Kara, H.; Ali, M.A.; Khan, S.; Chu, Y. Fractional Hermite-Hadamard-type inequalities for interval-valued co-ordinated convex functions. Open Math. 2021, 19, 1081–1097. [Google Scholar] [CrossRef]
- Hyder, A.; Barakat, M.A.; Fathallah, A.; Cesarano, C. Further Integral Inequalities through Some Generalized Fractional Integral Operators. Fractal Fract. 2021, 5, 282. [Google Scholar] [CrossRef]
- Gürbüz, M.; Akdemir, A.O.; Rashid, S.; Set, E. Hermite–Hadamard inequality for fractional integrals of Caputo–Fabrizio type and related inequalities. J. Inequalities Appl. 2020, 2020, 172. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Khan, A.; Rahman, G.; Nisar, K.S.; Abouzaid, M.S.; Khan, I. Fractional integral inequalities involving Marichev–Saigo–Maeda fractional integral operator. J. Inequalities Appl. 2020, 2020, 185. [Google Scholar] [CrossRef]
- Aljaaidi, T.A.; Pachpatte, D.B.; Abdeljawad, T.; Abdo, M.S.; Almalahi, M.A.; Redhwan, S.S. Generalized proportional fractional integral Hermite–Hadamard’s inequalities. Adv. Differ. Equ. 2021, 2021, 493. [Google Scholar] [CrossRef]
- Set, E.; Choi, J.; Gözpinar, A. Hermite–Hadamard Type Inequalities for New Conformable Fractional Integral Operator, ResearchGate Preprint. 2018. Available online: https://www.researchgate.net/publication/322936389 (accessed on 8 May 2012).
- Gözpınar, A. Some Hermite-Hadamard type inequalities for convex functions via new fractional conformable integrals and related inequalities. AIP Conf. Proc. 2018, 1991, 020006. [Google Scholar]
- Qaisar, S.; Hussain, S. On hermite-hadamard type inequalities for functions whose first derivative absolute values are convex and concave. Fasc. Math. 2017, 58, 155–166. [Google Scholar] [CrossRef]
- Kirmaci, U.S. Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula. Appl. Math. Comput. 2004, 147, 137–146. [Google Scholar] [CrossRef]
- Budak, H.; Agarwal, P. New generalized midpoint type inequalities for fractional integral. Miskolc Math. Notes 2019, 20, 781–793. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyder, A.-A.; Budak, H.; Almoneef, A.A. Further Midpoint Inequalities via Generalized Fractional Operators in Riemann–Liouville Sense. Fractal Fract. 2022, 6, 496. https://doi.org/10.3390/fractalfract6090496
Hyder A-A, Budak H, Almoneef AA. Further Midpoint Inequalities via Generalized Fractional Operators in Riemann–Liouville Sense. Fractal and Fractional. 2022; 6(9):496. https://doi.org/10.3390/fractalfract6090496
Chicago/Turabian StyleHyder, Abd-Allah, Hüseyin Budak, and Areej A. Almoneef. 2022. "Further Midpoint Inequalities via Generalized Fractional Operators in Riemann–Liouville Sense" Fractal and Fractional 6, no. 9: 496. https://doi.org/10.3390/fractalfract6090496
APA StyleHyder, A.-A., Budak, H., & Almoneef, A. A. (2022). Further Midpoint Inequalities via Generalized Fractional Operators in Riemann–Liouville Sense. Fractal and Fractional, 6(9), 496. https://doi.org/10.3390/fractalfract6090496






