The Nonlinear Dynamics Characteristics and Snap-Through of an SD Oscillator with Nonlinear Fractional Damping
Abstract
:1. Introduction
2. The Model of an SD Oscillator with Nonlinear Fractional Damping
3. The Bifurcation of the Amplitude–Frequency Response and the Stability Conditions of Steady-State Solutions
3.1. The Amplitude–Frequency Response Function of the Primary Resonance
3.2. The Stability Conditions of the Steady-State Solution
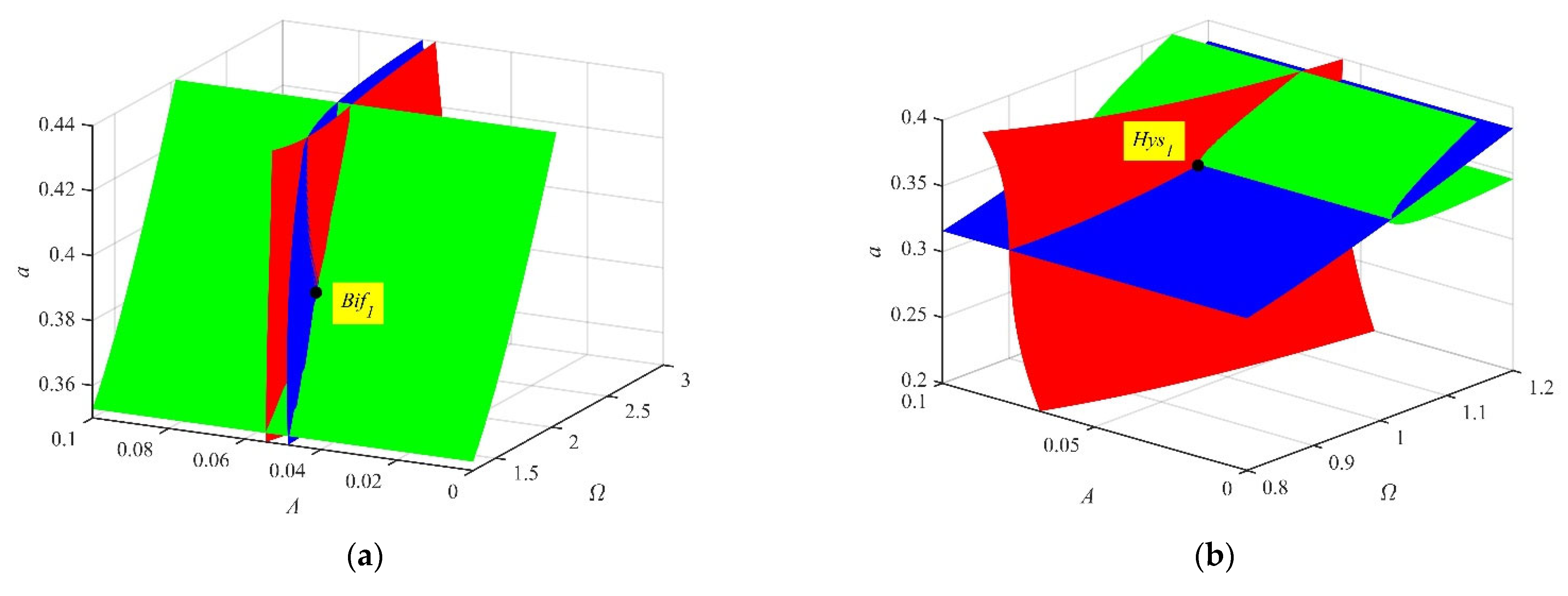
3.3. The Transition Set of the Amplitude–Frequency Response Function
4. The Nonlinear Characteristics Analysis of the SD Oscillator with Nonlinear Fractional Damping
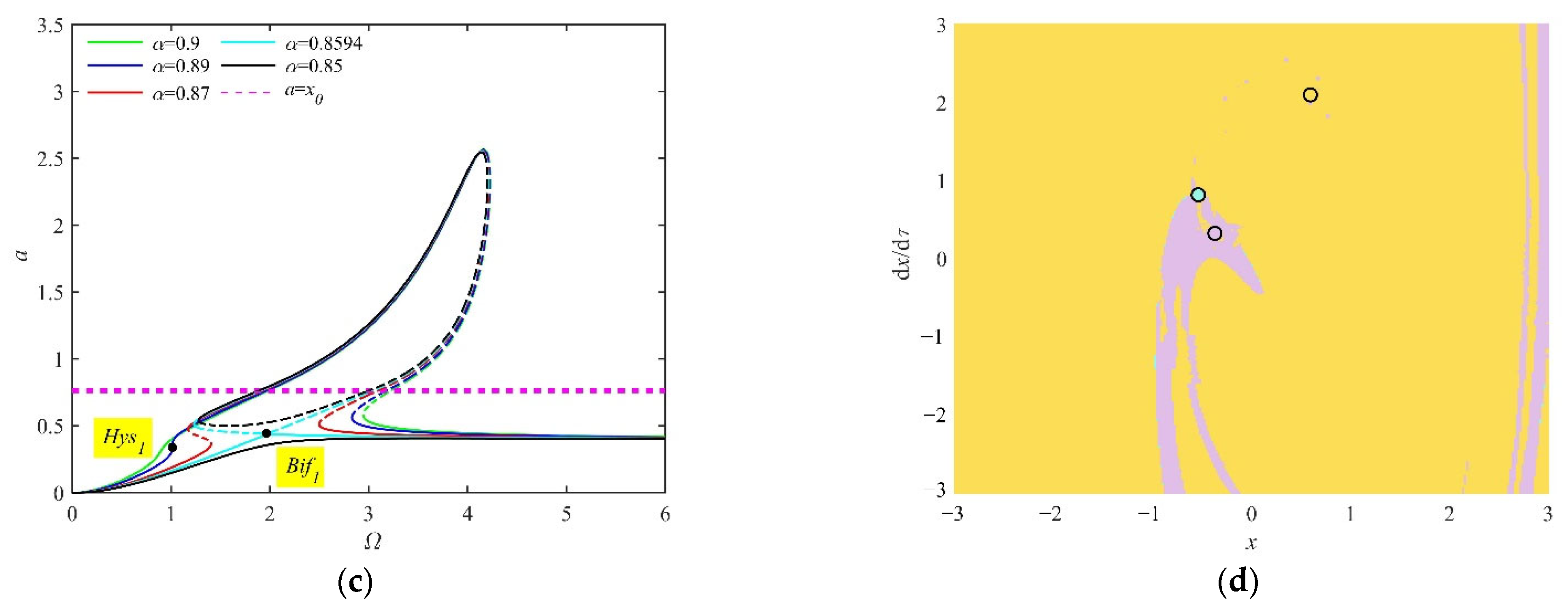
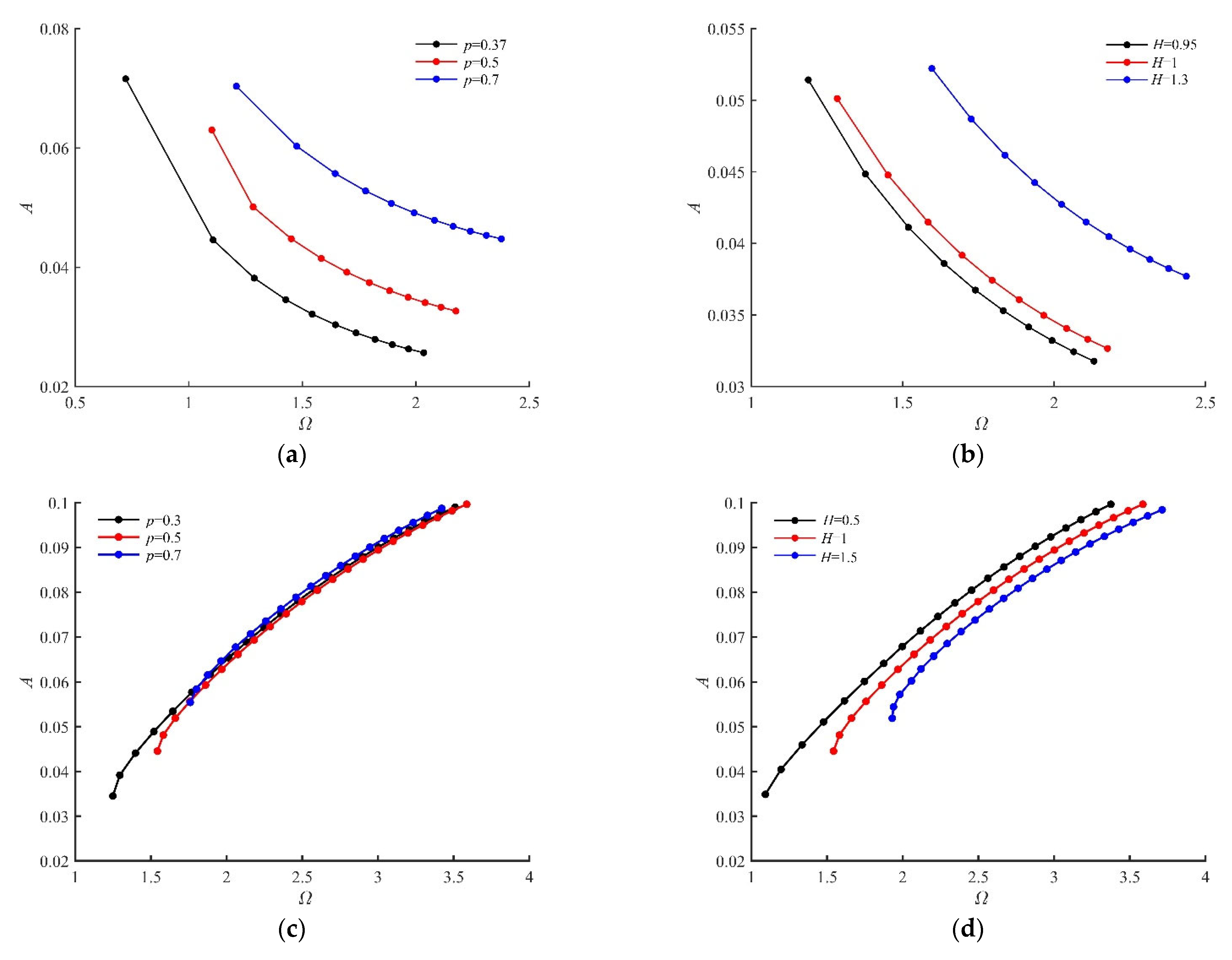
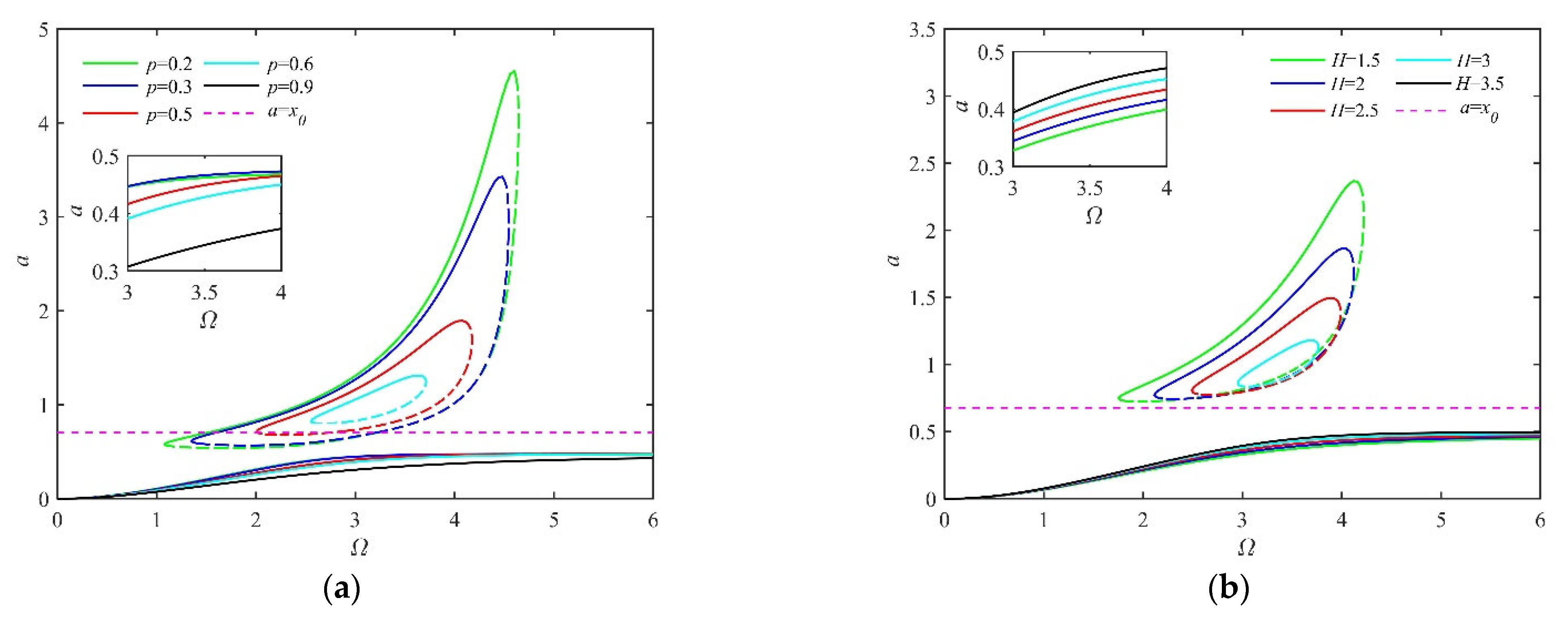
4.1. The Nonlinear Characteristics in the Resonant Region
4.1.1. The Influence of the Smooth Parameter in the Transition Set of the System
4.1.2. The Influence of the Fractional Damping Parameters in the Transition Set of the System
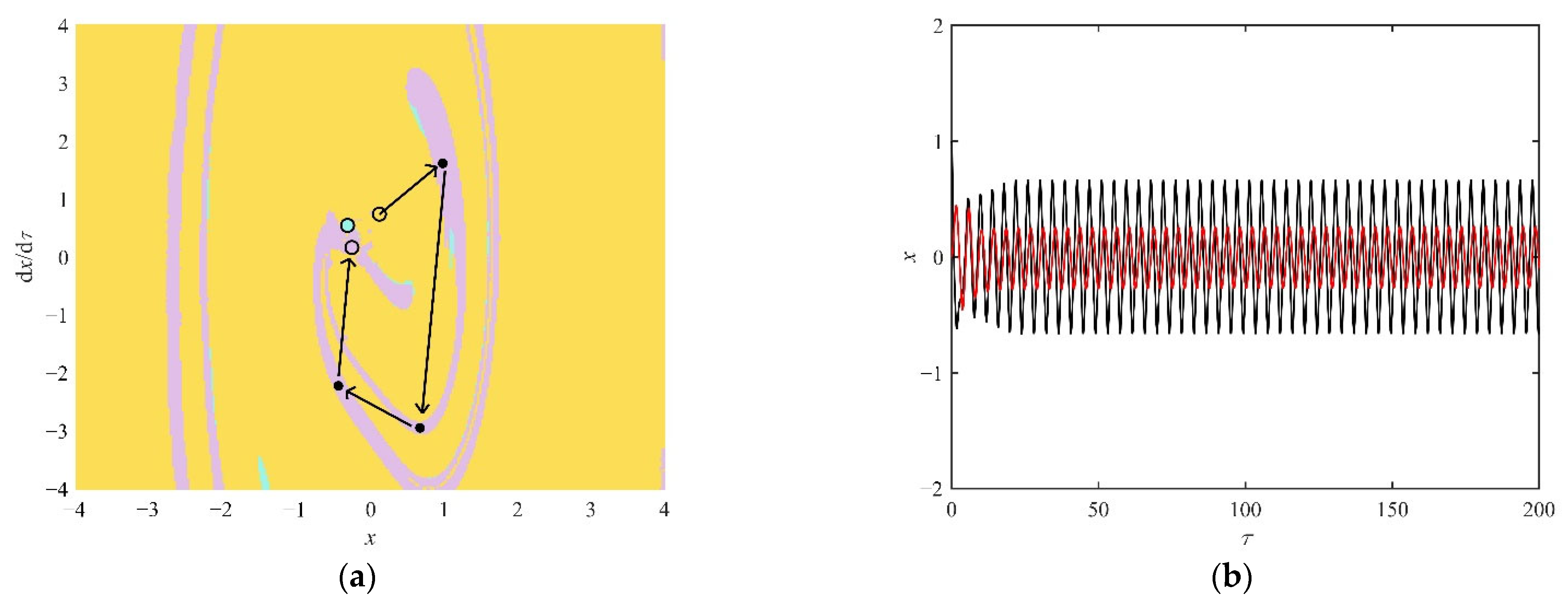
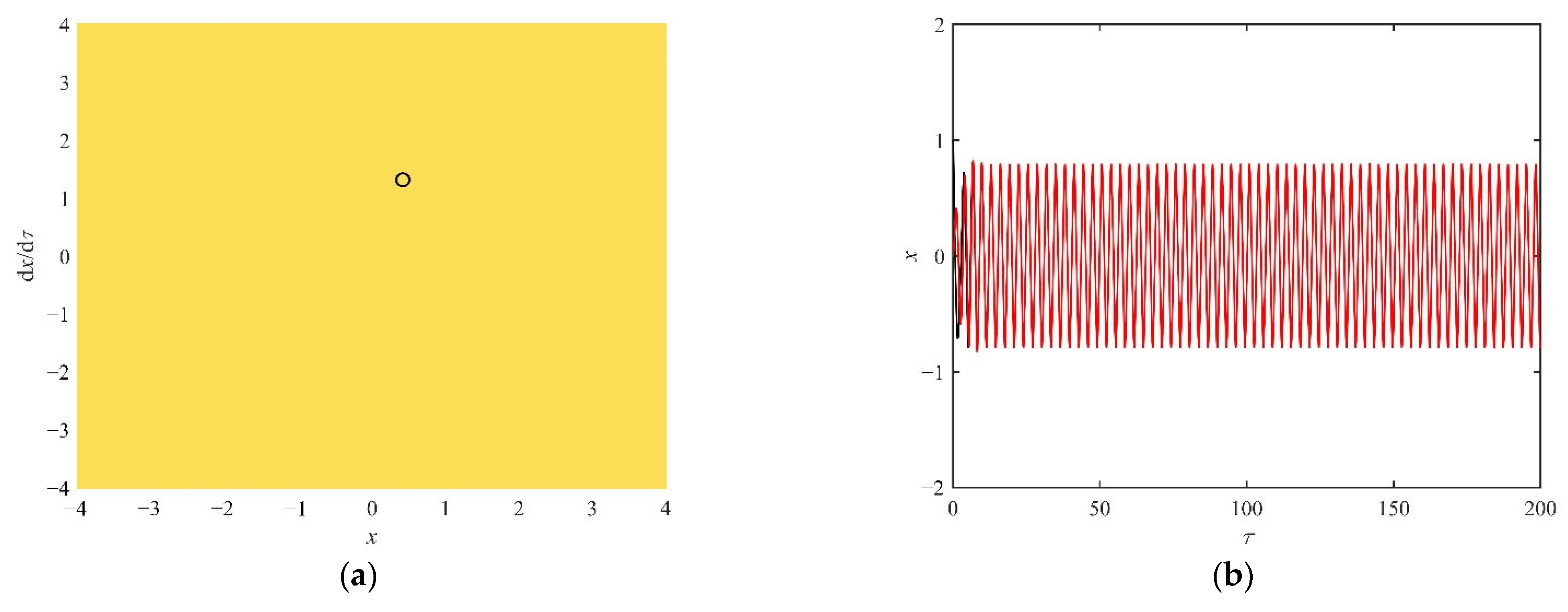
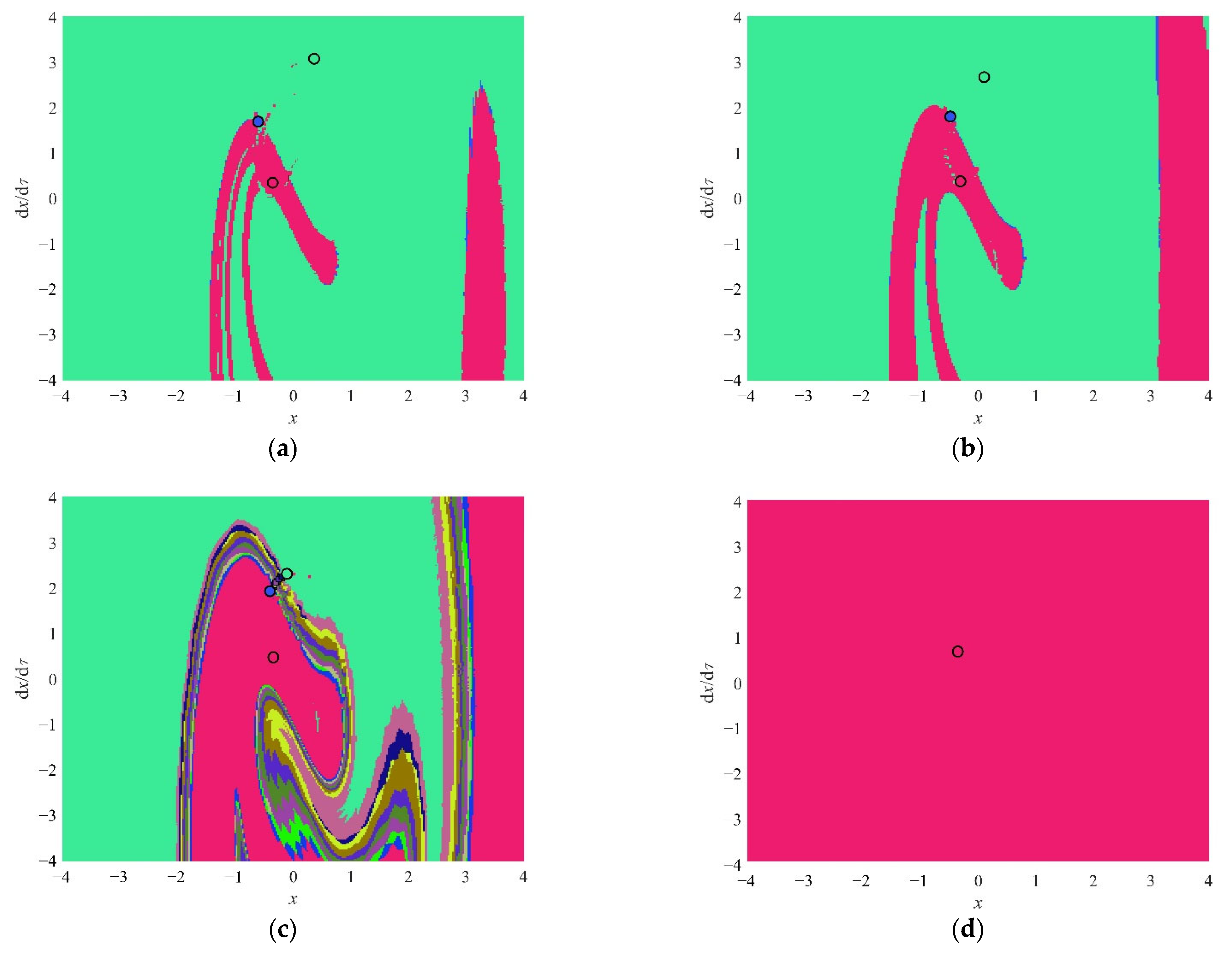
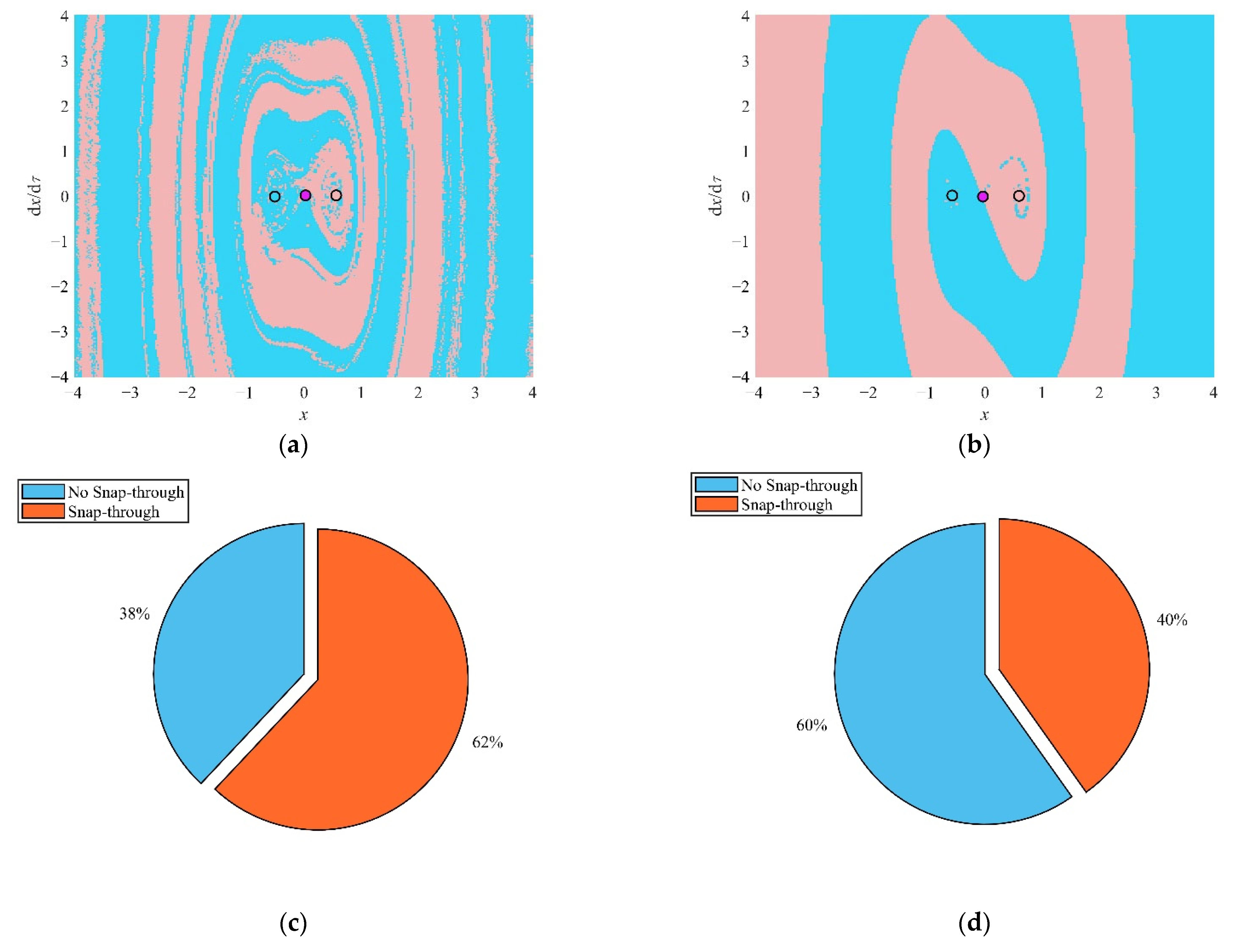
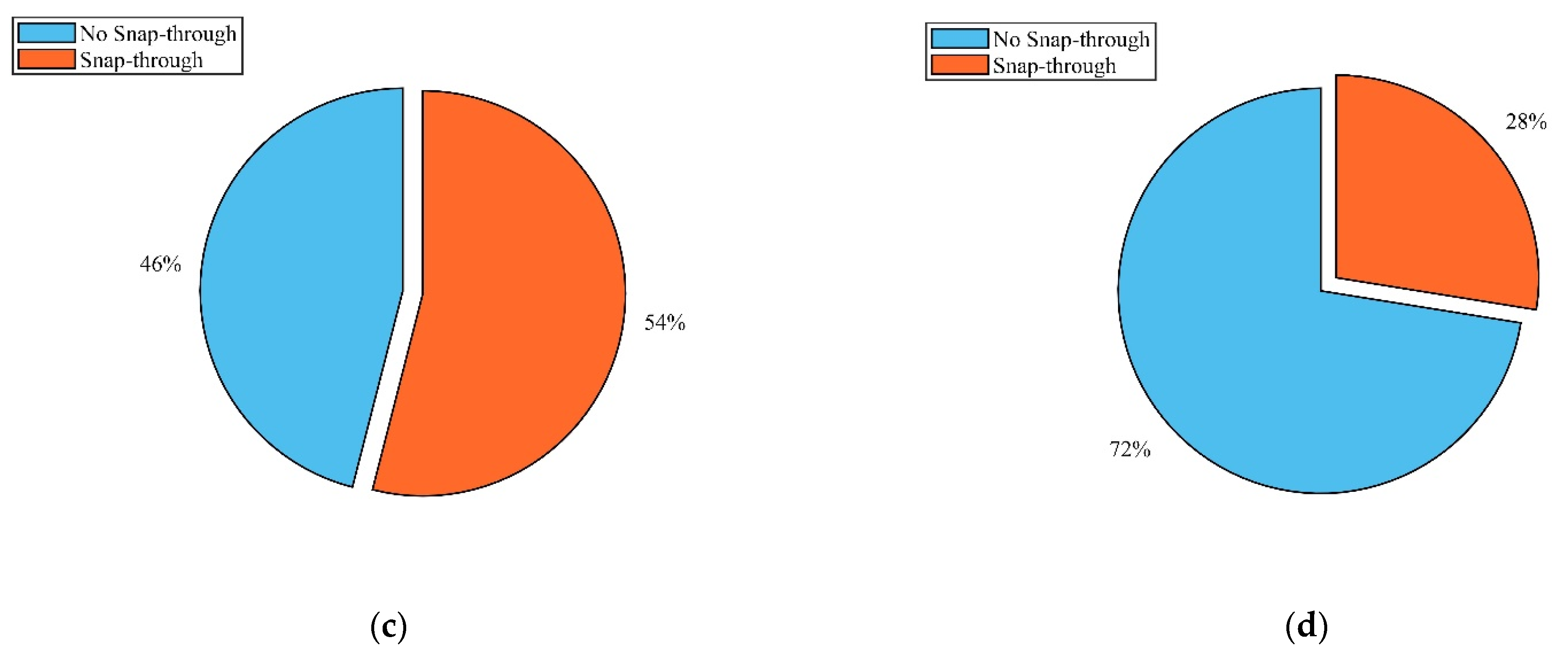
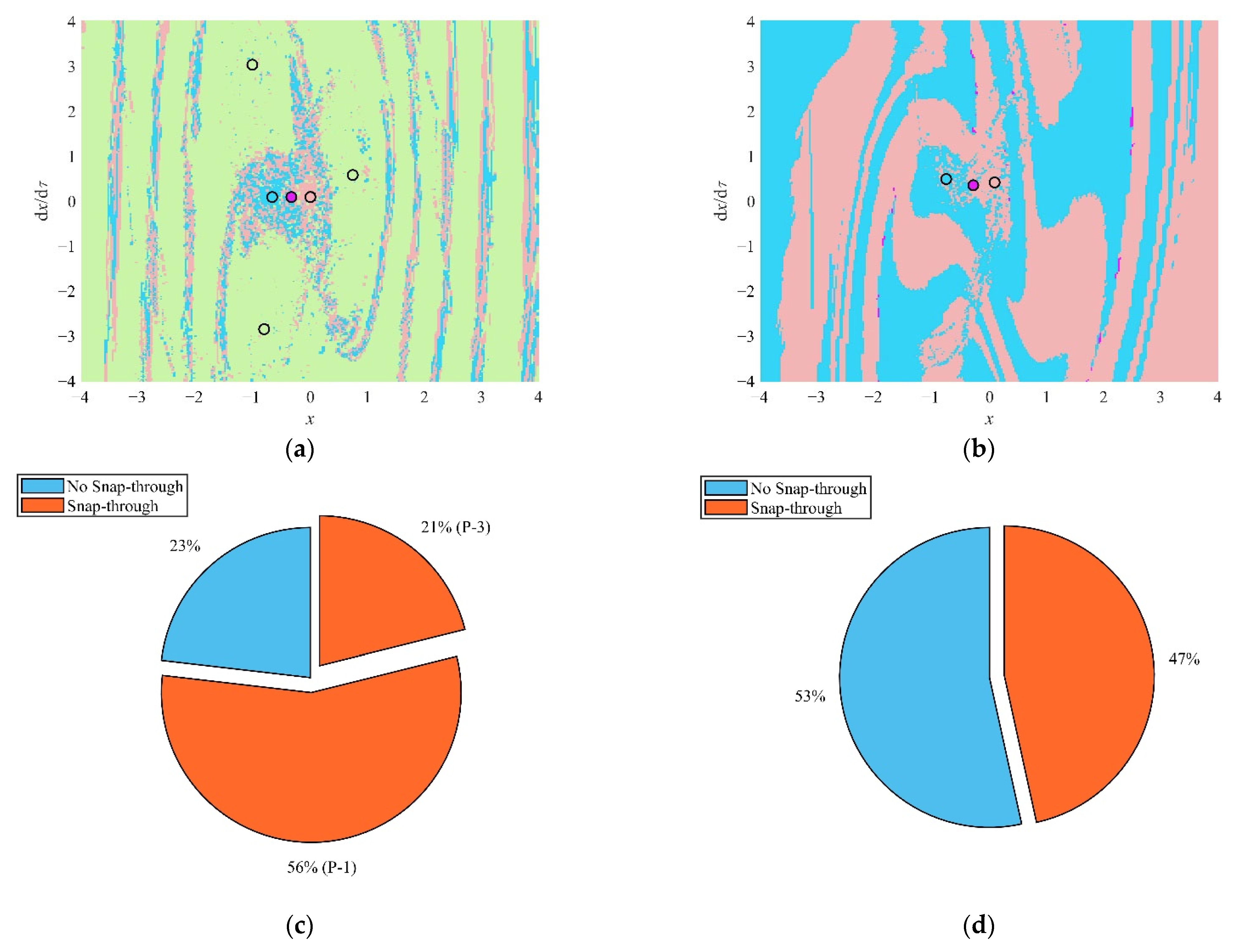
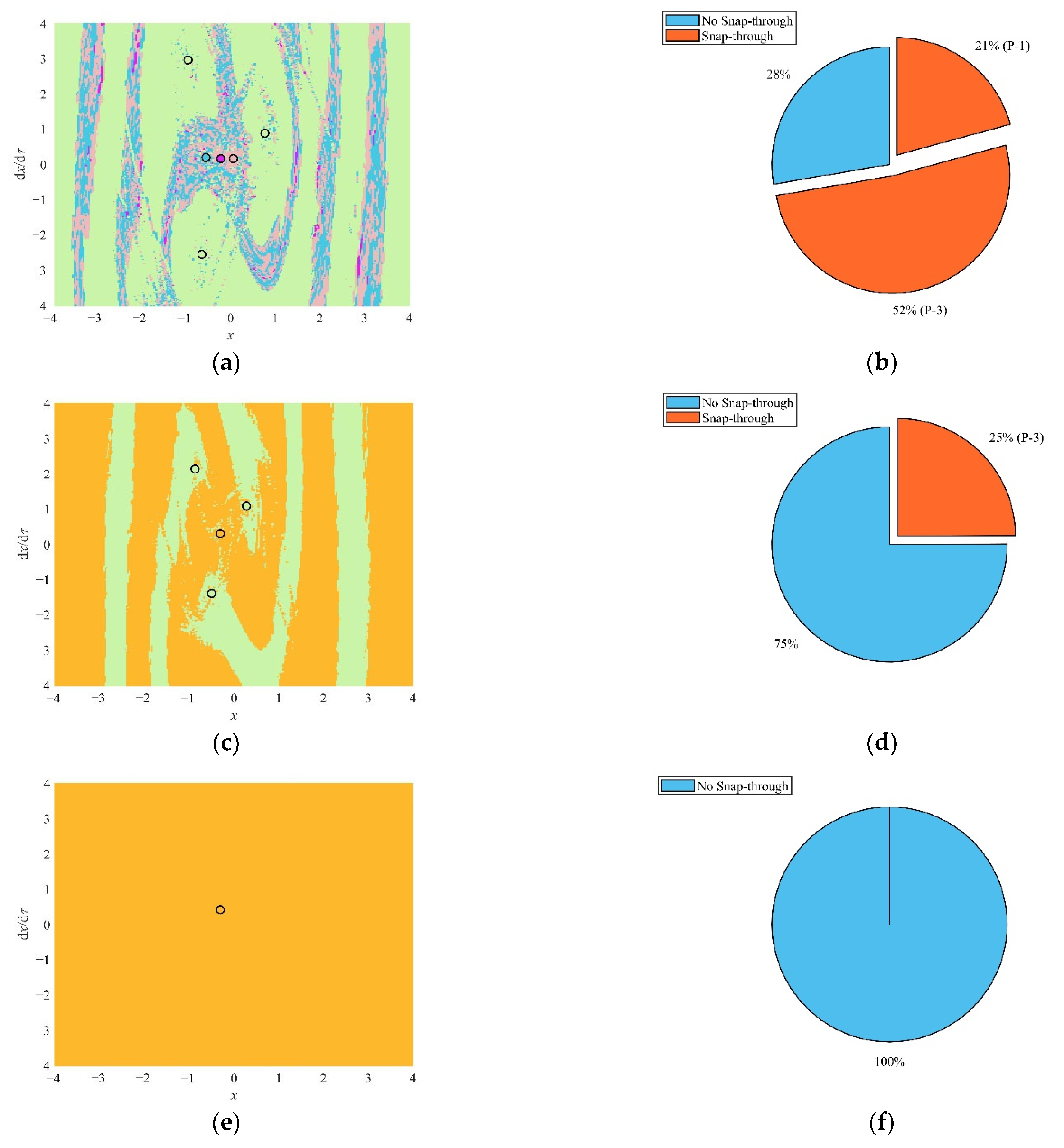
4.2. Analysis of the Snap-Through Phenomenon in the Non-Resonant Region
5. Conclusions
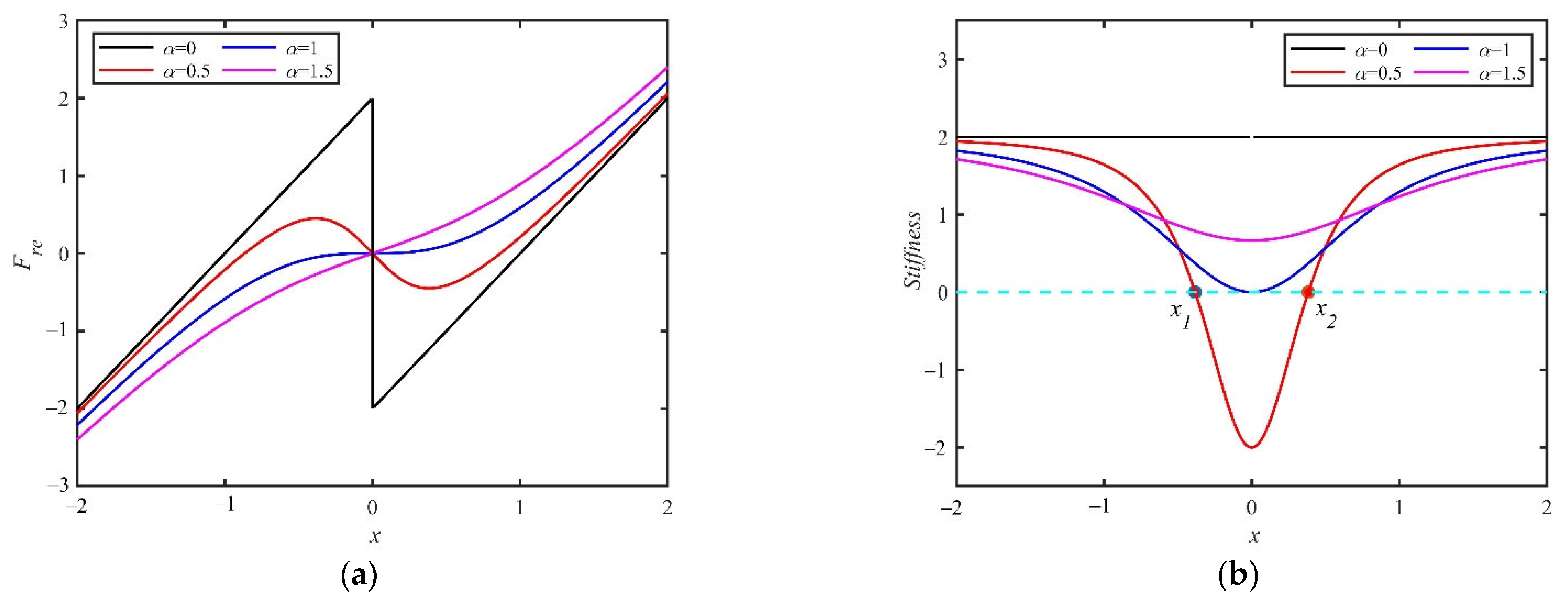
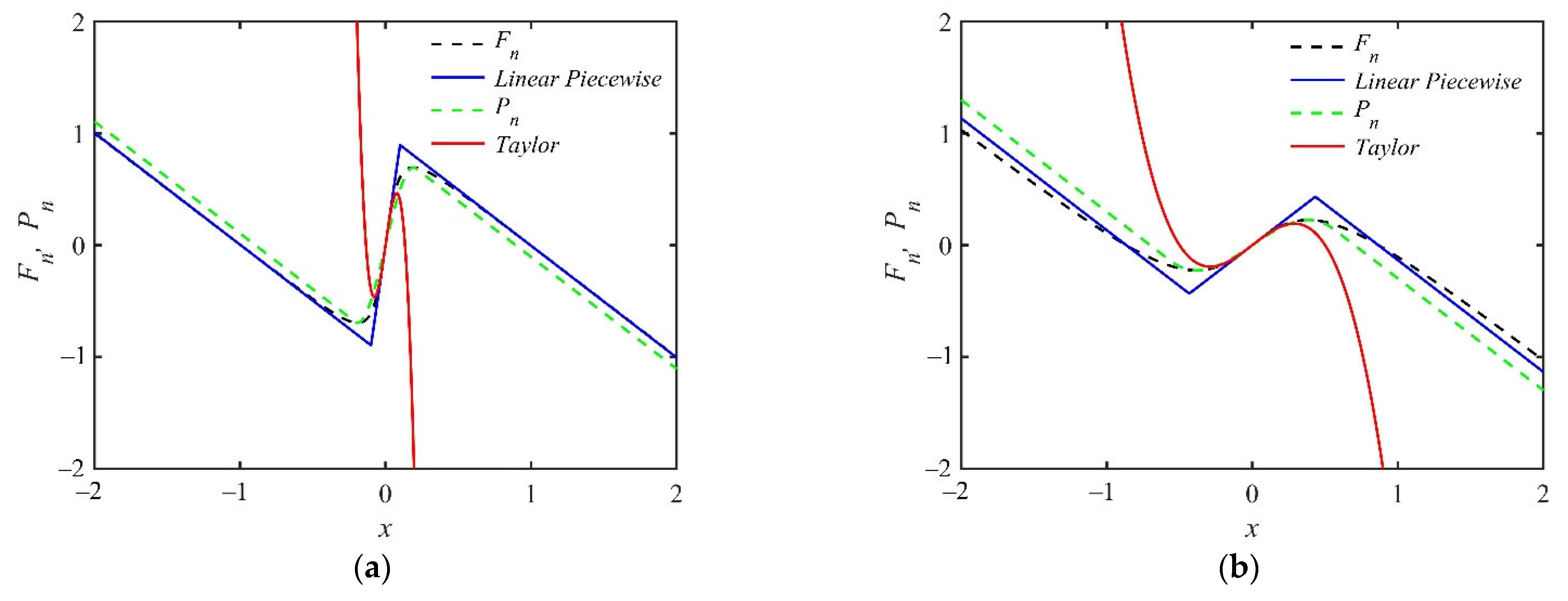
- The nonlinear restoring force is accurately represented by the piecewise nonlinear function. The nonlinear characteristics of the restoring force in the interval are retained, so that some novel nonlinear phenomena are found.
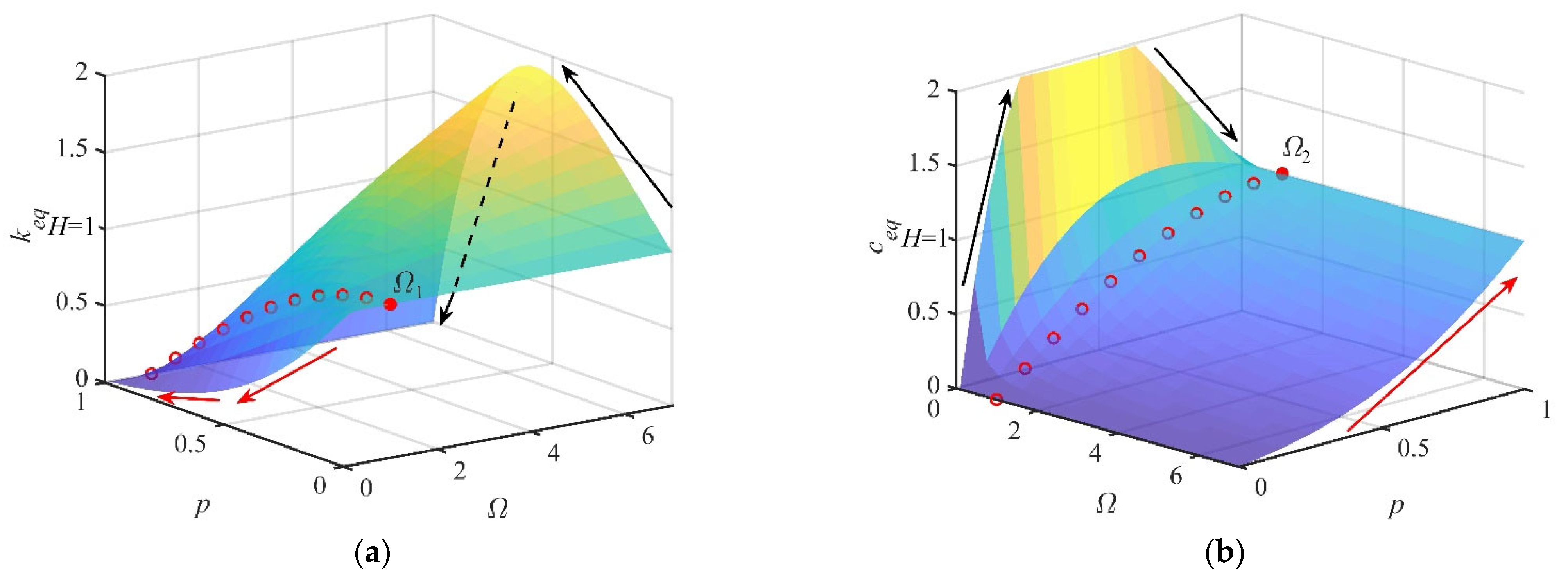
- The orthogonal function is used to calculate the equivalent fractional coefficients. The equivalent stiffness coefficient and the equivalent damping coefficient are variable with respect to the and the power of the excitation frequency. In the high-frequency region, the stiffness characteristic of the fractional model is dominant. The stiffness characteristic increases first and then decreases as the fractional order increases. In the low-frequency region, the damping characteristic of the fractional model is dominant. The damping characteristic increases first and then decreases as the fractional order increases. The fractional model affects the stiffness property and the damping property, simultaneously.
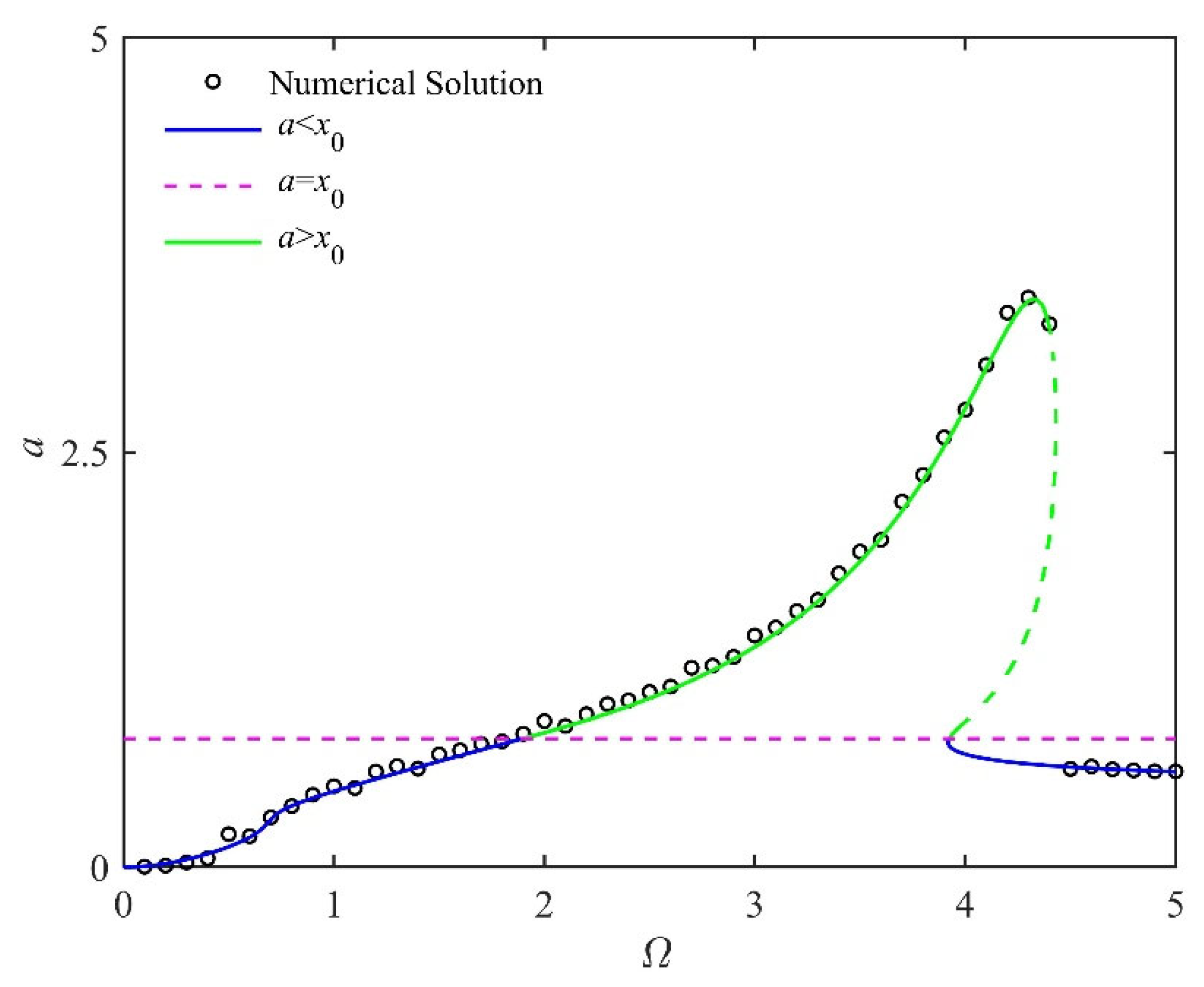
- Based on the amplitude–frequency response functions, a novel transition process is found. With the decrease in the smooth parameter, the nonlinearity of the system increases. A hysteresis point appears first, followed by a bifurcation point and a frequency island. There are three attractors (two stable attractors and one unstable attractor) in the frequency island. In addition, the variation in the number and the stable state of attractors means that pitchfork bifurcation and transcritical bifurcation are found. It is rare that the vibration amplitude of the system can be changed in the entire resonant region because of the frequency island.
- As the fractional parameters increase, the hysteresis point moves to the high-frequency and large-amplitude region, and the bifurcation point moves to the high-frequency and small-amplitude region. The frequency interval of the frequency island shortens. Finally, the frequency island disappears because the stable attractor and the unstable attractor collide.
- In the non-resonant region, the increase in the fractional parameters leads to the probability of the snap-through decreasing and the asymptotic stability of the steady-state solution increasing. When the excitation frequency is smaller than the natural frequency, the symmetry of the attraction domain enhances and the continuity increases. When the excitation frequency is larger than the natural frequency, the number of stable states of the system decreases. When the system is in a monostable state, no snap-through occurs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Cao, Q.J.; Wiercigroch, M.; Pavlovskaia, E.E.; Grebogi, C.; Thompson, J.M.T. Archetypal oscillator for smooth and discontinuous dynamics. Phys. Rev. E 2006, 74, 046218. [Google Scholar] [CrossRef]
- Ashwani, K.P.; Nalin, A.C.; Dennis, S.B.; Sanjay, P.B.; Anthony, M.W. Feedback stabilization of snap-through buckling in a preloaded two-bar linkage with hysteresis. Int. J. Nonlinear Mech. 2007, 43, 277–291. [Google Scholar]
- Yang, T.; Liu, J.Y.; Cao, Q.J. Response analysis of the archetypal smooth and discontinuous oscillator for vibration energy harvesting. Phys. A Stat. Mech. Its Appl. 2018, 507, 358–373. [Google Scholar] [CrossRef]
- Hao, Z.F.; Cao, Q.J.; Wiercigroch, M. Two-sided damping constraint control for high-performance vibration isolation and end-stop impact protection. Nonlinear Dyn. 2016, 86, 2129–2144. [Google Scholar] [CrossRef]
- Avramov, K.V.; Mikhlin, Y.V. Snap-through truss as a vibration absorber. J. Vib. Control 2004, 10, 291–308. [Google Scholar] [CrossRef]
- Brennan, M.J.; Elliott, S.J.; Bonello, P.; Vincent, J.F.V. The “click” mechanism in dipteran flight: If it exists, then what effect does it have? J. Theor. Biol. 2003, 224, 205–213. [Google Scholar] [CrossRef]
- Ichiro, A.; Nakazawa, M. Non-linear dynamic behavior of multi-folding microstructure systems based on origami skill. Int. J. Non-Linear Mech. 2010, 45, 337–347. [Google Scholar]
- Waite, J.J.; Virgin, L.N.; Wiebe, R. Competing responses in a discrete mechanical system. Int. J. Bifurc. Chaos 2014, 24, 1430003. [Google Scholar] [CrossRef]
- Hao, Z.F.; Cao, Q.J. The isolation characteristics of an archetypal dynamical model with stable-quasi-zero-stiffness. J. Sound Vib. 2015, 340, 61–79. [Google Scholar] [CrossRef]
- Hao, Z.F.; Cao, Q.J. A novel dynamical model for GVT nonlinear supporting system with stable-quasi-zero-stiffness. J. Theor. Appl. Mech. 2014, 52, 199–213. [Google Scholar]
- Currier, T.M.; Lheron, S.; Modarres-Sadeghi, Y. A bio-inspired robotic fish utilizes the snap-through buckling of its spine to generate accelerations of more than 20 g. Bioinspir. Biomim. 2020, 15, 055006. [Google Scholar] [CrossRef]
- Ding, H.; Chen, L.Q. Designs, analysis, and applications of nonlinear energy sinks. Nonlinear Dyn. 2020, 100, 3061–3107. [Google Scholar] [CrossRef]
- Geng, X.F.; Ding, H.; Mao, X.Y.; Chen, L.Q. Nonlinear energy sink with limited vibration amplitude. Mech. Syst. Signal Process. 2021, 156, 107625. [Google Scholar] [CrossRef]
- Jiang, W.A.; Chen, L.Q. Snap-through piezoelectric energy harvesting. J. Sound Vib. 2014, 333, 4314–4325. [Google Scholar] [CrossRef]
- Speciale, A.; Ardito, R.; Marco, B.; Ferrari, M.; Ferrari, V.; Frangi, A.A. Snap-through buckling mechanism for frequency-up conversion in piezoelectric energy harvesting. Appl. Sci. 2020, 10, 3614. [Google Scholar] [CrossRef]
- Myongwon, H.; Andres, F. Topological wave energy harvesting in bistable lattices. Smart Mater. Struct. 2022, 31, 015021. [Google Scholar]
- Tan, D.G.; Zhou, J.X.; Wang, K.; Zhao, X.; Wang, Q.; Xu, D. Bow-type bistable triboelectric nanogenerator for harvesting energy from low-frequency vibration. Nano Energy 2022, 92, 106746. [Google Scholar] [CrossRef]
- Cao, Q.J.; Wiercigroch, M.; Pavlovskaia, E.E.; Thompson, J.M.T.; Grebogi, C. Piecewise linear approach to an archetypal oscillator for smooth and discontinuous dynamics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 635–652. [Google Scholar] [CrossRef]
- Tian, R.L.; Cao, Q.J.; Li, Z.X. Hopf bifurcations for the recently proposed smooth-and-discontinuous oscillator. Chin. Phys. Lett. 2010, 27, 074701. [Google Scholar]
- Tian, R.L.; Cao, Q.J.; Yang, S.P. The codimension-two bifurcation for the recent proposed SD oscillator. Nonlinear Dyn. 2010, 59, 19–27. [Google Scholar] [CrossRef]
- Cao, Q.J.; Wiercigroch, M.; Pavlovskaia, E.E.; Grebogi, C.; Thompson, J.M.T. The limit case response of the archetypal oscillator for smooth and discontinuous dynamics. Int. J. Non-Linear Mech. 2008, 43, 462–473. [Google Scholar] [CrossRef]
- Shen, J.; Li, Y.; Du, Z. Subharmonic and grazing bifurcations for a simple bilinear oscillator. Int. J. Non-Linear Mech. 2014, 60, 70–82. [Google Scholar] [CrossRef]
- Han, Y.W.; Cao, Q.J.; Chen, Y.S.; Wiercigroch, M. A novel smooth and discontinuous oscillator with strong irrational nonlinearities. Sci. China Phys. Mech. Astron. 2012, 55, 1832–1843. [Google Scholar] [CrossRef]
- Cao, Q.J.; Han, Y.W.; Liang, T.W.; Wiercigroch, M.; Piskarev, S. Multiple buckling and codimension-three bifurcation phenomena of a nonlinear oscillator. Int. J. Bifurc. Chaos 2014, 24, 1430005. [Google Scholar] [CrossRef]
- Han, Y.W.; Cao, Q.; Chen, Y.S.; Wiercigroch, M. Chaotic thresholds for the piecewise linear discontinuous system with multiple well potentials. Int. J. Non-Linear Mech. 2015, 70, 145–152. [Google Scholar] [CrossRef]
- Han, Y.W.; Cao, Q.J.; Ji, J. Nonlinear dynamics of a smooth and discontinuous oscillator with multiple stability. Int. J. Bifurc. Chaos 2015, 25, 1530038. [Google Scholar] [CrossRef]
- Tian, R.L.; Wu, Q.L.; Yang, X.W.; Si, C.D. Chaotic threshold for the smooth-and-discontinuous oscillator under constant excitations. Eur. Phys. J. Plus 2013, 128, 80–91. [Google Scholar] [CrossRef]
- Yue, X.L.; Xu, W.; Wang, L. Stochastic bifurcations in the SD (smooth and discontinuous) oscillator under bounded noise excitation. Sci. China Phys. 2013, 56, 1010–1016. [Google Scholar] [CrossRef]
- Santhosh, B.; Padmanabhan, C.; Narayanan, S. Numeric-analytic solutions of the smooth and discontinuous oscillator. Int. J. Mech. Sci. 2014, 84, 102–119. [Google Scholar] [CrossRef]
- Chen, H. Global analysis on the discontinuous limit case of a smooth oscillator. Int. J. Bifurc. Chaos 2016, 26, 1650061. [Google Scholar] [CrossRef]
- Chen, H.B.; Jaume, L.; Tang, Y.L. Global dynamics of a SD oscillator. Nonlinear Dyn. 2018, 91, 1755–1777. [Google Scholar] [CrossRef]
- Wang, L.; Xue, L.; Xu, W.; Yue, X. Stochastic P-bifurcation analysis of a fractional smooth and discontinuous oscillator via the generalized cell mapping method. Int. J. Non-Linear Mech. 2017, 96, 56–63. [Google Scholar] [CrossRef]
- Chang, Y.J.; Chen, E.L.; Feng, M. Experimental study of the nonlinear dynamics of a smooth and discontinuous oscillator with different smoothness parameters and initial values. J. Theor. Appl. Mech. 2019, 57, 935–946. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Padovan, J.; Sawicki, J.T. Nonlinear vibrations of fractionally damped systems. Nonlinear Dyn. 1998, 16, 321–336. [Google Scholar] [CrossRef]
- Chang, Y.J.; Tian, W.W.; Chen, E.L.; Shen, Y.J.; Xing, W.C. Dynamic model for the nonlinear hysteresis of metal rubber based on the fractional-order derivative. J. Vib. Shock 2020, 39, 233–241. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Ann. Geophys. 1966, 19, 383–393. [Google Scholar] [CrossRef]
- Caputo, M. Linear model of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 2007, 13, 239–529. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Zaslavsky, G.M. Dynamics with low-level fractionality. Phys. A Stat. Mech. Its Appl. 2006, 368, 399–415. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Chen, E.; Tian, R.; Wang, C. The Nonlinear Dynamics Characteristics and Snap-Through of an SD Oscillator with Nonlinear Fractional Damping. Fractal Fract. 2022, 6, 493. https://doi.org/10.3390/fractalfract6090493
Wang M, Chen E, Tian R, Wang C. The Nonlinear Dynamics Characteristics and Snap-Through of an SD Oscillator with Nonlinear Fractional Damping. Fractal and Fractional. 2022; 6(9):493. https://doi.org/10.3390/fractalfract6090493
Chicago/Turabian StyleWang, Minghao, Enli Chen, Ruilan Tian, and Cuiyan Wang. 2022. "The Nonlinear Dynamics Characteristics and Snap-Through of an SD Oscillator with Nonlinear Fractional Damping" Fractal and Fractional 6, no. 9: 493. https://doi.org/10.3390/fractalfract6090493
APA StyleWang, M., Chen, E., Tian, R., & Wang, C. (2022). The Nonlinear Dynamics Characteristics and Snap-Through of an SD Oscillator with Nonlinear Fractional Damping. Fractal and Fractional, 6(9), 493. https://doi.org/10.3390/fractalfract6090493



