Solving Two-Sided Fractional Super-Diffusive Partial Differential Equations with Variable Coefficients in a Class of New Reproducing Kernel Spaces
Abstract
:1. Introduction
2. Main Notations
3. A Class of Fractional Reproducing Kernel Space
4. Representation of Solutions
5. Numerical Experiment
6. Conclusions and Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pal, K.; Fang, L.; Yan, Y. Finite difference method for two-sided space-fractional partial differential equations. In International Conference on Finite Difference Methods; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Tadjeran, M. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar]
- Aronszajn, N. Theory of reproducing kernels. Trans. Amer. Math. Soc. 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Cui, M.G. Two-dimensional reproducing kernel and surface interpolation. J. Comp. Math. 1986, 4, 177–181. [Google Scholar]
- Geng, F.Z.; Wu, X.Y. Reproducing kernel function-based Filon and Levin methods for solving highly oscillatory integral. Appl. Math. Comput. 2021, 397, 125980. [Google Scholar] [CrossRef]
- Li, X.Y.; Wu, B.Y. A kernel regression approach for identification of first order differential equations based on functional data. Appl. Math. Lett. 2022, 127, 107832. [Google Scholar] [CrossRef]
- Geng, F.Z.; Qian, S.P. An optimal reproducing kernel method for linear nonlocal boundary value problems. Appl. Math. Lett. 2018, 77, 49–56. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, Z. Solving a system of linear Volterra integral equations using the reproducing kernel method. Appl. Math. Comput. 2013, 219, 10225–10230. [Google Scholar] [CrossRef]
- Dai, D.D.; Ban, T.T.; Wang, Y.L.; Zhang, W. The piecewise reproducing kernel method for the time variable fractional order advection-reaction-diffusion equations. Therm. Sci. 2021, 25, 1261–1268. [Google Scholar] [CrossRef]
- Geng, F.Z.; Tang, Z.Q. Piecewise shooting reproducing kernel method for linear singularly perturbed boundary value problems. Appl. Math. Lett. 2016, 62, 1–8. [Google Scholar] [CrossRef]
- Arqub, O.A.; Maayah, B. Fitted fractional reproducing kernel algorithm for the numerical solutions of ABC-Fractional Volterra integro-differential equations. Chaos Solitons Fractals 2019, 126, 394–402. [Google Scholar] [CrossRef]
- Geng, F.Z.; Wu, X.Y. Reproducing kernel functions based univariate spline interpolation. Appl. Math. Lett. 2021, 122, 107525. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. J. Nonl. Scien. Appl. 2017, 10, 2607–2619. [Google Scholar] [CrossRef] [Green Version]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Wang, Y.L.; Du, M.J.; Tan, F.G. Using reproducing kernel for solving a class of fractional partial differential equation with non-classical conditions. Appl. Math. Comput. 2013, 219, 5918–5925. [Google Scholar] [CrossRef]
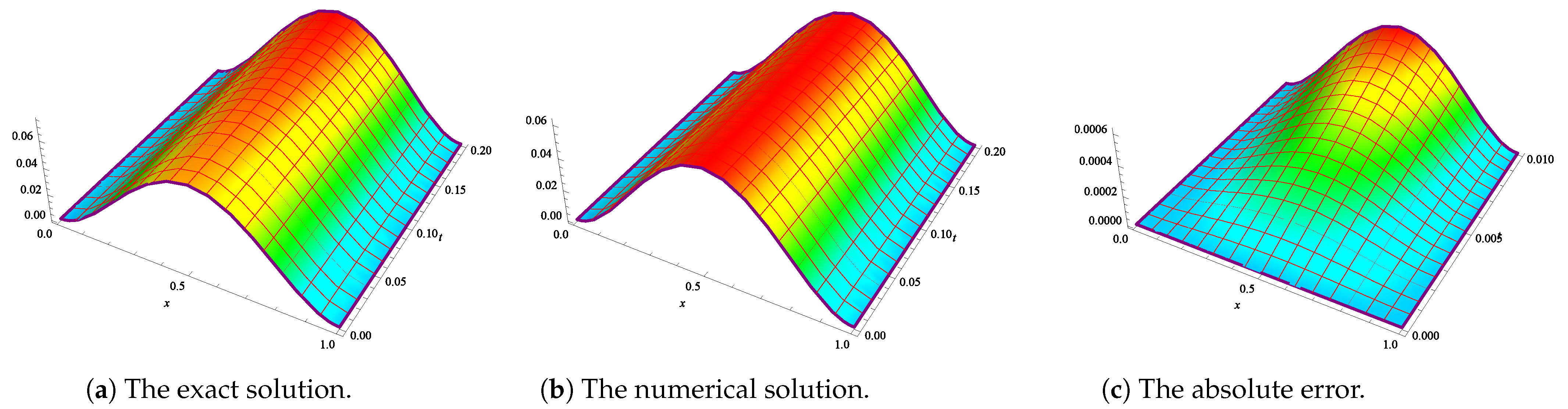
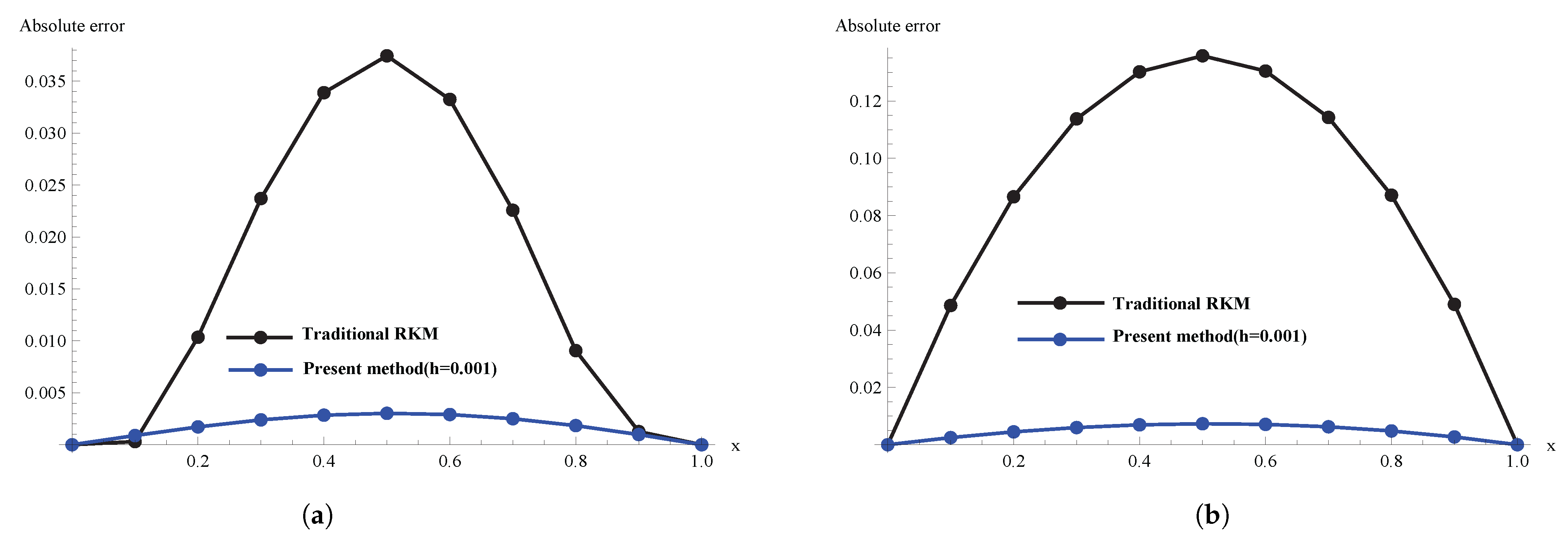
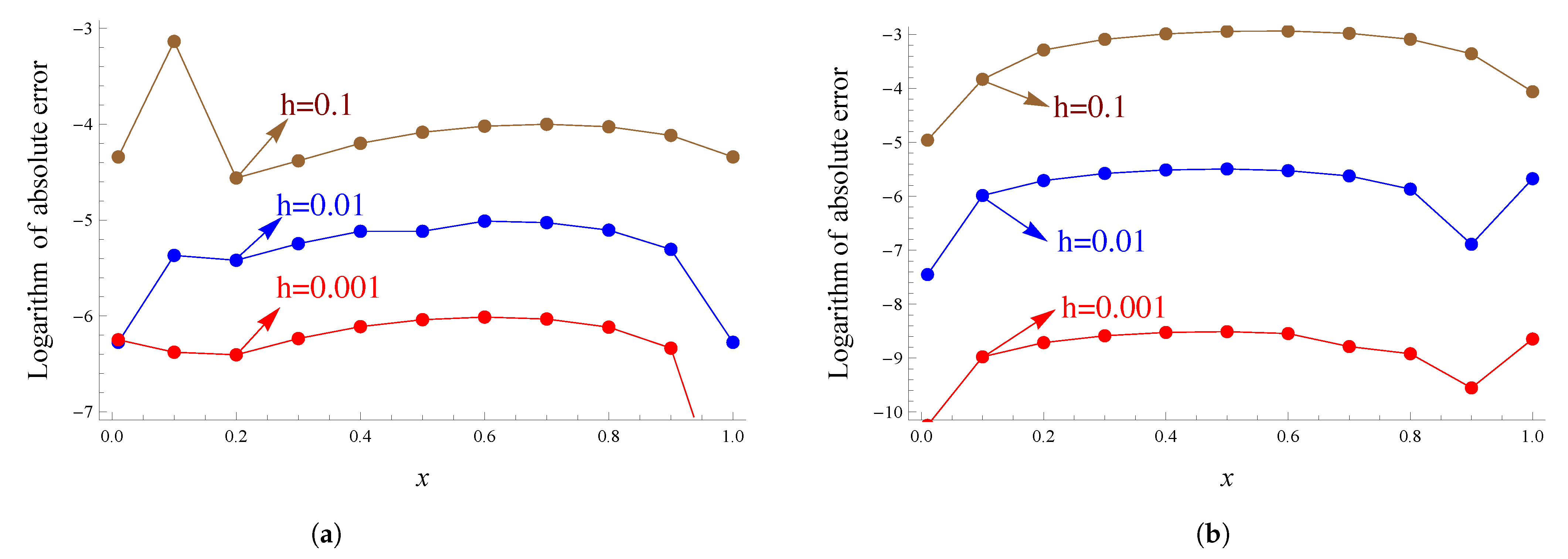
| m | |||
|---|---|---|---|
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 2 | |||
| 2 | |||
| 2 | |||
| 2 | |||
| 3 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 5 |
| Reproducing Kernel l () | Reproducing Kernel 2 () | |||||
|---|---|---|---|---|---|---|
| (0.1, 0.1) | 1.4440 × 10 | 2.8809 × 10 | 3.0098 × 10 | 1.4464 × 10 | 1.0353 × 10 | 1.0435 × 10 |
| (0.3, 0.3) | 2.0026 × 10 | 2.2921 × 10 | 2.3158 × 10 | 3.6627 × 10 | 1.1251 × 10 | 1.1362 × 10 |
| (0.5, 0.5) | 4.8845 × 10 | 5.0010 × 10 | 5.0002 × 10 | 1.1624 × 10 | 3.1989 × 10 | 3.0835 × 10 |
| (0.6, 0.6) | 6.1882 × 10 | 6.0286 × 10 | 5.9944 × 10 | 1.5634 × 10 | 4.0257 × 10 | 3.8357 × 10 |
| (0.7, 0.7) | 7.0611 × 10 | 6.4478 × 10 | 6.3604 × 10 | 1.8338 × 10 | 4.1408 × 10 | 3.8142 × 10 |
| (0.9, 0.9) | 6.3208 × 10 | 4.0652 × 10 | 3.7896 × 10 | 1.1447 × 10 | 3.4362 × 10 | 7.5174 × 10 |
| (1.0, 1.0) | 4.0413 × 10 | 4.7204 × 10 | 4.7920 × 10 | 2.8127 × 10 | 6.8379 × 10 | 7.3464 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, Q.; Wang, Y.; Li, X. Solving Two-Sided Fractional Super-Diffusive Partial Differential Equations with Variable Coefficients in a Class of New Reproducing Kernel Spaces. Fractal Fract. 2022, 6, 492. https://doi.org/10.3390/fractalfract6090492
Li Z, Chen Q, Wang Y, Li X. Solving Two-Sided Fractional Super-Diffusive Partial Differential Equations with Variable Coefficients in a Class of New Reproducing Kernel Spaces. Fractal and Fractional. 2022; 6(9):492. https://doi.org/10.3390/fractalfract6090492
Chicago/Turabian StyleLi, Zhiyuan, Qintong Chen, Yulan Wang, and Xiaoyu Li. 2022. "Solving Two-Sided Fractional Super-Diffusive Partial Differential Equations with Variable Coefficients in a Class of New Reproducing Kernel Spaces" Fractal and Fractional 6, no. 9: 492. https://doi.org/10.3390/fractalfract6090492
APA StyleLi, Z., Chen, Q., Wang, Y., & Li, X. (2022). Solving Two-Sided Fractional Super-Diffusive Partial Differential Equations with Variable Coefficients in a Class of New Reproducing Kernel Spaces. Fractal and Fractional, 6(9), 492. https://doi.org/10.3390/fractalfract6090492







