Collective Behaviors of Star-Coupled Harmonic Oscillators with Fluctuating Frequency in the Presence of Stochastic Resonance

Abstract

The stochastic resonance (SR) of a star-coupled harmonic oscillator subject to multiplicative fluctuation and periodic force in viscous media is studied. The multiplicative noise is modeled as a dichotomous noise and the memory of viscous media is characterized by a fractional power kernel function. By using the Shapiro–Loginov formula and Laplace transform, we obtain the analytical expressions of the first moment of the steady-state response and study the relationship between the system response and the system parameters in the long-time limit. The simulation results show the nonmonotonic dependence between the response output gain and the input signal frequency, the noise parameters of the system, etc., which indicates that the bona fide resonance and the generalized SR phenomena appear. Furthermore, the fluctuation noise, the number of particles, and the fractional order work together, producing more complex dynamic phenomena compared with the integral-order system. In addition, all the theoretical analyses are supported by the corresponding numerical simulations. We believe that the results that we have found may be a certain reference value for the research and development of the SR.

1. Introduction

Stochastic resonance (SR) is an important nonlinear phenomenon which has been paid considerable attention in the past few decades [1,2,3]. This phenomenon shows that appropriate noise can enhance the response of a system; therefore, it overturns people’s previous understanding that noise is only destructive [4,5,6]. In recent years, SR has been intensively investigated. In particular, early investigations indicate that three basic conditions must be met for SR to occur: (i) the nonlinearity of the system, (ii) a weak coherent signal, and (iii) a noise source [7,8,9]. Thus, early studies focused on nonlinear systems driven by additive white noise, while more recent works have found that multiplicative colored noise can lead to SR even in linear systems [10,11,12].

The classical integer-order Langevin equation inherits and develops Einstein’s theoretical research on Brownian motion and simplifies the fact of a large number of molecular collisions into the random perturbation force of the systems, which can be expressed as follows:

$$m\ddot{x}\left(t\right)+\gamma \dot{x}\left(t\right)=F\left(x\left(t\right)\right)+\eta \left(t\right)$$

(1)

Here, m represents the mass of the particle, and $x\left(t\right)$, $\dot{x}\left(t\right)$, and $\ddot{x}\left(t\right)$ are the displacement, the corresponding velocity, and the acceleration of the time-dependent particle. $m\ddot{x}\left(t\right)$ represents the inertia force, $\gamma \dot{x}\left(t\right)$ represents the damping force, and $F\left(x\right(t\left)\right)$ represents the deterministic driving force which usually contains the potential field force and the applied driving force. $\eta \left(t\right)$ is internal noise which will usually be modeled as Gaussian noise.

Considering the system disturbed by multiplicative noise, the potential field tends to fluctuate randomly (i.e., fluctuating frequency). For example, an ATP-ADP potential produced by the repeated binding-release cycle can be considered as a randomly fluctuating potential field [13,14,15]. For this reason, some scholars describe the fluctuating frequency by introducing multiplicative noise into the Langevin equation. In early studies, the fluctuating frequency of the system was often modeled as Gaussian white noise. This approach can simplify the solution of the model, but it ideally assumes the potential field of the system is in a Gaussian distribution. In fact, the potential field force of a real system usually exists in a color noise distribution. Therefore, we model the fluctuating frequency as a dichotomous noise in this paper. In particular, dichotomous noise can be reduced to Gaussian white noise or white shot noise under limited conditions [15,16].

Since most stochastic systems consist of particles that do not always work independently but operate in groups, the investigations of SR have been extended to coupled stochastic systems [17,18]. Until now, many significant results, such as mean-field-coupling-induced SR, coupling-induced cooperative behavior, coherent and coupling-enhanced resonance, etc., have been obtained by combining the study of SR with coupling systems. In addition, the investigations of coupled stochastic systems have suggested that both the noise and the coupling coefficient can affect the response of the system. Therefore, to study coupled systems’ SR behaviors and the influences of coupling is surely of great interest. To analyze the collective behavior, we introduce star-coupled oscillators, which can be regarded as special cases of many complex coupling systems, such as global coupling systems.

The SR phenomenon driven by frequency fluctuation in coupled- or single-oscillator(s) systems disturbed by multiplicative noise has been extensively explored by integer-order Langevin equations. The integer-order differential operator restricts the evolution state of the particle to the state of the present moment only. For example, in the above model (1), the term of the damping force is equivalent to the following expression:

$$\gamma \dot{x}\left(t\right)=\gamma {\int }_0^t\delta (t-\tau )\dot{x}\left(\tau \right)d\tau .$$

(2)

This means that the damping force is dependent only on its current velocity $\dot{x}\left(t\right)$. However, more studies indicate that in heterogeneous media, especially in viscous media and fluids with internal degrees of freedom, most physical and biochemical reaction processes show the power-law memory of historical states, which means the closer to the current moment, the stronger its memory and the greater the impact on the system.

Therefore, the following damping kernel function with power-law memory, which is the famous Caputo fractional derivative, is introduced [19,20]:

$${}_0{}^{C}D_t^{\alpha }x\left(t\right):=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\tau )}^{-\alpha }\dot{x}\left(\tau \right)d\tau ,(0<\alpha \le 1).$$

(3)

In fact, previous studies have shown that the change in fractional order $\alpha$ can effectively enlarge the resonance region and enhance the resonance intensity under certain circumstances [21,22,23,24,25,26]. Hence, it is interesting to study the roles of fractional order in a system’s dynamical behaviors.

From these above discussions, an intriguing and significant question arises naturally of whether the presence of the potential fluctuations and star coupling can affect the dynamical properties of overdamped Brownian particles. Regrettably, as far as we know, related research reports associated with star coupling systems are currently missing in the existing literature. To elaborate on this question, we firstly investigate a simple model for coupled Brownian particles moving in a harmonic potential driven by periodic force and the potential fluctuations generated by a dichotomous colored noise.

This paper is organized in five sections. After the introduction, the system model is solved analytically in Section 2. In Section 3 and Section 4, applying analytical results and numerical simulations, we discuss the impacts of system parameters, noise intensity, and external driving frequency on the output gain G, respectively. Finally, some conclusions are summarized in Section 5.

2. System Model and Methods

In this section, as the model of an $N+1$ star-coupled oscillatory system is subjected to fluctuation frequency and driven by periodic force, the generalized Langevin equations with power-law type memory friction kernel functions are considered as (in dimensionless form):

$$\left\{\begin{array}{c}{}_0{}^{C}D_t^{\alpha }{x}_0\left(t\right)=(\omega +{\xi }_t)x_0\left(t\right)+ϵ{\displaystyle \sum _{i=1}^n}(x_i-x_0)+A_{0}sin\left(\mathsf{\Omega }t\right);\hfill \\ {}_0{}^{C}D_t^{\alpha }{x}_k\left(t\right)=(\omega +{\xi }_t)x_k\left(t\right)+ϵ(x_0-x_k)+A_{0}sin\left(\mathsf{\Omega }t\right),k=1,2,\dots ,N.\hfill \end{array}\right.$$

(4)

Here, $x_i(i=0,1,2,\dots ,N)$ is the position of the ith particle at time t. Particularly, $x_0\left(t\right)$ and $x_i\left(t\right)$$(i\ne 0)$ represent the main particle and the general particles of the star-coupled oscillator, respectively (see Figure 1). The oscillators interact with each other through a linear coupling term $ϵ(x_0-x_i)$ or $ϵ{\sum }_{i=1}^n(x_i-x_0)$, and $ϵ$ is called the coupled coefficient. Moreover, the whole system is driven by the external periodic force $A_{0}sin\left(\mathsf{\Omega }t\right)$, with $A_0$ representing the amplitude and frequency, respectively.

Furthermore, ${\xi }_t$ is a symmetric dichotomous noise that randomly switches between two values $\pm \sigma (\sigma >0)$ with the mean value and correlation functions:

$$〈{\xi }_t〉=0,$$

(5)

and

$$〈{\xi }_t{\xi }_{\tau }〉={\sigma }^{2}exp(-\lambda |t-\tau \left|\right),$$

(6)

respectively. Here, $\lambda$ denotes the noise correlation rate.

For coupled particles with dichotomous noise in the dynamical system, we introduce star-coupled particles in a randomly switching potential. Hence, the fluctuation potential can be modeled as $(\omega +{\xi }_t)x_0\left(t\right)$ or $(\omega +{\xi }_t)x_i\left(t\right)$. Here, $\omega \ge 0$ is the intrinsic frequency of the system that is disturbed by the potential fluctuation ${\xi }_t$. In this manuscript, ${\xi }_{\left(t\right)}$ is modeled as a dichotomous Markov process, which is also called random telegraph noise.

2.1. Synchronization

To discuss the collective behavior of the coupled system, we firstly introduce the mean field defined as following formula:

$$S=\frac{{\sum }_{i=0}^N{x}_i}{N+1}$$

(7)

Here, S is a profile of the average displacement of all the $N+1$ particles.

By averaging all $N+1$ equations statistically with the mean field S, we have

$$D^{\alpha }S+(\omega +{\xi }_t)S=A_{0}sin\left(\mathsf{\Omega }t\right).$$

(8)

Next, we analyze the SR behavior of the coupling system based on the system model and the mean field equation in (8). Firstly, we need to check whether or not the average behaviors of the $N+1$ particles are synchronous. We know from previous studies that the stable response of the mean field is a sinusoidal wave, and thus the synchronization of the single particles is further considered, including both the main particle and the general particles in the coupled system.

2.1.1. Synchronization between the Main Particle and the Mean Field

Firstly, we consider the main particle which is governed by the following equation:

$$D^{\alpha }{x}_0+(\omega +{\xi }_t)x_0=ϵ\sum _{i=1}^N(x_i-x_0)+A_{0}sin\left(\mathsf{\Omega }t\right).$$

(9)

Denoting the deviation of the main particle’s displacement from the mean field as ${\Delta }_0=x_0-S$, using Equation (9) minus Equation (8) yields

$$D^{\alpha }{\Delta }_0+(\omega +{\xi }_t){\Delta }_0=ϵ\sum _{i=1}^N(x_i-x_0).$$

(10)

Note that

$${\Delta }_0=x_0-\frac{1}{N+1}\sum _{i=0}^N{x}_i=\frac{1}{N+1}\sum _{i=1}^N(x_0-x_i),$$

(11)

Then we have

$$\sum _{i=1}^N(x_i-x_0)=-{\Delta }_0(N+1).$$

(12)

Inserting Equation (12) into Equation (10) and simplifying the observed equation, we have

$$D^{\alpha }{\Delta }_0+[\omega +{\xi }_t+ϵ(N+1)]{\Delta }_0=0.$$

(13)

with the condition of the stability criterion of (10):

$${\sigma }^2<{[\omega +ϵ(N+1)]}^2+{\lambda }^{\alpha }[\omega +ϵ(N+1)],$$

(14)

Since Equation (13) is a homogeneous equation, it must have a zero solution which is globally and asymptotically stable when Equation (13) satisfies the condition of the stability criterion in Equation (14). Therefore, when $t\to \infty$, we have

$$\langle {\Delta }_0\rangle =0.$$

(15)

This indicates that the main particle will synchronize with the mean field of the system in expectation when the evolution time is long enough. In this paper, Inequality (14) is called the synchronous criterion of the main particle. This is one of the main results of this study.

2.1.2. Synchronization between the General Particles and the Mean Field

In this section, we further consider a general particle of the system equation in (1), say, the nth particle, which is governed by the following equation:

$$D^{\alpha }{x}_n+(\omega +{\xi }_t)x_n=ϵ(x_0-x_n)+A_{0}sin\left(\mathsf{\Omega }t\right),n=1,2,\dots ,N,$$

(16)

Let ${\Delta }_n=x_n-S$. Subtracting Equation (16) from Equation (8), we observe

$$D^{\alpha }{\Delta }_n+(\omega +{\xi }_t){\Delta }_n=ϵ(x_0-x_n).$$

(17)

When the synchronous criterion (14) of the main particle is satisfied, $x_0=S$ almost everywhere as t goes to infinity. Therefore, Equation (17) can be rewritten as:

$$D^{\alpha }{\Delta }_n+(\omega +{\xi }_t+ϵ){\Delta }_n=0.$$

(18)

Comparing with Equation (13), we obtain the first moment of the general particle’s deviation in the long-time limit $t\to \infty$

$$\langle {\Delta }_n\rangle =0,$$

(19)

and the corresponding synchronous condition of the general particle

$${\sigma }^2<{(\omega +ϵ)}^2+{\lambda }^{\alpha }(\omega +ϵ).$$

(20)

Since Inequality (20) holds, Inequality (14) must hold. Therefore, we call (20) the global synchronization condition and let

$${\sigma }_s^2={(\omega +ϵ)}^2+{\lambda }^{\alpha }(\omega +ϵ).$$

(21)

When the system satisfies the global synchronous condition, all the particles, including the main particle and the general particles, are synchronous with the main field of the system S as t becomes larger than a certain threshold.

Furthermore, the results Equations (15) and (19) show that the mean field is equal to the average of any single particle’s position in a certain threshold. This conclusion allows us to study the single particle through the mean field. Thus, in the rest of this paper, the behaviors of the mean field are analyzed and these analyses are the main basis of the SR research in Section 4.

2.2. The Output Amplitude Gain of the Mean Field

The output amplitude gain (OAG) is very important for system dynamics analysis. Therefore, based on the completely synchronous condition given in Inequality (20), we calculate $〈S〉$ and then derive an analytical expression of OAG in this section. Then, we firstly average all realizations of the trajectory in Equation (8), and thus we obtain

$$D^{\alpha }〈S〉+\omega 〈S〉+〈{\xi }_{t}S〉=A_{0}sin\left(\mathsf{\Omega }t\right).$$

(22)

Since Equation (22) contains a new correlator, $〈{\xi }_{t}S〉$, we establish another equation by multiplying Equation (8) by ${\xi }_t$ and averaging the obtained equation, which yields

$$〈{\xi }_t{D}^{\alpha }S〉+\omega 〈{\xi }_{t}S〉+{\sigma }^2〈S〉=0.$$

(23)

Using the well-known Shapiro–Loginov formulas [27], we have

$$〈{\xi }_t{D}^{\alpha }S〉=e^{-\lambda t}{D}^{\alpha }\left({\xi }_{t}S{e}^{\lambda t}\right).$$

(24)

Inserting Equation (24) into Equation (23), we obtain the following expression:

$$e^{\lambda t}{D}^{\alpha }\left({\xi }_{t}S{e}^{\lambda t}\right)+\omega 〈{\xi }_{t}S〉+{\sigma }^2〈S〉=0.$$

(25)

Let $y_1=〈S〉$ and $y_2=〈{\xi }_{t}S〉$. We obtain closed equations for two variables $y_1$ and $y_2$ according to Equations (22) and (25):

$$\left\{\begin{array}{c}{D}^{\alpha }{y}_1+\omega y_1+y_2=A_{0}sin\left(\mathsf{\Omega }t\right),\hfill \\ e^{\lambda t}{D}^{\alpha }\left(y_2{e}^{\lambda t}\right)+\omega y_2+{\sigma }^2{y}_1=0.\hfill \end{array}\right.$$

(26)

Then the corresponding characteristic equation of (26) is

$$(s^{\alpha }+\omega )({(s+\lambda )}^{\alpha }+\omega )-{\sigma }^2=0.$$

(27)

According to the Routh–Hurwitz criterion, we obtain the necessary and sufficient condition of the stability criterion of Equation (26):

$${\sigma }^2<{\omega }^2+\omega {\lambda }^{\alpha }$$

(28)

Especially when $\alpha =1$, (28) will degrade into the stability criterion of the integer-order system. Applying the Laplace transform technique to the closed Equations (22) and (25), we have:

$$C\left(\begin{array}{c}{Y}_1\\ Y_2\end{array}\right)=\left(\begin{array}{c}{s}^{\alpha -1}{y}_1\left(0\right)+\frac{A_0\mathsf{\Omega }}{s^2+{\mathsf{\Omega }}^2}\\ {(s+\lambda )}^{\alpha -1}{y}_2\left(0\right)\end{array}\right)$$

(29)

Here, $Y_1$ and $Y_2$ are the Laplace transformations of $y_1$ and $y_2$ and $y_1\left(0\right)$ and $y_2\left(0\right)$ are the initial conditions. $C=\left(c_{ij}\right),i=1,2,j=1,2$, and

$$C=\left(\begin{array}{cc}{s}^{\alpha }+\omega & 1\\ {\sigma }^2& {(s+\lambda )}^{\alpha }+\omega \end{array}\right)$$

(30)

Solving Equation (29), we obtain

$$Y_1\left(s\right)=H_1\left(s\right)y_1\left(0\right)-H_2\left(s\right)y_2\left(0\right)+H_0\frac{A_0\mathsf{\Omega }}{s^2+{\mathsf{\Omega }}^2},$$

(31)

where

$$\begin{array}{cc}\hfill H_0& =\frac{c_{22}}{c_{11}{c}_{22}-c_{12}{c}_{21}},\hfill \\ \hfill H_1& =\frac{-c_{21}}{c_{11}{c}_{22}-c_{12}{c}_{21}}{s}^{\alpha -1},\hfill \\ \hfill H_2& =\frac{-c_{12}}{c_{11}{c}_{22}-c_{12}{c}_{21}}{(s+\lambda )}^{\alpha -1}.\hfill \end{array}$$

(32)

Solving Equation (31) and applying the inverse Laplace transform to Equation (29),

$$〈S〉=y_1=A_0{\int }_0^t{h}_0(t-\tau )sin\left(\mathsf{\Omega }\tau \right)d\tau .$$

(33)

Here, $h_0$ is the inverse Laplace transform of $H_0$.

Therefore, the first moment $〈S〉$ of the stable-state mean field system can be considered as the output of the linear time-invariant system (8) with the transform function $h_0\left(t\right)$. On the other hand, according to the response theory of a linear time-invariant system, the output can be written as:

$$〈S〉=A_0\left|H_0\left(j\mathsf{\Omega }\right)\right|sin(\mathsf{\Omega }t+\varphi ).$$

(34)

where j is the imaginary unit which means $j^2=-1$ and $A_1=A_0\left|H_0\left(j\mathsf{\Omega }\right)\right|$ and $\varphi$ are the amplitude and the phase angle of $〈S〉$, respectively. Moreover,

$$\left|H_0\right(j\mathsf{\Omega }\left)\right|=\sqrt{\frac{f_1^2+f_2^2}{f_3^2+f_4^2}},\varphi =arctan\left(\frac{f_2{f}_3-f_1{f}_4}{f_1{f}_3+f_2{f}_4}\right).$$

(35)

Finally, we obtain the output gain (OAG) of the mean field:

$$G=\frac{A_1}{A_0}=\left|H_0\left(j\mathsf{\Omega }\right)\right|=\sqrt{\frac{f_1^2+f_2^2}{f_3^2+f_4^2}}.$$

(36)

where the explicit expression of $f_i(i=1,2,3,4)$ is given below:

$$\begin{array}{cc}\hfill & f_1=r^{\alpha }cos\left(\alpha \theta \right),\hfill \\ \hfill & f_2=r^{\alpha }sin\left(\alpha \theta \right),\hfill \\ \hfill & f_3=r^{\alpha }{\mathsf{\Omega }}^{\alpha }cos(\alpha \theta +\frac{\alpha \pi }{2})+\omega {\mathsf{\Omega }}^{\alpha }cos\left(\frac{\alpha \pi }{2}\right)+\omega f_1+{\omega }^2-{\sigma }^2,\hfill \\ \hfill & f_4=r^{\alpha }{\mathsf{\Omega }}^{\alpha }sin(\alpha \theta +\frac{\alpha \pi }{2})+\omega {\mathsf{\Omega }}^{\alpha }sin\left(\frac{\alpha \pi }{2}\right)+\omega f_2,\hfill \\ \hfill & r=\sqrt{{\mathsf{\Omega }}^2+{\lambda }^2},\hfill \\ \hfill & \theta =arctan\left(\frac{\mathsf{\Omega }}{\lambda }\right).\hfill \end{array}$$

(37)

It should be noted that the results in this section recover the previously published results for a single oscillator without any memory effect when both $ϵ=0$ and $\alpha =1$.

3. Collective Behaviors of the Coupled System

The analytical expressions of the system are too complex to be intuitively understood. Therefore, in this section, the collective behaviors of the coupled system based on the above results are provided through the corresponding accurate analytical expressions. Based on the previous theoretical results and numerical analyses, we firstly discuss the stability criterion.

The general stability criterion satisfies (28). In fact, the general criterion for stability is that all the roots of the characteristic equation of Equation (26), seeing that $\left|D\right(\alpha \left)\right|=0$, have negative real parts. This requires the system parameters to satisfy stability conditions which can be induced by the well-known Routh–Hurwitz theorem. In the following discussion, all the groups of parameters satisfy the stable condition.

Next, we focus on the synergistic effect of the fractional order $\alpha$ and the noise intensity $\sigma$ and the noise correlation rate $\lambda$ on SR behavior, including the bona fide resonance (BSR) [28] presented by adjusting the external driving frequency with fixed system parameters, the conventional stochastic resonance (CSR) presented by adjusting the noise intensity with fixed system parameters, and the parameter-induced stochastic resonance (PSR) by adjusting the system parameters.

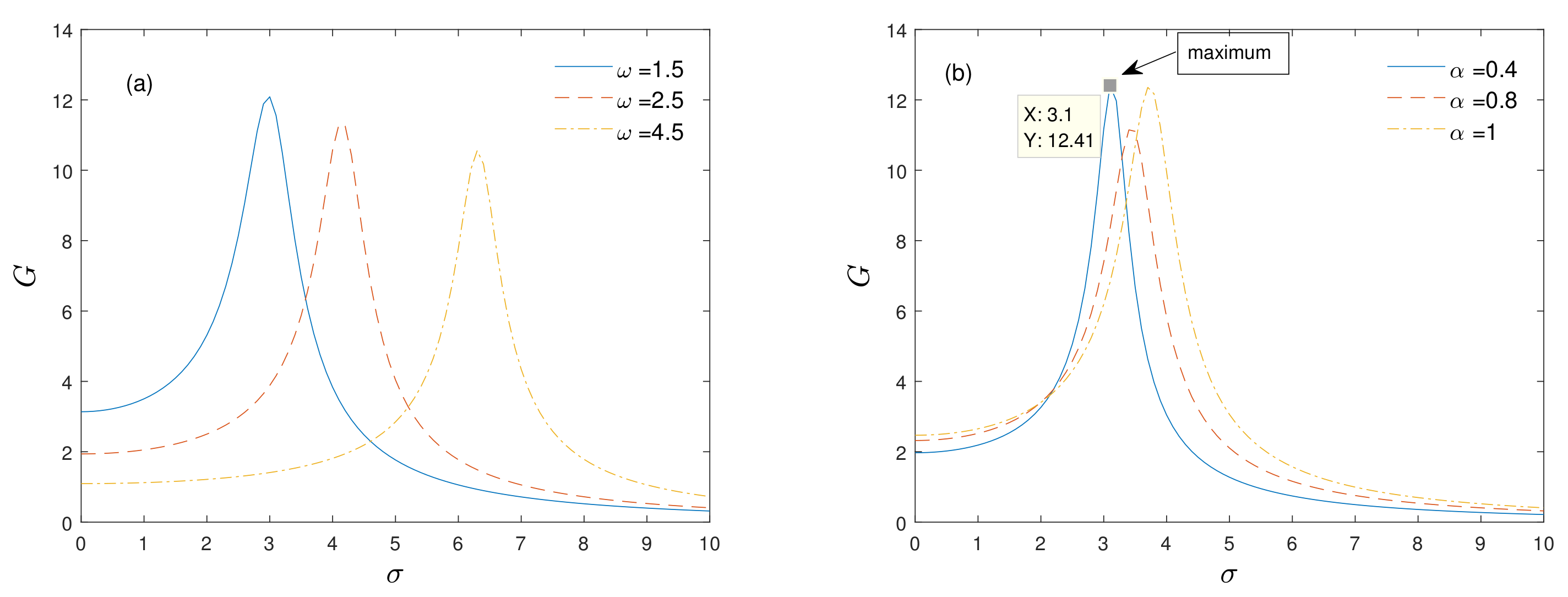
3.1. Bona Fide Stochastic Resonance: BSR

In Figure 2, the relationship between the OAG of the mean field and the external driving frequency $\mathsf{\Omega }$ has been displayed. From the curves of different noise correlation coefficients $\lambda$ and the fractional order $\alpha$, it can be seen that in all the cases, the OAG shows nonmonotonic dependence on $\mathsf{\Omega }$, which indicates that the BSR phenomenon has occurred. In Figure 2a, increasing the noise correlation coefficient $\lambda$ while the other parameters remain unchanged, we find the one-peak and one-valley SR which was rarely reported in the single-particle system. Moreover, when $\lambda =2$, the BSR disappears. This effect comes from the fact that since $\lambda$ increases, the correlation time decreases, and then the oscillators constantly jump from one state to the other and the time to build up a proper response to an external field might be insufficient; therefore, the SR disappears. In Figure 2b,c, when the parameters $\sigma$ and $\omega$ take appropriate values, the output gain G will cause obvious SR phenomena to occur, but when these two parameters are smaller or larger than some threshold, the SR will vanish. In Figure 2d, with the increase in $\alpha$, the maximum value of SR decreases and the formant position gradually shifts to the right. These phenomena indicate that the memory effect can enhance the SR behavior. In general, the case of a coupled oscillator with fluctuation frequency can contribute to the existence of classical BSR, but it can also contribute to one-peak and one-valley BSR.

3.2. Conventional Stochastic Resonance: CSR

We provide the $G-\sigma$ in Figure 3 to analyze the influence of the noise intensity $\sigma$ on the CSR under different values of $\omega$ and $\alpha$. Figure 3a shows that as $\omega$ increases, the resonance curves switch to the right hand and the peak value decreases, which indicates that increasing $\omega$ can weaken the resonance intensity. From Figure 3b, the resonance curve decreases almost linearly with the increase in the fractional order $\alpha$ under some conditions, namely, CSR becomes weak. When $\alpha =0.3$, the curves exhibit the biggest resonance peak. On the other hand, the above results are consistent with the result shown in Figure 2d, that is, changing $\alpha$ can control the emergence of SR.

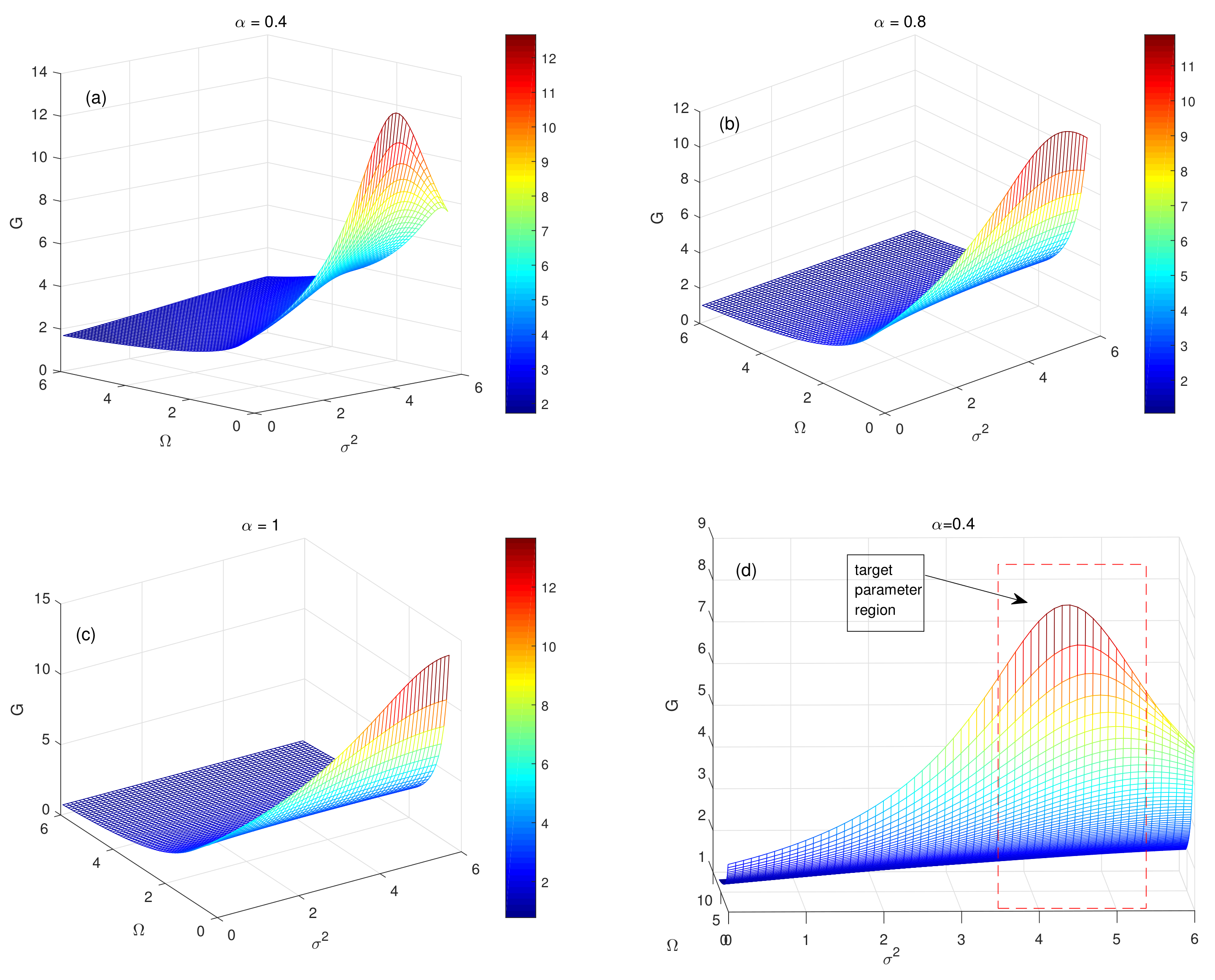
3.3. Parameter-Induced Stochastic Resonance: PSR

We already know from Figure 2 and Figure 3 that both $\mathsf{\Omega }$ and $\sigma$ affect the SR phenomenon significantly, respectively. A natural thought is how these two parameters can synergistically influence the steady-state output gain of the system under other parameters. In Figure 4, we discuss the dependence of the output gain G on the parameters $\mathsf{\Omega }$, $\sigma$, as well as $\alpha$. As shown in Figure 4, for a fixed $\alpha$ all the curves show that the evolution of G with $\mathsf{\Omega }$ and $\sigma$ presents nonmonotonous behaviors, which indicates a typical resonance structure, i.e., the parameter-induced SR phenomenon occurs. It is noticed that with the increase in $\alpha$, the intensity of the SR of G gradually decreases until the SR phenomenon disappears when $\alpha =1$. In other words, there is no SR phenomenon when the memory effect is ignored in the classical integer-order Langevin equation system.

4. Numerical Simulation

In order to verify the correctness of the theoretical results, the evolutions of the particles depicted by the system model equation in (4) were simulated by numerical simulation. In addition to that, we used MATLAB R2020b as the simulation tool. Specifically, the numerical simulations of the system are presented to check whether the theoretical results containing Equations (15), (19) and (36) are in accordance with the numerical simulations. For the numerical simulation, we applied the fractional predictor-corrector method [29,30], and the simulation parameters were: simulation duration $t=15$, time step $dt=0.01$, and simulation time $N=3000$. Moreover, we assumed that the initial positions of all the particles in the system obeyed the normal distribution with mean zero and standard deviation one.

Firstly, in Figure 5a,b, due to the influence of noise, the evolution of the system at the initial stage has great randomness, but as time goes on, all particles, including the main particle and the general particles, achieve synchronization, which is in good consistency with our analytical conclusions of Equations (15) and (19). Moreover, we mention that the coupling only affects the relaxation time for synchronization, and the essential reason for the synchronization is the uniform influence of the randomly switching potential, which can be inferred from Inequality (14) by using a zero-coupling intensity. As a result, in the stationary regime, we can analyze the behavior of all of the particles just by analyzing the mean field. Therefore, in the previous and subsequent discussions, we focus on the dynamic behaviors of the mean field.

Secondly, in Figure 5c,d, the red solid line depicts the theoretical trajectory of the first moment of the mean field, which is a sine wave expressed by Equation (36). We all see the realizations of the deviation are zero in the long-time regime except for a set of measure zero, showing that every single particle of Equation (4) is almost synchronized with the mean field S after a certain time. This indicates the theoretical analyses are consistent with the corresponding numerical simulations. Furthermore, we infer that particles with different initial conditions will move together with the mean field in the stationary regime.

5. Discussion and Conclusions

To summarize, we have explored, in the long-time regime, the collective behaviors of coupled oscillators with frequency fluctuation driven by periodic signal in the presence of the SR phenomenon. The coupling form is the star-coupled oscillator, and the frequency fluctuation is modeled as a dichotomous noise. We detect three different forms of SRs existing in this system: the bona fide SR, the conventional SR, and the parameter-induced SR. Specially, the one-peak and one-valley SR phenomenon between G and $\mathsf{\Omega }$ has not been reported in classical Langevin systems before. Moreover, we find that there is no SR phenomenon when the memory effect is ignored, i.e., $\alpha =1$. Importantly, we can enhance the SR phenomenon by appropriately controlling the values in the proposed system, which has potential implications in the real world.

It has been found that the stochastic resonance of the fractional coupled oscillator has more important and abundant SR behaviors than the integer-order and single oscillator. With the proper adjustments of the parameters mentioned above, we can effectively control the SR of the system within a certain range and further broaden the application scope of the SR phenomenon in some fields.