Local Fractional Homotopy Perturbation Method for Solving Coupled Sine-Gordon Equations in Fractal Domain
Abstract
1. Introduction
2. Local Fractional Calculus
2.1. Local Fractional Derivatives
2.2. Local Fractional Integral
2.3. Basic Operation
3. Local Fractional Homotopy Perturbation Method
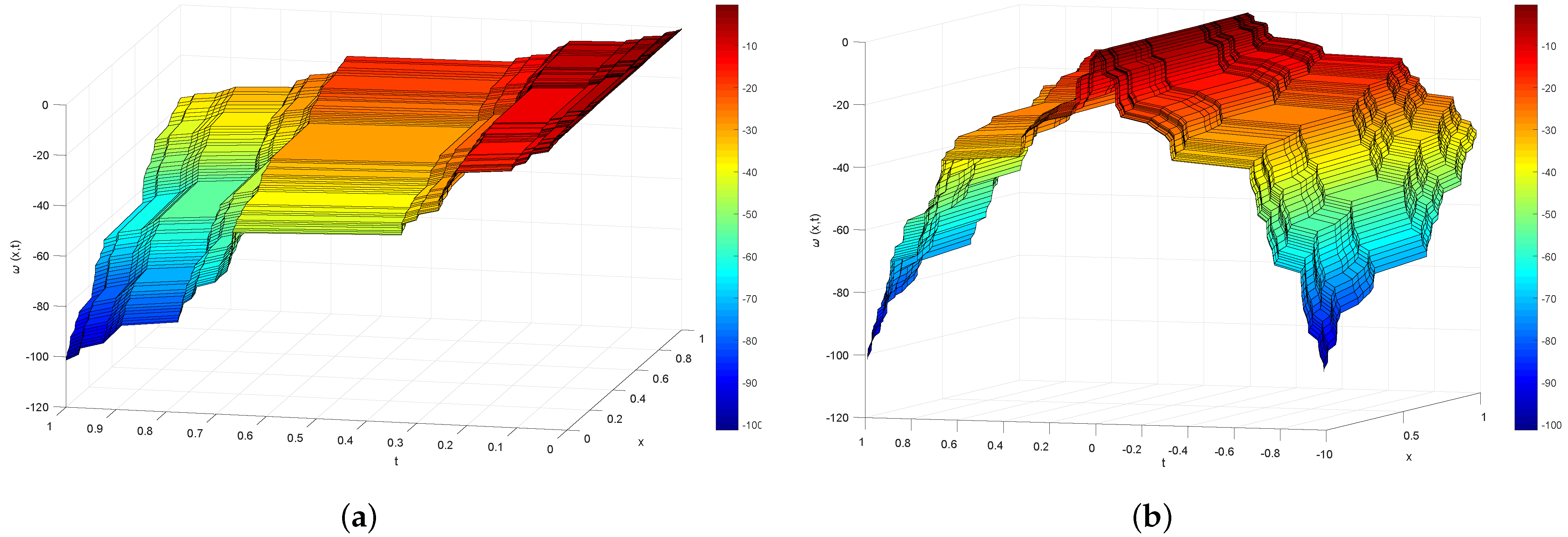
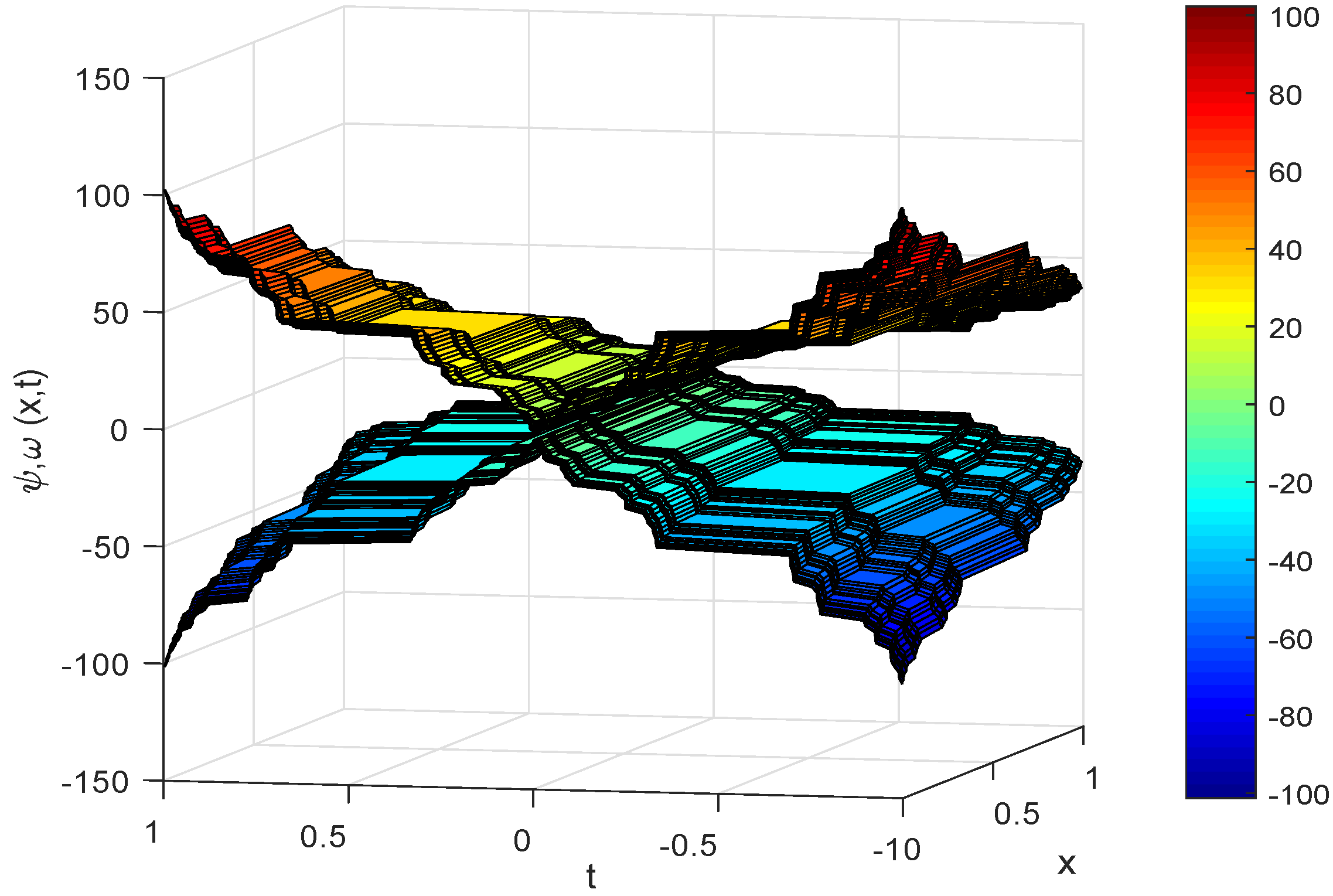
4. Solution of System of Equations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HPM | homotopy perturbation method |
| LFHP | local fractional homotopy perturbation |
References
- Charpentier, I. On Higher-order Differentiation in Nonlinear Mechanics. Optim. Methods Softw. 2012, 27, 221–232. [Google Scholar] [CrossRef]
- Viana, R.L.; Silva, E.; Kroetz, T.; Caldas, I.T.; Roberto, M.; Sanjuan, A.F. Fractal Structures in Nonlinear Plasma Physics. Philos. Trans. R. Soc. A 2011, 369, 371–395. [Google Scholar] [CrossRef] [PubMed]
- Kalashnikov, A.S. The Propagation of Disturbances in Problem of Nonlinear Heat Conduction with Absorption. Comput. Math. Math. Phys. 1974, 14, 70–85. [Google Scholar] [CrossRef]
- Chowdhury, A.R.; Pal, S.K. N-fold Backlund Transformation for Deformed Nonlinear Schrödinger Equation. Int. J. Theor. Phys. 1997, 36, 1021–1031. [Google Scholar] [CrossRef]
- Liu, W.J.; Tian, B.; Zhang, H.Q.; Li, L.L.; Xue, Y.S. Soliton Interaction in the Higher-order Nonlinear Schrodinger equation Investigated with Hirota’s Bilinear Method. Phys. Rev. E 2008, 77, 066605. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A Sine-cosine Method for Handling Nonlinear Wave Equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R.K. An Approximate Solution of a Nonlinear Fractional Differential Equation by Adomian Decomposition Method. Appli. Math. Comp. 2005, 167, 561–571. [Google Scholar]
- Askari, H.; Zhang, D.; Esmailzadeh, E. Periodic Solutions for Nonlinear Oscillations of Nanowires Using Variational Iteration Method. In Proceedings of the 2013 13th IEEE International Conference on Nanotechnology (IEEE-NANO 2013), Beijing, China, 5–8 August 2013. [Google Scholar]
- Wu, X.H.; He, J.H. EXP-function Method and its Application to Nonlinear Equations. Chaos Solitons Fractals 2008, 38, 903–910. [Google Scholar]
- Rajabi, A.; Ganji, D.D.; Taherian, H. Application of Homotopy Perturbation Method in Nonlinear Heat Conduction and Convection Equations. Phys. Lett. 2007, 360, 570–573. [Google Scholar] [CrossRef]
- Asllanaj, F.; Jeandel, G.; Roche, J.R. Numerical Solution of Radiative Transfer Equation Coupled with Nonlinear Heat Conduction Equation. Int. J. Numer. Methods Heat Fluid Flow 2015, 11, 449–473. [Google Scholar] [CrossRef]
- He, J.H. Application of Homotopy Perturbation Method to Nonlinear Wave Equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- Ganji, D.D.; Sadighi, A.; Ganjavi, B. Traveling Wave Solutions of the Sine-gordon and the Coupled Sine-gordon Equations Using the Homotopy-perturbation Method. Sci. Iran. 2009, 16, 189–195. [Google Scholar]
- Mustafa Inc. He’s Homotopy Perturbation Method for Solving Korteweg-de Vries Burgers Equation with Initial Condition. Numer. Methods Partial. Differ. Equ. 2010, 26, 1224–1235. [Google Scholar]
- Ganji, D.D. The Application of He’s Homotopy Perturbation Method to Nonlinear Equations Arising in Heat Transfer-Science Direct. Phys. Lett. A 2006, 355, 337–341. [Google Scholar] [CrossRef]
- Ganji, D.D.; Sadighi, A. Application of He’s Homotopy-perturbation Method to Nonlinear Coupled Systems of Reaction-diffusion Equations. Int. J. Nonlinear Sci. Num. Simul. 2006, 7, 411–418. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; Orld Science: New York, NY, USA, 2012. [Google Scholar]
- Yang, X.J.; Srivastava, H.M.; Cattani, C. Local Fractional Homotopy Perturbation Method for Solving Fractal Partial Differential Equation Arising in Mathematical Physics. Rom. Rep. Phys. 2015, 67, 752–761. [Google Scholar]
- Zhang, Y.; Carlo, C. and Yang, X.J. Local Fractional Homotopy Perturbation Method for Solving Non-Homogeneous Heat Conduction Equations in Fractal Domains. Entropy 2015, 17, 6753–6764. [Google Scholar] [CrossRef]
- Braun, O.M.; Kivshar, Y.S. Nonlinear Dynamics of the Frenkel-Kontorova Model with Impurities. Phys. Rev. B Condens Matter 1998, 306, 1060–1073. [Google Scholar] [CrossRef]
- Saha, S.; Ray. A Numerical Solution of the Coupled Sine-Gordon Equation Using the Modified Decomposition Method. Appl. Math. Comput. 2006, 175, 1046–1054. [Google Scholar]
- Hosseini, K.; Mayeli, P.; Kumar, D. New exact solutions of the coupled sine-Gordon equations in nonlinear optics using the modified Kudryashov method. J. Mod. Opt. 2017, 65, 361–364. [Google Scholar] [CrossRef]
- Salas, A.H. Exact Solutions of Coupled Sine-Gordon Equations. Nonlinear Anal.-Real 2010, 11, 3930–3935. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Liu, H.H.; Yang, Y.J. Exact Solutions for the Coupled Sine-Gordon Equations by a New Hyperbolic Auxiliary Function Method. Appl. Math. Sci. 2011, 5, 1621–1629. [Google Scholar]
- Yang, X.J.; Machado, J.A.T.; Hristov, J. Nonlinear Dynamics for Local Fractional Burgers’ equation Arising in Fractal Flow. Nonlinear Dyn. 2016, 84, 3–7. [Google Scholar] [CrossRef]
- Ghanbari, B. On Novel Nondifferentiable Exact Solutions to Local Fractional Gardner’s Equation Using an Effective Technique. Math. Method Appl. Sci. 2021, 44, 4673–4685. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.T.; Baleanu, D.; Cattani, C. On Exact Traveling-wave Solutions for Local Fractional Korteweg-de Vries Equation. Chaos 2016, 26, 110–118. [Google Scholar] [CrossRef]
- Yang, X.J. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Quintero, R.N.; Sánchez, A. Ac driven sine-Gordon solitons: Dynamics and stability. Eur. Phys. J. B 1998, 6, 133–142. [Google Scholar] [CrossRef][Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Liu, Q. Local Fractional Homotopy Perturbation Method for Solving Coupled Sine-Gordon Equations in Fractal Domain. Fractal Fract. 2022, 6, 404. https://doi.org/10.3390/fractalfract6080404
Chen L, Liu Q. Local Fractional Homotopy Perturbation Method for Solving Coupled Sine-Gordon Equations in Fractal Domain. Fractal and Fractional. 2022; 6(8):404. https://doi.org/10.3390/fractalfract6080404
Chicago/Turabian StyleChen, Liguo, and Quansheng Liu. 2022. "Local Fractional Homotopy Perturbation Method for Solving Coupled Sine-Gordon Equations in Fractal Domain" Fractal and Fractional 6, no. 8: 404. https://doi.org/10.3390/fractalfract6080404
APA StyleChen, L., & Liu, Q. (2022). Local Fractional Homotopy Perturbation Method for Solving Coupled Sine-Gordon Equations in Fractal Domain. Fractal and Fractional, 6(8), 404. https://doi.org/10.3390/fractalfract6080404





