Permeability Prediction of Saturated Geomaterials with Revised Pore–Solid Fractal Model and Critical Path Analysis
Abstract
:1. Introduction
2. Revised PSF Model
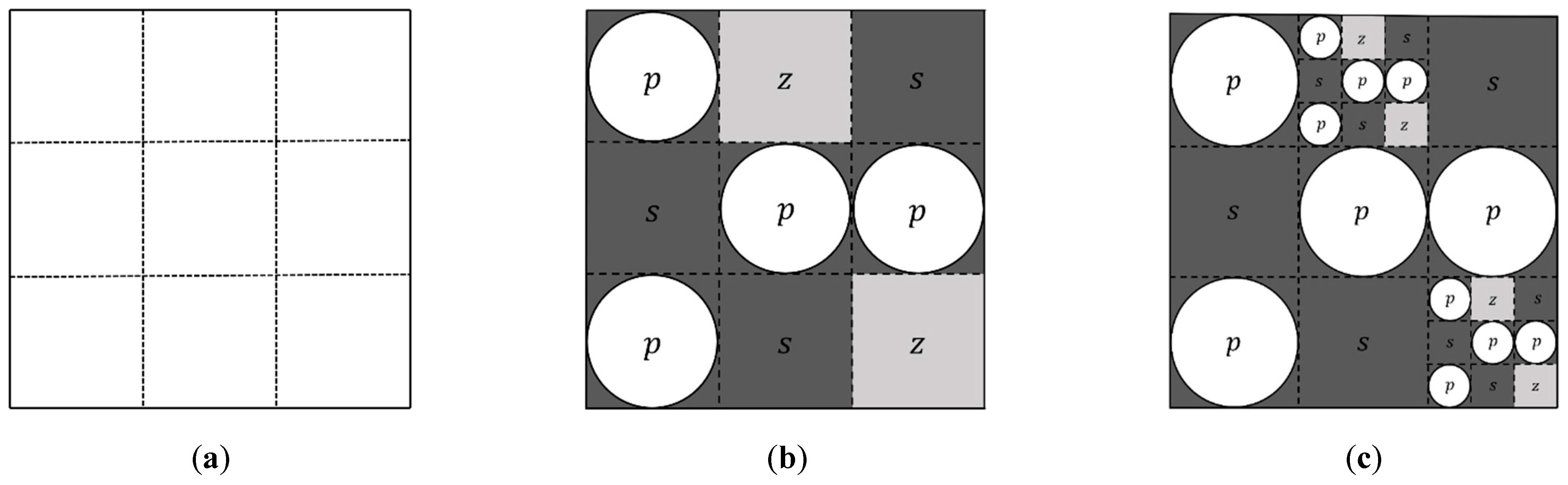
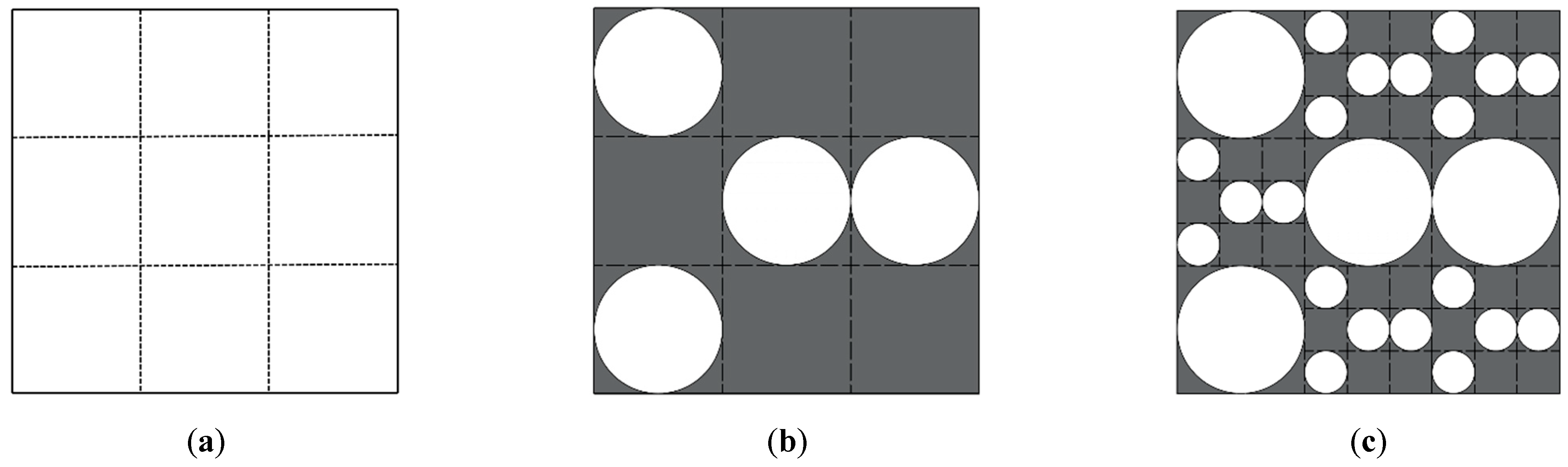
2.1. PSF Model with Circular-Based Pores
2.2. PSF Model with Circular-Based Solid Particles
3. Permeability for Revised PSF Model
3.1. Fragmented Pore or Solid Phase
3.2. Continuous Geomaterials
4. Discussion and Results
4.1. General Pore or Solid Fractal Model
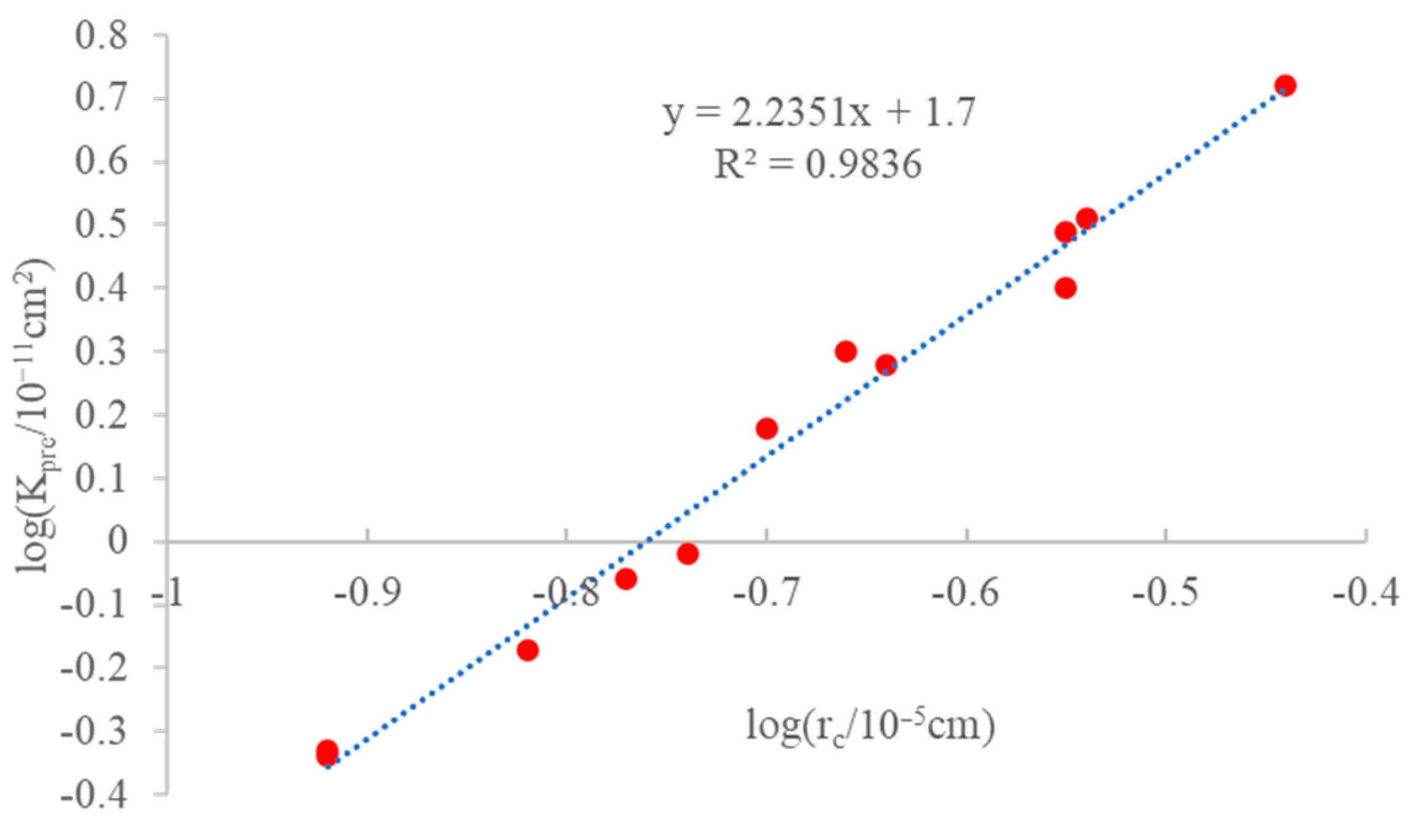
4.2. Permeability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Katz, A.J.; Thompson, A.H. Quantitative prediction of permeability in porous rock. Phys. Rev. B 1986, 34, 8179–8181. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Torres-Verdín, C.; Lake, L.W.; Marder, M. Gas permeability in unconventional tight sandstones: Scaling up from pore to core. J. Pet. Sci. Eng. 2018, 173, 1163–1172. [Google Scholar] [CrossRef] [Green Version]
- Coates, G.; Xiao, L.; Prammer, M. NMR Logging: Principles and Applications; Haliburton Energy Services: Houston, TX, USA, 1999; Volume 344. [Google Scholar]
- Glover, P.W.; Zadjali, I.I.; Frew, K.A. Permeability prediction from MICP and NMR data using an electrokinetic approach. Geophysics 2006, 71, F49–F60. [Google Scholar] [CrossRef]
- Kozeny, J. Ueber kapillare leitung des wassers im boden. Stizungsber. Akad. Wien Akad. Wiss 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Permeability of saturated sands, soils and clays. J. Agric. Sci. 1939, 29, 262–273. [Google Scholar] [CrossRef]
- Brutsaert, W. Some Methods of Calculating Unsaturated Permeability. Trans. ASAE 1967, 10, 400–404. [Google Scholar] [CrossRef]
- Mishra, S.; Parker, J.C. On the Relation Between Saturated Conductivity and Capillary Retention Characteristics. Ground Water 1990, 28, 775–777. [Google Scholar] [CrossRef]
- Sahimi, M. Applications of Percolation Theory; Taylor and Francis: London, UK, 1994. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor and Francis: London, UK, 1994. [Google Scholar]
- Ghanbarian, B.; Hunt, A.; Skinner, T.; Ewing, R. Saturation dependence of transport in porous media predicted by percolation and effective medium theories. Fractals 2015, 23, 1540004. [Google Scholar] [CrossRef]
- Richesson, S.; Sahimi, M. Hertz-Mindlin Theory of Contacting Grains and the Effective-Medium Approximation for the Permeability of Deforming Porous Media. Geophys. Res. Lett. 2019, 46, 8039–8045. [Google Scholar] [CrossRef]
- Sahimi, M. Heterogeneous Materials I: Linear Transport and Optical Properties; Springer: New York, NY, USA, 2003. [Google Scholar]
- Hunt, A. Applications of percolation theory to porous media with distributed local conductances. Adv. Water Resour. 2001, 24, 279–307. [Google Scholar] [CrossRef]
- Hunt, A. Comments on “Fractal Fragmentation, Soil Porosity, and Soil Water Properties: I. Theory”. Soil Sci. Soc. Am. J. 2007, 71, 1418–1419. [Google Scholar] [CrossRef]
- Cai, J.; Luo, L.; Ye, R.; Zeng, X.; Zhang, L.; Hu, Z. Recent advances on fractal modeling of permeability for fibrous porous media. Fractals 2015, 23, 1540006. [Google Scholar] [CrossRef]
- Daigle, H. Application of critical path analysis for permeability prediction in natural porous media. Adv. Water Resour. 2016, 96, 43–54. [Google Scholar] [CrossRef]
- Skaggs, T. Assessment of critical path analyses of the relationship between permeability and electrical conductivity of pore networks. Adv. Water Resour. 2011, 34, 1335–1342. [Google Scholar] [CrossRef]
- Hunt, A.; Ghanbarian, B.; Saville, K.C. Unsaturated hydraulic conductivity modeling for porous media with two fractal regimes. Geoderma 2013, 207–208, 268–278. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.; Skaggs, T.H.; Jarvis, N. Upscaling soil saturated hydraulic conductivity from pore throat characteristics. Adv. Water Resour. 2017, 104, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Sergeyev, Y. Evaluating the exact infinitesimal values of area of Sierpinski’s carpet and volume of Menger’s sponge. Chaos Solitons Fractals 2009, 42, 3042–3046. [Google Scholar] [CrossRef] [Green Version]
- Perrier, E.; Bird, N.; Rieu, M. Generalizing the fractal model of soil structure: The pore–solid fractal approach. Geoderma 1999, 88, 137–164. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Kou, L.; Miao, R.H.; Miao, F.Y. Fractal analysis of non-Newton fluid grouting through soil composed of arbitrary cross-sectional capillaries. Fractals 2021, 29, 2150139. [Google Scholar] [CrossRef]
- Perfect, E.; Gentry, R.; Sukop, M.; Lawson, J. Multifractal Sierpinski carpets: Theory and application to upscaling effective saturated hydraulic conductivity. Geoderma 2006, 134, 240–252. [Google Scholar] [CrossRef]
- Pia, G.; Sanna, U. An intermingled fractal units model and method to predict permeability in porous rock. Int. J. Eng. Sci. 2014, 75, 31–39. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, R. Evaluation of soil water retention curve with the pore–solid fractal model. Geoderma 2005, 127, 52–61. [Google Scholar] [CrossRef]
- Hwang, S.I.; Yun, E.Y.; Ro, H.M. Estimation of soil water retention function based on asymmetry between particle- and pore-size distributions. Eur. J. Soil Sci. 2011, 62, 195–205. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Hunt, A. Unsaturated hydraulic conductivity in porous media: Percolation theory. Geoderma 2012, 187–188, 77–84. [Google Scholar] [CrossRef]
- Bird, N.; Perrier, E.; Rieu, M. The water retention function for a model of soil structure with pore and solid fractal distributions. Eur. J. Soil Sci. 2000, 51, 55–63. [Google Scholar] [CrossRef]
- Hunt, A. Continuum percolation theory for transport properties in porous media. Philos. Mag. 2005, 85, 3409–3434. [Google Scholar] [CrossRef]
- Hunt, A.; Sahimi, M. Flow, Transport, and Reaction in Porous Media: Percolation Scaling, Critical-Path Analysis, and Effective Medium Approximation. Rev. Geophys. 2017, 55, 993–1078. [Google Scholar] [CrossRef]
- Ghanbarian, B. Predicting Single-Phase Permeability of Porous Media Using Critical-Path Analysis. In Complex Media and Percolation Theory; Sahimi, M., Hunt, A.G., Eds.; Encyclopedia of Complexity and Systems Science Series; Springer: New York, NY, USA, 2021. [Google Scholar]
- Khabbazi, A.E.; Hinebaugh, J.; Bazylak, A. Analytical tortuosity–porosity correlations for Sierpinski carpet fractal geometries. Chaos Solitons Fractals 2015, 78, 124–133. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kou, L.; Li, W.; Wu, J. Permeability Prediction of Saturated Geomaterials with Revised Pore–Solid Fractal Model and Critical Path Analysis. Fractal Fract. 2022, 6, 351. https://doi.org/10.3390/fractalfract6070351
Kou L, Li W, Wu J. Permeability Prediction of Saturated Geomaterials with Revised Pore–Solid Fractal Model and Critical Path Analysis. Fractal and Fractional. 2022; 6(7):351. https://doi.org/10.3390/fractalfract6070351
Chicago/Turabian StyleKou, Lei, Wuxue Li, and Jujie Wu. 2022. "Permeability Prediction of Saturated Geomaterials with Revised Pore–Solid Fractal Model and Critical Path Analysis" Fractal and Fractional 6, no. 7: 351. https://doi.org/10.3390/fractalfract6070351
APA StyleKou, L., Li, W., & Wu, J. (2022). Permeability Prediction of Saturated Geomaterials with Revised Pore–Solid Fractal Model and Critical Path Analysis. Fractal and Fractional, 6(7), 351. https://doi.org/10.3390/fractalfract6070351




