Asymptotic and Finite-Time Synchronization of Fractional-Order Memristor-Based Inertial Neural Networks with Time-Varying Delay
Abstract
:1. Introduction
- The Caputo fractional-order memristor-based inertial network model is constructed. Compared with the inertial integer-order neural network, the Caputo fractional-order memristor-based inertial network model can be widely and flexibly used. In addition, the advantage of this model is that it has a practical engineering background and is relatively easy to implement in engineering.
- By utilizing the properties of fractional calculus, two lemmas on asymptotic stability and finite-time stability are given, which are crucial to the proofs of our principal theorems.
- Based on the two proposed lemmas and Lyapunov direct methods, some new asymptotic and finite-time synchronization control strategies for inertial memristor-based Caputo fractional-order neural networks are proposed.
- The direct analysis method is adopted to analyze the dynamic performance of the inertial system without using the reduced-order method based on variable substitution, which not only avoids increasing the system’s dimension, thereby increasing the difficulty of analysis, but also avoids the loss of system inertia; thus, it has more important practical significance.
2. Problem Statement and Preliminaries
2.1. Basic Knowledge
2.2. Problem Formulation
3. Main Results
3.1. Asymptotic Synchronization
3.2. Finite-Time Synchronization
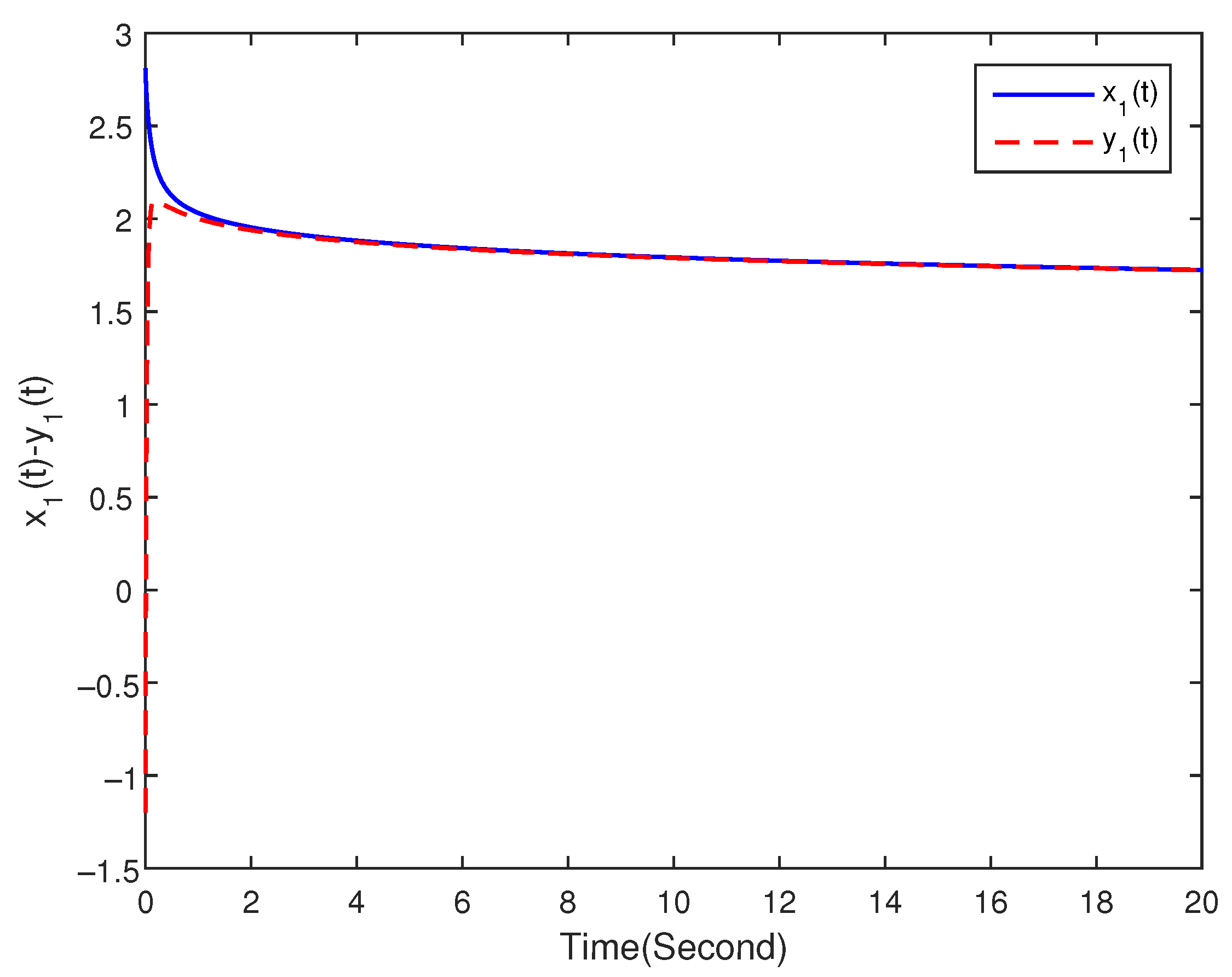
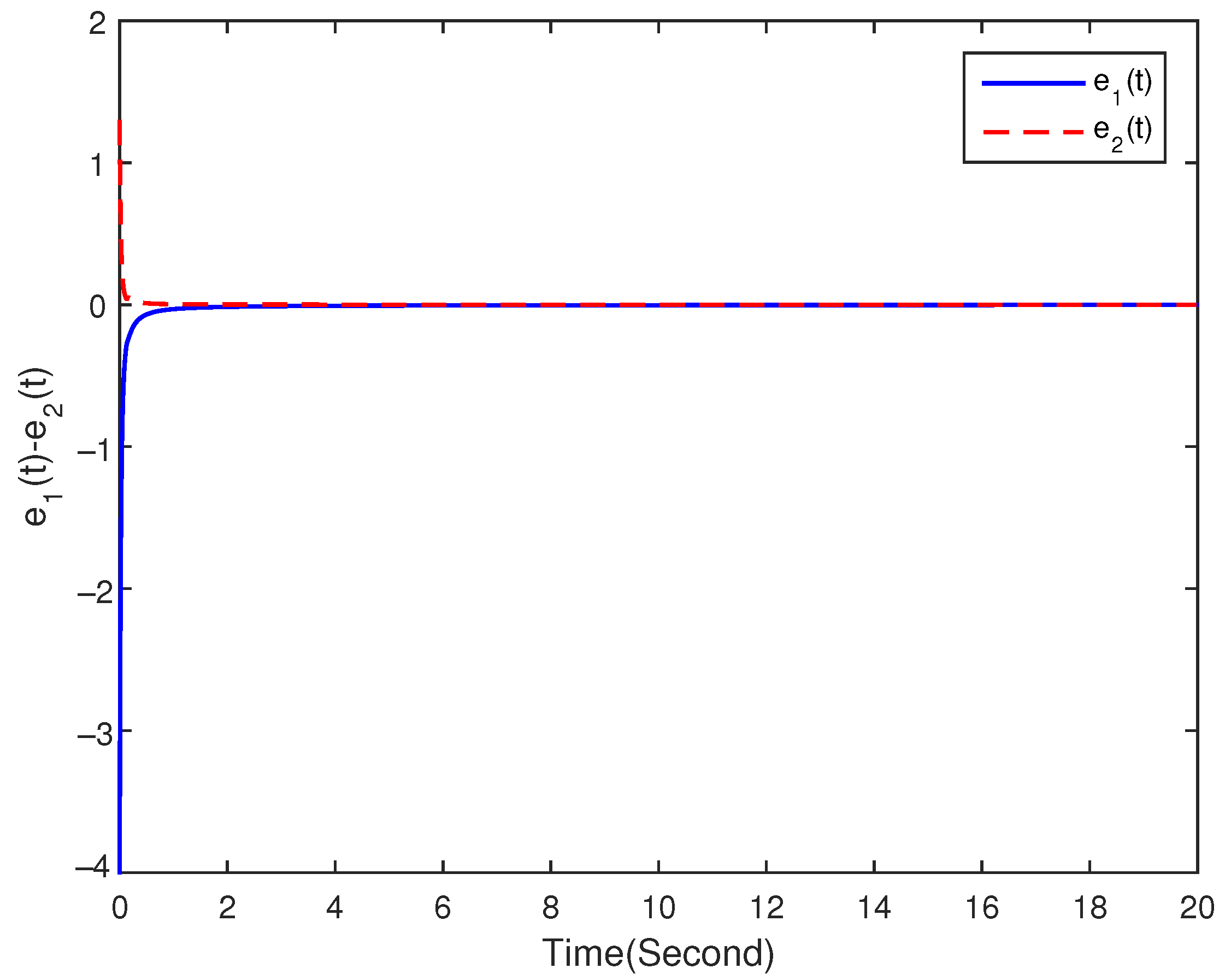
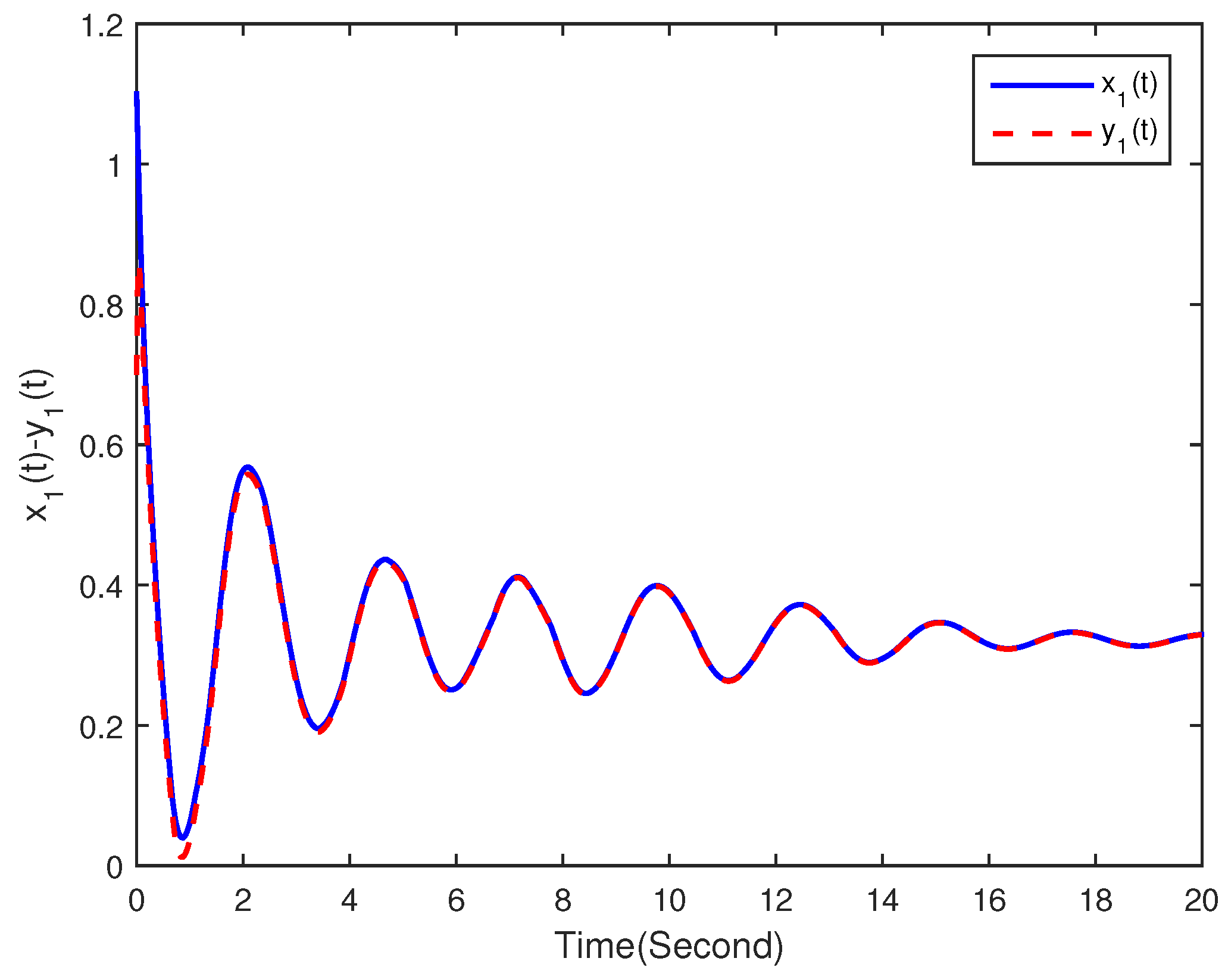
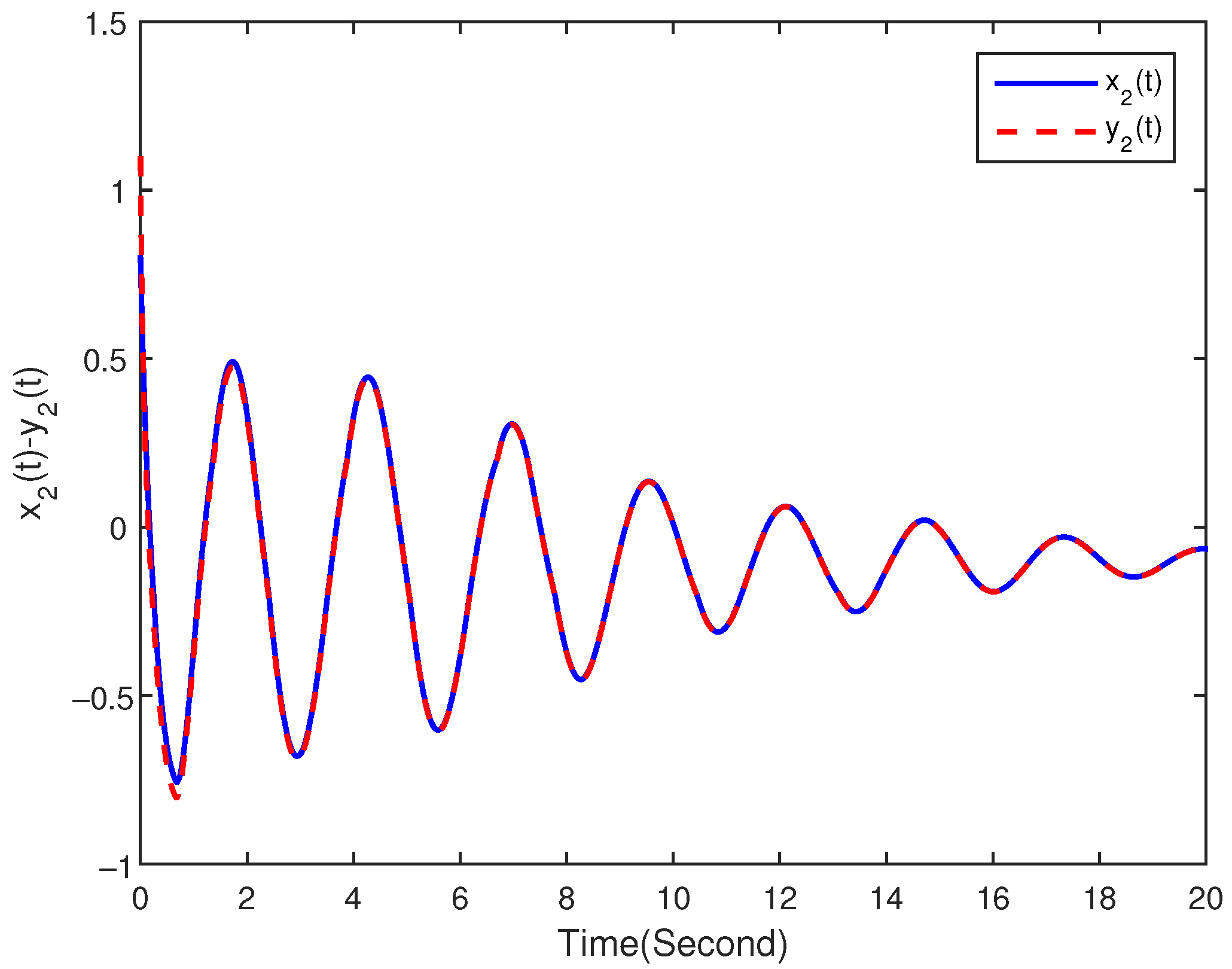
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Badcock, K.L.; Westervelt, R.M. Dynamics of simple electronic neural networks. J. Phys. D 1987, 28, 305–316. [Google Scholar] [CrossRef]
- Mauro, A.; Conti, F.; Dodge, F. Subthreshold behavior and phenomenological impedance of the squid giant axon. J. Gen. Phys. 1970, 55, 497–523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Angelaki, D.E.; Correia, M.J. Models of membrane resonance in pigeon semicircular canal type II hair cell. Biol. Cybernet 1991, 65, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, C. Dynamics analysis on a class of delayed neural networks involving inertial terms. Adv. Differ. Equ. 2020, 2020, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ke, Y.; Miao, C. Anti-periodic solutions of inertial neural networks with time delays. Neural Process Lett. 2017, 45, 523–538. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, J.; Zeng, Z. New criteria on global stabilization of delayed memristive neural networks with inertial item. IEEE Trans. Cybern. 2020, 50, 2770–2780. [Google Scholar] [CrossRef]
- Wan, P.; Jian, J. Global convergence analysis of impulsive inertial neural networks with timevarying delays. Neurocomputing 2017, 245, 68–76. [Google Scholar] [CrossRef]
- Duan, L.; Jian, J.; Wang, B. Global exponential dissipativity of neutral-type BAM inertial neural networks with mixed time-varying delays. Neurocomputing 2020, 378, 399–412. [Google Scholar] [CrossRef]
- Huang, Q.; Cao, J. Stability analysis of inertial Cohen-Grossberg neural networks with Markovian jumping parameters. Neurocomputing 2018, 282, 89–97. [Google Scholar] [CrossRef]
- Cui, N.; Jiang, H.; Hu, C.; Abdurahman, A. Global asymptotic and robust stability of inertial neural networks with proportional delays. Neurocomputing 2018, 272, 326–333. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, J. Novel finite-time synchronization criteria for inertial neural networks with time delays via integral inequality method. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1476–1485. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Li, J. Fixed-time synchronization of fuzzy neutral-type BAM memristive inertial neural networks with proportional delays. Inf. Sci. 2021, 576, 522–541. [Google Scholar] [CrossRef]
- Lin, D.; Chen, X.; Yu, G.; Li, Z.; Xia, Y. Global exponential synchronization via nonlinear feedback control for delayed inertial memristor-based quaternion-valued neural networks with impulses. Appl. Math. Comput. 2021, 401, 126093. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y. Fixed-time synchronization of delayed fractional-order memristor-based fuzzy cellular neural networks. IEEE Access 2020, 8, 165951–165962. [Google Scholar] [CrossRef]
- Du, F.; Lu, J. New criterion for finite-time synchronization of fractional order memristor-based neural networks with time delay. Appl. Math. Comput. 2021, 389, 125616. [Google Scholar] [CrossRef]
- Li, N.; Zheng, W. Bipartite synchronization of multiple memristor-based neural networks with antagonistic interactions. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1642–1653. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Sun, Y.; Liu, Y. Adaptive synchronization control and parameters identification for chaotic fractional neural networks with time-varying delays. Neural Process. Lett. 2021, 53, 2729–2745. [Google Scholar] [CrossRef]
- Tavazoei, M.; Asemani, M.H. Stability analysis of time-delay incommensurate fractional-order systems. Commun. Nonlinear Sci. Numer. Simul. 2022, 109, 106270. [Google Scholar] [CrossRef]
- Wei, Y.; Cao, J.; Chen, Y.; Wei, Y. The proof of Lyapunov asymptotic stability theorems for Caputo fractional order systems. Appl. Math. Lett. 2022, 129, 107961. [Google Scholar] [CrossRef]
- Li, L.; Sun, Y. Adaptive fuzzy control for nonlinear fractional-order uncertain systems with unknown uncertainties and external disturbance. Entropy 2015, 17, 5580–5592. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Y.; Huang, T.; Zeng, Z.; Li, P. Exponential Stabilization of Inertial Memristive Neural Networks With Multiple Time Delays. IEEE Trans. Cybern. 2021, 51, 579–588. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, X.; Wang, X.; Yang, X. L2–L∞ state estimation of the high-order inertial neural network with time-varying delay: Non-reduced order strategy. Inf. Sci. 2022, 607, 62–78. [Google Scholar] [CrossRef]
- Han, J.; Chen, G.; Hu, J. New results on anti-synchronization in predefined-time for a class of fuzzy inertial neural networks with mixed time delays. Neurocomputing 2022, 495, 26–36. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.; Hu, J. Fixed-time stabilization and synchronization for fuzzy inertial neural networks with bounded distributed delays and discontinuous activation functions. Neurocomputing 2022, 495, 86–96. [Google Scholar] [CrossRef]
- Li, H.; Li, C.; Ouyang, D.; Nguang, S. Impulsive Synchronization of Unbounded Delayed Inertial Neural Networks with Actuator Saturation and Sampled-Data Control and Its Application to Image Encryption. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1460–1473. [Google Scholar] [CrossRef]
- Lu, Z.; Ge, Q.; Li, Y.; Hu, J. Finite-Time Synchronization of Memristor-Based Recurrent Neural Networks With Inertial Items and Mixed Delays. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2701–2711. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, H.; Yu, Y. Stability and synchronization for Riemann-Liouville fractional-order time-delayed inertial neural networks. Neurocomputing 2019, 340, 270–280. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y. The Boundedness and the Global Mittag-Leffler Synchronization of Fractional-Order Inertial Cohen-Grossberg Neural Networks with Time Delays. Neural Process. Lett. 2022, 54, 597–611. [Google Scholar] [CrossRef]
- Ke, L. Mittag-Leffler stability and asymptotic ω-periodicity of fractional-order inertial neural networks with time-delays. Neurocomputing 2021, 465, 53–62. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, M.; Liu, X. Synchronization of a Riemann-Liouville fractional time-delayed neural network with two inertial terms. Circuits Syst. Signal Process. 2021, 40, 5280–5308. [Google Scholar] [CrossRef]
- Yang, X.; Lu, J. Synchronization of fractional order memristor-based inertial neural networks with time delay. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 3853–3858. [Google Scholar]
- Yang, C.; Huang, L.; Cai, Z. Fixed-time synchronization of coupled memristor-based neural networks with time-varying delays. Neural Netw. 2019, 116, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Andreev, A.; Sedova, N. The method of Lyapunov-Razumikhin functions in stability analysis of systems with delay. Autom. Remote Control 2019, 80, 1185–1229. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Liu, Y.; Liu, L. Asymptotic and Finite-Time Synchronization of Fractional-Order Memristor-Based Inertial Neural Networks with Time-Varying Delay. Fractal Fract. 2022, 6, 350. https://doi.org/10.3390/fractalfract6070350
Sun Y, Liu Y, Liu L. Asymptotic and Finite-Time Synchronization of Fractional-Order Memristor-Based Inertial Neural Networks with Time-Varying Delay. Fractal and Fractional. 2022; 6(7):350. https://doi.org/10.3390/fractalfract6070350
Chicago/Turabian StyleSun, Yeguo, Yihong Liu, and Lei Liu. 2022. "Asymptotic and Finite-Time Synchronization of Fractional-Order Memristor-Based Inertial Neural Networks with Time-Varying Delay" Fractal and Fractional 6, no. 7: 350. https://doi.org/10.3390/fractalfract6070350
APA StyleSun, Y., Liu, Y., & Liu, L. (2022). Asymptotic and Finite-Time Synchronization of Fractional-Order Memristor-Based Inertial Neural Networks with Time-Varying Delay. Fractal and Fractional, 6(7), 350. https://doi.org/10.3390/fractalfract6070350





