Cluster Oscillation of a Fractional-Order Duffing System with Slow Variable Parameter Excitation
Abstract
:1. Introduction
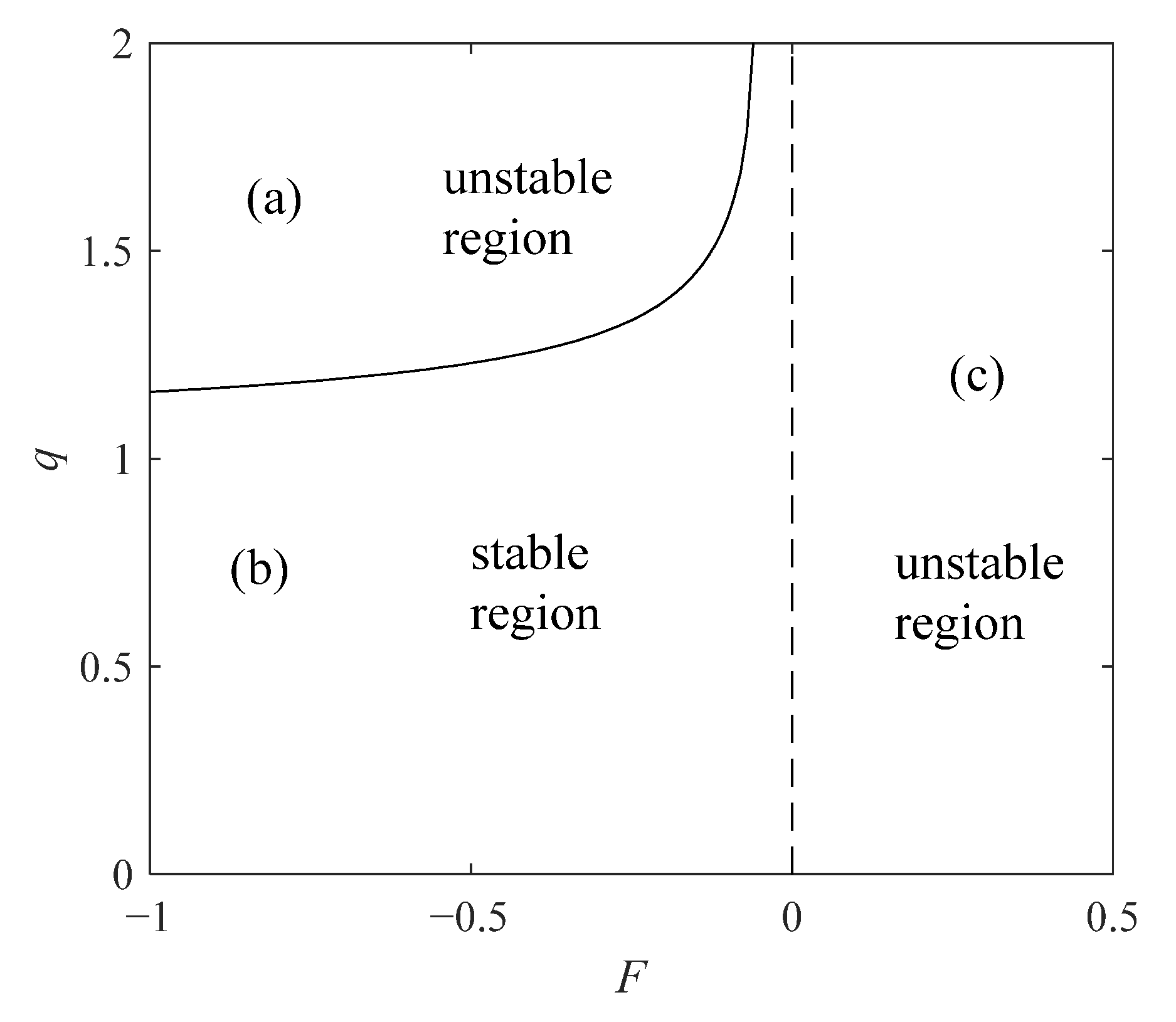
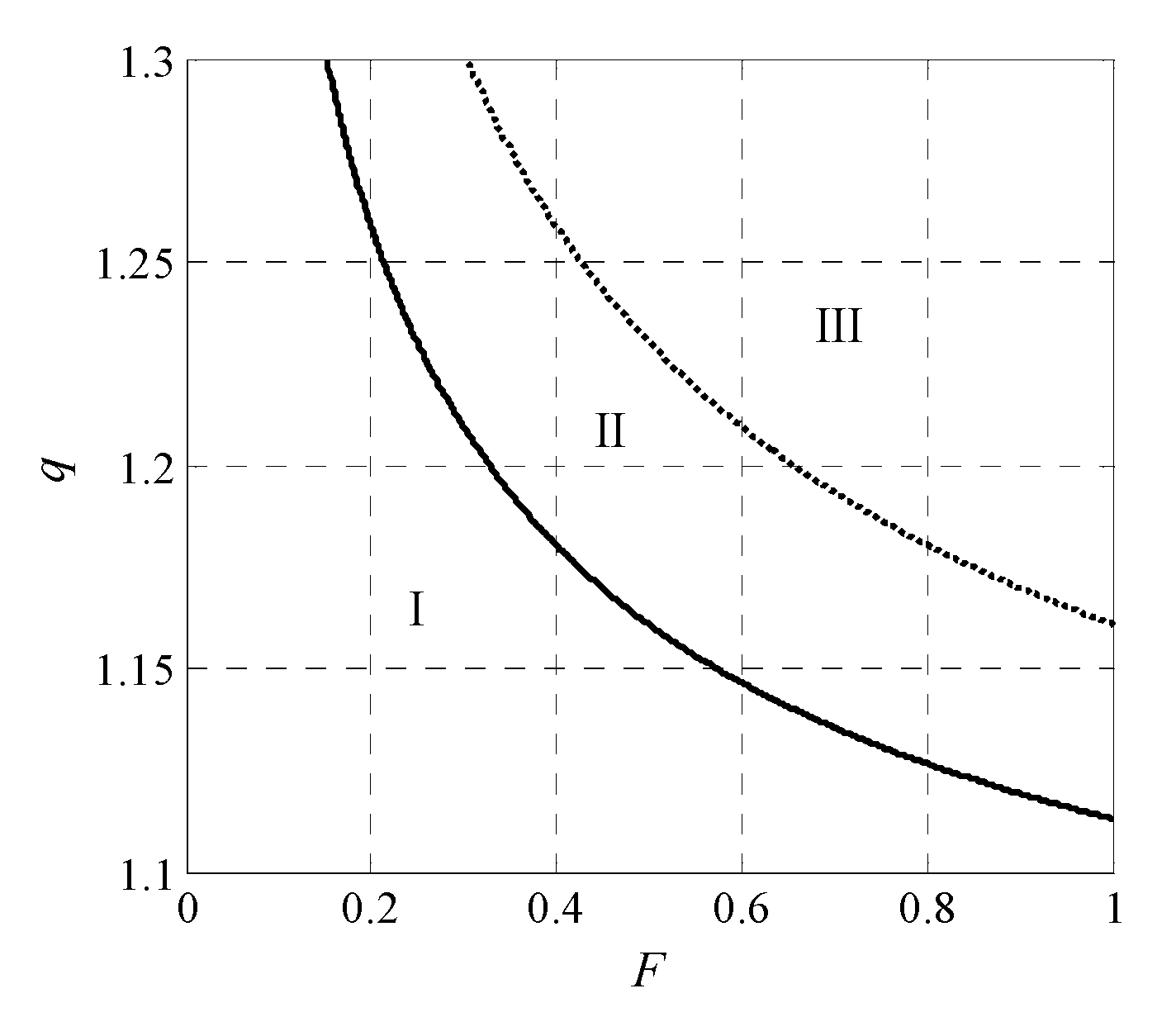
2. Bifurcation Analysis
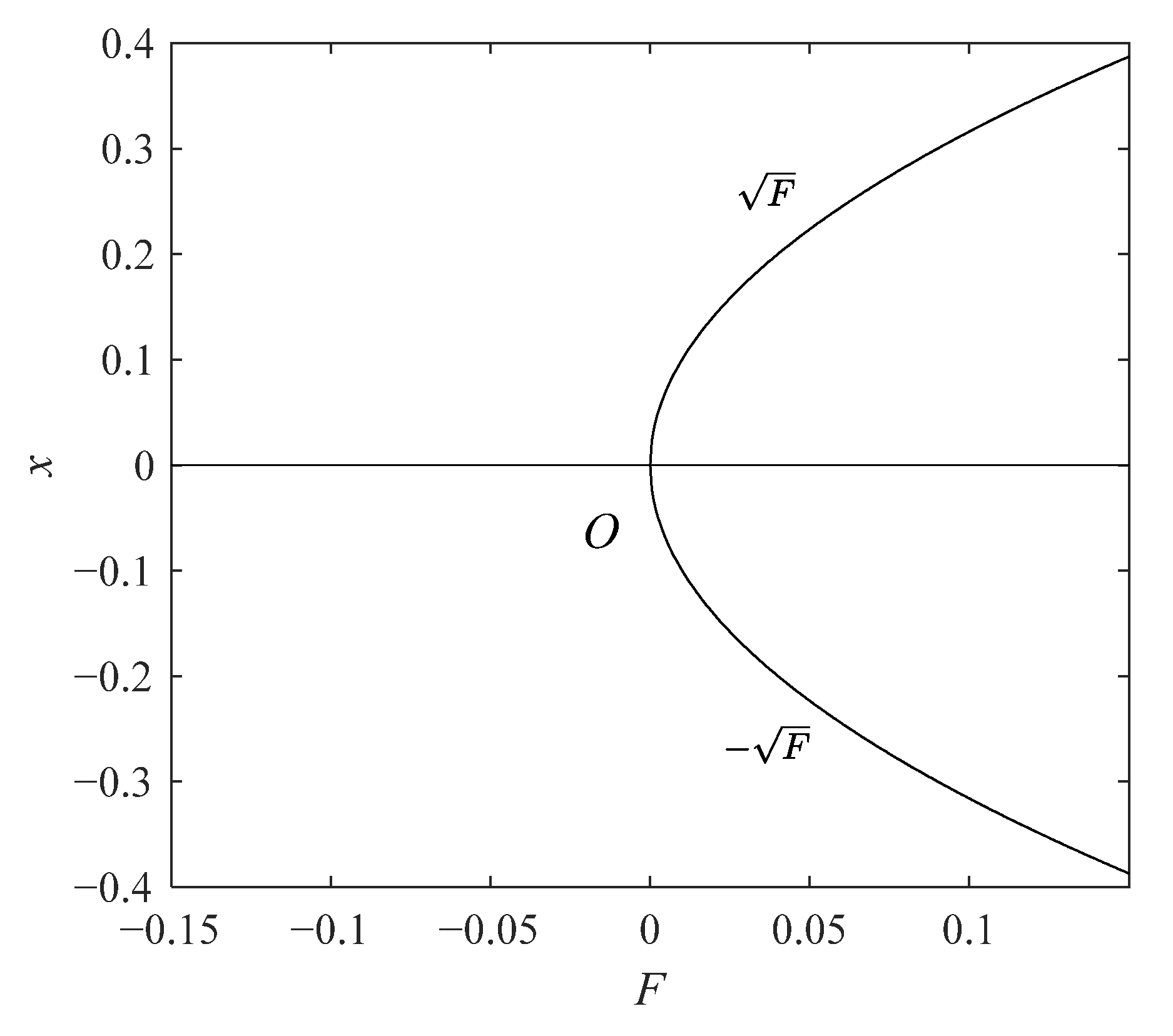
2.1. Pitchfork Bifurcation
2.2. Hopf Bifurcation
2.3. Limit Cycle Bifurcation
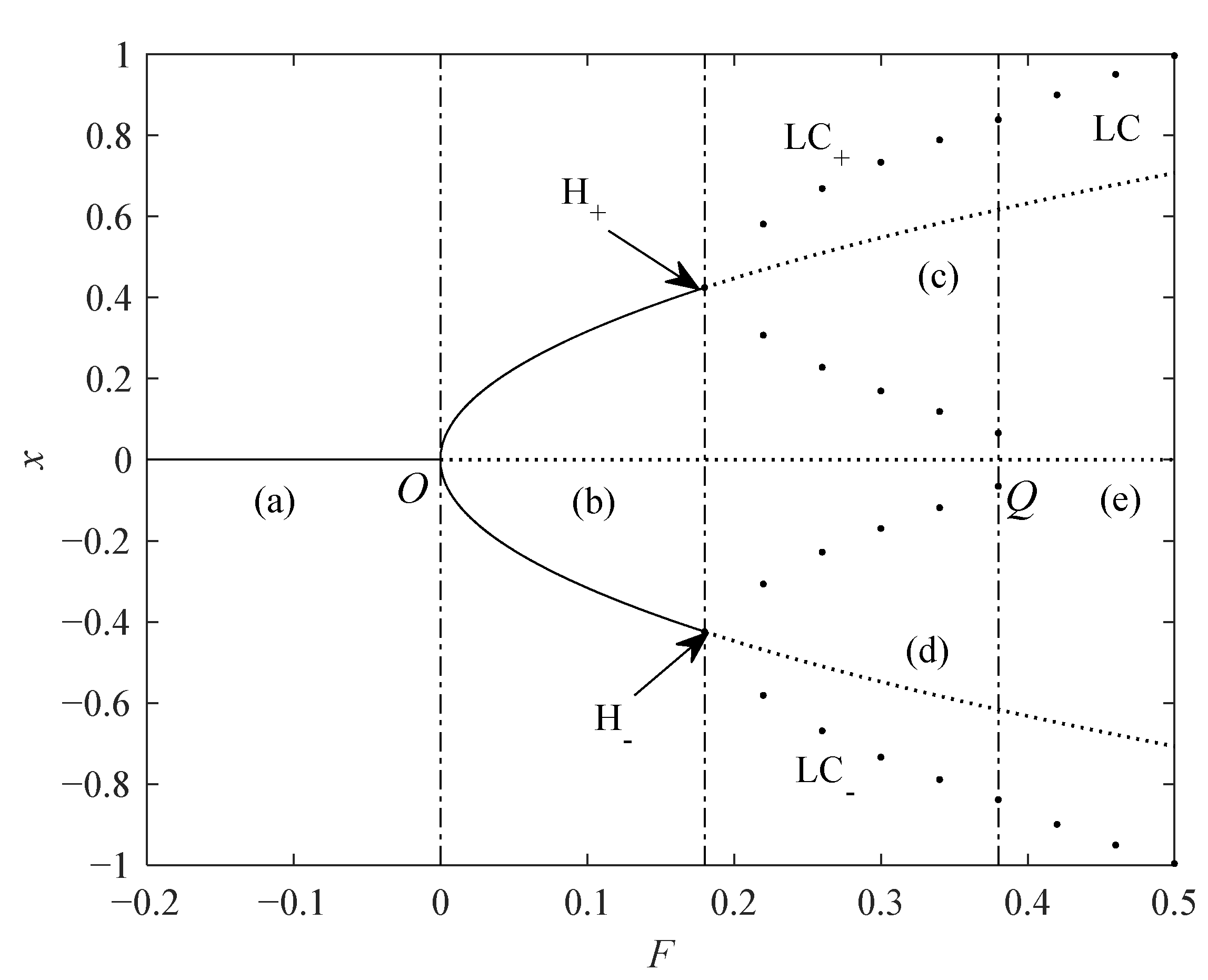
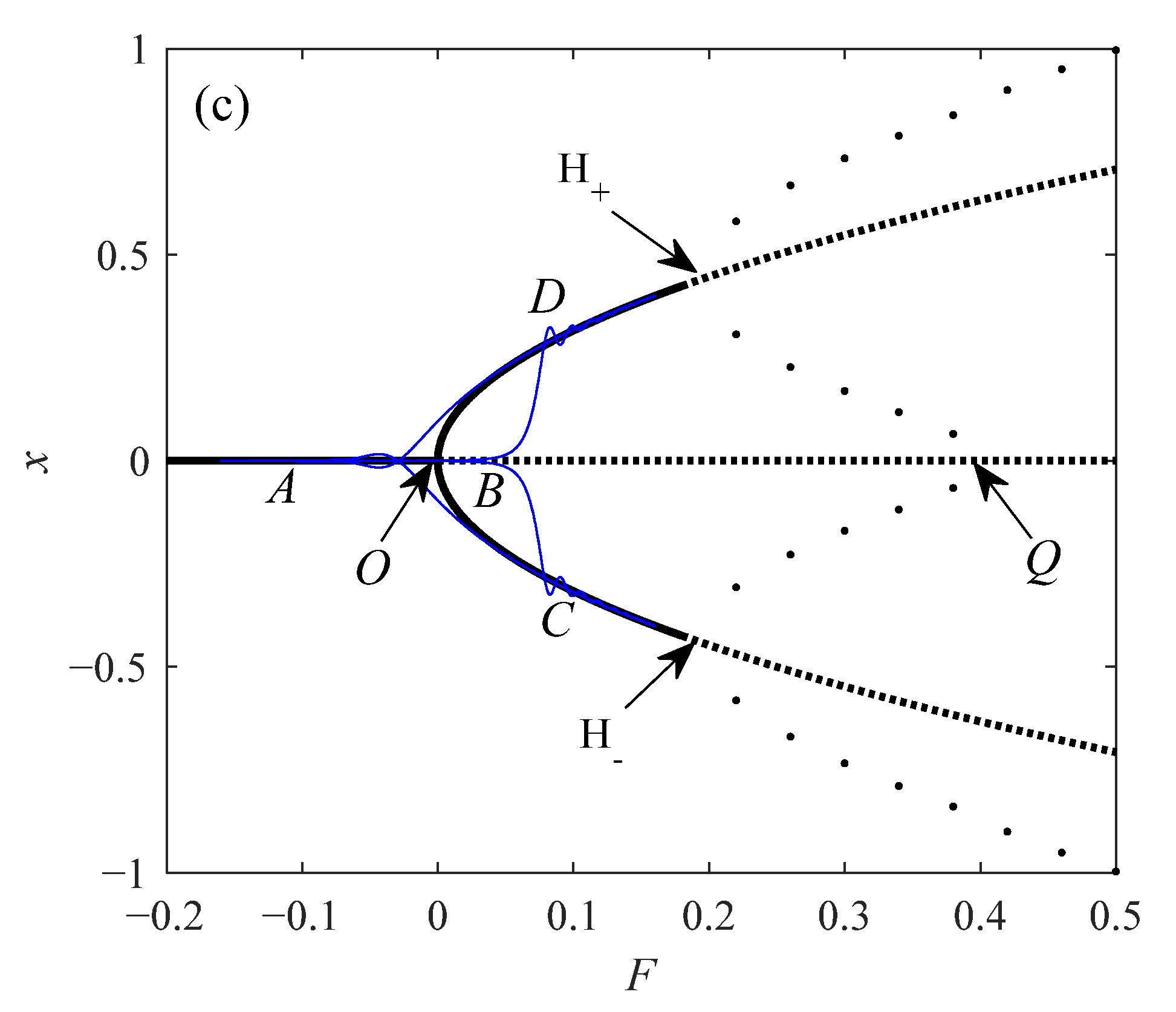
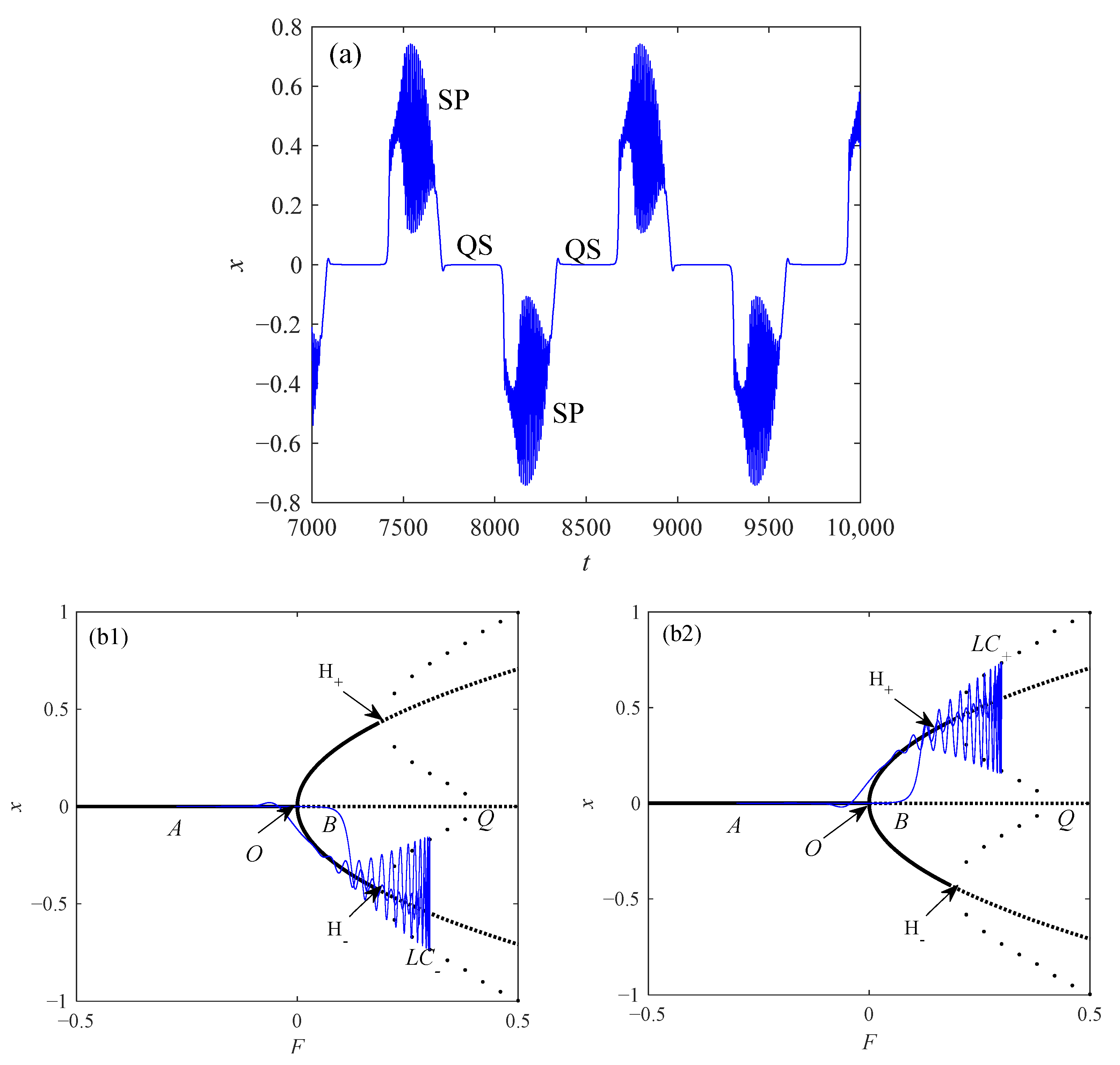
3. Analysis of Cluster Oscillation
3.1. The Point–Point Cluster Oscillation and Pitchfork Bifurcation
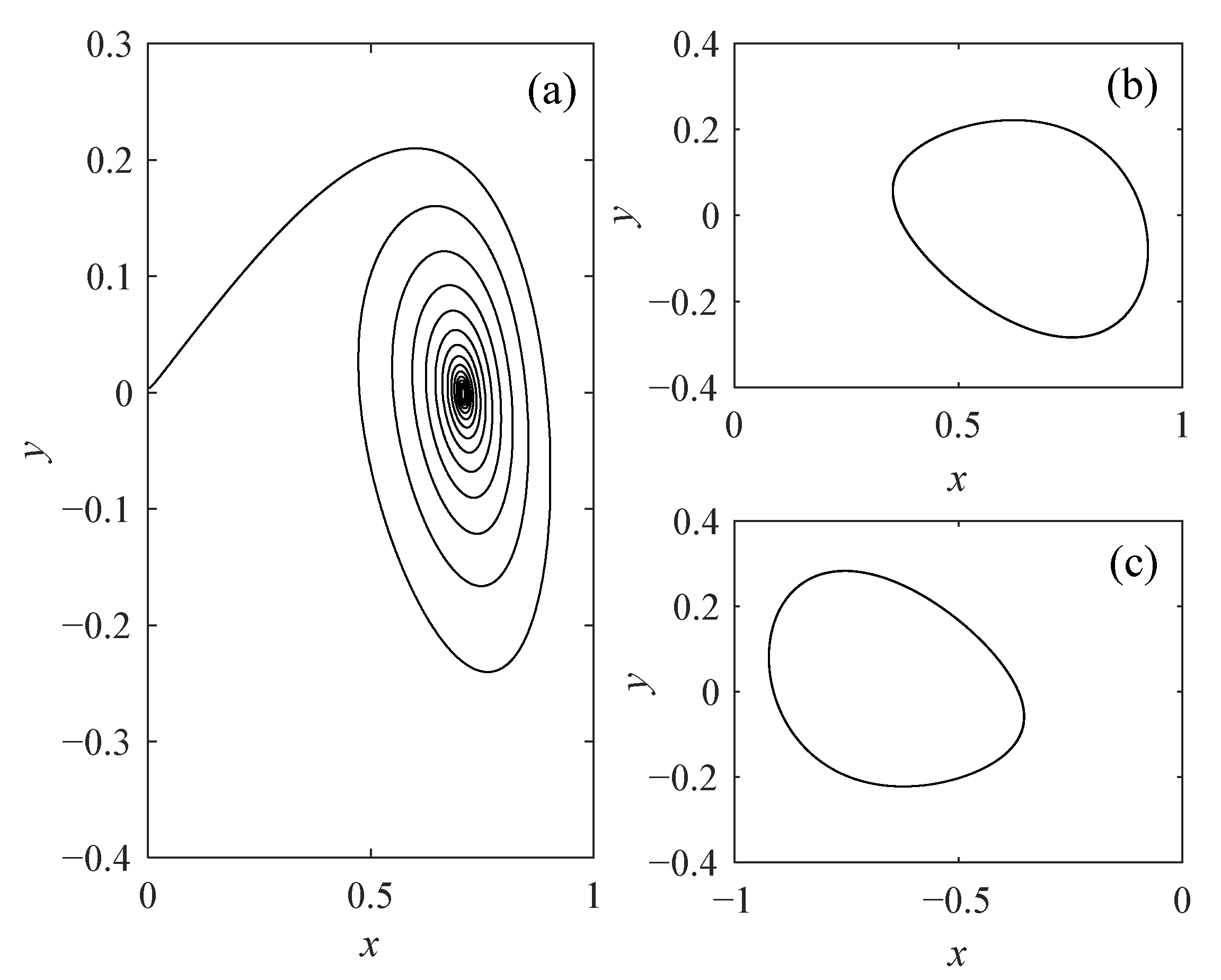
3.2. The Point–Cycle Cluster Oscillation and Pitchfork/Hopf Bifurcation
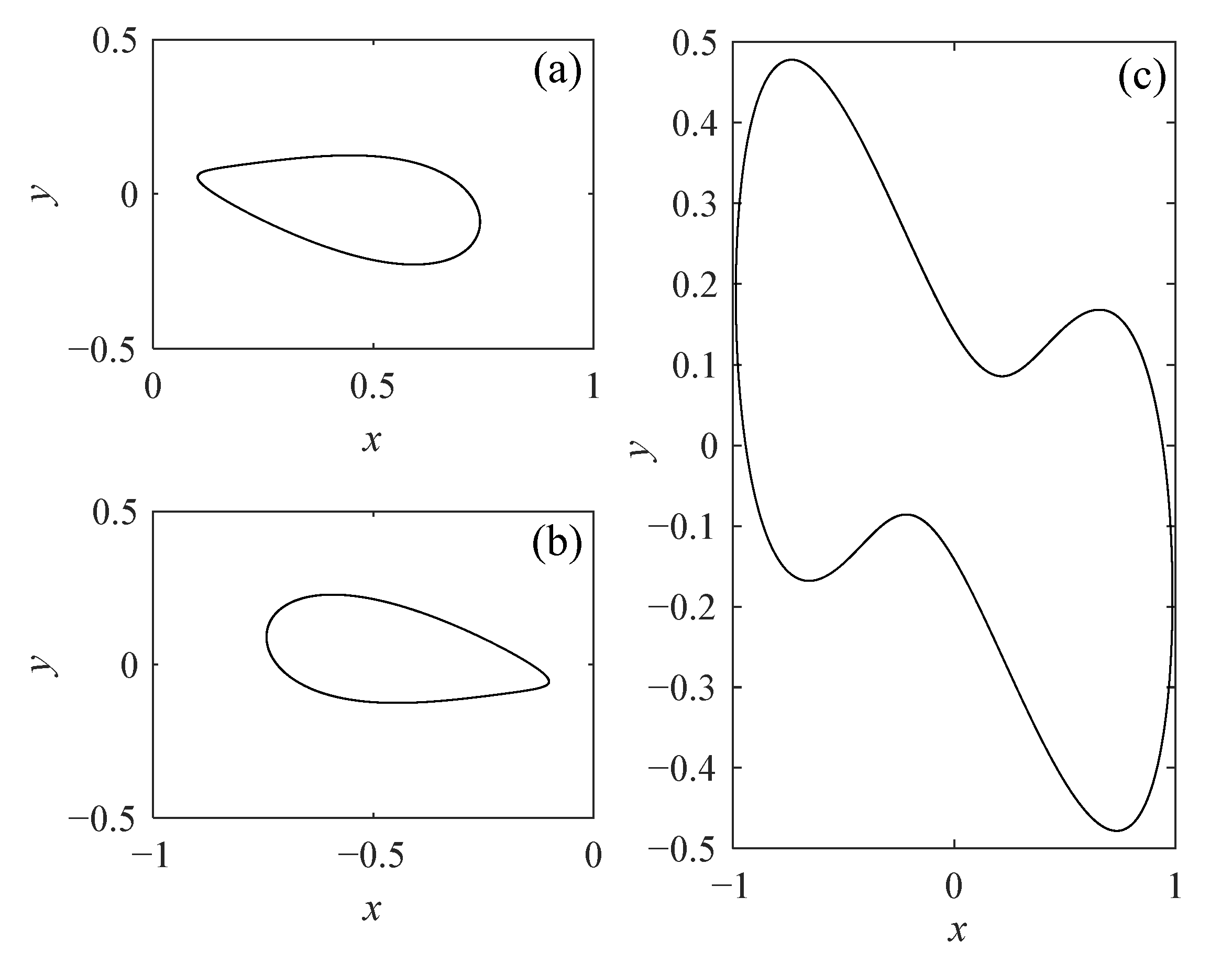
3.3. The Point–Cycle–Cycle Cluster Oscillation and Pitchfork/Hopf/Limit Cycle Bifurcation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tarasov, V.E. Generalized Memory: Fractional Calculus Approach. Fractal Fract. 2018, 2, 23. [Google Scholar] [CrossRef] [Green Version]
- Simo, H.; Siewe, R.T.; Dutt, J.K.; Woafo, P. Effects of delay, noises and fractional-order on the peaks in antiperiodic oscillations in Duffing oscillator. Indian J. Phys. 2019, 94, 2005–2015. [Google Scholar] [CrossRef]
- Shen, Y.J.; Li, H.; Yang, S.P.; Peng, M.F.; Han, Y.J. Primary and subharmonic simultaneous resonance of fractional-order Duffing oscillator. Nonlinear Dyn. 2020, 102, 1485–1497. [Google Scholar] [CrossRef]
- Shen, Y.J.; Yang, S.P.; Xing, H.J.; Ma, H.X. Primary resonance of Duffing oscillator with fractional-order derivative. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3092–3100. [Google Scholar] [CrossRef]
- Shen, Y.J.; Yang, S.P.; Xing, H.J.; Ma, H.X. Primary resonance of Duffing oscillator with two kinds of fractional-order derivatives. Int. J. Non-Linear Mech. 2012, 47, 975–983. [Google Scholar] [CrossRef]
- Nguyen, V.K.; Chien, T.Q. Subharmonic resonance of Duffing oscillator with fractional-order derivative. J. Comput. Nonlinear Dyn. 2016, 11, 051018. [Google Scholar]
- Lai, L.; Ji, Y.D.; Zhong, S.C.; Zhang, L. Sequential Parameter Identification of Fractional-Order Duffing System Based on Differential Evolution Algorithm. Math. Probl. Eng. 2017, 20, 3572365. [Google Scholar] [CrossRef] [Green Version]
- Ei-Sayed, A.; Ei-Raheem, Z.F.; Salman, S.M. Discretization of Forced Duffing System with Fractional-Order Damping; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; p. 66. [Google Scholar]
- Li, R.H.; Li, J.; Huang, D.M. Static bifurcation and vibrational resonance in an asymmetric fractional-order delay Duffing system. Phys. Scr. 2021, 96, 085214. [Google Scholar] [CrossRef]
- Lei, Y.M.; Wang, Y.Y. Period-Doubling Bifurcation of Stochastic Fractional-Order Duffing System via Chebyshev Polynomial Approximation. Shock. Vib. 2017, 2017, 4162363. [Google Scholar] [CrossRef]
- Liu, X.J.; Hong, L.; Jiang, J. Global Bifurcations in Fractional-Order Chaotic Systems with an Extended Generalized Cell Mapping Method; Chaos: Woodbury, NY, USA, 2016; Volume 26, p. 084304. [Google Scholar]
- Li, Z.S.; Chen, D.Y.; Zhu, J.W.; Liu, Y.J. Nonlinear dynamics of fractional order Duffing system. Chaos Solitons Fractals 2015, 81, 111–116. [Google Scholar] [CrossRef]
- Yaghooti, B.; Shadbad, A.S.; Safavigerdini, K.; Salarieh, H. Adaptive synchronization of uncertain fractional-order chaotic systems using sliding mode control techniques. Proc. Inst. Mech. Eng. 2020, 234, 3–9. [Google Scholar] [CrossRef]
- Niu, J.C.; Shen, Y.J.; Yang, S.P.; Li, S.J. Analysis of Duffing oscillator with time-delayed fractional-order PID controller. Int. J. Non-Linear Mech. 2017, 92, 66–75. [Google Scholar] [CrossRef]
- Peters, A.; Moctar, O.E. Numerical assessment of cavitation-induced erosion using a multi-scale Euler–Lagrange method. J. Fluid Mech. 2020, 894, 1–54. [Google Scholar] [CrossRef]
- Harzallah, M.; Pottier, T.; Gilblas, R.; Landon, Y. Thermomechanical coupling investigation in Ti-6Al-4V orthogonal cutting: Experimental and numerical confrontation. Int. J. Mech. Sci. 2019, 169, 105322. [Google Scholar] [CrossRef]
- Fei, Y.; Batty, C.; Grinspun, E.; Zheng, C.X. A multi-scale model for coupling strands with shear-dependent liquid. ACM Trans. Graph. (TOG) 2019, 38, 190. [Google Scholar] [CrossRef] [Green Version]
- Li, S.B.; Roy, S.; Unnikrishnan, V. Modeling of fracture behavior in polymer composites using concurrent multi-scale coupling approach. Mech. Adv. Mater. Struct. 2018, 25, 1342–1350. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, W.B.; Bao, H.; Shen, Q. Bifurcation mechanism of periodic bursting in a simple three-element-based memristive circuit with fast-slow effect. Chaos Solitons Fractals 2020, 131, 109524. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.Y.; Xu, B.B.; Wu, C.Z.; Wang, X.Y. The slow-fast dynamical behaviors of a hydro-turbine governing system under periodic excitations. Nonlinear Dyn. 2017, 87, 2519–2528. [Google Scholar] [CrossRef]
- Wang, H.X.; Lu, Q.S.; Shi, X. Comparison of Synchronization Ability of Four Types of Regular Coupled Networks. Commun. Theor. Phys. 2012, 58, 681–685. [Google Scholar] [CrossRef]
- Han, X.J.; Zhang, Y.; Bi, Q.S.; Kurths, J. Two novel bursting patterns in the Duffing system with multiple-frequency slow parametric excitations. Chaos 2018, 28, 43111. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Stability of Generalized Proportional Caputo Fractional Differential Equations by Lyapunov Functions. Fractal Fract. 2022, 6, 34. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Wang, Y.L.; Li, X.H.; Shen, Y.J. Cluster oscillation and bifurcation of fractional-order Duffing system with two time scales. Acta Mech. Sin. 2020, 36, 926–932. [Google Scholar] [CrossRef]

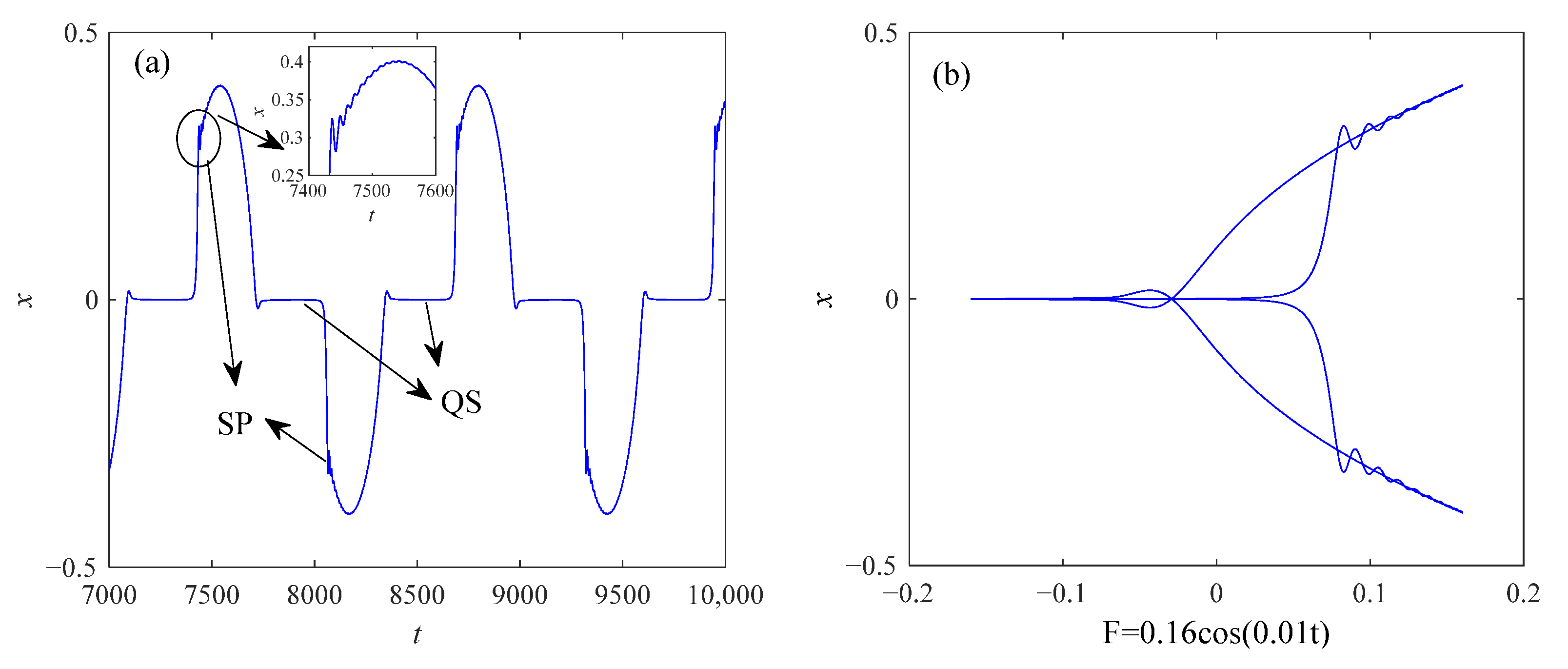

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, Y.; Shen, Y. Cluster Oscillation of a Fractional-Order Duffing System with Slow Variable Parameter Excitation. Fractal Fract. 2022, 6, 295. https://doi.org/10.3390/fractalfract6060295
Li X, Wang Y, Shen Y. Cluster Oscillation of a Fractional-Order Duffing System with Slow Variable Parameter Excitation. Fractal and Fractional. 2022; 6(6):295. https://doi.org/10.3390/fractalfract6060295
Chicago/Turabian StyleLi, Xianghong, Yanli Wang, and Yongjun Shen. 2022. "Cluster Oscillation of a Fractional-Order Duffing System with Slow Variable Parameter Excitation" Fractal and Fractional 6, no. 6: 295. https://doi.org/10.3390/fractalfract6060295





