Stochastic Optimal Control Analysis of a Mathematical Model: Theory and Application to Non-Singular Kernels
Abstract
:1. Introduction to the Problem and Model Formulation
2. Qualitative Analysis of the Global Non-Negative Solution
3. Extinction of the Proposed Model
4. The Stationary Distribution of the Disease
- 1.
- In the set U and its neighbor thereof, the eigenvalue of the diffusion matrix that has the smallest magnitude is bounded away from the origin;
- 2.
- If x is in , the average time τ in which a path starts from x reaching U is , and where K is compact. Besides, for an integrable function w.r.t measure Π, we have:
5. Stochastic Optimal Control
- The control measure shows physically the discussion about non-singular and singular kernels on social research forums such as Google scholar and Researchgate for example "https://pubpeer.com/";
- The variable describes the size of papers published/accepted, the books, etc., about non-singular and singular kernels;
- The variable stands for the qualitative aspects such as the fairness of publishers and the editorial board;
- The measure denotes a conference presenting good talks on the subject of fractional derivatives and integrals.
6. Numerical Simulations
6.1. Numerical Simulations for the Stationary Distribution and Extinction
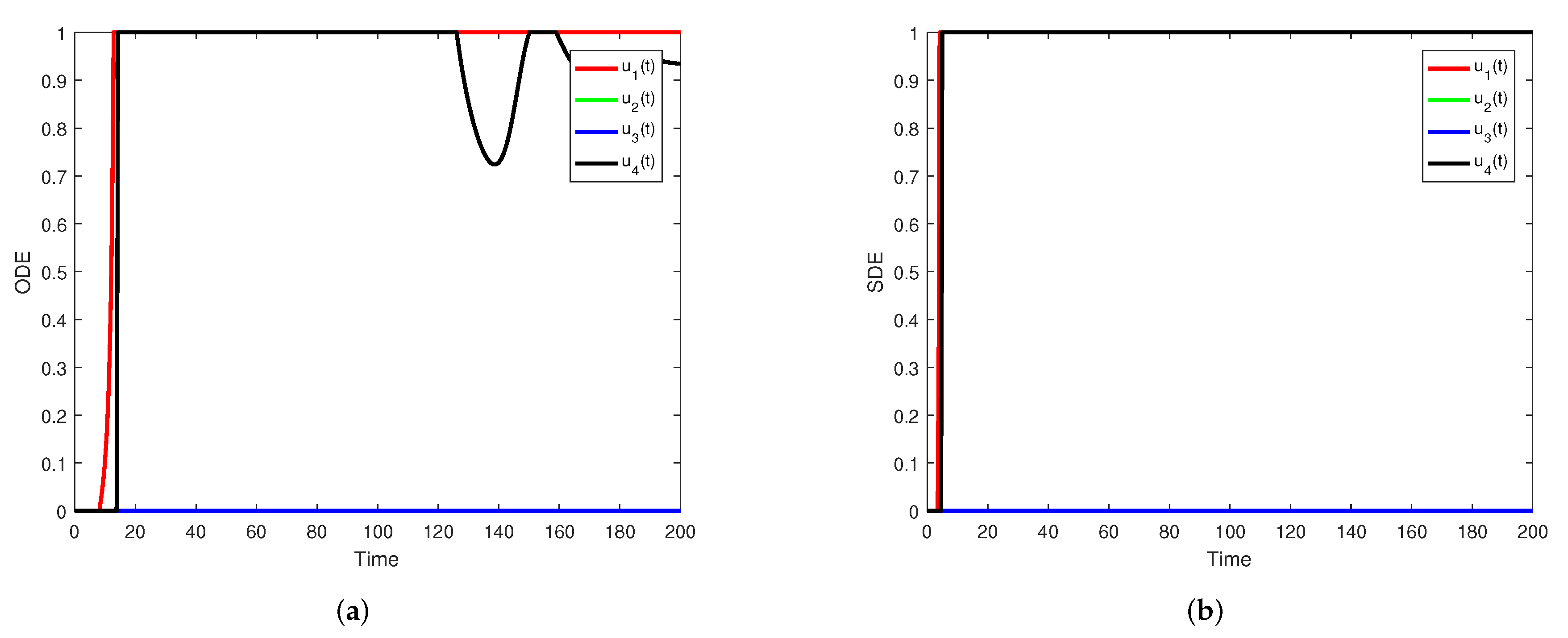
6.2. Numerical Simulations for Stochastic Optimality
7. Conclusions and Prediction
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Din, A.; Li, Y. Stationary distribution extinction and optimal control for the stochastic hepatitis B epidemic model with partial immunity. Phys. Scr. 2021, 96, 074005. [Google Scholar] [CrossRef]
- Li, Y.X.; Rauf, A.; Naeem, M.; Binyamin, M.A.; Aslam, A. Valency-based topological properties of linear hexagonal chain and hammer-like benzenoid. Complexity 2021, 2021, 9939469. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Badshah, Q.; Rahman, G.; Islam, S. Optimal control and dynamical aspects of a stochastic pine wilt disease model. J. Frankl. Inst. 2019, 356, 3991–4025. [Google Scholar] [CrossRef]
- Chen, S.-B.; Soradi-Zeid, S.; Jahanshahi, H.; Alcaraz, R.; Gómez-Aguilar, J.F.; Bekiros, S.; Chu, Y.-M. Optimal control of time-delay fractional equations via a joint application of radial basis functions and collocation method. Entropy 2020, 22, 1213. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-P.; al Bayatti, H.; Din, A.; Zeb, A. A vigorous study of fractional order COVID-19 model via ABC derivatives. Results Phys. 2021, 29, 104737. [Google Scholar] [CrossRef]
- Chen, S.-B.; Rajaee, F.; Yousefpour, A.; Alcaraz, R.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Bekiros, S.; Aly, A.A.; Jahanshahi, H. Antiretroviral therapy of HIV infection using a novel optimal type-2 fuzzy control strategy. Alex. Eng. J. 2021, 60, 1545–1555. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. Controlling heroin addiction via age-structured modeling. Adv. Differ. Equ. 2020, 2020, 521. [Google Scholar] [CrossRef]
- Chen, S.-B.; Rashid, S.; Hammouch, Z.; Noor, M.A.; Ashraf, R.; Chu, Y. Integral inequalities via Raina’s fractional integrals operator with respect to a monotone function. Adv. Differ. Equ. 2020, 2020, 647. [Google Scholar] [CrossRef]
- Ye, W.; Khan, M.A.; Alshahrani, M.Y.; Muhammad, T. A dynamical study of SARS-COV-2: A study of third wave. Results Phys. 2021, 29, 104705. [Google Scholar]
- Din, A.; Khan, A.; Zeb, A.; Ammi, M.R.S.; Tilioua, M.; Torres, D.F.M. Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application. Axioms 2021, 10, 290. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel, Theory and Application to Heat Transfer Model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Caputo, M. Linear model of dissipation whoseQ is almost frequency independent. II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Leibniz, G.W. Letter from Hanover, Germany to G.F.A. L’Hospital, September 30, 1695. Math. Schr. 1849, 2, 301–302. [Google Scholar]
- Abel, N.H. Oplösning af et par opgaver ved hjelp af bestemte integraler (Solution de quelques problèmes à l’aide d’int égrales définies, Solution of a couple of problems by means of definite integrals). Mag. Nat. 1823, 2, 55–68. [Google Scholar]
- Depnath, L. A brief historical introduction to fractional calculus. Int. J. Math. Educ. Sci. Technol. 2004, 35, 487–501. [Google Scholar] [CrossRef]
- Chen, S.-B.; Beigi, A.; Yousefpour, A.; Rajaee, F.; Jahanshahi, H.; Bekiros, S.; Martínez, R.A.; Chu, Y. Recurrent neural network-based robust non-singular sliding mode control with input saturation for a non-holonomic spherical robot. IEEE Access 2020, 8, 188441–188453. [Google Scholar] [CrossRef]
- Shen, Z.-H.; Chu, Y.; Khan, M.A.; Muhammad, S.; Al-Hartomy, O.A.; Higazy, M. Mathematical modeling and optimal control of the COVID-19 dynamics. Results Phys. 2021, 31, 105028. [Google Scholar] [CrossRef]
- Saima, R.; Noor, M.A.; Ashraf, R.; Chu, Y.-M. A new approach on fractional calculus and probability density function. AIMS Math. 2020, 5, 7041–7054. [Google Scholar]
- Rashid, S.; Sultana, S.; Karaca, Y.; Khalid, A.; Chu, Y.-M. Some further extensions considering discrete proportional fractional operators. Fractals 2021, 2240026. [Google Scholar] [CrossRef]
- Balzotti, C.; D’Ovidio, M.; Loreti, P. Fractional SIS epidemic models. Fractal Fract. 2020, 4, 44. [Google Scholar] [CrossRef]
- Almeida, R.; Qureshi, S. A fractional measles model having monotonic real statistical data for constant transmission rate of the disease. Fractal Fract. 2019, 3, 53. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chen, Y. Dynamic analysis of the viscoelastic pipeline conveying fluid with an improved variable fractional order model based on shifted Legendre polynomials. Fractal Fract. 2019, 3, 52. [Google Scholar] [CrossRef] [Green Version]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Hristov, J. Steady-state heat conduction in a medium with spatial non-singular fading memory: Derivation of Caputo-Fabrizio space-fractional derivative from Cattaneo concept with Jeffreys Kernel and analytical solutions. Therm. Sci. 2017, 21, 827–839. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A. Mathematical model of survival of fractional calculus, critics and their impact: How singular is our world? Results Phys. 2021, 31, 105208. [Google Scholar] [CrossRef]
- Khasminskii, R. Stochastic Stability of Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 66. [Google Scholar]
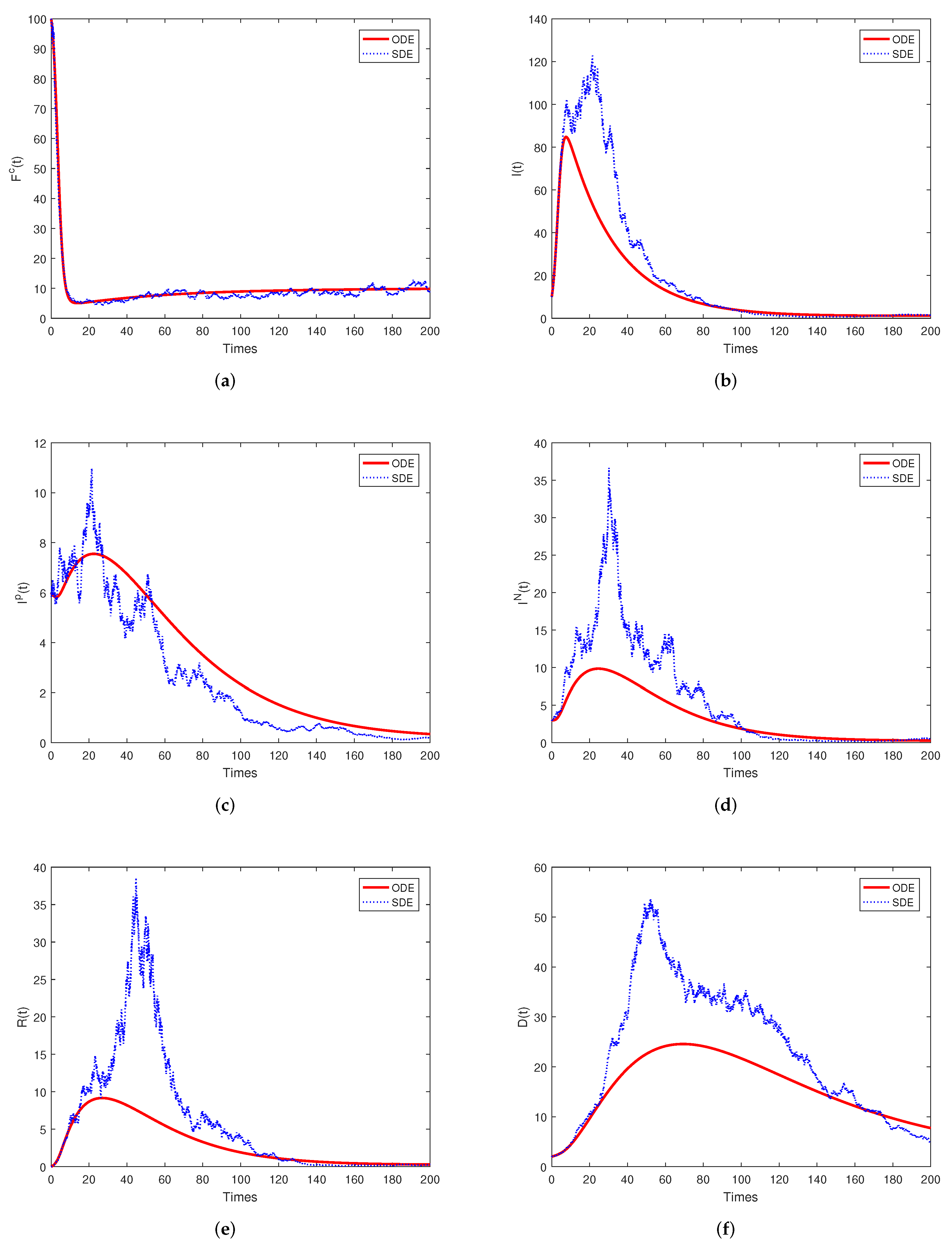
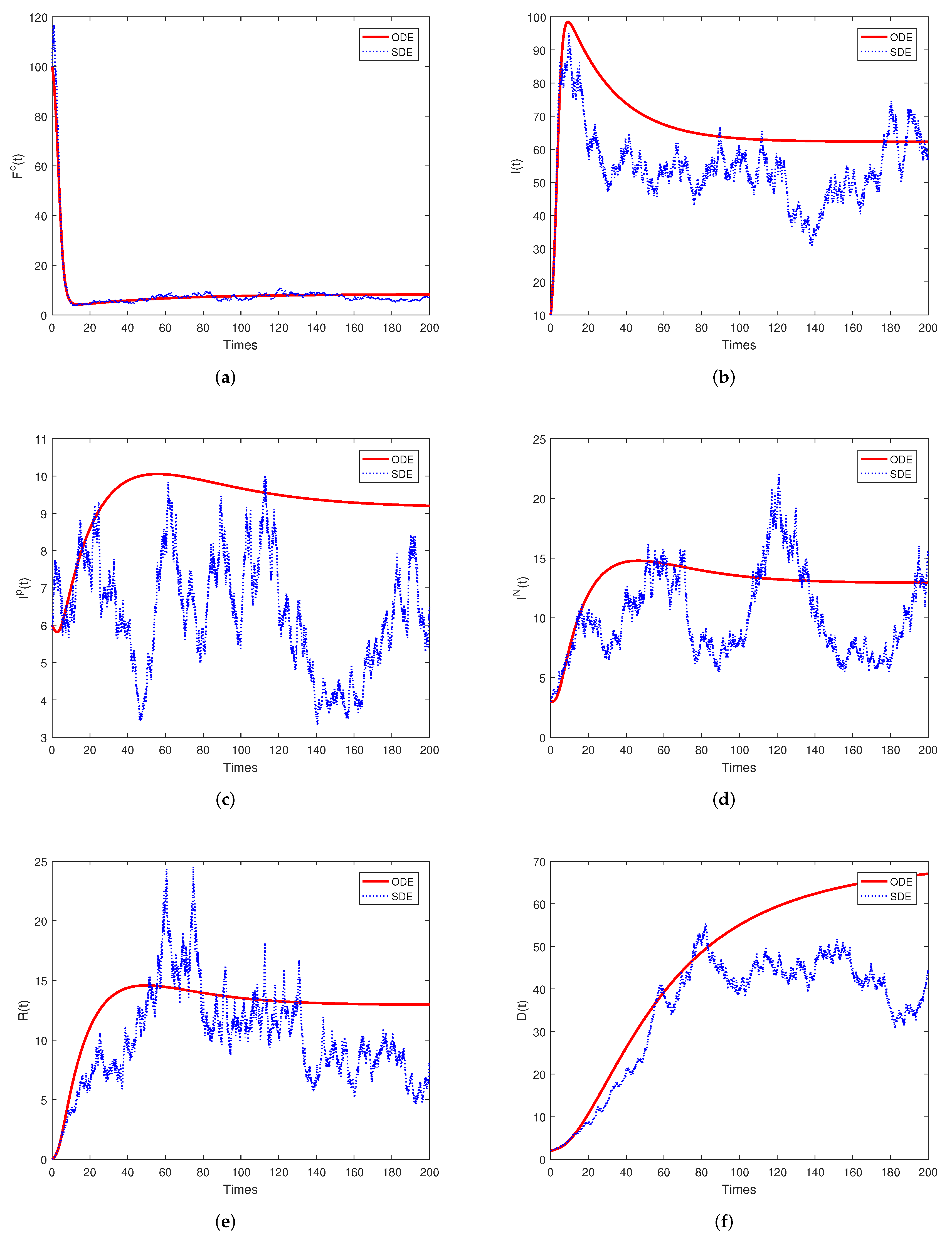
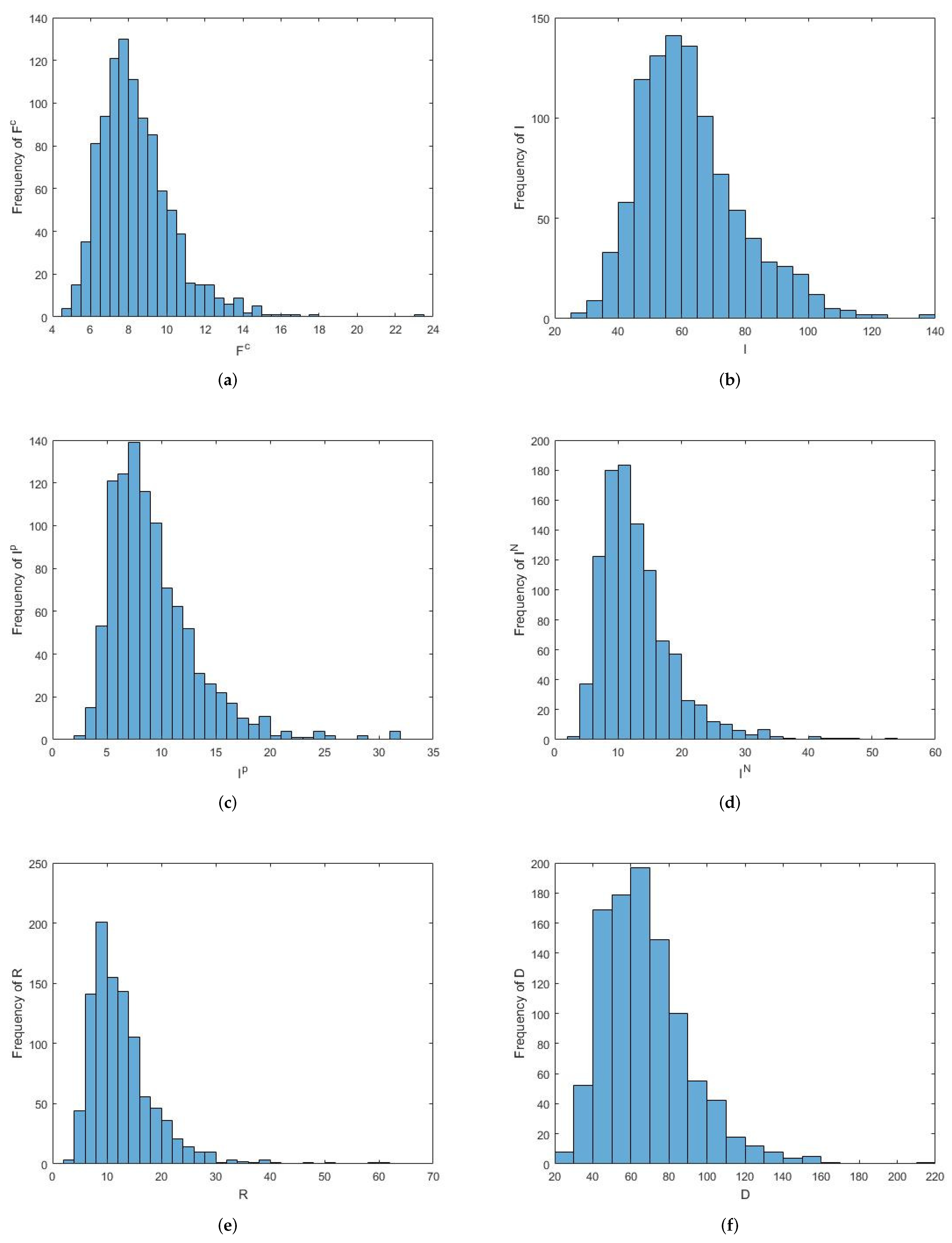

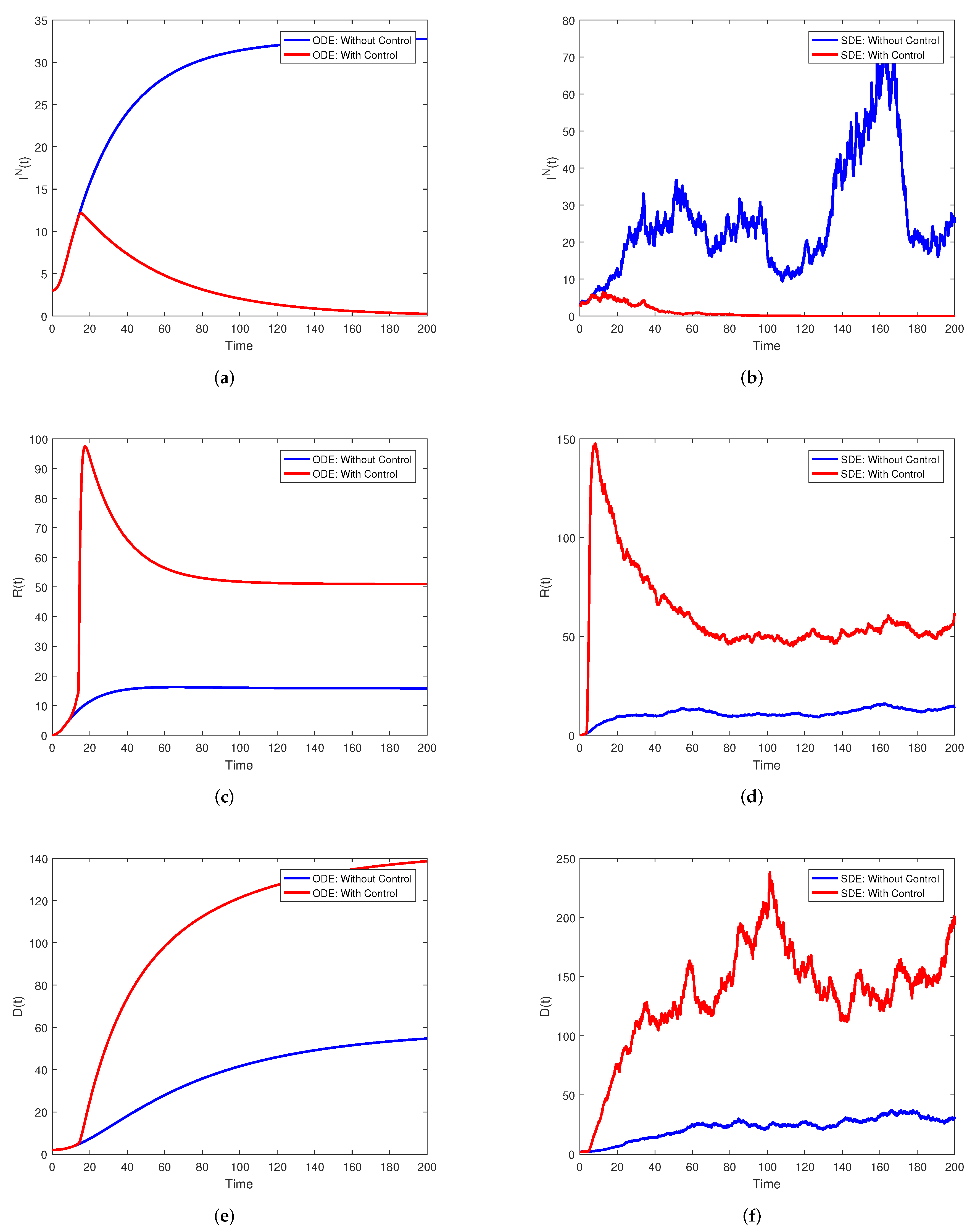
| Parameters | Unite | |||
|---|---|---|---|---|
| Per week | 0.05 | 2.5 | 2.8 | |
| d | Per week | 1/170.365 | 1/70.365 | 1/70.365 |
| Per week | 0.08 | 0.9 | 0.8 | |
| Per week | 0.01 | 0.08 | 0.8 | |
| Per week | 0.04 | 0.07 | 0.5 | |
| Per week | 0.004 | 0.07 | 0.004 | |
| Per week | 0.02 | 0.04 | 0.04 | |
| Per week | 0.004 | 0.004 | 0.005 | |
| Per week | 0.01 | 0.03 | 0.03 | |
| Per week | 0.03 | 0.1 | 0.1 | |
| v | Per week | 0.01 | 0.01 | 0.01 |
| Per week | 0.02 | 0.001 | 0.01 | |
| Noise intensity | 0.4 | 0.4 | 2 | |
| Noise intensity | 0.3 | 0.2 | 0.3 | |
| Noise intensity | 0.4 | 0.5 | 0.4 | |
| Noise intensity | 0.5 | 0.5 | 0.5 | |
| Noise intensity | 0.6 | 0.6 | 0.1 | |
| Noise intensity | 0.2 | 0.1 | 0.2 | |
| Initial value | 100 | 60 | 430 | |
| Initial value | 10 | 50 | 10 | |
| Initial value | 06 | 40 | 30 | |
| Initial value | 03 | 35 | 20 | |
| Initial value | 00 | 15 | 10 | |
| Initial value | 02 | 15 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Din, A.; Ain, Q.T. Stochastic Optimal Control Analysis of a Mathematical Model: Theory and Application to Non-Singular Kernels. Fractal Fract. 2022, 6, 279. https://doi.org/10.3390/fractalfract6050279
Din A, Ain QT. Stochastic Optimal Control Analysis of a Mathematical Model: Theory and Application to Non-Singular Kernels. Fractal and Fractional. 2022; 6(5):279. https://doi.org/10.3390/fractalfract6050279
Chicago/Turabian StyleDin, Anwarud, and Qura Tul Ain. 2022. "Stochastic Optimal Control Analysis of a Mathematical Model: Theory and Application to Non-Singular Kernels" Fractal and Fractional 6, no. 5: 279. https://doi.org/10.3390/fractalfract6050279
APA StyleDin, A., & Ain, Q. T. (2022). Stochastic Optimal Control Analysis of a Mathematical Model: Theory and Application to Non-Singular Kernels. Fractal and Fractional, 6(5), 279. https://doi.org/10.3390/fractalfract6050279







