A New Adaptive Robust Sliding Mode Control Approach for Nonlinear Singular Fractional-Order Systems
Abstract
:1. Introduction
2. Preliminaries
3. Main Results
3.1. The Design of Sliding Mode State Feedback Controller
3.2. The Design of Sliding Mode Output Feedback Controller
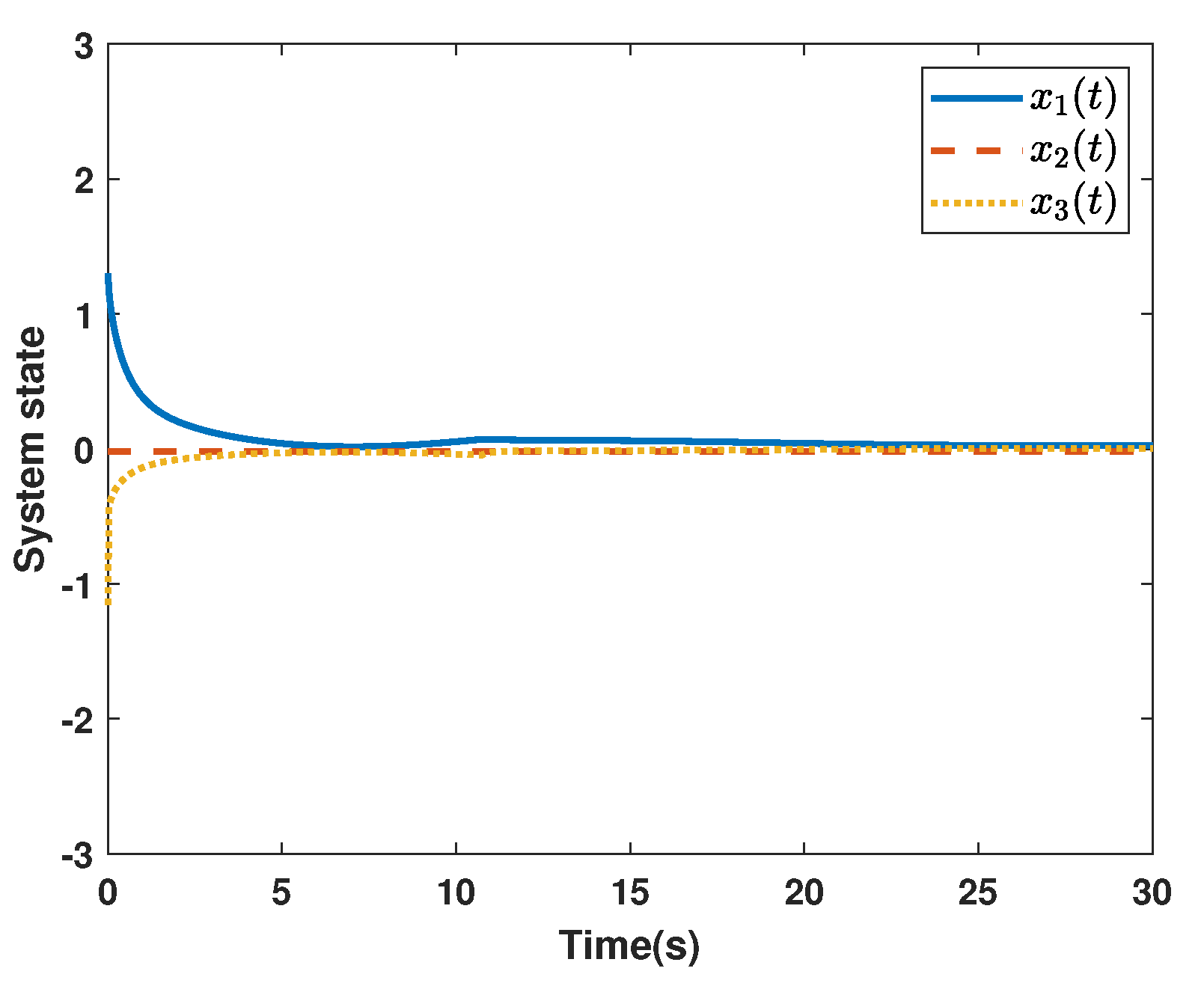
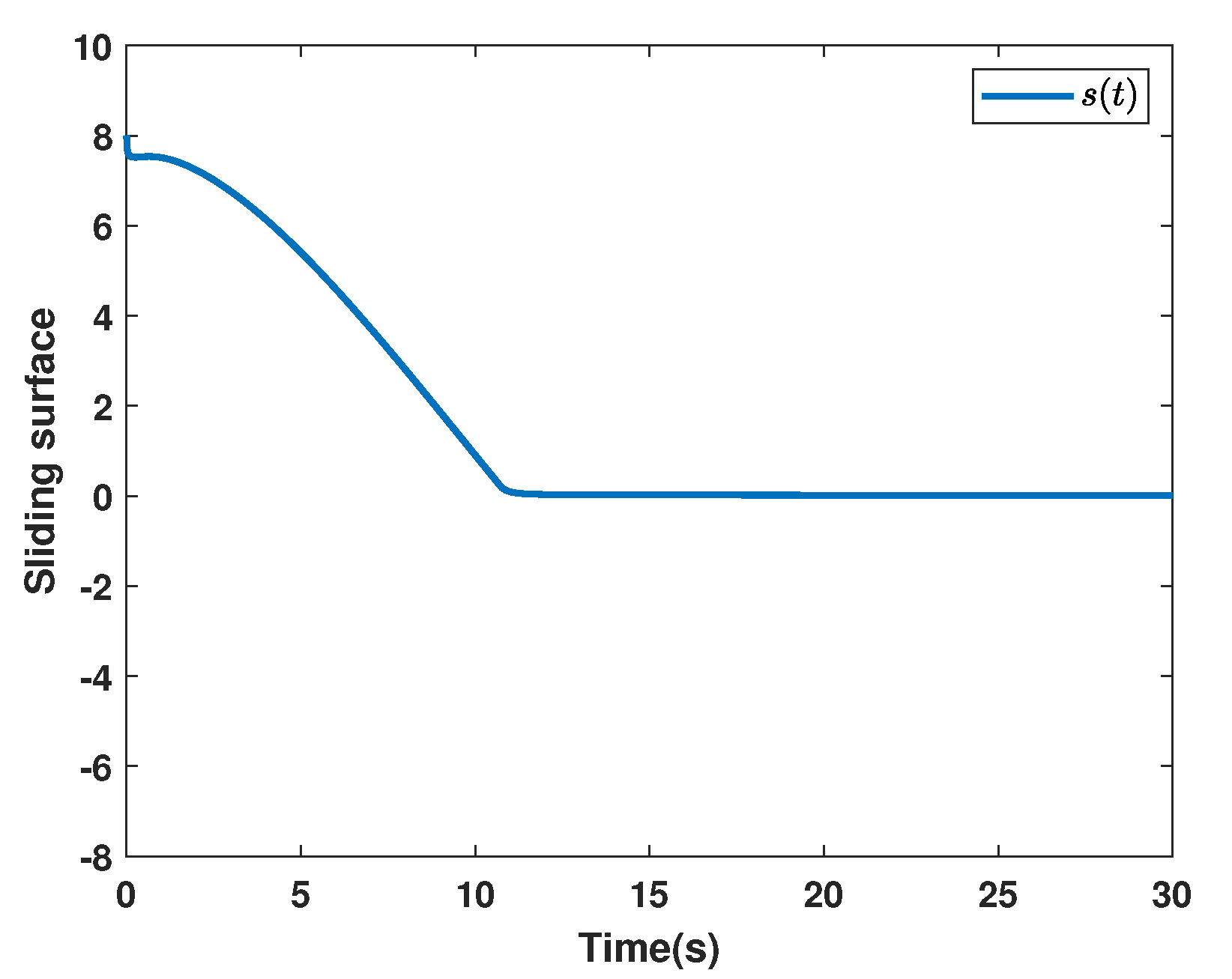
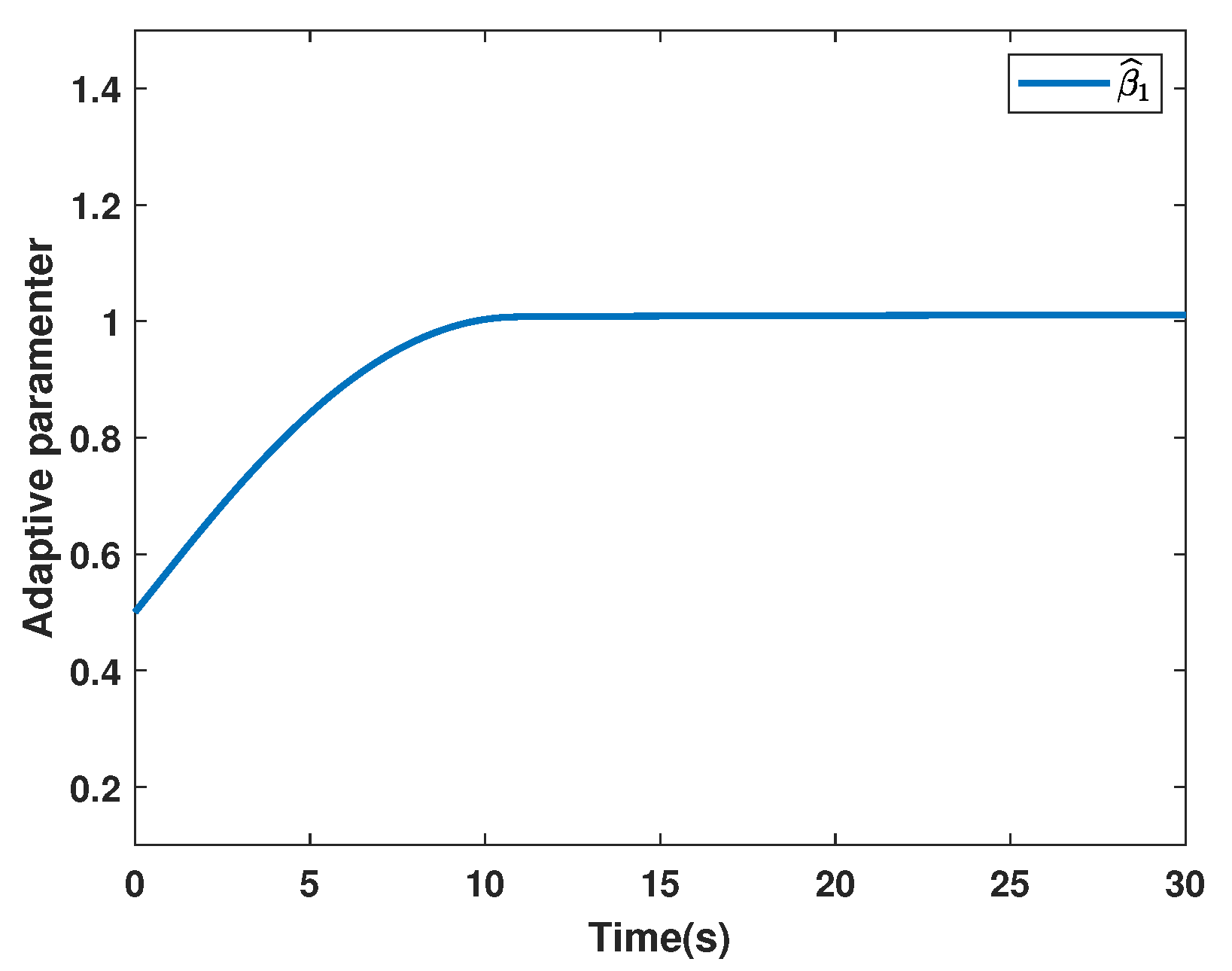
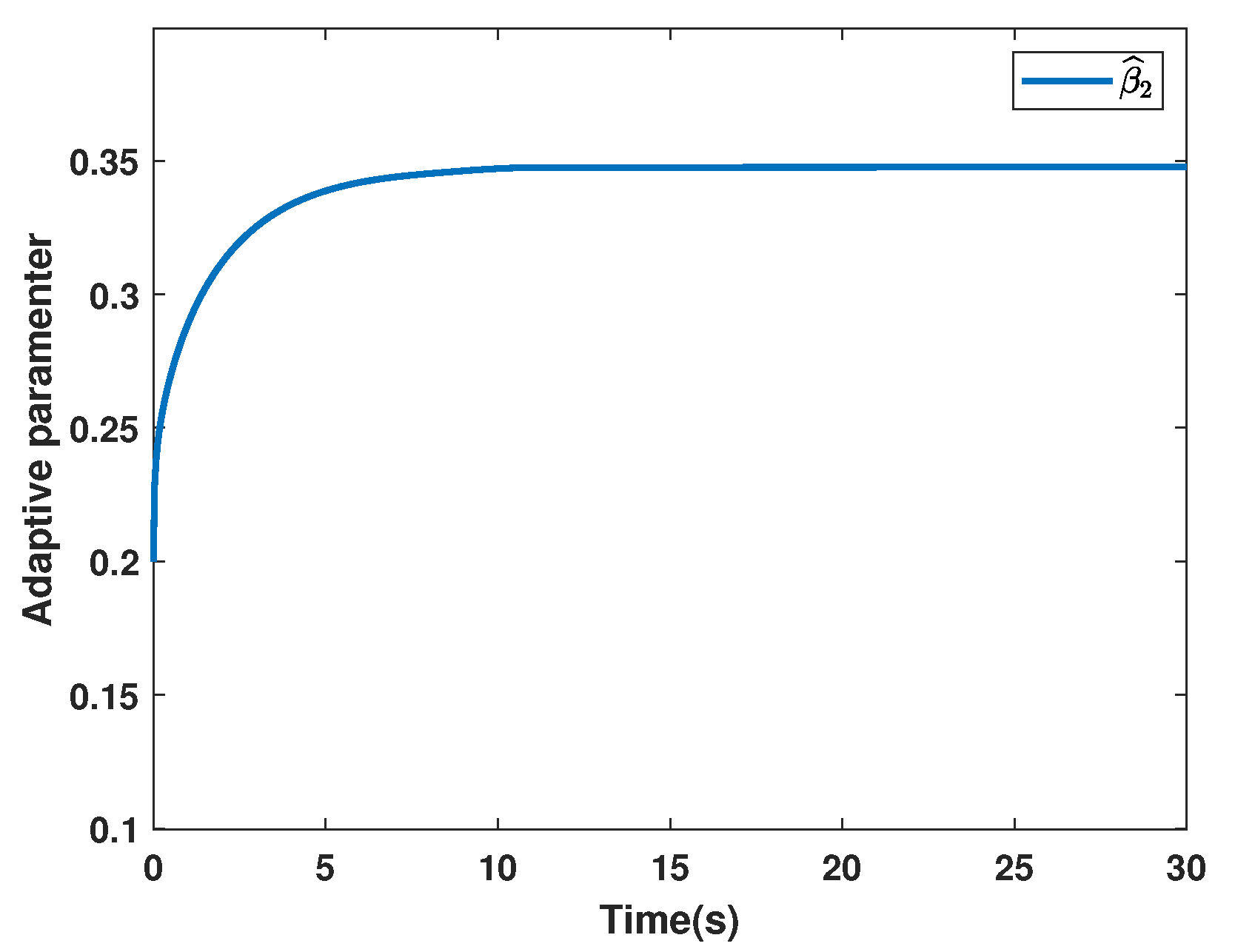
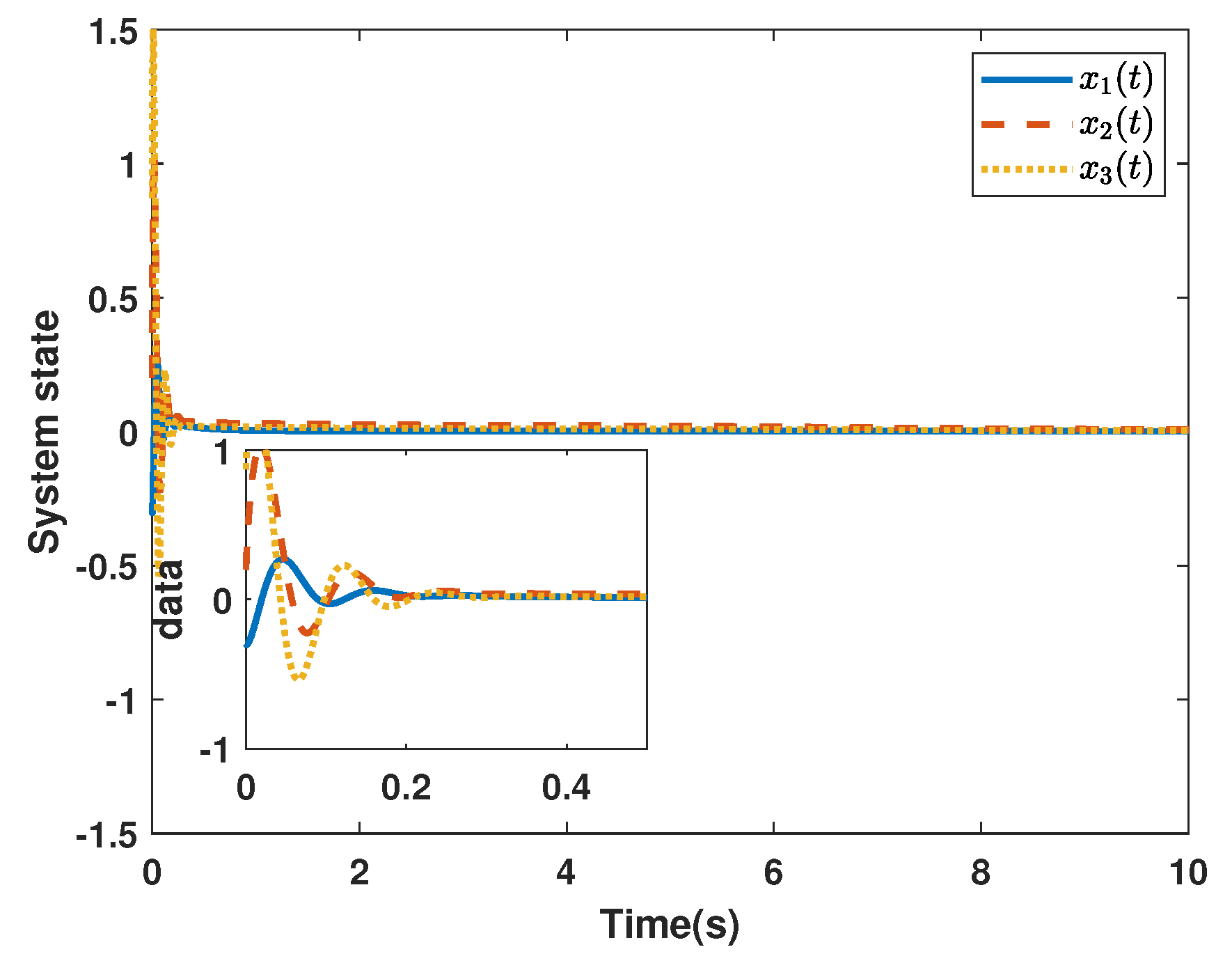
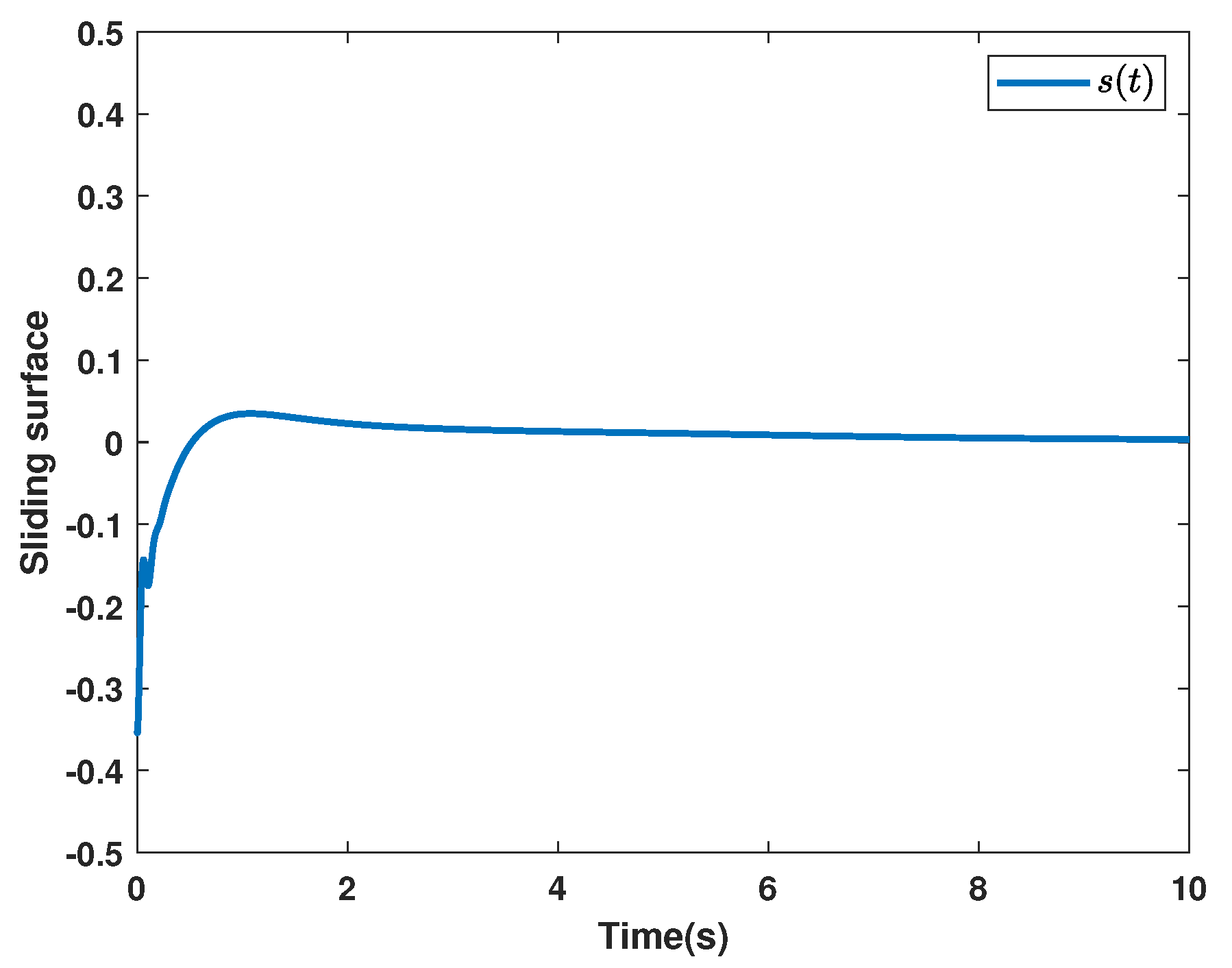
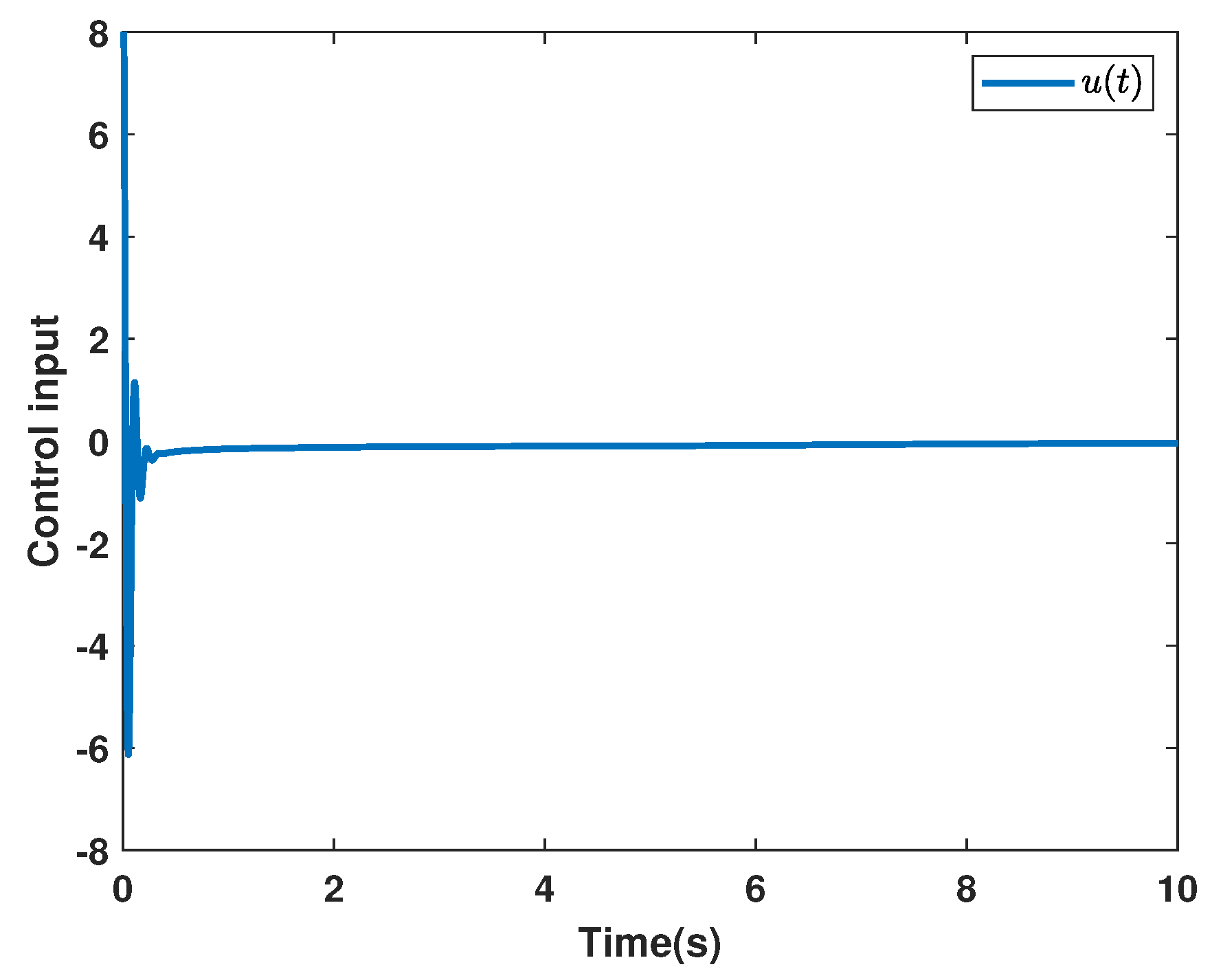
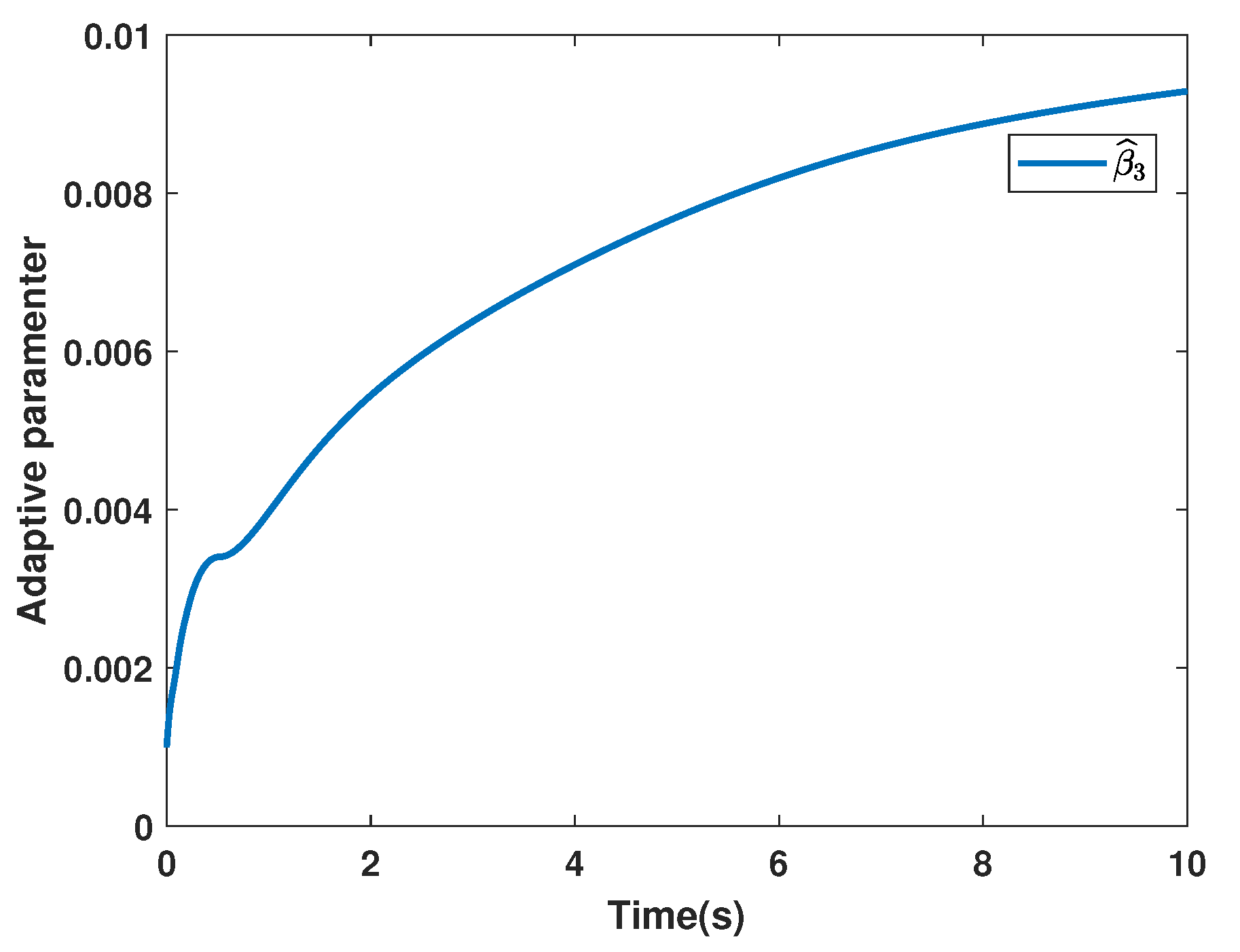
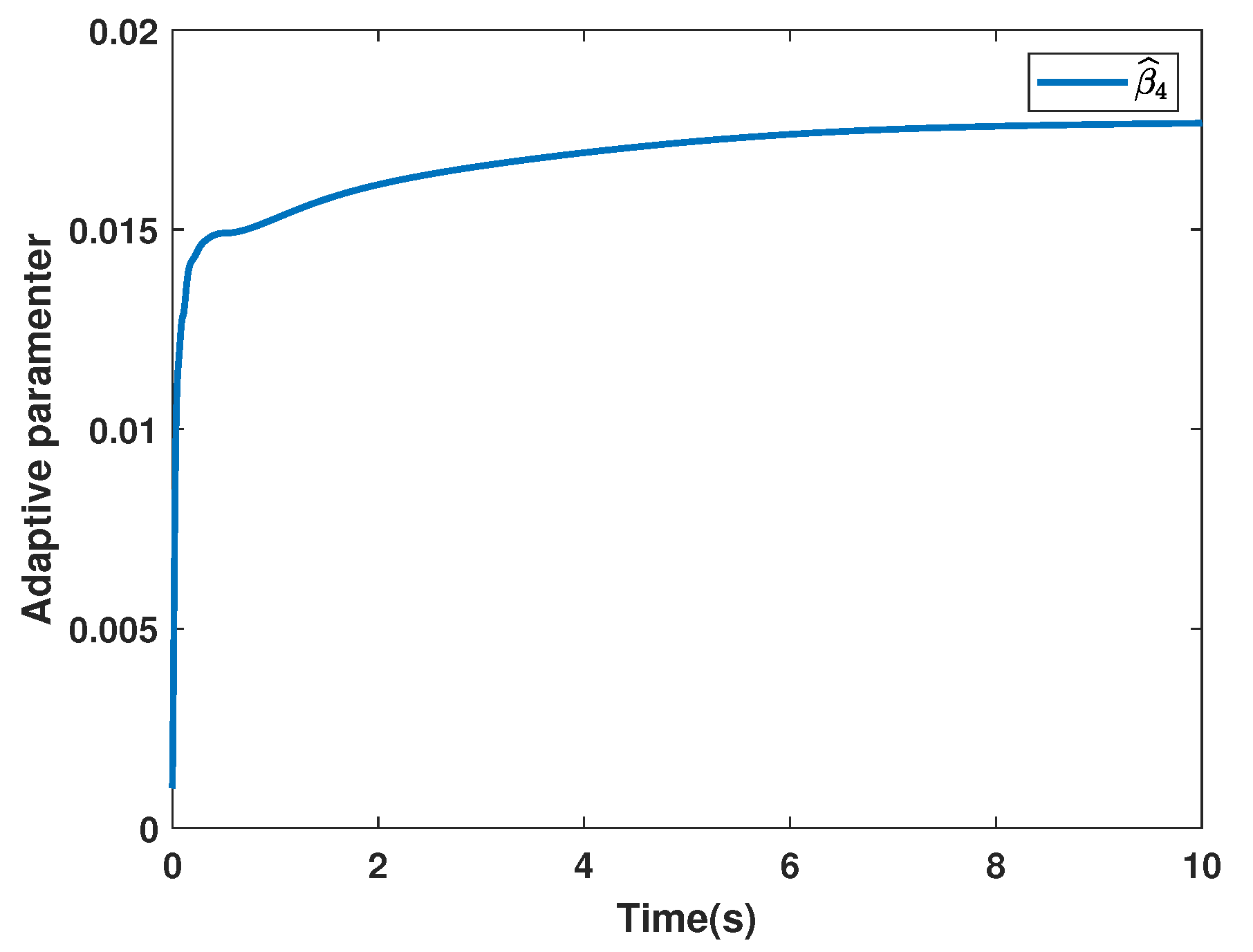
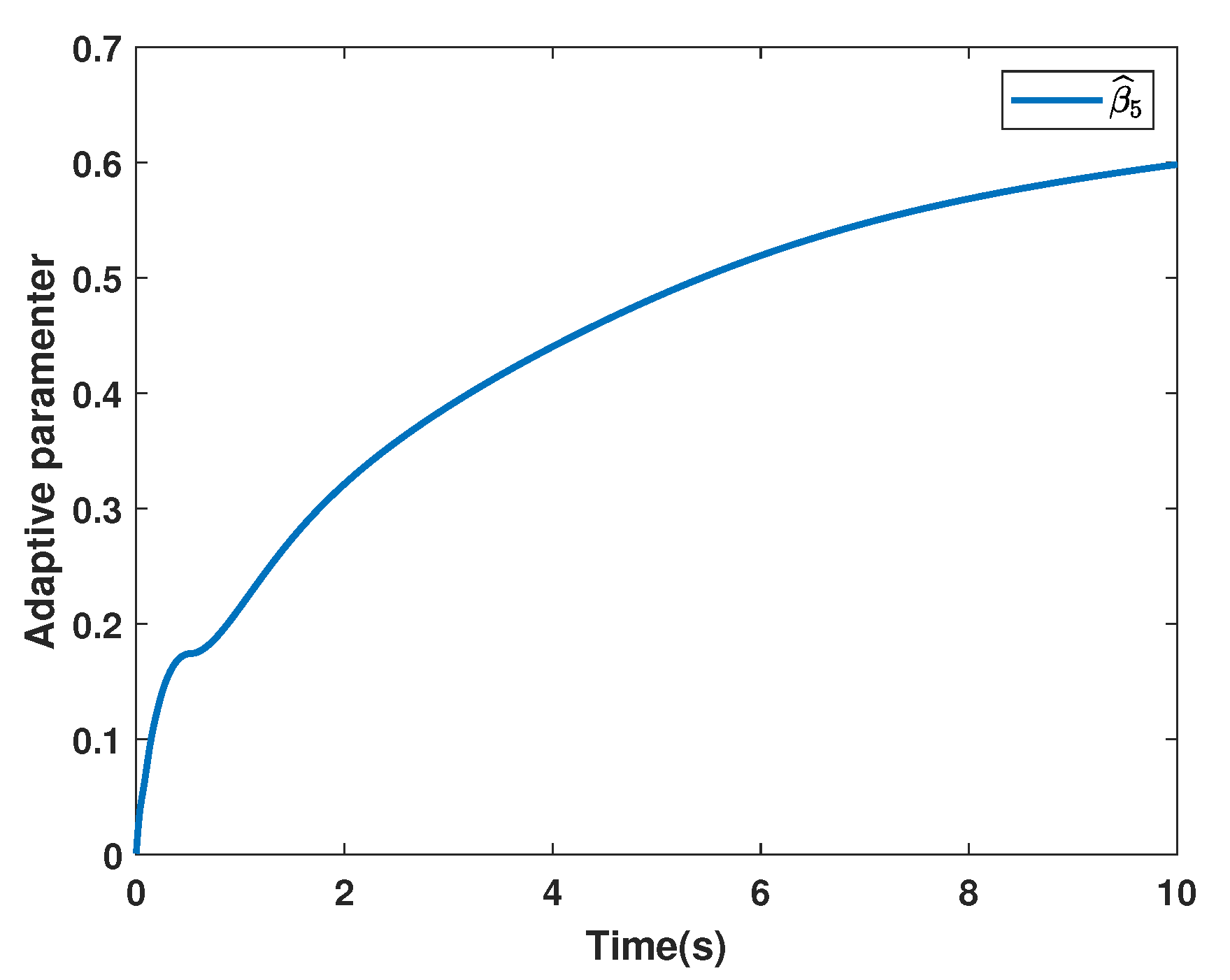
4. Simulation Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- function dx1 = fcn(x1,x2,x3,s1,u)
- A = [-1 0 -1;0 0 0;0 -1 -1];
- B = [1;0;1];
- V1 = [2 4 6];
- OO = A+U*s1*V1;
- dx1 = OO(1,1)*x1+OO(1,2)*x2+OO(1,3)*x3+B(1,1)*(u+x1*sin(x1));


References
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef] [Green Version]
- Kaczorek, T. Singular fractional linear systems and electrical circuits. Int. J. Appl. Math. Comput. Sci. 2011, 21, 379–384. [Google Scholar] [CrossRef]
- Zhang, X.F.; Huang, W.K. Adaptive neural network sliding mode control for nonlinear singular fractional order systems with mismatched uncertainties. Fractal Fract. 2020, 4, 50. [Google Scholar] [CrossRef]
- Li, R.C.; Zhang, Q.L. Robust H∞ sliding mode observer design for a class of Takagi-Sugeno fuzzy descriptor systems with time-varying delay. Appl. Math. Comput. 2018, 337, 158–178. [Google Scholar] [CrossRef]
- Boukal, Y.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Robust H∞ Observer-based control of fractional-order systems with gain parametrization. IEEE Trans. Autom. Control 2017, 62, 5710–5723. [Google Scholar] [CrossRef]
- Ibrir, S.; Bettayeb, M. New sufficient conditions for observer-based control of frational order uncertain systems. Automatica 2015, 59, 216–223. [Google Scholar] [CrossRef]
- Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0<α<2. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3237–3241. [Google Scholar]
- Qi, W.H.; Zong, G.D.; Karimi, H.R. Sliding mode control for nonlinear stochastic singular semi-markov jump systems. IEEE Trans. Autom. Control 2019, 65, 361–368. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Xie, X.P.; Chadli, M.; Xie, S.R.; Peng, Y. Sliding mode control of fuzzy singularly perturbed descriptor systems. IEEE Trans. Fuzzy Syst. 2020, 29, 2349–2360. [Google Scholar] [CrossRef]
- Zhang, X.F.; Dong, J. LMI criteria for admissibility and robust stabilization of singular fractional-order systems possessing poly-topic uncertainties. Fractal Fract. 2020, 4, 58. [Google Scholar] [CrossRef]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Wei, Y.; Tse, P.W.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Trans. 2017, 69, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Meng, B.; Wang, X.H.; Zhang, Z.Y.; Wang, Z. Necessary and sufficient conditions for normalization and sliding mode control of singular fractional-order systems with uncertainties. Sci. China Inf. Sci. 2020, 63, 152202. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0<α<1 case. ISA Trans. 2017, 82, 42–50. [Google Scholar] [PubMed]
- Zhang, X.F.; Yan, Y.Q. Admissibility of fractional order descriptor systems based on complex variables: An LMI approach. Fractal Fract. 2020, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Marir, S.; Chadli, M.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. J. Frankl. Inst. 2017, 354, 752–766. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhao, Z.L.; Wang, Q.G. Static and dynamic output feedback stabilisation of descriptor fractional order systems. IET Control Theory Appl. 2020, 14, 324–333. [Google Scholar] [CrossRef]
- Lin, C.; Chen, B.; Wang, Q.G. Static output feedback stabilization for fractional-order systems in T-S fuzzy models. Neurocomputing 2016, 2016 218, 354–358. [Google Scholar] [CrossRef]
- Ji, Y.D.; Su, L.Q.; Qiu, Q. Design of fuzzy output feedback stabilization for uncertain fractional-order systems. Neurocomputing 2016, 173, 1683–1693. [Google Scholar] [CrossRef]
- Jiang, J.F.; Li, H.K.; Zhao, K.; Cao, D.Q.; Guirao, J.L. Finite time stability and sliding mode control for uncertain variable fractional order nonlinear systems. Adv. Differ. Equ. 2021, 127. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, M.H.; Zheng, X.M.; Han, F.L.; Yu, X.H. Full-order terminal sliding-mode control of MIMO systems with unmatched uncertainties. J. Frankl. Inst. 2018, 355, 653–674. [Google Scholar] [CrossRef]
- Sheng, Y.Z.; Bai, W.J.; Xie, Y.W. Fractional-order (PID)-D-lambda sliding mode control for hypersonic vehicles with neural network disturbance compensator. Nonlinear Dyn. 2021, 103, 849–863. [Google Scholar] [CrossRef]
- Jiang, J.F.; Cao, D.Q.; Chen, H.T. Sliding mode control for a class of variable-order fractional chaotic systems. J. Frankl. Inst. 2020, 357, 10127–10158. [Google Scholar] [CrossRef]
- Zhan, T.; Liu, X.; Ma, S. A new singular system approach to output feedback sliding mode control for fractional order nonlinear systems. J. Frankl. Inst. 2018, 355, 6746–6762. [Google Scholar] [CrossRef]
- Fei, J.T.; Lu, C. Adaptive fractional order sliding mode controller with neural estimator. J. Frankl. Inst. 2018, 355, 2369–2391. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Autom. Control 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Pisano, A.; Rapaić, M.R.; Jelićić, Z.D.; Usai, E. Sliding mode control approaches to the robust regulation of linear multivariable fractional-order dynamics. Int. J. Robust Nonlinear Control 2010, 20, 2045–2056. [Google Scholar] [CrossRef]
- Sun, G.; Wu, L.; Kuang, Z.; Ma, Z.; Liu, J. Practical tracking control of linear motor via fractional-order sliding mode. Automatica 2018, 94, 221–235. [Google Scholar] [CrossRef]
- Dadras, S.; Momeni, H.R. Control of a fractional-order economical system via sliding mode. Phys. A Stat. Mech. Its Appl. 2010, 389, 2434–2442. [Google Scholar] [CrossRef]
- Li, R.C.; Zhang, X.F. Adaptive sliding mode observer design for a class of T-S fuzzy descriptor fractional order systems. IEEE Trans. Fuzzy Syst. 2020, 28, 1951–1960. [Google Scholar] [CrossRef]
- Han, H.G.; Wu, X.L.; Qiao, J.F. Design of robust sliding mode control with adaptive reaching Law. IEEE Trans Cybern. 2020, 50, 4415–4424. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Robust adaptive fault-tolerant control for a class of unknown nonlinear systems. IEEE Trans. Ind. Electron. 2017, 64, 585–594. [Google Scholar] [CrossRef]
- Sheng, D.; Wei, Y.; Cheng, S.; Wang, Y. Observer-based adaptive backstepping control for fractional order systems with input saturation. ISA Trans. 2018, 82, 18–29. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.X.; Yang, G.H. Fuzzy adaptive output feedback control of uncertain nonlinear systems with prescribed performance. IEEE Trans. Cybern. 2018, 48, 1342–1354. [Google Scholar] [CrossRef] [PubMed]
- Bigdeli, N.; Ziazi, H.A. Finite-time fractional-order adaptive intelligent backstepping sliding mode control of uncertain fractional-order chaotic systems. J. Frankl. Inst. 2017, 354, 160–183. [Google Scholar] [CrossRef]
- Mirzajani, S.; Aghababa, M.P.; Heydari, A. Adaptive T-S fuzzy control design for fractional-order systems with parametric uncertainty and input constraint. Fuzzy Sets Syst. 2019, 365, 22–39. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Ghaemi, S. A modified sliding mode approach for synchronization of fractional-order chaotic/hyperchaotic systems by using new self-structuring hierarchical type-2 fuzzy neural network. Neurocomputing 2016, 191, 200–213. [Google Scholar] [CrossRef]
- Hosseinnia, S.H.; Ghaderi, R.; Ranjbar, A.N.; Mahmoudian, M.; Momani, S. Sliding mode synchronization of an uncertain fractional order chaotic system. Comput. Math. Appl. 2010, 59, 1637–1643. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.C.; Lee, T.Y. Chaos synchronization of uncertain fractional-order chaotic systems with time delay based on adaptive fuzzy sliding mode control. IEEE Trans. Fuzzy Syst. 2011, 19, 623–635. [Google Scholar]
- Aghababa, M.P. Design of a chatter-free terminal sliding mode controller for nonlinear fractional-order dynamical systems. Int. J. Control 2013, 86, 1744–1756. [Google Scholar] [CrossRef]
- Wang, J.; Shao, C.; Chen, Y.Q. Fractional order sliding mode control via disturbance observer for a class of fractional order systems with mismatched disturbance. Mechatronics 2018, 53, 8–19. [Google Scholar] [CrossRef]
- Pashaei, S.; Badamchizadeh, M. A new fractional-order sliding mode controller via a nonlinear disturbance observer for a class of dynamical systems with mismatched disturbances. ISA Trans. 2016, 63, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Li, R.C.; Zhang, Q.L.; Li, J.X. Adaptive robust H∞ sliding mode control for singular systems with time-varying delay and uncertain derivative matrix. Int. J. Control Autom. Syst. 2019, 17, 3179–3193. [Google Scholar] [CrossRef]
- Cuong, H.M.; Dong, H.Q.; Trieu, P.V.; Tuan, L.A. Adaptive fractional-order terminal sliding mode control of rubber-tired gantry cranes with uncertainties and unknown disturbances. Mech. Syst. Signal Process. 2021, 154, 107601. [Google Scholar] [CrossRef]
- Tuan, L.A. Neural observer and adaptive fractional-order backstepping fast-terminal sliding-mode control of RTG cranes. IEEE Trans. Ind. Electron. 2021, 68, 434–442. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef] [PubMed]
- Dassios, I.; Baleanu, D. Caputo and related fractional derivatives in singular systems. Appl. Math. Comput. 2018, 337, 591–606. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Huang, W.; Liu, Q. A New Adaptive Robust Sliding Mode Control Approach for Nonlinear Singular Fractional-Order Systems. Fractal Fract. 2022, 6, 253. https://doi.org/10.3390/fractalfract6050253
Chen S, Huang W, Liu Q. A New Adaptive Robust Sliding Mode Control Approach for Nonlinear Singular Fractional-Order Systems. Fractal and Fractional. 2022; 6(5):253. https://doi.org/10.3390/fractalfract6050253
Chicago/Turabian StyleChen, Shunan, Wenkai Huang, and Qiang Liu. 2022. "A New Adaptive Robust Sliding Mode Control Approach for Nonlinear Singular Fractional-Order Systems" Fractal and Fractional 6, no. 5: 253. https://doi.org/10.3390/fractalfract6050253
APA StyleChen, S., Huang, W., & Liu, Q. (2022). A New Adaptive Robust Sliding Mode Control Approach for Nonlinear Singular Fractional-Order Systems. Fractal and Fractional, 6(5), 253. https://doi.org/10.3390/fractalfract6050253




