Abundant Exact Travelling Wave Solutions for a Fractional Massive Thirring Model Using Extended Jacobi Elliptic Function Method
Abstract
1. Introduction
2. Preliminaries
- (I)
- Ifthenfor
- (II)
- (III)
3. The Extended Jacobi Elliptic Equation Method
3.1. The Jacobi Elliptic Functions
| , | , | , |
| , | ||
| , | . |
| , | , | , |
| , | ||
| , | . |
| , | , | , |
| , | ||
| , | . |
3.2. Extended Jacobi Elliptic Function Expansion Method
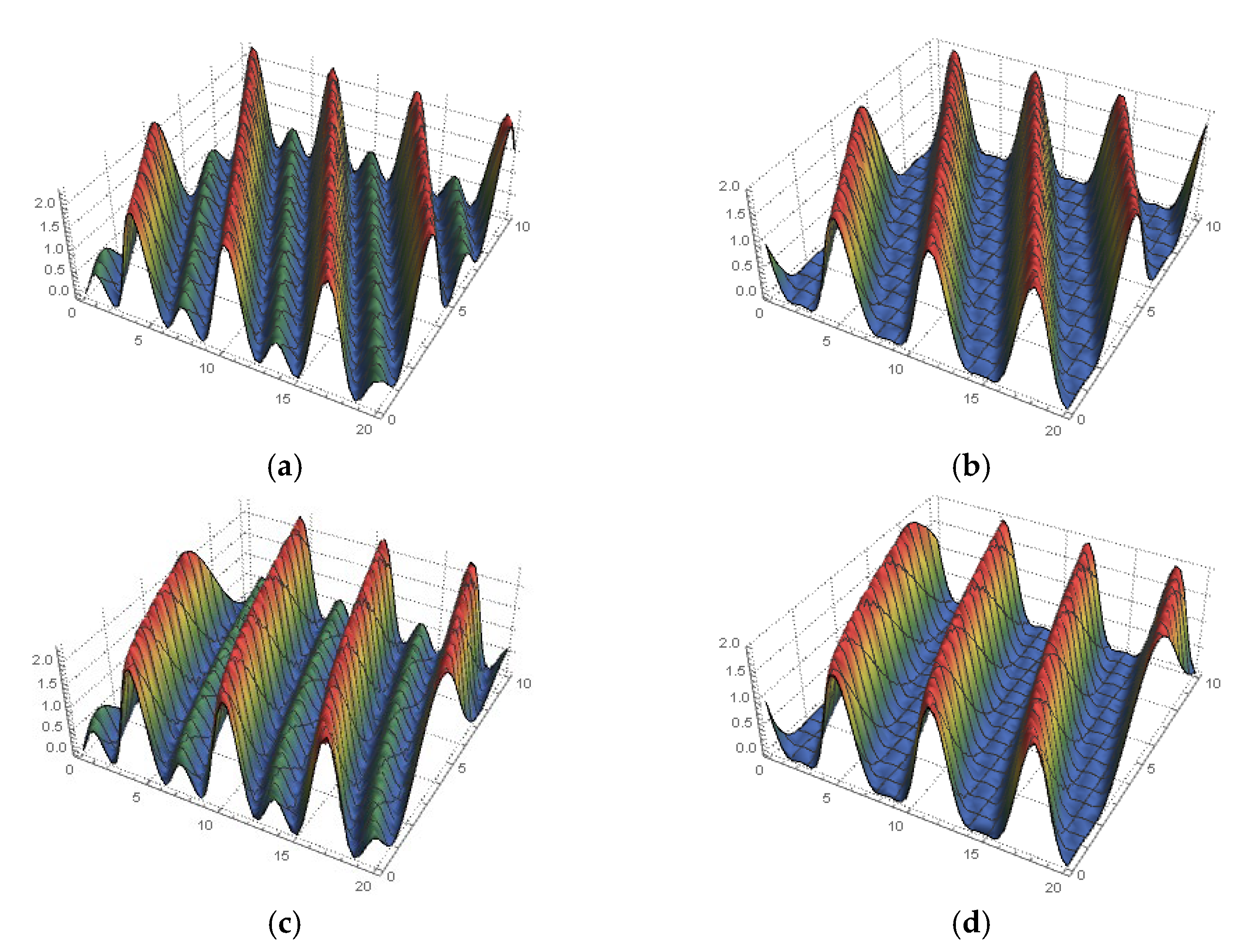
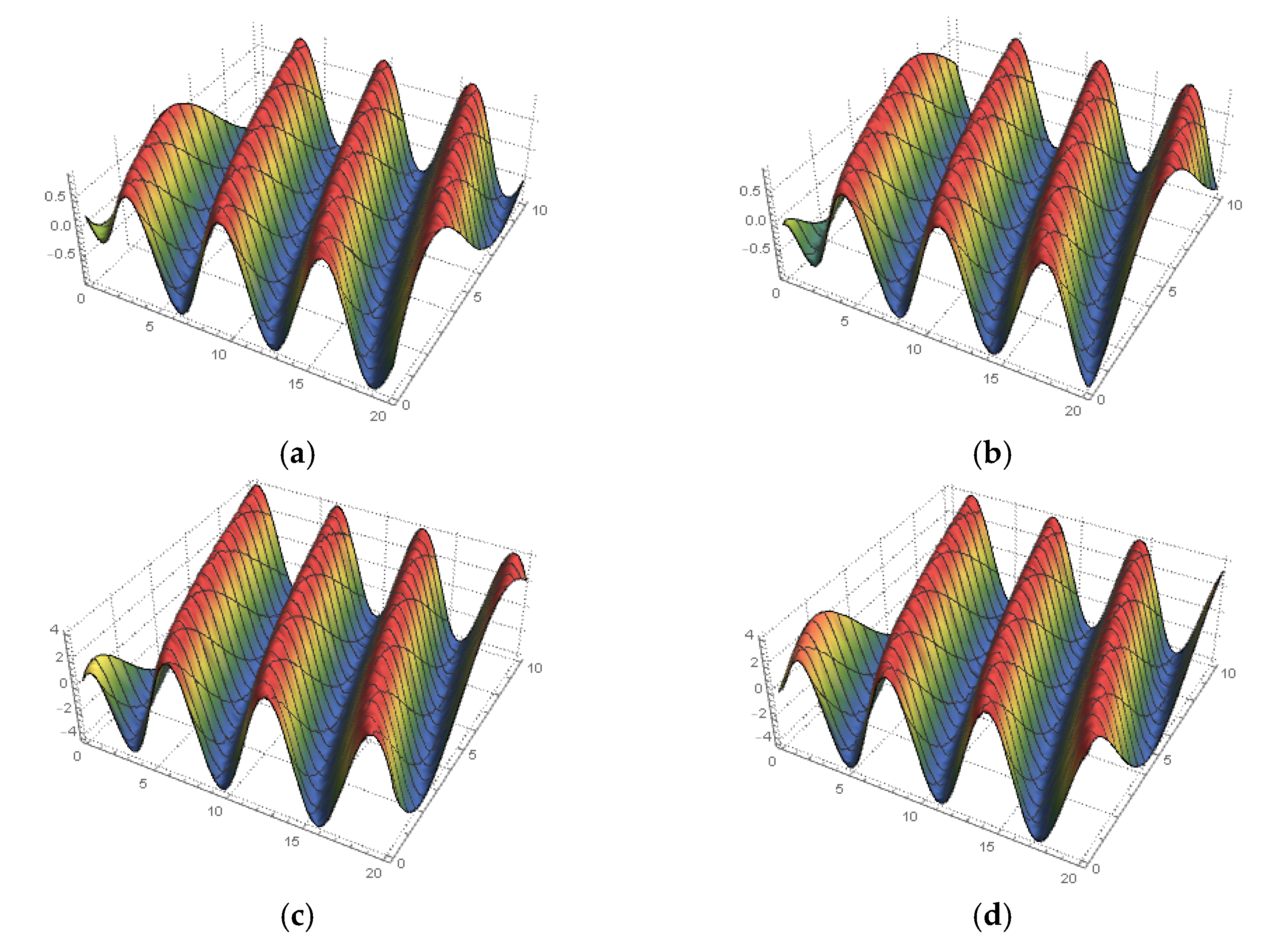
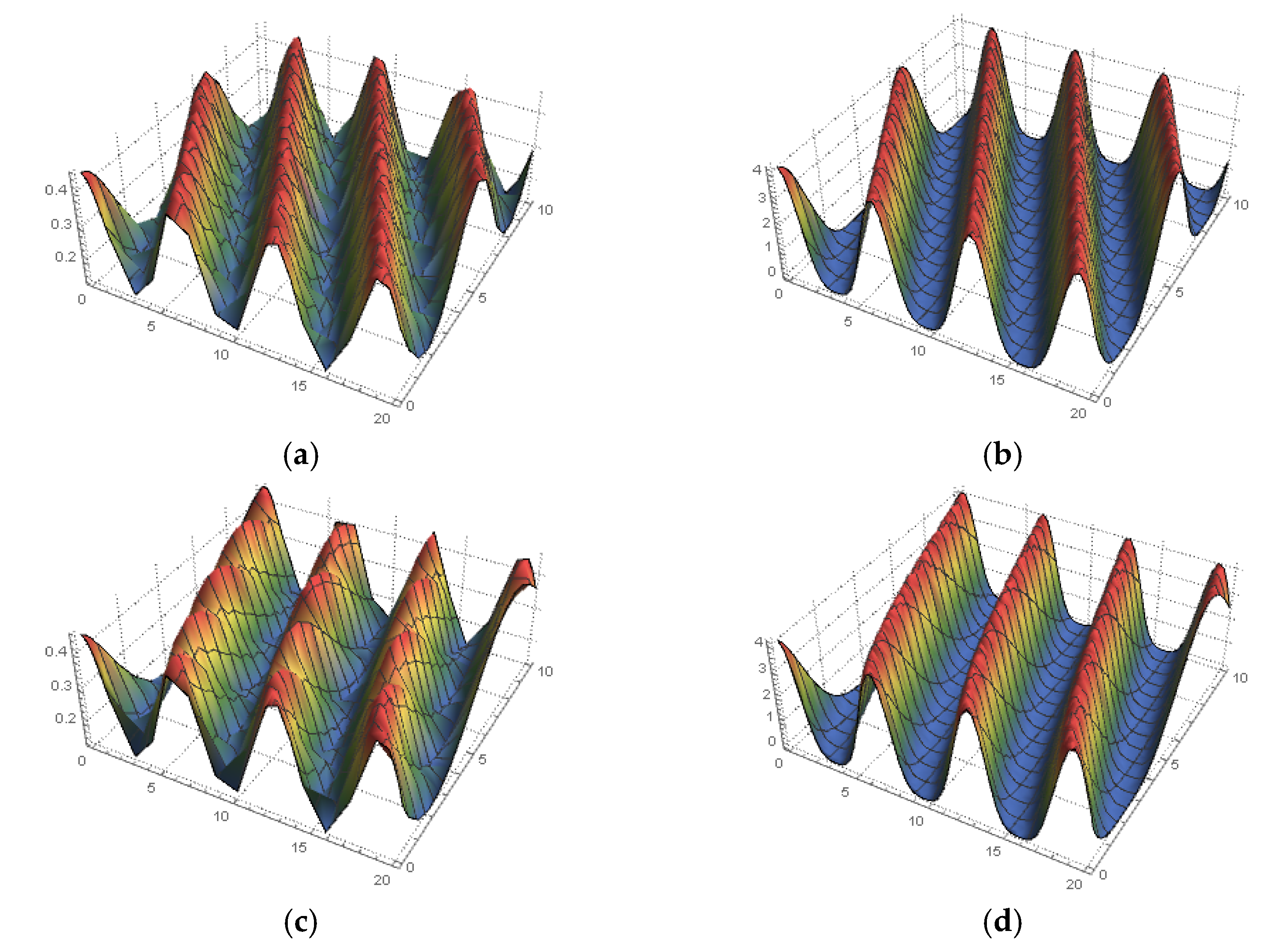
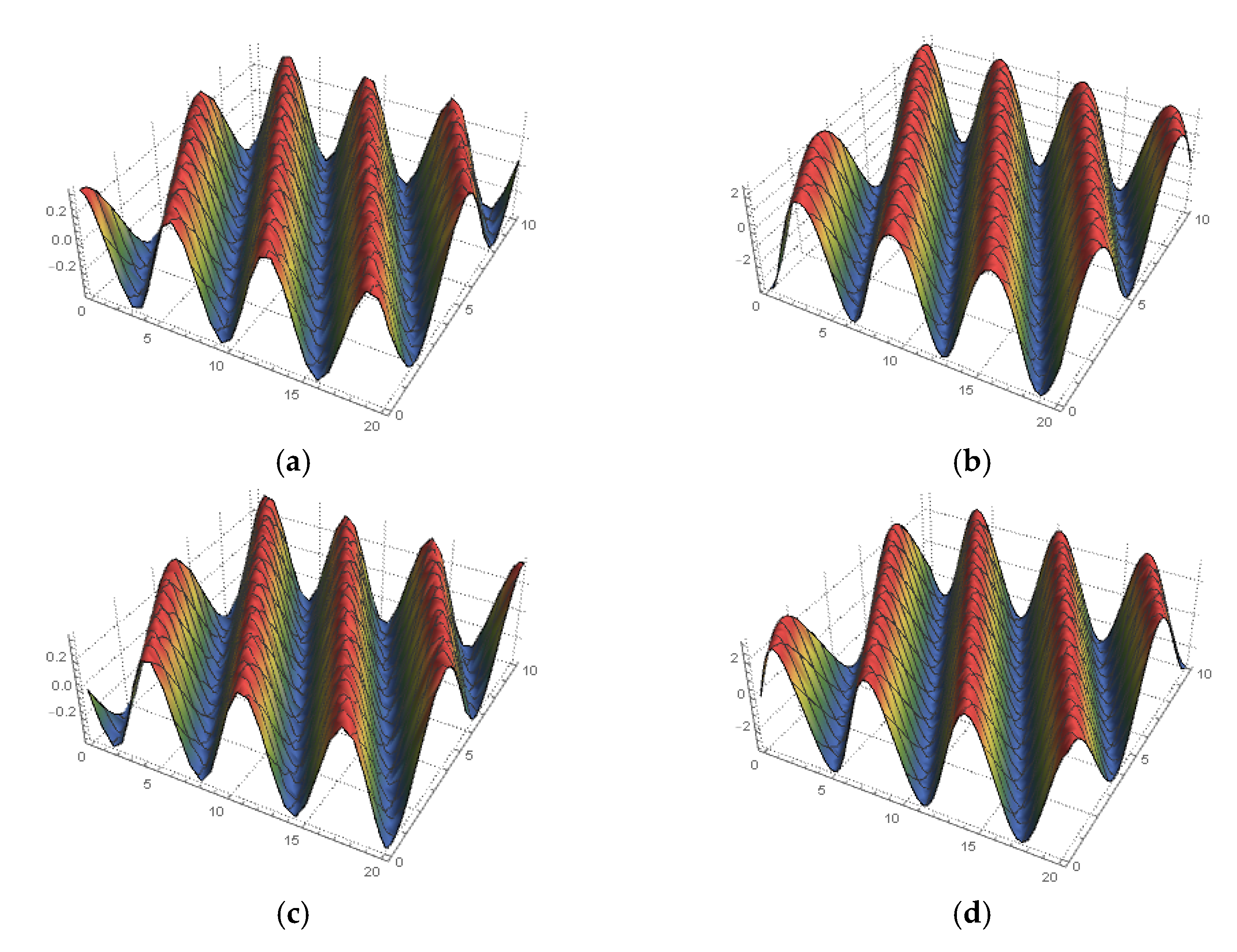
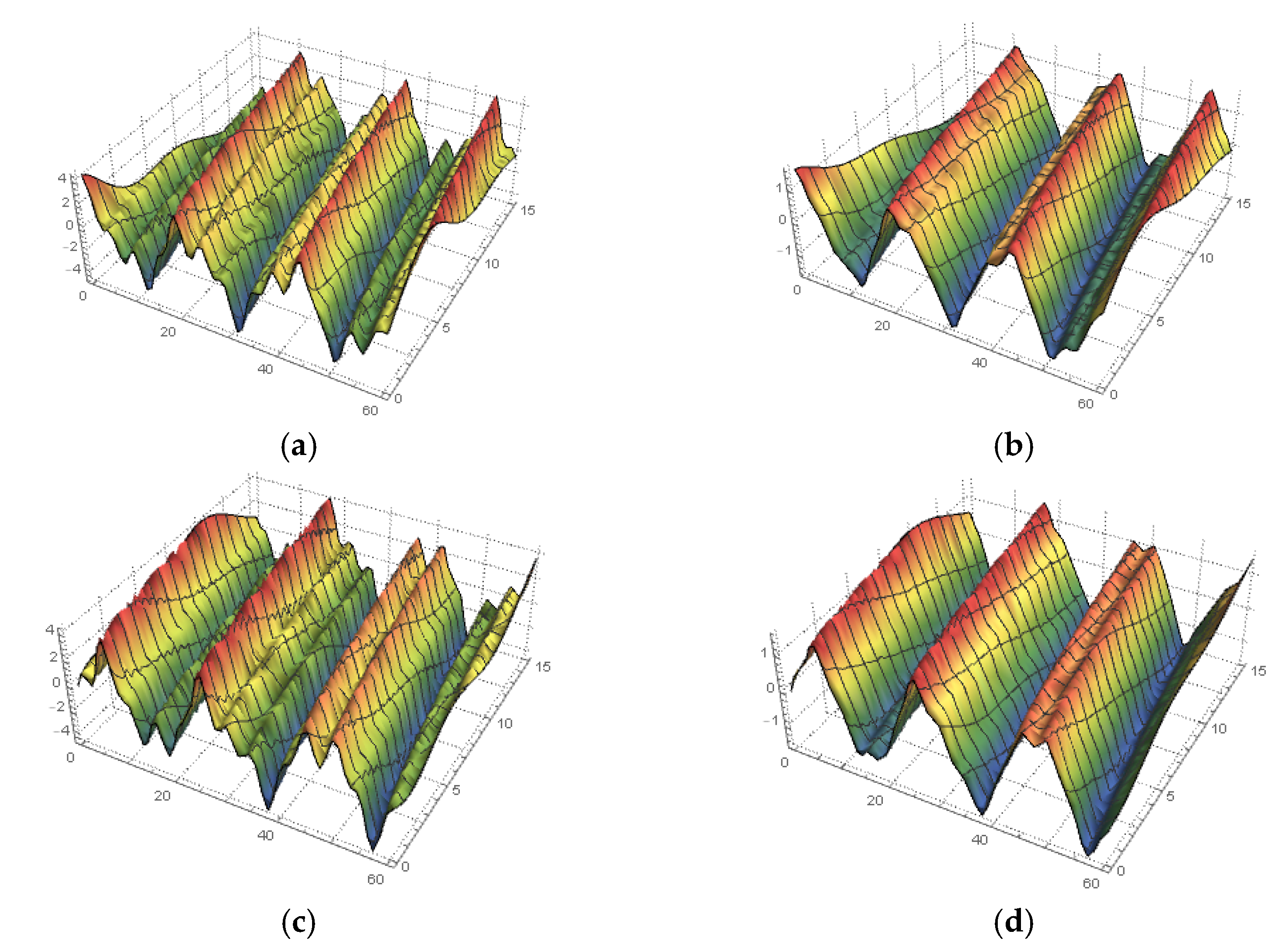
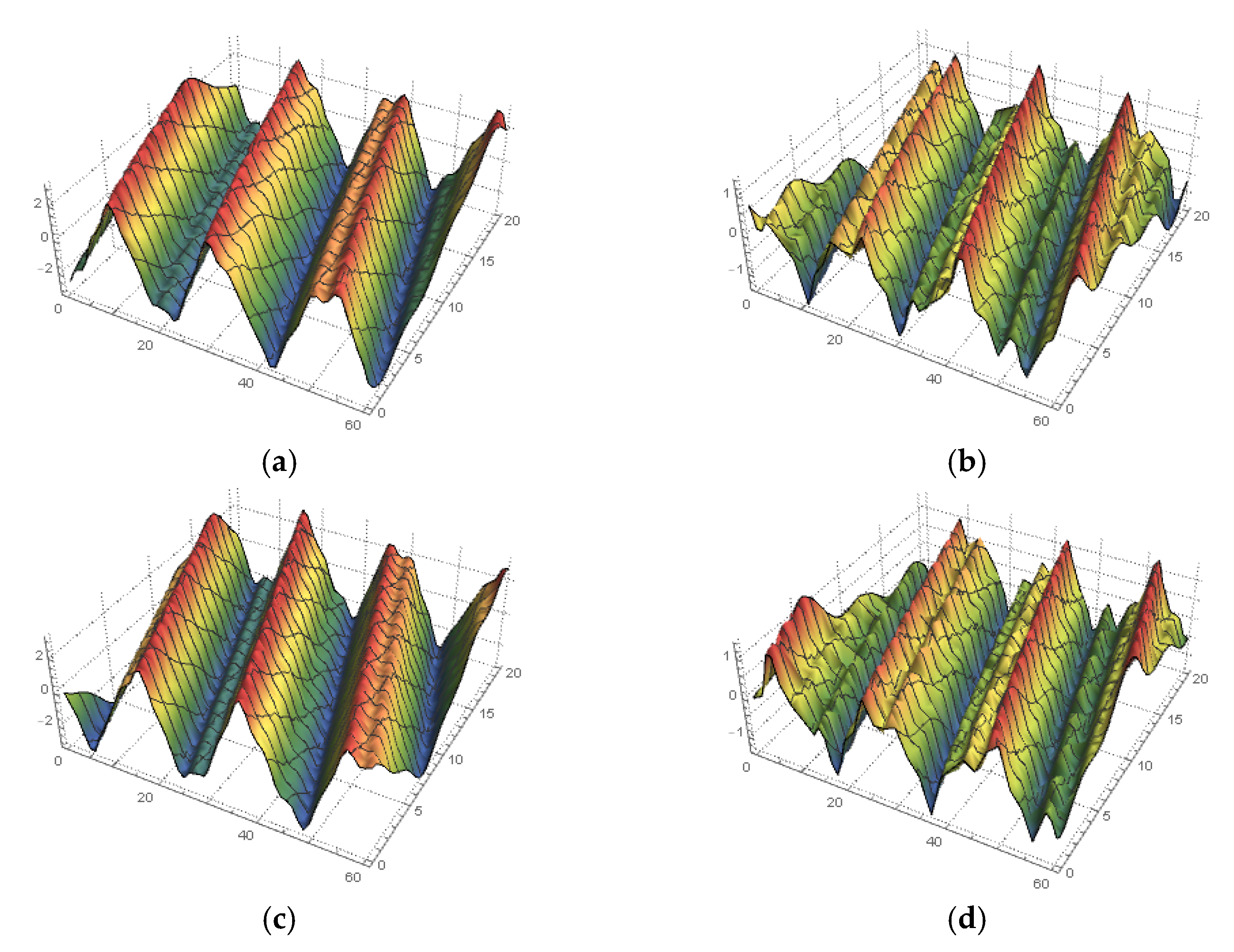
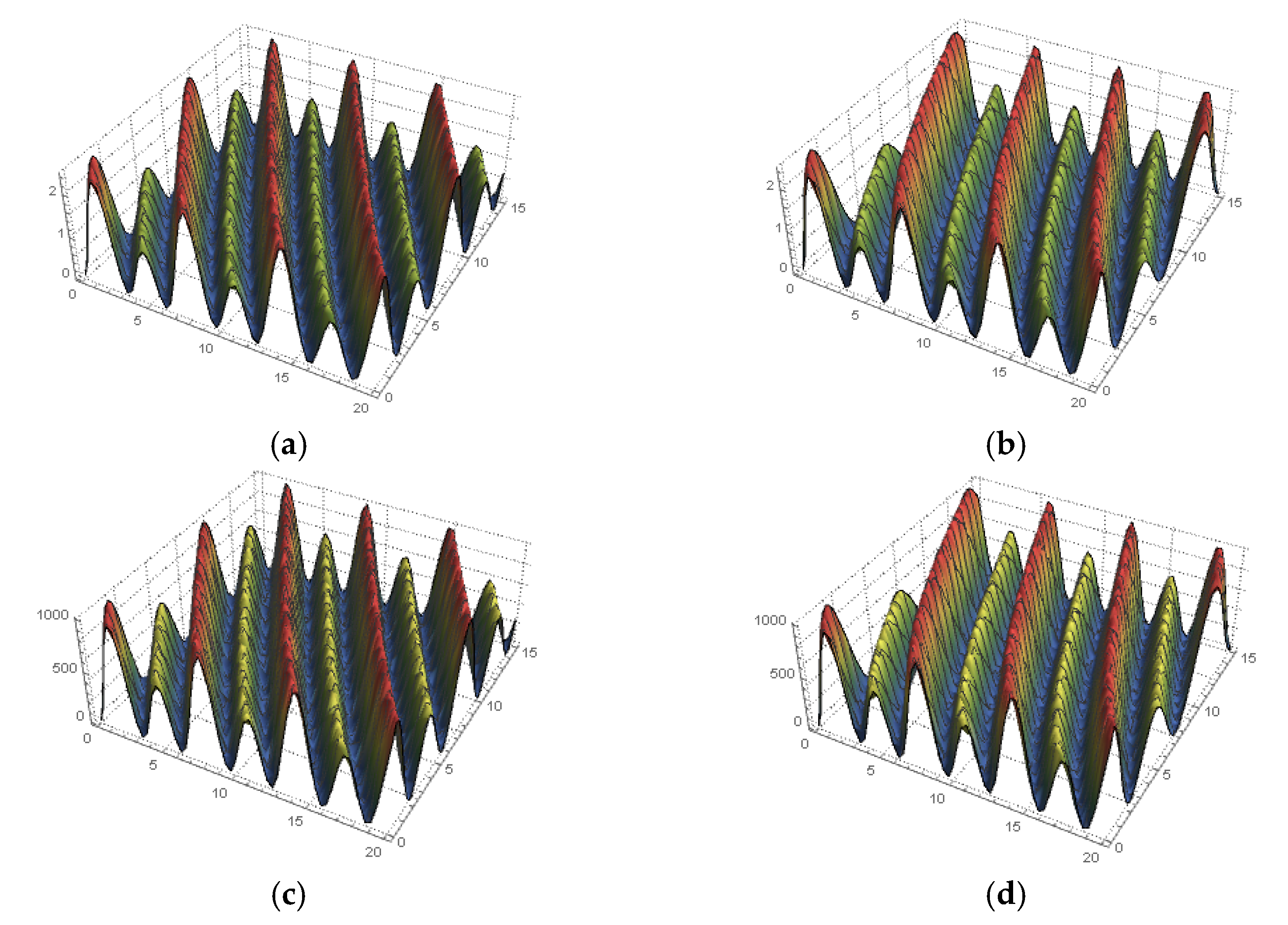
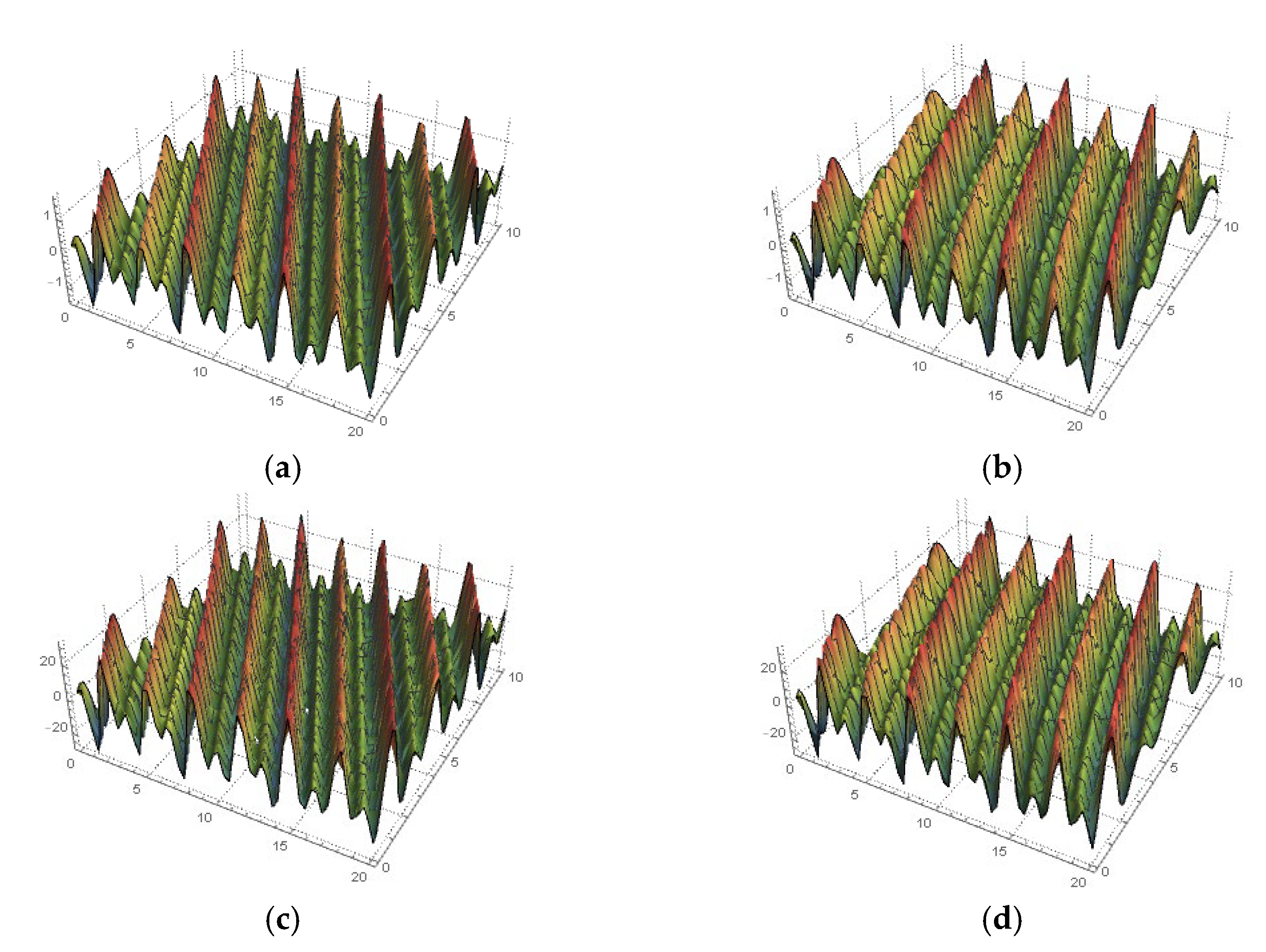
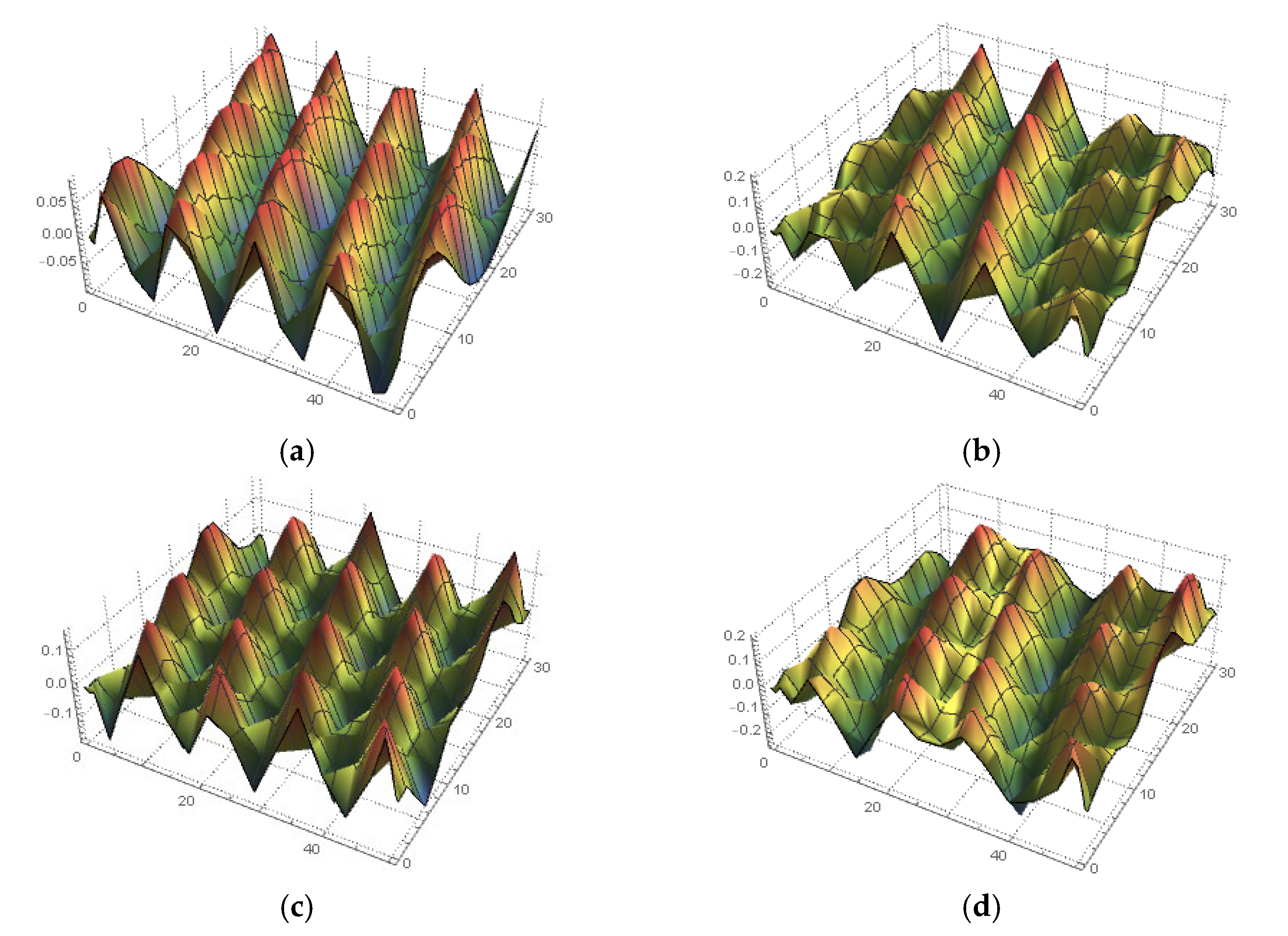
4. Solving the Space–Time Fractional MTM
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Beiser, A. Concepts of Modern Physics, 6th ed.; McGraw-Hill: New York, NY, USA, 1994; ISBN 978-0072448481. [Google Scholar]
- Kiselev, V.; Shnir, Y.; Tregubovich, A. Introduction to Quantum Field Theory, 1st ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar] [CrossRef]
- Thirring, W. A soluble relativistic field theory. Ann. Phys. 1958, 3, 91–112. [Google Scholar] [CrossRef]
- Kondo, K.-I. Bosonization and Duality of Massive Thirring Model. Prog. Theor. Phys. 1995, 94, 899–914. [Google Scholar] [CrossRef][Green Version]
- Kondo, K.-I. Thirring model as a gauge theory. Nucl. Phys. B 1995, 450, 251–266. [Google Scholar] [CrossRef]
- Joshi, N.; Pelinovsky, D.E. Integrable semi-discretization of the massive Thirring system in laboratory coordinates. J. Phys. A Math. Theor. 2019, 52, 03LT01. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Quantum Mechanics; World Scientific Publishing Co. Pte., Ltd.: Singapore, 2018. [Google Scholar]
- Lu, B. Bäcklund transformation of fractional Riccati equation and its applications to nonlinear fractional partial differential equations. Phys. Lett. A 2012, 376, 2045–2048. [Google Scholar] [CrossRef]
- Zahran, E.H.M.; Khater, M.M.A. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Model. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- Dubey, V.P.; Kumar, R.; Kumar, D.; Khan, I.; Singh, J. An efficient computational scheme for nonlinear time fractional systems of partial differential equations arising in physical sciences. Adv. Differ. Equat. 2020, 2020, 46. [Google Scholar] [CrossRef]
- Gaber, A.A.; Aljohani, A.F.; Ebaid, A.; Machado, J.T. The generalized Kudryashov method for nonlinear space–time fractional partial differential equations of Burgers type. Nonlinear Dyn. 2019, 95, 361–368. [Google Scholar] [CrossRef]
- Benfatto, G.; Falco, P.; Mastropietro, V. Functional Integral Construction of the Massive Thirring model: Verification of Axioms and Massless Limit. Commun. Math. Phys. 2007, 273, 67–118. [Google Scholar] [CrossRef]
- Bergknoff, H.; Thacker, H.B. Structure and solution of the massive Thirring model. Phys. Rev. D 1979, 19, 3666–3681. [Google Scholar] [CrossRef]
- Fujita, T.; Sekiguchi, Y.; Yamamoto, K. A New Interpretation of Bethe Ansatz Solutions for Massive Thirring Model. Ann. Phys. 1997, 255, 204–227. [Google Scholar] [CrossRef][Green Version]
- Delépine, D.; Felipe, R.G.; Weyers, J. Equivalence of the sine-Gordon and massive Thirring models at finite temperature. Phys. Lett. B 1998, 419, 296–302. [Google Scholar] [CrossRef]
- Aydogmus, F.; Tosyali, E. Numerical Analysis of Thirring Model under White Noise. J. Phys. Conf. Ser. 2015, 633, 012022. [Google Scholar] [CrossRef]
- Bañuls, M.C.; Cichy, K.; Kao, Y.-J.; Lin, C.-J.D.; Lin, Y.-P.; Tan, D.T.-L. Phase structure of the (1+1)-dimensional massive Thirring model from matrix product states. Phys. Rev. D 2019, 100, 094504. [Google Scholar] [CrossRef]
- Guo, L.; Wang, L.; Cheng, Y.; He, J. High-order rogue wave solutions of the classical massive Thirring model equations. Commun. Nonlinear Sci. Numer. Simul. 2017, 52, 11–23. [Google Scholar] [CrossRef]
- Arafa, A.A.M.; Hagag, A.M.S. Q-homotopy analysis transform method applied to fractional Kundu–Eckhaus equation and fractional massive Thirring model arising in quantum field theory. Asian Eur. J. Math. 2019, 12, 1950045. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O.; Hadid, S. Approximate solutions of nonlinear fractional Kundu-Eckhaus and coupled fractional massive Thirring equations emerging in quantum field theory using conformable residual power series method. Phys. Scr. 2020, 95, 105205. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Freihat, A.; Khalil, H.; Momani, S.; Khan, R.A. Numerical multistep approach for solving fractional partial dif-ferential equations. Int. J. Comput. Meth. 2017, 14, 1750029. [Google Scholar] [CrossRef]
- Hasan, S.; El-Ajou, A.; Hadid, S.; Al-Smadi, M.; Momani, S. Atangana-Baleanu fractional framework of reproducing kernel technique in solving fractional population dynamics system. Chaos Solitons Fractals 2020, 133, 109624. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O. Computational algorithm for solving fredholm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O.; Momani, S. Numerical computations of coupled fractional resonant Schrödinger equations arising in quantum mechanics under conformable fractional derivative sense. Phys. Scr. 2020, 95, 075218. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O.; Hadid, S. An attractive analytical technique for coupled system of fractional partial differential equations in shallow water waves with conformable derivative. Commun. Theor. Phys. 2020, 72, 085001. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O.; Gaith, M. Numerical simulation of telegraph and Cattaneo fractional-type models using adaptive reproducing kernel framework. Math. Methods Appl. Sci. 2020, 44, 8472–8489. [Google Scholar] [CrossRef]
- Nairat, M.; Shqair, M.; Alhalholy, T. Cylindrically Symmetric Fractional Helmholtz Equation. Appl. Math. 2019, 19, 708–717. [Google Scholar]
- Shqair, M. Developing a new approaching technique of homotopy perturbation method to solve two-group reflected cy-lindrical reactor. Results Phys. 2019, 12, 1880–1887. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. A variety of multiple-soliton solutions for the integrable (4+1)-dimensional Fokas equation. Waves Random Complex Media 2021, 31, 46–56. [Google Scholar] [CrossRef]
- Wen, X.; Feng, R.; Lin, J.; Liu, W.; Chen, F.; Yang, Q. Distorted light bullet in a tapered graded-index waveguide with PT symmetric potentials. Optik 2021, 248, 168092. [Google Scholar] [CrossRef]
- Fang, J.J.; Mou, D.S.; Zhang, H.C.; Wang, Y.Y. Discrete fractional soliton dynamics of the fractional Ablowitz-Ladik model. Optik 2021, 228, 166186. [Google Scholar] [CrossRef]
- Liu, C.-S. Counterexamples on Jumarie’s two basic fractional calculus formulae. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 92–94. [Google Scholar] [CrossRef]
- Liu, C.-S. Counterexamples on Jumarie’s three basic fractional calculus formulae for non-differentiable continuous functions. Chaos Solitons Fractals 2018, 109, 219–222. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simulat. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Tarasov, V.E. No violation of the Leibniz rule. No fractional derivative. Commun. Nonlinear. Sci. Numer. Simulat. 2013, 18, 2945–2948. [Google Scholar] [CrossRef]
- Yu, L.-J.; Wu, G.-Z.; Wang, Y.-Y.; Chen, Y.-X. Traveling wave solutions constructed by Mittag–Leffler function of a (2+1)-dimensional space-time fractional NLS equation. Results Phys. 2020, 17, 103156. [Google Scholar] [CrossRef]
- Wu, G.-Z.; Yu, L.-J.; Wang, Y.-Y. Fractional optical solitons of the space-time fractional nonlinear Schrödinger equation. Int. J. Light Electron Opt. 2020, 207, 164405. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, N. Bifurcation of traveling waves and exact solutions of Kadomtsev–Petviashvili modified equal width equation with fractional temporal evolution. Comput. Appl. Math. 2019, 38, 9. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, Y.; Li, S. Improved Fractional Subequation Method and Exact Solutions to Fractional Partial Differential Equations. J. Funct. Spaces 2020, 2020, 5840920. [Google Scholar] [CrossRef]
- Li, C.; Guo, Q.; Zhao, M. On the solutions of (2+1)-dimensional time-fractional Schrödinger equation. Appl. Math. Lett. 2019, 94, 238–243. [Google Scholar] [CrossRef]
- Aksoy, E.; Bekir, A.; Çevikel, A.C. Study on Fractional Differential Equations with Modified Riemann–Liouville Derivative via Kudryashov Method. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 511–516. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shqair, M.; Alabedalhadi, M.; Al-Omari, S.; Al-Smadi, M. Abundant Exact Travelling Wave Solutions for a Fractional Massive Thirring Model Using Extended Jacobi Elliptic Function Method. Fractal Fract. 2022, 6, 252. https://doi.org/10.3390/fractalfract6050252
Shqair M, Alabedalhadi M, Al-Omari S, Al-Smadi M. Abundant Exact Travelling Wave Solutions for a Fractional Massive Thirring Model Using Extended Jacobi Elliptic Function Method. Fractal and Fractional. 2022; 6(5):252. https://doi.org/10.3390/fractalfract6050252
Chicago/Turabian StyleShqair, Mohammed, Mohammed Alabedalhadi, Shrideh Al-Omari, and Mohammed Al-Smadi. 2022. "Abundant Exact Travelling Wave Solutions for a Fractional Massive Thirring Model Using Extended Jacobi Elliptic Function Method" Fractal and Fractional 6, no. 5: 252. https://doi.org/10.3390/fractalfract6050252
APA StyleShqair, M., Alabedalhadi, M., Al-Omari, S., & Al-Smadi, M. (2022). Abundant Exact Travelling Wave Solutions for a Fractional Massive Thirring Model Using Extended Jacobi Elliptic Function Method. Fractal and Fractional, 6(5), 252. https://doi.org/10.3390/fractalfract6050252





