The Sharp Bounds of the Third-Order Hankel Determinant for Certain Analytic Functions Associated with an Eight-Shaped Domain

Abstract

The main focus of this research is to solve certain coefficient-related problems for analytic functions that are subordinated to a unique trigonometric function. For the class ${\mathcal{S}}_{sin}^{*}$, with the quantity $\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}$ subordinated to $1+sinz$, we obtain an estimate on the initial coefficient $a_4$ and an upper bound of the third Hankel determinant. For functions in the class ${\mathcal{BT}}_{sin}$, with $f^{\prime }\left(z\right)$ lie in an eight-shaped domain in the right-half plane, we prove that its upper bound of third Hankel determinant is $\frac{1}{16}$. All the results are proven to be sharp.

1. Introduction and Definitions

The purpose of this section is to provide some basic concepts about geometric function theory that will help with understanding the main findings of the article. In this regard, let the set that consists of analytic functions in the region $\mathbb{U}:=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$ with the below Taylor’s series form

$$f\left(z\right)=z+\sum _{l=2}^{\infty }{a}_l{z}^l(z\in \mathbb{U})$$

(1)

be denoted by $\mathcal{A}$. Additionally, the subset $\mathcal{S}$ of $\mathcal{A}$ represents the set of normalized univalent functions. This class was introduced by Köebe [1] in 1907 and has become the core ingredient of advanced research in this field. Many people were interested in this concept, but within a short period, Bieberbach [2] published a paper in which the famous coefficient hypothesis was proposed. This conjecture states that if $f\left(z\right)\in \mathcal{S}$ and has the series form 1, then $\left|a_n\right|\le n$ for all $n\ge 2$. Many mathematicians worked hard to solve this problem, which remained a challenge for function theorists for 69 years. In 1985, it was de-Branges [3], who settled this long-lasting conjecture. During these 69 years, there were a lot of papers devoted to this conjecture and its related coefficient problems. New subfamilies of $\mathcal{S}$ were defined and their coefficient problems were discussed.

For the given functions $g_1,g_2\in \mathcal{A}$, $g_1$ is said to be subordinated to $g_2$ (mathematically written as $g_1\prec g_2$), if an analytic function $\kappa$ appears in $\mathbb{U}$ with the restrictions $\kappa \left(0\right)=0$ and $\left|\kappa \left(z\right)\right|<1$ in such a manner that $g_1\left(z\right)=g_2\left(\kappa \left(z\right)\right)$ holds. Moreover, if $g_2$ in $\mathbb{U}$ is univalent, then

$$g_1\left(z\right)\prec g_2\left(z\right)\left(z\in \mathbb{U}\right)$$

if and only if

$$g_1\left(0\right)=g_2\left(0\right)\&g_1\left(\mathbb{U}\right)\subset g_2\left(\mathbb{U}\right)$$

.

In 1992, Ma and Minda [4] presented a unified version of the class ${\mathcal{S}}^{*}\left(\mathrm{\Lambda }\right)$ using subordination terminology. It was defined by

$${\mathcal{S}}^{*}\left(\mathrm{\Lambda }\right)=\left\{f\in \mathcal{S}:\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \mathrm{\Lambda }\left(z\right)\left(z\in \mathbb{U}\right)\right\},$$

(2)

where $\mathrm{\Lambda }\left(z\right)$ is a univalent function with ${\mathrm{\Lambda }}^{\prime }\left(0\right)>0$ and $Re\left(\mathrm{\Lambda }\right(z\left)\right)>0$. Additionally, the region $\mathrm{\Lambda }\left(\mathbb{U}\right)$ is star-shaped about the point $\mathrm{\Lambda }\left(0\right)=1$ and is symmetric along the real-line axis. They obtained some interesting results on the distortion, growth, and the theorem of covering for this family. In the past few years, numerous subfamilies of the collection $\mathcal{S}$ have been introduced as special choices of the class ${\mathcal{S}}^{*}\left(\mathrm{\Lambda }\right)$. For example, by choosing the function

$$\Lambda \left(z\right)=\frac{1+\mathcal{M}z}{1+\mathcal{N}z}(\mathcal{M}\in \mathbb{C},-1\le \mathcal{N}\le 0,\mathcal{M}\ne \mathcal{N}),$$

we obtain the class ${\mathcal{S}}^{*}[\mathcal{M},\mathcal{N}]\equiv {\mathcal{S}}^{*}\left(\frac{1+\mathcal{M}z}{1+\mathcal{N}z}\right)$ which was studied in [5]. For $-1\le \mathcal{N}<\mathcal{M}\le 1$, we get the class of Janowski starlike functions investigated in [6]. See also [7]. Assuming that $\mathcal{M}=1-2{\xi }_1$ and $\mathcal{N}=-1$ with $0\le {\xi }_1<1$ lead to the class ${\mathcal{S}}^{*}\left({\xi }_1\right)\equiv {\mathcal{S}}^{*}[1-2{\xi }_1,-1]$ of starlike function of order ${\xi }_1$. The following are the recently studied relevant subclasses of the class ${\mathcal{S}}^{*}\left(\mathrm{\Lambda }\right)$.

(i).

${\mathcal{SS}}^{*}\left({\xi }_2\right)\equiv {\mathcal{S}}^{*}\left(\mathrm{\Lambda }\left(z\right)\right)$ with $\mathrm{\Lambda }\left(z\right)={\left(\frac{1+z}{1-z}\right)}^{{\xi }_2}$ and $0<{\xi }_2\le 1$ (see [8]).

(ii).

${\mathcal{S}}_{\mathcal{L}}^{*}\equiv {\mathcal{S}}^{*}\left(\sqrt{1+z}\right)$ (see [9]), ${\mathcal{S}}_{car}^{*}\equiv {\mathcal{S}}^{*}\left(1+\frac{4}{3}z+\frac{2}{3}{z}^2\right)$ (see [10]).

(iii).

${\mathcal{S}}_{\rho }^{*}\equiv {\mathcal{S}}^{*}\left(1+{sinh}^{-1}z\right)$ (see [11]), ${\mathcal{S}}_e^{*}\equiv {\mathcal{S}}^{*}\left(e^z\right)$ (see [12,13]).

(iv).

${\mathcal{S}}_{cos}^{*}\equiv {\mathcal{S}}^{*}\left(cosz\right)$ (see [14]), ${\mathcal{S}}_{cosh}^{*}\equiv {\mathcal{S}}^{*}\left(coshz\right)$ (see [15]).

(v).

${\mathcal{S}}_{tanh}^{*}\equiv {\mathcal{S}}^{*}\left(1+tanhz\right)$ (see [16]).

Finding bounds for the function coefficients in a given collection is one of the most fundamental problems in geometric function theory, since it impacts geometric features. For example, the constraint on the second coefficient provides the growth and distortion features. The Hankel determinant ${\mathcal{H}}_{q,n}\left(f\right)$ $\left(n,q\in \mathbb{N}=\left\{1,2,\dots \right\}\right)$ for the function $f\in \mathcal{S}$ was introduced by Pommerenke [17,18] defined by

$$H_{q,n}\left(f\right)=\left|\begin{array}{cccc}{a}_n\hfill & a_{n+1}\hfill & \dots \hfill & a_{n+q-1}\hfill \\ a_{n+1}\hfill & a_{n+2}\hfill & \dots \hfill & a_{n+q}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ a_{n+q-1}\hfill & a_{n+q}\hfill & \dots \hfill & a_{n+2q-2}\hfill \end{array}\right|.$$

It is not hard to note that the first, second, and third order of Hankel determinants of f can be given by

$$\begin{array}{ccc}\hfill H_{2,1}\left(f\right)& =& a_3-a_2^2,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill H_{2,2}\left(f\right)& =& a_2{a}_4-a_3^2,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill H_{3,1}\left(f\right)& =& 2a_2{a}_3{a}_4-a_3^3-a_4^2+a_3{a}_5-a_2^2{a}_5.\hfill \end{array}$$

(5)

There are relatively few results about the Hankel determinant for functions belonging to the general family class $\mathcal{S}$. The first sharp inequality for the function $f\in \mathcal{S}$ is given by

$$\left|H_{2,n}\left(f\right)\right|\le \left|\nu \right|\sqrt{n},$$

where $\nu$ is constant. This result is due to Hayman [19]. Additionally, for $f\in \mathcal{S}$, it is calculated in [20] that

$$\begin{array}{ccc}\hfill \left|H_{2,2}\left(f\right)\right|& \le & \lambda ,\mathrm{for}1\le \lambda \le \frac{11}{3},\hfill \\ \hfill \left|H_{3,1}\left(f\right)\right|& \le & \mu ,\mathrm{for}\frac{4}{9}\le \mu \le \frac{32+\sqrt{285}}{15}.\hfill \end{array}$$

The challenges of determining the bounds of Hankel determinants for a certain set of complex valued functions have attracted the interests of many researchers. For example, Janteng et al. [21,22] obtained the sharp bounds of $\left|H_{2,2}\left(f\right)\right|$ for the subfamilies $\mathcal{C}$, ${\mathcal{S}}^{*}$ and $\mathcal{BT}$ of $\mathcal{S}$, where $\mathcal{BT}$ is the set of bounded turning functions. They give the following estimates

$$\left|H_{2,2}\left(f\right)\right|\le \left\{\begin{array}{ccc}\frac{1}{8},\hfill & \mathrm{for}\hfill & f\in \mathcal{C},\hfill \\ 1,\hfill & \mathrm{for}\hfill & f\in {\mathcal{S}}^{*},\hfill \\ \frac{4}{9},\hfill & \mathrm{for}\hfill & f\in \mathcal{BT}.\hfill \end{array}\right.$$

For the subclasses ${\mathcal{S}}^{*}\left({\xi }_1\right)$ $\left(0\le {\xi }_1<1\right)$ and ${\mathcal{SS}}^{*}\left({\xi }_2\right)$ $\left(0<{\xi }_2\le 1\right)$ of $\mathcal{S}$, Cho et al. [23,24] prove that $\left|H_{2,2}\left(f\right)\right|$ is bounded by ${\left(1-{\xi }_1\right)}^2$ and ${\xi }_2^2$, respectively. This determinant was also investigated in [25,26,27,28,29] for some other interested function classes.

The Formulae (3)–(5) make it obvious that determining the bounds of $\left|H_{3,1}\left(f\right)\right|$ is substantially more difficult than finding the bounds of $\left|H_{2,2}\left(f\right)\right|$. Babalola [30] first studied the third-order Hankel determinant for the $\mathcal{C}$, ${\mathcal{S}}^{*}$ and $\mathcal{BT}$ families. Later, many researchers [31,32,33,34] obtained many other results on $\left|H_{3,1}\left(f\right)\right|$ using a similar approach for specific subclasses of univalent functions. After that, the readers’ attention was drawn to Zaprawa’s work [35], in which he enhanced Babalola’s conclusions by employing a new approach to demonstrate that

$$\left|H_{3,1}\left(f\right)\right|\le \left\{\begin{array}{ccc}\frac{49}{540},\hfill & \mathrm{for}\hfill & f\in \mathcal{C},\hfill \\ 1,\hfill & \mathrm{for}\hfill & f\in {\mathcal{S}}^{*},\hfill \\ \frac{41}{60},\hfill & \mathrm{for}\hfill & f\in \mathcal{BT}.\hfill \end{array}\right.$$

Furthermore, he pointed that these results are not sharp. In 2018, Kwon et al. [36] improved Zaprawa’s inequality for $f\in {\mathcal{S}}^{*}$ and showed that $\left|H_{3,1}\left(f\right)\right|\le \frac{8}{9}$. Zaprawa et al. [37] refined this bound in 2021 by proving that $\left|H_{3,1}\left(f\right)\right|\le \frac{5}{9}$. Many researchers attempted to obtain the determinant’s sharp bounds. In 2018, Kowalczyk et al. [38] and Lecko et al. [39] obtained the sharp bounds of $\left|H_{3,1}\left(f\right)\right|$ for the subclasses $\mathcal{C}$ and ${\mathcal{S}}^{*}\left(\frac{1}{2}\right)$. They proved that

$$\left|H_{3,1}\left(f\right)\right|\le \left\{\begin{array}{ccc}\frac{4}{135},\hfill & \mathrm{for}\hfill & f\in \mathcal{C},\hfill \\ \frac{1}{9},\hfill & \mathrm{for}\hfill & f\in {\mathcal{S}}^{*}\left(\frac{1}{2}\right).\hfill \end{array}\right.$$

In 2021, Barukab and his coauthors [40] obtained the sharp bounds of $\left|H_{3,1}\left(f\right)\right|$ for a collection of bounded turning functions associated with the petal-shaped domain. At the end of 2021, Ullah et al. [41] and Wang et al. [42] obtained the following sharp bounds of the third-order Hankel determinant given by

$$\left|H_{3,1}\left(f\right)\right|\le \left\{\begin{array}{ccc}\frac{1}{16},\hfill & \mathrm{for}\hfill & f\in {\mathcal{BT}}_L,\hfill \\ \frac{1}{9},\hfill & \mathrm{for}\hfill & f\in {\mathcal{S}}_{tanh}^{*},\hfill \end{array}\right.$$

where the family ${\mathcal{BT}}_L$ is defined as

$${\mathcal{BT}}_L=\left\{f\in \mathcal{A}:f^{\prime }\left(z\right)\prec \sqrt{1+z}(z\in \mathbb{U})\right\}.$$

In 2018, Cho et al. [43] introduced the function classes ${\mathcal{S}}_{sin}^{*}$ defined by

$${\mathcal{S}}_{sin}^{*}:=\left\{z\in \mathcal{A}:\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec 1+sinz(z\in \mathbb{U})\right\}.$$

(6)

For functions belonging to this class, it means that $\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}$ lie in an eight-shaped region in the right-half plane (see Figure 1).

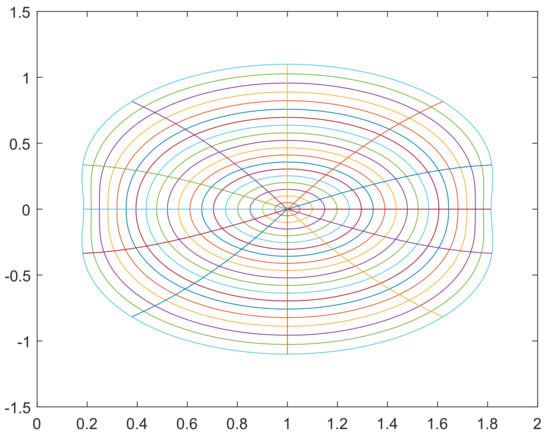
Figure 1. Image of $\mathbb{U}$ under $1+sinz$.

Recently, Arif et al. [44] investigated the family ${\mathcal{BT}}_{sin}$ of analytic functions defined by

$${\mathcal{BT}}_{sin}=\left\{f\in \mathcal{A}:f^{\prime }\left(z\right)\prec 1+sinz(z\in \mathbb{U})\right\}.$$

As $Re\left(1+sinz\right)>0\left(z\in \mathbb{U}\right)$, it is noted that ${\mathcal{S}}_{sin}^{*}$ is a subclass of starlike functions and ${\mathcal{BT}}_{sin}$ is subclass of functions with bounded turning.

Some interesting geometry properties of the two subclasses of univalent functions have been discussed. For two subclasses of $T_1$ and $T_2$ of $\mathcal{S}$, the $T_1$ radius of $T_2$ is the largest number $\nu \in (0,1)$ such that $r^{-1}f\left(rz\right)\in T_1$, $0<r\le \nu$ for all $f\in T_2$ and the number $\nu$ is called the $T_1$ radius of the class $T_2$. It is proved that the ${\mathcal{S}}^{*}$-radius for the class ${\mathcal{S}}_{sin}^{*}$ is $r_0={sinh}^{-1}\left(1\right)\approx 0.88$ and the $\mathcal{K}$-radius for the class ${\mathcal{S}}_{sin}^{*}$ is ${\widehat{r}}_0\approx 0.345$. The non-sharp upper bounds of the third Hankel determinant were also determined for the family ${\mathcal{S}}_{sin}^{*}$. The authors proved that $\left|H_{3,1}\left(f\right)\right|\le 0.51856$ for $f\in {\mathcal{S}}_{sin}^{*}$.

The aim of the present work is to obtain the sharp bounds of an initial coefficient and the third Hankel determinants for the classes of ${\mathcal{S}}_{sin}^{*}$ and ${\mathcal{BT}}_{sin}$.

2. A Set of Lemmas

Let $\mathcal{P}$ be the class of analytic functions with positive real parts. From the subordination principle, we have

$$\mathcal{P}=\left\{q\in \mathcal{A}:q\left(z\right)\prec \frac{1+z}{1-z}(z\in \mathbb{U})\right\},$$

where q has the series expansion of the form

$$q\left(z\right)=1+\sum _{n=1}^{\infty }{p}_n{z}^n\left(z\in \mathbb{U}\right).$$

(7)

The subsequent Lemmas are essential for the proof of our main results. It includes the well-known $p_2$ formula [45], the $p_3$ formula introduced by Libera and Zlotkiewicz [46], and the $p_4$ formula proven in [47].

Lemma 1.

Let $q\in \mathcal{P}$ be the form of (7). Then, for $x,\sigma ,\rho \in \overline{\mathbb{U}}$, we have

$$\begin{array}{ccc}\hfill 2p_2& =& p_1^2+x\left(4-p_1^2\right),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill 4p_3& =& p_1^3+2\left(4-p_1^2\right)p_{1}x-p_1\left(4-p_1^2\right)x^2+2\left(4-p_1^2\right)\left(1-{\left|x\right|}^2\right)\sigma ,\hfill \\ \hfill 8p_4& =& p_1^4+(4-p_1^2)x\left[p_1^2\left(x^2-3x+3\right)+4x\right]-4(4-p_1^2)(1-{\left|x\right|}^2)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & \left[p(x-1)\sigma +\overline{x}{\sigma }^2-(1-{\left|\sigma \right|}^2)\rho \right].\hfill \end{array}$$

(10)

Lemma 2

(see [48]). Let $q\in \mathcal{P}$ be the form of (7). If $B\in \left[0,1\right]$ with $B\left(2B-1\right)\le D\le B$, we have

$$\left|p_3-2B{p}_1{p}_2+D{p}_1^3\right|\le 2.$$

(11)

3. Coefficient Related Problems for the Family ${\mathcal{S}}_{sin}^{*}$

We start by determining the bound of an initial coefficient $a_4$ for the function $f\in {\mathcal{S}}_{sin}^{*}$.

Theorem 1.

If $f\in {\mathcal{S}}_{sin}^{*}$ has the series expansion of the form (1), then

$$\left|a_4\right|\le \frac{1}{3}.$$

(12)

The bound is sharp.

Proof. 

From the definition of the class ${\mathcal{S}}_{sin}^{*}$ along with subordination principal, there is a Schwarz function $\omega \left(z\right)$, such that

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}=1+sin\left(\omega \left(z\right)\right).$$

Assuming that $p\in \mathcal{P}$. By writing p in terms of Schwarz function $\omega$, we have

$$p\left(z\right)=\frac{1+w\left(z\right)}{1-w\left(z\right)}=1+p_{1}z+p_2{z}^2+p_3{z}^3+\dots .$$

(13)

It is equivalent to

$$\omega \left(z\right)=\frac{p\left(z\right)-1}{p\left(z\right)+1}=\frac{p_{1}z+p_2{z}^2+p_3{z}^3+p_4{z}^4+\dots }{2+p_{1}z+p_2{z}^2+p_3{z}^3+p_4{z}^4+\dots }.$$

Using (1), we easily obtain

$$\begin{array}{ccc}\hfill \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}& =& 1+a_{2}z+(2a_3-a_2^2)z^2+(3a_4-3a_2{a}_3+a_2^3)z^3\hfill \\ & & +(4a_5-2a_3^2-4a_2{a}_4+4a_2^2{a}_3-a_2^4)z^4+\dots .\hfill \end{array}$$

(14)

From the series expansion of $\omega \left(z\right)$, we have

$$\begin{array}{ccc}\hfill 1+sin\left(\omega \left(z\right)\right)& =& 1+\frac{1}{2}{p}_{1}z+\left(\frac{1}{2}{p}_2-\frac{1}{4}{p}_1^2\right)z^2+\left(\frac{1}{2}{p}_3+\frac{5}{48}{p}_1^3-\frac{1}{2}{p}_1{p}_2\right)z^3\hfill \\ & & +\left(\frac{1}{2}{p}_4-\frac{1}{4}{p}_2^2-\frac{1}{32}{p}_1^4+\frac{5}{16}{p}_1^2{p}_2-\frac{1}{2}{p}_1{p}_3\right)z^4+\dots .\hfill \end{array}$$

(15)

By comparing (14) and (15), it follows that

$$\begin{array}{ccc}\hfill a_2& =& \frac{1}{2}{p}_1,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill a_3& =& \frac{1}{4}{p}_2,\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill a_4& =& \frac{1}{6}{p}_3-\frac{1}{144}{p}_1^3-\frac{1}{24}{p}_1{p}_2,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill a_5& =& \frac{1}{4}\left(\frac{1}{2}{p}_4-\frac{1}{8}{p}_2^2+\frac{5}{288}{p}_1^4-\frac{1}{48}{p}_1^2{p}_2-\frac{1}{6}{p}_1{p}_3\right).\hfill \end{array}$$

(19)

From (18), we deduce that

$$\left|a_4\right|=\frac{1}{6}\left|p_3-\frac{1}{4}{p}_1{p}_2-\frac{1}{24}{p}_1^3\right|.$$

(20)

Let $B=\frac{1}{8}$ and $D=-\frac{1}{24}$. It is clear that $0\le B\le 1$, $B\ge D$ and

$$B(2B-1)=\frac{1}{8}(\frac{1}{4}-1)=-\frac{3}{32}\le D.$$

Thus, all the conditions of Lemma 2 are satisfied. Hence, we have

$$\left|a_4\right|\le \frac{1}{3}.$$

The result is sharp with the extremal defined by

$$f\left(z\right)=zexp\left(\underset{0}{\overset{z}{\int }}\frac{sin\left(t^3\right)}{t}dt\right)=z+\frac{z^4}{3}+\dots .$$

(21)

□

4. Third Hankel Determinant for the Class ${\mathcal{S}}_{sin}^{*}$

In this portion, we investigate the sharp bounds of third-order Hankel determinant for $f\in {\mathcal{S}}_{sin}^{*}$.

Theorem 2.

Let $f\in {\mathcal{S}}_{sin}^{*}$ be the series representation (1). Then

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{9}.$$

Equality can be obtained with the extremal function given by (21).

Proof. 

From the definition, we know that

$$H_{3,1}\left(f\right)=2a_2{a}_3{a}_4-a_3^3-a_4^2+a_3{a}_5-a_2^2{a}_5.$$

In virtue of (16)–(19) along with $p_1=p\in \left[0,2\right]$, it can be obtained that

$$\begin{array}{ccc}\hfill H_{3,1}\left(f\right)& =& \frac{1}{41472}\left(-47p^6+3p^4{p}_2+528p^3{p}_3-234p^2{p}_2^2-1296p^2{p}_4\right.\hfill \\ & & \left.+1872p{p}_2{p}_3-972p_2^3+1296p_2{p}_4-1152p_3^2\right).\hfill \end{array}$$

(22)

Let $t=4-p^2$. Using (8)–(10) along with straightforward algebraic computations, we have

$$\begin{array}{ccc}\hfill 3p^4{p}_2& =& \frac{3}{2}\left(p^6+p^{4}tx\right),\hfill \\ \hfill 528p^3{p}_3& =& 132\left(p^6+2p^{4}tx-p^{4}t{x}^2+2p^{3}t\left(1-{\left|x\right|}^2\right)\sigma \right),\hfill \\ \hfill 234p^2{p}_2^2& =& \frac{117}{2}\left(p^6+2p^{4}tx+p^2{t}^2{x}^2\right),\hfill \\ \hfill 1296p^2{p}_4& =& 162p^{4}t{x}^3-648p^{3}tx\left(1-{\left|x\right|}^2\right)\sigma -648p^{2}t\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2-486p^{4}t{x}^2\hfill \\ & & +648p^{2}t\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho +648p^{3}t\left(1-{\left|x\right|}^2\right)\sigma +486p^{4}tx\hfill \\ & & +162p^6+648p^{2}t{x}^2,\hfill \\ \hfill 1872p{p}_2{p}_3& =& -234p^2{t}^2{x}^3-234p^{4}t{x}^2+468p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma +468p^2{t}^2{x}^2\hfill \\ & & +468p^{3}t\left(1-{\left|x\right|}^2\right)\sigma +702p^{4}tx+234p^6,\hfill \\ \hfill 972p_2^3& =& \frac{243}{2}\left(t^3{x}^3+3p^2{t}^2{x}^2+3p^{4}tx+p^6\right),\hfill \\ \hfill 1296p_2{p}_4& =& 324p^{2}t{x}^2+324t^2{x}^3+81p^6+324p^{4}tx+324p^{3}t\left(1-{\left|x\right|}^2\right)\sigma \hfill \\ & & +324p^{2}t\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho +243p^2{t}^2{x}^2+324p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma \hfill \\ & & +324t^{2}x\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho -243p^{4}t{x}^2-324p^{2}t\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2\hfill \\ & & -324p^{3}tx\left(1-{\left|x\right|}^2\right)\sigma -243p^2{t}^2{x}^3-324t^{2}x\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2+81p^{4}t{x}^3\hfill \\ & & +81p^2{t}^2{x}^4-324p{t}^2{x}^2\left(1-{\left|x\right|}^2\right)\sigma ,\hfill \\ \hfill 1152p_3^2& =& 72p^2{t}^2{x}^4-288p{t}^2{x}^2\left(1-{\left|x\right|}^2\right)\sigma -288p^2{t}^2{x}^3-144p^{4}t{x}^2\hfill \\ & & +288t^2{\left(1-{\left|x\right|}^2\right)}^2{\sigma }^2+576p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma +288p^2{t}^2{x}^2\hfill \\ & & +288p^{3}t\left(1-{\left|x\right|}^2\right)\sigma +288p^{4}tx+72p^6.\hfill \end{array}$$

Inserting these formulae into (22), it follows that

$$\begin{array}{ccc}\hfill H_{3,1}\left(f\right)& =& \frac{1}{41472}\left\{-\frac{25}{2}{p}^6+324t^2{x}^3-\frac{243}{2}{t}^3{x}^3-324p^{2}t{x}^2-81p^{4}t{x}^3+21p^{4}t{x}^2\right.\hfill \\ & & +36p^{4}tx+9p^2{t}^2{x}^4-189p^2{t}^2{x}^3-288t^2{\left(1-{\left|x\right|}^2\right)}^2{\sigma }^2+120p^{3}t\left(1-{\left|x\right|}^2\right)\sigma \hfill \\ & & +324p^{3}tx\left(1-{\left|x\right|}^2\right)\sigma +324p^{2}t\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2-324p^{2}t\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho \hfill \\ & & -36p{t}^2{x}^2\left(1-{\left|x\right|}^2\right)\sigma -324t^{2}x\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2+216p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma \hfill \\ & & \left.+324t^{2}x\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho \right\}.\hfill \end{array}$$

Thus, we have

$$H_{3,1}\left(f\right)=\frac{1}{41472}\left(v_1\left(p,x\right)+v_2\left(p,x\right)\sigma +v_3\left(p,x\right){\sigma }^2+\mathrm{\Psi }\left(p,x,\sigma \right)\rho \right),$$

where $\rho ,x,\sigma \in \overline{\mathbb{U}}$, and

$$\begin{array}{ccc}\hfill v_1\left(p,x\right)& =& -\frac{25}{2}{p}^6+\left(4-p^2\right)\left[\left(4-p^2\right)\left(-162x^3-\frac{135}{2}{p}^2{x}^3+9p^2{x}^4\right)\right.\hfill \\ & & \left.-324p^2{x}^2-81p^4{x}^3+21p^4{x}^2+36p^{4}x\right],\hfill \\ \hfill v_2\left(p,x\right)& =& \left(4-p^2\right)\left(1-{\left|x\right|}^2\right)\left[\left(4-p^2\right)\left(216px-36p{x}^2\right)+324p^{3}x+120p^3\right],\hfill \\ \hfill v_3\left(p,x\right)& =& \left(4-p^2\right)\left(1-{\left|x\right|}^2\right)\left[\left(4-p^2\right)\left(-36{\left|x\right|}^2-288\right)+324p^2\overline{x}\right],\hfill \\ \hfill \mathrm{\Psi }\left(p,x,\sigma \right)& =& \left(4-p^2\right)\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\left[-324p^2+324x\left(4-p^2\right)\right].\hfill \end{array}$$

Let $\left|x\right|=x$ and $\left|\sigma \right|=y$. By noting that $\left|\rho \right|\le 1$, we obtain

$$\begin{array}{ccc}\hfill \left|H_{3,1}\left(f\right)\right|& \le & \frac{1}{41472}\left(\left|v_1\left(p,x\right)\right|+\left|v_2\left(p,x\right)\right|y+\left|v_3\left(p,x\right)\right|y^2+\left|\mathrm{\Psi }\left(p,x,\sigma \right)\right|\right).\hfill \\ & \le & \frac{1}{41472}\mathrm{\Gamma }\left(p,x,y\right),\hfill \end{array}$$

(23)

where

$$\mathrm{\Gamma }\left(p,x,y\right)=h_1\left(p,x\right)+h_2\left(p,x\right)y+h_3\left(p,x\right)y^2+h_4\left(p,x\right)\left(1-y^2\right),$$

with

$$\begin{array}{ccc}\hfill h_1\left(p,x\right)& =& \frac{25}{2}{p}^6+\left(4-p^2\right)[\left(4-p^2\right)\left(162x^3+\frac{135}{2}{p}^2{x}^3+9p^2{x}^4\right)\hfill \\ & & +324p^2{x}^2+81p^4{x}^3+21p^4{x}^2+36p^{4}x],\hfill \\ \hfill h_2\left(p,x\right)& =& \left(4-p^2\right)\left(1-x^2\right)\left[\left(4-p^2\right)\left(216px+36p{x}^2\right)+324p^{3}x+120p^3\right],\hfill \\ \hfill h_3\left(p,x\right)& =& \left(4-p^2\right)\left(1-x^2\right)\left[\left(4-p^2\right)\left(36x^2+288\right)+324p^{2}x\right],\hfill \\ \hfill h_4\left(p,x\right)& =& \left(4-p^2\right)\left(1-x^2\right)\left[324p^2+324x\left(4-p^2\right)\right].\hfill \end{array}$$

Now, we have to maximize $\mathrm{\Gamma }\left(p,x,y\right)$ in the closed cuboid $\mathrm{{\rm Y}}:\left[0,2\right]\times \left[0,1\right]\times \left[0,1\right]$.

For this, we have to discuss the maximum values of $\mathrm{\Gamma }\left(p,x,y\right)$ in the interior of $\mathrm{{\rm Y}}$, in the interior of its six faces and on its twelve edges.

1. Interior points of cuboid $\mathrm{{\rm Y}}$:

Let $\left(p,x,y\right)\in \left(0,2\right)\times \left(0,1\right)\times \left(0,1\right).$ By taking a partial derivativeof $\mathrm{\Gamma }\left(p,x,y\right)$ with respect to y, we get

$$\begin{array}{ccc}\hfill \frac{\partial \mathrm{\Gamma }}{\partial y}& =& 12\left(4-p^2\right)(1-x^2)\left\{6y(x-1)\left[\left(4-p^2\right)\left(x-8\right)+9p^2\right]\right.\hfill \\ & & \left.+3p\left[x\left(4-p^2\right)\left(x+6\right)+p^2\left(9x+\frac{10}{3}\right)\right]\right\}.\hfill \end{array}$$

Plugging $\frac{\partial \mathrm{\Gamma }}{\partial y}=0$ yields

$$y=\frac{3p\left[x\left(4-p^2\right)\left(x+6\right)+p^2\left(9x+\frac{10}{3}\right)\right]}{6(x-1)\left[\left(4-p^2\right)\left(8-x\right)-9p^2\right]}=y_0.$$

If $y_0$ is a critical point inside $\mathrm{{\rm Y}}$, then $y_0\in \left(0,1\right)$, which is possible only if

$$3p^3\left(9x+\frac{10}{3}\right)+3px\left(4-p^2\right)\left(x+6\right)+6(1-x)\left(4-p^2\right)\left(8-x\right)<54p^2(1-x).$$

(24)

and

$$p^2>\frac{4\left(8-x\right)}{17-x}.$$

(25)

Now, we have to obtain the solutions which satisfy both inequalities (24) and (25) for the existence of the critical points.

Let $g\left(x\right)=\frac{4\left(8-x\right)}{17-x}$. Since $g^{\prime }\left(x\right)<0$ for $\left(0,1\right)$, $g\left(x\right)$ is decreasing in $\left(0,1\right)$. Hence $p^2>\frac{7}{4}$ and a simple exercise shows that (24) does not hold in this case for all values of $x\in [\frac{1}{3},1)$ and there is no critical point of $\mathrm{\Gamma }$ in $\left(0,2\right)\times [\frac{1}{3},1)\times \left(0,1\right)$.

Suppose that there is a critical point $(\tilde{p},\tilde{x},\tilde{y})$ of $\mathrm{\Gamma }$ existing in the interior of cuboid $\mathrm{{\rm Y}}$. Clearly, it must satisfy that $\tilde{x}<\frac{1}{3}$. From the above discussion, it is also known that ${\tilde{p}}^2>\frac{46}{25}$ and $\tilde{y}\in (0,1)$. In the following, we will prove that $\mathrm{\Gamma }(\tilde{p},\tilde{x},\tilde{y})<4608$.

For $(p,x,y)\in \left(\frac{\sqrt{46}}{5},2\right)\times (0,\frac{1}{3})\times \left(0,1\right)$, by invoking $x<\frac{1}{3}$ and $1-x^2<1$ it is not hard to observe that

$$\begin{array}{ccc}\hfill h_1\left(p,x\right)& \le & \frac{25}{2}{p}^6+\left(4-p^2\right)[\left(4-p^2\right)\left(162{(1/3)}^3+\frac{135}{2}{p}^2{(1/3)}^3+9p^2{(1/3)}^4\right)\hfill \\ & & +324p^2{(1/3)}^2+81p^4{(1/3)}^3+21p^4{(1/3)}^2+36p^4(1/3)]\hfill \\ & =& \frac{25}{2}{p}^6+\frac{1}{18}\left(4-p^2\right)\left(265p^4+728p^2+432\right):={\varphi }_1\left(p\right),\hfill \\ \hfill h_2\left(p,x\right)& \le & \left(4-p^2\right)\left[\left(4-p^2\right)\left(216p(1/3)+36p{(1/3)}^2\right)+324p^3(1/3)+120p^3\right],\hfill \\ & =& (4-p^2)\left(152p^3+304p\right):={\varphi }_2\left(p\right),\hfill \\ \hfill h_3\left(p,x\right)& \le & (4-p^2)\left[\left(4-p^2\right)\left(36{(1/3)}^2+288\right)+324p^2(1/3)\right],\hfill \\ & =& (4-p^2)\left(-184p^2+1168\right):={\varphi }_3\left(p\right),\hfill \\ \hfill h_4\left(p,x\right)& =& (4-p^2)\left[324p^2+324(1/3)\left(4-p^2\right)\right]\hfill \\ & =& (4-p^2)\left(216p^2+432\right):={\varphi }_4\left(p\right).\hfill \end{array}$$

Therefore, we have

$$\mathrm{\Gamma }(p,x,y)\le {\varphi }_1\left(p\right)+{\varphi }_4\left(p\right)+{\varphi }_2\left(p\right)y+\left[{\varphi }_3\left(p\right)-{\varphi }_4\left(p\right)\right]y^2:=\mathrm{\Xi }(p,y).$$

Obviously, it can be seen that

$$\frac{\partial \mathrm{\Xi }}{\partial y}={\varphi }_2\left(p\right)+2\left[{\varphi }_3\left(p\right)-{\varphi }_4\left(p\right)\right]y$$

and

$$\frac{{\partial }^2\mathrm{\Xi }}{\partial y^2}=2\left[{\varphi }_3\left(p\right)-{\varphi }_4\left(p\right)\right]=2(4-p^2)(-400p^2+736).$$

Since ${\varphi }_3\left(p\right)-{\varphi }_4\left(p\right)\le 0$ for $p\in (\frac{\sqrt{46}}{5},2)$, we obtain that $\frac{{\partial }^2\mathrm{\Xi }}{\partial y^2}\le 0$ for $y\in (0,1)$ and thus it follows that

$$\frac{\partial \mathrm{\Xi }}{\partial y}\ge \frac{\partial \mathrm{\Xi }}{\partial y}{|}_{y=1}=(4-p^2)(152p^3-800p^2+304p+1472)\ge 0,p\in (\frac{\sqrt{46}}{5},2).$$

Therefore, we have

$$\mathrm{\Xi }(p,y)\le \mathrm{\Xi }(p,1)={\varphi }_1\left(p\right)+{\varphi }_2\left(p\right)+{\varphi }_3\left(p\right):=\iota \left(p\right).$$

It is easy to calculate that $\iota \left(p\right)$ attains its maximum value $3899.867$ at $p\approx 1.356466$. Thus, we have

$$\mathrm{\Gamma }(p,x,y)<4608,(p,x,y)\in \left(\frac{\sqrt{46}}{5},2\right)\times (0,\frac{1}{3})\times \left(0,1\right).$$

Hence $\mathrm{\Gamma }(\tilde{p},\tilde{x},\tilde{y})<4608$. This implies that $\mathrm{\Gamma }$ is less than 4608 at all the critical points in the interior of $\mathrm{{\rm Y}}$. Therefore, $\mathrm{\Gamma }$ has no optimal solution in the interior of $\mathrm{{\rm Y}}$.

2. Interior of all the six faces of cuboid $\mathrm{{\rm Y}}$:

On $p=0,$$\mathrm{\Gamma }(p,x,y)$ reduces to

$$\begin{array}{ccc}\hfill T_1(x,y)& =& \mathrm{\Gamma }(0,x,y)=2592x^3+(1-x^2)\left(576x^2{y}^2-5184x{y}^2+4608y^2\right.\hfill \\ & & \left.+5184x\right),x,y\in \left(0,1\right).\hfill \end{array}$$

(26)

Then

$$\frac{\partial T_1}{\partial y}=(1-x^2)y\left(1152x^2-10368x+9216\right),x,y\in \left(0,1\right).$$

$T_1(x,y)$ has no critical point in $\left(0,1\right)\times \left(0,1\right).$

On $p=2,$$\mathrm{\Gamma }(p,x,y)$ reduces to

$$\mathrm{\Gamma }(2,x,y)=800.$$

(27)

Thus

$$\left|H_{3,1}\left(f\right)\right|\le \frac{25}{1296}.$$

On $x=0,$$\mathrm{\Gamma }(p,x,y)$ reduces to $\mathrm{\Gamma }(p,0,y)$ given by

$$\begin{array}{ccc}\hfill T_2(p,y)& =& \mathrm{\Gamma }(p,0,y)=\frac{25}{2}{p}^6+(4-p^2)\left(120p^{3}y+(1152-288p^2)y^2\right.\hfill \\ & & \left.+324p^2(1-y^2)\right).\hfill \end{array}$$

(28)

Solving $\frac{\partial T_2}{\partial y}=0$, we get

$$y=\frac{5p^3}{3(17p^2-32)}=y_1.$$

For the given range of $y$, $y_1$ should belong to $\left(0,1\right)$, which is possible only if $p>p_0$, $p_0\approx 1.484217030.$ Another derivative of $T_2(p,y)$, partially with respect to p, is

$$\begin{array}{ccc}\hfill \frac{\partial T_2}{\partial p}& =& 75p^5+\left(4-p^2\right)\left(360p^{2}y-576p{y}^2+648p\left(1-y^2\right)\right)\hfill \\ & & -648p^3\left(1-y^2\right)-240p^{4}y+2p\left(288p^2-1152\right)y^2.\hfill \end{array}$$

(29)

By substituting the value of y in (29), plugging $\frac{\partial T_2}{\partial p}=0$ and simplifying, we obtain

$$\frac{\partial T_2}{\partial p}=9p\left(1275p^8-44816p^6+239904p^4-460800p^2+294912\right)=0.$$

(30)

A calculation gives the solution of (30) in $\left(0,2\right)$ that is $p\approx 1.20622871$. Thus $T_2(p,y)$ has no optimal point in $\left(0,2\right)\times \left(0,1\right)$.

On $x=1,$$\mathrm{\Gamma }(p,x,y)$ reduces to

$$T_3(p,y)=\mathrm{\Gamma }(p,1,y)=-49p^6-222p^4+1224p^2+2592.$$

(31)

Solving $\frac{\partial T_3}{\partial p}=0$, we reach the critical point at $p_0\approx 1.32161749$. Thus, $T_3(p,y)$ achieves its maximum at $p_0$ that is $3791.5209$. Hence

$$\left|H_{3,1}\left(f\right)\right|\le 0.09142363.$$

On $y=0,$$\mathrm{\Gamma }(p,x,y)$ yields

$$\begin{array}{ccc}\hfill T_4(p,x)& =& \mathrm{\Gamma }(p,x,0)=\frac{25}{2}{p}^6-378p^4{x}^3+2376p^2{x}^3-2592x^3-\frac{27}{2}{p}^6{x}^3\hfill \\ & & +9p^6{x}^4-72p^4{x}^4+144p^2{x}^4+84p^4{x}^2-21p^6{x}^2-36p^{6}x\hfill \\ & & +468p^{4}x-324p^4-2592p^{2}x+1296p^2+5184x.\hfill \end{array}$$

A calculation shows that there is no existing solution for the system of equations $\frac{\partial T_4}{\partial x}=0$ and $\frac{\partial T_4}{\partial p}=0$ in $\left(0,2\right)\times \left(0,1\right)$.

On $y=1$, $\mathrm{\Gamma }(p,x,y)$ reduces to

$$\begin{array}{ccc}\hfill T_5(p,x)& =& \mathrm{\Gamma }(p,x,1)=4608-120p^5-\frac{27}{2}{p}^6{x}^3+9p^6{x}^4-21p^6{x}^2\hfill \\ & & -36p^{6}x-36p^5{x}^4+108p^5{x}^3+156p^5{x}^2+288p^3{x}^4\hfill \\ & & -108p^{5}x+432p^3{x}^3-768p^3{x}^2-576p{x}^4-3456p{x}^3\hfill \\ & & -108p^4{x}^4-576x^4+288p^4+\frac{25}{2}{p}^6-2304p^2\hfill \\ & & +2592x^3-4032x^2+480p^3-1512p^2{x}^3+432p^2{x}^4\hfill \\ & & +3312p^2{x}^2+270p^4{x}^3-492p^4{x}^2-180p^{4}x+3456px\hfill \\ & & +576p{x}^2-432p^{3}x+1296p^{2}x.\hfill \end{array}$$

A calculation shows that there is no existing solution for the system of equations $\frac{\partial T_5}{\partial x}=0$ and $\frac{\partial T_5}{\partial p}=0$ in $\left(0,2\right)\times \left(0,1\right)$.

3. On the edges of cuboid $\mathrm{{\rm Y}}$:

Putting $y=0$ in $\mathrm{\Gamma }(p,x,y),$ we have

$$\mathrm{\Gamma }(p,0,0)=\frac{25}{2}{p}^6-324p^4+1296p^2=T_6\left(p\right).$$

Clearly $T_6^{\prime }\left(p\right)=0$ for $p_0\approx 1.51933049$ in $\left[0,2\right]$, where the maximum point of $T_6\left(p\right)$ is achieved at $p_0$. Thus, we say that

$$\left|H_{3,1}\left(f\right)\right|\le 0.0342145.$$

By putting $y=1$ in $\mathrm{\Gamma }(p,x,y)$, we get

$$\mathrm{\Gamma }(p,0,1)=\frac{25}{2}{p}^6-120p^5+480p^3+288p^4-2304p^2+4608=T_7\left(p\right).$$

Since $T_7^{\prime }\left(p\right)<0$ for $\left[0,2\right]$. Therefore, $T_7\left(p\right)$ decreases in $\left[0,2\right]$ and hence, maximum is achieved at $p=0$. Thus,

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{9}.$$

By putting $p=0$ in $\mathrm{\Gamma }(p,x,y)$, we get

$$\mathrm{\Gamma }(0,0,y)=4608y^2.$$

A simple calculation gives

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{9}.$$

Since $\mathrm{\Gamma }(p,1,y)$ is independent of $y$, we have

$$\mathrm{\Gamma }(p,1,0)=\mathrm{\Gamma }(p,1,1)=-49p^6-222p^4+1224p^2+2592=T_8\left(p\right).$$

Now, $T_8^{\prime }\left(p\right)=0$, for $p_0\approx 1.321617491$ in $\left[0,2\right]$, where the maximum point of $T_8\left(p\right)$ is achieved at $p_0$. We conclude that

$$\left|H_{3,1}\left(f\right)\right|\le 0.09142363.$$

By putting $p=0$ in $\mathrm{\Gamma }(p,x,y)$, we obtain

$$\mathrm{\Gamma }(0,1,y)=2592.$$

Hence,

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{16}.$$

$\mathrm{\Gamma }(2,x,y)$ is independent of x and $y$, therefore

$$\mathrm{\Gamma }(2,1,y)=\mathrm{\Gamma }(2,0,y)=\mathrm{\Gamma }(2,x,0)=\mathrm{\Gamma }(2,x,1)=800.$$

Thus,

$$\left|H_{3,1}\left(f\right)\right|\le \frac{25}{1296}.$$

By putting $y=1$ in $\mathrm{\Gamma }(p,x,y)$, we get

$$\mathrm{\Gamma }(0,x,1)=-576x^4+2592x^3-4032x^2+4608=T_9\left(x\right).$$

Since $T_9^{\prime }\left(x\right)<0$ for $\left[0,1\right]$. Therefore, $T_9\left(x\right)$ is decreasing in $\left[0,1\right]$ and hence maximum is achieved at $x=0$. Thus

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{9}.$$

By putting $y=0$ in $\mathrm{\Gamma }(p,x,y)$, we get

$$\mathrm{\Gamma }(0,x,0)=-2592x^3+5184x=T_{10}\left(x\right).$$

Clearly $T_{10}^{\prime }\left(x\right)=0$ for $x_0\approx 0.8164965$ in $\left[0,1\right]$, where the maximum point of $T_{10}\left(x\right)$ is achieved at $x_0$. We conclude that

$$\left|H_{3,1}\left(f\right)\right|\le 0.06804138.$$

Thus, from the above cases we conclude that

$$\mathrm{\Gamma }\left(p,x,y\right)\le 4608\mathrm{on}\left[0,2\right]\times \left[0,1\right]\times \left[0,1\right].$$

Therefore, we can write

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{41472}\left(\mathrm{\Gamma }\left(p,x,y\right)\right)\le \frac{1}{9}.$$

If $f\in {\mathcal{S}}_{sin}^{*}$, then the sharp bound for this Hankel determinant is determined by

$$\left|H_{3,1}\left(f\right)\right|=\frac{1}{9}\approx 0.1111,$$

with an extremal function

$$f\left(z\right)=zexp\left({\int }_0^z\frac{sin\left(t^3\right)}{t}dt\right)=z+\frac{1}{3}{z}^4+\dots .$$

□

5. Third Hankel Determinant for the Class ${\mathcal{BT}}_{sin}$

In the following, we discuss the bounds of the third-order Hankel determinant for $f\in {\mathcal{BT}}_{sin}$.

Theorem 3.

Let $f\in {\mathcal{BT}}_{sin}$ be the series representation (1). Then

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{16}.$$

This bound is sharp.

Proof. 

Suppose that $f\in {\mathcal{BT}}_{sin}$. From the definition, we know that there is a Schwarz function $\omega \left(z\right)$, such that

$$f^{\prime }\left(z\right)=1+sin\left(\omega \left(z\right)\right).$$

(32)

From (1), we easily have

$$f^{\prime }\left(z\right)=1+2a_{2}z+3a_3{z}^2+4a_4{z}^3+5a_5{z}^4+\dots .$$

(33)

Combing (32), (33) and the series expansion of $1+sin\left(\omega \right(z\left)\right)$ in (15), we obtain that

$$\begin{array}{ccc}\hfill a_2& =& \frac{1}{4}{p}_1,\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill a_3& =& \frac{1}{3}\left(\frac{1}{2}{p}_2-\frac{1}{4}{p}_1^2\right),\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill a_4& =& \frac{1}{4}\left(\frac{1}{2}{p}_3+\frac{5}{48}{p}_1^3-\frac{1}{2}{p}_1{p}_2\right),\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill a_5& =& \frac{1}{5}\left(\frac{1}{2}{p}_4-\frac{1}{4}{p}_2^2-\frac{1}{32}{p}_1^4+\frac{5}{16}{p}_1^2{p}_2-\frac{1}{2}{p}_1{p}_3\right).\hfill \end{array}$$

(37)

Substituting (34)–(37) into the expression of $H_{3,1}\left(f\right)$ along with $p_1=p\in \left[0,2\right]$, we get

$$\begin{array}{ccc}\hfill H_{3,1}\left(f\right)& =& \frac{1}{552960}\left(-151p^6+144p^4{p}_2+1584p^3{p}_3-768p^2{p}_2^2-8064p^2{p}_4\right.\hfill \\ & & \left.+13824p{p}_2{p}_3-7168p_2^3+9216p_2{p}_4-8640p_3^2\right).\hfill \end{array}$$

(38)

Let $t=4-p^2$. Using (8)–(10) along with the straightforward algebraic computations, we have

$$\begin{array}{ccc}\hfill 144p^4{p}_2& =& 72\left(p^6+p^{4}tx\right),\hfill \\ \hfill 1584p^3{p}_3& =& 396p^6+792p^{4}tx-396p^{4}t{x}^2+792p^{3}t\left(1-{\left|x\right|}^2\right)\sigma ,\hfill \\ \hfill 768p^2{p}_2^2& =& 192p^6+384p^{4}tx+192p^2{t}^2{x}^2,\hfill \\ \hfill 8064p^2{p}_4& =& 1008p^{4}t{x}^3-4032p^{3}tx\left(1-{\left|x\right|}^2\right)\sigma -4032p^{2}t\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2\hfill \\ & & -3024p^{4}t{x}^2+4032p^{2}t\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho +4032p^{3}t\left(1-{\left|x\right|}^2\right)\sigma \hfill \\ & & +3024p^{4}tx+1008p^6+4032p^{2}t{x}^2,\hfill \\ \hfill 13824p{p}_2{p}_3& =& -1728p^2{t}^2{x}^3-1728p^{4}t{x}^2+3456p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma +3456p^2{t}^2{x}^2\hfill \\ & & +3456p^{3}t\left(1-{\left|x\right|}^2\right)\sigma +5184p^{4}tx+1728p^6,\hfill \\ \hfill 7168p_2^3& =& 896t^3{x}^3+2688p^2{t}^2{x}^2+2688p^{4}tx+896p^6,\hfill \\ \hfill 9216p_2{p}_4& =& 2304p^{2}t{x}^2+2304t^2{x}^3+576p^6+2304p^{4}tx+2304p^{3}t\left(1-{\left|x\right|}^2\right)\sigma \hfill \\ & & +2304p^{2}t\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho +1728p^2{t}^2{x}^2+2304p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma \hfill \\ & & +2304t^{2}x\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho -1728p^{4}t{x}^2-2304p^{2}t\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2\hfill \\ & & -2304p^{3}tx\left(1-{\left|x\right|}^2\right)\sigma -1728p^2{t}^2{x}^3-2304t^{2}x\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2\hfill \\ & & +576p^{4}t{x}^3+576p^2{t}^2{x}^4-2304p{t}^2{x}^2\left(1-{\left|x\right|}^2\right)\sigma ,\hfill \\ \hfill 8640p_3^2& =& 540p^2{t}^2{x}^4-2160p{t}^2{x}^2\left(1-{\left|x\right|}^2\right)\sigma -2160p^2{t}^2{x}^3-1080p^{4}t{x}^2\hfill \\ & & +2160t^2{\left(1-{\left|x\right|}^2\right)}^2{\sigma }^2+4320p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma +2160p^2{t}^2{x}^2\hfill \\ & & +2160p^{3}t\left(1-{\left|x\right|}^2\right)\sigma +2160p^{4}tx+540p^6.\hfill \end{array}$$

By plugging these expressions into (38) and performing some basic computations, we can get

$$\begin{array}{ccc}\hfill H_{3,1}\left(f\right)& =& \frac{1}{552960}\left\{-15p^6+2304t^2{x}^3-896t^3{x}^3-1728p^{2}t{x}^2-432p^{4}t{x}^3+252p^{4}t{x}^2\right.\hfill \\ & & +96p^{4}tx+36p^2{t}^2{x}^4-1296p^2{t}^2{x}^3+144p^2{t}^2{x}^2-2160t^2{\left(1-{\left|x\right|}^2\right)}^2{\sigma }^2\hfill \\ & & +360p^{3}t\left(1-{\left|x\right|}^2\right)\sigma +1728p^{3}tx\left(1-{\left|x\right|}^2\right)\sigma +1728p^{2}t\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2\hfill \\ & & -1728p^{2}t\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho -144p{t}^2{x}^2\left(1-{\left|x\right|}^2\right)\sigma -2304t^{2}x\overline{x}\left(1-{\left|x\right|}^2\right){\sigma }^2\hfill \\ & & \left.+1440p{t}^{2}x\left(1-{\left|x\right|}^2\right)\sigma +2304t^{2}x\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\rho \right\}.\hfill \end{array}$$

Therefore,

$$H_{3,1}\left(f\right)=\frac{1}{552960}\left(v_1\left(p,x\right)+v_2\left(p,x\right)\sigma +v_3\left(p,x\right){\sigma }^2+\mathrm{\Psi }\left(p,x,\sigma \right)\rho \right),$$

where $\rho ,x,\sigma \in \overline{\mathbb{U}},$ and

$$\begin{array}{ccc}\hfill v_1\left(p,x\right)& =& -15p^6+\left(4-p^2\right)\left[\left(4-p^2\right)\left(-1280x^3-400p^2{x}^3+36p^2{x}^4+144p^2{x}^2\right)\right.\hfill \\ & & \left.-1728p^2{x}^2-432p^4{x}^3+252p^4{x}^2+96p^{4}x\right],\hfill \\ \hfill v_2\left(p,x\right)& =& \left(4-p^2\right)\left(1-{\left|x\right|}^2\right)\left[\left(4-p^2\right)\left(1440px-144p{x}^2\right)+1728p^{3}x+360p^3\right],\hfill \\ \hfill v_3\left(p,x\right)& =& \left(4-p^2\right)\left(1-{\left|x\right|}^2\right)\left[\left(4-p^2\right)\left(-144{\left|x\right|}^2-2160\right)+1728p^2\overline{x}\right],\hfill \\ \hfill \mathrm{\Psi }\left(p,x,\sigma \right)& =& \left(4-p^2\right)\left(1-{\left|x\right|}^2\right)\left(1-{\left|\sigma \right|}^2\right)\left[-1728p^2+2304x\left(4-p^2\right)\right].\hfill \end{array}$$

Now, employing $\left|x\right|=x$, $\left|\sigma \right|=y$, and utilizing the assumption $\left|\rho \right|\le 1,$ we obtain

$$\begin{array}{ccc}\hfill \left|H_{3,1}\left(f\right)\right|& \le & \frac{1}{552960}\left(\left|v_1\left(p,x\right)\right|+\left|v_2\left(p,x\right)\right|y+\left|v_3\left(p,x\right)\right|y^2+\left|\mathrm{\Psi }\left(p,x,\sigma \right)\right|\right).\hfill \end{array}$$

(39)

$$\begin{array}{ccc}& \le & \frac{1}{552960}G\left(p,x,y\right),\hfill \end{array}$$

(40)

where

$$G\left(p,x,y\right)=k_1\left(p,x\right)+k_2\left(p,x\right)y+k_3\left(p,x\right)y^2+k_4\left(p,x\right)\left(1-y^2\right),$$

with

$$\begin{array}{ccc}\hfill k_1\left(p,x\right)& =& 15p^6+\left(4-p^2\right)\left[\left(4-p^2\right)\left(1280x^3+400p^2{x}^3+36p^2{x}^4+144p^2{x}^2\right)\right.\hfill \\ & & \left.+1728p^2{x}^2+432p^4{x}^3+252p^4{x}^2+96p^{4}x\right],\hfill \\ \hfill k_2\left(p,x\right)& =& \left(4-p^2\right)\left(1-x^2\right)\left[\left(4-p^2\right)\left(1440px+144p{x}^2\right)+1728p^{3}x+360p^3\right],\hfill \\ \hfill k_3\left(p,x\right)& =& \left(4-p^2\right)\left(1-x^2\right)\left[\left(4-p^2\right)\left(144x^2+2160\right)+1728p^{2}x\right]\hfill \\ \hfill k_4\left(p,x\right)& =& \left(4-p^2\right)\left(1-x^2\right)\left[1728p^2+2304x\left(4-p^2\right)\right].\hfill \end{array}$$

Now, we have to maximize $G\left(p,x,y\right)$ in the closed cuboid $\mathrm{{\rm Y}}:\left[0,2\right]\times \left[0,1\right]\times \left[0,1\right]$.

For this, we have to discuss the maximum values of $G\left(p,x,y\right)$ in the interior of $\mathrm{{\rm Y}}$, in the interior of its six faces and on its twelve edges.

1. Interior points of cuboid $\mathrm{{\rm Y}}$:

Let $\left(p,x,y\right)\in \left(0,2\right)\times \left(0,1\right)\times \left(0,1\right)$. By taking partial derivativeof $G\left(p,x,y\right)$ with respect to y, we get

$$\begin{array}{ccc}\hfill \frac{\partial G}{\partial y}& =& 72\left(4-p^2\right)(1-x^2)\left\{4y(x-1)\left[\left(4-p^2\right)\left(x-15\right)+12p^2\right]\right.\hfill \\ & & \left.+2p\left[x\left(4-p^2\right)\left(x+10\right)+p^2\left(12x+\frac{5}{2}\right)\right]\right\}.\hfill \end{array}$$

Plugging $\frac{\partial G}{\partial y}=0$ yields

$$y=\frac{2p\left[x\left(4-p^2\right)\left(x+10\right)+p^2\left(12x+\frac{5}{2}\right)\right]}{4(x-1)\left[\left(4-p^2\right)\left(15-x\right)-12p^2\right]}=y_0.$$

If $y_0$ is a critical point inside $\mathrm{{\rm Y}}$, then $y_0\in \left(0,1\right)$. This is possible only if

$$2p^3\left(12x+\frac{5}{2}\right)+2px\left(4-p^2\right)\left(x+10\right)+4(1-x)\left(4-p^2\right)\left(15-x\right)<48p^2(1-x).$$

(41)

and

$$p^2>\frac{4\left(15-x\right)}{27-x}.$$

(42)

Now, we have to obtain the solutions which satisfy both inequalities (41) and (42) for the existence of the critical points.

Let $g\left(x\right)=\frac{4\left(15-x\right)}{27-x}$. Since $g^{\prime }\left(x\right)<0$ for $\left(0,1\right)$, $g\left(x\right)$ is decreasing in $\left(0,1\right)$. Hence $p^2>\frac{28}{13}$ and a simple exercise shows that (41) does not hold in this case for all values of $x\in [\frac{2}{5},1)$, and there is no critical point of G in $\left(0,2\right)\times [\frac{2}{5},1)\times \left(0,1\right)$.

For any critical point $(\widehat{p},\widehat{x},\widehat{y})$ of G existing in the interior of cuboid $\mathrm{{\rm Y}}$, it is obvious that $\widehat{x}<\frac{2}{5}$. Then we see ${\widehat{p}}^2>\frac{292}{133}$ and $\widehat{y}\in (0,1)$. Now we are going to prove that $G(\widehat{p},\widehat{x},\widehat{y})<34560$.

Let $(p,x,y)\in \left(\sqrt{\frac{292}{133}},2\right)\times (0,\frac{2}{5})\times \left(0,1\right)$. Using $x<\frac{2}{5}$ and $1-x^2<1$, it follows that

$$\begin{array}{ccc}\hfill k_1\left(p,x\right)& \le & 15p^6+\left(4-p^2\right)\left[\left(4-p^2\right)\left(1280{(2/5)}^3+400p^2{(2/5)}^3+36p^2{(2/5)}^4+144p^2{(2/5)}^2\right)\right.\hfill \\ & & \left.+1728p^2{(2/5)}^2+432p^4{(2/5)}^3+252p^4{(2/5)}^2+96p^4(2/5)\right]\hfill \\ & =& 15p^6+\frac{1}{625}\left(4-p^2\right)\left(23504p^4+245504p^2+204800\right):={\zeta }_1\left(p\right),\hfill \\ \hfill k_2\left(p,x\right)& \le & \left(4-p^2\right)\left[\left(4-p^2\right)\left(1440p(2/5)+144p{(2/5)}^2\right)+1728p^3(2/5)+360p^3\right]\hfill \\ & =& \frac{1}{25}(4-p^2)(11304p^3+59904p):={\zeta }_2\left(p\right),\hfill \\ \hfill k_3\left(p,x\right)& \le & (4-p^2)\left[\left(4-p^2\right)\left(144{(2/5)}^2+2160\right)+1728p^2(2/5)\right]\hfill \\ & =& \frac{1}{25}(4-p^2)\left(-37296p^2+218304\right):={\zeta }_3\left(p\right),\hfill \\ \hfill k_4\left(p,x\right)& \le & (4-p^2)\left[1728p^2+2304(2/5)\left(4-p^2\right)\right]\hfill \\ & =& \frac{1}{5}(4-p^2)\left(4032p^2+18432\right):={\zeta }_4\left(p\right).\hfill \end{array}$$

This yields

$$G(p,x,y)\le {\zeta }_1\left(p\right)+{\zeta }_4\left(p\right)+{\zeta }_2\left(p\right)y+\left[{\zeta }_3\left(p\right)-{\zeta }_4\left(p\right)\right]y^2:=\mathrm{\Theta }(p,y).$$

It is noted that

$$\frac{\partial \mathrm{\Theta }}{\partial y}={\zeta }_2\left(p\right)+2\left[{\zeta }_3\left(p\right)-{\zeta }_4\left(p\right)\right]y$$

and

$$\frac{{\partial }^2\mathrm{\Theta }}{\partial y^2}=2\left[{\zeta }_3\left(p\right)-{\zeta }_4\left(p\right)\right]=\frac{2}{25}\left(-57456p^2+126144\right).$$

In virtue of ${\zeta }_3\left(p\right)-{\zeta }_4\left(p\right)\le 0$ for $p\in (\sqrt{\frac{292}{133}},2)$, we find that $\frac{{\partial }^2\mathrm{\Theta }}{\partial y^2}\le 0$ for $y\in (0,1)$ and thus

$$\frac{\partial \mathrm{\Theta }}{\partial y}\ge \frac{\partial \mathrm{\Theta }}{\partial y}{|}_{y=1}=\frac{1}{25}\left(4-p^2\right)\left(11304p^3-114912p^2+59904p+252288\right)\ge 0,p\in (\sqrt{\frac{292}{133}},2).$$

Then, we have

$$\mathrm{\Theta }(p,y)\le \mathrm{\Theta }(p,1)={\zeta }_1\left(p\right)+{\zeta }_2\left(p\right)+{\zeta }_3\left(p\right):=\varpi \left(p\right).$$

Some simple calculations show that $\varpi \left(p\right)$ attains its maximum value $21708.38$ at $p\approx 1.481718$. Hence, we see that

$$G(p,x,y)<34560,(p,x,y)\in \left(\sqrt{\frac{292}{133}},2\right)\times (0,\frac{2}{5})\times \left(0,1\right).$$

This means that $G(\widehat{p},\widehat{x},\widehat{y})<34560$. Thus, we know G is less than 34560 at all the critical points in the interior of $\mathrm{{\rm Y}}$. That is to say that G has no optimal solution in the interior of $\mathrm{{\rm Y}}$.

2. Interior of all the six faces of cuboid $\mathrm{{\rm Y}}$:

On $p=0$, $G(p,x,y)$ reduces to

$$\begin{array}{ccc}\hfill T_1(x,y)& =& G(0,x,y)=20480x^3+(1-x^2)\left(2304x^2{y}^2-36864x{y}^2+34560y^2\right.\hfill \\ & & \left.+36864x\right),x,y\in \left(0,1\right).\hfill \end{array}$$

(43)

Then

$$\frac{\partial T_1}{\partial y}=(1-x^2)y\left(1152x^2-10368x+9216\right),x,y\in \left(0,1\right).$$

$T_1(x,y)$ has no critical point in $\left(0,1\right)\times \left(0,1\right)$.

On $p=2$, $G(p,x,y)$ reduces to

$$G(2,x,y)=960.$$

(44)

Thus

$$\left|{\mathcal{H}}_3\left(1\right)\right|\le \frac{1}{576}.$$

On $x=0$, $G(p,x,y)$ reduces to $G(p,0,y)$, given by

$$\begin{array}{ccc}\hfill T_2(p,y)& =& G(p,0,y)=15p^6+(4-p^2)\left(360p^{3}y+(8640-2160p^2)y^2\right.\hfill \\ & & \left.+1728p^2(1-y^2)\right).\hfill \end{array}$$

(45)

Solving $\frac{\partial T_2}{\partial y}=0$, we get

$$y=\frac{5p^3}{12(9p^2-20)}=y_1.$$

For the given range of $y$, $y_1$ should belong to $\left(0,1\right)$, which is possible only if $p>p_0$, $p_0\approx 1.547150535.$ Also derivative of $T_2(p,y)$ partially with respect to p is

$$\begin{array}{ccc}\hfill \frac{\partial T_2}{\partial p}& =& 90p^5+\left(4-p^2\right)\left(1080p^{2}y-4320p{y}^2+3456p\left(1-y^2\right)\right)\hfill \\ & & -3456p^3\left(1-y^2\right)-720p^{4}y+2p\left(2160p^2-8640\right)y^2.\hfill \end{array}$$

(46)

By substituting the value of y in (46), plugging $\frac{\partial T_2}{\partial p}=0$ and simplifying, we get

$$\frac{\partial T_2}{\partial p}=24p\left(135p^8-23728p^6+150336p^4-322560p^2+230400\right)=0.$$

(47)

A calculation gives the solution of (47) in $\left(0,2\right)$; that is, $p\approx 1.338189368$. Thus, $T_2(p,y)$ has no optimal point in $\left(0,2\right)\times \left(0,1\right)$.

On $x=1$, $G(p,x,y)$ reduces to

$$T_3(p,y)=G(p,1,y)=-185p^6-1968p^4+5952p^2+20480.$$

(48)

Solving $\frac{\partial T_3}{\partial p}=0$, we get the critical point at $p_0\approx 1.131750917.$ Thus, $T_3(p,y)$ achieves its maximum at $p_0$ that is $24486.2176$. Hence,

$$\left|H_{3,1}\left(f\right)\right|\le 0.0442820.$$

On $y=0$, $G(p,x,y)$ yields

$$\begin{array}{ccc}\hfill T_4(p,x)& =& G(p,x,0)=36p^6{x}^4-32p^6{x}^3-108p^6{x}^2-288p^4{x}^4-96p^{6}x\hfill \\ & & -2496p^4{x}^3+15p^6-144p^4{x}^2+576p^2{x}^4+2688p^{4}x\hfill \\ & & +14592p^2{x}^3-1728p^4+2304p^2{x}^2-18432p^{2}x\hfill \\ & & -16384x^3+6912p^3+36864x.\hfill \end{array}$$

A calculation shows that there is no existing solution for the system of equations $\frac{\partial T_4}{\partial x}=0$ and $\frac{\partial T_4}{\partial p}=0$ in $\left(0,2\right)\times \left(0,1\right)$.

On $y=1$, $G(p,x,y)$ reduces to

$$\begin{array}{ccc}\hfill T_5(p,x)& =& G(p,x,1)=36p^6{x}^4-32p^6{x}^3-144p^5{x}^4-108p^6{x}^2+288p^5{x}^3\hfill \\ & & -432p^4{x}^4-96p^{6}x+504p^5{x}^2+1536p^4{x}^3+1152p^3{x}^4\hfill \\ & & +15p^6-288p^{5}x-3888p^4{x}^2+4608p^3{x}^3+1728p^2{x}^4\hfill \\ & & -360p^5-1344p^{4}x-2592p^3{x}^2-10752p^2{x}^3-2304p{x}^4\hfill \\ & & +2160p^4-4608p^{3}x+25344p^2{x}^2-23040p{x}^3-2304x^4\hfill \\ & & +1440p^3+6912p^{2}x+2304p{x}^2+20480x^3-17280p^2\hfill \\ & & +23040px-32256x^2+34560.\hfill \end{array}$$

A calculation shows that there is no existing solution for the system of equations $\frac{\partial T_5}{\partial x}=0$ and $\frac{\partial T_5}{\partial p}=0$ in $\left(0,2\right)\times \left(0,1\right)$.

3. On the edges of cuboid $\mathrm{{\rm Y}}$:

By putting $y=0$ in $G(p,x,y)$, we have

$$G(p,0,0)=15p^6-1728p^4+6912p^2=T_6\left(p\right).$$

Clearly $T_6^{\prime }\left(p\right)=0$ for $p_0\approx 1.433522440$ in $\left[0,2\right]$, where the maximum point of $T_6\left(p\right)$ is achieved at $p_0$. Thus, we say that

$$\left|H_{3,1}\left(f\right)\right|\le 0.01272596.$$

By putting $y=1$ in $G(p,x,y)$, we get

$$G(p,0,1)=15p^6-360p^5+2160p^4+1440p^3-17280p^2+34560=T_7\left(p\right).$$

since $T_7^{\prime }\left(p\right)<0$ for $\left[0,2\right]$. Therefore, $T_7\left(p\right)$ is decreasing in $\left[0,2\right]$, and hence the maximum is achieved at $p=0$. Thus,

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{16}.$$

By putting $p=0$ in $G(p,x,y)$, we get

$$G(0,0,y)=34560y^2.$$

A simple calculation gives

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{16}.$$

We see that $G(p,1,y)$ is independent of $y$, we have

$$G(p,1,0)=G(p,1,1)=-185p^6-1968p^4+5952p^2+20480=T_8\left(p\right).$$

Now, $T_8^{\prime }\left(p\right)=0$, for $p_0\approx 1.13175091$ in $\left[0,2\right]$, where the maximum point of $T_8\left(p\right)$ is achieved at $p_0$. We conclude that

$$\left|H_{3,1}\left(f\right)\right|\le 0.04428207.$$

By putting $p=0$ in $G(p,x,y)$, we get

$$G(0,1,y)=20480.$$

Hence,

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{27}.$$

As $G(2,x,y)$ is independent of x and $y$, therefore

$$G(2,1,y)=G(2,0,y)=G(2,x,0)=G(2,x,1)=960.$$

Thus,

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{576}.$$

By putting $y=1$ in $G(p,x,y)$, we get

$$G(0,x,1)=-2304x^4+20480x^3-32256x^2+34560=T_9\left(x\right)$$

since $T_9^{\prime }\left(x\right)<0$ for $\left[0,1\right]$. Therefore, $T_9\left(x\right)$ is decreasing in $\left[0,1\right]$, and hence the maximum is achieved at $x=0$. Thus,

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{16}.$$

By putting $y=0$ in $G(p,x,y)$, we get

$$G(0,x,0)=-16384x^3+36864x=T_{10}\left(x\right).$$

Clearly $T_{10}^{\prime }\left(x\right)=0$ for $x_0\approx 0.8660254$ in $\left[0,1\right]$, where the maximum point of $T_{10}\left(x\right)$ is achieved at $x_0$. We know that

$$\left|H_{3,1}\left(f\right)\right|\le 0.03849001.$$

Thus, from the above cases, we conclude that

$$G\left(p,x,y\right)\le 34560\mathrm{on}\left[0,2\right]\times \left[0,1\right]\times \left[0,1\right].$$

Hence, we can write

$$\left|H_{3,1}\left(f\right)\right|\le \frac{1}{552960}\left(G\left(p,x,y\right)\right)\le \frac{1}{16}.$$

If $f\in {\mathcal{BT}}_{sin}$, then sharp bound for this Hankel determinant is determined by

$$\left|H_{3,1}\left(f\right)\right|=\frac{1}{16}\approx 0.0625,$$

with an extremal function

$$f\left(z\right)={\int }_0^z\left(1+sin\left(t^3\right)\right)dt=z+\frac{1}{4}{z}^4+\dots .$$

□

6. Conclusions

In the current article, we considered a subclass of starlike functions denoted as ${\mathcal{S}}_{sin}^{*}$ and a subclass of functions with bounded turning denoted as ${\mathcal{BT}}_{sin}$. The two subfamilies of univalent functions were all connected with an eight-shaped domain with $\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}$ and $f^{\prime }\left(z\right)$ subordinated to $1+sinz$, respectively. We gave an estimate for an initial coefficient and the bounds of the third-order Hankel determinant for these classes were determined. All the estimations were proven to be sharp.

In proving our main results, the third Hankel determinant of functions belonging to ${\mathcal{S}}_{sin}^{*}$ and ${\mathcal{BT}}_{sin}$ were represented in terms of the well-known formulas for the coefficient $c_2$, $c_3$ and $c_4$ of functions with positive real part, respectively. Using triangle inequalities, the problem of finding the upper bound of the third Hankel determinant is reducing it to discuss the maximum values of a function with three variables. Based on analysis of all the possibilities that the maxima might occur, we obtained the sharp upper bounds of third Hankel determinant. Clearly, this method can be extended to find upper bounds for functions of different subfamilies of univalent functions. The difficulty is that formulae for the coefficient $c_2$, $c_3$ and $c_4$ consist of three complex variables in the closed-unit disk. It is not easy to get sharp results.