Abstract
We conduct cluster analysis of a class of locally asymptotically self-similar stochastic processes with finite covariance structures, which includes Brownian motion, fractional Brownian motion, and multifractional Brownian motion as paradigmatic examples. Given the true number of clusters, a new covariance-based dissimilarity measure is introduced, based on which we obtain approximately asymptotically consistent algorithms for clustering locally asymptotically self-similar stochastic processes. In the simulation study, clustering data sampled from fractional and multifractional Brownian motions with distinct Hurst parameters illustrates the approximated asymptotic consistency of the proposed algorithms. Clustering global financial markets’ equity indexes returns and sovereign CDS spreads provides a successful real world application. Implementations in MATLAB of the proposed algorithms and the simulation study are publicly shared in GitHub.
1. Introduction
Learning stochastic processes is a fast growing research area in machine learning, as there is a considerable number of machine learning problems that involve the time variable as a component of datasets [1,2,3,4,5]. Due to the nature of the time index, stochastic processes often possess “path features” [6]. This additional information provided by the time index makes performing machine learning on stochastic processes quite different from other types of objects. Several new techniques are developed alongside studying such machine learning problems [7,8,9,10]. In this paper, we focus our study on a particular unsupervised learning problem: clustering of stochastic processes. Recently, clustering distribution stationary ergodic time series were motivated by and discussed in [11,12]. Later, Peng et al. [13] developed Khaleghi et al. [12]’s consistent clustering algorithms in order to cluster covariance stationary ergodic (discrete-time or continuous-time) stochastic processes. Please note that a distribution stationary ergodic stochastic process is not necessarily covariance stationary. Therefore, Peng et al. [13] enlarged the class of stochastic processes for which one can apply the consistent clustering algorithms.
The motivation for this paper lies in the fact that assuming the observed data to follow a covariance stationary stochastic process seems still unrealistic. Our paper then tries to overcome this issue through developing a promising algorithm to cluster a more general class of stochastic processes, the so-called locally asymptotically self-similar processes. More precisely, the key path features of the observed stochastic processes are assumed to be known as Assumption 1 (see Section 2). Compared to the stationarity, Assumption 1 is a much weaker constraint, for the reason that in many fields it was proved that the observed paths are sampled from functions (or functionals) of well-known locally asymptotically self-similar processes. For example, dynamics in financial markets (equity returns and interest rates) can be described based on geometric Brownian motions (gBm); long-term dependent or self-similar phenomena are often modeled by fractional Brownian motions (fBm) [14]. The long-term financial indexes and curves, such as S&P 500, Dow Jones, NASDAQ, interest rates, VIX rates, and currency exchange rates can be modeled using multifractional Brownian motions (mBm) [15,16,17,18,19,20]. Modeling events using locally asymptotically self-similar processes can be widely found in other fields such as geology, biology, power, and energy [21,22]. Recently, there was growth of investigations on how to test and estimate locally asymptotically self-similar processes, and on how to apply machine learning analysis to such processes [23,24,25,26,27,28,29,30]. However, in as far as we know, there has not yet been a study on clustering locally asymptotically self-similar processes in the literature. Our paper then aims at shedding some light on clustering such processes.
Contrary to the conventional clustering of finite-dimensional data, clustering based on the paths’ features of the processes largely removes the noise by capturing the observations’ path features. Therefore, a nice dissimilarity measure should be the one that well characterizes the path features. In this context, “nice” refers to the property that the computational complexity and the prediction errors caused by the over-fitting issues are expected to be largely reduced. Moreover, with some path features, consistency of the clustering algorithm [11,12] may be obtained. Among all the stochastic process features, we focus on characterizing the property of ergodicity in this paper. However similar analysis can be made for other patterns of process features such as seasonality, Markov property and martingale property.
Ergodicity [31] is a very typical feature possessed by several well-known processes, which is applied to financial time series analysis. It is tightly related to other process features, such as stationarity, long-term memory, and self-similarity [32,33]. In [12,13], it is shown that both distribution ergodicity and covariance ergodicity lead to obtaining an asymptotically consistent clustering algorithms for clustering processes. In this paper, we take one step further to relax the condition of ergodicity to the “local asymptotic ergodicity” [34] and obtain the so-called “approximately asymptotically consistent algorithms” for clustering processes having such path property. This setting presents such a large class of processes that includes the well-known Lévy processes, some self-similar processes and some multifractional processes [34].
Each clustering stochastic processes problem involves handling data, defining clusters, measuring dissimilarities, and finding groups efficiently; therefore, we organize the paper as follows. Section 2 is devoted to introducing a class of locally asymptotically self-similar processes to which our clustering approaches apply. In Section 3, a covariance-based dissimilarity measure is suggested and in Section 4, the approximately asymptotically consistent algorithms for clustering both offline and online datasets are designed. A simulation study is performed in Section 5, where the algorithms are applied to cluster multifractional Brownian motions (mBm), an excellent representative of the class of locally asymptotically self-similar processes. In Section 6, we perform cluster analysis over a global equity return data. Conventionally, stock returns of countries in the same region are considered to have similar patterns due to the common regional economic factors. However, recent empirical evidence shows that, as financial market globalization increases, global economic clusters switch from “geographical centriods” to “economic development centriods”. Our clustering algorithms show how “geography” and “economic development” jointly impact the equity returns of countries or regions. Considering the equities as stochastic processes in the clustering makes the analysis more promising. Finally, Section 7 concludes and provides future prospects.
2. A Class of Locally Asymptotically Self-Similar Processes
Self-similar processes are a class of processes that are invariant in distribution under suitable scaling of time [35,36,37]. These processes have been used to successfully model various time-scaling random phenomena observed in high frequency data, especially in the financial data and geological data.
Definition 1
(Self-similar process). A stochastic process (here the time indexes set is not necessarily continuous) is self-similar to self-similarity index if, for all , all and all ,
where denotes the equality in joint probability distribution of two finite-dimensional random vectors.
When for , it follows from (1) that for any ,
Therefore taking at both hand sides of (2) yields
Self-similar processes are generally not distribution stationary but their increment processes can be distribution stationary (any finite subset’s joint distribution is invariant subject to time shift) or covariance stationary (its mean and covariance structure exist and are an invariant subject to time shift). From now on we restrict our setting to stochastically continuous-time self-similar processes only [37]. i.e., a process is stochastically continuous at if
This assumption is weaker than the almost sure continuity. The process is called (stochastically) continuous time over if it is continuous at each . For , we call the increment process (or simply the increments) of . If a continuous-time self-similar process’ all increment processes are covariance stationary, its covariance structure can be explicitly given below:
Theorem 1.
Let be a self-similar process with index and with covariance stationary increments. Then
and
Theorem 1 can be obtained by replacing the distribution stationary increments assumption in Theorem 1.2 in [36] with covariance stationary increments assumption. We briefly provide the proof below.
Proof.
We highlight that, contrary to Theorem 1.2 in [36], the covariance stationary increment process of in Theorem 1 is not necessarily distribution stationary. This fact inspires us to relax the distribution stationarity of the processes to the covariance stationarity in the forthcoming Assumption (). Below, we introduce a natural extension of self-similar processes, the so-called locally asymptotically self-similar processes [34,38,39].
Definition 2
(Locally asymptotically self-similar process). A continuous-time stochastic process with its index being a continuous function valued in , is called locally asymptotically self-similar, if for each , there exists a non-degenerate self-similar process with self-similarity index , such that
where the convergence is in the sense of all the finite-dimensional distributions.
In (10), is called the tangent process of at t [38,39]. Moreover, it is shown (see Theorem 3.8 in [39]) that, if is unique in law, it is then self-similar to index and it has distribution stationary increments. Then the local asymptotic self-similarity generalizes the conventional self-similarity, in the sense that, any non-degenerate self-similar process with distribution stationary increments is locally asymptotically self-similar and its tangent process is itself. Furthermore, in a weaker sense, it is not difficult to show the following:
Proposition 1.
Let be a continuous-time self-similar process with self-similarity index and with covariance stationary increments. Then all its tangent processes share the same mean and covariance function.
Proof.
Since is locally asymptotically self-similar, by definition at each there exists a tangent process such that
Next we show s mean and covariance structure are uniquely determined.
We remark from Proposition 1 that the tangent processes of may not be unique in law, but their finite-dimensional subsets have unique first and second order moments.
Based on the above discussion, throughout this paper, we assume that the observed datasets are sampled from a known number (denoted by ) of continuous-time processes satisfying the following condition:
Assumption 1.
The processes are locally asymptotically self-similar; their tangent processes’ increment processes are autocovariance ergodic.
In Assumption 1, the autocovariance-ergodicity means that the sample autocovariance functions of the covariance stationary process converges in squared mean to the autocovariance functions of the process, i.e., a zero-mean (that is the case for the tangent processes’ increments) continuous-time process is autocovariance ergodic if it is covariance stationary and satisfies
where denotes the mean squared convergence: . Please note that the above convergence (15) yields
Thus, Assumption 1 says that the observed processes’ tangent processes have covariance stationary increments. The typical examples of locally asymptotically self-similar processes satisfying Assumption 1 are fractional Brownian motion (fBm) [40], multifractional Brownian motion (mBm) [41,42,43] and the generalized multifractional Brownian motion introduced in [44]. Below, we focus our attention on mBm, which is used in our simulation study and real world application (see Section 5 and Section 6). MBm is a paradigmatic example of both multifractional stochastic processes and locally asymptotically self-similar processes. It naturally extends the classical fBm by allowing its Hurst parameter to vary with time. The mBm was introduced independently by Peltier and Lévy-Véhel [41] and Benassi et al. [42], using, respectively, integral moving average type representation and harmonizable integral representation of the fBm. These two types of mBms share several core features and their precise connection was studied by Stoev and Taqqu [43], who show that the two types of mBms generally have different correlation structures. The most recent discussion on the definition of mBm is also made in [43], where they define a general class of multifractional Gaussian processes which includes the above two types of mBms as two particular cases. In this paper, we adopt a definition of mBm through the so-called harmonizable integral representation (see (1.3) in [43] or see [42,44]). Please note that our analysis and approaches are valid for all other versions of mBms in the literature.
Definition 3
(Multifractional Brownian motion). A multifractional Brownian motion is a continuous-time Gaussian process defined by:
where:
- denotes a complex-valued Gaussian measure (see Proposition 2.1 in [43]) satisfyingfor anywith being the Fourier transform of f and being a standard Brownian motion.
- The Hurst functional parameter is a Hölder function with exponent . Subject to this constraint the paths of mBm are almost surely continuous functions.
Theorem 4.1 in [43] gives the covariance function of : for ,
where
It is known that the pointwise Hölder exponent (pHe) of is almost surely equal to at each t [42]. Recall that, for a continuous-time nowhere differentiable process , its local Hölder regularity can be measured by the pHe defined by: for each ,
For a continuous but undifferentiable function, the pHe measures its “local roughness”: the smaller the pHe is at time t, the more “fractals” should be observed around t in the path. When becomes a constant, mBm reduces to an fBm with Hurst parameter equal to H. More generally, it can be seen from [34] that mBm is locally asymptotically self-similar satisfying Assumption 1. Its tangent process at each t is an fBm with index :
where is a deterministic function only depending on . In the literature, some studies are particularly focused on the statistical inference problems around the pHe of processes and their applications. This study is motivated by modeling using locally asymptotically self-similar processes as well. We refer the readers to [45,46,47,48,49,50].
As one of the most natural extensions of fBm, mBm has, at present, broad applications. Unlike fBm, mBm allows its Hurst parameter H to change with time. This allows us to model different regimes of the stochastic process with one single model. For example, during a financial crisis, asset volatility may rise significantly, while it is much lower in the peaceful period. Likewise, empirical evidence shows that there have been periods of different volatilities in either exchange rates or interest rates. An fBm (or a self-similar process) is unable to capture the above phenomena. This motivates researchers to introduce mBm into finance as an alternative or improvement of fBm.
The assumption of covariance stationarity inspires us to introduce a covariance-based dissimilarity measure between the sample paths, in order to capture the level of differences between the two corresponding covariance stationary processes. Later we show that the assumption of autocovariance-ergodicity is sufficient for the clustering algorithms to be approximately asymptotically consistent.
3. Clustering Stochastic Processes
3.1. Covariance-Based Dissimilarity Measure between Autocovariance Ergodic Processes
Let Z be a process satisfying Assumption 1. Denote by Y its tangent process (see (10)) and denote by X an increment process of Y, i.e., there is some such that for all . In Assumption 1, X is autocovariance ergodic. Since we will show that clustering distinct Zs is approximately asymptotically equivalent to clustering the corresponding increment processes Xs, then the dissimilarity measures of Zs can be constructed based on those of the autocovariance ergodic processes Xs. From (4) we know that the autocovariance process X is zero-mean. Our first main result is then introduction to the following covariance-based dissimilarity measure between autocovariance ergodic processes. We refer the readers to [13] for more features of this dissimilarity measure.
Definition 4.
The covariance-based dissimilarity measure d between the discrete-time stochastic processes , (in fact , denote two covariance structures, each class may contain different process distributions but they share the same autocovariance function) is defined by
where:
- For any integers , , is the shortcut notation of the row vector .
- The distance ρ between two equal-sized covariance matrixes denotes the Frobenius norm of . Recall that for a matrix , its Frobenius norm is defined by where for each , denotes the -coefficient of .
Remark 1.
It is important to note that Definition 4 only defines the dissimilarity measures between discrete-time stochastic processes (time series). This is the most common object studied in the literature on clustering stochastic processes. Studying clustering of time series is sufficient for practical applications for at least two reasons. First, a continuous-time path is not observable in the real world. Second, any (stochastically) continuous-time process can be well approximated by its discrete-time paths. In what follows, we will find a mean sample path by a finite-length subsequence of a discretized stochastic process.
Thanks to the autocovariance-ergodicity of the sample processes, the dissimilarity measure d can be estimated by the empirical dissimilarity measure below:
Definition 5.
Given two processes’ discrete-time sample paths for , let , then the empirical covariance-based dissimilarity measure between and is given by
where:
- () is the largest dimension of the covariance matrix considered by ; in this framework we take , i.e., the floor number of [12,13].
- For , and , denotes the empirical covariance matrix of the process s path , which is given below:where denotes the transpose of a matrix.
Remark 2.
Since X is autocovariance ergodic, every empirical covariance matrix is a consistent estimator of the covariance matrix under Frobenius norm and in probability, i.e.,
Furthermore, the fact that both d and satisfy the triangle inequalities implies that is a consistent estimator of d. The proof is quite similar to that of Lemma 1 in [13], except that in the former statement the convergence holds in probability. These ergodicity and triangle inequalities are the keys to demonstrate that our algorithms in the next section are approximately asymptotically consistent. We list them in the following paragraphs.
Remark 3.
For every pair of paths
sampled from two autocovariance ergodic processes and , respectively, we have
and
where the dissimilarity measure between the sample path and the stochastic process is defined to be
Remark 4.
In the next section, we define a proper covariance-based dissimilarity measure between locally asymptotically self-similar processes satisfying Assumption (), based on the dissimilarity measure d.
3.2. Covariance-Based Dissimilarity Measure between Locally Asymptotically Self-Similar Processes
Now under Assumption (), we study the asymptotic relationship between the locally asymptotically self-similar process in (10) and its tangent process’ increment process. The following result reveals the relationship between local asymptotic self-similarity and covariance stationarity.
Proposition 2.
Let be a locally asymptotically self-similar process satisfying Assumption (). For each ,
where (see (10)) is an autocovariance ergodic process.
Proof.
Let us fix and pick any finite discrete-time indexes set . In Assumption (), the f.d.d. convergence (10) holds. It then implies
where we adopt the notation to denote the vector
From a statistical point of view, the sequence at the left-hand side of (25) cannot straightforwardly serve to estimate the distribution of the right-hand side , because the functional index at the left-hand side is not observable in practice. To overcome this inconvenience, we note that (25) can be interpreted as follows: when is sufficiently small,
where K is an arbitrary positive integer. Smaller is , closer are the two hand sides of (28). However in practice has its optimal value, due to the sample size limitation. Therefore, when applied to the real world, (28) says that: given a discrete-time path with for each , sampled from a locally asymptotically self-similar process , its localized increment paths with time index around , i.e.,
is approximately distributed as an autocovariance ergodic increment process of the self-similar process . In this example, is the smallest value one can consider for in (28). This fact drives us to define the empirical covariance-based dissimilarity measure between two paths of locally asymptotically self-similar processes and as follows:
where:
- L is chosen from .
- , are the localized increment paths defined as in (29). Heuristically speaking, for , computes the “distance” between the two covariance structures (of the increments of ) indexed by the time in the neighborhood of , and averages the above distances. It is worth noting that the value K describes the “sample size” used to approximate each local distance . Therefore, its value should be picked neither too large nor too small and it can depend on n. It is suggested that in order that the result of estimating the dissimilarity measure is acceptable. The largest value one can set for K is (correspondingly, ).
The following observation is straightforward.
Remark 5.
Based on the definition (30) and Remark 2, is also a (weakly) consistent estimator of d (see Remark 3) and it also satisfies the triangle inequalities as in Remark 4.
Through employing the dissimilarity measure on locally asymptotically self-similar processes, we obtain the so-called “approximately asymptotically consistent algorithms”, which are introduced in the following section.
4. Approximately Asymptotically Consistent Algorithms
4.1. Offline and Online Algorithms
Please note that the covariance-based dissimilarity measure defined in (30) will aim to cluster covariance structures, not process distributions; therefore the ground truths of clustering should be those of covariance structures. We thus define the ground truth as follows [13].
Definition 6
(Ground truth of covariance structures). Let be a partitioning of into κ disjoint sets , , such that the means and covariance structures of , are identical, if and only if for some . Such G is called ground truth of covariance structures. For , we denote by the restriction of G to the first N sequences:
The processes Z satisfying Assumption 1 are generally not covariance stationary; however, their tangent processes’ increments X are covariance stationary. In view of (25) and (28), clustering these processes Z is equivalent to clustering X, based on the covariance structure ground truth of the latter increments. Below we will introduce algorithms aiming to approximate the covariance structure ground truth of X.
Depending on how the information is collected, the processes clustering problems consist of dealing with two separate model settings: the offline and online settings. In the offline setting, the sample size and each path length are time-independent. However, in the online setting, they may both grow with time. As stated in [12], using the offline algorithm in the online setting by simply applying it to the entire data observed at every time step, does not result in an asymptotically consistent algorithm. As a result, we consider clustering offline and online datasets as two approaches and study them separately. Hence the approximated asymptotic consistency will be described in Theorems 2 and 3 below, respectively, for offline and online clustering algorithms. Our offline and online clustering algorithms below are obtained by replacing the dissimilarity measures in Algorithms 1 and 2 in [13] with .
For the offline setting, we cluster observed data using Algorithm 1 below. It is a 2-point initialization centroid-based clustering approach. From the distance defined in (30), the algorithm picks the farthest two points to be the first two cluster centers (Lines 1–2). Then, iteratively, each following cluster center is chosen to be the point farthest to all the previously assigned cluster centers (Lines 3–5). Finally, the algorithm assigns each remaining point to the nearest cluster (Lines 7–10).
The strategy for clustering online data is presented in Algorithm 2 as follows. At each time t, first update the collection of sample paths (Lines 1–2); then for each , use Algorithm 1 to group the first j paths in into clusters (Lines 6–7); for each cluster the center is selected as the point having the smallest index among that cluster, and sort these indexes increasingly (Line 8); calculate the minimum inter-cluster distance and update the normalization factor (Lines 9–11). Finally, every sample path in is assigned to the “nearest” cluster, based on the weighted combination of the distances (given in Line 15) between this observation and the candidate cluster centers obtained at each iteration on j (Lines 14–17).
| Algorithm 1: Offline clustering. |
 |
| Algorithm 2: Online clustering. |
 |
4.2. Computational Complexity and Consistency of the Algorithms
We describe the computational complexity based on the number of computations of the distance . For Algorithm 1, the 2-point initialization requires times calculations of . From (30) we see that each calculation of consists of times computations of . By (20), can be obtained through computing times distances . Therefore, the total number of computations of is not greater than . For Algorithm 2, since at each step , Algorithm 1 is run on j observations, the total number of s computations is then less than . The computational complexity is acceptable in practice, and it is quite competitive compared with existing algorithms for clustering stochastic processes.
Now we introduce the notion of approximately asymptotic consistency. Fix a positive integer K. Let , be two locally asymptotically self-similar processes with respect functional indexes , . Furthermore, let
be, respectively, their sample paths , ’ increments, defined as in (29). For , we define the normalized increments by taking the following linear transformation:
Then using (25) we obtain
where denotes a discrete-time path of the increment of a self-similar process with self-similarity index . Fix . For each empirical dissimilarity measure , we correspondingly define
is another dissimilarity measure between , which has a tight relationship to the distance between their tangent processes’ increments. Indeed using (32) and the continuous mapping theorem, it is easy to derive the following result.
Proposition 3.
For any N independent sample paths ,
where are the increments of the tangent processes corresponding to , respectively.
In particular, when , . In this sense, “approximates” . cannot be observed in practice since the functional indexes of the locally asymptotically self-similar processes are supposed to be unknown. In what follows, only serves to define the approximate asymptotic consistency. In this concept, “approximate” means the clustering locally asymptotically self-similar processes problem is “approximately” equivalent to the clustering their tangent processes problem.
Now we state the consistency theorems. Through Theorems 2 and 3, below we show that Algorithms 1 and 2 are both approximately asymptotically consistent. Their proofs are inspired by the ones in [12,13]. However different from the consistency theorems in [12,13], the convergences in Theorems 2 and 3 have weaker senses, which are in probability, not almost sure.
Theorem 2.
In Assumption 1, Algorithm 1 is approximately asymptotically consistent for clustering the offline sample paths . This means: if is replaced with in Algorithm 1, the output clusters converge to the covariance structure ground truths of the increments of the corresponding tangent processes in probability, as and . More formally,
where f is given in Algorithm 1 and denotes the ground truths of the covariance structures that generate the set of paths .
Proof.
First, we show
where denotes any -partition of . Since if the estimated clusters , the samples in S that are generated by the same cluster in G are closer under to each other than to the rest of the samples. Hence we can write
It follows from (37) and (34) that
which proves (36).
Next we show that Algorithm 1 is asymptotically consistent on clustering under :
Denote by
Fix . Let denote the shortest path length in :
Denote by the minimal non-zero dissimilarity measure between the processes with different covariance structures:
Fix and let be arbitrarily small. Since there are a finite number N of samples, by Remark 3 there is such that for we have
On one hand, by applying the triangle inequalities (see Remark 5), we obtain
Then by (41) and the fact that , the following inclusion holds:
On the other hand, by applying the triangle inequalities (see Remark 5) and the fact that , we also obtain: if
then
Equivalently,
It follows from (42), (43) and (40) that for ,
Please note that (44) is equivalent to
This tells us that the sample paths in S that are generated by the same covariance structures are closer to each other than to the rest of sample paths. Then, by (44), for , each sample path should be “close” enough to its cluster center, i.e.,
where the cluster centers’ indexes are determined by Algorithm 1 in the following way:
and
These are chosen to index sample paths generated by different process covariance structures. Then by (44), each remaining sample path will be assigned to the cluster center corresponding to the sample path generated by the same process covariance structure. Finally, (38) results from (44) and (45); and (35) is proved by combining (36) and (38). □
Below we state the consistency theorem concerning the online clustering algorithm.
Theorem 3.
In Assumption 1, Algorithm 2 is approximately asymptotically consistent for clustering the online sample paths , . This means: if is replaced with in Algorithm 2, for any integer , the output clusters of the first N paths in
converge to the covariance structure ground truths of the increments of the corresponding tangent processes in probability, as and . In other words,
where denotes the clustering restricted to the first N sample paths in . We also recall that is the restriction of to the first N sample paths in (see Definition 6).
Proof.
Let us fix . First, similar to the derivation of (36) in the proof of Theorem 2, we can obtain
Then it remains to prove
In what follows we prove (48).
Let be arbitrarily small. Fix , where is defined as in (39).
Denote by
For , denote by the index of the first path in sampled from , i.e.,
Please note that does not depend on t but only on k. Then denote by
For denote by the first j sample paths in . Then from (51) we see that, and contains paths sampled from all distinct processes (covariance structures). Using the fact that , we can find a fixed value such that
Recall that in the online setting, the ith sample path’s length grows with time t. Therefore, by Remark 5, for every there exists some such that
Since , by Theorem 2 for every there exists such that is asymptotically consistent for all . Since is increasing as , there is such that for . Let
From Algorithm 2 (Lines 9, 11) we see
Below we provide upper bounds in probability of and .
- Upper bound of: Similar to how (43) is derived, we use the triangle inequalities (Remark 5) and (39) to obtain:Since the clusters are sorted in the order of appearance of the distinct process covariance structures, we have for all and , where we recall that the index is defined in (50). It follows from (55), the fact that and (53) thatFor , by (54), the triangle inequality, (49) and (56), we have
- Upper bound of the first term: Using (53) and the fact that we obtain
- Upper bound of the second term: Recall that for all and . Therefore, by (52) and the fact that for every we have
Combining (59)–(62) we obtain, for ,
Now we explain how to use (63) to prove the asymptotic consistency of Algorithm 2. Consider an index for some . On one hand, using the triangle inequalities, we obtain for , ,
Then applying (53) and (63) we obtain
On the other hand, from (53) we see for any ,
Using again the triangle inequalities, we obtain
Let . It results from (66), (65) and (63) that
Since and can be chosen arbitrarily small, it follows from (64) and (67) that
for all . (47) as well as Theorem 3 is proved. □
5. Tests on Simulated Data: Clustering Multifractional Brownian Motions
5.1. Efficiency Improvement: -Transformation
In this section, we show the performance of the proposed clustering approaches (Algorithms 1 and 2) on clustering simulated mBms given in Definition 3. Recall that mBm is a paradigmatic example of locally asymptotically self-similar processes. Its tangent process is an fBm, which is self-similar. Since the covariance structure of the fBm is nonlinearly dependent on its self-similarity index, we can then apply the so-called -transformation to the covariance matrixes of its increments, in order to improve the efficiency of the clustering algorithms. More precisely, in our clustering algorithms, we replace in the coefficients of all the covariance matrixes and their estimators with their -transformations. For , its -transformation is defined to be
By applying such transformation, the observations assigned to any two clusters by the covariance structure ground truths become well separated thus the clustering algorithms become more efficient. For more detail on this efficiency enhancement approach, we refer the reader to Section 3 in [13].
5.2. Simulation Methodology
We select Wood–Chan’s method [51,52] to simulate mBm, and use the implementation (MATLAB) of Wood–Chan’s method in FracLab (version 2.2) by INRIA in our simulation study (https://project.inria.fr/fraclab/download/overview/, accessed on 1 January 2022). This method outputs independent sample paths of the following form:
where is an input integer. Now we would select so that d (see (19)) is a convergent series (well-defined). To show that this choice is reasonable, we consider the stochastic process
where is some given mesh. For each , the increments of the tangent process (see the right-hand side of (28))
is given by: for ,
As increments of fBm, is autocovariance ergodic. Moreover for , we have, using the definition of (see (67)), the covariance function of fBm (see (5)) and the fact that ,
From the definition of d in (19) and (72) we can see that, by taking and using (72), for any ,
where
Therefore, we showed that the choice makes d well-defined.
5.3. Synthetic Datasets
To construct a collection of the mBm paths with distinct functional indexes , we set the function form of in each of the predetermined clusters. Two functional forms of are selected for synthetic data study:
- Case 1 (Monotonic function): The general form is taken to bewhere is a fixed integer and different values of h correspond to different clusters. We then predetermine five clusters with various hs to separate different clusters. In this study, we set , and . The trajectories of the five functional forms of in different clusters are illustrated in the left graph of Figure 1.
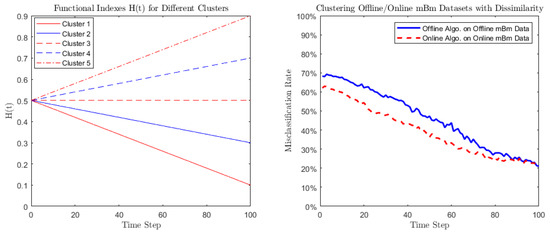 Figure 1. The functional form of follows Equation (73): with . The left graph plots correspond to 5 different clusters. The right graph illustrates the misclassification rates output by (i) offline algorithm on offline dataset (solid line) and (ii) online algorithm on online dataset (dashed line). Both algorithms are performed based on the - transformed covariance-based dissimilarity measure.
Figure 1. The functional form of follows Equation (73): with . The left graph plots correspond to 5 different clusters. The right graph illustrates the misclassification rates output by (i) offline algorithm on offline dataset (solid line) and (ii) online algorithm on online dataset (dashed line). Both algorithms are performed based on the - transformed covariance-based dissimilarity measure. - Case 2 (Periodic function): The general form is taken to bewhere different values of h lead to different clusters. Specifically, we take , and . The trajectories of the corresponding five functional forms of are illustrated in the left graph of Figure 2.
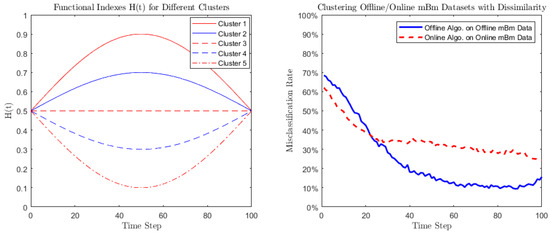 Figure 2. The functional form of follows Equation (74): with . The left graph plots corresponding to 5 different clusters. The right graph illustrates the misclassification rates output by (i) offline algorithm on offline dataset (solid line) and (ii) online algorithm on online dataset (dashed line). Both algorithms are performed based on the - transformed covariance-based dissimilarity measure.
Figure 2. The functional form of follows Equation (74): with . The left graph plots corresponding to 5 different clusters. The right graph illustrates the misclassification rates output by (i) offline algorithm on offline dataset (solid line) and (ii) online algorithm on online dataset (dashed line). Both algorithms are performed based on the - transformed covariance-based dissimilarity measure. - Case 3 (Small turbulence on ): We proceed to examine if the proposed algorithm has the capacity of distinguishing processes with very similar behaviors. To this end we take consider clustering an fBm with Hurst parameter , and an mBm with the Hurst functional parameterWe perform the tests using two values of : (i) and (ii) . In both cases, the index of the corresponding mBm is regarded to be plus some noise.
We demonstrate the approximated asymptotic consistency of the proposed algorithms by conducting both offline and online clustering analysis. We denote the number of observed data points in each time series by , and denote the number of time series paths by .
In the offline setting, the number of observed paths does not depend on time t; however, the lengths do. To construct offline datasets, we perform the following:
- 1.
- For , simulate 20 mBm paths in group i (corresponding to ), each path is with length of 305. Then the total number of paths . To be more explicit we denote bywhere each row is an mBm discrete-time path. For , the data from the ith group are given as:
- 2.
- At each , we observe the first values of each path, i.e.,
The online dataset does not require observed paths to be of equal length, and can be regarded as an extension of the offline case. Introducing the online dataset aims at mimicking the situation where new time series are observed as time goes. In our simulation study, we use the following method to construct online datasets:
- 1.
- 2.
- At each and , we observe the following dataset in the ith group:where
- s are the -coefficients in given in (75).
- denotes the number of paths in the ith group. Here denotes the floor number. That is, starting from 6 paths in each group, 1 new path will be added into each group as t increases by 10.
- , with . This means each path observes three new values as t increases by 1.
Since at each time t, the covariance structure ground truth being known, we can then evaluate the clustering performance in terms of the so-called “misclassification rate”, which is calculated based on averaging the proportion of mis-clustered paths in each scenario. For more detail on this notion of misclassification rate we refer the readers to Section 4 in [13].
5.4. Experimental Results
We demonstrate the asymptotic consistency of our clustering algorithms by computing the misclassification rates using simulated offline and online datasets. Below we summarize the simulation study results.
Case 1 (Monotonic function):
When s are chosen to be give monotonic functionals of the form (73) (see the left graph in Figure 1), the right graph in Figure 1 illustrates the behavior of the misclassification rates corresponding to Algorithm 1 applied to offline data setting (solid line), and Algorithm 2 applied to online data setting (dashed line). From this result we observe the following:
- (1)
- Both algorithms attempt to be consistent in their circumstances, as the time t increases, in the sense that the corresponding misclassification rates decrease to 0.
- (2)
- Clustering mBms are asymptotically equivalent to clustering their tangent processes’ increments.
- (3)
- The online algorithm seems to have an overall better performance: its misclassification rates are 5– lower than that of offline algorithm. The reason may be that at early time steps the differences among the s are not significant. Unlike the offline clustering algorithm, the online one is flexible enough to catch these small differences.
Case 2 (Periodic function):
The same converging behaviors are found in the case of periodic functional form of as specified in (74). Their trajectories are illustrated in the left graph of Figure 2. The clustering performance shown in the right graph of Figure 2 indicates the following:
- (1)
- Both misclassification rates of the clustering algorithms have generally a declining trend as time increases.
- (2)
- As the differences among the periodic function s values go up and down, the misclassification rates go down and up accordingly.
- (3)
- The online clustering algorithm has an overall worse performance than the offline one. This may be because starting from the differences among s become significantly large. In this situation, the offline clustering algorithm can better catch these differences, since it has a larger sample size (20 paths in each group) than the online one.
Case 3 (Small turbulence on ):
We continue the simulation analysis using the case where we intend to distinguish the classical fBm process with the mBm process with similar function H. We take two values of (as a constant) for the fBm: (i) and (ii) . In both cases, the corresponding mBm has the H function slightly different with . The functional form of H for mBm is specified in Equation (75).
The clustering results are presented in Figure 3. We find general convergence performance in both cases (for ). More specifically, the online algorithm outperforms the offline algorithm for both datasets. The misclassification rate is lower than 20% when for the online algorithm results. In both cases, as the difference between the two Hurst parameters goes up and down, we see the corresponding misclassification rates go down and up, which is in line with the consistency of our clustering algorithms. When , the percent changes between the Hurst parameters of fBm and mBm are smaller than those for , therefore the performance of clustering presented in the right graph is slightly worse. In conclusion, the proposed algorithms demonstrate a robust convergence feature when clustering fBm and mBm with similar Hurst parameters.
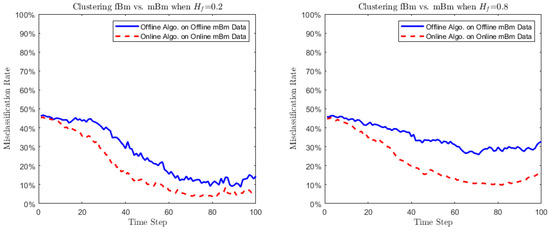
Figure 3.
The clustering performance using fBm with and mBm with given in Equation (74): with . The left graph is the case where , and the right graph is the case where . Both graphs illustrate the misclassification rates output by offline algorithm on offline dataset (solid line) and online algorithm on online dataset (dashed line). Both algorithms are performed based on the - transformed covariance-based dissimilarity measure.
Please note that for each pair of paths with length , we took and in ; however, any other value of K could be taken. We have provided easily readable and editable MATLAB codes of the proposed algorithms and simulation study replications. All the codes used in this section can be found publicly online (https://github.com/researchcoding/clustering_locally_asymptotically_self_similar_processes/, accessed on 1 January 2022).
5.5. Comparison to Traditional Approaches Designed for Clustering Finite-Dimensional Vectors
In this section, we use the benchmark methods to cluster the simulated dataset proposed in Section 5.3 and compare them to our novel approach. For the specification of the benchmark method, we select K-means and hierarchical clustering with Euclidean distance, which are commonly used in clustering analysis of non-stochastic vectors or processes. First of all, performing both approaches is more time-consuming than our clustering algorithms. More importantly, the misclassification rates from these two traditional algorithms are plotted in Figure 4 and Figure 5.
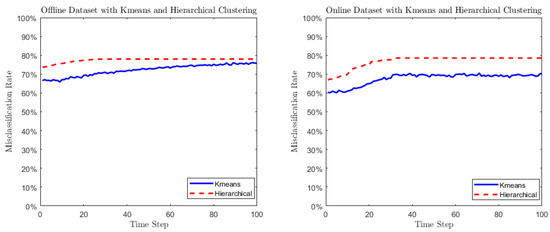
Figure 4.
The functional form of follows Equation (73): with . The left graph plots the misclassification rates output by K-means and hierarchical clustering methods using the offline dataset. The right graph shows the misclassification rates using the online dataset.
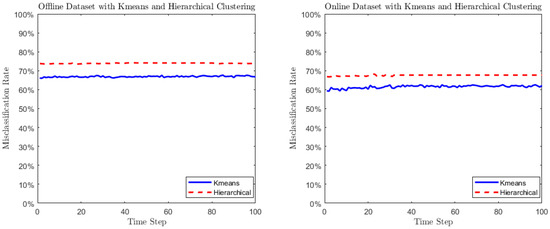
Figure 5.
The functional form of follows Equation (74): with . The left graph plots the misclassification rates output by K-means and hierarchical clustering methods using the offline dataset. The right graph shows the misclassification rates using the online dataset.
As opposed to the performance shown in Figure 1 and Figure 2, the benchmark algorithms do not converge when clustering locally asymptotically self-similar processes. Though the numbers of clusters are clearly predetermined in both algorithms, none of the benchmark algorithm demonstrates declining misclassification rate with the increased number of observations. Figure 4 shows the diverging performance of the clustering algorithm with an increased then flat misclassification over time. Figure 5 shows almost flat misclassification rates. None of the results shows a misclassification rate lower than 60%.
From the simulation analysis, we conclude that the conventional approaches have failed to cluster the locally asymptotically self-similar processes (with different functional forms of ) in this particular case. The proposed methods in this paper are tailored to cluster the locally asymptotically self-similar stochastic processes with known number of clusters.
6. Real World Application: Clustering Global Financial Markets
6.1. Motivation
In this section, we apply the proposed clustering algorithm on the real world datasets. We select a global equity return data to perform the clustering analysis. Conventionally, stock returns of countries in the same region are considered to have similar patterns due to the common regional economic factors. In other words, economic entities in close geographical distance have potentially more trades and other economic ties. Therefore, these countries are influenced by similar economic and finance factors. However, recent empirical evidence regarding the financial markets show that globalization has broken the geographical barrier and creates new economic factors in contrast to the geographical ones. As a result, global economic clusters switch from “geographical centriods” to “economic development centriods”. Emerging markets demonstrate increasingly similar financial market patterns and correlations [53], whereas developed economic entities share increasing financial market similarity [54].
Bianchi and Pianese [15] pioneered the stock returns modeling using locally asymptotically self-similar processes (e.g., mBm process). Bianchi et al. [18] and Peng and Zhao [27] provide empirical support on this time-varying self-similar feature of the financial time series. Given this fact, the financial market index is a perfect example of stochastic processes, where our proposed clustering algorithms are applicable. We examine the connection of global financial markets by answering as to whether economic entities are well-behaved and clustered by geographical distribution or by development level.
6.2. Data and Methodology
In empirical cluster analysis, we use two asset classes from global financial markets: the country-level stock index and the sovereign credit default swap spread. The stock index return captures the upside (growth) characteristics, and the sovereign CDS spread captures the downside (credit risk) characteristics of underlying economic entities. We provide a more detailed description below.
- Equity indexes returns: We cluster the global stock indexes based on their empirical time-varying covariance structure. We use Algorithms 1 and 2 as the clustering approach. We select the index constituents of MSCI ACWI (All Country World Index) as the underlying stochastic processes in the datasets for clustering analysis. Each of the indexes is a realized path representing the historical monthly returns of the underlying economic entities. MSCI ACWI is the leading global equity market index and covers more than 85% of the market capitalization of the global stock market (As of December 2018, as reported on https://www.msci.com/acwi, accessed on 1 January 2022).
- Sovereign CDS spreads: We cluster the sovereign credit default swap (CDS) spreads of global economic entities. The sovereign CDS is an insurance-like financial product that provides default protection of treasury bonds for the economic entity (e.g., the government). The CDS spread reflects the cost to insurer of the exposure on a sovereign entity’s default. We select a five-year sovereign CDS spread as the indicator of sovereign credit risk, as the five-year product has the best liquidity on the CDS market. We overlap the sample of economic entities between the stock and CDS datasets, and the same set of underlying economics entities are present in the clustering analysis. Our CDS data source is Bloomberg.
The extant literature [15,18,27] shows that these types of financial time series demonstrate a “long memory” path feature. These stochastic processes are naturally modeled as locally asymptotically self-similar processes such as fBm and mBm. In the fBm and mBm cases, the proposed algorithms are applicable to cluster the stock returns and CDS spreads. Similar to Section 5, we cluster the increments of the indexes returns with the -transformed dissimilarity measure. The data sample consists of stock indexes and sovereign CDS spreads including 23 developed economic entities and 24 emerging markets. The detailed constituents are present in Table 1 from the data source at https://www.msci.com/acwi, accessed on 1 January 2022. The geographical regions include the Americas, EMEA (Europe, Middle East and Africa), the Pacific, and Asia.

Table 1.
The categories of major stock and sovereign CDS markets in the MSCI ACWI (All Country World Index). There are 23 developed economic entities and 24 emerging countries or areas. The geographical regions contain Americas, EMEA (Europe, Middle East and Africa), Pacific and Asia. Markets with * have missing sovereign CDS data in our data sample.
We construct both offline and online datasets using monthly returns of stock indexes and monthly spreads of sovereign CDS. The offline dataset of the monthly return of stock index data starts in June 2005, includes the financial crisis period in September 2007, and ends in November 2019. We include the global financial market crisis to present the systematic risk contagion effect in our clustering analysis. The online dataset starts on January 1989, which covers the 1997 Asian financial crisis, 2003 dot-com bubble andthe 2007 subprime mortgage crisis, and ends in November 2019. The offline dataset contains 47 observed paths, and each has 174 time points. In the online setting, the longest stochastic path has 371 observations, and the shortest time series have 174 observations. The online dataset begins with 33 economic entities and ends with 47 economic entities.
As for monthly sovereign CDS spreads, we remove the Netherlands, Qatar, Singapore, Greece and United Arabic from the sample due to insufficient observations. We end up with 42 economic entities with CDS spread in the clustering analysis. The offline dateset starts in June 2005 and ends in November 2019, and each economic entity has 174 observations.
6.3. Clustering Results
We compare the clustering results using offline and online datasets with the number of clusters based on (i) geographical regions (four groups: Americas, Europe and the Middle East, the Pacific, and Asia) and (ii) development level (two groups: emerging markets and developed markets). The clustering factor (geographical region or development level) with the lower misclassification rate represents the most relevant partition of the economics entities. We examine whether the geographical region or development level differentiates between the financial market’s behaviors the most.
Table 2 shows that the misclassification rates for clustering using development levels are significantly and consistently lower than that of the geographical region. The empirical result is robust, using offline or online settings and using stock indexes or sovereign CDS spreads. The clustering performance tends to support the dominance of the development level in comparison to the geographical region, in terms of characterizing the financial market features in recent decades. The best results (lowest misclassification rate) are (i) clustering the offline dataset using offline algorithm, and (ii) clustering the online dataset using an online algorithm, when the cluster factor is using the development level (emerging markets vs. developed markets). There are 30% to 50% decreases on misclassification rates when clustering using development level compared to when clustering using region.

Table 2.
The misclassification rates of clustering algorithms on different datasets. The clustering facts are geographical region and development level, respectively. Panel A presents the results from clustering global stock indexes, and Panel B presents the results from clustering sovereign CDS spreads.
Table 3 presents misclassified economic entities in the cluster analysis, when we use the development level as the clustering factor. For global stock indexes, the misclassification often occurs in the case where developed economic entities is clustered into the emerging market group. Stock index returns from Austria, Finland, and Portugal are clustered in the emerging market group in both offline and online algorithms. The misclassification within the developed market group demonstrates a more random pattern. For sovereign CDS spreads, the misclassification occurs in the cases where emerging economic entities are clustered into the developed market group. Sovereign CDS spreads of Chile, China (Mainland), Czech Republic, Korea, Malaysia, Mexico, Poland, and Thailand are consistently misclassified into the developed market group. A plausible reason is that these economic entities have low sovereign credit risk compared to their peers in the most recent years.

Table 3.
The misclassification cases when using offline algorithm on offline dataset and online algorithm on online dataset. Panel A reports the mis-categorized economics entities in the stock index clustering case, and Panel B reports the mis-categorized economics entities in the sovereign CDS spreads clustering case. The algorithm clusters the dataset into two groups: emerging market group and developed market group. The mis-categorized outcome are reported, where (i) entities from developed markets incorrectly clusters in emerging market, or (ii) vice versa.
In both stock and CDS cases, we show that clustering financial time series by development level outperforms geographical region in our sample. This empirical evidence supports that economic globalization is breaking the geographic barrier and enhances the comovement of financial market performance by economics development status.
7. Conclusions and Future Prospects
In this paper, we introduce the problem of clustering locally asymptotically self-similar processes. A novel covariance-based dissimilarity measure is proposed to obtain approximately asymptotically consistent clustering algorithms for both offline and online settings. We showed that the recommended algorithms are competitive for at least three reasons:
- (1)
- Given their flexibility, our algorithms are applicable to clustering any distribution stationary ergodic processes with finite variances, any autocovariance ergodic processes, and locally asymptotically self-similar processes whose tangent processes have autocovariance ergodic increments. Multifractional Brownian motion (mBm) is an excellent representative of the latter class of processes.
- (2)
- Our algorithms are efficient enough in terms of their computational complexity. A simulation study is performed on clustering mBm. The results show that both offline and online algorithms are approximately asymptotically consistent.
- (3)
- Our algorithms are successfully applied to cluster the real world financial time series (equity returns and sovereign CDS spreads) via the development level and via regions. The outcomes are self-consistent with the financial markets behavior and they reveal the level of impact between the economic development and regions on equity returns.
Finally, we list the following open problems which could be left for future research.
- (1)
- The clustering framework proposed in our paper only focuses on the cases where the true number of clusters is known. The problem for which is supposed to be unknown remains open.
- (2)
- If we drop the Gaussianity assumption, the class of stationary incremental self-similar processes becomes much larger. This will yield an introduction to a more general class of locally asymptotically self-similar processes, whose autocovariances do not exist. This class includes linear multifractional stable motion [55,56] as a paradigmatic example. Cluster analysis of such stable processes will no doubt lead to a wide range of applications, especially when the process distributions exhibit heavy-tailed phenomena. Neither the distribution dissimilarity measure introduced in [12] nor the covariance-based dissimilarity measures used in this paper would work in this case, hence new techniques are required to cluster such processes, such as considering replacing the covariances with covariations [35] or symmetric covariations [57] in the dissimilarity measures.
Author Contributions
Conceptualization and Methodology: N.R. and Q.P.; Formal analysis and investigation: N.R., Q.P. and R.Z.; Writing: N.R., Q.P. and R.Z.; Data collection and analysis: R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in the simulation study are available at https://github.com/researchcoding/clustering_locally_asymptotically_self_similar_processes/, accessed on 1 January 2022. The datasets used in the real world application are available at https://www.msci.com/acwi, accessed on 1 January 2022.
Acknowledgments
The authors would like to express their special thanks to the assistant editor Finley Shen and the three anonymous reviewers for their careful reading of the manuscript and many insightful feedback and suggestions, which have led to a significant improvement of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| fBm | fractional Brownian motion |
| mBm | multifractional Brownian motion |
| gBm | geometric Brownian motion |
References
- Cotofrei, P. Statistical temporal rules. In Proceedings of the 15th Conference on Computational Statistics–Short Communications and Posters, Berlin, Germany, 24–28 August 2002. [Google Scholar]
- Harms, S.K.; Deogun, J.; Tadesse, T. Discovering sequential association rules with constraints and time lags in multiple sequences. In International Symposium on Methodologies for Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2002; pp. 432–441. [Google Scholar]
- Jin, X.; Lu, Y.; Shi, C. Distribution discovery: Local analysis of temporal rules. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2002; pp. 469–480. [Google Scholar]
- Jin, X.; Wang, L.; Lu, Y.; Shi, C. Indexing and mining of the local patterns in sequence database. In International Conference on Intelligent Data Engineering and Automated Learning; Springer: Berlin/Heidelberg, Germany, 2002; pp. 68–73. [Google Scholar]
- Keogh, E.; Kasetty, S. On the need for time series data mining benchmarks: A survey and empirical demonstration. Data Min. Knowl. Discov. 2003, 7, 349–371. [Google Scholar] [CrossRef]
- Lin, J.; Keogh, E.; Lonardi, S.; Patel, P. Finding motifs in time series. In Proceedings of the 2nd Workshop on Temporal Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 53–68. [Google Scholar]
- Li, C.S.; Yu, P.S.; Castelli, V. MALM: A framework for mining sequence database at multiple abstraction levels. In Proceedings of the Seventh International Conference on Information and Knowledge Management, Bethesda, MA, USA, 2–7 November 1998; pp. 267–272. [Google Scholar]
- Bradley, P.S.; Fayyad, U.M. Refining Initial Points for K-Means Clustering. ICML 1998, 98, 91–99. [Google Scholar]
- Keogh, E.; Chakrabarti, K.; Pazzani, M.; Mehrotra, S. Dimensionality reduction for fast similarity search in large time series databases. Knowl. Inf. Syst. 2001, 3, 263–286. [Google Scholar] [CrossRef]
- Java, A.; Perlman, E.S. Predictive Mining of Time Series Data. Bull. Am. Astron. Soc. 2002, 34, 741. [Google Scholar]
- Khaleghi, A.; Ryabko, D.; Mary, J.; Preux, P. Online clustering of processes. In Proceedings of the Fifteenth International Conference on Artificial Intelligence and Statistics, La Palma, Canary Islands, 21–23 April 2012; pp. 601–609. [Google Scholar]
- Khaleghi, A.; Ryabko, D.; Mary, J.; Preux, P. Consistent algorithms for clustering time series. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Peng, Q.; Rao, N.; Zhao, R. Covariance-based dissimilarity measures applied to clustering wide-sense stationary ergodic processes. Mach. Learn. 2019, 108, 2159–2195. [Google Scholar] [CrossRef]
- Comte, F.; Renault, E. Long memory in continuous-time stochastic volatility models. Math. Financ. 1998, 8, 291–323. [Google Scholar] [CrossRef]
- Bianchi, S.; Pianese, A. Multifractional properties of stock indices decomposed by filtering their pointwise Hölder regularity. Int. J. Theor. Appl. Financ. 2008, 11, 567–595. [Google Scholar] [CrossRef]
- Bianchi, S.; Pantanella, A.; Pianese, A. Modeling and simulation of currency exchange rates using multifractional process with random exponent. Int. J. Model. Optim. 2012, 2, 309–314. [Google Scholar] [CrossRef]
- Bertrand, P.R.; Hamdouni, A.; Khadhraoui, S. Modelling NASDAQ series by sparse multifractional Brownian motion. Methodol. Comput. Appl. Probab. 2012, 14, 107–124. [Google Scholar] [CrossRef]
- Bianchi, S.; Pantanella, A.; Pianese, A. Modeling stock prices by multifractional Brownian motion: An improved estimation of the pointwise regularity. Quant. Financ. 2013, 13, 1317–1330. [Google Scholar] [CrossRef]
- Bianchi, S.; Frezza, M. Fractal stock markets: International evidence of dynamical (in) efficiency. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 071102. [Google Scholar] [CrossRef] [PubMed]
- Pianese, A.; Bianchi, S.; Palazzo, A.M. Fast and unbiased estimator of the time-dependent Hurst exponent. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 031102. [Google Scholar] [CrossRef] [PubMed]
- Marquez-Lago, T.T.; Leier, A.; Burrage, K. Anomalous diffusion and multifractional Brownian motion: Simulating molecular crowding and physical obstacles in systems biology. IET Syst. Biol. 2012, 6, 134–142. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Cattani, C.; Chi, C.H. Multifractional Brownian motion and quantum-behaved particle swarm optimization for short term power load forecasting: An integrated approach. Energy 2020, 194. [Google Scholar] [CrossRef]
- Sikora, G. Statistical test for fractional Brownian motion based on detrending moving average algorithm. Chaos Solitons Fractals 2018, 116, 54–62. [Google Scholar] [CrossRef]
- Balcerek, M.; Burnecki, K. Testing of fractional Brownian motion in a noisy environment. Chaos Solitons Fractals 2020, 140, 110097. [Google Scholar] [CrossRef]
- Balcerek, M.; Burnecki, K. Testing of multifractional Brownian motion. Entropy 2020, 22, 1403. [Google Scholar] [CrossRef]
- Jin, S.; Peng, Q.; Schellhorn, H. Estimation of the pointwise Hölder exponent of hidden multifractional Brownian motion using wavelet coefficients. Stat. Inference Stoch. Process. 2018, 21, 113–140. [Google Scholar] [CrossRef]
- Peng, Q.; Zhao, R. A general class of multifractional processes and stock price informativeness. Chaos Solitons Fractals 2018, 115, 248–267. [Google Scholar] [CrossRef]
- Vu, H.T.; Richard, F.J. Statistical tests of heterogeneity for anisotropic multifractional Brownian fields. Stoch. Process. Their Appl. 2020, 130, 4667–4692. [Google Scholar] [CrossRef]
- Bicego, M.; Trudda, A. 2D shape classification using multifractional Brownian motion. In Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR); Springer: Berlin/Heidelberg, Germany, 2008; pp. 906–916. [Google Scholar]
- Kirichenko, L.; Radivilova, T.; Bulakh, V. Classification of fractal time series using recurrence plots. In Proceedings of the 2018 International Scientific-Practical Conference Problems of Infocommunications. Science and Technology (PIC S&T), Kharkiv, Ukraine, 9–12 October 2018; pp. 719–724. [Google Scholar]
- Krengel, U. Ergodic Theorems; de Gruyter Studies in Mathematics; de Gruyter: Berlin, Germany, 1985. [Google Scholar]
- Grazzini, J. Analysis of the emergent properties: Stationarity and ergodicity. J. Artif. Soc. Soc. Simul. 2012, 15, 7. [Google Scholar] [CrossRef]
- Samorodnitsky, G. Extreme value theory, ergodic theory and the boundary between short memory and long memory for stationary stable processes. Ann. Probab. 2004, 32, 1438–1468. [Google Scholar] [CrossRef]
- Boufoussi, B.; Dozzi, M.; Guerbaz, R. Path properties of a class of locally asymptotically self-similar processes. Electron. J. Probab. 2008, 13, 898–921. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Embrechts, P.; Maejima, M. An introduction to the theory of self-similar stochastic processes. Int. J. Mod. Phys. B 2000, 14, 1399–1420. [Google Scholar] [CrossRef]
- Embrechts, P.; Maejima, M. Selfsimilar Processes; Princeton Series in Applied Mathematics; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Falconer, K. Tangent fields and the local structure of random fields. J. Theor. Probab. 2002, 15, 731–750. [Google Scholar] [CrossRef]
- Falconer, K. The local structure of random processes. J. Lond. Math. Soc. 2003, 67, 657–672. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Peltier, R.F.; Lévy-Véhel, J. Multifractional Brownian Motion: Definition and Preliminary Results; Technical Report 2645; Institut National de Recherche en Informatique et en Automatique, INRIA: Roquecourbe, France, 1995. [Google Scholar]
- Benassi, A.; Jaffard, S.; Roux, D. Elliptic Gaussian random processes. Revista Matemática Iberoamericana 1997, 13, 19–90. [Google Scholar] [CrossRef]
- Stoev, S.A.; Taqqu, M.S. How rich is the class of multifractional Brownian motions? Stoch. Process. Their Appl. 2006, 116, 200–221. [Google Scholar] [CrossRef]
- Ayache, A.; Véhel, J.L. On the identification of the pointwise Hölder exponent of the generalized multifractional Brownian motion. Stoch. Process. Their Appl. 2004, 111, 119–156. [Google Scholar] [CrossRef]
- Ayache, A.; Taqqu, M.S. Multifractional processes with random exponent. Publicacions Matemàtiques 2005, 49, 459–486. [Google Scholar] [CrossRef]
- Bianchi, S.; Pantanella, A. Pointwise regularity exponents and well-behaved residuals in stock markets. Int. J. Trade Econ. Financ. 2011, 2, 52–60. [Google Scholar] [CrossRef][Green Version]
- Cadoni, M.; Melis, R.; Trudda, A. Financial crisis: A new measure for risk of pension fund portfolios. PLoS ONE 2015, 10, e0129471. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Frezza, M. Modeling the time-changing dependence in stock markets. Chaos Solitons Fractals 2012, 45, 1510–1520. [Google Scholar] [CrossRef]
- Frezza, M.; Bianchi, S.; Pianese, A. Forecasting Value-at-Risk in turbulent stock markets via the local regularity of the price process. Comput. Manag. Sci. 2022, 19, 99–132. [Google Scholar] [CrossRef]
- Garcin, M. Fractal analysis of the multifractality of foreign exchange rates. Math. Methods Econ. Financ. 2020, 13–14, 49–73. [Google Scholar]
- Wood, A.T.; Chan, G. Simulation of stationary Gaussian processes in [0,1]d. J. Comput. Graph. Stat. 1994, 3, 409–432. [Google Scholar] [CrossRef]
- Chan, G.; Wood, A.T. Simulation of multifractional Brownian motion. In COMPSTAT; Springer: Berlin/Heidelberg, Germany, 1998; pp. 233–238. [Google Scholar]
- Demirer, R.; Omay, T.; Yuksel, A.; Yuksel, A. Global risk aversion and emerging market return comovements. Econ. Lett. 2018, 173, 118–121. [Google Scholar] [CrossRef]
- Ang, A.; Longstaff, F.A. Systemic sovereign credit risk: Lessons from the US and Europe. J. Monet. Econ. 2013, 60, 493–510. [Google Scholar] [CrossRef]
- Stoev, S.; Taqqu, M.S. Stochastic properties of the linear multifractional stable motion. Adv. Appl. Probab. 2004, 36, 1085–1115. [Google Scholar] [CrossRef]
- Stoev, S.; Taqqu, M.S. Path properties of the linear multifractional stable motion. Fractals 2005, 13, 157–178. [Google Scholar] [CrossRef]
- Ding, Y.; Peng, Q. Series representation of jointly SαS distribution via a new type of symmetric covariations. Commun. Math. Stat. 2021, 9, 203–238. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).