Fixed-Time Fractional-Order Global Sliding Mode Control for Nonholonomic Mobile Robot Systems under External Disturbances
Abstract
:1. Introduction
- The fixed-time convergence is fully addressed in this work, taking into consideration real system needs.
- In contrast to previous finite-time/fixed-time control methods, the present paper combines fixed-time control and fractional theory.
- Two FO fixed-time controllers are designed for first/second order systems, and two switching strategies are suggested to ensure the fixed-time stability of uncertain chained-form nonholonomic systems.
- The second-order controller proposed in this work possesses better performance with regard to reduction of the chattering phenomenon and global stabilization.
- The theory results are confirmed by numerical results for various cases and are compared with recent fixed-time controls [30].
2. Preliminaries and Conceptualization of the Problem
2.1. Preliminary Considerations on Fractional Calculus
2.2. Preliminary Considerations for Finite/fixed-Time Stability
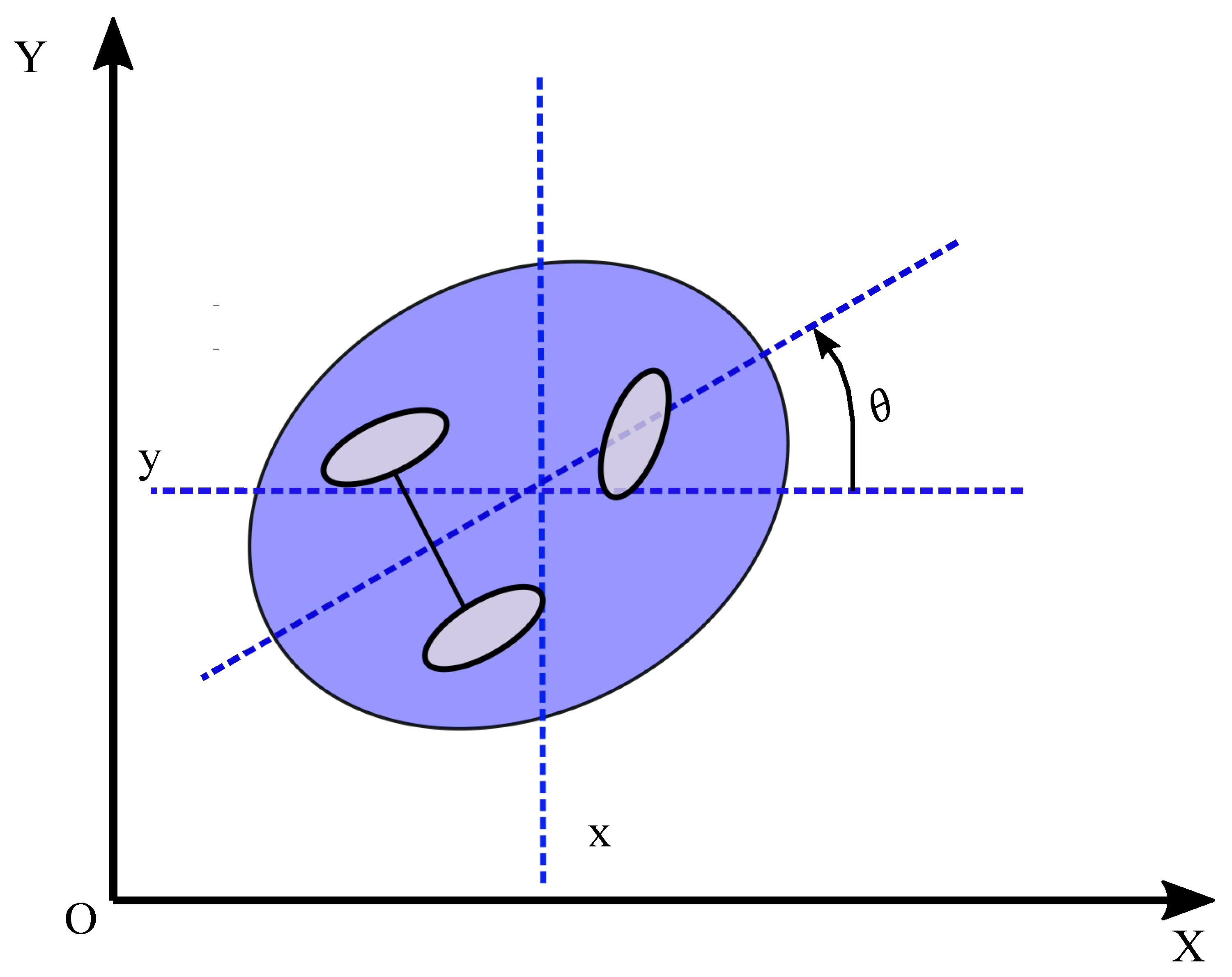
2.3. Problem Formulation
3. Main Results
3.1. Stabilization of the First-Order System (FOS) of the MR in the Presence of Perturbation
3.2. Stabilization of the (FOS) of the MR Based on FO Control Method in the Presence of Perturbation
3.3. Design of FO Global Sliding Mode Controller for SOS
3.4. Stabilization of Nonholonomic Chained-Form Systems with Unknown Perturbations
- (1)
- For , is used as a constant control input. Then, in the presence of a disturbance, one may deduce that and converge to zero in the fixed finite time , based on the result of Theorem 2.
- (2)
- For , the control signal is developed to drive . Consider the candidate LF and its time-derivative . We choose , then for all .
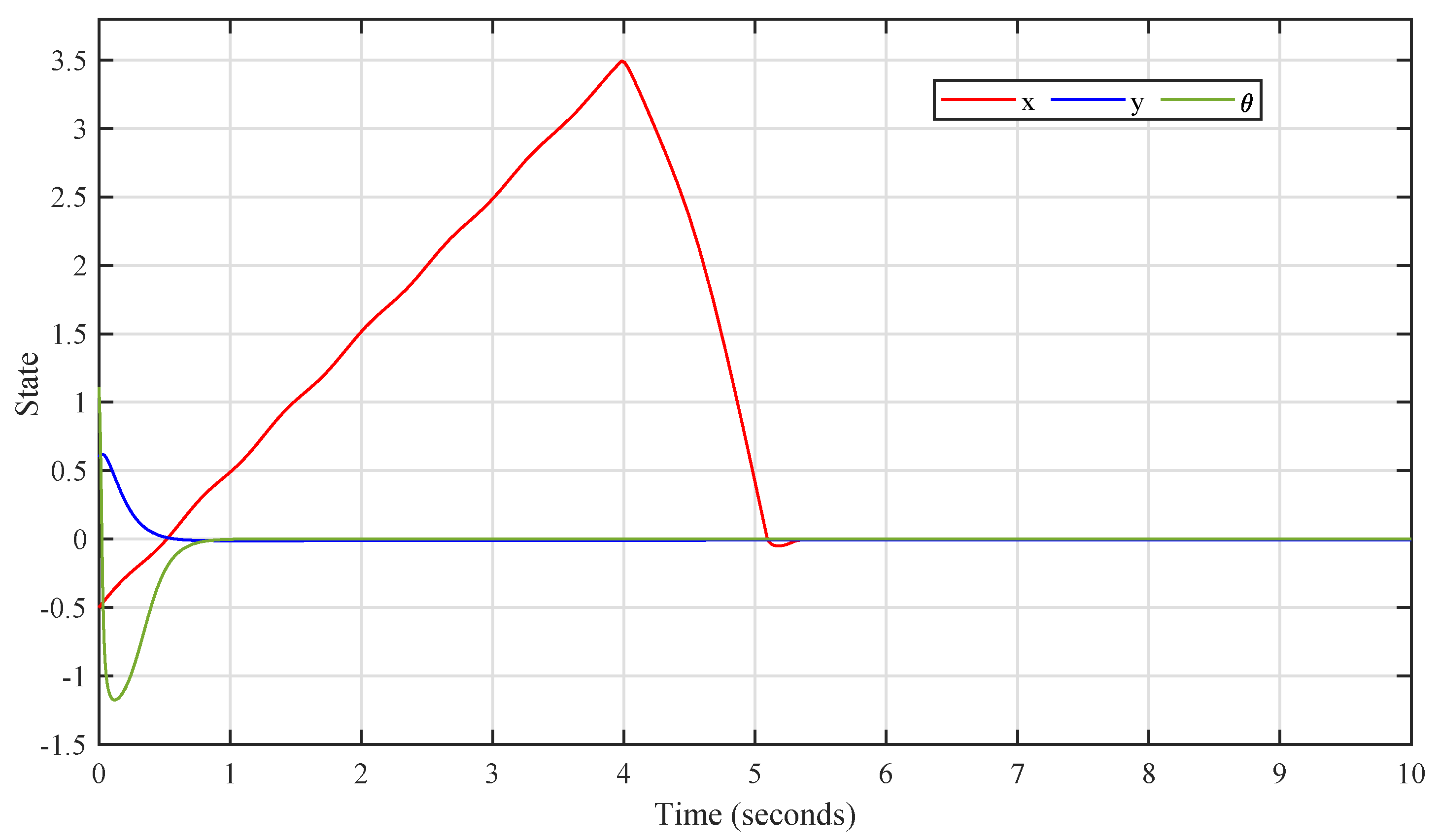
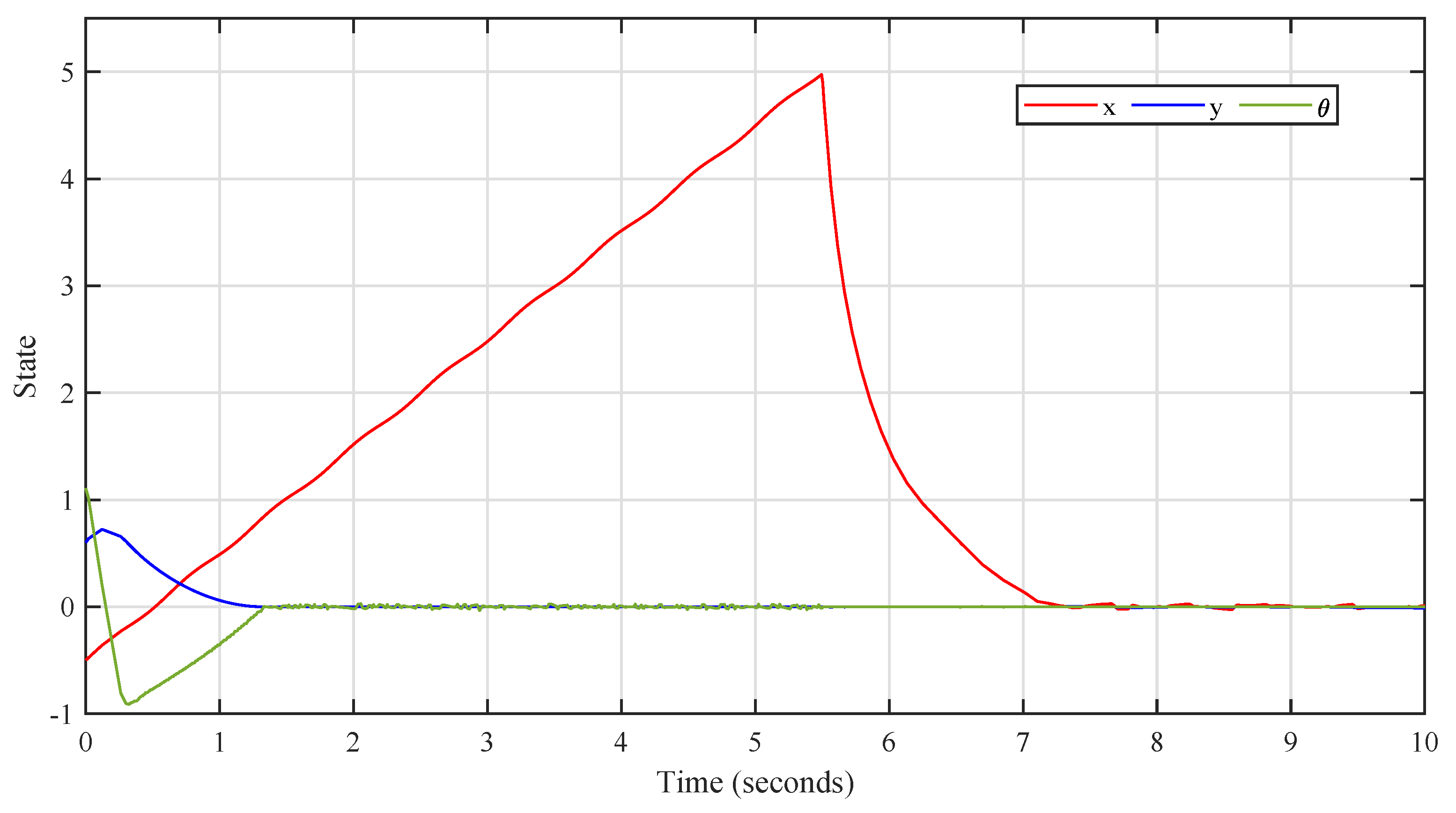
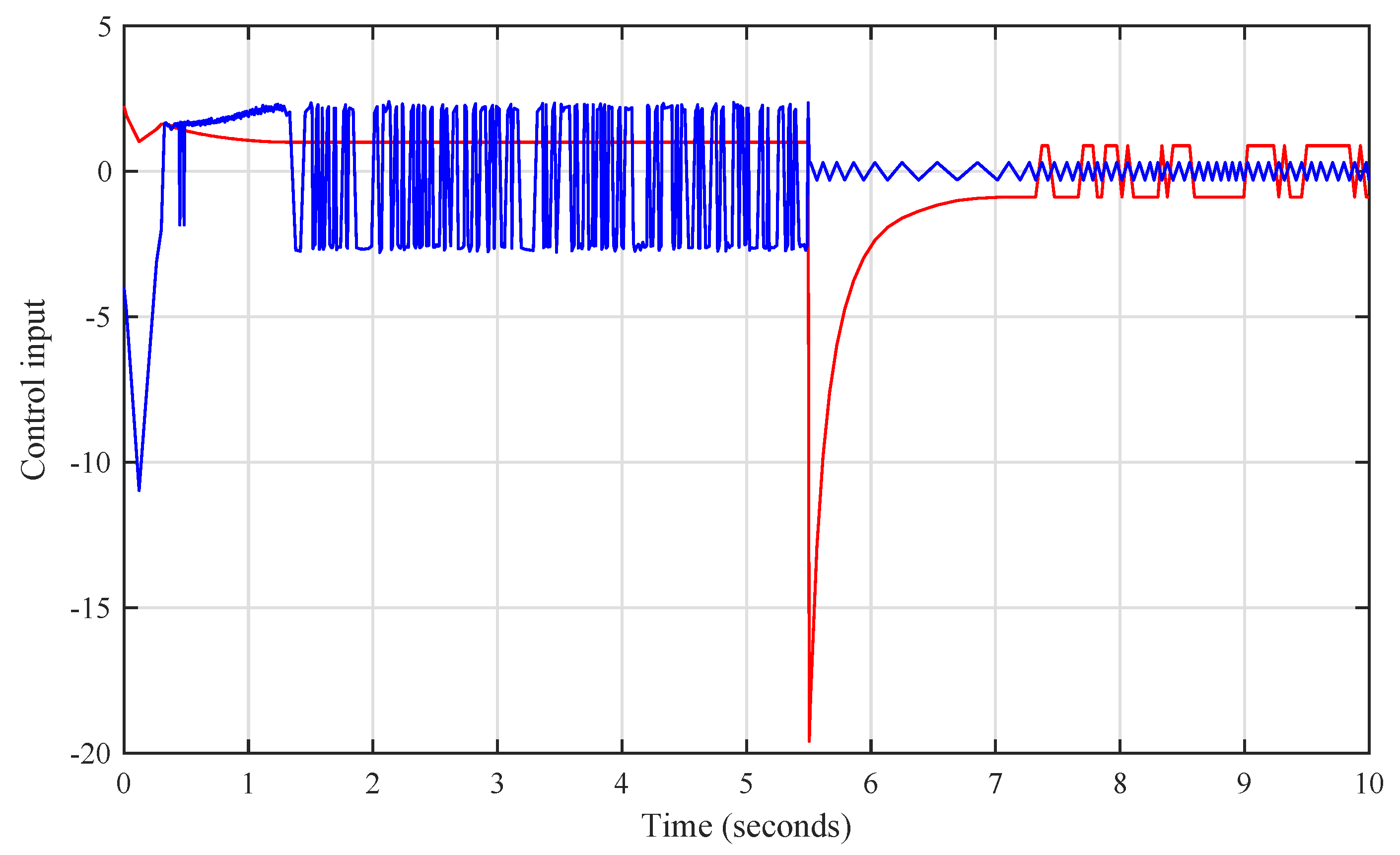
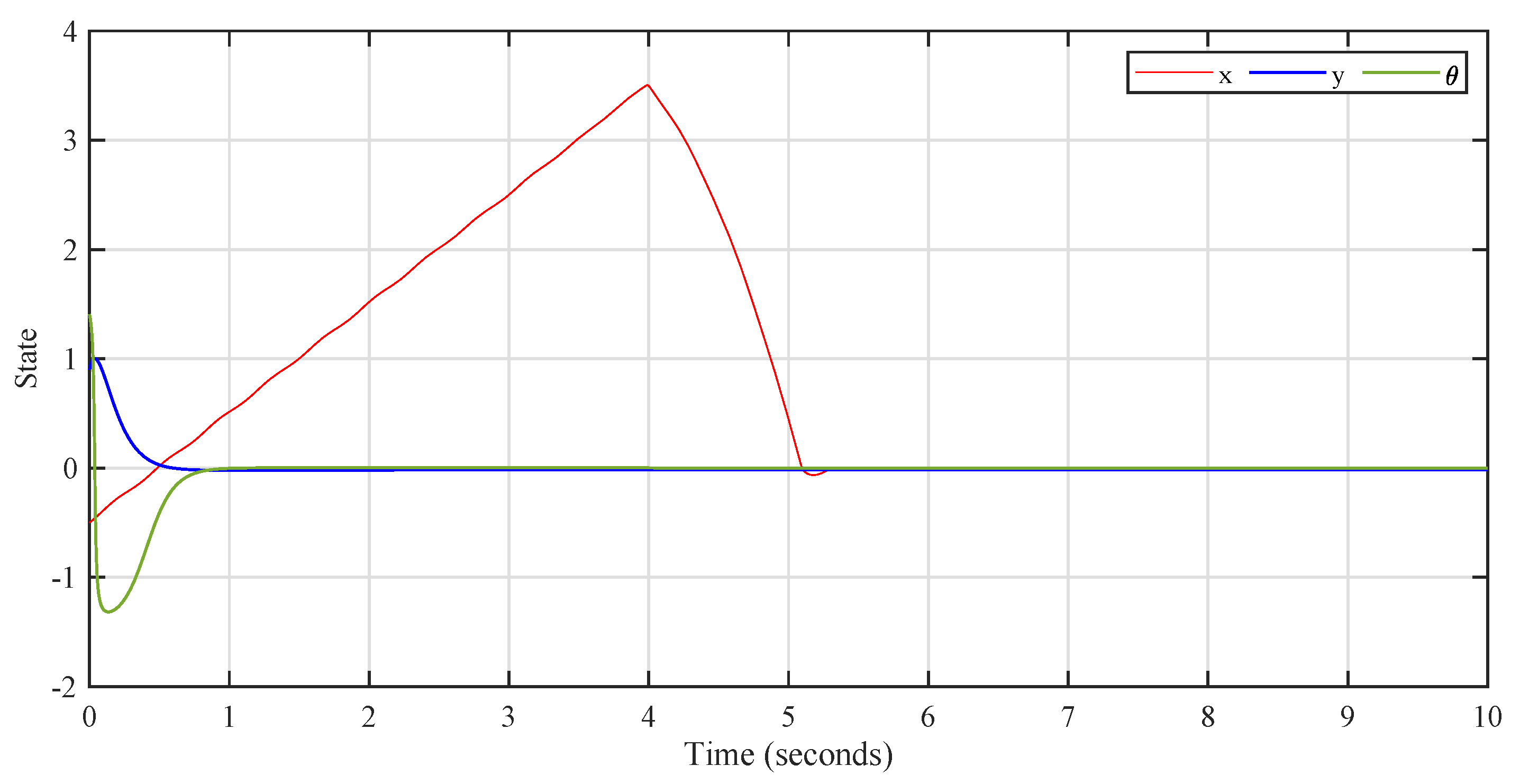
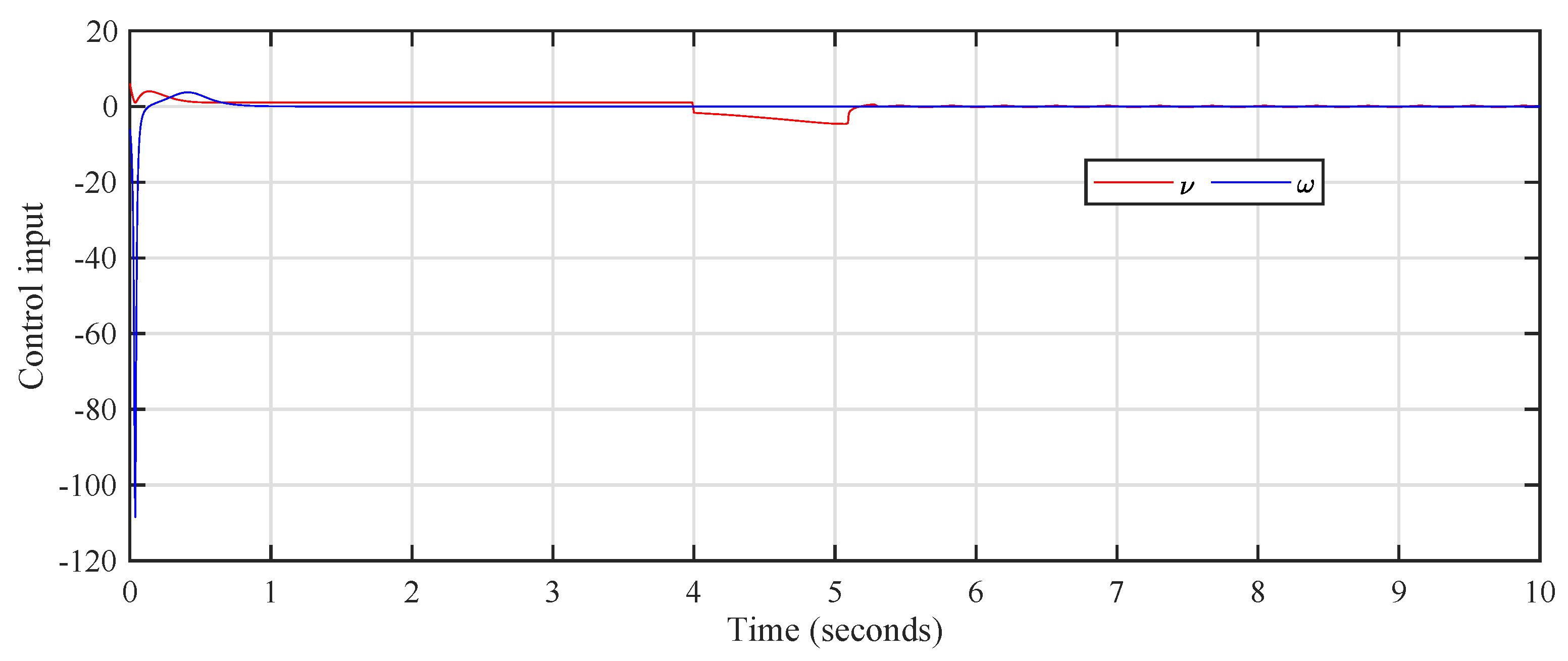
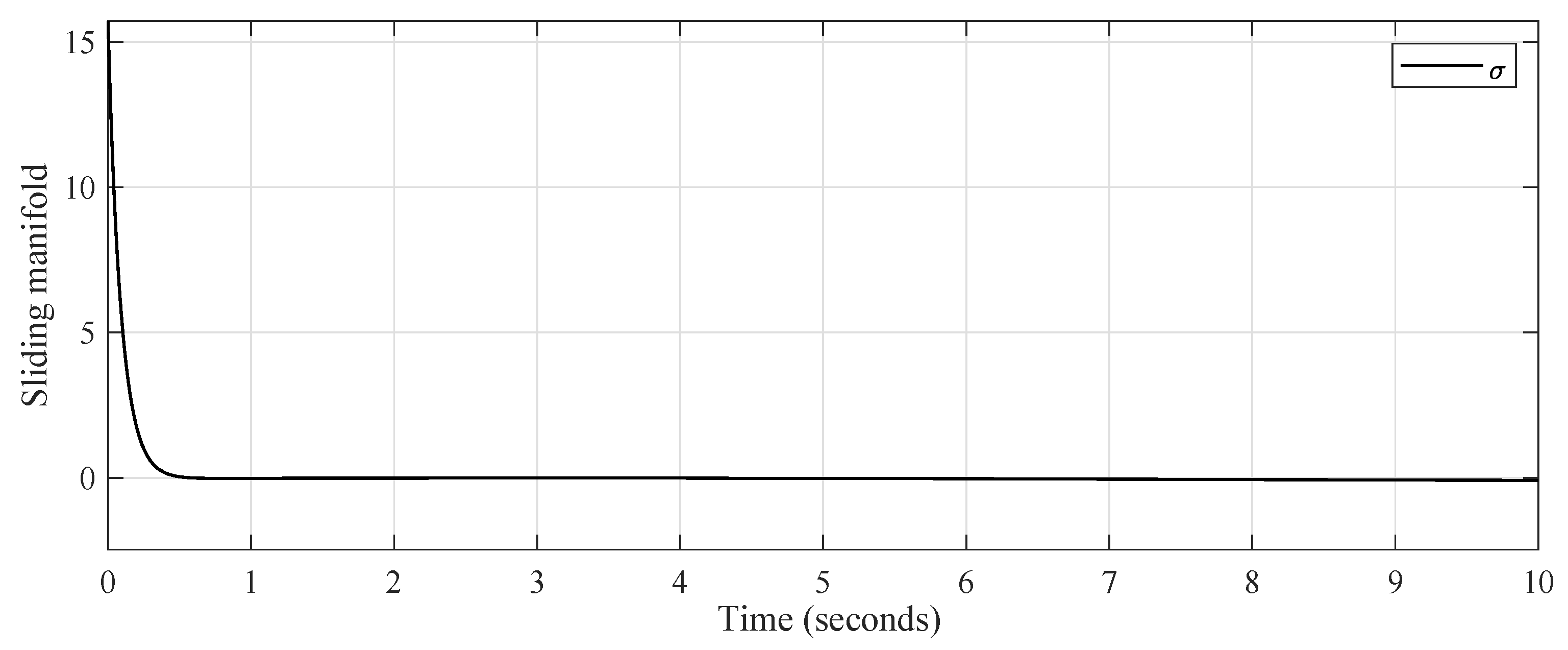
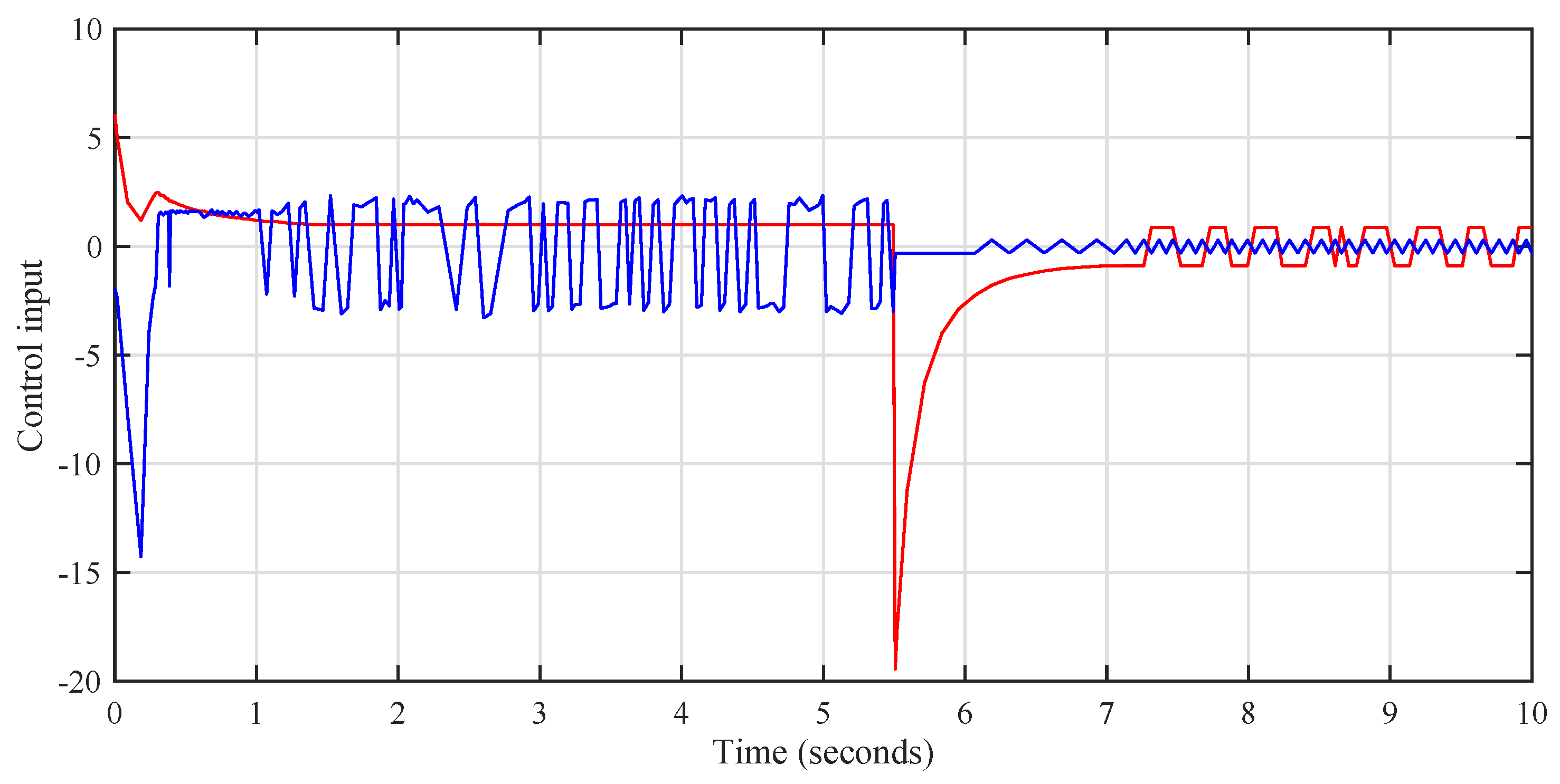
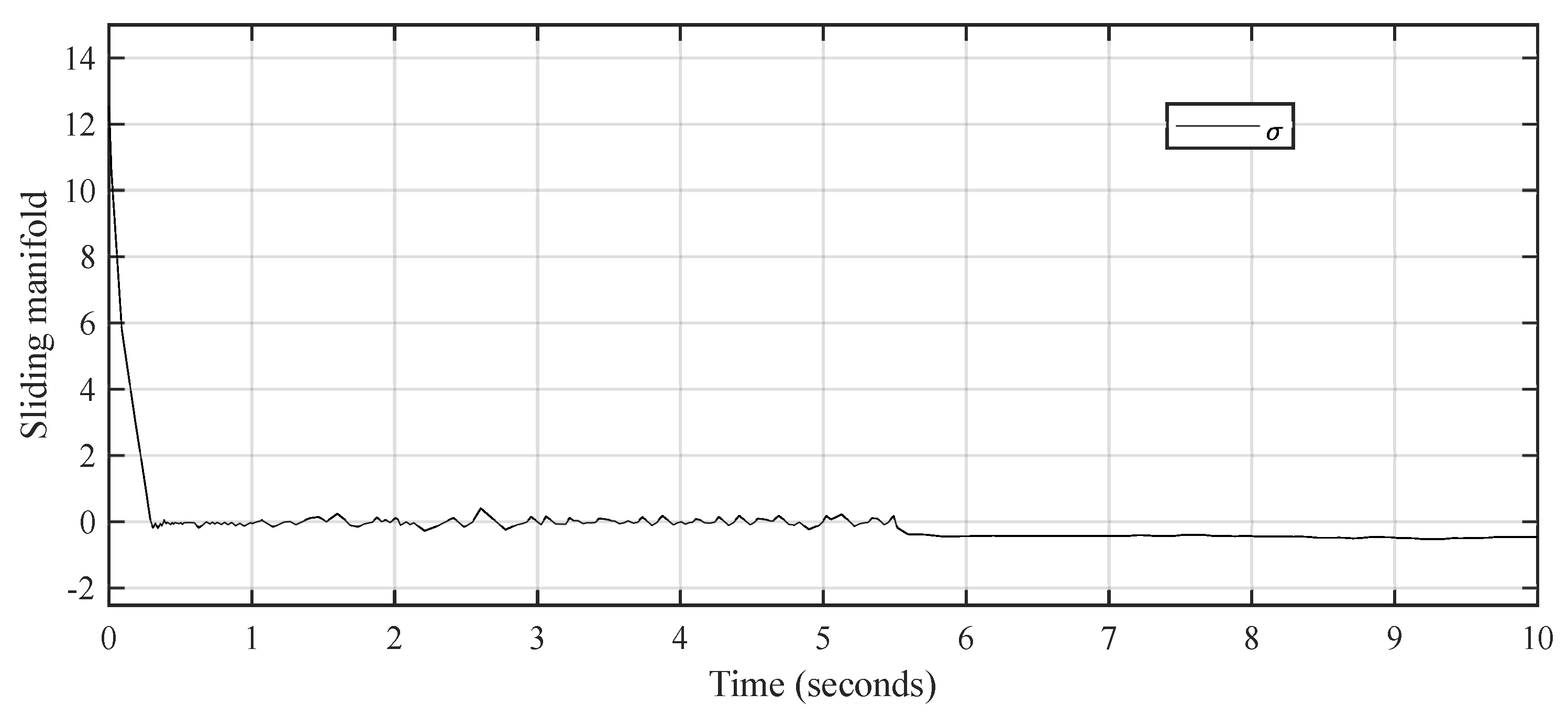
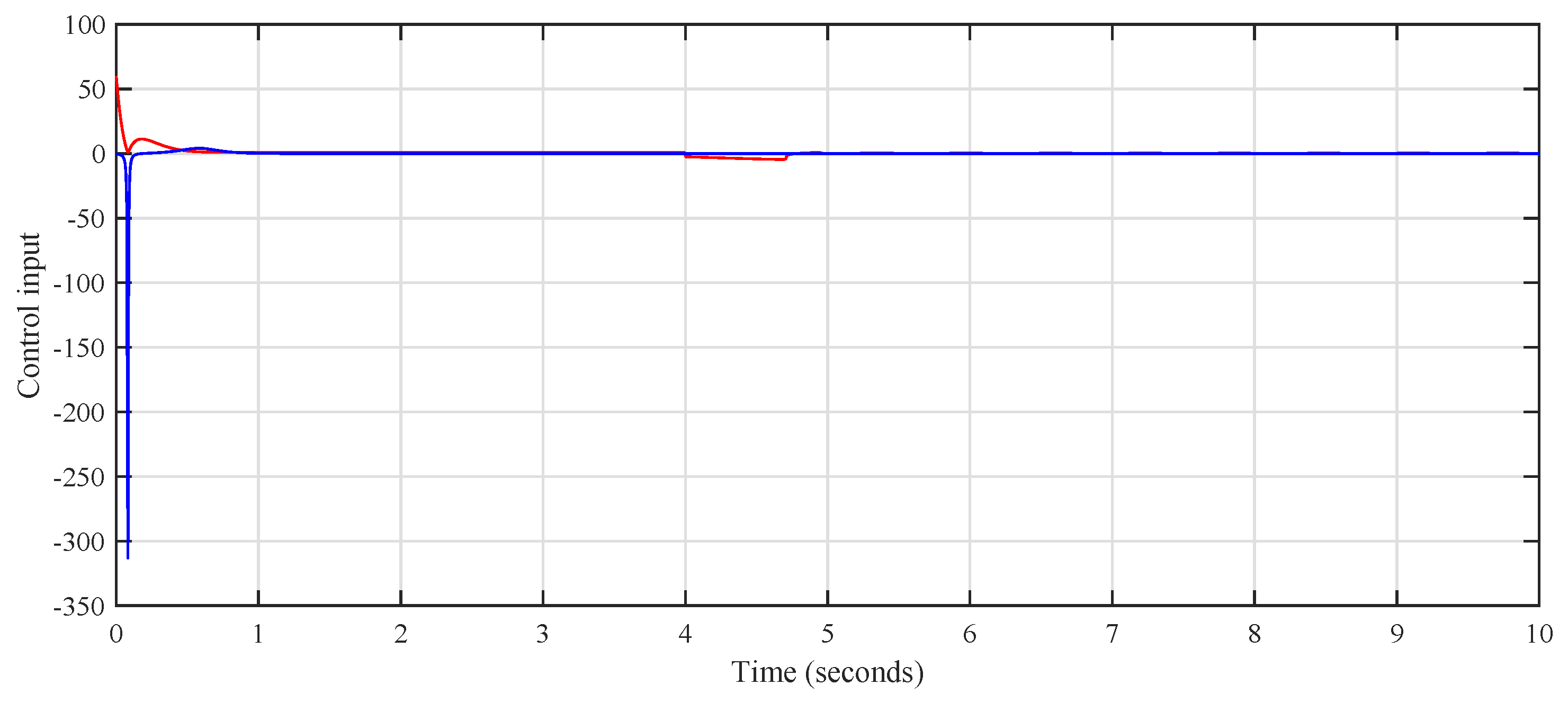
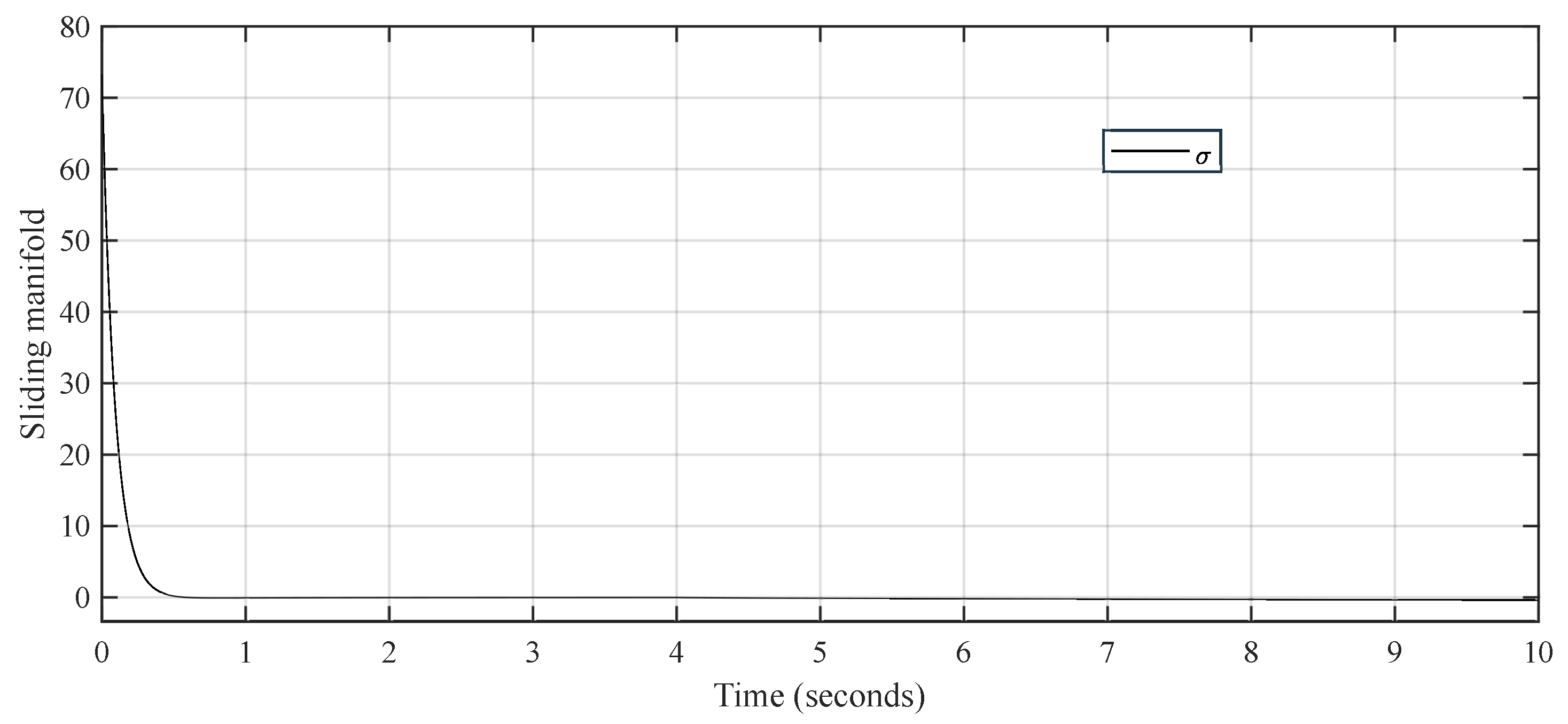
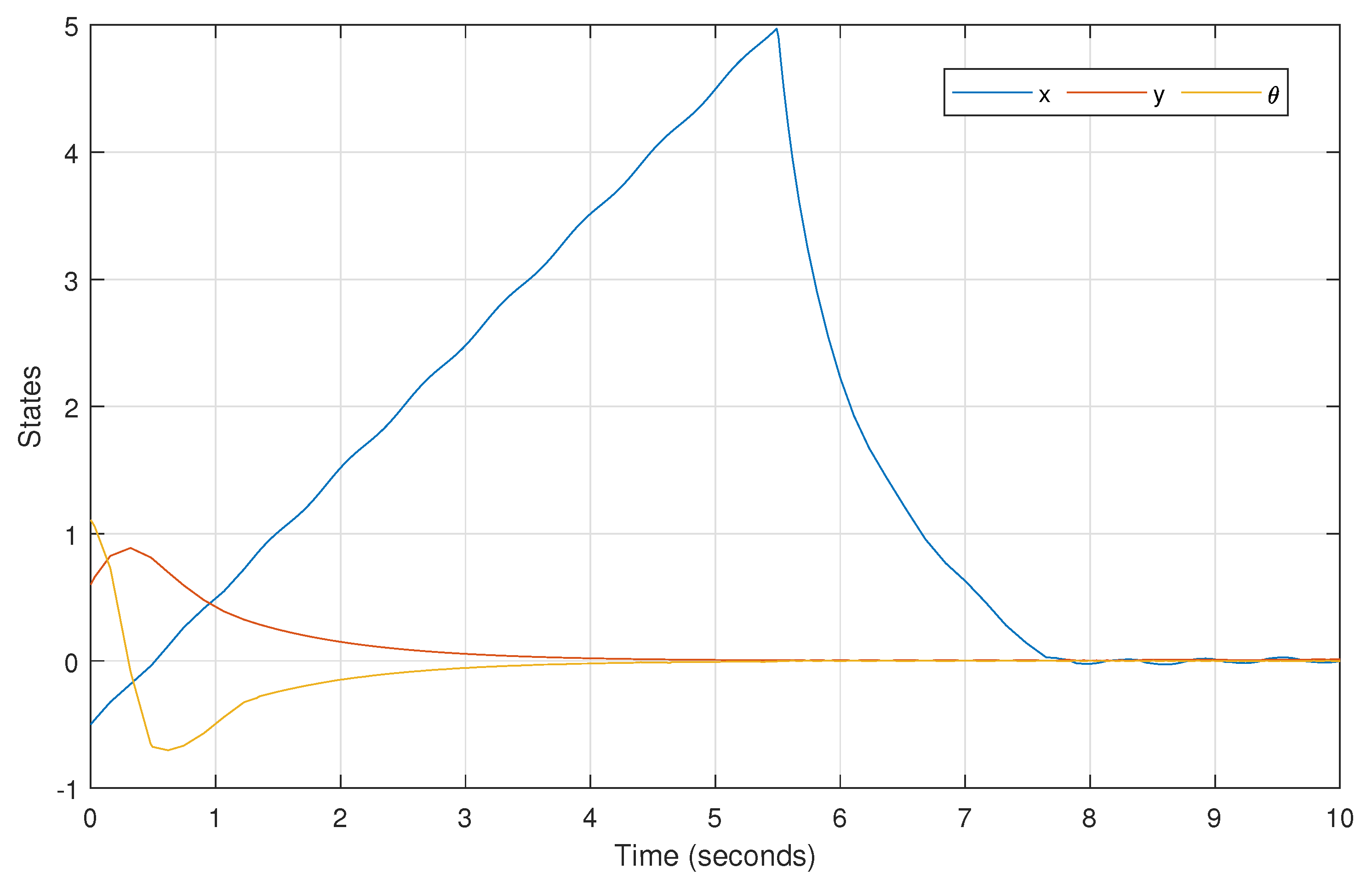
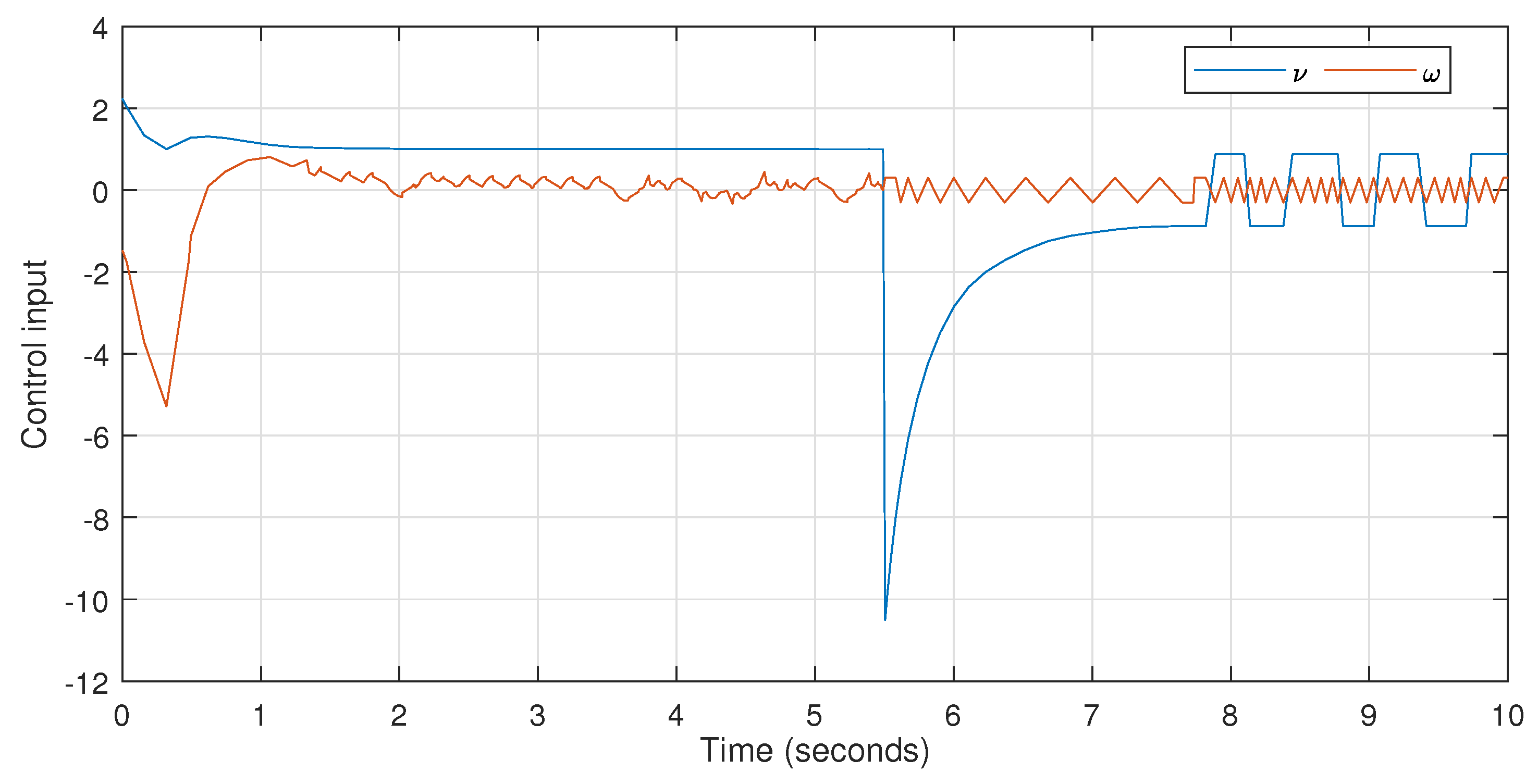
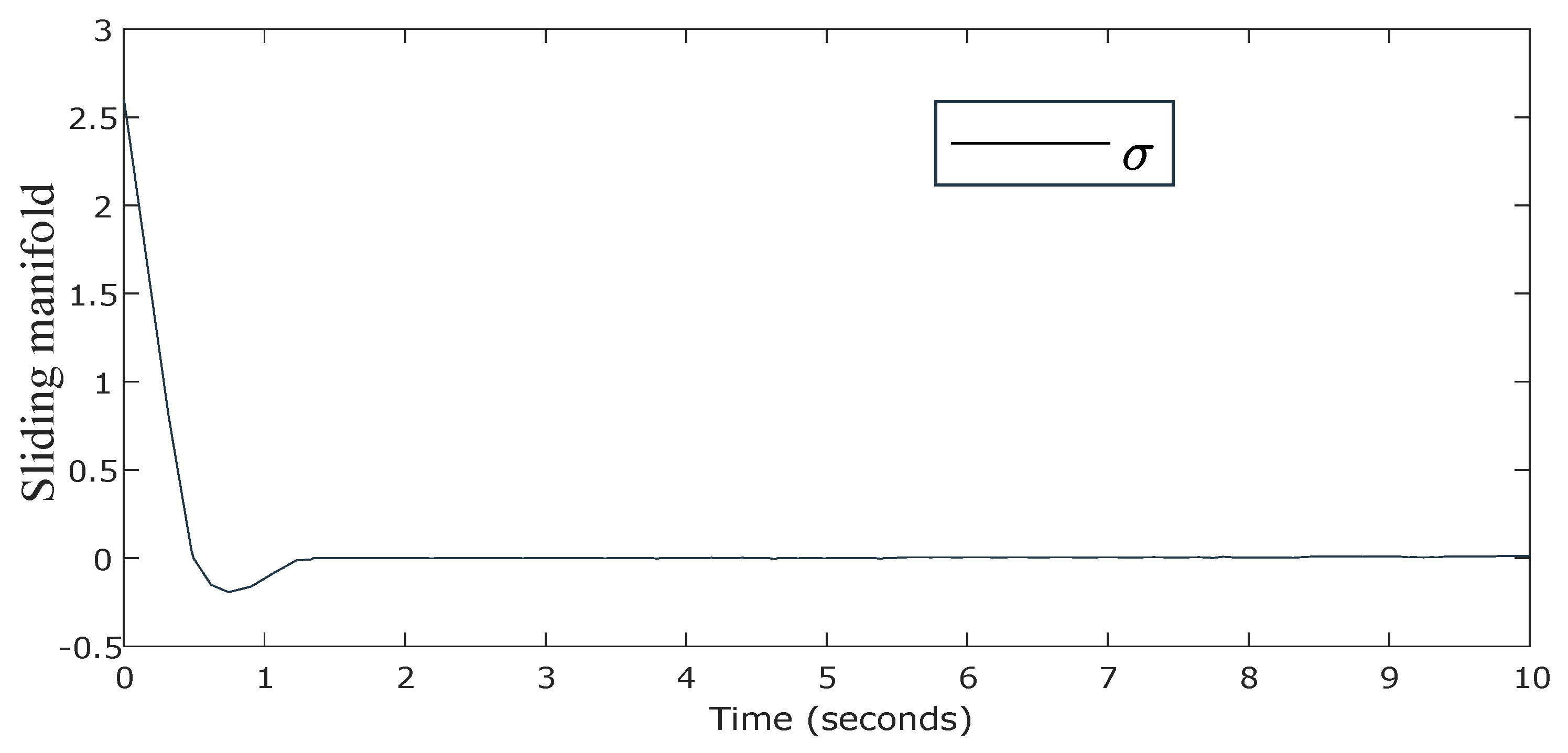
4. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fragapane, G.; de Koster, R.; Sgarbossa, F.; Strandhagen, J.O. Planning and control of autonomous mobile robots for intralogistics: Literature review and research agenda. Eur. J. Oper. Res. 2021, 294, 405–426. [Google Scholar] [CrossRef]
- Zhu, A.; Pauwels, P.; De Vries, B. Smart component-oriented method of construction robot coordination for prefabricated housing. Autom. Constr. 2021, 129, 103778. [Google Scholar] [CrossRef]
- Lee, W.J.; Ill Kwag, S.; Ko, Y.D. Optimal capacity and operation design of a robot logistics system for the hotel industry. Tour. Manag. 2020, 76, 103971. [Google Scholar] [CrossRef]
- Gao, F.; Wu, Y.; Huang, J.; Liu, Y. Output feedback stabilization within prescribed finite time of asymmetric time-varying constrained nonholonomic systems. Int. J. Robust Nonlinear Control 2021, 31, 427–446. [Google Scholar] [CrossRef]
- Stolfi, A. Discontinuous control of nonholonomic systems. Syst. Control Lett. 1996, 27, 37–45. [Google Scholar] [CrossRef]
- Brockett, R.W. Asymptotic stability and feedback stabilization. Differ. Geom. Control. Theory 1983, 27, 181–191. [Google Scholar]
- Sánchez-Torres, J.D.; Defoort, M.; Muñoz-Vázquez, A.J. Predefined-time stabilisation of a class of nonholonomic systems. Int. J. Control 2020, 93, 2941–2948. [Google Scholar] [CrossRef]
- Huang, Y.; Su, J. Output feedback stabilization of uncertain nonholonomic systems with external disturbances via active disturbance rejection control. ISA Trans. 2020, 104, 245–254. [Google Scholar] [CrossRef]
- Ge, S.S.; Wang, Z.; Lee, T.H. Adaptive stabilization of uncertain nonholonomic systems by state and output feedback. Automatica 2003, 39, 1451–1460. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Q. Adaptive output feedback control of stochastic nonholonomic systems with nonlinear parameterization. Automatica 2018, 98, 247–255. [Google Scholar] [CrossRef]
- Liu, Z.G.; Wu, Y.Q.; Sun, Z.Y. Output feedback control for a class of high-order nonholonomic systems with complicated nonlinearity and time-varying delay. J. Frankl. Inst. 2017, 354, 4289–4310. [Google Scholar] [CrossRef]
- Jiang, Z.P. Robust exponential regulation of nonholonomic systems with uncertainties. Automatica 2000, 36, 189–209. [Google Scholar] [CrossRef]
- Tian, Y.P.; Li, S. Exponential stabilization of nonholonomic dynamic systems by smooth time-varying control. Automatica 2002, 38, 1139–1146. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, Y. Global robust stabilization for nonholonomic systems with dynamic uncertainties. J. Frankl. Inst. 2020, 357, 1357–1377. [Google Scholar] [CrossRef]
- Gao, F.; Yuan, F. Adaptive finite-time stabilization for a class of uncertain high order nonholonomic systems. ISA Trans. 2015, 54, 75–82. [Google Scholar] [CrossRef]
- Gao, F.; Wu, Y.; Zhang, Z. Finite-time stabilization of uncertain nonholonomic systems in feedforward-like form by output feedback. ISA Trans. 2015, 59, 125–132. [Google Scholar] [CrossRef]
- Gao, F.; Yuan, Y.; Wu, Y. Finite-time stabilization for a class of nonholonomic feedforward systems subject to inputs saturation. ISA Trans. 2016, 64, 193–201. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Zhang, C.; Chang, L. A time-varying high-gain approach to feedback regulation of uncertain time-varying nonholonomic systems. ISA Trans. 2020, 98, 110–122. [Google Scholar] [CrossRef]
- Wu, D.; Cheng, Y.; Du, H.; Zhu, W.; Zhu, M. Finite-time output feedback tracking control for a nonholonomic wheeled mobile robot. Aerosp. Sci. Technol. 2018, 78, 574–579. [Google Scholar] [CrossRef]
- Gao, F.; Huang, J.; Zhu, X.; Wu, Y. Output feedback stabilization via nonlinear mapping for time-varying constrained nonholonomic systems in prescribed finite time. Inf. Sci. (NY) 2021, 550, 297–312. [Google Scholar] [CrossRef]
- Gao, F.; Huang, J.; Shi, X.; Zhu, X. Nonlinear mapping-based fixed-time stabilization of uncertain nonholonomic systems with time-varying state constraints. J. Frankl. Inst. 2020, 357, 6653–6670. [Google Scholar] [CrossRef]
- Guo, Y.; Ma, B.L. Global sliding mode with fractional operators and application to control robot manipulators. Int. J. Control 2019, 92, 1497–1510. [Google Scholar] [CrossRef]
- Labbadi, M.; Boukal, Y.; Cherkaoui, M.; Djemai, M. Fractional-order global sliding mode controller for an uncertain quadrotor UAVs subjected to external disturbances. J. Frankl. Inst. 2021, 358, 4822–4847. [Google Scholar] [CrossRef]
- Nojavanzadeh, D.; Badamchizadeh, M. Adaptive fractional-order non-singular fast terminal sliding mode control for robot manipulators. IET Control Theory Appl. 2016, 10, 1565–1572. [Google Scholar] [CrossRef]
- Aghababa, M.P. A fractional sliding mode for finite-time control scheme with application to stabilization of electrostatic and electromechanical transducers. Appl. Math. Model. 2015, 39, 6103–6113. [Google Scholar] [CrossRef]
- Labbadi, M.; Boukal, Y.; Taleb, M.; Cherkaoui, M. Fractional order sliding mode control for the tracking problem of Quadrotor UAV under external disturbances. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; pp. 1595–1600. [Google Scholar]
- Labbadi, M.; Boukal, Y.; Cherkaoui, M. Path Following Control of Quadrotor UAV With Continuous Fractional-Order Super Twisting Sliding Mode. J. Intell. Robot. Syst. Theory Appl. 2020, 100, 1429–1451. [Google Scholar] [CrossRef]
- Labbadi, M.; Nassiri, S.; Bousselamti, L.; Bahij, M.; Cherkaoui, M. Fractional-order fast terminal sliding mode control of uncertain quadrotor UAV with time-varying disturbances. In Proceedings of the 2019 8th International Conference on Systems and Control (ICSC 2019), Marrakesh, Morocco, 23–25 October 2019. [Google Scholar]
- Labbadi, M.; El Moussaoui, H. An improved adaptive fractional-order fast integral terminal sliding mode control for distributed quadrotor. Math. Comput. Simul. 2021, 188, 120–134. [Google Scholar] [CrossRef]
- Defoort, M.; Demesure, G.; Uo, Z.; Zuo, Z.; Polyakov, A.; Djemai, M. Fixed-time stabilisation and consensus of non-holonomic systems. IET Control Theory Appl. 2016, 10, 2497–2505. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic: New York, NY, USA, 1999. [Google Scholar]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fract. Calc. Appl. Anal. 2002, 5, 367–386. [Google Scholar]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Bhat, S.; Bernstein, D. Geometric homogeneity with applications to finite time stability. Math. Control Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Yu, X.; Stonier, R. Continuous finite-time control for robotic manipulators with terminal sliding modes. In Proceedings of the Sixth International Conference of Information Fusion, Cairns, QLD, Australia, 8–11 July 2003; pp. 1433–1440. [Google Scholar]
- Moulay, E.; Perruquetti, W. Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 2006, 323, 1430–1443. [Google Scholar] [CrossRef] [Green Version]
- Yin, C.; Chen, Y.; Zhong, S.M. Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems. Automatica 2014, 50, 3173–3181. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Labbadi, M.; Boubaker, S.; Djemai, M.; Mekni, S.K.; Bekrar, A. Fixed-Time Fractional-Order Global Sliding Mode Control for Nonholonomic Mobile Robot Systems under External Disturbances. Fractal Fract. 2022, 6, 177. https://doi.org/10.3390/fractalfract6040177
Labbadi M, Boubaker S, Djemai M, Mekni SK, Bekrar A. Fixed-Time Fractional-Order Global Sliding Mode Control for Nonholonomic Mobile Robot Systems under External Disturbances. Fractal and Fractional. 2022; 6(4):177. https://doi.org/10.3390/fractalfract6040177
Chicago/Turabian StyleLabbadi, Moussa, Sahbi Boubaker, Mohamed Djemai, Souad Kamel Mekni, and Abdelghani Bekrar. 2022. "Fixed-Time Fractional-Order Global Sliding Mode Control for Nonholonomic Mobile Robot Systems under External Disturbances" Fractal and Fractional 6, no. 4: 177. https://doi.org/10.3390/fractalfract6040177
APA StyleLabbadi, M., Boubaker, S., Djemai, M., Mekni, S. K., & Bekrar, A. (2022). Fixed-Time Fractional-Order Global Sliding Mode Control for Nonholonomic Mobile Robot Systems under External Disturbances. Fractal and Fractional, 6(4), 177. https://doi.org/10.3390/fractalfract6040177






