Robust H_∞ Control of Fractional-Order Switched Systems with Order 0 < α < 1 and Uncertainty

Abstract

In this paper, robust $H_{\infty }$ control for fractional-order switched systems (FOSSs) with uncertainty is studied. Firstly, the fractional-order switching law for FOSSs is proposed. Then, $H_{\infty }$ control for FOSSs is proven based on the switching law and linear matrix inequalities (LMIs). Moreover, $H_{\infty }$ control for FOSSs with a state feedback controller is extended. Furthermore, the LMI-based condition of robust $H_{\infty }$ control for FOSSs with uncertainty is proven. Furthermore, the condition of robust $H_{\infty }$ control is proposed to design the state feedback controller. Finally, four simulation examples verified the effectiveness of the proposed methods.

1. Introduction

Switched systems, as a kind of hybrid system, are composed of multiple subsystems and switching rules [1]. They have attracted the interest of many researchers, not only because they are more complex than other control systems [2], but also because they are widely used in engineering and social sciences [3,4]. A large part of control systems, such as network-based systems [5,6], can be represented by switching systems. Stability analysis is the most fundamental for switched systems. Hence, a large number of results have been published in the field. Adaptive control has been studied for switched systems by using the average dwell time approach in [7,8]. The approach is usually used to judge the stability of switched systems [9]. Finding the Lyapunov function to guarantee the stability for all constituent subsystems is the other typical method for switched systems [10]. Based on the Lyapunov function method, nonlinear and linear switched systems with uncertainties were studied in [11,12,13,14]. Tracking control is an effective control technique [15] and was studied for switched systems in [16]. Moreover, the results of finite-time stability and sliding mode control for switched systems were reported in [17,18], respectively.

Fractional-order systems can describe physical phenomena in the real world and are widely considered by the academic community to be more accurate [19,20]. Since the necessary tools for simulation verification are lacking, the development of fractional-order theory is slow. In the past two decades, with the development of advanced computers, many conditions have been published about the stability and stabilization of fractional-order systems. From Figure 1, the stable area of order $0<\alpha <1$ is not convex. Hence, the stability analysis of order $0<\alpha <1$ is more difficult than order $1<\alpha <2$. In [21,22,23], the results based on linear matrix inequalities (LMI) were proposed to analyze stability for order $0<\alpha <1$. In [21], the direct introduction of complex variables brought difficulties to the solution process. Therefore, in [22,23], by using more real variables to replace the complex variables, the results could solve the difficulties of complex variables, but these results introduce more variables. To solve these problems, Reference [24] provided new LMI-based results to solve the stability and stabilization for order $0<\alpha <2$ by using two real variables. Although Atangana–Baleanu and Riemann–Liouville definitions of the fractional operator were used in some papers, such as [25], the Caputo definition of the fractional operator is commonly used in the field of control [24,26], since it has a well-understood physical sense and wide applications in engineering [27]. $H_{\infty }$ control is a great method to counteract the effects of disturbances. The conditions of $H_{\infty }$ control for fractional-order systems were published in [28,29]. State feedback, dynamic output, and robust $H_{\infty }$ control for fractional-order systems were studied in [30,31,32], respectively.

Figure 1. Stable region of fractional-order systems with: (a) order $0<\alpha <1$; (b) order $1<\alpha <2$.

Recently, many researchers have tried to introduce fractional calculus into switched systems, to more accurately describe the phenomenon and properties of switched systems. The description is indeed better than the effect of integer-order switched systems, because the physical characteristics of the actual system are more accurately described by the fractional order. Stability and stabilization for fractional switched systems (FOSSs) were studied in [33,34,35]. State-dependent control and finite-time stability for positive FOSSs were studied in [36,37,38]. Moreover, References [39,40,41] studied the stability and robust stabilization for nonlinear and uncertain FOSSs. The results of observer-based and guaranteed cost control for FOSSs were reported in [42,43]. Fault-tolerant control is widely used in the control field [44]. By using the Lyapunov method in [33], fault estimation was investigated for nonlinear fractional-order systems in [45]. Furthermore, decentralized control and state-dependent switching control of nonlinear FOSSs were reported in [46,47].

However, $H_{\infty }$ control and robust $H_{\infty }$ for FOSSs with uncertainty have not been reported yet. The main contributions of this paper are as follows:

(1)

The fractional-order switching law is proven for FOSSs. From the stable region of order $\alpha \in (0,1)$ in Figure 1, if the fractional-order systems have positive characteristic roots, they may be stable. The characteristic roots in the right stable region were not considered in [45,46,47]. The fractional-order switching law proposed in this paper overcomes this shortcoming. Hence, it is less conservative;

(2)

$H_{\infty }$ control for FOSSs is proposed under the fractional-order switching law. Then, the controller for closed-loop FOSSs is designed. Furthermore, the conditions based on LMIs are proposed to solve the problem of robust $H_{\infty }$ control for FOSSs with uncertainty.

The outline of this paper is as follows. The preliminaries and problem descriptions are presented in Section 2. In Section 3, the switching law is proven for FOSSs. In Section 4 and Section 5, $H_{\infty }$ control and robust $H_{\infty }$ control for FOSSs are studied under the switching law, respectively. In Section 6, four numerical examples are shown to prove the effectiveness of the conditions in the paper.

Notations: In this paper, $X^T$ is the transpose of X. $A>0$ denotes positive definite. $\mathrm{sym}\left(X\right)=X+X^T$. $\mathrm{spec}\left(X\right)$ denotes the spectrum (set of all eigenvalues) of X. $min\left\{N\right\}$ and $argmin\left\{N\right\}$ are the minimum value and minimum index of the set N, and ${\parallel G\left(s\right)\parallel }_{\infty }$ denotes the $H_{\infty }$-norm of $G\left(s\right)$. Let $\left[\begin{array}{cc}P& Q\\ *& P\end{array}\right]=\left[\begin{array}{cc}P& Q\\ Q^T& P\end{array}\right]$.

2. Preliminaries and Problem Descriptions

2.1. Preliminaries

The Caputo definition [19] is shown as follows:

$$\begin{array}{cc}& D^{\alpha }f\left(t\right)=\frac{1}{\Gamma (n-\alpha )}{\int }_0^t\frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}d\tau \end{array}$$

(1)

where $n-1<\alpha <n$ and $\Gamma (.)$ is the Gamma function.

Remark 1.

In general, the Caputo derivative has a clear physical meaning at the initial value. Hence, the Caputo derivative is widely used in the control field.

Consider the following fractional-order system:

$$\begin{array}{c}{D}^{\alpha }x\left(t\right)=Ax\left(t\right)+B_{w}w\left(t\right)\hfill \\ z\left(t\right)=Cx\left(t\right)+Dw\left(t\right)\hfill \end{array}$$

(2)

where $0<\alpha <1$. $x\left(t\right)$, $w\left(t\right)$, and $y\left(t\right)$ denote the state, exogenous input, and output vectors. A, $B_w$, C, and D are appropriate dimension matrices. $G\left(s\right)=C{(s^{\alpha }I-A)}^{-1}{B}_w+D$ denotes the transfer matrix.

Then, some lemmas and the $H_{\infty }$-norm definition is introduced in the following part.

Definition 1

([29]). The $H_{\infty }$-norm is defined as:

$$\begin{array}{c}\hfill {\parallel G\left(s\right)\parallel }_{\infty }=\underset{Re\left(s\right)\ge 0}{sup}\sigma \left(G\left(s\right)\right)\end{array}$$

Lemma 1

([32]). For given $\gamma >0$, System (2) is asymptotically stable and ${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$ iff there exist two matrices $X,Y\in {\mathbf{R}}^{n\times n}$ such that:

$$\begin{array}{c}\hfill \left[\begin{array}{cc}X& Y\\ -Y& X\end{array}\right]>0\\ \hfill \end{array}$$

(3)

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}\mathrm{sym}(aAX+bAY)& (aX-bY)C^T& B_w\\ *& -\gamma I& D\\ *& *& -\gamma I\end{array}\right]<0\\ \hfill \end{array}$$

(4)

where $a=sin\left(\alpha \frac{\pi }{2}\right)$ and $b=cos\left(\alpha \frac{\pi }{2}\right)$.

Remark 2.

Lemma 1 is different from the results in [28,29]; it avoids the trouble of solving the complex matrix. Lemma 1 can be easier to solve by using the LMI toolbox. When $\alpha =1$, Lemma 1 is equivalent to the results of the integer order. For brevity, a and b denote $sin\left(\alpha \frac{\pi }{2}\right)$ and $cos\left(\alpha \frac{\pi }{2}\right)$ in this paper.

Lemma 2

([19]). For System (2), if $\alpha <2$, β is an arbitrary real number, ρ is such that $\pi \alpha /2<\rho <min\{\pi ,\pi \alpha \}$, and C is a real constant, then:

$$\parallel E_{\alpha ,\beta }\left(z\right)\parallel \le \frac{C}{1+\parallel z\parallel },(\rho \le \parallel arg\left(z\right)\parallel \le \pi ),\parallel z\parallel \ge 0.$$

Lemma 3

([48]). (Schur complement) Matrices $W_1$, $W_2$ and $W_3$ satisfy $W_1=W_1^T$, $W_3>0$.

$$W_1+W_2{W}_3^{-1}{W}_2^T<0$$

if and only if:

$$\left[\begin{array}{cc}{W}_1& W_2\\ W_2^T& -W_3\end{array}\right]<0$$

Lemma 4

([49]). For matrices H, E, $F^T\left(t\right)F\left(t\right)\le I$, and one constant $ϵ>0$, then:

$$HF\left(t\right)E+E^T{F}^T\left(t\right)H^T\le ϵH{H}^T+{ϵ}^{-1}{E}^{T}E$$

2.2. Problem Descriptions

Consider the following general FOSS:

$$\begin{array}{c}{D}^{\alpha }x\left(t\right)=A_{\sigma }x\left(t\right)+B_{\sigma }{u}_{\sigma }\left(t\right)+B_{\sigma w}w\left(t\right)\hfill \\ z\left(t\right)=C_{\sigma }x\left(t\right)\hfill \end{array}$$

(5)

where $0<\alpha <1$, $\sigma \in J=\{1,2,\dots ,N\}$ is the piecewise constant switching signal. $\sigma =i$ denotes that the i-th subsystem is activated. $A_i,B_i,B_{iw}$, and $C_i$$(i\in J)$ are real matrices. The transfer matrix between $w\left(t\right)$ and $z\left(t\right)$ is $G\left(s\right)=C_{\sigma }{(s^{\alpha }I-A_{\sigma })}^{-1}{B}_{\sigma w}$.

Then, the necessary lemma is introduced as follows.

Lemma 5

([41]). System (5) with $u_{\sigma }\left(t\right)=0$ is asymptotically stable iff there exist $X,Y\in {\mathbf{R}}^{n\times n}$ such that:

$$\left[\begin{array}{cc}X& Y\\ -Y& X\end{array}\right]>0$$

$$a{A}_{i}X+b{A}_{i}Y+aX{A}_i^T-bY{A}_i^T<0$$

where $i\in J=\{1,2,\dots ,N\}$.

Our primary aim in this paper was to design a switching law to ensure FOSSs’ stability. In addition, $H_{\infty }$ and robust $H_{\infty }$ performance for FOSSs should be guaranteed.

3. Formal Description of the Switching Law

In this section, the switching signal should be designed. Therefore, the average matrix can be expressed as:

$$\overline{A}=\sum _{i=1}^N{\lambda }_i{A}_i,i\in J=\{1,2,\dots ,N\}$$

We can obtain the equation below:

$$\overline{A}(aX+bY)+(aX-bY){\overline{A}}^T=-I_n$$

where X, Y satisfy (3). According to Lemma 5, we denote:

$$\begin{array}{cc}& P_i=A_i(aX+bY)+(aX-bY)A_i^T,\forall i\in J\end{array}$$

(6)

Assume $r_i\in (0,1),i\in J$, and $x\left(t_0\right)=x_0$, and set:

$$\begin{array}{c}\hfill \sigma \left(t_0\right)=argmin\{x_0^T{P}_1{x}_0,\dots ,x_0^T{P}_N{x}_0\}\end{array}$$

(7)

Next, let $t_1$ be:

$$t_1=\{t>t_0:x^T\left(t\right)P_{\sigma \left(t_0\right)}x\left(t\right)>-r_{\sigma \left(t_0\right)}{x}^T\left(t\right)x\left(t\right)\}$$

If the set is empty, $t_1=\infty$. If the set is not empty, the switching index can be defined as:

$$\sigma \left(t_1\right)=argmin\left\{x^T\left(t_1\right)P_{i}x\left(t_1\right)\right\}$$

Therefore, we obtain:

$$\begin{array}{ccc}\hfill t_{k+1}& =& \{t>t_k:x^T\left(t\right)P_{\sigma \left(t_k\right)}x\left(t\right)>-r_{\sigma \left(t_k\right)}{x}^T\left(t\right)x\left(t\right)\}\hfill \\ \hfill \sigma \left(t_{k+1}\right)& =& argmin\left\{x^T\left(t_{k+1}\right)P_{i}x\left(t_{k+1}\right)\right\}k,i\in J=\{1,2,\dots ,N\}\hfill \\ \hfill \end{array}$$

(8)

Theorem 1.

Under the fractional-order switching law (8), System (5) is asymptotically stable and well-posed.

Proof. 

Firstly, let $i={\sigma }_{t_k+}$. Based on the switching signal, we can obtain:

$$\begin{array}{cc}& \left(1\right)x^T\left(t_k\right)P_{i}x\left(t_k\right)=\underset{j\in J}{min}\left\{x^T\left(t_k\right)P_{j}x\left(t_k\right)\right\}\\ \hfill & \left(2\right)x^T(t_k+1)P_{i}x(t_k+1)\ge -r_i{x}^T(t_k+1)x(t_k+1)\end{array}$$

According to ${\sum }_{j\in J}{\lambda }_j{P}_j=-I_n$, ${\sum }_{j\in J}{\lambda }_j=1$, and (1), we obtain:

$$\begin{array}{cc}& x^T\left(t_k\right)P_{i}x\left(t_k\right)\le -x^T\left(t_k\right)x\left(t_k\right)\end{array}$$

(9)

Let $\mu >1$, $x_k=x\left(t_k\right)$, and $x_{k+1}=x\left(t_{k+1}\right)$. Then,

$$\begin{array}{cc}& \mu \parallel x_{k+1}\parallel \ge \parallel x\left(t\right)\parallel \end{array}$$

(10)

where $t\in [t_k,t_{k+1}]$.

From the above condition, we can define:

$$\begin{array}{cc}& f\left(t\right)=x^T\left(t\right)(P_i+I_n)x\left(t\right)\end{array}$$

(11)

Based on (9) and (2), we obtain:

$$\begin{array}{cc}& f\left(t_k\right)\le 0,f\left(t_{k+1}\right)\ge (1-r_i)x_{k+1}^T{x}_{k+1}\end{array}$$

(12)

Hence, we have:

$$\begin{array}{cc}& \dot{f}\left(t\right)=x^T\left(t\right)(A_i^T(P_i+I_n)+{(P_i+I_n)}^T{A}_i)x\left(t\right)\end{array}$$

(13)

Denote ${\rho }_i=\parallel A_i^T(P_i+I_n)+{(P_i+I_n)}^T{A}_i\parallel$; from (10) and Lemma 3, we have:

$$\begin{array}{cc}& |\dot{f}\left(t\right)|\le {\mu }^2{\rho }_i{x}_{k+1}^T{x}_{k+1}\end{array}$$

From (12), we can obtain:

$$\begin{array}{cc}& {\mu }^2{\rho }_i(t_{k+1}-t_k)\ge (1-r_i)\end{array}$$

(14)

that is to say,

$$\begin{array}{cc}& (1-r_i)/\left({\mu }^2{\rho }_i\right)\le t_{k+1}-t_k\end{array}$$

(15)

Assume (10) does not hold. Then, $t^{*}\in [t_k,t_{k+1}]$ can be found to satisfy:

$$\begin{array}{cc}& \mu \parallel x_{k+1}\parallel <\parallel x\left(t^{*}\right)\parallel \end{array}$$

(16)

From the Mittag–Leffler function [19], we can obtain:

$$\begin{array}{cc}& x\left(t^{*}\right)=E_{\alpha }\left(A_i{(t^{*}-t_{k+1})}^{\alpha }\right)x_{k+1}\end{array}$$

According to (16) and Lemma 2, we can obtain $C>\mu$ and:

$$\begin{array}{c}\hfill \mu <\parallel E_{\alpha }\left(A_i{(t^{*}-t_{k+1})}^{\alpha }\right)\parallel \le \frac{C}{1+\parallel A_i{(t^{*}-t_{k+1})}^{\alpha }\parallel }\end{array}$$

Then,

$$\begin{array}{cc}& D^{\alpha }\frac{C-\mu }{\mu \parallel A_i\parallel }<t_{k+1}-t^{*}\le t_{k+1}-t_k\ge \end{array}$$

In summary,

$$\begin{array}{cc}& \varphi =\underset{\mu >1}{sup}\underset{i\in J}{min}(\frac{(1-r_i}{{\mu }^2{\rho }_i},D^{\alpha }\frac{C-\mu }{\mu \parallel A_i\parallel })\le t_{k+1}-t_k\end{array}$$

Therefore, $\varphi >0$, and the switching signal is well-defined.

From (6), define $V\left(x\right)=x^T(aX+bY)x$. Then, we obtain:

$$\begin{array}{cc}& \dot{V}=x^T\left(t\right)P_{\sigma }x\left(t\right)\le -r_{\sigma }{x}^T\left(t\right)x\left(t\right)\le -r{x}^T\left(t\right)x\left(t\right)\end{array}$$

where $r=min\{r_1,\dots ,r_N\}$. From Lemma 5, we can prove that System (5) is asymptotically stable. Hence, we complete the proof. □

4. ${\mathbf{H}}_{\infty }$ Control

In this section, $H_{\infty }$ control for FOSSs is studied. According to Theorem 1 and Lemma 1 proposed in the paper, the following theorems are derived.

Theorem 2.

Given any constant $\gamma >0$, N, matrices X, Y, and scalars ${\lambda }_i\ge 0(i\in J=\{1,2,\dots ,N\})$, ${\sum }_{i=1}^N{\lambda }_i=1$, System (5) is asymptotically stable, and ${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$, if:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}X& Y\\ -Y& X\end{array}\right]>0\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \left[\begin{array}{ccc}\mathrm{sym}(a\overline{A}X+bX{\overline{A}}^T)& (aX-bY){\overline{C}}^T& {\overline{B}}_w\\ *& -\gamma I& 0\\ *& *& -\gamma I\end{array}\right]<0\hfill \end{array}$$

(18)

where:

$$\overline{A}=\sum _{i=1}^N{\lambda }_i{A}_i,{\overline{B}}_w=\sum _{i=1}^N\sqrt{{\lambda }_i}{B}_{iw},\overline{C}=\sum _{i=1}^N\sqrt{{\lambda }_i}{C}_i$$

$$i\in J=\{1,2,\dots ,N\}.$$

Then, the switching law is:

$$\begin{array}{ccc}\hfill \sigma \left(t\right)& =& arg\underset{i\in J}{min}\left\{x^T\right(A_i(aX+bY)\hfill \\ \hfill & +& (aX-bY)A_i^T+{\gamma }^{-1}{B}_{iw}{B}_{iw}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\left)x\right\}\hfill \end{array}$$

(19)

Proof. 

From Theorem 1, (19) can be proven easily. Then, we prove that System (5) is asymptotically stable, and ${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$.

Suppose that $\left\{(t_k,r_k)\right|r_k\in J,k=1,2,\dots ,N\}$ is the switching sequence in $[0,T)$. Then, from Lemma 3, (18) is equivalent to the following equation:

$$\left[\begin{array}{cc}\mathrm{sym}(a\overline{A}X+bX{\overline{A}}^T)& (aX-bY){\overline{C}}^T\\ *& -\gamma I\end{array}\right]+\frac{1}{\gamma }\left[\begin{array}{c}{\overline{B}}_w\\ 0\end{array}\right]\left[\begin{array}{cc}{\overline{B}}_w^T& 0\end{array}\right]<0$$

(20)

Owing to the existing matrices X and Y, Inequality (20) is equivalent to Inequality (21), when Inequality (20) is multiplied by $\gamma$.

$$\gamma \left[\begin{array}{cc}\mathrm{sym}(a\overline{A}X+bX{\overline{A}}^T)& (aX-bY){\overline{C}}^T\\ *& 0\end{array}\right]+\left[\begin{array}{cc}{\overline{B}}_w{\overline{B}}_w^T& 0\\ 0& -{\gamma }^{2}I\end{array}\right]<0$$

(21)

Let $P=X\gamma$ and $Q=Y\gamma$, to make the proof simple. From (21), we have:

$$\begin{array}{c}{\left[\begin{array}{cc}{\overline{A}}^T& {\overline{C}}^T\\ I_n& 0\end{array}\right]}^T\left(\left[\begin{array}{cc}0& aP+bQ\\ aP-bQ& 0\end{array}\right]\otimes I_m\right)\\ \left[\begin{array}{cc}{\overline{A}}^T& {\overline{C}}^T\\ I_n& 0\end{array}\right]+\left[\begin{array}{cc}{\overline{B}}_w{\overline{B}}_w^T& 0\\ 0& -{\gamma }^{2}I\end{array}\right]<0\hfill \\ \end{array}$$

(22)

where $a=sin\left(\alpha \frac{\pi }{2}\right)$ and $b=cos\left(\alpha \frac{\pi }{2}\right)$.

According to Lemmas 1 and 2 in [28], when $0<\alpha <1$, let ${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$, and consider the curve:

$${\Gamma }_{11}=(\left[\begin{array}{cc}0& aP+bQ\\ aP-bQ& 0\end{array}\right],0).$$

Since ${\Gamma }_{11}\left(s\right)\subset \{s^{\alpha }:Re\left(s\right)\ge 0\}$, we can obtain:

$$\overline{H}\left(\lambda \right)={(\lambda I-{\overline{A}}^T)}^{-1}{\overline{C}}^T$$

and we have:

$${\left[\begin{array}{c}\overline{H}\left(\lambda \right)\\ I_n\end{array}\right]}^T\left[\begin{array}{cc}{\overline{B}}_w{\overline{B}}_w^T& 0\\ 0& -{\gamma }^{2}I\end{array}\right]\left[\begin{array}{c}\overline{H}\left(\lambda \right)\\ I_n\end{array}\right]<0$$

(23)

Unfolding Equality (23), we can obtain:

$$\begin{array}{cc}& {\overline{H}}^T\left(\lambda \right){\overline{B}}_w{\overline{B}}_w^T\overline{H}\left(\lambda \right)-{\gamma }^{2}I<0\end{array}$$

(24)

From Equality (24):

$$\begin{array}{cc}& \left[\overline{C}{(\lambda I-\overline{A})}^{-1}{\overline{B}}_w\right]{\left[\overline{C}{(\lambda I-\overline{A})}^{-1}{\overline{B}}_w\right]}^T-{\gamma }^{2}I<0\end{array}$$

(25)

According to Equality (25):

$$\begin{array}{ccc}\hfill {\gamma >\parallel G\left(s\right)\parallel }_{H_{\infty }}& =& \underset{Re\left(s\right)\ge 0}{sup}\left[\overline{C}{(s^{\alpha }I-\overline{A})}^{-1}{\overline{B}}_w\right]\hfill \\ \hfill & \ge & \underset{\lambda \in {\Gamma }_{11}}{sup}\left[\overline{C}{(s^{\alpha }I-\overline{A})}^{-1}{\overline{B}}_w\right]\hfill \\ \hfill \end{array}$$

(26)

The proof is complete. □

Based on Theorem 2, $H_{\infty }$ control of FOSSs with the state feedback controller is given as follows.

Theorem 3.

Given any constant $\gamma >0$, N, matrices X, Y, Z, and scalars ${\lambda }_i\ge 0(i\in J=\{1,2,\dots ,N\})$, ${\sum }_{i=1}^N{\lambda }_i=1$, System (5) with state feedback $u_{\sigma }\left(t\right)=Kx\left(t\right)$ is asymptotically stabilizable, and ${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$, if:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}X& Y\\ -Y& X\end{array}\right]>0\hfill \end{array}$$

(27)

$$\left[\begin{array}{ccc}\mathrm{sym}(a\overline{A}X+bX{\overline{A}}^T+\overline{B}Z)& (aX-bY){\overline{C}}^T& {\overline{B}}_w\\ *& -\gamma I& 0\\ *& *& -\gamma I\end{array}\right]<0$$

(28)

where:

$$\overline{A}=\sum _{i=1}^N{\lambda }_i{A}_i,{\overline{B}}_w=\sum _{i=1}^N\sqrt{{\lambda }_i}{B}_{iw},\overline{C}=\sum _{i=1}^N\sqrt{{\lambda }_i}{C}_i,$$

$$i\in J=\{1,2,\dots ,N\}.$$

Then, the gain matrix is:

$$\begin{array}{cc}& K=Z{(aX+bY)}^{-1}\end{array}$$

(29)

The switching law is:

$$\begin{array}{ccc}\hfill \sigma \left(t\right)& =& arg\underset{i\in J}{min}\left\{x^T\right((A_i+B_{i}K)(aX+bY)\hfill \\ \hfill & +& (aX-bY){(A_i+B_{i}K)}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\hfill \\ \hfill & +& {\gamma }^{-1}{B}_{iw}{B}_{iw}^T\left)x\right\}\hfill \end{array}$$

(30)

Proof. 

Let $\widehat{A}=\overline{A}+\overline{B}K$; the proof of Theorem 3 is directly derived from Theorem 2. □

5. Robust ${\mathbf{H}}_{\infty }$ Control

In this section, robust $H_{\infty }$ control of FOSSs with uncertainty is studied.

Consider the following FOSS with uncertainty:

$$\begin{array}{ccc}\hfill D^{\alpha }x\left(t\right)& =& (A_{\sigma }+\Delta A)x\left(t\right)+(B_{\sigma }+\Delta B)u_{\sigma }\left(t\right)\hfill \\ \hfill & +& B_{\sigma w}w\left(t\right)\hfill \\ \hfill z\left(t\right)& =& C_{\sigma }x\left(t\right)\hfill \end{array}$$

(31)

where $G\left(s\right)=C_{\sigma }{(s^{\alpha }I-A_{\sigma }-\Delta A)}^{-1}{B}_{\sigma w}$. $\Delta A$ and $\Delta B$ are the norm-bounded uncertainties, and:

$$[\Delta A \Delta B]=MF\left(t\right)[N_1 N_2]$$

(32)

where $M,N_1$ and $N_2$ are constant matrices of appropriate dimensions. $F\left(t\right)$ satisfies $F^T\left(t\right)F\left(t\right)\le I$.

According to Theorem 1, Theorem 2, and Lemma 5, the following theorem is derived.

Theorem 4.

Given any constant $\gamma >0$, N, matrices X, Y, and scalars ${\lambda }_i\ge 0(i\in J=\{1,2,\dots ,N\})$, ${\sum }_{i=1}^N{\lambda }_i=1$, ϵ, System (31) is quadratically stable, and ${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$, if:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}X& Y\\ -Y& X\end{array}\right]>0\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}{\Pi }_{11}& (aX-bY){\overline{C}}^T& {\overline{B}}_w& N_1(aX+bY)\\ *& -\gamma I& 0& 0\\ *& *& -\gamma I& 0\\ *& *& *& -ϵI\end{array}\right]<0\hfill \end{array}$$

(34)

where:

$${\Pi }_{11}=\mathit{sym}(a\overline{A}X+bX{\overline{A}}^T)+ϵM{M}^T,$$

$$\overline{A}=\sum _{i=1}^N{\lambda }_i{A}_i,{\overline{B}}_w=\sum _{i=1}^N\sqrt{{\lambda }_i}{B}_{iw},\overline{C}=\sum _{i=1}^N\sqrt{{\lambda }_i}{C}_i,$$

$$i\in J=\{1,2,\dots ,N\}.$$

Then, the switching law is:

$$\begin{array}{ccc}\hfill \sigma \left(t\right)& =& arg\underset{i\in J}{min}\left\{x^T\right(A_i(aX+bY)\hfill \\ \hfill & +& (aX-bY)A_i^T+{\gamma }^{-1}{B}_{iw}{B}_{iw}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\left)x\right\}\hfill \end{array}$$

(35)

Proof. 

Let $\overline{A}=A_{\sigma }+\Delta A$, and substitute $\overline{A}$ into Theorem 2. We can obtain:

$$\left[\begin{array}{ccc}{\Phi }_{11}& (aX-bY){\overline{C}}^T& {\overline{B}}_w\\ *& -\gamma I& 0\\ *& *& -\gamma I\end{array}\right]<0$$

where ${\Phi }_{11}=a(\overline{A}+\Delta A)X+bX{(\overline{A}+\Delta A)}^T+b(\overline{A}+\Delta A)Y-bY{(\overline{A}+\Delta A)}^T$.

Then, by applying Lemma 4, the above inequality can be expressed as (34). Theorem 4 can be easily proven. □

Based on Theorems 2 and 4, robust $H_{\infty }$ control of FOSSs with the state feedback controller and uncertainty is given as follows.

Theorem 5.

Given any constant $\gamma >0$, N, matrices X, Y, Z, W, and scalars ${\lambda }_i\ge 0(i\in J=\{1,2,\dots ,N\})$, ${\sum }_{i=1}^N{\lambda }_i=1$, ϵ, System (31) with state feedback $u_{\sigma }\left(t\right)=Kx\left(t\right)$ is quadratically stabilizable, and ${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$, if:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}X& Y\\ -Y& X\end{array}\right]>0\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}{\Pi }_{11}& (aX-bY){\overline{C}}^T& {\overline{B}}_w& N_1(aX+bY)+N_{2}W\\ *& -\gamma I& 0& 0\\ *& *& -\gamma I& 0\\ *& *& *& -ϵI\end{array}\right]<0\hfill \end{array}$$

(37)

where:

$${\Pi }_{11}=\mathit{sym}(a\overline{A}X+b\overline{A}Y+\overline{B}Z)+ϵM{M}^T,$$

$$\overline{A}=\sum _{i=1}^N{\lambda }_i{A}_i,{\overline{B}}_w=\sum _{i=1}^N\sqrt{{\lambda }_i}{B}_{iw},\overline{C}=\sum _{i=1}^N\sqrt{{\lambda }_i}{C}_i$$

$$i\in J=\{1,2,\dots ,N\}.$$

Then, the gain matrix is:

$$\begin{array}{cc}& K=Z{(aX+bY)}^{-1}\end{array}$$

(38)

The switching law is:

$$\begin{array}{ccc}\hfill \sigma \left(t\right)& =& arg\underset{i\in J}{min}\left\{x^T\right((A_i+B_{i}K)(aX+bY)\hfill \\ \hfill & +& (aX-bY){(A_i+B_{i}K)}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\hfill \\ \hfill & +& {\gamma }^{-1}{B}_{iw}{B}_{iw}^T\left)x\right\}\hfill \end{array}$$

(39)

Proof. 

Let $\hat{A}=(A_{\sigma }+\Delta A)+(B_{\sigma }+\Delta B)K$; substitute $\hat{A}$ into Theorem 2, and set $W=K(aX+bY)$. Theorem 5 is directly derived from Theorems 2 and 5. □

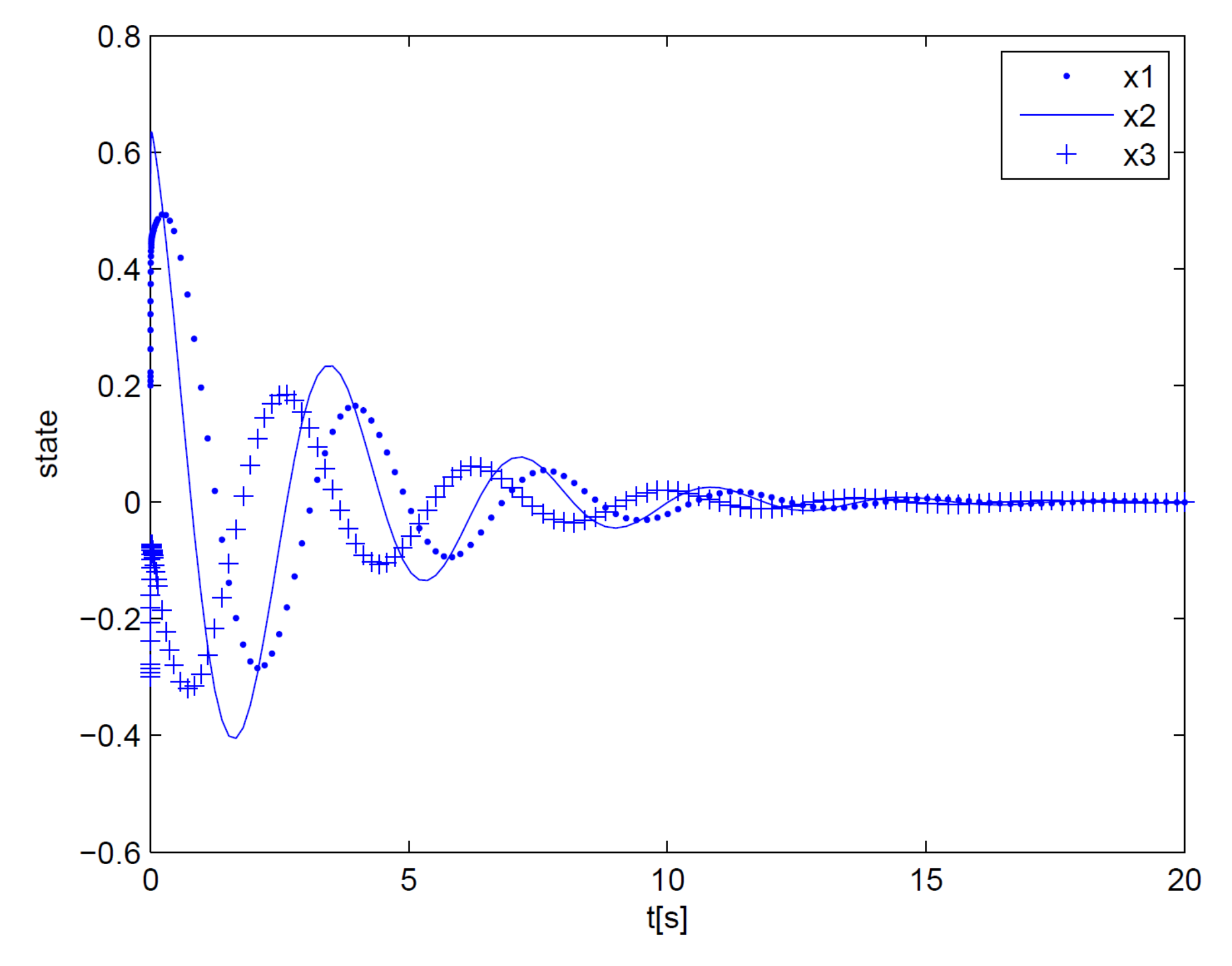
6. Examples

6.1. Example 1

Consider System (5) with order $\alpha =0.5$, $N=2$, and:

$$A_1=\left[\begin{array}{cc}-1.9& 1\\ 2& 1\end{array}\right],A_2=\left[\begin{array}{cc}-3& -4.3\\ -1& -0.5\end{array}\right],B_1=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]$$

$$B_2=\left[\begin{array}{cc}0& -1\\ 1& 1\end{array}\right],B_{1w}=\left[\begin{array}{c}0.5\\ 1\end{array}\right],B_{2w}=\left[\begin{array}{c}1\\ 0.1\end{array}\right]$$

$$C_1=\left[\begin{array}{cc}-1& 2\end{array}\right],C_2=\left[\begin{array}{cc}2& 1\end{array}\right]$$

Set ${\lambda }_1=0.7,{\lambda }_2=0.3$ and the disturbance attenuation level $\gamma =0.8$, according to Theorem 3; we can obtain:

$$X=\left[\begin{array}{cc}0.7717& 0.0430\\ 0.0430& 0.0024\end{array}\right],Y=\left[\begin{array}{cc}0& -0.0024\\ 0.0024& 0\end{array}\right]$$

$$K=\left[\begin{array}{cc}2.5946& -3.1100\\ -2.5777& -0.9836\end{array}\right]$$

Let:

$$\begin{array}{ccc}\hfill P_i& =& (A_i+B_{i}K)(aX+bY)\hfill \\ \hfill & +& (aX-bY){(A_i+B_{i}K)}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\hfill \\ \hfill & +& {\gamma }^{-1}{B}_{iw}{B}_{iw}^T\hfill \end{array}$$

Then, obtain the switching law:

$$\begin{array}{c}\hfill \sigma \left(t\right)=i=\left\{\begin{array}{cc}1,\hfill & x^T(P_1-P_2)x<0;\hfill \\ 2,\hfill & x^T(P_1-P_2)x\ge 0\hfill \end{array}\right.\end{array}$$

Figure 2 shows that the state trajectory converges to zero, and the designed controllers make the associated subsystems asymptotically stable by the switching strategy (30).

Figure 2. State trajectories of Example 1.

6.2. Example 2

Consider System (5) with order $\alpha =0.23$, $N=2$, and:

$$A_1=\left[\begin{array}{ccc}-1& 1& -2\\ 2& 1& 1\\ 0& 2& 2\end{array}\right],A_2=\left[\begin{array}{ccc}-3& -2& -2\\ -1& -2& 1\\ -1& -1& 2\end{array}\right],B_1=\left[\begin{array}{c}1\\ 2\\ 1\end{array}\right]$$

$$B_2=\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right],B_{1w}=\left[\begin{array}{c}2\\ 1\\ 2\end{array}\right],B_{2w}=\left[\begin{array}{c}1\\ 0.5\\ 1\end{array}\right]$$

$$C_1=\left[\begin{array}{ccc}-1& 2& 2\end{array}\right],C_2=\left[\begin{array}{ccc}1& 2& 1\end{array}\right]$$

Set ${\lambda }_1=0.4,{\lambda }_2=0.6$ and the disturbance attenuation level $\gamma =1.2$; from Theorem 3, we can obtain:

$$X=\left[\begin{array}{ccc}13.6532& 3.6714& -0.0721\\ 3.6714& 3.5815& -2.0306\\ -0.0721& -2.0306& -1.0467\end{array}\right],Y=\left[\begin{array}{ccc}0& 0.0721& 2.0306\\ -0.0721& 0& 1.0467\\ -2.0306& -1.0467& 0\end{array}\right]$$

$$K=\left[\begin{array}{ccc}-4.4841& -96.8927& -77.1058\end{array}\right]$$

Let:

$$\begin{array}{ccc}\hfill P_i& =& (A_i+B_{i}K)(aX+bY)\hfill \\ \hfill & +& (aX-bY){(A_i+B_{i}K)}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\hfill \\ \hfill & +& {\gamma }^{-1}{B}_{iw}{B}_{iw}^T\hfill \end{array}$$

Then, we obtain the switching law:

$$\begin{array}{c}\hfill \sigma \left(t\right)=i=\left\{\begin{array}{cc}1,\hfill & x^T(P_1-P_2)x<0;\hfill \\ 2,\hfill & x^T(P_1-P_2)x\ge 0\hfill \end{array}\right.\end{array}$$

Figure 3 shows that the state trajectory converges to zero, and the designed controllers make the associated subsystems asymptotically stable by the switching strategy (30).

Figure 3. State trajectories of Example 2.

Remark 3.

The characteristic roots of $A_2+B_{2}K$ are $\{-3.0638,9.9254+20.4436i,9.9254-20.4436i\}$ and $\left|\arg (9.9254+20.4436i)\right|=1.1188>\frac{0.23\pi }{2}=0.3613$. Although there are positive real roots, the second subsystem is stable under our results. Hence, compared with the results in [45,46,47], the results in this paper are less conservative.

6.3. Example 3

Consider System (31) with order $\alpha =0.3$, $N=2$, and:

$$A_1=\left[\begin{array}{ccc}-1& 0& 1\\ 2& 1& 2\\ 2& 1& 0\end{array}\right],A_2=\left[\begin{array}{ccc}2& -1& 1\\ 0& 2& 1\\ 0& 1& 1\end{array}\right],B_1=\left[\begin{array}{ccc}0& 1& 1\\ 1& 0& 1\\ 1& 1& 1\end{array}\right]$$

$$B_2=\left[\begin{array}{ccc}0& -1& 1\\ 1& 0& -1\\ 1& 1& 1\end{array}\right],B_{1w}=\left[\begin{array}{c}0.5\\ 1\\ 0.75\end{array}\right],B_{2w}=\left[\begin{array}{c}0.2\\ 0.5\\ 0.1\end{array}\right]$$

$$C_1=\left[\begin{array}{ccc}-1& 0& 1\end{array}\right],C_2=\left[\begin{array}{ccc}0& 1& 1\end{array}\right]$$

$$M=\left[\begin{array}{ccc}-2& 2& 2\\ -3& -2& 2\\ -2& -2& -4\end{array}\right],N_1=I_3,N_2=\left[\begin{array}{ccc}0.1& 0.15& 0.2\\ 0.2& 0.1& 0.1\\ 0.15& 0.25& 0.3\end{array}\right]$$

Set ${\lambda }_1=0.8,{\lambda }_2=0.2$ and the disturbance attenuation level $\gamma =1.2$; according to Theorem 5, we can obtain:

$$X=\left[\begin{array}{ccc}1.0667& 0.0976& 0.2477\\ 0.0976& -0.1708& 0.1370\\ 0.2477& 0.1370& -0.1728\end{array}\right]$$

$$Y=\left[\begin{array}{ccc}0& -0.2477& -0.1370\\ 0.2477& 0& 0.1728\\ 0.1370& -0.1728& 0\end{array}\right]$$

$$K=\left[\begin{array}{ccc}-9.3285& 108.9177& 240.5395\\ -255.9823& 317.2618& 521.5005\\ 149.9447& -279.5623& -481.4994\end{array}\right]$$

Let:

$$\begin{array}{ccc}\hfill W_i& =& (A_i+B_{i}K)(aX+bY)\hfill \\ \hfill & +& (aX-bY){(A_i+B_{i}K)}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\hfill \\ \hfill & +& {\gamma }^{-1}{B}_{iw}{B}_{iw}^T\hfill \end{array}$$

Then, we obtain the switching law:

$$\begin{array}{c}\hfill \sigma \left(t\right)=i=\left\{\begin{array}{cc}1,\hfill & x^T(W_1-W_2)x<0;\hfill \\ 2,\hfill & x^T(W_1-W_2)x\ge 0\hfill \end{array}\right.\end{array}$$

Figure 4 shows that System (31) with gain K is quadratically stable by switching strategy (39), when the system initializes at $x\left(0\right)={\left[\begin{array}{ccc}0.7& 0.4& -0.5\end{array}\right]}^T$.

Figure 4. State trajectories of Example 3.

6.4. Example 4

Consider System (31) with order $\alpha =0.63$, $N=2$, and:

$$A_1=\left[\begin{array}{ccc}-2& 2& 1.5\\ 1.2& 0.1& 2.1\\ 2& 1& 1\end{array}\right],A_2=\left[\begin{array}{ccc}1.2& -2.1& 0.2\\ 0.12& 2.2& 1.1\\ 0.3& 1.2& 1.5\end{array}\right],B_1=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]$$

$$B_2=\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right],B_{1w}=\left[\begin{array}{c}1.5\\ 1\\ 2.75\end{array}\right],B_{2w}=\left[\begin{array}{c}1\\ 2.5\\ 1\end{array}\right]$$

$$C_1=\left[\begin{array}{ccc}-1& 2& 1\end{array}\right],C_2=\left[\begin{array}{ccc}3& 1& 1\end{array}\right]$$

$$M=\left[\begin{array}{ccc}1.2& 0.2& 2.2\\ 1.3& 0.2& 1.2\\ 1.2& 0.2& 2.4\end{array}\right],N_1=\left[\begin{array}{ccc}0.1& 0.2& 0.1\\ 0.2& 0.1& 0.3\\ 0.1& 0.2& 0.3\end{array}\right],N_2=\left[\begin{array}{ccc}0.21& 0.13& 0.12\\ 0.23& 0.21& 0.11\\ 0.35& 0.22& 0.31\end{array}\right]$$

Set ${\lambda }_1=0.25,{\lambda }_2=0.75$ and the disturbance attenuation level $\gamma =2.5$; according to Theorem 5, we can obtain:

$$X=\left[\begin{array}{ccc}2.4811& 2.3268& 1.2724\\ 2.3268& 17.5209& -16.7539\\ 1.2724& -16.7539& -10.0580\end{array}\right]$$

$$Y=\left[\begin{array}{ccc}0& -1.2724& 16.7539\\ 1.2724& 0& 10.0580\\ -16.7539& -10.0580& 0\end{array}\right]$$

$$K=\left[\begin{array}{ccc}41.8007& 27.9848& 22.9541\end{array}\right]$$

Let:

$$\begin{array}{ccc}\hfill W_i& =& (A_i+B_{i}K)(aX+bY)\hfill \\ \hfill & +& (aX-bY){(A_i+B_{i}K)}^T\hfill \\ \hfill & +& {\gamma }^{-1}(aX-bY)C_i^T{C}_i(aX+bY)\hfill \\ \hfill & +& {\gamma }^{-1}{B}_{iw}{B}_{iw}^T\hfill \end{array}$$

Then, we obtain the switching law:

$$\begin{array}{c}\hfill \sigma \left(t\right)=i=\left\{\begin{array}{cc}1,\hfill & x^T(W_1-W_2)x<0;\hfill \\ 2,\hfill & x^T(W_1-W_2)x\ge 0\hfill \end{array}\right.\end{array}$$

Figure 5 shows that System (31) with gain K is quadratically stable by the switching strategy (39).

Figure 5. State trajectories of Example 4.

7. Conclusions

In this paper, the fractional-order switching law was derived for fractional-order switched systems (FOSSs) with order $0<\alpha <1$. Under the above switching law, stability and well-posedness can be proven for FOSSs. Then, the conditions of $H_{\infty }$ control and controller design for FOSSs were proposed based on linear matrix inequalities (LMIs) in the paper, which can ensure the $H_{\infty }$ performance for closed-loop FOSSs. Furthermore, the LMI-based conditions of robust $H_{\infty }$ control and performance analysis were proven for FOSSs with uncertainty. Four the numerical simulation, results were given to verify the validity of the results proposed in this paper.

In the future, output feedback $H_{\infty }$ control for FOSSs and robust $H_{\infty }$ control for FOSSs with poly-topic uncertainty are the desired research directions.