Abstract
In this paper, we investigate the numerical valuation of European and American options under the time fractional Black-Scholes model. We first apply a coordinate stretching transformation to the asset price so that the spatial region can focus on the vicinity of singularities, which are usually found in the payoff function. The radial basis function finite difference method is used for the spatial discretization, and the improved L1 method is used to deal with the reduced order of convergence for the nonsmooth initial data. We use the operator splitting method for solving the linear complementary problem of American options. The proposed scheme leads to a sparse linear system which is trivial to solve. Moreover, the stability of the proposed numerical scheme is analyzed using Fourier analysis. Numerical experiments demonstrate the accuracy and efficiency of the proposed method.
1. Introduction
Since the classical Black-Scholes (B-S) model based on Brownian motion and normal distribution was proposed by Black and Scholes [1], it has achieved unprecedented success in computational finance because of its simplicity and clarity. Recent empirical evidence suggests that the B-S model fails to reflect the asymmetric leptokurtic features and the volatility smile observed in the real market. Therefore, many studies have been conducted to modify and improve the B-S model, such as the jump diffusion models [2,3], the constant elasticity of variance model [4], the stochastic volatility models [5,6,7] and the fractional models [8,9,10,11,12].
In recent years, there has been an increasing interest in fractional differential equations. Due to the non-locality of fractional derivatives, researchers observed that they provide a powerful tool to describe memory effect [13]. The fractional partial differential equations have been introduced more and more into financial theory. Wyss [8] gave the first time fractional B-S model for European call options. Cartea and del-Castillo-Negrete [9] successfully connected the FMLS process [14], KoBoL process [15] and CGMY process [16,17] with the space fractional derivatives for pricing exotic options. Jumarie [10,18] derived two new families of fractional B-S equations by using the new fractional Taylor’s series. Liang et al. [11] established the bi-fractional B-S model and obtained the explicit option pricing formulas for European options. The time-space fractional option pricing models were discussed in [19,20,21].
In general, as it is extremely difficult to obtain analytical solutions for the fractional B-S model, the efficient numerical method is essential. Song and Wang [22] used an implicit finite difference method for European and American put options under the Jumarie time fractional B-S model. Zhang et al. [23] constructed an implicit numerical scheme using the finite difference method for European options under the Wyss time fractional B-S model. De Staelen and Hendy [24] derived a compact difference scheme for European double barrier options under the Wyss time fractional B-S model. Koleva and Vulkov [25] presented the weighted finite difference scheme for European options under the Jumarie time fractional B-S model. Golbabai et al. [26] developed a numerical method, using the meshless method based on the radial basis function (RBF) collocation method for European options under the Wyss time fractional B-S model. Chen et al. [27] established a new operator splitting method for American options under the Jumarie model, Farhadi model [28] and Wyss model. Huang et al. [29] presented a numerical method based on an adaptive moving mesh for European options under the Wyss time fractional B-S model. Almushaira et al. [30] proposed the improved L1 operator splitting and spectral methods for American options under the time-space fractional B-S model.
In this paper, the numerical valuation of European and American options under the Wyss time fractional B-S model is studied. It is well known that the American options pricing problem can be stated as the linear complementary problem. We propose a new combination of the radial basis function finite difference (RBF-FD) and the improved L1 operator splitting methods for American options, inspired by [27,30,31]. We first apply a coordinate stretching transformation to the asset price so that the spatial region can focus on the vicinity of the points of singularity usually found in the payoff function. Then, the RBF-FD method is used for space discretization. As a meshless method, the RBF-FD [32,33,34] method is a local method resulting in a sparse linear system, while the global RBF method results in a dense linear system showing ill conditioning. The operator splitting method is an effective method for the American options pricing problem. Chen et al. [27] extended the technique to the fractional B-S models. However, the method is only first-order accurate for American options when . We improve on their results by constructing a scheme of order in time.
The paper is organized as follows. Section 2 describes the time fractional B-S model. In Section 3, the discretization scheme is constructed. The stability of the proposed numerical scheme is given in Section 4. In Section 5, we present some numerical experiments to assess the accuracy and efficiency of the proposed method. Conclusions are drawn in Section 6.
2. Time Fractional B-S Model
In this paper, we focus on the following Wyss time fractional B-S model. Let denote the price of a European option with strike price K on the underlying asset S and time t. It is easy to show that is governed by
where is the volatility of the returns, r is the risk-free interest rate and T is the expiry date. The fractional derivative is the modified right Riemann-Liouville derivative defined as
when , the model (1) is the classical B-S model. Note that we consider in the following. The boundary conditions and depend on the type of option, and is the payoff function. In this paper, we focus on the put options, where . As pointed out in [35], this model assumes that the underlying asset follows the classical Brownian motion, whereas the change in the option price is a fractal transmission system. For more information on the Wyss time fractional B-S model, see [8,23,35].
To solve the above model numerically, we truncate the original unbounded region into a bounded interval . Since the payoff function is nonsmooth at , we employ the following change of variables so that the spatial region can focus on the vicinity of the nonsmooth point ,
where is the stretching parameter, which determines the concentration near . The inverse transformation of is
Finally, applying the chain rule, model (1) can be reformulated into
where
The fractional derivative coincides with the Caputo derivative for , that is
The corresponding boundary and initial conditions for European put options are given as
The value of American options satisfies the following linear complementary problem
The boundary and initial conditions for American put options are given as
3. Discretization Scheme
3.1. The Improved L1 Scheme and Operator Splitting Method
Let be any given uniform temporal grid with step size . We first introduce the following L1 scheme for the approximation of the fractional derivative.
where and
For the temporal discretization of Equations (3) and (6), we employ the improved L1 scheme [36] to obtain a higher order method for the nonsmooth initial condition.
Let , it is easy to obtain
and then the model (3) for European options is equivalent to
We consider the improved L1 scheme with a correction at the starting steps of the L1 scheme as used by Ford and Yan [36]. Denoting , then , and the model (9) is approximated by
where
For American options, we introduce a slack function , then (6) can be reformulated as follows
Let , then (11) for American options is equivalent to
The operator splitting method for American options splits the equation into two easy discrete equations on each time level. Let , in the first substep, we solve for an intermediate solution from the following boundary value problem:
In the second substep, we solve for from the following system
The solution of (14) is given by
3.2. The Radial Basis Function Finite Difference Method
In this subsection, we present the RBF-FD formulas for the first and second derivatives. Let be any given uniform spatial grid with mesh width . We consider the equidistant grid of nodes , and the following multiquadrics RBF.
where c is the shape parameter. The first order derivative is approximated by
Lemma 1
([32]). For a given smooth function, the resulting error by approximating the first derivative with the RBF-FD formulation (17) is expressed by
and the weighting coefficients are given by
Proof.
The following linear algebraic system is required to be solved in order to determine the weighting coefficients .
where is the RBF collocation point at . It is easy to obtain the first derivative of .
Substituting (16) and (21) into (20), and letting we have
and the solutions of Equation (22) are given by
However, the obtained solution may not be used in practice due to its complexity, and a more useful formula can be obtained by Taylor expansion under the condition .
Moreover, we can obtain the error by the Taylor expansion
which shows the quadratic convergence for our RBF-FD approximation (17). □
We can write the RBF-FD approximation for the second derivatives in a similar way as follows:
Lemma 2
([32]). For a given smooth function, the resulting error by approximating the second derivative with the RBF-FD formulation (23) is expressed by
and the weighting coefficients are given by
Proof.
The proof is similar to Lemma 1. The following linear algebraic system is required to be solved in order to determine the weighting coefficients .
It is easy to obtain the second derivative of .
Substituting (16) and (27) into (26), and letting then we have
and the solutions of Equation (28) are given by
We obtain a useful formula by the Taylor expansion under the condition .
and the resulting error can be obtained by the Taylor expansion
The proof is now complete. □
Let denote a numerical approximation to for and . We use the RBF-FD formulas to approximate the space derivatives.
where the weighting coefficients are given in (19) and (25), and then we obtain the following discrete implicit scheme for European options:
where , and .
Rearranging the above Equation (31), we have
where
The corresponding boundary and initial conditions can be discretized as
4. Stability Analysis
In this section, we consider the stability of the proposed implicit discrete scheme (32) using the Fourier analysis method. Let be an approximate solution of the implicit discrete scheme (32), and define for , , then satisfies the following equation:
and . We define a grid function as follows:
Then can be expanded in a Fourier series
where and . Let ; the norm of is defined by
Furthermore, using the Parseval identity,
Based on the above analysis and , we suppose that the solution of (33) has the following form:
Then, substituting the above formula into (33), we have
That is
Lemma 3.
The following estimate holds:
Proof.
By writing and , we obtain
Note that , and ([31], Lemma 2), then
This completes the proof. □
Lemma 4.
If is the solution of (37) for , we have .
Proof.
For in (37), by Lemma 3, we have
Suppose that , . By Lemma 3, we have
Note that and , then we have . □
Theorem 1.
The difference scheme (32) is unconditionally stable.
Proof.
By Lemmas 3 and 4, we obtain
which implies the stability of the numerical method. □
5. Numerical Experiment
In this section, we illustrate the performance of the proposed approach, which consists of the RBF-FD discretization in space coupled with the improved L1 method in time (RBF-FD-IL1). The numerical experiments for European and American options are presented to indicate the efficiency and accuracy of our numerical scheme.
5.1. European Options
We consider the following parameters for European put options, which are also used in Chen et al. [27]
The order of convergence is computed by
where is defined as , and is the numerical solution with step size at the terminal time T.
Chen et al. [27] proposed a method for European options based on finite difference discretization in space combined with the L1 method (FD-L1), and the reported results for the FD-L1 method in this paper are taken from Chen et al. [27]. We first compare the values of European put options using the RBF-FD-IL1 and FD-L1 methods. As shown in Table 1, the RBF-FD-IL1 and FD-L1 methods produce prices that are in good agreement. Next, we investigate the error and convergence rate in time for European put options. The RBF-FD discretization in space coupled with the L1 method (RBF-FD-L1) and the FD-L1 method are used for comparison. It can be observed in Table 2 that the option prices using our RBF-FD-IL1 method are in general more accurate than those computed by the RBF-FD-L1 or FD-L1 methods. Table 3 shows that a order convergence in time is attained for our numerical scheme with different values of , while first-order convergence is observed for the RBF-FD-L1 or FD-L1 methods. Further, the numerical solutions for and are plotted in Figure 1. We use the following parameter set:
and European option prices at the terminal time T with different values of for the parameter set (41) are shown in Figure 2.

Table 1.
Values of European put options using the RBF-FD-IL1 and FD-L1 methods, where M and N are the number of points in S and t, respectively.

Table 2.
The numerical error for European put options using the RBF-FD-IL1, RBF-FD-L1 and FD-L1 methods with .

Table 3.
The order of convergence for European put options using the RBF-FD-IL1, RBF-FD-L1 and FD-L1 methods with .
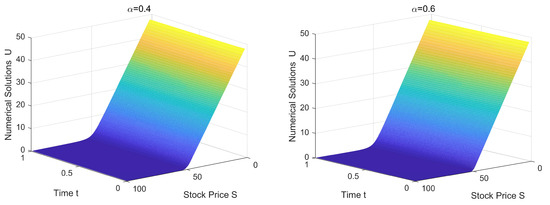
Figure 1.
Numerical solutions of European put options with for and .
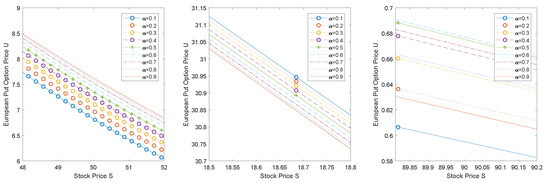
Figure 2.
European put option prices at the terminal time T with for different values.
5.2. American Options
For American put options, we use the same parameters as in (39). Table 4 compares the values of American put options obtained by the RBF-FD-IL1 method coupled with the operator splitting method (RBF-FD-IL1-OS) and the FD-L1 method combined with the operator splitting method (FD-L1-OS). From the table, we can see that they are in good agreement. Table 5 and Table 6 present the numerical error and the order of convergence for our numerical scheme with different values of . It can be seen from these tables that the order of convergence for the proposed numerical scheme is almost , while the FD-L1-OS method in Chen et al. [27] is only first-order accurate when . Further, Figure 3 shows the numerical solutions of American put options for and , and Figure 4 displays the option prices at the terminal time T with different values of for the parameter set (41). The optimal exercise prices with different values of are presented in Figure 5.

Table 4.
Values of American put options using the RBF-FD-IL1-OS and FD-L1-OS methods, where M and N are the number of points in S and t, respectively.

Table 5.
The numerical error for American put options using the RBF-FD-IL1-OS method with .

Table 6.
The order of convergence for American put options using the RBF-FD-IL1-OS method with .
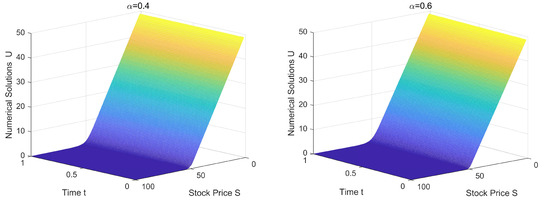
Figure 3.
Numerical solutions of American put options with for and .
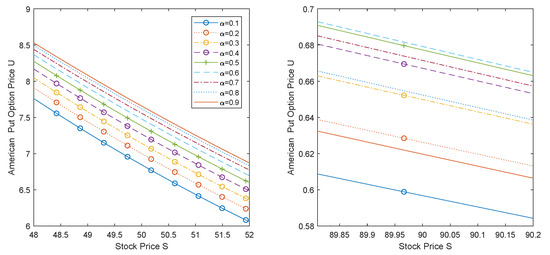
Figure 4.
American put option prices at the terminal time T with for different values.
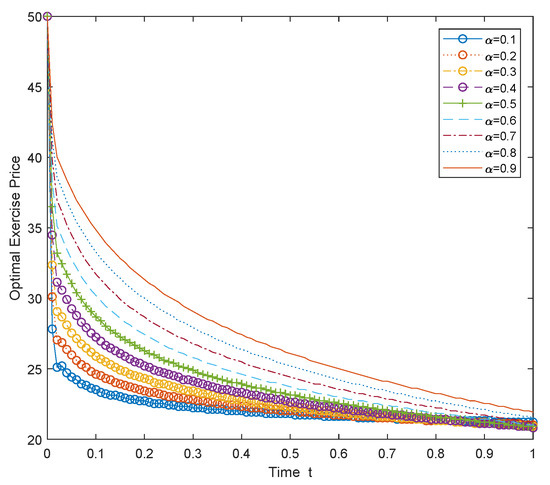
Figure 5.
Optimal exercise prices for American put options with different values.
6. Conclusions
In this paper, we investigate the numerical valuation of European and American options under the time fractional Black-Scholes model. The radial basis function finite difference discretization with a coordinate stretching transformation in space coupled with the improved L1 scheme is introduced for European options. The operator splitting method is proposed for American options. The proposed scheme leads to a sparse linear system, which is trivial to solve. Moreover, we prove that the proposed numerical scheme is unconditionally stable for European options. Numerical experiments demonstrate that a order convergence in time is attained, which improves the results of Chen et al. [27]. The option prices and optimal exercise prices with different values of for American options are presented. We can observe that the proposed method is very accurate and efficient. The numerical technique presented in this paper can be extended to other higher dimensional fractional models for pricing European and American options.
Author Contributions
P.Y.: conceptualization, methodology, software, validation, writing—original draft preparation, writing—review and editing; Z.X.: conceptualization, methodology, funding acquisition, supervision, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 12071479), and the Outstanding Innovative Talents Cultivation Funded Programs 2019 of Renmin University of China.
Acknowledgments
The authors thank the referees for their comments and detailed suggestions. These have significantly improved the presentation of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Merton, R.C. Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef] [Green Version]
- Kou, S.G. A jump-diffusion model for option pricing. Manag. Sci. 2002, 48, 1086–1101. [Google Scholar] [CrossRef] [Green Version]
- Cox, J.C.; Ross, S.A. The valuation of options for alternative stochastic processes. J. Financ. Econ. 1976, 3, 145–166. [Google Scholar] [CrossRef]
- Hull, J.; White, A. The pricing of options on assets with stochastic volatilities. J. Financ. 1987, 42, 281–300. [Google Scholar] [CrossRef]
- Stein, E.M.; Stein, J.C. Stock price distributions with stochastic volatility: An analytic approach. Rev. Financ. Stud. 1991, 4, 727–752. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef] [Green Version]
- Wyss, W. The fractional Black-Scholes equation. Fract. Calc. Appl. Anal. 2000, 3, 51–61. [Google Scholar]
- Cartea, A.; del-Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Physical A 2007, 2, 749–763. [Google Scholar] [CrossRef] [Green Version]
- Jumarie, G. Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black-Scholes equations. Insur. Math. Econ. 2008, 42, 271–287. [Google Scholar] [CrossRef]
- Liang, J.R.; Wang, J.; Zhang, W.J.; Qiu, W.Y.; Ren, F.Y. The solution to a bi-fractional Black–Scholes–Merton differential equation. Int. J. Pure Appl. Math. 2010, 58, 99–112. [Google Scholar]
- Aguilar, J.P.; Kirkby, J.L.; Korbel, J. Pricing, risk and volatility in subordinated market models. Risks 2020, 8, 124. [Google Scholar] [CrossRef]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef] [Green Version]
- Carr, P.; Wu, L. The finite moment log stable process and option pricing. J. Financ. 2003, 58, 753–777. [Google Scholar] [CrossRef] [Green Version]
- Carr, P.; Geman, H.; Madan, D.; Yor, M. Stochastic volatility for Lévy processes. Math. Financ. 2003, 13, 345–382. [Google Scholar] [CrossRef] [Green Version]
- Koponen, I. Analytic approach to the problem of convergence of truncated Lévy flights towards the Gaussian stochastic process. Phys. Rev. E. 1995, 52, 1197–1199. [Google Scholar] [CrossRef]
- Boyarchenko, S.I.; Levendorskiǐ, S.Z. Non-Gaussian Merton-Black-Scholes Theory; World Scientific: Singapore, 2002. [Google Scholar]
- Jumarie, G. Derivation and solutions of some fractional Black Scholes equations in coarse-grained space and time. Application to Mertons optimal portfolio. Comput. Math. Appl. 2010, 59, 1142–1164. [Google Scholar] [CrossRef] [Green Version]
- Kleinert, H.; Korbel, J. Option pricing beyond Black-Scholes based on double-fractional diffusion. Physical A 2016, 449, 200–214. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liu, F.; Chen, S.; Anh, V.; Chen, J. Fast numerical simulation of a new time-space fractional option pricing model governing European call option. Appl. Math. Comput. 2018, 339, 186–198. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, J.P.; Korbel, J.; Pesci, N. On the quantitative properties of some market models involving fractional derivatives. Mathematics 2021, 9, 3198. [Google Scholar] [CrossRef]
- Song, L.; Wang, W. Solution of the fractional Black-Scholes option pricing model by finite difference method. Abstr. Appl. Anal. 2013, 2013, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liu, F.; Turner, I.; Yang, Q. Numerical solution of the time fractional Black-Scholes model governing European options. Comput. Math. Appl. 2016, 71, 1772–1783. [Google Scholar] [CrossRef]
- De Staelen, R.H.; Hendy, A.S. Numerically pricing double barrier options in a time-fractional Black-Scholes model. Comput. Math. Appl. 2017, 74, 1166–1175. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical solution of time-fractional Black-Scholes equation. Comput. Appl. Math. 2017, 36, 1699–1715. [Google Scholar] [CrossRef]
- Golbabai, A.; Nikan, O.; Nikazad, T. Numerical analysis of time fractional Black-Scholes European option pricing model arising in financial market. Comput. Appl. Math. 2019, 38, 173. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Z.; Yang, Y. A new operator splitting method for American options under fractional Black-Scholes models. Comput. Math. Appl. 2019, 77, 2130–2144. [Google Scholar] [CrossRef]
- Farhadi, A.; Salehi, M.; Erjaee, G.H. A new version of Black–Scholes equation presented by time-fractional derivative. Iran. J. Sci. Technol. A. 2018, 42, 2159–2166. [Google Scholar] [CrossRef]
- Huang, J.; Cen, Z.; Zhao, J. An adaptive moving mesh method for a time-fractional Black-Scholes equation. Adv. Differ. Equ. 2019, 2019, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Almushaira, M.; Chen, F.; Liu, F. Efficient operator splitting and spectral methods for the time-space fractional Black-Scholes equation. Resul. Appl. Math. 2021, 10, 100149. [Google Scholar] [CrossRef]
- Haghi, M.; Mollapourasl, R.; Vanmaele, M. An RBF-FD method for pricing American options under jump-diffusion models. Comput. Math. Appl. 2018, 76, 2434–2459. [Google Scholar] [CrossRef] [Green Version]
- Bayona, V.; Moscoso, M.; Carretero, M.; Kindelan, M. RBF-FD formulas and convergence properties. J. Comput. Phys. 2010, 229, 8281–8295. [Google Scholar] [CrossRef]
- Saib, A.A.E.F.; Tangman, D.Y.; Bhuruth, M. A new radial basis functions method for pricing American options under Merton’s jump-diffusion model. Inter. J. Comput. Math. 2012, 89, 1164–1185. [Google Scholar] [CrossRef]
- Soleymani, F.; Zhu, S. RBF-FD solution for a financial partial-integro differential equation utilizing the generalized multiquadric function. Comput. Math. Appl. 2021, 82, 161–178. [Google Scholar] [CrossRef]
- Chen, W.; Xu, X.; Zhu, S. Analytically pricing double barrier options based on a time-fractional Black-Scholes equation. Comput. Math. Appl. 2015, 69, 1407–1419. [Google Scholar] [CrossRef]
- Ford, N.J.; Yan, Y. An approach to construct higher order time discretisation schemes for time fractional partial differential equations with nonsmooth data. Fract. Calc. Appl. Anal. 2017, 20, 1076–1105. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).