Novel Patterns in Fractional-in-Space Nonlinear Coupled FitzHugh–Nagumo Models with Riesz Fractional Derivative
Abstract
:1. Introduction
2. Numerical Method
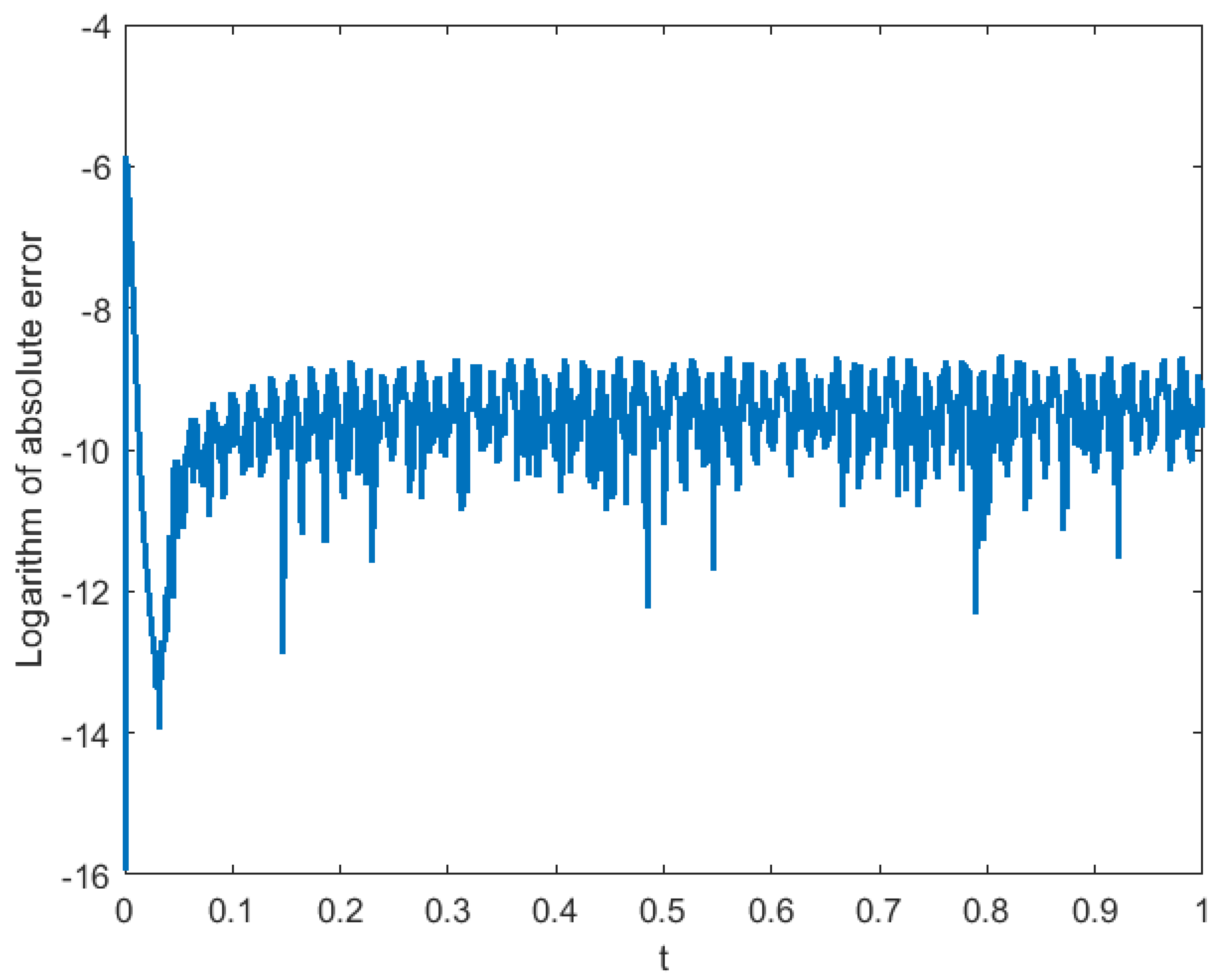
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Tan, W.; Xu, M. Plane surface suddenly set in motion in a viscoelastic fluid with fractional Maxwell model. Acta Mech. Sin. 2002, 18, 342–349. [Google Scholar]
- Scott-Blair, G.W. The role of psychophysics in rheology. J. Colloid Sci. 1947, 2, 21–32. [Google Scholar] [CrossRef]
- Ding, C.; Cao, J.; Chen, Y.Q. Fractional-order model and experimental verification for broadband hysteresis in piezoelectric actuators. Nonlinear Dyn. 2019, 98, 3143–3153. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J.; Blumen, A. Fractional kinetics. Phys. Today 2002, 55, 48–54. [Google Scholar] [CrossRef]
- Gerasimov, A.N. A generalization of linear laws of deformation and its application to inner friction problems. Prikl. Math. Mekh. 1948, 12, 251–259. [Google Scholar]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Metzler, R.; Glockle, W.G.; Nonnenmacher, T.F. Fractional model equation for anomalous diffusion. Phys. A Stat. Mech. Its Appl. 1994, 211, 13–24. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, M.; Qi, H. The fractional diffusion model with an absorption term and modified Fick’s law for non-local transport processes. Nonlinear Anal. Real World Appl. 2010, 11, 262–269. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems in Physics: The Decomposition Method; Kluwer Academic: Boston, MA, USA, 1994. [Google Scholar]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations differential equations. J. Math. Anal. Appl. 2006, 316, 321–354. [Google Scholar] [CrossRef] [Green Version]
- He, J.H.; El-Dib, Y.O.; Mady, A.A. Homotopy perturbation method for the fractal toda oscillator. Fractal Fraction 2021, 5, 93. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, J.; Bu, W.; Xiao, A. A fast finite difference/finite element method for the two-dimensional distributed-order time-space fractional reaction-diffusion equation. Int. J. Model. Simul. Sci. Comput. 2020, 11, 2050016. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Sukale, Y.; Bhalekar, S. A new predictor-corrector method for fractional differential equations. Appl. Math. Comput. 2014, 244, 158–182. [Google Scholar] [CrossRef]
- Jhinga, A.; Daftardar-Gejji, V. A new finite difference predictor-corrector method for fractional differential equations. Appl. Math. Comput. 2018, 336, 418–432. [Google Scholar] [CrossRef]
- Wang, Y.L.; Jia, L.N.; Zhang, H.L. Numerical solution for a class of space-time fractional equation in reproducing. Int. J. Comput. Math. 2019, 96, 2100–2111. [Google Scholar] [CrossRef]
- Dai, D.D.; Ban, T.T.; Wang, Y.L.; Zhang, W. The piecewise reproducing kernel method for the time variable fractional order advection-reaction-diffusion equations. Therm. Sci. 2021, 25, 1261–1268. [Google Scholar] [CrossRef]
- Podlubny, I. Matrix approach to discrete fractional calculus. Fract. Calc. Appl. Anal. 2000, 3, 359–386. [Google Scholar]
- Wang, J.J.; Xiao, A.G. Conservative Fourier spectral method and numerical investigation of space fractional Klein-Gordon-Schrödinger equations. Appl. Math. Comput. 2019, 350, 348–365. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, B.; Zhang, P.; Zhang, W.; Liu, F. Fourier spectral method for the modified Swift-Hohenberg equation. Adv. Differ. Equ. 2013, 2013, 156. [Google Scholar] [CrossRef] [Green Version]
- Bueno-Orovio, A.; Kay, D.; Burrage, K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. Bit Numer. Math. 2014, 54, 937–954. [Google Scholar] [CrossRef]
- Pelz, R.B. Fourier spectral method on ensemble architectures. Comput. Methods Appl. Mech. Eng. 1991, 89, 529–542. [Google Scholar] [CrossRef]
- Xue, D.Y. Fractional Calculus and Fractional-Order Control; Science Press: Beijing, China, 2018. [Google Scholar]
- Owolabi, K.M.; Atangana, A. Numerical Methods for Fractional Differentiation; Springer: Singapore, 2019. [Google Scholar]
- Atangana, A.; Alqahtani, R.T. New numerical method and application to Keller-Segel model with fractional order derivative. Chaos Solitons Fractals 2018, 116, 14–21. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett. 2015, 47, 54–60. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Podlubny, I. Geometric and physical interpretations of fractional integration and differentiation. Fract. Calc. Appl. Anal. 2001, 5, 230–237. [Google Scholar]
- Yang, X.J. General Fractional Derivatives: Theory, Methods and Applications; CRC Press: New York, NY, USA, 2019. [Google Scholar]
- Han, C.; Wang, Y.L.; Li, Z.Y. Numerical solutions of space fractional variable-coefficient KdV-modified KdV equation by Fourier spectral method. Fractals 2021, 29, 2150246. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.L.; Li, Z.Y. A high-precision numerical approach to solving space fractional Gray-Scott model. Appl. Math. Lett. 2022, 125, 107759. [Google Scholar] [CrossRef]
- Fitzhugh, R. Mathematical models of threshold phenomena in the nerve membrane. Bull. Math. Biophys. 1995, 17, 257–269. [Google Scholar] [CrossRef]
- Nagumo, J.; Arimoto, S.; Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. IRE 1962, 50, 2061–2070. [Google Scholar] [CrossRef]
- Magin, R.L.; Abdullah, O.; Baleanu, D.; Zhou, X.J. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J. Magn. Reson. 2008, 190, 255–270. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Mortensen, J.; Wheatcraft, S.W. Fractional vector calculus for fractional advection-dispersion. Phys. A Stat. Mech. Its Appl. 2006, 367, 181–190. [Google Scholar] [CrossRef]
- Liu, F.W.; Zhuang, P.H.; Turner, I.; Anh, V.; Burrage, K. A semi-alternating direction method for a 2-D fractional FitzHugh-Nagumo monodomain model on an approximate irregular domain. J. Comput. Phys. 2015, 293, 252–263. [Google Scholar] [CrossRef] [Green Version]
- Lee, G.H. A second-order operator splitting Fourier spectral method for fractional-in-space reaction-diffusion equations. J. Comput. Appl. Math. 2018, 33, 395–403. [Google Scholar] [CrossRef]
- Wang, T.T.; Song, F.Y.; Wang, H.; Karniadakis, G.E. Fractional Gray-Scott model: Well-posedness, discretization, and simulations. Comput. Methods Appl. Mech. Eng. 2019, 347, 1030–1049. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Fan, E.Y.; Yin, B.L.; Li, H.; Wang, J. TT-M finite element algorithm for a two-dimensional space fractional Gray-Scott model. Comput. Math. Appl. 2020, 80, 1793–1809. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X.Y.; Zeng, F.H.; Karniadakis, G.E. A stabilized semi-implicit Fourier spectral method for nonlinear space-fractional reaction-diffusion equations. J. Comput. Phys. 2019, 405, 109141. [Google Scholar] [CrossRef] [Green Version]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Atanackovic, T.M.; Pilipovic, S.; Stankovic, B.; Zorica, D. Fractional Calculus with Applications in Maechanics; John Willey Sons Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ruiz-Ramirez, J.; Macias-Diaz, J.E. A finite-difference scheme to approximate non-negative and bounded solutions of a FitzHugh-Nagumo equation. Int. J. Comput. Math. 2011, 88, 3186–3201. [Google Scholar] [CrossRef]
- INan, B.; Ali, K.K.; Saha, A.; Ak, T. Analytical and numerical solutions of the Fitzhugh-Nagumo equation and their multistability behavior. Numer. Methods Partial Differ. Equ. 2021, 37, 7–23. [Google Scholar] [CrossRef]
- Engler, H. On the speed of spread for fractional reaction-diffusion equations. Int. J. Differ. Equ. 2010, 315, 315–421. [Google Scholar] [CrossRef] [Green Version]

















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Han, C.; Wang, Y. Novel Patterns in Fractional-in-Space Nonlinear Coupled FitzHugh–Nagumo Models with Riesz Fractional Derivative. Fractal Fract. 2022, 6, 136. https://doi.org/10.3390/fractalfract6030136
Li X, Han C, Wang Y. Novel Patterns in Fractional-in-Space Nonlinear Coupled FitzHugh–Nagumo Models with Riesz Fractional Derivative. Fractal and Fractional. 2022; 6(3):136. https://doi.org/10.3390/fractalfract6030136
Chicago/Turabian StyleLi, Xiaoyu, Che Han, and Yulan Wang. 2022. "Novel Patterns in Fractional-in-Space Nonlinear Coupled FitzHugh–Nagumo Models with Riesz Fractional Derivative" Fractal and Fractional 6, no. 3: 136. https://doi.org/10.3390/fractalfract6030136
APA StyleLi, X., Han, C., & Wang, Y. (2022). Novel Patterns in Fractional-in-Space Nonlinear Coupled FitzHugh–Nagumo Models with Riesz Fractional Derivative. Fractal and Fractional, 6(3), 136. https://doi.org/10.3390/fractalfract6030136






