Abstract
In this article, unsteady free convective heat transport of copper-water nanofluid within a square-shaped enclosure with the dominance of non-uniform horizontal periodic magnetic effect is investigated numerically. Various nanofluids are also used to investigate temperature performance. The Brownian movement of nano-sized particles is included in the present model. A sinusoidal function of the y coordinate is considered for the magnetic effect, which works as a non-uniform magnetic field. The left sidewall is warmed at a higher heat, whereas the right sidewall is cooled at a lower heat. The upper and bottom walls are insulated. For solving the governing non-linear partial differential equation, Galerkin weighted residual finite element method is devoted. Comparisons are made with previously published articles, and we found there to be excellent compliance. The influence of various physical parameters, namely, the volume fraction of nanoparticles, period of the non-uniform magnetic field, Rayleigh number, the shape and diameter of nanoparticles, and Hartmann number on the temperature transport and fluid flow are researched. The local and average Nusselt number is also calculated to investigate the impact of different parameters on the flow field. The results show the best performance of heat transport for the Fe3O4-water nanofluid than for other types of nanofluids. The heat transport rate increases 20.14% for Fe3O4-water nanofluid and 8.94% for TiO2-water nanofluid with 1% nanoparticles volume. The heat transportation rate enhances with additional nanoparticles into the base fluid whereas it decreases with the increase of Hartmann number and diameter of particles. A comparison study of uniform and non-uniform magnetic effects is performed, and a higher heat transfer rate is observed for a non-uniform magnetic effect compared to a uniform magnetic effect. Moreover, periods of magnetic effect and a nanoparticle’s Brownian movement significantly impacts the temperature transport and fluid flow. The solution reaches unsteady state to steady state within a very short time.
1. Introduction
Nanofluids are a novel fluid class with a higher thermal conductivity than conventional fluids. Nanofluids are formed by using nanoparticles with a size of 1–100 nm, which are made from different materials and base fluids, for example, Au, Ag, Cu, SiC, TiC, CuO, Al2O3, SiN, TiO2, pump oil, ethylene glycol, water, engine oil, glycerol, etc. Choi [1,2] first introduced this new novel class of fluids. Different researchers [3,4,5,6,7] investigated the convective heat transfer of different nanofluids with different conditions and its various applications. Khan et al. [8] investigated numerical investigation of second order velocity flow of micropolar ferrofluid inside a permeable medium. Khan et al. [9] also performed chemical reaction of energy diffusion flow of non-Newtonian nano-sized material with Brownian diffusion. They showed that MHD encounters heat transport. Khan et al. [10] also researched entropy generation of hybrid nanomaterials considering Brownian movement and thermophoresis. They found that the temperature transport rate rises with the maximum Eckert number. Hayat et al. [11] performed impact of magnetic and thermal radiation of viscous liquid inside the boundary layer flow. They found that the heat enhances and the velocity diminishes with the increment of magnetic nanoparticles. Hayat et al. [12] also investigated ferromagnetic nano-sized particles flow considering thermophoretic and Brownian movement. They showed that the velocity profile is larger for a higher value of thermophoresis variables. Mahian et al. [13,14] investigated mathematical modeling of nanofluids and its simulation. Shah et al. [15] investigated time-dependent flow of nanofluids with various conventional fluids considering electrically conducting nanoparticles. Rahman et al. [16] performed magneto-hydrodynamics convective flow of nanofluids within the triangular cavity. The outcome predicted that the Brownian effects of the nanoparticles and the nanoparticle diameter significantly impact the temperature transport. Kalbani et al. [17] performed the buoyancy-driven heat transport of different nanofluids with various shape factors of nanoparticles within the cavity with magnetic effects. Higher temperature transmission is audited for the particles of blade shape compared to another shape of nanoparticles. Mojumder et al. [18] studied convective temperature transport in a half-moon-shaped enclosure charged by the ferrofluid. The results show that heat transportation diminishes with a higher magnetic effect.
Natural convective temperature transport has become an essential topic to the researcher. It has wide applications such as nuclear waste management, electronic equipment cooling, biomedical systems, chemical reactors, heat exchangers, medicine-drug delivery, solar thermal systems, photovoltaic systems, car radiators, refrigerators, and boilers, etc. Parveen and Mahapatra [19] studied the convective flow within a square vessel with magnetic effects. The outcome depicted that heat transport augments with additional nanoparticles into base fluid and higher Rayleigh number. Dogonchi et al. [20] performed convection temperature transport of water-copper nanofluids by employing a magnetic field. They investigated how the streamline strength diminishes with the increment of the buoyancy-driven parameter. Billah et al. [21] performed time-dependent temperature transport augmentation of nanofluids in a triangle shape cavity. Li et al. [22] performed a convective flow of a nanofluid within the square vessel through the magnetic field. The result predicted that the heat transport rate reduces with the Hartmann number, whereas it increases with the additional nanoparticles. Basak et al. [23] researched the natural convective flow of the nanofluid in the cavity, including both non-uniform and uniform thermal systems. Al-Weheibi et al. [24] researched the free convectional temperature transport of nanofluids. They show that additional nanoparticles and their size have a dominant influence on temperature transport. Alam et al. [25] investigated the convection flow of kerosene-cobalt nanofluid considering the Brownian movement of particles.
By magnetic effects, convection heat transport has practical engineering applications in areas such as biomechanics, healthcare devices, microscope design, etc. Mehryan et al. [26] performed the convective temperature transport of ferrofluid with the effect of periodic magnetic effect. Haq and Aman [27] studied how the additional nano-sized particles into the base fluid diminishes the temperature transport rate and reverse with higher Rayleigh number. Chamkha et al. [28] researched copper-water nanofluid flow by the dominance of magneto-hydrodynamics. The results show that more particles into base liquid reduce the temperature transfer rate. Uddin [29] also studied the hydrodynamic natural convective temperature transport of Cu-H2O nanofluid in the semicircular enclosure. Zahan et al. [30] performed the temperature transport in the chamber for the different parameters with magnetic effect. The outcome predicted that the performance of temperature flow diminishes with the higher Hartmann number. Abedini et al. [31] researched the convection temperature transport of nanofluids for uniform magnetic effect. Marzougui et al. [32] performed magneto-hydrodynamics convection temperature transport of Cu-H2O nanofluid. Balushi and Rahman [33] studied the convective heat transport of nanofluids with magnetic fields. The result predicted that the addition of nanoparticles intensifies the average temperature flow rate and kerosene-based nanofluids perform better heat transfer. Al-Kalbani and Rahman [34] investigated the convection heat transport of nanofluids by various nanoparticles, including the nanoparticles’ Brownian movement. The results showed that the temperature flow depends on Hartmann number and nanoparticles size.
Recently, Dutta et al. [35] performed free convection temperature transport of nanofluids by the impression of non-uniform heated boundary system in the rhombic enclosure. Uddin and Rasel [36] investigated the convective heat transport of nanofluids in the quadrilateral cavity by the magnetic field. Uddin et al. [37] also researched the convective temperature transport of nanofluids in a square vessel with a magnetic effect. Islam et al. [38,39,40] conducted MHD convective temperature transport of nanofluids with various geometries and heated systems. Mullick et al. [41] performed the convective flow of nanofluid inside the chamber. Rostami et al. [42] performed the heat transport phenomenon of magnetic nanoparticles. The thermal performance of Al2O3 nanoparticles was performed by Alsabery et al. [43]. The result showed that the size of the particles enhances the temperature flow rate. Uddin and Rahman [44] also performed the heat transportation of nanofluids within triangular cavities. Qayyum et al. [45] studied a comparison study of viscous liquid including Joule heating for various nano-sized particles. They showed that higher temperature transport is conformed for water-silver nanofluid. Gireesha et al. [46] investigated free convectional flowing of hybrid nanofluids. They found that the temperature transport rate is greater for a convective fin than an insulated fin. Waqas et al. [47] performed convective energy transport of viscoelastic nanofluid. They showed the impact of convective conditions and viscous dissipation and opposite behavior of radiation against thermal field. Mansour et al. [48] investigated time-dependent convective of nanofluids in a chamber. They found that MHD has a significant impact on streamlines and isotherms. Alsoy-Akgün et al. [49] performed influence of uniform MHD on time-dependent free convectional flow of nanofluids. The results showed that MHD and Rayleigh number influence the flow behavior. By assessing the literature papers [50,51,52,53,54,55,56,57], it has been found that convection and finite element methods are described.
Therefore, this study investigated the natural convection flow and temperature transport of nanofluids into a square enclosure with the dominance of periodic magnetic effects, including the nanoparticles’ Brownian movement. The magnetic field can create an encounter with the physical environment that can affect any chemical and physical processes, which can be useful in material processes, heat exchangers, and other scientific research. The periodic magnetic field can create a periodic force. This periodic magnetic field is used in water evaporation, silver deposition, and protein crystallization, etc. The encountered periodic forces of the sinusoidal magnetic field are the key to the differences in temperature between the non-uniform (sinusoidal) magnetic field and uniform MHD. The Brownian movement of nano-sized particles has various applications in natural random phenomena such as flower pollen in water, chaotic oscillations of microscopic objects, etc. Therefore, the buoyancy introduced heat transfer in the square enclosure is a crucial engineering phenomenon with direct applications in solar thermal collectors, heat exchangers, nuclear reactors, cooling of electronic devices, and greenhouses. Therefore, this work has engineering importance and practical applications in the natural field. Thus, the heat transfer in a square enclosure is analyzed in the present study to visualize the heat flow and find an efficient way of transferring heat in the chamber under the influence of the periodic MHD effect. The results of various parameters such as nanoparticle diameter, the nanoparticles volume, Rayleigh number, Hartmann number, and nanoparticles diameter by streamline contours, isothermal lines, and Nusselt number are investigated numerically.
2. Physical and Mathematical Model
We consider a time-dependent two-dimensional free convective flow of nanofluids inside a square enclosure, where copper (Cu) is taken as the nanoparticles and water (H2O) is taken as the base fluid, considering that the nano-sized particles are dispersed into the base fluid homogenously. The other type of nano-sized particles and base fluid are considered in this study. The upper and bottom walls are insulated. The right vertical sidewall is cooled at lower heat Tc, whereas the left vertical side is warmed at higher heat Th (Tc < Th). The magnetic field is employed non-uniformly, which is horizontally periodic. The relation of the magnetic term is represented by , where B0 represents the periodic magnetic field amplitude and represents the magnetic field period. It is also assumed that no thermal and no dynamical slip occurs within the base fluid and nanoparticles. The acceleration of gravitational force works at the negative y-axis. All rigid boundaries are supposed as no-slip walls. The coordinate systems and geometry are schematically represented in Figure 1, where x and y represent the Cartesian coordinates. The properties of different nano-sized particles and water are given in Table 1. Moreover, six types of nanofluids are deliberated to survey the best performance of temperature transport augmentation compared to the base fluid.
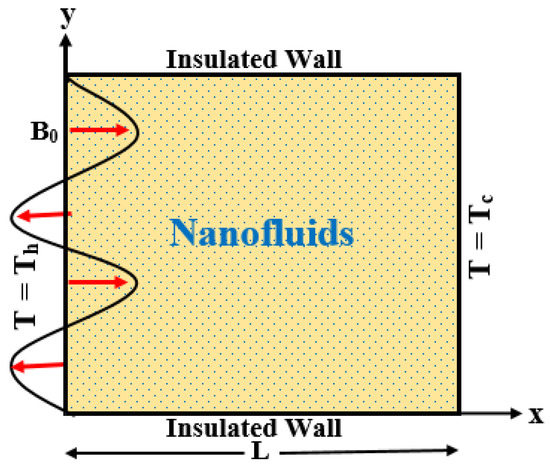
Figure 1.
Schematic flow configuration and geometry.

Table 1.
Thermo-physical properties of the different nanoparticles and base fluids (see [17,24]).
To drive the nonlinear governing PDEs in dimensional form for this study, we apply the aforementioned considerations as follows (see Al-Weheibi et al. [24], Mehryan et al. [26]):
Continuity equation [24,26,49]:
.
Momentum equation in x direction [24,26,49]:
Momentum equation in y direction [24,26,49]:
Energy equation [17,24,26,49]:
The usual meanings of the symbols are listed in the nomenclature.
2.1. Dimensional Boundary Conditions
For the above narrated model, the boundary conditions are represented as:
For ; entire domain:
.
For ;
At the left vertical sidewall:
At the right vertical sidewall:
At the top and bottom walls:
2.2. Physical and Thermal Properties of Nanofluids
The nanofluid properties, namely density, thermal diffusivity, thermal conductivity, electrical conductivity, heat capacitance, and thermal expansion coefficient, are enlisted below for the present calculations (Al-Balushi et al. [33]).
where the values of n in Equation (11), i.e., n = 8.6, 5.7, 4.9, 3.7, 3, represents blade, platelet, brick, cylinder, and sphere shape nanoparticles, respectively. The first term of the right-hand of Equation (11) describes Maxwell’s static part. The second part represents the Brownian part where the irregular motion of suspended nanoparticles has been taken into account, including particle size, nanoparticles volume, and temperature of the mixture where KB represents the Boltzmann constant and dp represents size of nanoparticles where KB represents the Boltzmann constant and dp represents the size of the nanoparticles.
2.3. Dimensional Analysis
The following dimensionless variables are introduced in the current investigation to convert the governing Equations (1)–(4), including boundary conditions (5)–(8), into dimensionless form.
We employ Equation (15) into (1)–(4) and (5)–(8) as follows:
The dimensionless boundary condition becomes
For ; entire domain:
.
For ;
On the left vertical sidewall:
.
On the right vertical sidewall:
.
On the top and bottom walls:
.
For this model, the local Nusselt number along the left vertical warmed sidewall is defined as:
The average Nusselt number on the left vertical warmed sidewall is defined as:
3. Computational Procedure
The square cavity is discretized into many triangle shape elements, where the governing Equations (16)–(19), including the boundary conditions (20)–(23), are employed for the numerical calculations. The Galerkin weighted residual finite element technique has been employed for solving this model. This numerical method is narrated well in the text of Zienkiewicz and Taylor [58]. The domain of the solution is discretized within a limited number of grids, firstly determined from non-uniform three-cornered elements in this method. A triangular component of six nodes is exercised for the improvement of the finite element equations. The Galerkin weighted residual method is appointed, which transfers Equations (16)–(17) into the integral equation system. Integral parts of these equations are accomplished, employing Gauss’s quadrature technique. After that, boundary conditions are also used to modify the nonlinear algebraic equations. To solve these algebraic equations in matrix form, Newton-Raphson iteration is devoted. The convergent criteria for the numerical solution procedure have been estimated as , where Γ represents the subordinate variables, U, V, θ, and n represents the iteration number.
3.1. Grid Independence Test
A comprehensive grid testing procedure has been devoted for the square cavity of the current problem when ϕ = 0.04, Ha = 30, Ra = 105, d = 10 nm and n = 3. Five different non-uniform grid systems containing element numbers 1726, 2790, 7192, 18,206, and 27,510 are examined in this study. For the element numbers mentioned earlier, the Average Nusselt number (Nuav) has been calculated for checking the development of fineness of the grid. In this study, the element size 18,206 depicts an ordinary variety of outcomes concerning the average Nusselt number (Nuav) with other elements, 27,510, presented in Figure 2. Therefore, the element size 18,206 is employed for a grid-independent solution.
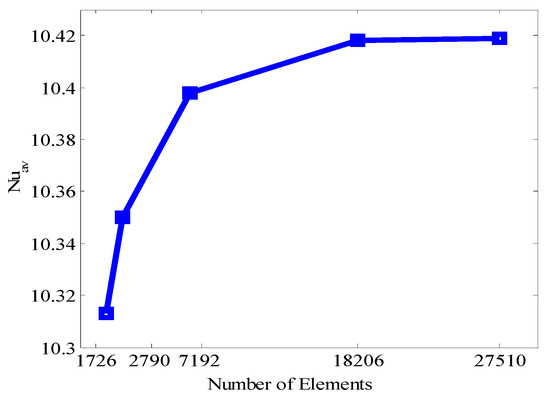
Figure 2.
Grid sensitivity test.
3.2. Validation of Code
For verifying the present numerical code, the average Nusselt number (Nuav) has been obtained from the current numerical code by Ghasemi et al. [50] for the steady-state case. Ghasemi et al. [50] studied the two-dimensional free convection flow of Al2O3-water nanofluid in the square cavity. The current numerical code is transferred into the Al2O3-water nanofluids charged inside the square chamber. The mean Nusselt number for the nanoparticles volume and Hartmann number has been presented in Table 2. This validation motivates us, as it shows an excellent agreement to use the present numerical code for the current investigation.

Table 2.
Comparison of average Nusselt number (Nuav) of the current code with Ghasemi et al. [50] for different nanoparticles volume (ϕ), and Hartmann number (Ha) when Ra = 105.
4. Results and Discussion
In this study, an unsteady natural convectional temperature transport in Cu-H2O nanofluids under the influence of a non-uniform horizontally periodic magnetic field has been analyzed numerically. More than six types of nanofluids have also been used to examine the best performance of enhancing temperature transport compared to the base fluid. The value of the Prandtl number (Pr = 6.8377) is constant for copper-water nanofluid and it is varied with other nanofluids. The range of the values of the model dimensionless physical parameters are the Hartmann number (0 ≤ Ha ≤ 80), Rayleigh number (103 ≤ Ra ≤ 106), nanoparticles volume fraction (0 ≤ ϕ ≤ 0.1), period of magnetic field (0.1 ≤ λ ≤ 1), and nanoparticles diameter (1 nm ≤ d ≤ 100 nm). The streamline contours, isotherms, and local and mean Nusselt numbers are calculated to understand the impact of different non-dimensional physical parameters on temperature transport. The square enclosure is essential because it is a common physical problem in different engineering applications. For example, it is very commonly used in the thermal collector, heat exchangers, etc. Furthermore, we know that the buoyancy introduced heat transfer is a crucial engineering phenomenon with direct applications in solar thermal collectors, heat exchangers, nuclear reactors, cooling of electronic devices, and greenhouses. Therefore, this work has engineering importance and practical applications in the natural field. Thus, the heat transfer in a square enclosure is analyzed in the present study to visualize the heat flow and find an efficient way of transferring heat in the chamber under the influence of the periodic MHD effect.
Figure 3 illustrates the variation in the streamlines with the period of the magnetic effect and Hartmann number when ϕ = 0.04, Ra = 106, n = 3, and d = 10 nm. The outcome shows that the classical natural convection occurs inside the enclosure at Hartmann number Ha = 0, but the patterns of the streamlines completely change by employing magnetic effects. A strong counteraction force is generated by Lorentz forces of the applied magnetic field for the increment of Ha, and as a result, the flow circulation diminishes. Furthermore, the flow circulation changes from horizontal to vertical state with the increment of the Hartmann number (Ha). Furthermore, an interesting pattern of the streamlines is seen for the changes of the period of the magnetic effect (λ). The streamline figure for uniform magnetic field (umf) is listed in the first row of Figure 3. At low period λ (λ = 0.1), the streamlines are almost similar to the uniform magnetic field because the volume force employed by the low periodic magnetic effect and the uniform magnetic field is almost the same. At λ = 0.1, the streamlines neighboring the vertical walls are deviated from the straight lines because of the gradient of the interchanging magnitude of Lorentz forces employed by the flow field along the y coordinate. Consequently, the streamlines create a sawtooth form. With the increase of the period of the magnetic field (λ), the Lorentz force gradient decreases along the vertical walls, and the streamline patterns become straight lines. Moreover, the circulation strength within the enclosure is enhanced by amplifying the period of the magnetic effect because. With the increase of λ, the average Lorentz forces in the flow field diminishes. The streamlines are more squeezed near the hot wall for λ = 0.25, and λ = 0.5. For the period λ = 1, two symmetrical vortex cells are generated neighborly in the cavity’s bottom and upper regions. Furthermore, at the period λ = 0.25, three central circulation cells with similar patterns are seen for a higher Hartmann number (Ha).

Figure 3.
Effect of streamline contours for various Hartmann number (Ha) for (a) uniform magnetic field (umf), (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ra = 106, d = 10 nm, ϕ = 0.04, n = 3, Pr = 6.8377, and τ = 1.
The influence of isotherms on Hartmann number (Ha) and magnetic field period (λ) is represented in Figure 4 when Ra = 106, ϕ = 0.04, and τ = 1. The isothermal lines change their direction from a horizontal to a vertical state with the increase of Ha, which represents convection as the principal mode of temperature transport. In addition, the denseness of the isotherms at the down and top of the warm and cold walls, respectively, increases with the decrease of magnetic effect (Ha). At λ = 0.1, the denseness of isotherms increases the neighbor warmed wall compared to the uniform magnetic effect since the convective temperature transport is enriched in that region, and the rate of temperature transfer is also increased. At λ = 0.25 and λ = 0.5, the isotherm contours become a waveform under employed sinusoidal Lorentz force on the flow domain. The compactness of isotherm contours is also enhanced at the neighboring hot wall. At λ = 1, a horizontal state of isothermal lines is observed because of the existence of two vortices of streamlines (Figure 3) at the upper and lowermost sides within the enclosure. However, the isothermal lines become a vertical state at the cavity center for a higher Hartman number, caused by the dominance of conductive heat transport. The magnetic field is useful in material processes, heat exchangers, and various scientific research. The periodic magnetic field can create a periodic force. This periodic magnetic field is used in water evaporation, silver deposition, and protein crystallization, etc.
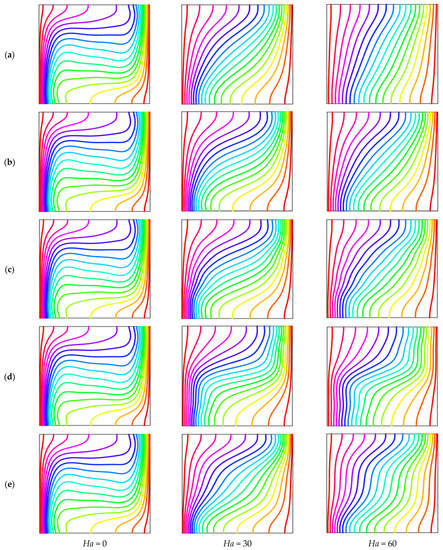
Figure 4.
Effect of isotherms for various Hartmann number (Ha) for (a) uniform magnetic field (umf), (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ra = 106, d = 10 nm, ϕ = 0.04, n = 3, Pr = 6.8377, and τ = 1.
Figure 5 exhibits the influence of streamlines on Rayleigh number (Ra) and a period of the magnetic field (λ) when Ha = 30, ϕ = 0.04, n = 3, and d = 10 nm. The circulation strength of the vortices increases for upper Ra because the natural convective force enhances with the increment of Ra. Usually, the mean Nusselt number and vortex intensities enhance for the increment of Ra. For Ra = 104, the streamline contours are horizontally symmetrical to the horizontal middle crossing of the cavity. For this condition, a little variation is observed in the local Nu on warmed and cold walls. In addition, for Ra = 104, the intensity of the vortex enhances with the increment of λ up to 0.5, whereas a discernment is seen at λ = 1. Therefore, in this condition, Nuav, as well as convective temperature transport, can be increased until λ receives 0.5. Furthermore, the flow intensity is highly influenced by the period of the applied magnetic field; consequently, this turns into natural convection. On the other hand, the symmetry pattern of the streamline along the central line diminishes with the increment of the buoyancy force induced by Ra, and the streamline compactness is enhanced when neighboring the lower left and upper right corner inside the vessel. This means that the local Nu is higher in that region. At Ra = 105 and Ra = 106, the streamline compactness decreases near the enclosure’s lower right and upper left corners. In addition, at λ = 0.25, under the existence of strong vortices and higher free convective temperature flow, the oscillation increases in the local Nu. The flow pattern changes as λ enhances up to 0.5 because of the changes in the magnetic effects that simultaneously affect Nu changes.

Figure 5.
Effect of streamline contours for various Rayleigh number (Ra) for (a) uniform magnetic field (umf), (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ha = 30, d = 10 nm, ϕ = 0.04, n = 3, Pr = 6.8377, and τ = 1.
The isotherms for various Rayleigh numbers (Ra) and the magnetic field period (λ) when Ha = 30, ϕ = 0.04, and d = 10 nm are displayed in Figure 6. The configuration of the isothermal lines changes with the variations of the period of the magnetic field. For different λ, a changing variety of isothermal lines is observed from the vertical position to the horizontal for the increase of Ra. This outcome is a result of the augmentation of buoyancy forces. Therefore, convection is a significant mood of temperature distribution and its dominance over conduction. The uniform state of the isothermal line changes its uniform status at Ra = 105, and it is also more distorted, and the flow intensity enhances with higher Ra (Ra = 106). In addition, at different λ, the isothermal lines change completely with the enhancement of Ra because of the growth of the buoyancy force and dominance of convection over conduction temperature transport.
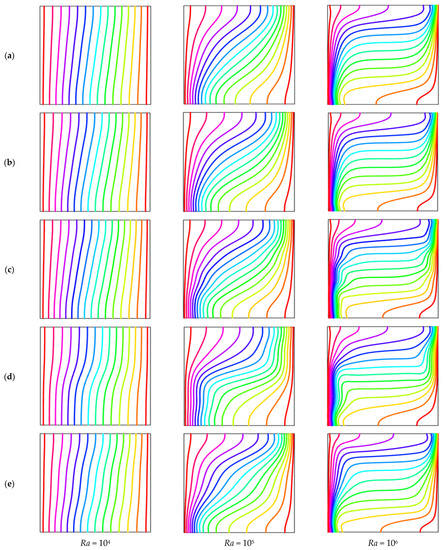
Figure 6.
Effect of isotherms for various Rayleigh number (Ra) for (a) uniform magnetic field (umf), (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ha = 30, d = 10 nm, ϕ = 0.04, n = 3, Pr = 6.8377, and τ = 1.
The local Nusselt number (NuL) along the warmed wall for Rayleigh number, Hartmann number, nanoparticle volume fraction, and nanoparticles diameter are presented in Figure 7, Figure 8, Figure 9 and Figure 10 at various periods of the magnetic field (λ). At λ = 0.25 and λ = 0.5, these figures show a damping periodic diminishing tendency in NuL. The maximum NuL exists for these cases. The streamline’s compactness is a high neighboring warmed wall and significantly enhances the free convective temperature transport. The temperature of the nanofluids neighbors the bottom part of the heated wall is cooler than the other warmed wall region. This is the cause of a higher temperature gradient between the wall and adjacent nanofluids, which leads a higher value of NuL. The local Nu is significantly affected by non-uniform magnetic effects by the mentioned values of Ha, Ra, ϕ, and d. Usually, the local Nu variations are diminished smoothly with the increase of non-uniform magnetic fields. Figure 7 represents a uniform variation for lower Ra (Ra = 104) due to the dominating conduction to convection temperature flow in the non-uniform magnetic field. However, a falling change of NuL is observed on the warmed side for higher Ra (Ra = 105 and 106). In addition, the nanofluid is moved away from the hot bottom wall to the upward wall by buoyant forces, which significantly improves the local Nusselt number.
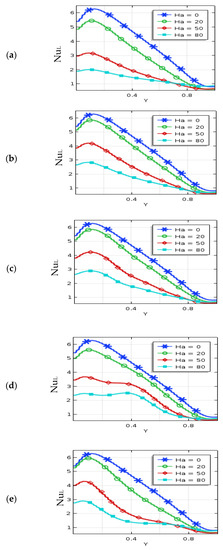
Figure 7.
Local Nusselt number for Hartmann number (Ha) and (a) umf, (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ra = 106, ϕ = 0.04, d = 10 nm, n = 3, and τ = 1.
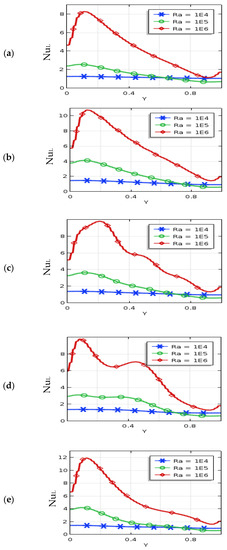
Figure 8.
Local Nusselt number for Rayleigh number (Ra) and (a) umf, (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ha = 30, d = 10 nm, ϕ = 0.04, n = 3, and τ = 1.
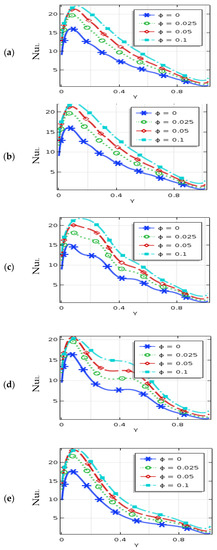
Figure 9.
Local Nusselt number for nanoparticles volume (ϕ), and (a) umf, (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ra = 106, Ha = 30, d = 10 nm, n = 3, and τ = 1.
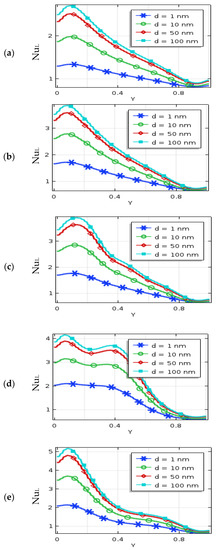
Figure 10.
Local Nusselt Number for nanoparticles diameter (d) and (a) umf, (b) λ = 0.1, (c) λ = 0.25, (d) λ = 0.5, and (e) λ = 1 when Ra = 106, Ha = 30, n = 3, ϕ = 0.04, and τ = 1.
Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 illustrate the mean Nusselt number (Nuav) on the warmed sidewall for various parameters. Figure 11 and Figure 15 show the mean Nusselt number (Nuav) drops with the growth of the Hartmann number, whereas it upturns for the rise of Ra. The Lorentz forces increased by the addition of nano-sized particles into the base fluid, which produced a stronger resistance to the movement of the liquid. Consequently, the thermal efficiency of the nanofluid reduces compared to the base fluid. A higher average rate of temperature transport is observed for the non-uniform magnetic effect when λ = 0.75 than the uniform magnetic effect. Figure 12 shows that the accumulation of nano-sized particles augments the average temperature transfer rate. Figure 13 shows that the size of the nanoparticles is a important for making a stable nanofluid. The nanoparticles are highly affected by the rate of heat transfer of a nanofluid. Above all, the outcomes are calculated for the spherical shape of the nanoparticles. Figure 14 shows that the mean Nusselt number is significantly greater for nano-sized particles with a blade shape compared to a spherical shape. This is because the total surface area of the blade-shaped particles is higher compared to other shapes of nano-sized particles. Table 3 represents the mean Nusselt number for various water-based nanofluids. It shows a higher average rate of heat transport for nanofluids than the base fluid, even with a 1% volume fraction of nanoparticles. It also illustrates that the mean Nusselt number (Nuav) is higher for Fe3O4-water nanofluids than the six other varieties of nanofluids, although the CNT nano-sized particles exhibits higher thermal conductivity.
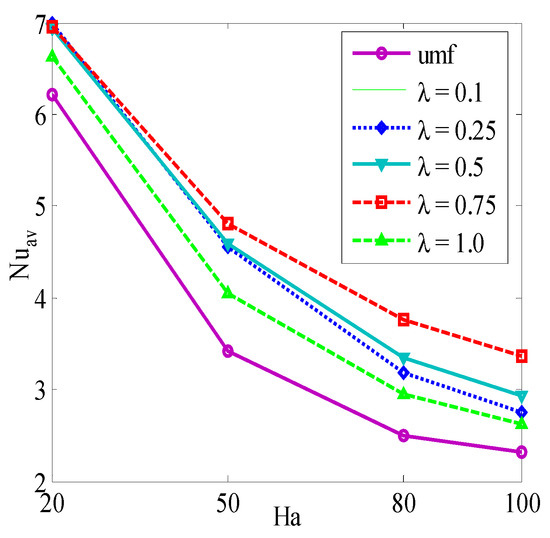
Figure 11.
Average Nusselt number (Nuav) with Hartmann number for uniform magnetic field and different periods of the magnetic field when Ra = 106, Ha = 30, d = 10 nm, n = 3, ϕ = 0.04, and τ = 1.
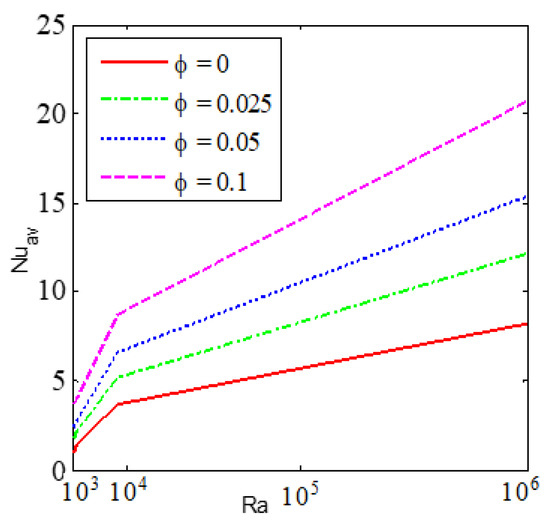
Figure 12.
Average Nusselt number (Nuav) for different Rayleigh number (Ra) and nanoparticles volume fraction (ϕ) when λ = 0.5, Ha = 30, d = 10 nm, n = 3, and τ = 1.
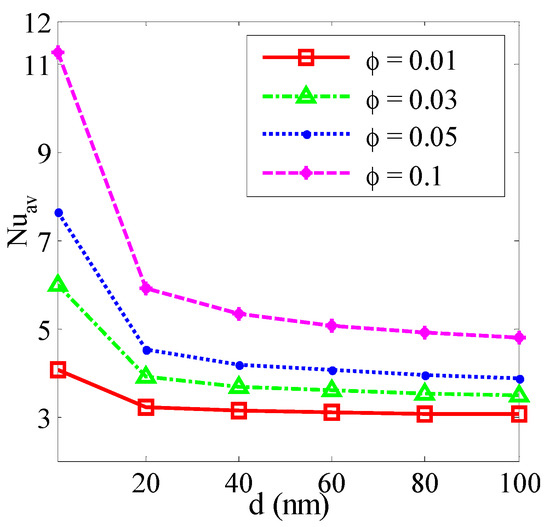
Figure 13.
Average Nusselt number (Nuav) for different nanoparticles diameter (d) and nanoparticles volume fraction (ϕ) when Ra = 106, Ha = 30, λ = 0.5, d = 10 nm, n = 3, and τ = 1.
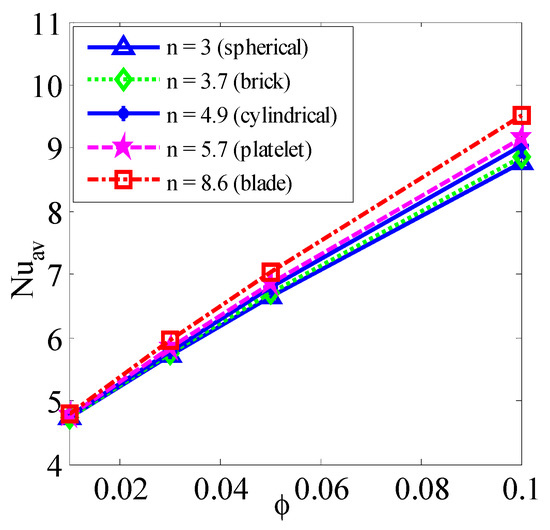
Figure 14.
Average Nusselt number (Nuav) for the nanoparticles shape (n) and nanoparticles volume fraction (ϕ) when Ra = 106, Ha = 30, d = 10 nm, n = 3, λ = 0.5, and τ = 1.
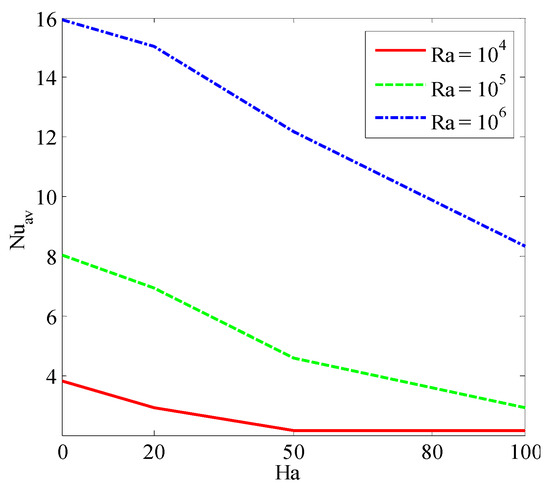
Figure 15.
Variation of mean Nusselt number (Nuav) for various Rayleigh numbers (Ra) and Hartmann number (Ha) when ϕ = 0.04, n = 3, d = 10 nm, n = 3, λ = 0.5, and τ = 1.

Table 3.
Variation of mean Nusselt number (Nuav) for various nanoparticles volume (ϕ), and various nanofluids when n = 3, Ra = 106, λ = 0.5, d = 10 nm, n = 3, Ha = 30, and τ = 1.
5. Conclusions
The primary purpose of this study was to explore the influence of periodic magnetic effect on free convective temperature transport considering the nanoparticles Brownian movement of Cu-water nanofluids within the square enclosure being performed numerically. The upper and lower sides were insulated. The left-hand and right-hand sidewalls were heated and cooled, respectively. The function of the magnetic field was measured as the sine function of y. The FEM of the Galerkin type was engaged for numerical calculations of the non-linear governing PDEs. The various physical model parameters’ influence was investigated using isotherms, streamlines, local and mean Nusselt numbers. The essential findings are recorded as follows:
- The non-uniform magnetic effect has a significant impact on controlling the nanofluid flow and temperature transport, which provides a greater temperature transfer rate than the uniform magnetic field;
- The nanoparticles significantly improve heat transport rate even with 1% of nanoparticles volume fraction. The heat transfer rate rises by 18.71% for Cu-water nanofluid with 1% nanoparticles volume;
- A higher Rayleigh number represents a higher free convective heat transfer and fluid flow, whereas a higher Hartmann number diminishes the heat transport rate;
- The intensity of flow changes significantly with the variation of the magnetic field period. The streamlines and isotherms are almost identical at the low period (λ = 0.1) and uniform magnetic field. The period λ = 0.75 represents the highest heat transport rate;
- The nanoparticle’s diameter has an influential effect on making the nanofluid stable. The heat transfer rate is more significant for a smaller size of nanoparticles (0–20 nm);
- The average heat transport is greater for blade-shaped nano-sized particles than other shapes. Therefore, shape and size of nanoparticles significantly influences the thermal performance;
- The highest heat transfer is obtained for Fe3O4-water and Cu-water nanofluids compared to other nanofluids. The heat transport rate increases by 20.14% for Fe3O4-water nanofluids, whereas it increases by 5.21% for CNT-water nanofluid;
- Brownian movement of nanoparticles has an influential role on heat transport.
Author Contributions
T.I. and M.F.-A.-A.: conceptualization, methodology, software, formal analysis, validation, visualization, data curation, and original draft preparation; M.F.-A.-A., M.Y. and N.P.: investigation resources, data curation, and original draft preparation; T.I., M.F.-A.-A. and M.Y.: review and editing; N.P. and M.F.-A.-A.: supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data sharing is applicable because no data were developed or investigated for this present article.
Acknowledgments
The authors are grateful to the editors and reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| B0 | magnitude of magnetic field [kg s−2 A−1] | |
| cp | specific heat at constant pressure [J kg−1 K−1] | |
| g | gravitational acceleration [m s−2] | |
| dp | nanoparticles diameter [m] | |
| Ha | Hartmann number | |
| k | thermal conductivity [W m−1 K−1] | |
| KB | Boltzmann constant [J K−1] | |
| L | length of the enclosure [m] | |
| Nuav | average Nusselt number | |
| NuL | local Nusselt number | |
| p | dimensional fluid pressure [Pa] | |
| P | dimensionless fluid pressure | |
| Pr | Prandtl number | |
| Ra | Rayleigh number | |
| T | fluid temperature [K] | |
| t | dimensional time [s] | |
| u, v | dimensional velocity components [m s−1] | |
| U, V | dimensionless velocity component | |
| x, y | dimensional coordinates | |
| X, Y | non-dimensional coordinates | |
| Greek symbols | ||
| α | thermal diffusivity [m2 s−1] | |
| β | thermal expansion coefficient [K−1] | |
| ϕ | Solid volume fraction | |
| μ | dynamic viscosity [kg m−1 s−1] | |
| υ | kinematic viscosity [m2 s−1] | |
| θ | non-dimensional temperature | |
| ρ | density [kgm−3] | |
| σ | electric conductivity | |
| ψ | stream function | |
| λ0 | period number | |
| λ | period of magnetic field | |
| τ | dimensionless time | |
| Subscript | ||
| h | heat surface | |
| c | cold surface | |
| nf | nanofluid | |
| bf | basefluid | |
| sp | solid particle | |
| av | average | |
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles, Developments and Applications of Non-Newtonian Flows; ASME. FED-231/MD-66; Springer, D.A., Wang, H.P., Eds.; Argonne National Lab.: Argonne, IL, USA, 1995; pp. 99–105. [Google Scholar]
- Choi, S.U.S. Nanofluid Technology: Current Status and Future Research; Energy Technology Division, Argonne National Laboratory: Argonne, IL, USA, 1999; pp. 604–639. [Google Scholar]
- Saidur, R.; Leong, K.Y.; Mohammed, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Wen, D.; Lin, G.; Vafaei, S.; Zhang, K. Review of nanofluids for heat transfer applications. Particuology 2009, 7, 141–150. [Google Scholar] [CrossRef]
- Yu, W.; France, D.M.; Routbort, J.L.; Choi, S.U.S. Review and Comparison of Nanofluid Thermal Conductivity and Heat Transfer Enhancements. Heat Transf. Eng. 2008, 29, 432–460. [Google Scholar] [CrossRef]
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 11, 519659. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective Transport in Nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A. Simulation and modeling of second order velocity slip flow of micropolar ferrofluid with Darcy–Forchheimer porous medium. J. Mater. Res. Technol. 2020, 9, 7335–7340. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Binary chemical reaction with activation energy in dissipative flow of non-Newtonian nanomaterial. J. Theor. Comput. Chem. 2020, 19, 2040006. [Google Scholar] [CrossRef]
- Khan, M.I.; Alsaedi, A.; Hayat, T.; Khan, N.B. Modeling and computational analysis of hybrid class nanomaterials subject to entropy generation. Comput. Methods Programs Biomed. 2019, 179, 104973. [Google Scholar] [CrossRef]
- Hayat, T.; Tamoor, M.; Khan, M.I.; Alsaedi, A. Numerical simulation for nonlinear radiative flow by convective cylinder. Results Phys. 2016, 6, 1031–1035. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. Simulation of ferromagnetic nanomaterial flow of Maxwell fluid. Results Phys. 2018, 8, 34–40. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows-Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Shah, Z.; Ullah, A.; Bonyah, E.; Ayaz, M.; Islam, S.; Khan, I. Hall effect on Titania nanofluids thin film flow and radiative thermal behavior with different base fluids on an inclined rotating surface. AIP Adv. 2019, 9, 055113. [Google Scholar] [CrossRef]
- Rahman, M.; Alam, M.; Al-Salti, N.; Eltayeb, I. Hydromagnetic natural convective heat transfer flow in an isosceles triangular cavity filled with nanofluid using two-component nonhomogeneous model. Int. J. Therm. Sci. 2016, 107, 272–288. [Google Scholar] [CrossRef]
- Kalbani, K.S.A.; Rahman, M.M.; Alam, M.S.; Salti, N.A.; Eltayeb, I.A. Buoyancy induced heat transfer flow inside a tilted square enclosure filled with nanofluids in the presence of oriented magnetic field. Heat Transf. Eng. 2017, 39, 511–525. [Google Scholar] [CrossRef]
- Mojumder, S.; Rabbi, K.M.; Saha, S.; Hasan, M.N.; Saha, S.C. Magnetic field effect on natural convection and entropy gener-ation in a half-moon shaped cavity with semi-circular bottom heater having different ferrofluid inside. J. Magn. Magn. Mater. 2016, 407, 412–424. [Google Scholar] [CrossRef]
- Parveen, R.; Mahapatra, T. Numerical simulation of MHD double diffusive natural convection and entropy generation in a wavy enclosure filled with nanofluid with discrete heating. Heliyon 2019, 5, e02496. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Ismael, M.A.; Chamkha, A.J.; Ganji, D.D. Numerical analysis of natural convection of Cu–water nanofluid filling triangular cavity with semicircular bottom wall. J. Therm. Anal. 2019, 135, 3485–3497. [Google Scholar] [CrossRef]
- Billah, M.; Rahman, M.; Razzak, M.; Saidur, R.; Mekhilef, S. Unsteady buoyancy-driven heat transfer enhancement of nanofluids in an inclined triangular enclosure. Int. Commun. Heat Mass Transf. 2013, 49, 115–127. [Google Scholar] [CrossRef]
- Li, Z.; Hussein, A.K.; Younis, O.; Afrand, M.; Feng, S. Natural convection and entropy generation of a nanofluid around a circular baffle inside an inclined square cavity under thermal radiation and magnetic field effects. Int. Commun. Heat Mass Transf. 2020, 116, 104650. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Babu, S.K.; Balakrishnan, A. Finite element analysis of natural convection flow in a isosceles triangular enclosure due to uniform and non-uniform heating at the side walls. Int. J. Heat Mass Transf. 2008, 51, 4496–4505. [Google Scholar] [CrossRef]
- Al-Weheibi, S.M.; Rahman, M.; Alam, M.; Vajravelu, K. Numerical simulation of natural convection heat transfer in a trapezoidal enclosure filled with nanoparticles. Int. J. Mech. Sci. 2017, 131-132, 599–612. [Google Scholar] [CrossRef]
- Alam, M.S. Natural convective heat transfer of cobalt-kerosene nanofluid inside a quarter-circular enclosure with uniform and non-uniform heated bottom wall using two-component nonhomogeneous model. Thammasat Int. J. Sci. Technol. 2017, 22, 45–66. [Google Scholar]
- Mehryan, S.; Izadi, M.; Chamkha, A.J.; Sheremet, M.A. Natural convection and entropy generation of a ferrofluid in a square enclosure under the effect of a horizontal periodic magnetic field. J. Mol. Liq. 2018, 263, 510–525. [Google Scholar] [CrossRef]
- Haq, R.U.; Aman, S. Water functionalized CuO nanoparticles filled in a partially heated trapezoidal cavity with inner heated obstacle: FEM approach. Int. J. Heat Mass Transf. 2019, 128, 401–417. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; Armaghani, T.; Mansour, M.A. Effects of partial slip on entropy generation and MHD combined convection in a lid-driven porous enclosure saturated with a Cu–water nanofluid. J. Therm. Anal. 2018, 132, 1291–1306. [Google Scholar] [CrossRef]
- Uddin, M.J. Numerical simulation on free convective heat transfer in a copper-water nanofluid filled semi-circular annulus with the magnetic field. Tec. Ital.-Ital. J. Eng. Sci. 2018, 62, 119–129. [Google Scholar] [CrossRef]
- Zahan, I.; Nasrin, R.; Alim, M.A. MHD effect on conjugate heat transfer in a nanofluid filled rectangular enclosure. Int. J. Petrochem. Sci. Eng. 2018, 3, 114–123. [Google Scholar] [CrossRef][Green Version]
- Abedini, A.; Armaghani, T.; Chamkha, A.J. MHD free convection heat transfer of a water–Fe3O4 nanofluid in a baffled C-shaped enclosure. J. Therm. Anal. 2018, 135, 685–695. [Google Scholar] [CrossRef]
- Marzougui, S.; Mebarek-Oudina, F.; Assia, A.; Magherbi, M.; Shah, Z.; Ramesh, K. Entropy generation on magneto-convective flow of copper–water nanofluid in a cavity with chamfers. J. Therm. Anal. 2021, 143, 2203–2214. [Google Scholar] [CrossRef]
- Balushi, L.M.A.; Rahman, M.M. Convective heat transfer utilizing magnetic nanoparticles in the presence of a sloping magnetic field inside a square enclosure. J. Therm. Sci. Eng. Appl. 2019, 11, 1–19. [Google Scholar]
- Al-Kalbani, K.S.; Rahman, M.M. Convective Heat Transfer in the Flow of a Nanofluid in an Inclined Square Enclosure. J. Eng. Phys. 2019, 92, 1150–1170. [Google Scholar] [CrossRef]
- Dutta, S.; Goswami, N.; Pati, S.; Biswas, A.K. Natural convection heat transfer and entropy generation in a porous rhombic enclosure: Influence of non-uniform heating. J. Therm. Anal. 2021, 144, 1493–1515. [Google Scholar] [CrossRef]
- Uddin, M.; Rasel, S. Numerical analysis of natural convective heat transport of copper oxide-water nanofluid flow inside a quadrilateral vessel. Heliyon 2019, 5, e01757. [Google Scholar] [CrossRef]
- Uddin, M.; Rasel, S.; Rahman, M.; Vajravelu, K. Natural convective heat transfer in a nanofluid-filled square vessel having a wavy upper surface in the presence of a magnetic field. Therm. Sci. Eng. Prog. 2020, 19, 100660. [Google Scholar] [CrossRef]
- Islam, T.; Akter, N.; Jahan, N. MHD free convective heat transfer in a triangular enclosure filled with copper-water nanofluid. Int. J. Mater. Math. Sci. 2020, 2, 29–38. [Google Scholar]
- Islam, T.; Parveen, N.; Asad, M.F.A. Hydromagnetic natural convection heat transfer of copper-water nanofluid within a right-angled triangular cavity. Int. J. Sci. Technol. 2020, 7, 070304. [Google Scholar]
- Islam, T.; Alam, N.; Asjad, M.I.; Parveen, N.; Chu, Y.-M. Heatline visualization of MHD natural convection heat transfer of nanofluid in a prismatic enclosure. Sci. Rep. 2021, 11, 1–18. [Google Scholar] [CrossRef]
- Mullick, S.H.; Kumar, A.; Kundu, P.K. Numerical Study of Natural Convection Inside a Square Cavity with Non-uniform Heating from Top. J. Inst. Eng. Ser. C 2020, 101, 1043–1050. [Google Scholar] [CrossRef]
- Rostami, S.; Ellahi, R.; Oztop, H.F.; Goldanlou, A.S. A study on the effect of magnetic field and the sinusoidal boundary con-dition on free convective heat transfer of non-Newtonian power-law fluid in a square enclosure with two constant-temperature obstacles using lattice Boltzmann method. J. Therm. Anal. Calorim. 2020, 144, 1–17. [Google Scholar]
- Alsabery, A.I.; Ismael, M.; Chamkha, A.J.; Hashim, I. Mixed convection of Al2O3-water nanofluid in a double lid-driven square cavity with a solid inner insert using Buongiorno’s two-phase model. Int. J. Heat Mass Transf. 2018, 119, 939–961. [Google Scholar] [CrossRef]
- Uddin, M.; Rahman, M. Heat Transportation in Copper Oxide-Water Nanofluid Filled Triangular Cavities. Int. J. Heat Technol. 2020, 38, 106–124. [Google Scholar] [CrossRef]
- Qayyum, S.; Khan, M.I.; Hayat, T.; Alsaedi, A. Comparative investigation of five nanoparticles in flow of viscous fluid with Joule heating and slip due to rotating disk. Phys. B Condens. Matter 2018, 534, 173–183. [Google Scholar] [CrossRef]
- Gireesha, B.; Sowmya, G.; Khan, M.I.; Öztop, H.F. Flow of hybrid nanofluid across a permeable longitudinal moving fin along with thermal radiation and natural convection. Comput. Methods Programs Biomed. 2020, 185, 105166. [Google Scholar] [CrossRef]
- Waqas, M.; Khan, M.I.; Hayat, T.; Gulzar, M.M.; Alsaedi, A. Transportation of radiative energy in viscoelastic nanofluid con-sidering buoyancy forces and convective conditions. Chaos Solitons Fractals 2020, 130, 109415. [Google Scholar] [CrossRef]
- Mansour, M.A.; Gorla, R.S.R.; Siddiqa, S.; Rashad, A.M.; Salah, T. Unsteady MHD natural convection flow of a nanofluid inside an inclined square cavity containing a heated circular obstacle. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Alsoy-Akgün, N. Effect of an uniform magnetic field on unsteady natural convection of nanofluid. J. Taibah Univ. Sci. 2019, 13, 1073–1086. [Google Scholar] [CrossRef]
- Ghasemi, B.; Aminossadati, S.; Raisi, A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int. J. Therm. Sci. 2011, 50, 1748–1756. [Google Scholar] [CrossRef]
- Martínez-Farías, F.J.; Alvarado-Sánchez, A.; Rangel-Cortes, E.; Hernández-Hernández, A. Bi-dimensional crime model based on anomalous diffusion with law enforcement effect. Math. Model. Numer. Simul. Appl. 2022, 2, 26–40. [Google Scholar] [CrossRef]
- Asad, M.F.A.; Alam, M.N.; Rashad, A.M.; Sarker, M.M.A. Impact of undulation on magneto-free convective heat transport in an enclosure having vertical wavy sides. Int. Comm. Heat Mass Trans. 2021, 127, 105579. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid with Newtonian heating under Caputo fractional derivative: Analytical investigations via Laplace transforms. Math. Model. Numer. Simul. Appl. 2022, 2, 13–25. [Google Scholar] [CrossRef]
- Fayz-Al-Asad, M.; Alam, N.; Ahmad, H.; Sarker, M.; Alsulami, M.; Gepreel, K.A. Impact of a closed space rectangular heat source on natural convective flow through triangular cavity. Results Phys. 2021, 23, 104011. [Google Scholar] [CrossRef]
- Khan, A.; Khan, A.; Sinan, M. Ion temperature gradient modes driven soliton and shock by reduction perturbation method for electron-ion magneto-plasma. Math. Model. Numer. Simul. Appl. 2022, 2, 1–12. [Google Scholar] [CrossRef]
- Asad, M.F.A.; Alam, M.N.; Tunç, C.; Sarker, M.M.A. Heat transport exploration of free convection flow inside enclosure having vertical wavy walls. J. Appl. Comput. Mech. 2021, 7, 520–527. [Google Scholar]
- Asad, M.F.A.; Yavuz, M.; Alam, M.N.; Sarker, M.M.A.; Bazighifan, O. Influence of fin length on magneto-combined con-vection heat transfer performance in a lid-driven wavy cavity. Fractal Fract. 2021, 5, 107. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 4th ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).