1. Introduction
A space-time panel dataset is a sample collected from a number of spatial units over time periods. Such data widely exist in various research fields. It is of great theoretical significance and practical value to conduct statistical modeling and analysis on space-time panel data. There are three branches of panel data which are defined as ordinary panel data, spatial panel data, and space-time panel data given the variety heterogeneities of existing panel datasets. The regression models established on basis of ordinary panel data are called ordinary panel data regression models. Ordinary panel data regression models date back to the 1950s when the pioneering paper (Bates et al. [
1]) was published. After that, the theories and methods of ordinary panel data regression models have been greatly enriched and they are widely available in many fields, such as economics, management and environmental science, see Chamberlain [
2], Baltagi [
3], Arellano [
4], Baldev and Baltagi [
5], and Hsiao [
6], among others. Panel data spatial regression models generated from the turn of this century when spatial econometrics literature has exhibited a particular interest in the specification and estimation of econometric relationships based on spatial panel data (Elhorst [
7]). Panel data spatial regression models deal with the spatial correlations between different individual units in panel data models and their theories have been well developed and widely used, see Druska and Horrace [
8]; Egger, Pfaffermayr, and Winner [
9]; Kapoor, Kelejian, and Prucha [
10]; Lee and Yu [
11], etc.
Two problems hampering when modeling with space-time panel data are serial correlation and spatial correlation. Serial correlation lies between the observations of each spatial unit over time, and it is the domain of the voluminous time-series econometrics literature. Spatial correlation lies between the observations of the spatial units at each time period, and it is of the spatial econometrics literature, a subfield of econometrics for dealing with spatial interaction effects among geographical units such as individuals, firms, governments, etc. In order to overcome the defects that the panel data spatial regression models do not account for serial correlation and the ordinary panel data regression models account for neither spatial correlation nor serial correlation, people have tried to combine serial correlation and spatial correlations, and established panel data paramertic regression models with separable/nonseparable space-time filters, which are used to do researches on estimation, testing and empirical analysis. Elhorst [
12] developed ML method of a panel data linear regression model with nonseparable space-time filters, while did not establish asymptotic properties of the estimators. Parent and LeSage [
13] explored Markov Chain Monte Carlo methods of random effects panel data linear regression models with separable space-time filters, and the performance of the method was demonstrated by both Monte Carlo simulations and an applied illustration. Lee and Yu [
14] studied MLE and its asymptotic properties of fixed and random effects panel data parametric regression models with separable space-time filters. Lee and Yu [
15] provided QMLE and its asymptotic properties for a fixed effects panel data linear regression model with disturbances contained both separable space-time filters and nonseparable space-time filters. Baltagi et al. [
16] derived several Lagrange Multiplier tests for panel data linear regression model with separable space-time fliters containing random effects. Cohen and Paul [
17] analysed the influencing factors of public infrastructure investment on the costs and productivity of private enterprises on basis of 1982–1996 state-level U.S. manufacturing data by panel data parametric regression model with separable space-time filters.
All literature on panel data regression models with separable/nonseparable space-time filters mentioned above focuses on panel data parametric regression models. Although the theories and applications of these models have been well developed, they are often unrealistic in real situations for the reason that they fail to capture complex structure (e.g., nonlinearity) owing to lacking of flexibility. Moreover, the form of parametric regression models may be misspecified, and estimators based on misspecified models are able to cause inconsistency and even erroneous conclusions. Driven by these reasons, Zhao et al. [
18] constructed semiparametric minimum average variance estimation method, and proposed a F-test statistic of partially linear single-index panel regression model with separable space-time filters, then proved the asymptotic properties of estimators and test statistic. Bai, Hu, and You [
19] established weighted semiparametric least squares and weighted polynomial spline series estimation method for parametric and nonparametric component, respectively, of panel data partially linear varying-coefficient regression model with separable space-time filters, and then proved their asymptotic normalities.
In this paper, we study estimation and testing of random effects semiparametric regression model (RESPRM) with separable space-time filters. By allowing a nonparametric component in parametric regression model with separable space-time filters, it can simultaneously capture the linear and nonlinear effects of covariates, spatial correlation of error structure, serial correlation of remainder error structure, and individual random effects. To the best of our knowledge, there is no related literature on this model. In this paper, we aim to study its profile quasi-maximum likelihood estimation (PQMLE) and hypothesis test methods, and then conduct systematic studies of the asymptotic properties and small sample performance for estimators and test statistic. Furthermore, we illustrate the proposed estimation and testing methods by using a real dataset.
The remainder of this paper is organized as follows.
Section 2 introduces the RESPRM with separable space-time filters, and estimators for the model and test statistic for nonparametric component are constructed.
Section 3 mainly provides asymptotic properties of estimators, asymptotic distribution of test statistic and conditional assumptions.
Section 4 presents the finite sample performance of estimates and F-test statistic through Monte Carlo simulations.
Section 5 illustrates the proposed methods by an application of Indonesian rice farming data. Conclusions are summarized in
Section 6. The proofs of some important lemmas and theorems are given in
Appendix A.
5. Real Data Analysis
In this section, we will illustrate the prescribed estimation and testing methods by Indonesian rice farming dataset with
N = 171 and
T = 6 which is a quintessential example of large N and small T in the stochastic frontier literature(see detail for Feng and Horrace [
35]). This dataset has five variables, one response variable and four covariates. The response variable is natural logarithm of output of Indonesian rice farming, and the covariates include high, mixed, seed, and land, which are defined in
Table 8. The dataset is from the agricultural economic research center of the Ministry of agriculture of Indonesia and compiled by the Agro Economic Survey. Based on the panel data of related variables of 171 farms over 6 growing seasons (three wet and three dry seasons), we will explore the influencing factors of output of Indonesian rice farming by RESPRM with separable space-time filters.
In order to take the proposed RESPRM with separable space-time filters to Indonesian rice farming dataset, we apply the F-test statistic proposed in
Section 2.3 to verify whether or not a nonlinear relationship between covariates and response variable exists. The test results are given in
Table 9. From
Table 9, we find that land (other covariates) has (have) significant nonlinear (linear) relationship with natural logarithm of output of Indonesian rice farming at significant level
.
Therefore, we consider the model (
1)–(
3), and set
,
,
is the
ith observation of
at
tth growing season,
are the
ith observation of high, mixed, and seed at
tth growing season, respectively,
is land for the
ith observation at
tth growing season.
equals 1 if farms
i and
j are in the same village, equals 0 otherwise (see detail for Druska and Horrace [
8]).
The parametric estimates results of the model (
1)–(
3) for fitting Indonesia rice farming data are described in
Table 10. Via
Table 10, we find that: (1)
show expectation of dummy variables for high, mixed, and seed have promotional effects on output of rice. (2)
presents that the output of rice in different farm is relatively unstable and is affected by external fluctuations.
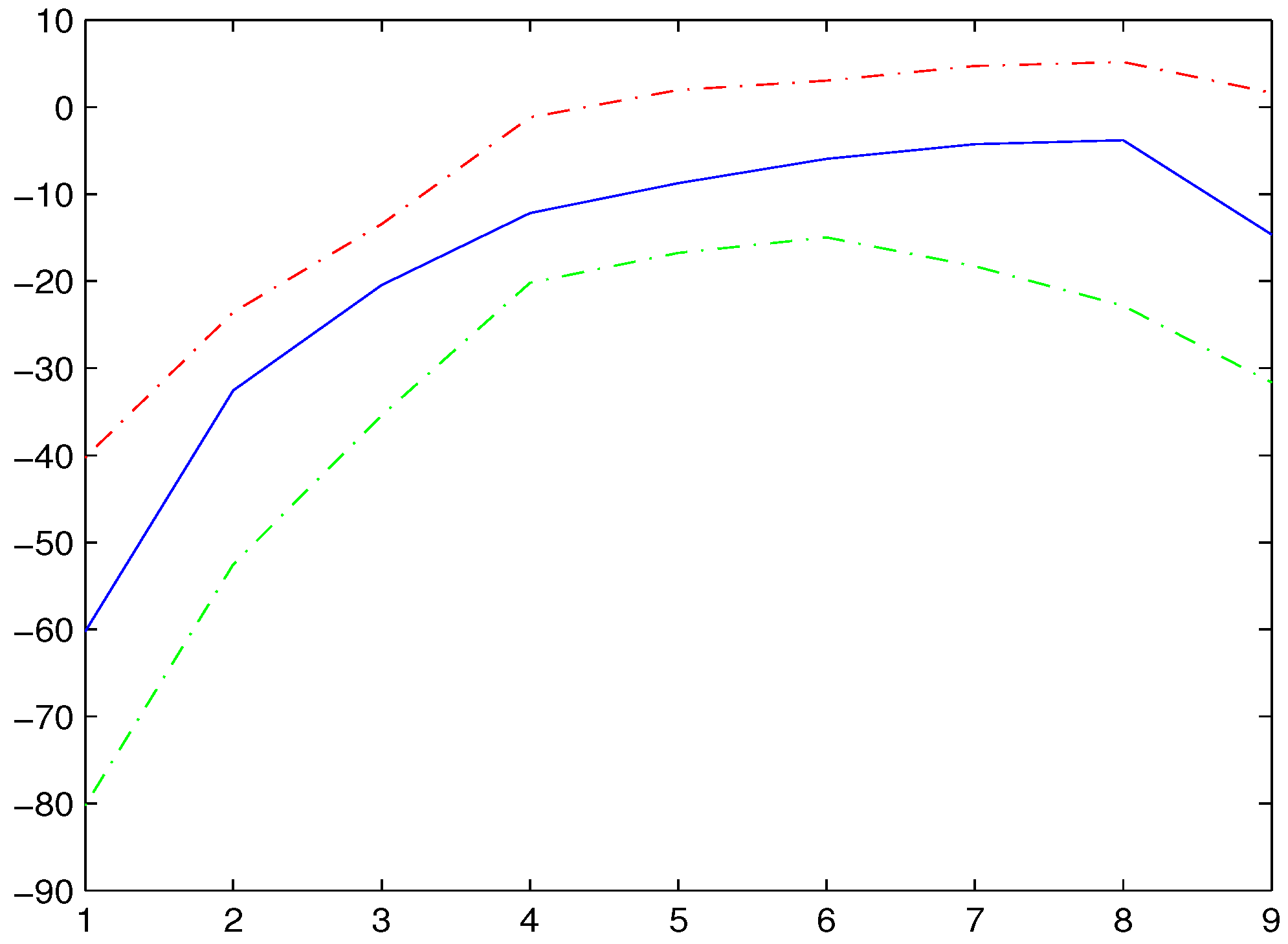
Figure 5 shows the results of estimation and corresponding 95% confidence intervals of
, where the blue solid line is the average fit over 500 simulations, the red and green dotted lines are the corresponding 95% confidence bands. From
Figure 5, we know that land has obvious nonlinear effects on output of rice, and output of rice increases with the increase in land.
6. Conclusions
In this paper, we study PQMLE and hypothesis test for RESPRM with separable space-time filters. The proposed model can simultaneously capture linear and nonlinear effects of covariates, spatial correlation of error structure, serial correlation of remainder error structure, and individual random effects. With the given conditional assumptions, asymptotic properties of PQMLE and asymptotic distribution of nonparametric components are proved. Monte Carlo simulations are applied to investigate the performance of estimators and test statistic under finite samples, and the results show that proposed estimators and test statistic are well-behaved under finite samples, and consistency of parametric estimates is hard to guarantee if spatial correlation and series correlation in the real model are ignored in some cases. In addition, the practicability of the proposed methods are also assessed by a real dataset.
This paper focuses only on RESPRM with separable space-time filters but does not account for spatially lagged response variables. How to extend our proposed estimation and testing methods to a random effects spatial lag semiparametric regression model with separable space-time filters is an open problem. In addition, we may combine generalized moment estimation method, quantile regression method and local linear method to estimate parametric and nonparametric components of the random effects spatial lag semiparametric regression model with separable space-time filters and RESPRM with separable space-time filters.