Investigation of the Oriented Structure Characteristics of Shale Using Fractal and Structural Entropy Theory
Abstract
1. Introduction
2. Geological Settings
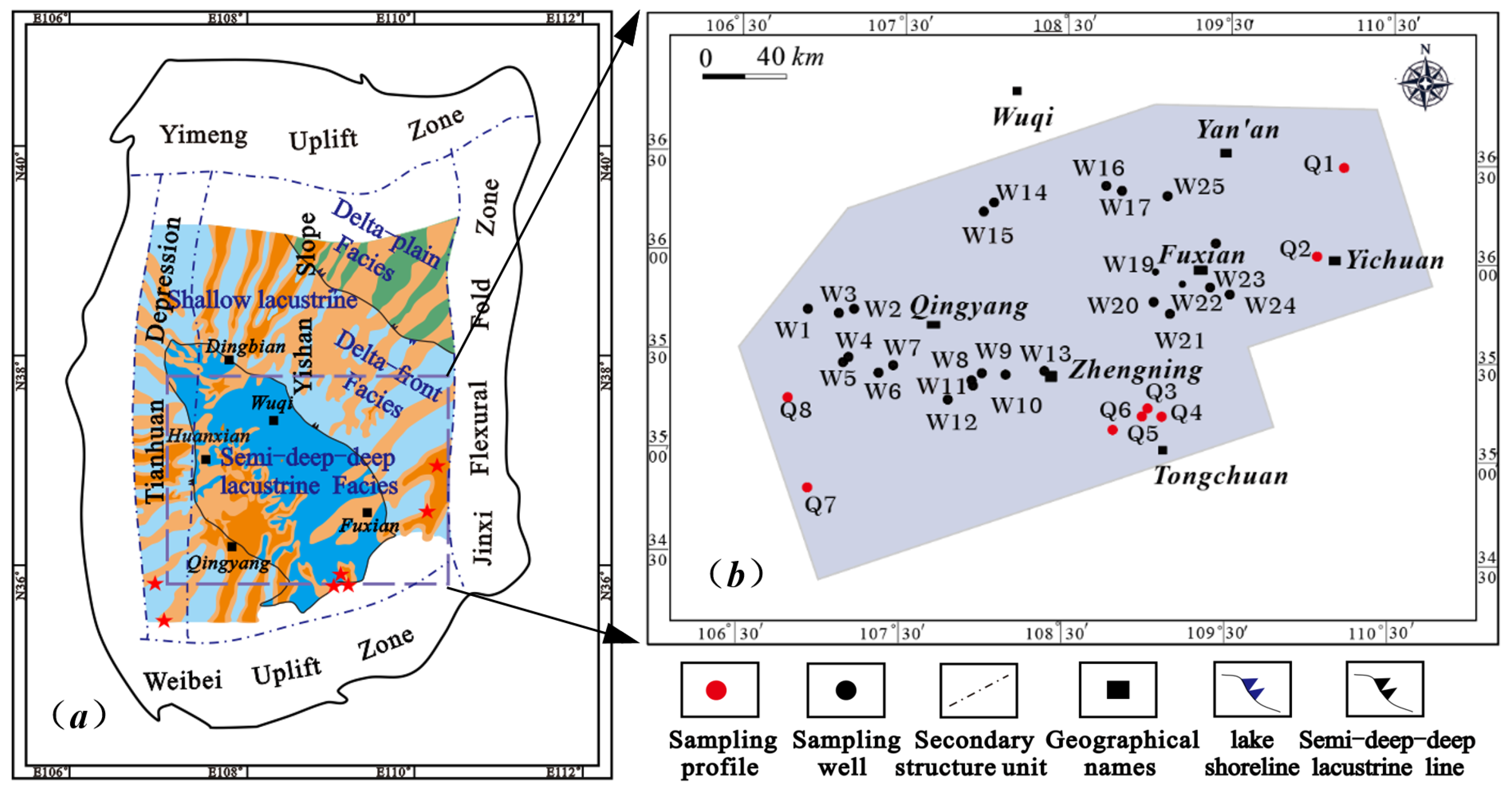
2.1. Geological Background
2.2. Sampling Location
3. Structure Entropy Model
3.1. Oriented-Structure Entropy Model
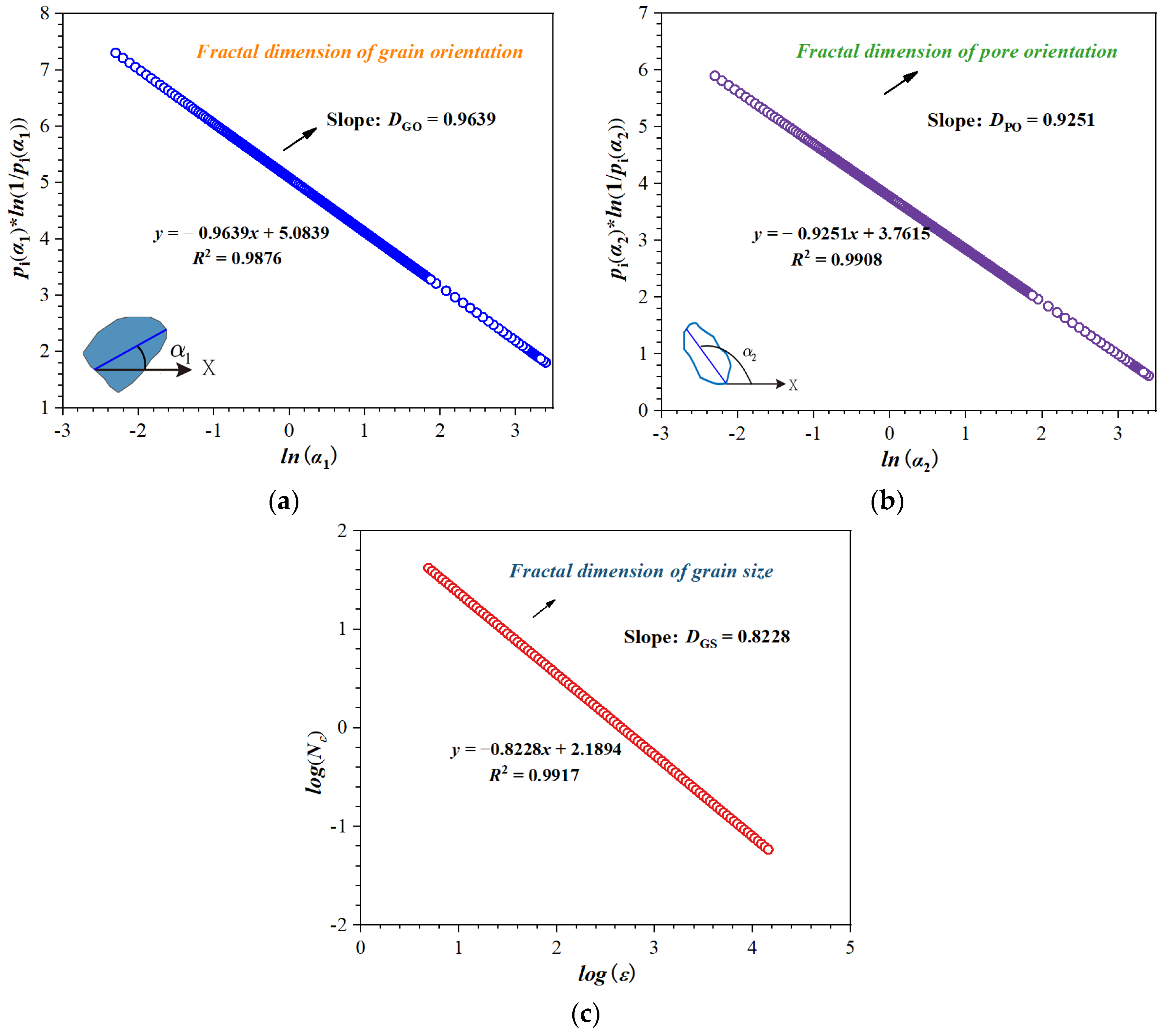
3.2. Fractal Dimension Selection for the Entropy Model
3.2.1. FE–SEM Characterization and Image Processing
- Grayscale conversion. The FE–SEM images of the shale samples were first transformed into 8-bit grayscale images.
- Grayscale threshold selection. The threshold values of the images can be tuned to display the morphologies of grains and pores. In this study, the threshold values of grains and pores are in the range of 0–73 and 88–255, respectively. The FE–SEM image showing the morphologies of grains is illustrated in Figure 4b. The black area represents grains, while the white ones stand for pores.
- Image noise reduction. After threshold processing, many noise spots are shown in the images, affecting the processing accuracy. The image after noise reduction is illustrated in Figure 4c.
3.2.2. Fractal Dimension Calculation
3.2.3. Oriented-Structure Entropy Model
3.2.4. Model Verification
4. Results and Discussions
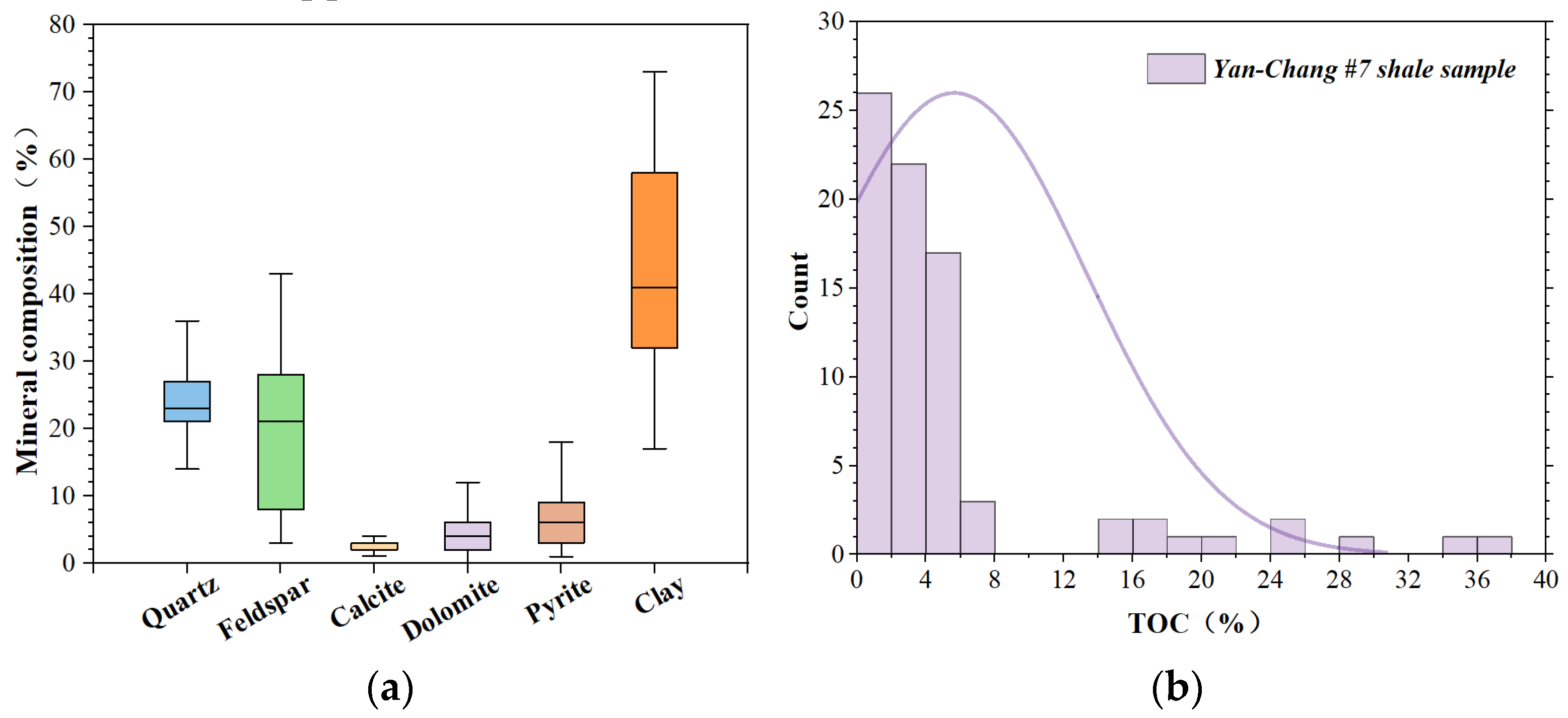
4.1. Sample Compositions
4.2. FE–SEM Characterization
4.3. Oriented Structure Characteristics of Shale
4.3.1. Multifractal and SOE
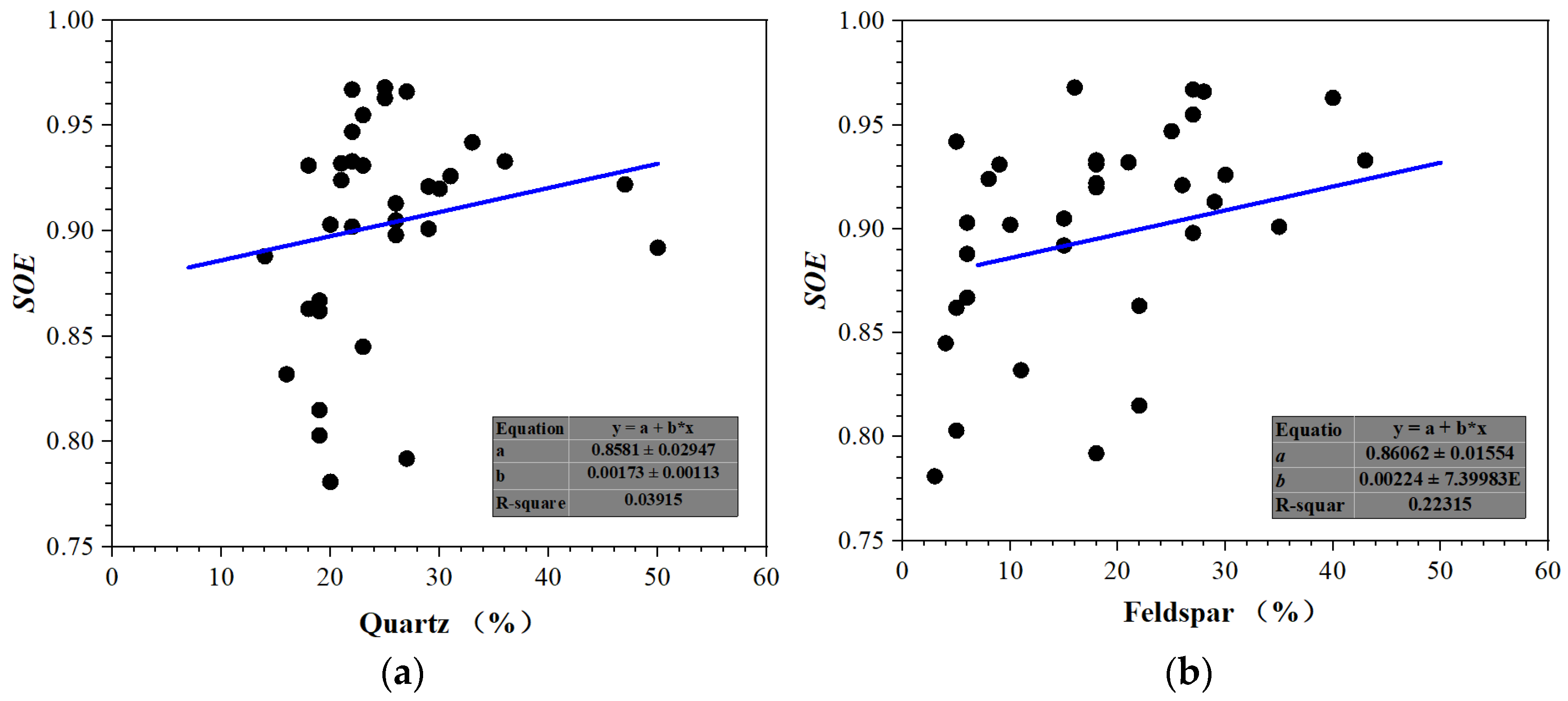
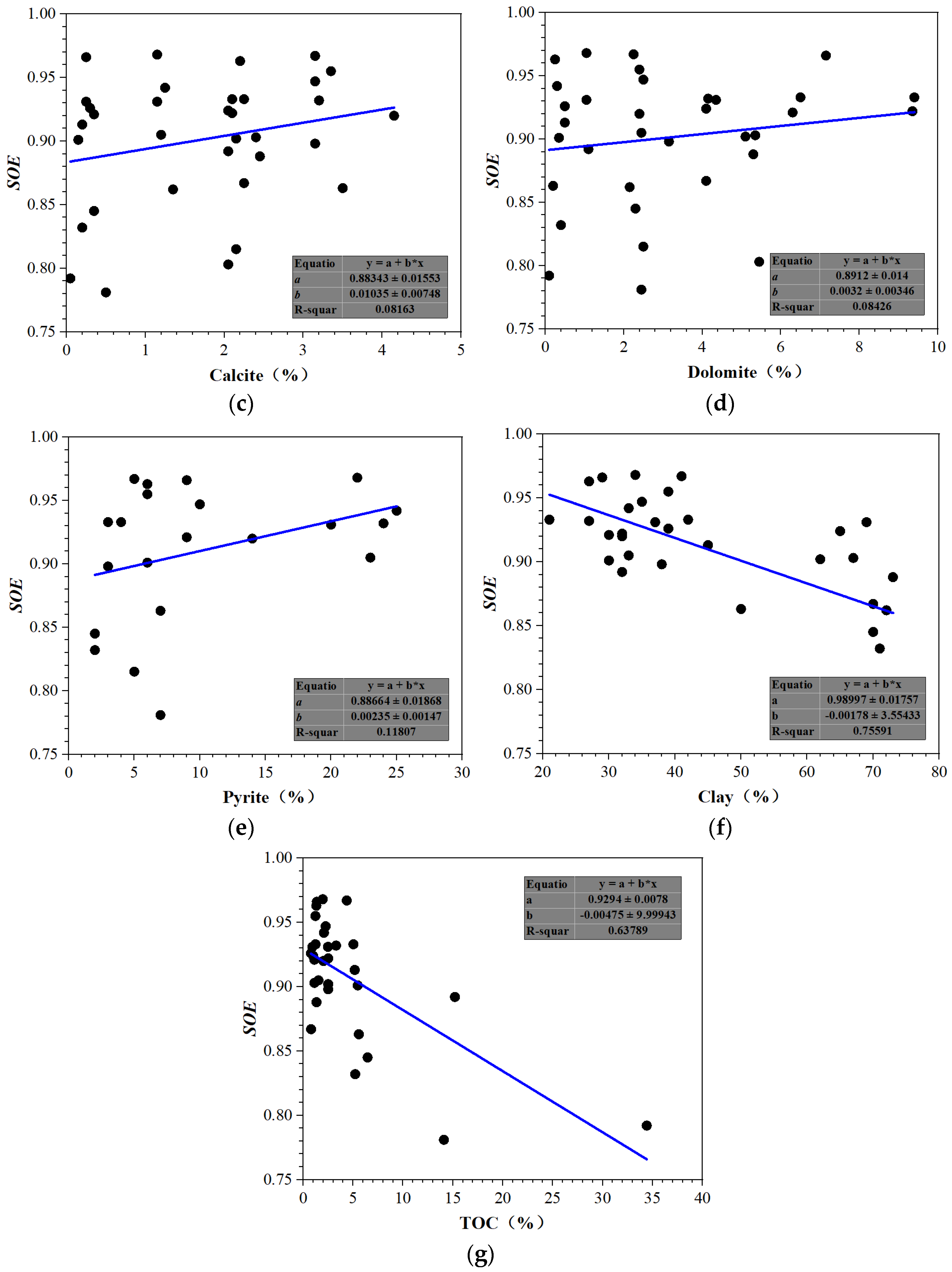
4.3.2. The Influential Factors of SOE
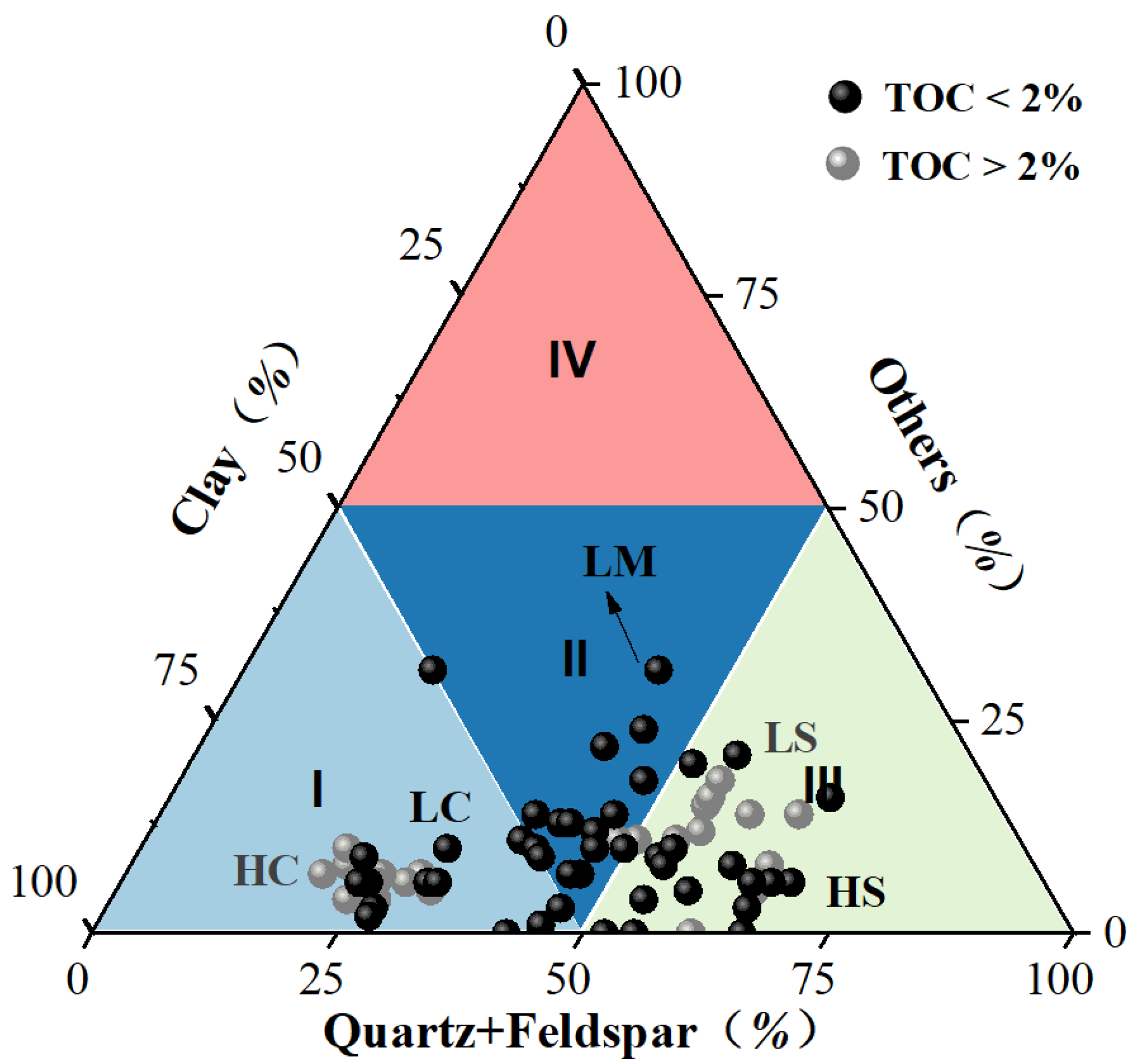
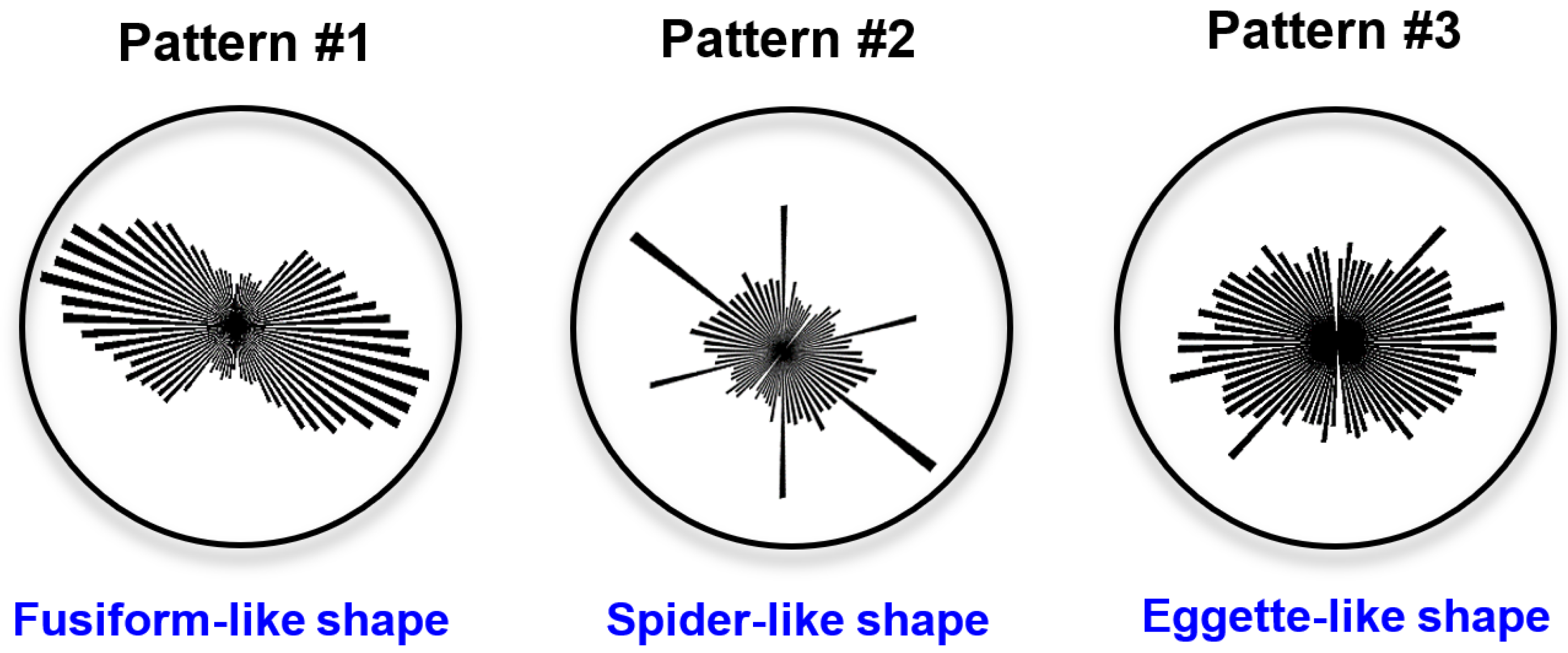
4.4. Directivity Patterns of Shale
5. Conclusions
- Based on many FE–SEM characterizations, the fractal dimensions of grain orientation, the fractal dimension of pore orientation and the fractal dimension of grain size were selected to form the oriented structure entropy model. The synthetic cores were prepared, and their permeabilities are measured to determine the coefficients in the SOE model.
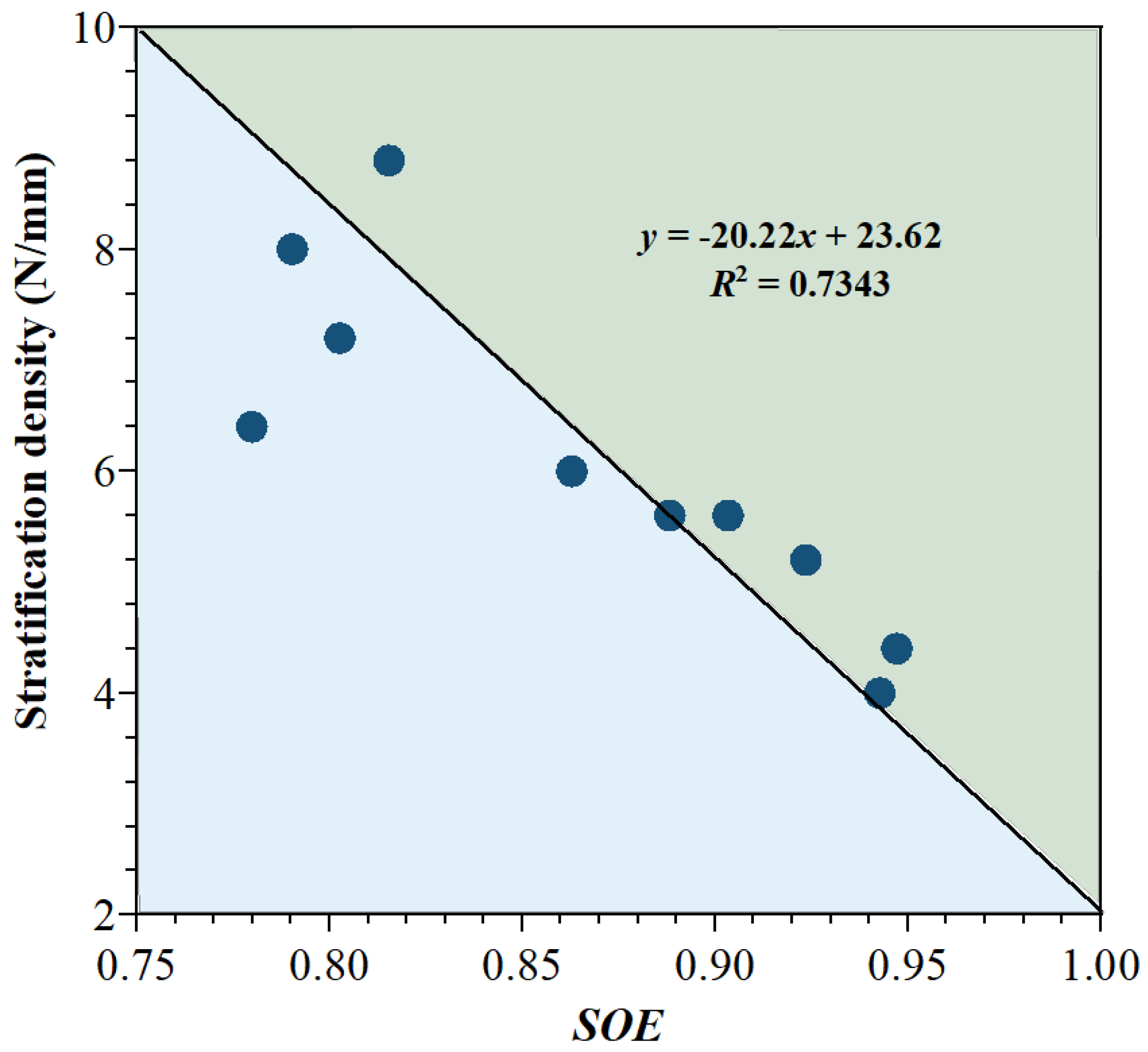
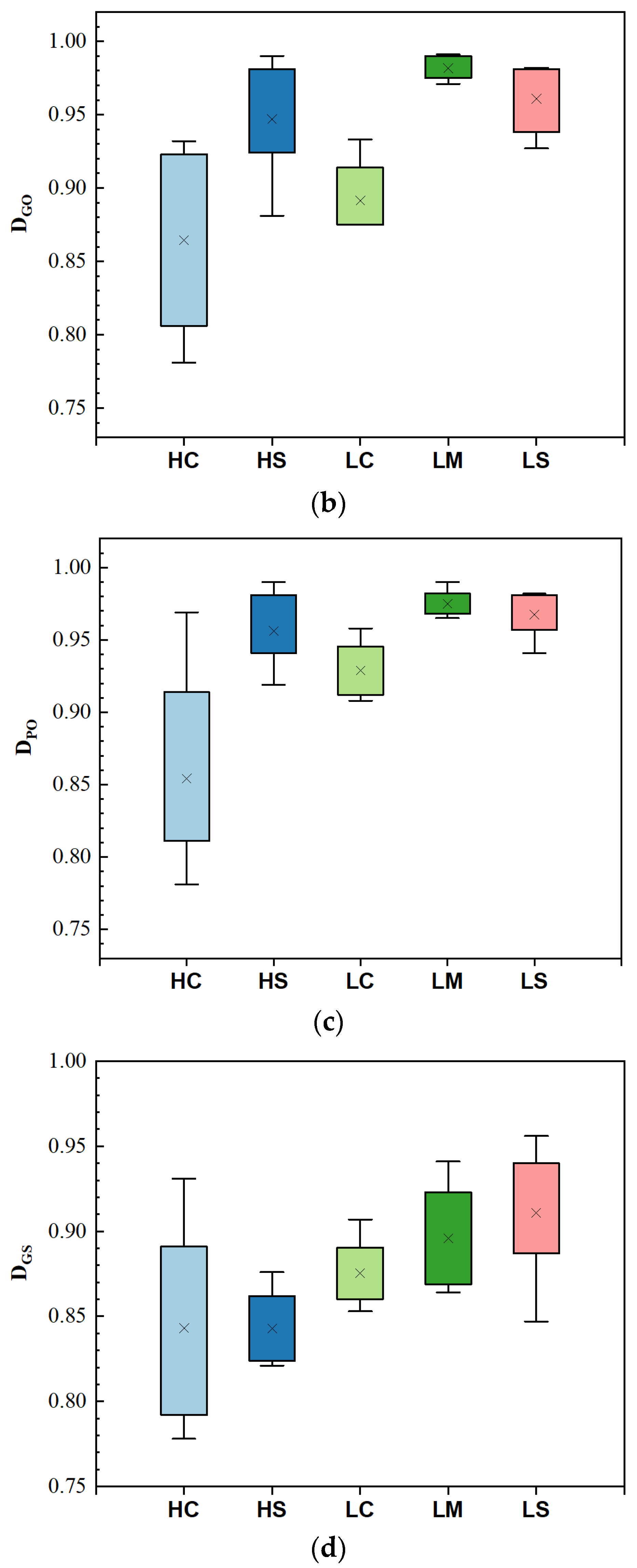
- The SOE model is applied to evaluate the oriented structures of Yan-Chang #7 Shale; the obtained SOE values are in the range of 0.780–0.968. The threshold value of SOE for the samples to exhibit directional features is 0.85; samples with SOEs larger than 0.85 demonstrate the random distribution of grains.
- The TOC and clay minerals are the crucial factors that affect the oriented structures of shale. The SOE values are both strongly correlated with the clay mineral and TOC contents with R2s of 0.7559 and 0.6379, respectively, but poorly related with other minerals.
- Grain alignment patterns can be classified as pattern #1 (fusiform-like shape), pattern #2 (spider-like shape) and pattern #3 (eggette-like shape). High-TOC clayey shales show the typical pattern #1 grain alignment. Low-TOC clayey shale, high-TOC sandy shale and low-TOC sandy shale have the characteristics of both patterns #1 and #2. The grain alignment of low-TOC mixed shales belongs to patterns #2 and #3.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Sample No. | Well Site | Formation | Depth (m) | Mineral Content (%) | TOC (%) | Ro (%) | Organic Type | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quartz | Feldspar | Calcite | Dolomite | Pyrite | Gypsum | Clay | |||||||
| #S1 | Q1 | Chang #7 | Outcrop | 26 | 29 | 0 | 0 | 0 | 0 | 45 | 5.17 | - | II1 |
| #S2 | Q1 | Chang #7 | Outcrop | 19 | 23 | 0 | 0 | 0 | 0 | 58 | 2.61 | - | II2 |
| #S3 | Q2 | Chang #7 | Outcrop | 32 | 33 | 3 | 2 | 0 | 0 | 30 | 1.26 | - | I |
| #S4 | Q3 | Chang #7 | Outcrop | 33 | 5 | 1 | 3 | 25 | 3 | 33 | 2.08 | - | II2 |
| #S5 | Q3 | Chang #7 | Outcrop | 47 | 4 | 2 | 1 | 17 | 0 | 29 | 29.34 | - | II1 |
| #S6 | Q3 | Chang #7 | Outcrop | 62 | 6 | 6 | 0 | 0 | 0 | 26 | 24.44 | - | II1 |
| #S7 | Q3 | Chang #7 | Outcrop | 22 | 25 | 3 | 5 | 10 | 3 | 35 | 2.25 | - | II1 |
| #S8 | Q4 | Chang #7 | Outcrop | 35 | 31 | 0 | 0 | 0 | 0 | 34 | 18.41 | - | II1 |
| #S9 | Q5 | Chang #7 | Outcrop | 25 | 16 | 1 | 2 | 22 | 1 | 34 | 1.96 | - | II1 |
| #S10 | Q5 | Chang #7 | Outcrop | 23 | 18 | 1 | 1 | 20 | 0 | 37 | 2.49 | - | II2 |
| #S11 | Q5 | Chang #7 | Outcrop | 58 | 8 | 5 | 0 | 2 | 0 | 28 | 21.49 | - | II2 |
| #S12 | Q5 | Chang #7 | Outcrop | 18 | 26 | 4 | 2 | 18 | 0 | 32 | 2.40 | - | I |
| #S13 | Q5 | Chang #7 | Outcrop | 26 | 29 | 4 | 2 | 15 | 0 | 24 | 24.78 | - | II1 |
| #S14 | Q6 | Chang #7 | Outcrop | 23 | 29 | 0 | 0 | 0 | 0 | 48 | 16.07 | - | II1 |
| #S15 | Q7 | Chang #7 | Outcrop | 31 | 30 | 0 | 0 | 0 | 0 | 39 | 0.78 | - | II1 |
| #S16 | Q8 | Chang #7 | Outcrop | 27 | 18 | 0 | 0 | 0 | 0 | 54 | 34.41 | - | II1 |
| #S17 | W1 | Chang #7 | 768.23 | 23 | 4 | 0 | 2 | 2 | 0 | 70 | 6.45 | - | II1 |
| #S18 | W2 | Chang #7 | 770.70 | 26 | 5 | 0 | 3 | 3 | 0 | 63 | 5.11 | 1.12 | II1 |
| #S19 | W2 | Chang #7 | 727.20 | 26 | 6 | 0 | 4 | 0 | 0 | 63 | 0.71 | 1.07 | II1 |
| #S20 | W2 | Chang #7 | 773.79 | 18 | 7 | 0 | 4 | 0 | 0 | 69 | 3.21 | 0.78 | I |
| #S21 | W2 | Chang #7 | 784.24 | 20 | 3 | 0 | 2 | 7 | 0 | 68 | 14.10 | 1.12 | I |
| #S22 | W2 | Chang #7 | 787.45 | 34 | 4 | 2 | 6 | 6 | 0 | 48 | 5.21 | 1.06 | II1 |
| #S23 | W3 | Chang #7 | 790.14 | 39 | 7 | 0 | 1 | 1 | 0 | 51 | 4.73 | 0.92 | II1 |
| #S24 | W4 | Chang #7 | 1224.04 | 36 | 18 | 2 | 6 | 4 | 0 | 42 | 17.03 | - | II1 |
| #S25 | W5 | Chang #7 | 1263.38 | 23 | 8 | 2 | 8 | 0 | 0 | 59 | 36.76 | - | II1 |
| #S26 | W5 | Chang #7 | 1276.32 | 16 | 6 | 2 | 6 | 0 | 0 | 70 | 0.85 | 1.20 | - |
| #S27 | W5 | Chang #7 | 1280.60 | 22 | 8 | 2 | 4 | 0 | 0 | 63 | 1.05 | 0.88 | - |
| #S28 | W5 | Chang #7 | 1239.70 | 21 | 8 | 2 | 4 | 0 | 0 | 65 | 0.99 | 1.30 | II1 |
| #S29 | W6 | Chang #7 | 1433.37 | 30 | 18 | 4 | 2 | 14 | 0 | 32 | 2.03 | - | II1 |
| #S30 | W6 | Chang #7 | 1435.34 | 22 | 10 | 2 | 5 | 0 | 0 | 62 | 2.51 | 0.72 | II1 |
| #S31 | W6 | Chang #7 | 1436.01 | 19 | 5 | 2 | 5 | 0 | 0 | 70 | 3.53 | 0.75 | II1 |
| #S32 | W6 | Chang #7 | 1437.88 | 20 | 6 | 2 | 5 | 0 | 0 | 67 | 1.13 | 1.12 | II1 |
| #S33 | W6 | Chang #7 | 1071.83 | 18 | 9 | 0 | 4 | 0 | 0 | 69 | 0.93 | 1.17 | II1 |
| #S34 | W7 | Chang #7 | 1084.49 | 16 | 5 | 0 | 7 | 2 | 0 | 69 | 1.24 | 0.83 | II1 |
| #S35 | W7 | Chang #7 | 1087.60 | 17 | 9 | 3 | 4 | 0 | 0 | 68 | 1.52 | 0.83 | - |
| #S36 | W7 | Chang #7 | 1912.09 | 19 | 5 | 1 | 2 | 0 | 0 | 72 | 1.29 | 0.87 | II2 |
| #S37 | W7 | Chang #7 | 1916.66 | 14 | 6 | 2 | 5 | 0 | 0 | 73 | 1.34 | 1.30 | - |
| #S38 | W7 | Chang #7 | 1919.04 | 19 | 6 | 2 | 4 | 0 | 0 | 70 | 0.79 | 1.02 | - |
| #S39 | W8 | Chang #7 | 1924.60 | 47 | 18 | 2 | 9 | 0 | 0 | 32 | 2.51 | - | II1 |
| #S40 | W8 | Chang #7 | 1921.50 | 7 | 12 | 1 | 2 | 28 | 0 | 50 | 3.24 | - | II1 |
| #S41 | W9 | Chang #7 | 1448.79 | 50 | 15 | 2 | 1 | 0 | 0 | 32 | 15.20 | - | II1 |
| #S42 | W10 | Chang #7 | 1450.75 | 25 | 35 | 5 | 9 | 0 | 0 | 26 | 1.31 | - | II1 |
| #S43 | W11 | Chang #7 | 1453.96 | 29 | 26 | 0 | 6 | 9 | 0 | 30 | 1.12 | - | II1 |
| #S44 | W12 | Chang #7 | 1439.60 | 22 | 43 | 2 | 9 | 3 | 0 | 21 | 1.24 | - | II1 |
| #S45 | W13 | Chang #7 | 1495.65 | 28 | 27 | 0 | 12 | 4 | 0 | 29 | 1.54 | - | II1 |
| #S46 | W13 | Chang #7 | 1497.79 | 21 | 20 | 15 | 18 | 2 | 0 | 24 | 0.79 | 1.01 | II2 |
| #S47 | W14 | Chang #7 | 1499.31 | 22 | 24 | 3 | 0 | 4 | 0 | 47 | 3.96 | 1.30 | II2 |
| #S48 | W15 | Chang #7 | 1396.04 | 20 | 22 | 3 | 3 | 7 | 0 | 45 | 5.62 | - | II2 |
| #S49 | W16 | Chang #7 | 1397.62 | 23 | 27 | 3 | 2 | 6 | 0 | 39 | 1.23 | - | II2 |
| #S50 | W17 | Chang #7 | 1399.10 | 25 | 40 | 2 | 0 | 6 | 0 | 27 | 1.32 | - | II1 |
| #S51 | W18 | Chang #7 | 1254.31 | 29 | 35 | 0 | 0 | 6 | 0 | 30 | 5.47 | 1.20 | II1 |
| #S52 | W19 | Chang #7 | 1151.32 | 22 | 27 | 3 | 2 | 5 | 0 | 41 | 4.37 | - | II1 |
| #S53 | W19 | Chang #7 | 1152.48 | 24 | 14 | 2 | 3 | 6 | 0 | 51 | 2.59 | - | II1 |
| #S54 | W19 | Chang #7 | 1188.03 | 24 | 37 | 2 | 0 | 6 | 0 | 31 | 3.24 | 1.26 | II1 |
| #S55 | W19 | Chang #7 | 1189.25 | 23 | 38 | 2 | 0 | 6 | 0 | 31 | 4.74 | - | II1 |
| #S56 | W19 | Chang #7 | 1220.21 | 30 | 28 | 3 | 0 | 2 | 0 | 37 | 2.94 | 1.08 | II2 |
| #S57 | W19 | Chang #7 | 1224.04 | 26 | 28 | 0 | 0 | 4 | 0 | 42 | 2.35 | 1.16 | II2 |
| #S58 | W19 | Chang #7 | 1263.38 | 23 | 22 | 2 | 2 | 8 | 0 | 43 | 4.21 | - | II2 |
| #S59 | W19 | Chang #7 | 1276.32 | 23 | 25 | 3 | 2 | 6 | 0 | 41 | 2.08 | 1.11 | II2 |
| #S60 | W19 | Chang #7 | 1280.60 | 26 | 27 | 3 | 3 | 3 | 0 | 38 | 2.51 | - | II2 |
| #S61 | W19 | Chang #7 | 1283.24 | 25 | 29 | 3 | 5 | 2 | 0 | 36 | 4.32 | - | II2 |
| #S62 | W20 | Chang #7 | 1446.21 | 26 | 28 | 3 | 5 | 3 | 0 | 35 | 2.19 | - | II2 |
| #S63 | W20 | Chang #7 | 1448.79 | 27 | 28 | 0 | 7 | 9 | 0 | 29 | 1.37 | 0.99 | II2 |
| #S64 | W20 | Chang #7 | 1450.75 | 26 | 30 | 0 | 8 | 4 | 0 | 32 | 1.24 | - | II2 |
| #S65 | W20 | Chang #7 | 1451.39 | 26 | 29 | 0 | 8 | 8 | 0 | 29 | 0.97 | - | - |
| #S66 | W20 | Chang #7 | 1453.96 | 20 | 34 | 3 | 3 | 2 | 0 | 38 | 5.35 | - | II1 |
| #S67 | W21 | Chang #7 | 1495.65 | 18 | 22 | 3 | 0 | 7 | 0 | 50 | 5.58 | - | II1 |
| #S68 | W21 | Chang #7 | 1497.79 | 20 | 21 | 3 | 0 | 10 | 0 | 46 | 7.47 | - | II1 |
| #S69 | W21 | Chang #7 | 1499.31 | 19 | 22 | 2 | 2 | 5 | 0 | 50 | 5.08 | - | II2 |
| #S70 | W21 | Chang #7 | 1350.24 | 22 | 23 | 3 | 0 | 4 | 0 | 48 | 5.34 | - | II2 |
| #S71 | W21 | Chang #7 | 1396.04 | 21 | 25 | 3 | 4 | 3 | 0 | 44 | 4.04 | - | II2 |
| #S72 | W21 | Chang #7 | 1397.62 | 25 | 21 | 3 | 4 | 7 | 0 | 40 | 4.46 | - | II2 |
| #S73 | W21 | Chang #7 | 1399.10 | 21 | 21 | 3 | 3 | 7 | 0 | 45 | 6.81 | - | II2 |
| #S74 | W22 | Chang #7 | 768.23 | 29 | 26 | 2 | 8 | 8 | 0 | 27 | 0.93 | 0.97 | II2 |
| #S75 | W22 | Chang #7 | 770.7 | 16 | 11 | 0 | 0 | 2 | 0 | 71 | 5.21 | - | II2 |
| #S76 | W23 | Chang #7 | 727.2 | 33 | 34 | 2 | 13 | 0 | 1 | 17 | 3.25 | - | II2 |
| #S77 | W23 | Chang #7 | 773.79 | 27 | 17 | 1 | 3 | 5 | 0 | 47 | 2.02 | - | - |
| #S78 | W24 | Chang #7 | 784.24 | 26 | 15 | 1 | 2 | 23 | 0 | 33 | 1.53 | - | - |
| #S79 | W25 | Chang #7 | 787.45 | 21 | 21 | 3 | 4 | 24 | 0 | 27 | 3.30 | - | II1 |
Appendix B
Appendix C
| Sample No. | Stitched FE–SEM Images | Processed FE–SEM Images | Grain Alignment Pattern Diagrams |
|---|---|---|---|
| #S1 | 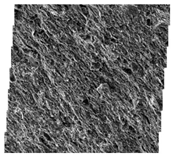 |  |  |
| #S4 |  | 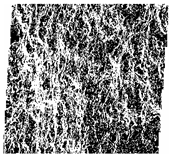 |  |
| #S9 |  |  |  |
| #S15 | 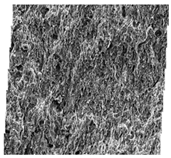 |  |  |
| #S17 |  |  |  |
| #S21 | 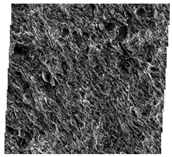 |  |  |
| #S24 | 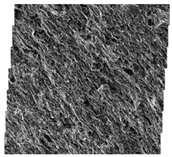 |  | 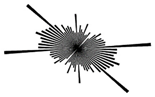 |
| #S30 | 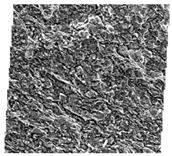 |  |  |
| #S32 |  |  |  |
| #S33 |  | 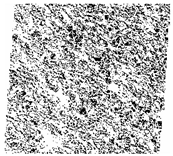 |  |
| #S38 | 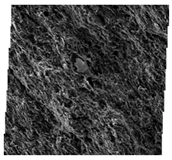 |  |  |
| #S39 |  |  |  |
| #S40 | 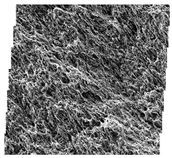 |  |  |
| #S41 |  |  |  |
| #S43 |  |  |  |
| #S44 |  |  |  |
| #S49 |  |  |  |
| #S50 |  |  |  |
| #S52 |  |  |  |
| #S63 | 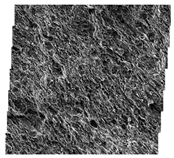 |  |  |
Appendix D
| Sample No. | Formation | Count | DmaxG (μm) | DminG (μm) | DaveG (μm) | AngleG (°) | PeriG (μm) | FlatG |
|---|---|---|---|---|---|---|---|---|
| #S1 | Chang #7 | 2659 | 53.138 | 0.756 | 15.462 | 77.721 | 18.640 | 1.193 |
| #S4 | Chang #7 | 2568 | 53.130 | 0.866 | 15.526 | 74.754 | 19.027 | 1.069 |
| #S9 | Chang #7 | 1718 | 64.910 | 0.123 | 20.889 | 88.267 | 20.876 | 1.069 |
| #S15 | Chang #7 | 2213 | 61.522 | 0.029 | 27.507 | 89.048 | 19.701 | 1.993 |
| #S17 | Chang #7 | 2046 | 55.946 | 0.465 | 21.615 | 84.663 | 17.599 | 2.130 |
| #S21 | Chang #7 | 2663 | 60.241 | 0.496 | 20.089 | 83.710 | 17.934 | 1.578 |
| #S24 | Chang #7 | 2936 | 51.674 | 0.091 | 16.025 | 80.341 | 16.129 | 1.974 |
| #S30 | Chang #7 | 2226 | 55.973 | 0.861 | 22.665 | 88.303 | 18.566 | 1.162 |
| #S32 | Chang #7 | 1946 | 53.928 | 0.565 | 10.694 | 87.338 | 12.192 | 1.208 |
| #S33 | Chang #7 | 1655 | 46.706 | 0.871 | 26.804 | 95.827 | 19.565 | 2.178 |
| #S38 | Chang #7 | 1696 | 57.061 | 0.282 | 20.574 | 91.708 | 21.274 | 1.532 |
| S#39 | Chang #7 | 1964 | 55.303 | 0.064 | 16.507 | 86.510 | 15.230 | 2.412 |
| S#40 | Chang #7 | 1824 | 50.123 | 0.014 | 14.271 | 85.211 | 15.214 | 1.795 |
| S#41 | Chang #7 | 2208 | 38.403 | 0.009 | 23.093 | 89.814 | 18.072 | 1.880 |
| S#43 | Chang #7 | 2993 | 60.682 | 0.064 | 15.325 | 85.962 | 19.636 | 2.000 |
| S#44 | Chang #7 | 1953 | 56.414 | 0.009 | 22.491 | 88.890 | 17.905 | 2.000 |
| S#49 | Chang #7 | 1690 | 55.925 | 0.039 | 18.579 | 89.953 | 19.358 | 2.271 |
| S#50 | Chang #7 | 2562 | 59.628 | 0.013 | 25.654 | 89.064 | 17.373 | 2.119 |
| S#52 | Chang #7 | 2509 | 55.476 | 0.008 | 35.13 | 86.690 | 18.676 | 1.334 |
| S#63 | Chang #7 | 2302 | 55.558 | 0.060 | 16.433 | 87.112 | 18.058 | 1.500 |
| Sample No. | Formation | Count | DmaxP (μm) | DminP (μm) | DaveP (μm) | AngleP (°) | PeriP (μm) | FlatP |
|---|---|---|---|---|---|---|---|---|
| #S1 | Chang #7 | 1894 | 52.561 | 0.001 | 18.640 | 85.202 | 8.143 | 2.979 |
| #S4 | Chang #7 | 2322 | 54.145 | 0.538 | 19.027 | 69.979 | 13.049 | 2.629 |
| #S9 | Chang #7 | 2221 | 52.962 | 0.077 | 20.876 | 88.208 | 9.173 | 1.131 |
| #S15 | Chang #7 | 1327 | 56.334 | 0.079 | 19.701 | 87.660 | 20.469 | 1.730 |
| #S17 | Chang #7 | 1983 | 63.631 | 0.028 | 17.599 | 86.326 | 11.086 | 2.016 |
| #S21 | Chang #7 | 1153 | 62.244 | 0.084 | 17.934 | 86.649 | 8.601 | 1.685 |
| #S24 | Chang #7 | 2296 | 55.418 | 0.076 | 16.129 | 72.340 | 16.457 | 1.211 |
| #S30 | Chang #7 | 2983 | 63.516 | 0.018 | 18.566 | 76.924 | 10.793 | 1.711 |
| #S32 | Chang #7 | 2865 | 57.283 | 0.025 | 12.192 | 66.133 | 21.929 | 1.209 |
| #S33 | Chang #7 | 1663 | 58.598 | 0.021 | 19.565 | 89.885 | 25.818 | 1.235 |
| #S38 | Chang #7 | 2004 | 58.061 | 0.028 | 21.274 | 85.114 | 15.589 | 1.700 |
| S#39 | Chang #7 | 2245 | 51.024 | 0.064 | 15.230 | 74.521 | 18.524 | 1.287 |
| S#40 | Chang #7 | 2502 | 54.442 | 0.014 | 15.214 | 84.441 | 19.884 | 2.620 |
| S#41 | Chang #7 | 1918 | 57.145 | 0.026 | 18.640 | 87.259 | 17.377 | 2.130 |
| S#43 | Chang #7 | 2384 | 57.901 | 0.062 | 25.462 | 85.778 | 16.774 | 1.102 |
| S#44 | Chang #7 | 2231 | 56.786 | 0.002 | 25.526 | 89.752 | 21.063 | 1.340 |
| S#49 | Chang #7 | 2576 | 58.667 | 0.018 | 24.839 | 89.421 | 17.694 | 3.136 |
| S#50 | Chang #7 | 2167 | 61.190 | 0.013 | 30.889 | 86.265 | 20.598 | 1.209 |
| S#52 | Chang #7 | 1885 | 61.760 | 0.019 | 27.507 | 88.356 | 20.137 | 2.770 |
| S#63 | Chang #7 | 2811 | 61.452 | 0.024 | 21.615 | 88.427 | 15.278 | 1.868 |
Appendix E
References
- U.S. Energy Information Administration. Annual Energy Outlook 2020 with Projections to 2050. Available online: http://www.eia.gov/aeo (accessed on 1 December 2020).
- Jiang, Z.; Song, Y.; Tang, X.; Li, Z.; Wang, X.; Wang, G.; Xue, Z.; Li, X.; Zhang, K.; Chang, J.; et al. Controlling factors of marine shale gas differential enrichment in southern China. Pet. Explor. Dev. 2020, 47, 661–673. [Google Scholar] [CrossRef]
- Liu, X.; Xiong, J.; Liang, L. Investigation of pore structure and fractal characteristics of organic-rich Yanchang formation shale in central China by nitrogen adsorption/desorption analysis. J. Nat. Gas Sci. Eng. 2015, 22, 62–72. [Google Scholar] [CrossRef]
- Liu, D.; Li, H.; Zhang, C.; Wang, Q.; Peng, P. Experimental investigation of pore development of the Chang 7 member shale in the Ordos basin under semi-closed high-pressure pyrolysis. Mar. Pet. Geol. 2019, 99, 17–26. [Google Scholar] [CrossRef]
- Jarvie, D.M.; Hill, R.J.; Ruble, T.E.; Pollastro, R.M. Unconventional shale-gas systems: The Mississippian Barnett Shale of north-central Texas as one model for thermogenic shale-gas assessment. AAPG Bull. 2007, 91, 475–499. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Elsworth, D.; Leong, Y.; Li, W.; Zeng, J. Shale gas production from reservoirs with hierarchical multiscale structural heterogeneities. J. Pet. Sci. Eng. 2022, 208, 109380. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Elsworth, D.; Leong, Y.; Li, W. An effective stress-dependent dual-fractal permeability model for coal considering multiple flow mechanisms. Fuel 2023, 224, 126800. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, S.; Lu, S.; He, Z.; Li, D.; Wang, Z.; Xiao, D. Investigation of mechanical properties of bedded shale by nanoindentation tests: A case study on Lower Silurian Longmaxi Formation of Youyang area in southeast Chongqing, China. Pet. Explor. Dev. 2019, 46, 155–164. [Google Scholar] [CrossRef]
- Wang, M.; Guo, Z.; Jiao, C.; Lu, S.; Li, J.; Xue, H.; Li, J.; Li, J.; Chen, G. Exploration progress and geochemical features of lacustrine shale oils in China. J. Pet. Sci. Eng. 2019, 178, 975–986. [Google Scholar] [CrossRef]
- Alexander, Z.; Adam, P.; Tracy, B.; John, A.; Selim, E. A robust algorithm to calculate parent β grain shapes and orientations from α phase electron backscatter diffraction data in α/β-titanium alloys. Scripta Mater. 2021, 191, 191–195. [Google Scholar]
- McDonald, S.A.; Reischig, P.; Holzner, C.; Lauridsen, E.M.; Withers, P.J.; Merkle, A.P.; Feser, M. Non-destructive mapping of grain orientations in 3D by laboratory X-ray microscopy. Sci. Rep. 2015, 5, 14665. [Google Scholar] [CrossRef]
- Gillott, J.E. Fabric of Leda clay investigated by optical, electron-optical, and X-ray diffraction methods. Eng. Geol. 1970, 4, 133–153. [Google Scholar] [CrossRef]
- Smeets, S.; Zou, X.; Wan, W. Serial electron crystallography for structure determination and phase analysis of nanocrystalline materials. J. Appl. Crystallogr. 2018, 51, 1262–1273. [Google Scholar] [CrossRef] [PubMed]
- Fredrik, K.; Mürer, A.S.M.; Kim, R.T.; Marco., D.; Pierre., C.; Basab, C.; Dag, W.B. Orientational mapping of minerals in Pierre shale using X-ray diffraction tensor tomography. IUCrJ 2021, 8, m0800747. [Google Scholar]
- Florio, B.J.; Fawell, P.D.; Small, M. The use of the perimeter-area method to calculate the fractal dimension of aggregates. Powder Technol. 2019, 343, 551–559. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-similarity of complex networks. Nature 2005, 433, 392. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Gallos, L.K.; Havlin, S.; Makse, H.A. How to calculate the fractal dimension of a complex network: The box covering algorithm. J. Stat. Mech. 2007, 7, P03006. [Google Scholar] [CrossRef]
- Neil, G.; Curtis, K.M. Shape recognition using fractal geometry. Pattern Recognit. 1997, 30, 1957–1969. [Google Scholar] [CrossRef]
- Montgomery, S.L.; Jarvie, D.M.; Bowker, K.A.; Pollastro, R.M. Mississippian Barnett shale, fortworth basin, north-central Texas: Gas-shale play with multi-trillion cubic foot potential. AAPG Bull. 2005, 89, 155–175. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, C.; Cai, X.; Huang, Y. Three-dimensional modeling and analysis of fractal characteristics of rupture source combined acoustic emission and fractal theory. Chaos Solitons Fractals 2022, 160, 112308. [Google Scholar] [CrossRef]
- Chaudhuri, B.B.; Sarkar, N. Texture segmentation using fractal dimension. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 72–77. [Google Scholar] [CrossRef]
- Wu, Y. Quantitative Research into the Microstructure of Clay Mineral. Ph.D. Thesis, Chinese Academy of Geological Sciences, Beijing, China, 1988. (In Chinese). [Google Scholar]
- Liu, A.C.; Missiaen, T.; Henriet, J.P. The morphology of the top-Tertiary erosion surface in the Belgian sector of the North Sea. Mar. Geol. 1992, 105, 275–284. [Google Scholar] [CrossRef]
- Xie, D. Thoughts on soil mechanics in the 21st century. J. Geotech. Eng. 1997, 19, 111–114. [Google Scholar]
- Xia, Y.; Wei, W.; Liu, Y.; Cai, Z.; Zhang, Q.; Cai, J. A fractal-based approach to evaluate the effect of microstructure on the permeability of two-dimensional porous media. Appl. Geochem. 2021, 131, 105013. [Google Scholar] [CrossRef]
- Zhu, W.; He, X.; Lei, G.; Wang, M. Complexity analysis of three-dimensional stochastic discrete fracture networks with fractal and multifractal techniques. J. Struct. Geol. 2022, 162, 104690. [Google Scholar] [CrossRef]
- Li, H.; Liang, J.; Li, C.; Li, G.; Meng, Y.; Yang, P. A novel method to improve mud pulse telemetuy performance during gaseated underbalanced drilling. J. Pet. Sci. Eng. 2022, 213, 110400. [Google Scholar] [CrossRef]
- Zhang, W.; Xie, L.; Yang, W.; Qin, Y.; Peng, P. Micro fractures and pores in lacustrine shales of the upper triassic yanchang Chang7 member, Ordos Basin, China. J. Pet. Sci. Eng. 2017, 156, 194–201. [Google Scholar] [CrossRef]
- Guo, H.; He, R.; Jia, W.; Peng, P.; Lei, Y.; Luo, X.; Wang, X.; Zhang, L.; Jiang, C. Pore characteristics of lacustrine shale within the oil window in the upper Triassic yanchang formation, southeastern Ordos Basin, China. Mar. Pet. Geol. 2018, 91, 279–296. [Google Scholar] [CrossRef]
- Qiu, Z.; Liu, B.; Lu, B.; Shi, Z.; Li, Z. Mineralogical and petrographic characteristics of the Ordovician-Silurian Wufeng-Longmaxi Shale in the Sichuan Basin and implications for depositional conditions and diagenesis of black shales. Mar. Pet. Geol. 2022, 135, 105428. [Google Scholar] [CrossRef]
- Li, X.; Tuo, J.; Wu, C.; Xin, H.; Zhang, M.; Zheng, J.; Ma, X. Organic matter heterogeneity and shale oil significance in Triassic Zhangjiatan shale, Ordos Basin, China. Energy Explor. Exploit. 2022, 40, 224–245. [Google Scholar] [CrossRef]
- Wang, R.; Singh, A.K.; Kolan, S.R.; Tsotsas, E. Fractal analysis of aggregates: Correlation between the 2D and 3D box-counting fractal dimension and power law fractal dimension. Chaos Solitons Fractals 2022, 160, 112246. [Google Scholar] [CrossRef]
- Bennett, R.H.; Hulbert, M.H. Clay Microstructure; International Human Resources Development Corporation: Boston, MA, USA, 1986. [Google Scholar]
- Deng, H.C.; Hu, X.F.; Li, H.A.; Luo, B.; Wang, W. Improved pore-structure characterization in shale formations with FESEM technique. J. Nat. Gas Sci. Eng. 2016, 35, 309–319. [Google Scholar] [CrossRef]
- Luan, X.; Di, B.; Wei, J.; Zhao, J.; Li, X. Creation of synthetic samples for physical modelling of natural shale. Geophys. Prospect. 2016, 898–914. [Google Scholar] [CrossRef]
- Xie, X. The Orientated Structure Characteristics of Fine-Grained Rock and Its Mechanism Research: A Case Study of Yanchang 7 Member Formation, Ordos Basin. Ph.D. Thesis, Chengdu University of Technology, Chengdu, China, 2022. (In Chinese). [Google Scholar]
- Lu, H.; Li, Q.; Yue, D.; Wu, Y.; Gao, J.; Wu, S.; Wang, W.; Li, M.; An., K. Quantitative characterization and formation mechanism of the pore system heterogeneity: Examples from organic-rich laminated and organic-poor layered shales of the upper triassic chang 7 member in the southern Ordos Basin, China. Mar. Pet. Geol. 2023, 147, 105999. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Z.; Zhang, L. Control actions of sedimentary environments and sedimentation rates on lacustrine oil shale distribution, an example of the oil shale in the Upper Triassic Yanchang Formation, southeastern Ordos Basin (NW China). Mar. Pet. Geol. 2019, 102, 508–520. [Google Scholar] [CrossRef]












| No. | Symbols | Interpretation | Note |
|---|---|---|---|
| 1 | DmaxG | The long axis of the ellipse |  |
| 2 | DminG | The short axis of the ellipse |  |
| 3 | Dave | The average of the short and long axis of the ellipse | / |
| 4 | AngleG | Dip angle | 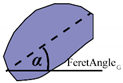 |
| 5 | PeriG | Perimeter of the ellipse | / |
| 6 | FlatG | The ratio between the long and short axis of the ellipse |
| No. | Fractal Dimension | Mathematic Formulas | Parameters 1 | Parameters 2 |
|---|---|---|---|---|
| 1 | Fractal dimension of grain flatness (DGF) | ε refers to grain flatness (FeretMaxG/FeretMinG) | Number of grain flatness that exceeds a specific flatness | |
| 2 | Fractal dimension of pore flatness (DPF) | ε refers to pore flatness (FeretMaxP/FeretMinP) | Number of pore flatness that exceeds a specific flatness | |
| 3 | Fractal dimension of grain size (DGS) | ε refers to the maximum diameter of shale grains (FeretMaxG) | Number of grains that exceed a specific grain diameter | |
| 4 | Fractal dimension of pore size (DPS) | ε refers to the maximum diameter of shale pores (FeretMaxP) | Number of pores that exceed a specific pore diameter | |
| 5 | Fractal dimension of the grain size distribution (DGD) | ε refers to grid length (FeretMaxP) | Number of boxes at grid length ε | |
| 6 | Fractal dimension of the pore size distribution (DPD) | ε refers to grid length (FeretMaxP) | Number of boxes at grid length ε | |
| 7 | Fractal dimension of grain orientation (DGO) | α refers to the angle between the maximum diameter of the grain and the horizontal plane (FeretAngleG) | The total number of grids on the image containing grains. | |
| 8 | Fractal dimension of pore orientation (DPO) | α refers to the angle between the maximum diameter of the pore and the horizontal plane (FeretAnglep) | The total number of grids on the image containing pores. | |
| 9 | Fractal dimension of surface roughness (DSR) | X refers to the horizontal distance of the sampling point. M denotes the total number of contour heights separated by a distance of h. | Z(x) represents the height of the roughness profile from the reference surface. |
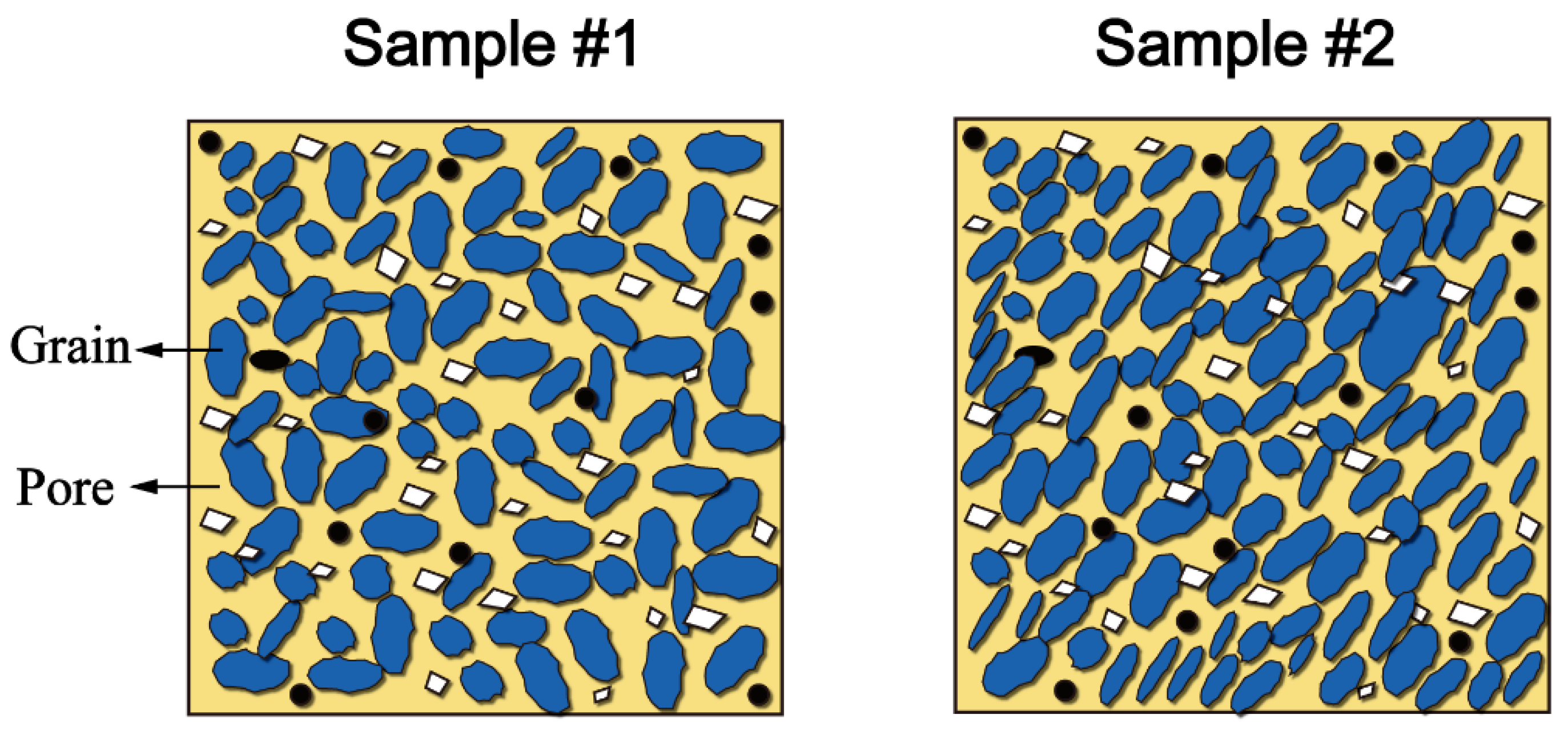
| No. | Parameters | Sample #1 | Sample #2 | Variation Rate * (%) |
|---|---|---|---|---|
| 1 | DGF | 0.9553 | 0.9648 | 1.21 |
| 2 | DPF | 0.9575 | 0.9644 | 0.71 |
| 3 | DGO | 0.9762 | 0.9149 | 6.28 |
| 4 | DPO | 0.9432 | 0.8787 | 6.83 |
| 5 | DGS | 0.8702 | 0.8054 | 7.46 |
| 6 | DPS | 0.9245 | 0.9225 | 2.06 |
| 7 | DGD | 1.8689 | 1.8288 | 2.15 |
| 8 | DPD | 1.9047 | 1.8765 | 1.48 |
| 9 | DSR | 1.2163 | 1.2048 | 0.94 |
| Sample No. | DGO | DPO | DGS | Permeability (mD) |
|---|---|---|---|---|
| #G1 | 0.781 | 0.771 | 0.792 | 0.219 |
| #G2 | 0.799 | 0.78 | 0.798 | 0.208 |
| #G3 | 0.811 | 0.819 | 0.778 | 0.197 |
| #G4 | 0.823 | 0.801 | 0.829 | 0.185 |
| #G5 | 0.852 | 0.847 | 0.894 | 0.137 |
| #G6 | 0.908 | 0.931 | 0.822 | 0.112 |
| #G7 | 0.892 | 0.973 | 0.831 | 0.099 |
| #G8 | 0.912 | 0.983 | 0.864 | 0.081 |
| #G9 | 0.99 | 0.974 | 0.867 | 0.058 |
| #G10 | 0.904 | 0.952 | 0.981 | 0.053 |
| Parameter | Function | Expression | R2 |
|---|---|---|---|
| DaveG | Gauss | 0.9852 | |
| PeriG | Gauss | 0.9814 | |
| FlatG | Lorentz | 0.9699 | |
| DaveP | Gauss | 0.9931 | |
| PeriP | Gauss | 0.9981 | |
| FlatP | Lorentz | 0.9681 |
| Sample No. | DGO | DPO | DGS | SOE |
|---|---|---|---|---|
| #S1 | 0.981 | 0.938 | 0.823 | 0.912 |
| #S4 | 0.990 | 0.974 | 0.867 | 0.943 |
| #S9 | 0.971 | 0.991 | 0.941 | 0.968 |
| #S15 | 0.990 | 0.968 | 0.821 | 0.925 |
| #S17 | 0.831 | 0.819 | 0.883 | 0.842 |
| #S21 | 0.781 | 0.771 | 0.792 | 0.780 |
| #S24 | 0.952 | 0.975 | 0.872 | 0.934 |
| #S30 | 0.914 | 0.892 | 0.891 | 0.897 |
| #S32 | 0.908 | 0.950 | 0.853 | 0.906 |
| #S33 | 0.933 | 0.958 | 0.907 | 0.934 |
| #S38 | 0.827 | 0.904 | 0.874 | 0.872 |
| #S39 | 0.954 | 0.957 | 0.852 | 0.921 |
| #S40 | 0.932 | 0.969 | 0.931 | 0.945 |
| #S41 | 0.881 | 0.919 | 0.876 | 0.894 |
| #S43 | 0.941 | 0.981 | 0.847 | 0.925 |
| #S44 | 0.927 | 0.967 | 0.906 | 0.935 |
| #S49 | 0.981 | 0.960 | 0.925 | 0.954 |
| #S50 | 0.982 | 0.953 | 0.956 | 0.961 |
| #S52 | 0.991 | 0.973 | 0.931 | 0.963 |
| #S63 | 0.981 | 0.971 | 0.940 | 0.963 |
| Mineral | Correlations | R2 | Relationship |
|---|---|---|---|
| Quartz | y = 0.8581 + 0.0017x | 0.0392 | Independent |
| Feldspar | y = 0.8606 + 0.0022x | 0.2231 | Independent |
| Calcite | y = 0.8834 + 0.0104x | 0.0816 | Independent |
| Dolomite | y = 0.8912 + 0.0032x | 0.0843 | Independent |
| Pyrite | y = 0.8866 + 0.0024x | 0.1181 | Independent |
| Clay | y = 0.9899 − 0.0018x | 0.7559 | Correlated |
| TOC | y = 0.9294 − 0.0048x | 0.6379 | Correlated |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Deng, H.; Li, Y.; Hu, L.; Mao, J.; Li, R. Investigation of the Oriented Structure Characteristics of Shale Using Fractal and Structural Entropy Theory. Fractal Fract. 2022, 6, 734. https://doi.org/10.3390/fractalfract6120734
Xie X, Deng H, Li Y, Hu L, Mao J, Li R. Investigation of the Oriented Structure Characteristics of Shale Using Fractal and Structural Entropy Theory. Fractal and Fractional. 2022; 6(12):734. https://doi.org/10.3390/fractalfract6120734
Chicago/Turabian StyleXie, Xinhui, Hucheng Deng, Yong Li, Lanxiao Hu, Jinxin Mao, and Ruixue Li. 2022. "Investigation of the Oriented Structure Characteristics of Shale Using Fractal and Structural Entropy Theory" Fractal and Fractional 6, no. 12: 734. https://doi.org/10.3390/fractalfract6120734
APA StyleXie, X., Deng, H., Li, Y., Hu, L., Mao, J., & Li, R. (2022). Investigation of the Oriented Structure Characteristics of Shale Using Fractal and Structural Entropy Theory. Fractal and Fractional, 6(12), 734. https://doi.org/10.3390/fractalfract6120734







