New Bright and Kink Soliton Solutions for Fractional Complex Ginzburg–Landau Equation with Non-Local Nonlinearity Term
Abstract
1. Introduction
2. Preliminaries
3. Transformation and Hamiltonian
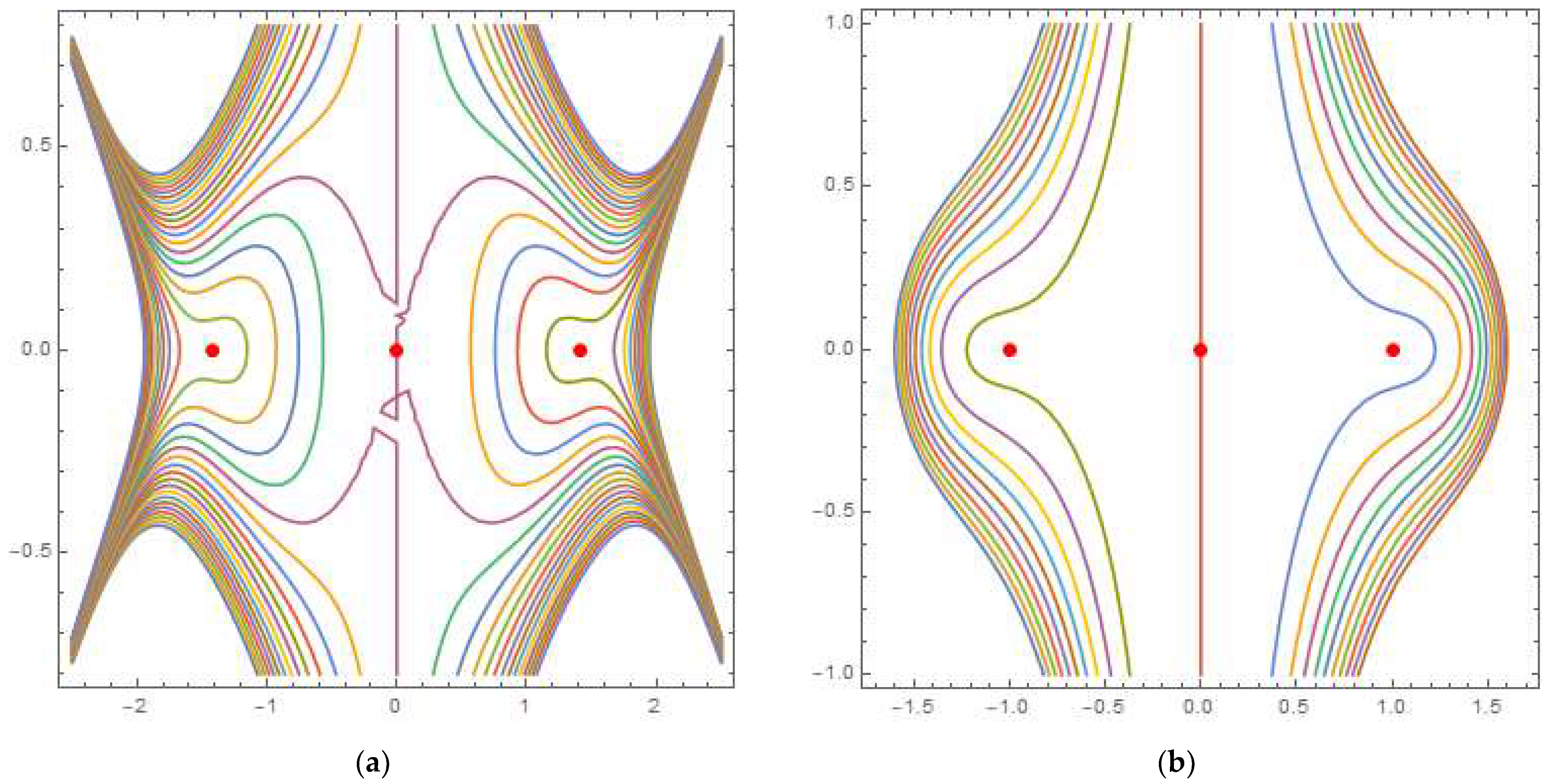
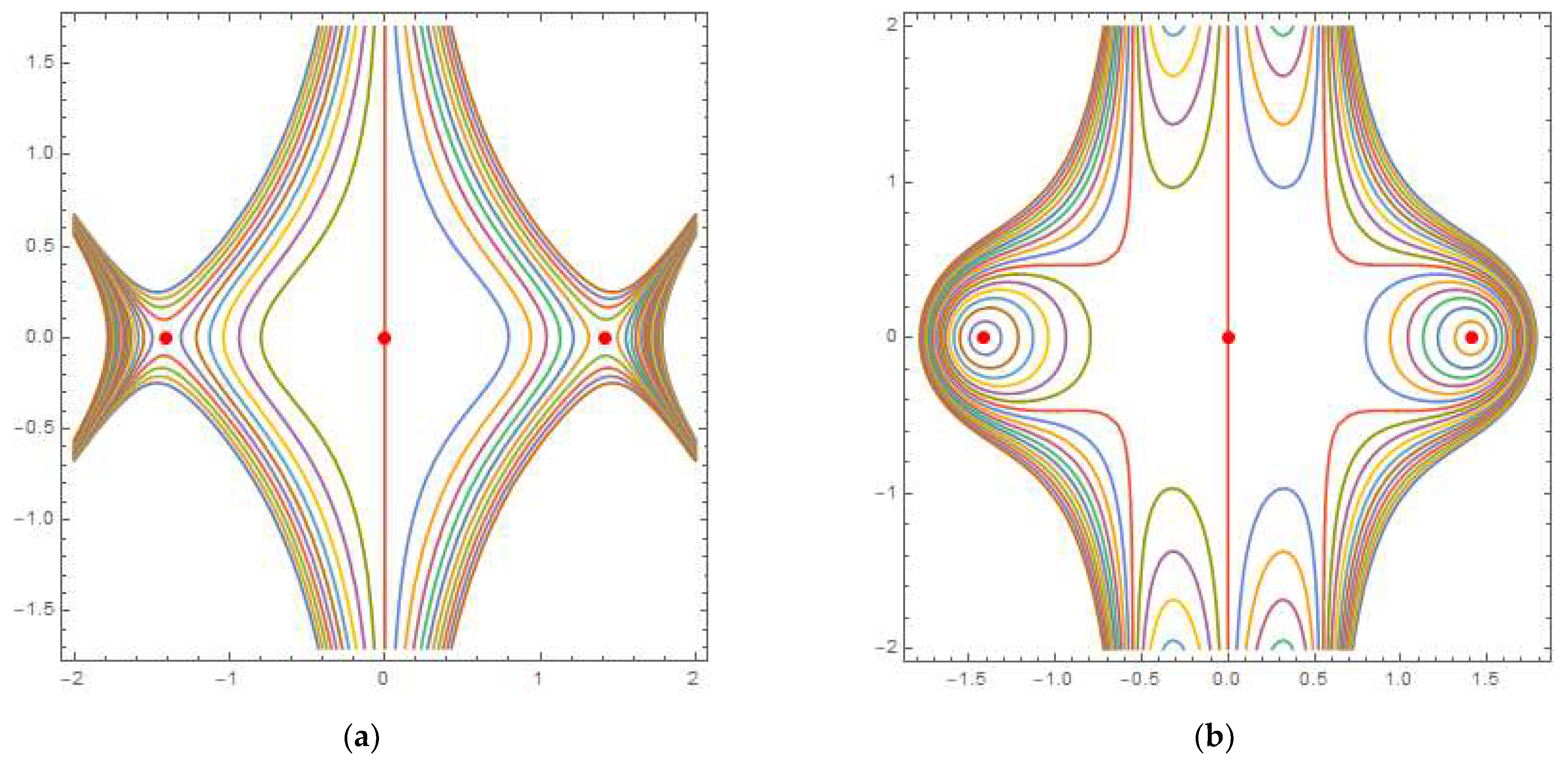
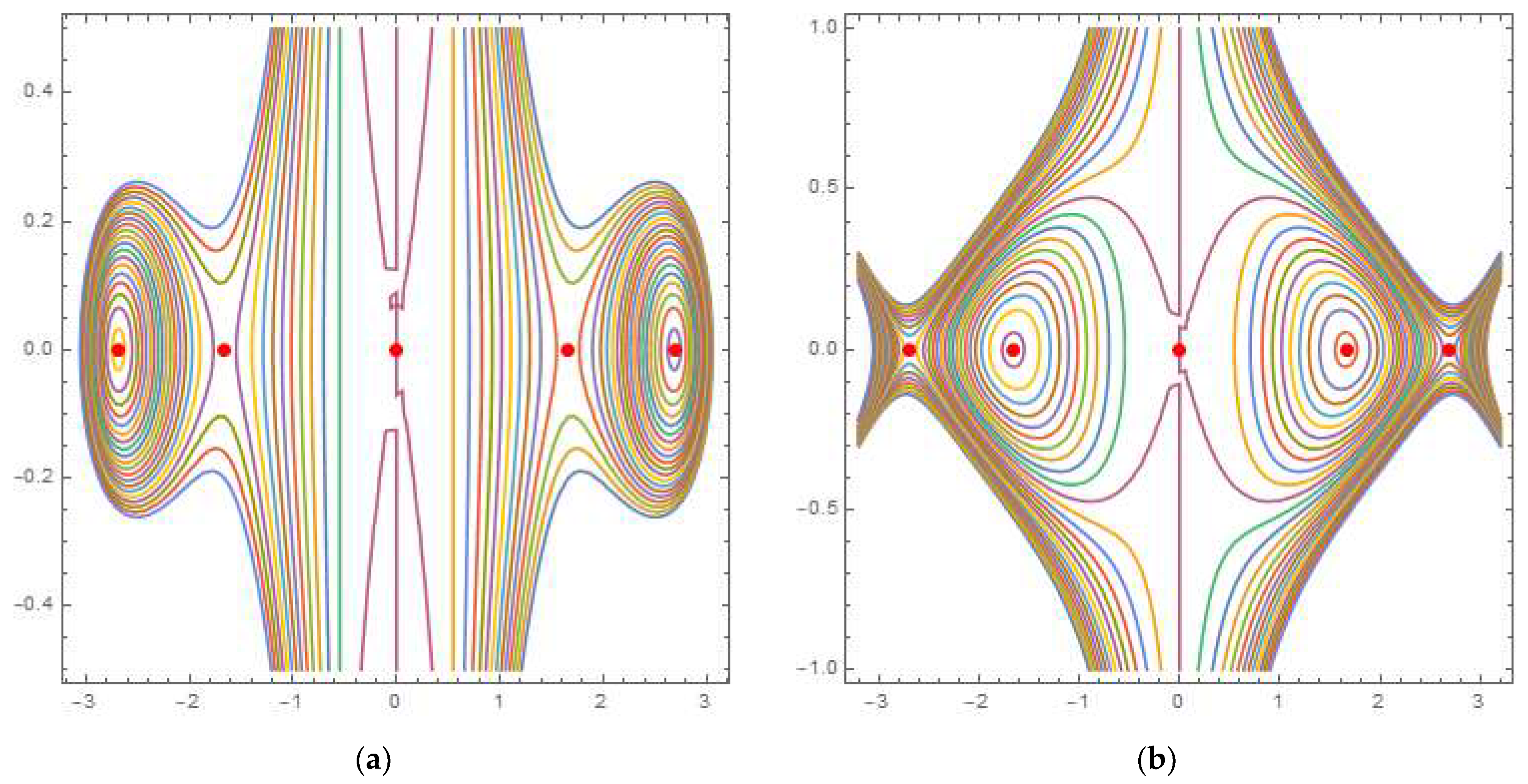
4. Equilibria Classification
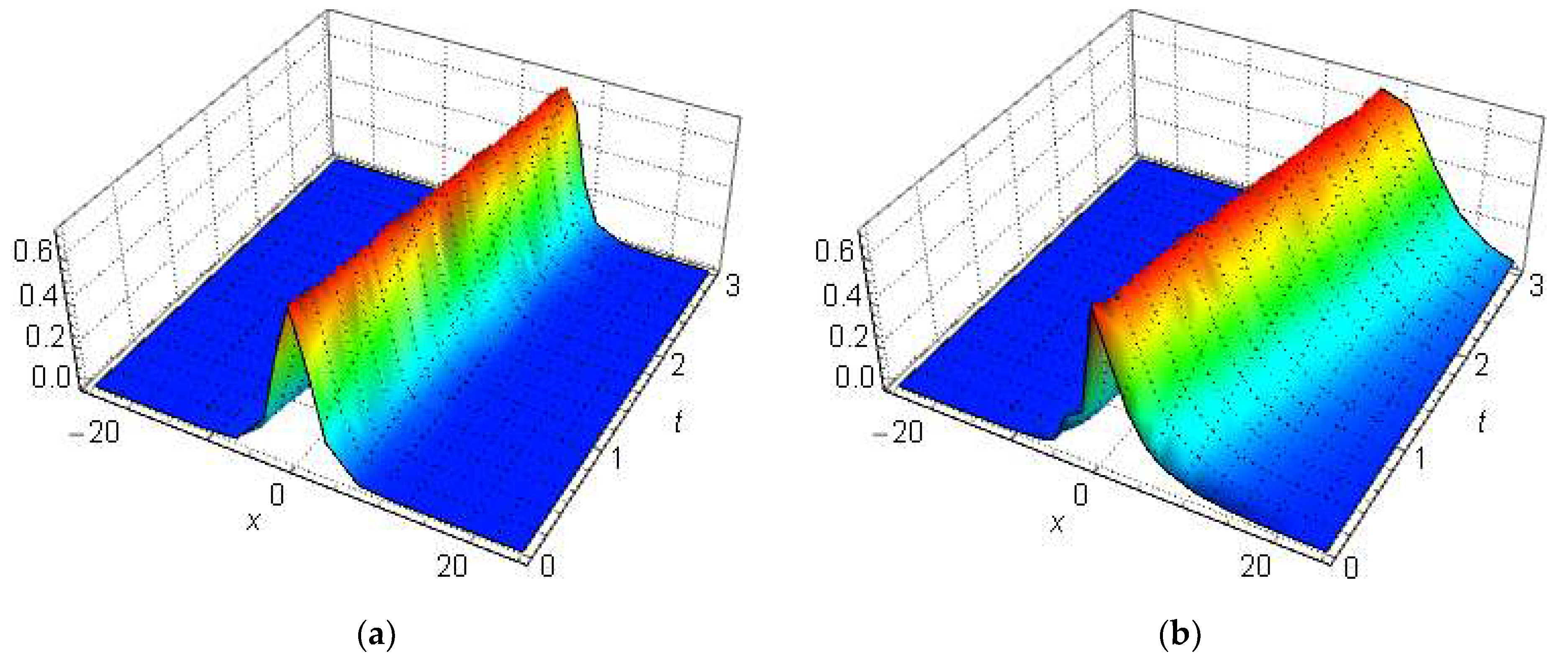
5. Bright and Kink Wave Solutions
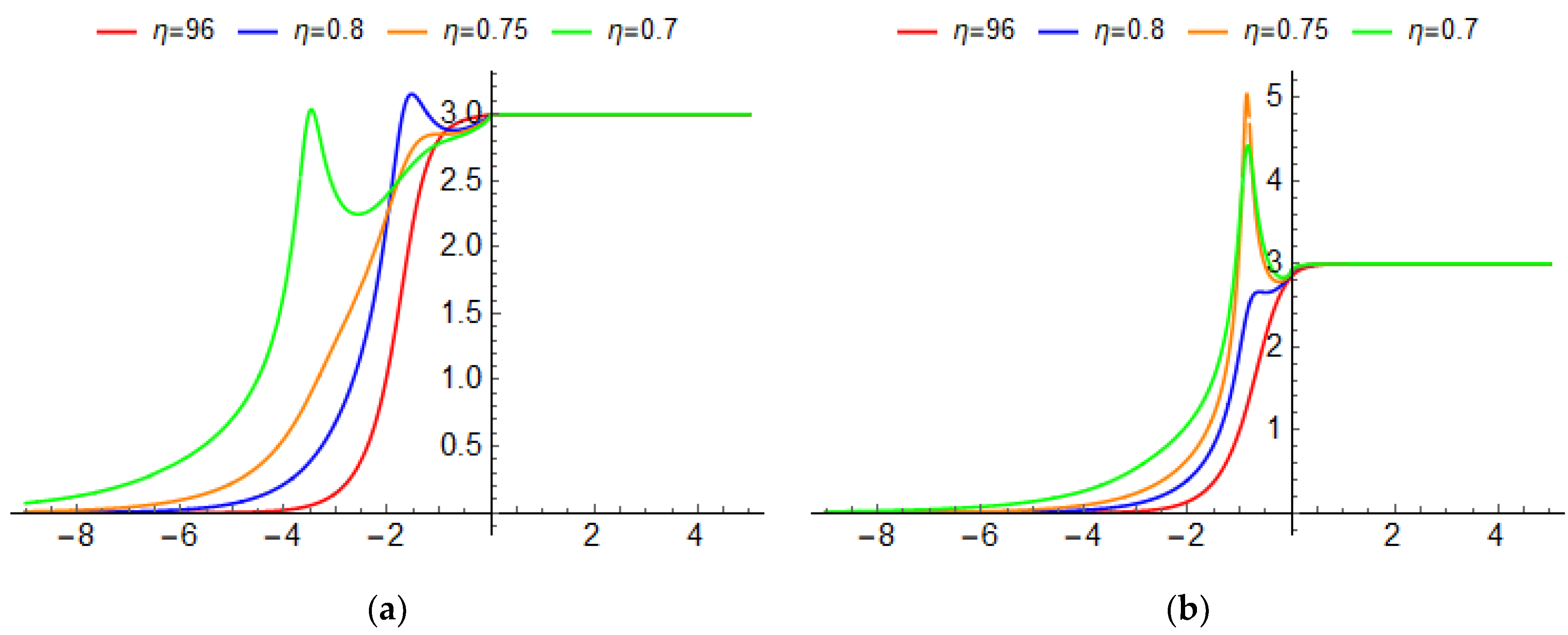
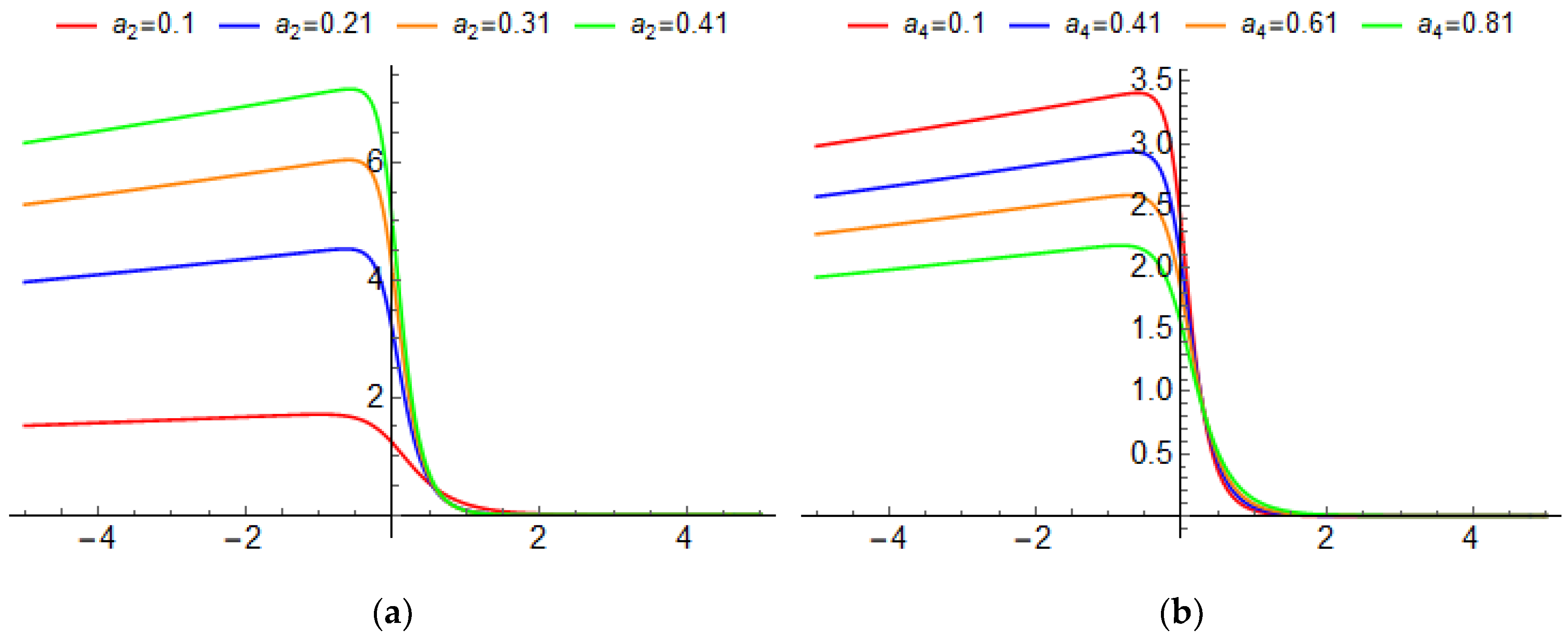
5.1. Bright Soliton
5.2. Kink Soliton
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goyal, A.; Alka; Raju, T.S.; Kumar, C.N. Lorentzian-type soliton solutions of ac-driven complex Ginzburg–Landau equation. Appl. Math. Comput. 2012, 218, 11931–11937. [Google Scholar] [CrossRef]
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef]
- Hasan, S.; Nadir Djeddi, N.; Al-Smadi, M.; Al-Omari, S.; Momani, S.; Fulga, A. Numerical solvability of generalized Bagley–Torvik fractional models under Caputo–Fabrizio derivative. Adv. Differ. Equ. 2022, 469, 1–21. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, A. Computational algorithm for solving fredholm time-fractional partial integro dif-ferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar] [CrossRef]
- García-Morales, V.; Krischer, K. The complex Ginzburg–Landau equation: An introduction. Contemp. Phys. 2012, 53, 79–95. [Google Scholar] [CrossRef]
- Shqair, M.; Alabedalhadi, M.; Al-Omari, S.; Al-Smadi, M. Abundant Exact Travelling Wave Solutions for a Fractional Massive Thirring Model Using Extended Jacobi Elliptic Function Method. Fractal Fract. 2022, 6, 252. [Google Scholar] [CrossRef]
- Sakaguchi, H. Phase dynamics of the coupled complex ginzburg-landau equations. Prog. Theor. Phys. 1995, 93, 491–502. [Google Scholar] [CrossRef]
- Megne, L.T.; Tabi, C.B.; Kofane, T.C. Modulation instability in nonlinear metamaterials modeled by a cubic-quintic complex Ginzburg-Landau equation beyond the slowly varying envelope approximation. Phys. Rev. E 2020, 102, 042207. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Y.; Li, J. Exact solitary wave and periodic-peakon solutions of the complex Ginzburg–Landau equation: Dynamical system approach. Math. Comput. Simul. 2022, 191, 157–167. [Google Scholar] [CrossRef]
- Yao, S.-W.; Ilhan, E.; Veeresha, P.; Baskonus, H.M. A powerful iterative approach for quintic complex ginzburg–landau equation within the frame of fractional operator. Fractals 2021, 29, 2140023. [Google Scholar] [CrossRef]
- Al-Smadi, M. Fractional residual series for conformable time-fractional Sawada–Kotera–Ito, Lax, and Kaup–Kupershmidt equations of seventh order. Math. Methods Appl. Sci. 2021. early view. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Osman, M.S.; Al Qurashi, M.; Baleanu, D. Solitons and Jacobi Elliptic Function Solutions to the Complex Ginzburg–Landau Equation. Front. Phys. 2020, 8, 225. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E.; El-Horbaty, M.; Biswas, A.; Alshomrani, A.S.; Ekici, M.; Yıldırım, Y.; Belic, M.R. Optical solitons with complex Ginzburg-Landau equation having a plethora of nonlinear forms with a couple of improved integration norms. Optik 2020, 207, 163804. [Google Scholar] [CrossRef]
- Zhu, W.; Xia, Y.; Bai, Y. Traveling wave solutions of the complex Ginzburg-Landau equation with Kerr law non-linearity. Appl. Math. Comput. 2020, 382, 125342. [Google Scholar] [CrossRef]
- Salete, E.; Vargas, A.M.; García, Á.; Negreanu, M.; Benito, J.J.; Ureña, F. Complex Ginzburg–Landau Equation with Generalized Finite Differences. Mathematics 2020, 8, 2248. [Google Scholar] [CrossRef]
- Diaz, J.I.; Padial, J.; Tello, J.I.; Tello, L. Complex Ginzburg-Landau equations with a delayed nonlocal perturbation. Electron. J. Differ. Equ. 2020, 40, 1–18. [Google Scholar]
- Matsuda, T. Global well-posedness of the two-dimensional stochastic complex Ginzburg-Landau equation with cubic nonlinearity. arXiv 2020, arXiv:2003.01569, preprint. [Google Scholar]
- Hosseini, K.; Mirzazadeh, M.; Baleanu, D.; Raza, N.; Park, C.; Ahmadian, A.; Salahshour, S. The generalized complex Ginzburg–Landau model and its dark and bright soliton solutions. Eur. Phys. J. Plus 2021, 136, 1–12. [Google Scholar] [CrossRef]
- Alneimat, M.; Moakher, M.; Djeddi, N.; Al-Omari, S. Numerical Solution of Fractional Model of Atangana-Baleanu-Caputo Integrodifferential Equations with Integral Boundary Conditions. J. Appl. Math. E-Notes 2022. to appear. [Google Scholar]
- Hussain, A.; Jhangeer, A.; Abbas, N.; Khan, I.; Sherif, E.S.M. Optical solitons of fractional complex Ginzburg–Landau equation with conformable, beta, and M-truncated derivatives: A comparative study. Adv. Differ. Equ. 2020, 2020, 612. [Google Scholar] [CrossRef]
- Qiu, Y.; Malomed, B.A.; Mihalache, D.; Zhu, X.; Zhang, L.; He, Y. Soliton dynamics in a fractional complex Ginz-burg-Landau model. Chaos Solitons Fractals 2020, 131, 109471. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Sun, H.-W. Exponential Runge–Kutta Method for Two-Dimensional Nonlinear Fractional Complex Ginzburg–Landau Equations. J. Sci. Comput. 2020, 83, 1–24. [Google Scholar] [CrossRef]
- Lu, P.; Wang, B.; Dai, C. Fractional traveling wave solutions of the (2 + 1)-dimensional fractional complex Ginzburg–Landau equation via two methods. Math. Methods Appl. Sci. 2020, 43, 8518–8526. [Google Scholar] [CrossRef]
- Zhang, Q.; Hesthaven, J.S.; Sun, Z.-Z.; Ren, Y. Pointwise error estimate in difference setting for the two-dimensional nonlinear fractional complex Ginzburg-Landau equation. Adv. Comput. Math. 2021, 47, 1–33. [Google Scholar] [CrossRef]
- Lu, H.; Bates, P.W.; Lü, S.; Zhang, M. Dynamics of the 3-D fractional complex Ginzburg–Landau equation. J. Differ. Equations 2015, 259, 5276–5301. [Google Scholar] [CrossRef]
- Huang, C.; Li, Z. New Exact Solutions of the Fractional Complex Ginzburg–Landau Equation. Math. Probl. Eng. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Layek, G.C. An Introduction to Dynamical Systems and Chaos; Springer: New Delhi, India, 2015; Volume 449. [Google Scholar]
- Chow, S.N.; Hale, J.K. Methods of Bifurcation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 251. [Google Scholar]
- Singh, S.; Kaur, L.; Sakkaravarthi, K.; Sakthivel, R.; Murugesan, K. Dynamics of higher-order bright and dark rogue waves in a new (2+1)-dimensional integrable Boussinesq model. Phys. Scr. 2020, 95, 115213. [Google Scholar] [CrossRef]
- Singh, S.; Sakkaravarthi, K.; Murugesan, K. Localized nonlinear waves on spatio-temporally controllable back-grounds for a (3 + 1)-dimensional Kadomtsev-Petviashvili-Boussinesq model in water waves. Chaos Solitons Fractals 2022, 155, 111652. [Google Scholar] [CrossRef]
- Sakkaravarthi, K.; Mareeswaran, R.B.; Kanna, T. Engineering optical rogue waves and breathers in a coupled non-linear Schrödinger system with four-wave mixing effect. Phys. Scr. 2020, 95, 095202. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Alhazmi, S.; Al-Omari, S.; Al-Smadi, M.; Momani, S. Novel bright and kink optical soliton solutions of fractional Lakshmanan-Porsezian-Daniel equation with kerr law nonlinearity in conformable sense. Fractals 2022. to appear. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Al-Omari, S.; Karaca, Y.; Momani, S. Effective analytical computational technique for conformable time-fractional nonlinear Gardner equation and Cahn-Hillard equations of fourth and sixth order emerging in dispersive media. J. Funct. Spaces 2022. to appear. [Google Scholar]
- Alaroud, M.; Ababneh, O.; Tahat, N.; Al-Omari, S. Analytic technique for solving temporal time-fractional gas dynamics equations with Caputo fractional derivative. AIMS Math. 2022, 7, 17647–17669. [Google Scholar] [CrossRef]
- Yang, X.-J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus: Theoretical Developments and Ap-plications in Physics and Engineering; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Baskonus, H.; Ruiz, L.S.; Ciancio, A. New Challenges Arising in Engineering Problems with Fractional and Integer Order. Fractal Fract. 2021, 5, 35. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A. Exact solutions to the time-fractional differential equations via local fractional derivatives. Waves Random Complex Media 2018, 28, 139–149. [Google Scholar] [CrossRef]
- Jia, Z.; Hu, M.; Chen, Q.; Jai, S. Local fractional differential equations by the Exp-function method. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1845–1849. [Google Scholar] [CrossRef]
- Bataiha, I.; Momani, S.; Quannas, A.; Momani, Z.; Hadid, S. Fractional-order COVID-19 pandamic outbreak: Modeling and stability analysis. Int. J. Biomath. 2022, 15, 2150090. [Google Scholar] [CrossRef]
- He, J.-H.; Elagan, S.; Li, Z. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 2012, 376, 257–259. [Google Scholar] [CrossRef]
- Saha, A. Bifurcation of travelling wave solutions for the generalized KP-MEW equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3539–3551. [Google Scholar] [CrossRef]
- Zhang, B.; Xia, Y.; Zhu, W.; Bai, Y. Explicit exact traveling wave solutions and bifurcations of the generalized com-bined double sinh–cosh-Gordon equation. Appl. Math. Comput. 2019, 363, 124576. [Google Scholar] [CrossRef]
- Al-qudah, Y.; Alaroud, M.; Qoqazeh, H.; Jaradat, A.; AlHazmi, S.; Al-Omari, S. Approximate Analytic-Numeric Fuzzy Solutions of Fuzzy Fractional, Equations Using Residual Power Series Approach. Symmetry 2022, 14, 804. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Smadi, M.; Al-Omari, S.; Momani, S. New optical soliton solutions for coupled resonant Davey-Stewartson system with conformable operator. Opt. Quantum Electron. 2022, 54, 392. [Google Scholar] [CrossRef]
- Hasan, S.; Harrouche, N.; Al-Omari, S.K.Q.; Al-Smadi, M.; Momani, S.; Cattani, C. Hilbert solution of fuzzy fractional boundary value problems. Comput. Appl. Math. 2022, 41, 1–22. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alabedalhadi, M.; Al-Smadi, M.; Al-Omari, S.; Karaca, Y.; Momani, S. New Bright and Kink Soliton Solutions for Fractional Complex Ginzburg–Landau Equation with Non-Local Nonlinearity Term. Fractal Fract. 2022, 6, 724. https://doi.org/10.3390/fractalfract6120724
Alabedalhadi M, Al-Smadi M, Al-Omari S, Karaca Y, Momani S. New Bright and Kink Soliton Solutions for Fractional Complex Ginzburg–Landau Equation with Non-Local Nonlinearity Term. Fractal and Fractional. 2022; 6(12):724. https://doi.org/10.3390/fractalfract6120724
Chicago/Turabian StyleAlabedalhadi, Mohammed, Mohammed Al-Smadi, Shrideh Al-Omari, Yeliz Karaca, and Shaher Momani. 2022. "New Bright and Kink Soliton Solutions for Fractional Complex Ginzburg–Landau Equation with Non-Local Nonlinearity Term" Fractal and Fractional 6, no. 12: 724. https://doi.org/10.3390/fractalfract6120724
APA StyleAlabedalhadi, M., Al-Smadi, M., Al-Omari, S., Karaca, Y., & Momani, S. (2022). New Bright and Kink Soliton Solutions for Fractional Complex Ginzburg–Landau Equation with Non-Local Nonlinearity Term. Fractal and Fractional, 6(12), 724. https://doi.org/10.3390/fractalfract6120724







