Adaptive Fuzzy Backstepping Control of Fractional-Order Chaotic System Synchronization Using Event-Triggered Mechanism and Disturbance Observer

Abstract

The synchronization of fractional-order chaotic systems is investigated using command-filtered adaptive fuzzy control with a disturbance observer, where an event-triggered mechanism and backstepping control technique are employed. In order to relieve the pressure of the continuous update of the controller and improve the resource utilization, an event-triggered control strategy is constructed to reduce the amount of communication for the actuator. Under the framework of adaptive fuzzy backstepping recursive design, fuzzy logical systems and disturbance observers are proposed to estimate the unknown parametric uncertainties and external disturbances, respectively. Moreover, a tracking differentiator is introduced to eliminate the drawback of the explosion of complexity in traditional backstepping. By applying the fractional-order stability theory, all closed-loop signals are bounded and chaos synchronization is achieved. Finally, a simulation example is provided to confirm the effectiveness of the designed method.

1. Introduction

Fractional calculus, one of the fields of mathematics, was first discussed in a letter in 1965 between the mathematicians Leibniz and L’Hospital [1]. However, it was initially confined to pure mathematical problems due to the lack of approaches for solving fractional differential equations, resulting in it not being applied to practical engineering. Due to advancements in computing technology, the memory and genetic properties of the essence of fractional calculus have been discovered, which in turn provide a forceful mathematical model for modeling actual systems [2,3,4,5]. Compared with traditional integer-order models, fractional-order (FO) differential equations can more accurately and effectively explain the dynamic behaviors of numerous physical phenomena such as electrical engineering, biological systems, and signal processing [6,7,8]. Consequently, in recent years, a growing number of researchers have studied their performance through stability analysis and control design, and many interesting results that integrate some classic control approaches and FO operators have been successively presented for FO systems in the fields of nonlinear and linear dynamics [9,10,11]. Correspondingly, a number of FO-based dynamic chaotic behaviors have been discovered to explain natural phenomena or model physical systems including the diffusion of liquid, FO Duffing’s oscillator, Rössler system, Chua’s circuit, and Chen system [4,9,12].

Chaos is an interesting phenomenon that displays a complicated, unpredictable, and sensitive dependence on the initial conditions; thus, the synchronization of chaotic systems has gained widespread attention and become a promising research topic. The primary intention of synchronization is to construct some control signals to make the synchronization errors between the drive and the response chaotic systems converge to zero. Over the past few decades, some effective control strategies have been reported to synchronize and control FO chaotic systems such as adaptive fuzzy control, sliding mode control, and backstepping control [13,14,15,16]. For two FO chaotic systems with unknown functions and external disturbances, an adaptive fuzzy synchronization control method with a fractional integral sliding mode surface was constructed so that the synchronization errors could rapidly converge to the origin [15]. The chaotic projective synchronization of incommensurate FO nonlinear systems was investigated via an adaptive fuzzy controller, where a generalized T-S fuzzy system that can approximate the arbitrary continuous function was studied in [16]. However, it is difficult to ensure that the system dimension matches the number of controllers due to the limitations of the actuator installation environment, information exchange, sensitivity identification, and other factors. Unlike [15,16], the synchronization of FO chaotic systems was studied with the help of the backstepping technique and Mittag–Leffler stability theory in [14]. An adaptive fuzzy synchronization controller using the backstepping approach was designed in [17] for FO chaotic systems with input constraints and time-varying external disturbances, where fuzzy logical systems (FLSs) were utilized to approximate system uncertainties and the FO derivative of the virtual control functions. It should be pointed out that under the backstepping control framework in [14], the repeated differentiation of virtual control signals resulted in the explosion of the complexity problem, which increased the computational burden and may have reduced control performance. Although a feasible method was mentioned in [17] to deal with unknown nonlinear functions and the derivative of virtual controllers by FLSs, the effect of fuzzy approximation was not satisfactory due to too many unknown items in the case of insufficient fuzzy rules (the number of rules is proportional to the amount of computation), which further reduced control performance or caused an exceedingly large control input. A composite learning adaptive dynamic surface control scheme was developed in [18] by utilizing the fractional dynamic surface, which not only avoided computing the fractional derivative of the virtual controller but also reduced the excessive computation burden. Based on dynamic surface control, some command-filtered control algorithms were developed to eliminate known filtering errors by constructing error compensation signals in [19,20,21]. Even though the burdensome calculation in the backstepping control algorithm has been relaxed, external disturbances have often been left out in practical chaotic systems. Disturbances, including noise, fiction, unmodeled dynamic, and parameter disturbances, generally exist in actual systems, which will bring about an undesirable effect. In [14,16,17], the maximum bound of disturbance compensated for the external disturbance. Although the external disturbance was copeddealt with, it also caused an unnecessary consumption of energy. To tackle external disturbances and improve control performance, the disturbance observer provides a reasonable anti-disturbance control strategy. In [22,23], disturbance observers were constructed to tackle external disturbances and controllers were designed based on the output of the observers. However, disturbance observers based on an adaptive command-filtered fuzzy synchronization control scheme for FO chaotic systems in the presence of disturbances and function uncertainties have rarely been studied, which motivated this work.

It needs to be pointed out that some controllers are continuously updated based on time in the aforementioned control scheme, which deviates from reality. In order to solve the problem of actuator limitations and resource limitations in practice, some sample date control strategies have been developed, where controllers are updated at periodical sampling instants. In [24,25], in view of the hereditary and memory properties of fractional calculus, FO multi-agent systems were studied using sampled date control approaches. Even though the desired control effect could be guaranteed by the sample date controllers, a small sampling period was often required, which resulted in unnecessary consumption. Hence, it is necessary to reduce similar or even identical data packages that are transmitted repeatedly in terms of saving energy. To obtain a sufficiently appropriate communication rate and ensure control performance, continuous control signals were quantized before being transmitted to the controlled system in [26]. In addition, the event-triggered strategy also provided an effective strategy for saving energy since the controller was updated only when the error-triggered mechanism was satisfied in [27,28,29]. In [27], an event-triggered control scheme with impulsive control technology was proposed to synchronize different FO chaotic systems, where the event-triggered condition depended on the state of the master and slave systems. In addition, if the difference between the states of the master and slave systems was very small, the controller output was unchanged. To obtain a sufficient networked synchronization condition for FO chaotic systems in the presence of function uncertainties and external disturbances, a novel event-triggered mechanism was designed in [28], which reduced the network transmission frequency of sampling data and ensured that the state information was transmitted in time. To synchronize FO-coupled neural networks, in [29], an event-triggered mechanism and an impulsive control algorithm were combined to control target systems, where a neural controller was activated only when certain predefined conditions were satisfied. According to the above-mentioned literature, the event-triggered control strategy has been demonstrated to be superior in reducing the usage of communication resources and decreasing network load. It should be mentioned that in the aforementioned results, the threshold parameters as the dynamic parameters are often selected as fixed constants, whereas in engineering applications, this may be unrealistic. Therefore, for FO chaotic system synchronization, it is a meaningful but challenging task to design disturbance-observer-based adaptive command-filtered synchronization control using the dynamic event-triggered mechanism, which is another motivation for this work.

Inspired by the above analysis, the synchronization of FO chaotic systems with function uncertainties and time-varying external disturbances is investigated on the basis of an adaptive command-filtered event-triggered control strategy. By constructing a disturbance observer and adopting an event-triggered algorithm, computing resources are utilized reasonably, the triggered time of the controller is decreased, and system robustness is improved. The main contributions are summarized as follows: (1) Unlike [14,15,16,17,30], the FLSs and the FO disturbance observer are employed to effectively deal with model uncertainty and external disturbances in every design step of the controller; (2) With the help of the FO differentiator, the tedious analytic computation is removed and error compensating signals are constructed to deal with known filtering errors, which is beneficial for obtaining a better tracking effect; and (3) A dynamic event-triggered mechanism is proposed for controlled systems. Compared with the traditional event-triggered method, a dynamic event-triggered controller not only balances control performance and control energy but also relieves the pressure of the continuous updating of the controller.

The rest of this paper is organized as follows. Section 2 presents some knowledge about fractional calculus and the problem statement. The disturbance-observer-based adaptive command-filtered synchronization control scheme with tan event-triggered mechanism and simulation example are given in Section 3 and Section 4, respectively. Section 5 summarizes the paper.

2. Preliminaries and Problem Formulation

Some useful definitions and lemmas for the fractional calculus and the FLSs, which will be used later, are provided below.

2.1. Knowledge of Fractional Calculus

The most commonly used definitions in fractional calculus are those of Riemann–Liouville, Grünwald–Letnikov, and Caputo. Compared with the other mentioned operators, the Caputo fractional operator is widely used in the field of engineering because the initial conditions for FO systems with Caputo derivatives have well-understood physical meanings and interpretations. Therefore, the Caputo FO operator is utilized throughout this research work.

Definition 1

([31]). The ϑ-th fractional integral of a smooth function $f\left(t\right)$ is defined as

$$I_t^{\vartheta }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\vartheta \right)}{\int }_0^t\frac{f\left(\tau \right)}{{(t-\tau )}^{1-\vartheta }}d\tau ,\hspace{1em}\vartheta >0,$$

(1)

where $\mathrm{\Gamma }\left(\vartheta \right)={\int }_0^{+\infty }{t}^{\vartheta -1}{e}^{-t}dt$ is the Euler Gamma function.

Definition 2

([31]). The Caputo fractional derivative with ϑ is given as

$$D_t^{\vartheta }f\left(t\right)=\frac{1}{\mathrm{\Gamma }(m-\vartheta )}{\int }_0^t\frac{f^{\left(m\right)}\left(\tau \right)}{{(t-\tau )}^{\vartheta +1-m}}d\tau ,$$

(2)

where $m-1<\vartheta <m$, $m\in {\mathbb{Z}}^{+}$. For convenience, only the case where $0<\vartheta <1$ is considered in the rest of this paper. Moreover, one has $I_t^{\vartheta }\left[D_t^{\vartheta }f\left(t\right)\right]=f\left(t\right)-f\left(0\right)$.

Definition 3

([31]). The Mittag-Leffler function is given as

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{+\infty }\frac{z^k}{\mathrm{\Gamma }(\alpha k+\beta )},\hspace{1em}\alpha ,\beta >0,$$

(3)

where z is a complex number. For $\beta =1$, one has $E_{\alpha ,1}\left(z\right)=E_{\alpha }\left(z\right)$ and $E_{\alpha ,1}\left(z\right)=e^z$. Usually, the Mittag–Leffler function $E_{\alpha ,1}(-\lambda t^{\alpha })$ appears in the stability analysis of FO systems; thus, some properties of this function are given as $0<E_{\alpha ,1}(-\lambda t^{\alpha })\le 1$ and ${lim}_{t\to \infty }{E}_{\alpha ,1}(-\lambda t^{\alpha })\to 0$ for $t\ge 0$ with $\lambda >0$.

Lemma 1

([18]). For $\alpha \in (0,2)$ and $\beta \in \mathbb{R}$, there exists a real number υ such that $\upsilon \in \left(\frac{\pi \alpha }{2},min\{\pi ,\pi \alpha \}\right)$. Then, one has

$$E_{\alpha ,\beta }\left(z\right)\le \frac{\sigma }{1+\left|z\right|},$$

(4)

where $\left|z\right|\ge 0$, $\upsilon \le |arg(z\left)\right|\le \pi$, and σ is a positive constant.

Lemma 2

([32]). Let the ϑ-order derivative of a smooth function $V\left(t\right):{\mathbb{R}}^{+}\to \mathbb{R}$ satisfy

$$D_t^{\vartheta }V\left(t\right)\le -cV\left(t\right)+r,$$

(5)

where c and r are positive constants. Then, one has

$$V\left(t\right)\le V\left(0\right)E_{\vartheta ,1}(-c{t}^{\vartheta })+\frac{\chi r}{c},\hspace{1em}t>0,$$

(6)

where $\chi >1$.

Lemma 3

([33]). For a variable $ϵ\in \mathbb{R}$ and $\kappa >0$, the hyperbolic tangent function $tanh(·)$ holds the following inequality

$$0\le \left|ϵ\right|-ϵtanh\frac{ϵ}{\kappa }\le \varrho \kappa ,$$

(7)

where $\varrho \approx 0.2785$ is the root of equation $\varrho =e^{-(\varrho +1)}$.

Lemma 4

([34]). Assume that $\mathit{x}\left(t\right)\in {\mathbb{R}}^n$ is a vector of differentiable function. Then, the relationship $\frac{1}{2}{D}_t^{\vartheta }\left({\mathit{x}}^T\left(t\right)\mathit{x}\left(t\right)\right)\le {\mathit{x}}^T\left(t\right)D_t^{\vartheta }\mathit{x}\left(t\right)$ holds for any time instant $t\ge t_0$.

Lemma 5

([19]). The FO-tracking differentiator (command filter) is utilized to circumvent the repeated differentiation of virtual controllers. Two variables ${\varsigma }_1\left(t\right)$ and ${\varsigma }_2\left(t\right)$ are designed, and the input of the command filter $\alpha \left(t\right)$ satisfies

$$\left\{\begin{array}{c}{D}_{t_0}^{\vartheta }{\varsigma }_1\left(t\right)=\omega {\varsigma }_2\left(t\right),\hfill \\ D_{t_0}^{\vartheta }{\varsigma }_2\left(t\right)=-2\omega \beta {\varsigma }_2\left(t\right)-\omega \left({\varsigma }_1\left(t\right)-\alpha \left(t\right)\right),\hfill \end{array}\right.$$

(8)

where ω, β are the positive accelerating factors of the differentiator, ${\varsigma }_1\left(0\right)=\alpha \left(0\right)$, and ${\varsigma }_2\left(0\right)=0$. If the input signal $\alpha \left(t\right)$ satisfies $|D_{t_0}^{\vartheta }\alpha \left(t\right)|\le {\omega }_1^{*}$ and $|D_{t_0}^{2\vartheta }\alpha \left(t\right)|\le {\omega }_2^{*}$, where ${\omega }_1^{*}$ and ${\omega }_2^{*}$ are positive constants, then, for a positive constant ${\iota }_1$, there exist $\omega >0$ and $0<\beta <1$ such that $|{\varsigma }_1\left(t\right)-\alpha \left(t\right)|\le {\iota }_1$.

2.2. FLSs

As we know, the inherent uncertainties of FO systems can be tackled using FLSs, which indicate a valid method for further stability analysis. Therefore, knowledge-system-based FLSs with a collection of if-then rules are expressed as

Rule ℓ: IF $x_1\left(t\right)$ is $F_1^{\ell }$ and $x_2\left(t\right)$ is $F_2^{\ell }$ and ⋯ and $x_n\left(t\right)$ is $F_n^{\ell }$, then $y\left(t\right)$ is $G^{\ell }$, $\ell =1,2,\dots ,m$, where $\mathit{x}\left(t\right)={[x_1\left(t\right),x_2\left(t\right),\dots ,x_n\left(t\right)]}^T$ denotes the FLS’s input, $y\left(t\right)$ is the output in the FLS, $F_i^{\ell }$$(i=1,2,\dots ,n)$ and $G^{\ell }$ are fuzzy sets, together with the fuzzy membership function ${\nu }_{F_i^{\ell }}\left(x_i\left(t\right)\right)$ and ${\nu }_{G^{\ell }}\left(y\left(t\right)\right)$, and m is the number of fuzzy rules.

In light of the singleton function, product inference, and center average defuzzification, the output $y\left(t\right)$ of the FLS is expressed as

$$\begin{array}{c}\hfill y\left(t\right)=\frac{{\sum }_{\ell =1}^m{\overline{y}}^{\ell }\left({\mathrm{\Pi }}_{i=1}^n{\nu }_{F_i^{\ell }}\left(x_i\left(t\right)\right)\right)}{{\sum }_{\ell =1}^m\left({\mathrm{\Pi }}_{i=1}^n{\nu }_{F_i^{\ell }}\left(x_i\left(t\right)\right)\right)},\end{array}$$

(9)

where ${\overline{y}}^{\ell }={max}_{y\in R}{\nu }_{G^{\ell }}\left(y\left(t\right)\right)$. Selecting the fuzzy basis function as

$$S_{\ell }\left(\mathit{x}\left(t\right)\right)=\frac{{\mathrm{\Pi }}_{i=1}^n{\nu }_{F_i^{\ell }}\left(x_i\left(t\right)\right)}{{\sum }_{\ell =1}^m\left({\mathrm{\Pi }}_{i=1}^n{\nu }_{F_i^{\ell }}\left(x_i\left(t\right)\right)\right)},$$

(10)

in which $\mathit{S}\left(\mathit{x}\left(t\right)\right)={[S_1\left(\mathit{x}\left(t\right)\right),S_2\left(\mathit{x}\left(t\right)\right),\dots ,S_m\left(\mathit{x}\left(t\right)\right)]}^T$, and the wight parameter vector is written as ${\mathit{W}}^T=[{\overline{y}}^1,{\overline{y}}^2,\dots ,{\overline{y}}^m]$, then (9) can be further represented as

$$y\left(\mathit{x}\left(t\right)\right)={\mathit{W}}^T\mathit{S}\left(\mathit{x}\left(t\right)\right).$$

(11)

It is worth emphasizing that based on the definition of fuzzy basis function $S_{\ell }\left(\mathit{x}\left(t\right)\right)$ in (10), one has $0<S_{\ell }\left(\mathit{x}\left(t\right)\right)\le 1$ and $0<{\mathit{S}}^T\left(\mathit{x}\left(t\right)\right)\mathit{S}\left(\mathit{x}\left(t\right)\right)\le 1$.

Lemma 6.

According to [17], if enough fuzzy rules are provided, the FLSs in (11) can approximate any continuous function $f\left(\mathit{x}\right(t\left)\right)$ on a compact set Ω with a desired precision. For $\forall \epsilon >0$, there exists an FLS such that

$$\underset{\mathit{x}\in \mathrm{\Omega }}{sup}|f\left(\mathit{x}\left(t\right)\right)-{\mathit{W}}^T\mathit{S}\left(\mathit{x}\left(t\right)\right)|\le \epsilon ,$$

(12)

where ε is the fuzzy approximation error.

2.3. System Model

In a synchronization task, two different FO chaotic systems are regarded as the drive system and response system. From a synchronous tracking perspective, the errand is to develop an efficient adaptive fuzzy control scheme that takes state signals from the drive system to regulate the behavior of the response system. The master chaotic system is written as

$$\left\{\begin{array}{c}{\mathcal{D}}_t^{\vartheta }{\xi }_i={\xi }_{i+1}+f_i\left(\mathbf{\xi }\right),\hfill \\ {\mathcal{D}}_t^{\vartheta }{\xi }_n=f_n\left(\mathbf{\xi }\right),i=1,2,\dots ,n-1,\hfill \end{array}\right.$$

(13)

and the slave chaotic system is considered as

$$\left\{\begin{array}{c}{\mathcal{D}}_t^{\vartheta }{\eta }_i={\eta }_{i+1}+g_i\left(\mathbf{\eta }\right)+\Delta g_i\left(\mathbf{\eta }\right)+d_i\left(t\right),\hfill \\ {\mathcal{D}}_t^{\vartheta }{\eta }_n=g_n\left(\mathbf{\eta }\right)+\Delta g_n\left(\mathbf{\eta }\right)+d_n\left(t\right)+u\left(t\right),\hfill \end{array}\right.$$

(14)

where $\mathbf{\xi }={[{\xi }_1,{\xi }_2,\dots ,{\xi }_n]}^T\in {\mathbb{R}}^n$ represents the state of the master system, $\mathbf{\eta }={[{\eta }_1,{\eta }_2,\dots ,{\eta }_n]}^T$$\in {\mathbb{R}}^n$ indicates the state vector of the slave system, $f_i\left(\mathbf{\xi }\right)\in \mathbb{R}$ and $g_i\left(\mathbf{\eta }\right)\in \mathbb{R}$ indicate specified nonlinear functions that are known, $u\left(t\right)$ demonstrates the input signal, and $\Delta g_i\left(\mathbf{\eta }\right)\in \mathbb{R}$ and $d_i\left(t\right)\in \mathbb{R}$ indicate unknown function and external disturbance, respectively.

The control objective is to develop an adaptive event-triggered fuzzy control scheme for (17) so that the synchronization error $z_i$ converges as much as possible to a small area of origin and all signals in the closed-system are bounded under the proposed controller.

Assumption A1.

The compound disturbance term ${\delta }_i=d_i\left(t\right)+{\epsilon }_i\left(\mathbf{\eta }\right)$ is an unknown bounded function, and the fractional derivative of ${\delta }_i$ is bounded so that $|{\mathcal{D}}_t^{\vartheta }{\delta }_i|\le {\overline{\delta }}_i$, where ${\overline{\delta }}_i$ is a positive constant.

Remark 1.

In practical applications, the external disturbance $d_i\left(t\right)$ is unavoidable and is generally difficult to measure directly using physical sensors. There are different types of disturbances including the harmonic disturbance, the constant value disturbance, and the constant value steady-state disturbance. It should be noted that external disturbances are bounded due to the fact that the energy of the external environment is finite and external disturbances have unknown bounded changing rates. However, it is not rigorous to assume that ${\epsilon }_i\left(\mathbf{\eta }\right)$ and its derivative are bounded; thus, one assumes that the compound disturbance ${\delta }_i$ and ${\mathcal{D}}_t^{\vartheta }{\delta }_i$ are bounded. In addition, Assumption A1 is a common condition, which has been widely used in some literature, for instance, in [35].

Considering the slave system (14) and master system (13), the synchronization error system is defined as

$$\left\{\begin{array}{c}{\mathcal{D}}_t^{\vartheta }{z}_i=z_{i+1}+g_i\left(\mathbf{\eta }\right)-f_i\left(\mathbf{\xi }\right)+\Delta g_i\left(\mathbf{\eta }\right)+d_i\left(t\right),\hfill \\ {\mathcal{D}}_t^{\vartheta }{z}_n=g_n\left(\mathbf{\eta }\right)-f_n\left(\mathbf{\xi }\right)+\Delta g_n\left(\mathbf{\eta }\right)+d_n\left(t\right)+u\left(t\right),\hfill \end{array}\right.$$

(15)

where $z_i={\mathbf{\eta }}_i-{\mathbf{\xi }}_i$. In view of (12), the unknown function $\Delta g_i\left(\mathbf{\eta }\right)$ can be approximated by

$$\Delta g_i\left(\mathbf{\eta }\right)={\mathit{W}}_i^{*T}{\mathit{S}}_i\left(\mathbf{\eta }\right)+{\epsilon }_i\left(\mathbf{\eta }\right),$$

(16)

where ${\epsilon }_i\left(\mathbf{\eta }\right)$ is the ideal approximation error, which satisfies $|{\epsilon }_i\left(\mathbf{\eta }\right)|\le {\overline{\epsilon }}_i$, and ${\overline{\epsilon }}_i$ is an unknown positive constant. The optimal parameter ${\mathit{W}}_i^{*}\in {\mathbb{R}}^m$ is expressed as

$${\mathit{W}}_i^{*}=arg\underset{{\mathit{W}}_i\in {\mathrm{\Phi }}_{1i}}{min}\left[\underset{\mathbf{\eta }\in {\mathrm{\Phi }}_{2i}}{sup}|\Delta g_i\left(\mathbf{\eta }\right)-{\mathit{W}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)|\right],$$

where ${\mathrm{\Phi }}_{1i}$ and ${\mathrm{\Phi }}_{2i}$ are the compact sets for ${\mathit{W}}_i$ and $\mathbf{\eta }$. Therefore, the synchronization error system (15) can be rewritten as

$$\left\{\begin{array}{c}{\mathcal{D}}_t^{\vartheta }{z}_i=z_{i+1}+g_i\left(\mathbf{\eta }\right)-f_i\left(\mathbf{\xi }\right)+{\mathit{W}}_i^{*T}{\mathit{S}}_i\left(\mathbf{\eta }\right)+{\delta }_i,\hfill \\ {\mathcal{D}}_t^{\vartheta }{z}_n=g_n\left(\mathbf{\eta }\right)-f_n\left(\mathbf{\xi }\right)+{\mathit{W}}_n^{*T}{\mathit{S}}_n\left(\mathbf{\eta }\right)+{\delta }_n+u\left(t\right),\hfill \end{array}\right.$$

(17)

where ${\delta }_i=d_i\left(t\right)+{\epsilon }_i\left(\mathbf{\eta }\right)$. According to the definitions of $d_i\left(t\right)$ and ${\epsilon }_i\left(\mathbf{\eta }\right)$ above, the time-varying unknown disturbance $d_i\left(t\right)$ and the ideal estimation error ${\epsilon }_i\left(\mathbf{\eta }\right)$ are both bounded.

In light of the state information and fuzzy output of (15), the disturbance observer is introduced as

$${\widehat{\delta }}_i={\widehat{\phi }}_i+l_i{z}_i,$$

(18)

where $l_i$ is a positive constant to be devised and ${\widehat{\phi }}_i$ is the estimated value of ${\phi }_i$ that is defined as ${\phi }_i={\delta }_i-l_i{z}_i$. Combined with the feedback control structure and the disturbance observer, an adaptive feedback control algorithm is constructed to regulate the closed-loop system and improve the anti-disturbance ability of the system. The intermedial variable ${\widehat{\phi }}_i$ is given by

$$\left\{\begin{array}{c}{\mathcal{D}}_t^{\vartheta }{\widehat{\phi }}_i=-l_i\left(z_{i+1}+g_i\left(\mathbf{\eta }\right)-f_i\left(\mathbf{\xi }\right)+{\mathit{W}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)+{\widehat{\delta }}_i\right),\hfill \\ {\mathcal{D}}_t^{\vartheta }{\widehat{\phi }}_n=-l_n\left(u\left(t\right)+g_n\left(\mathbf{\eta }\right)-f_n\left(\mathbf{\xi }\right)+{\mathit{W}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)+{\widehat{\delta }}_n\right),\hfill \end{array}\right.$$

(19)

in which $W_i$ is the estimation of ${\mathit{W}}_i^{*}$.

Remark 2.

For the error system in (15), the time-varying external disturbance is $d_i\left(t\right)$, whereas the estimation is ${\widehat{\delta }}_i$. In [17], a fractional adaptive update law was constructed to deal with external disturbances but the effect was not satisfactory. In this paper, based on the available information of system states, the control input, and the output of FLSs, a compensator that combines an approximation error and a time-varying disturbance is proposed to improve the robustness of the system in (15).

3. Event-Triggered Control Design

The aim of this section is to construct an adaptive event-triggered fuzzy control scheme in the framework of the backstepping dynamic surface control technique so that chaos synchronization between the drive system and response system will be come true. By introducing an event-triggered mechanism, the update frequency of the controller is reduced.

3.1. Event-Triggered Fuzzy Controller Design

Step 1: Define the first error surface as $s_1=z_1$, whose Caputo fractional derivative can be given by

$$\begin{array}{cc}\hfill D_t^{\vartheta }{s}_1& =s_2+z_2^c-{\alpha }_1+{\alpha }_1+g_1\left(\mathbf{\eta }\right)-f_1\left(\mathbf{\xi }\right)\hfill \\ \hfill & +{\mathit{W}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)+{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)+{\delta }_1,\hfill \end{array}$$

(20)

where $s_2=z_2-z_2^c$, ${\alpha }_1$ and $z_2^c$ are given later and ${\tilde{\mathit{W}}}_1={\mathit{W}}_1^{*}-{\mathit{W}}_1$.

The time derivative of the nonlinear disturbance observer ${\widehat{\delta }}_1$ is

$$\begin{array}{cc}\hfill D_t^{\vartheta }{\widehat{\delta }}_1& =D_t^{\vartheta }{\widehat{\phi }}_1+l_1{D}_t^{\vartheta }{z}_1\hfill \\ \hfill & =-l_1\left(z_2+g_1\left(\mathbf{\eta }\right)-f_1\left(\mathbf{\xi }\right)+{\mathit{W}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)+{\widehat{\delta }}_1\right)\hfill \\ \hfill & +l_1(z_2+g_1\left(\mathbf{\eta }\right)-f_1\left(\mathbf{\xi }\right)+{\mathit{W}}_1^{*T}{\mathit{S}}_1\left(\mathbf{\eta }\right)+{\delta }_1)\hfill \\ \hfill & =l_1{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)+l_1{\tilde{\delta }}_1,\hfill \end{array}$$

(21)

where ${\tilde{\delta }}_1={\delta }_1-{\widehat{\delta }}_1$. Choose the first virtual controller as

$${\alpha }_1=-c_1{s}_1-g_1\left(\mathbf{\eta }\right)+f_1\left(\mathbf{\xi }\right)-{\mathit{W}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)-{\widehat{\delta }}_1,$$

(22)

where $c_1$ is a positive designed parameter. The adaptive updated law of $D_t^{\vartheta }{W}_1$ is given as

$$D_t^{\vartheta }{\mathit{W}}_1={\gamma }_{11}{v}_1{\mathit{S}}_1\left(\mathbf{\eta }\right)-{\rho }_1{\mathit{W}}_1,$$

(23)

where ${\gamma }_{11}$ and ${\rho }_1$ are positive designed constants. Substituting (22) into (20) generates

$$\begin{array}{c}\hfill D_t^{\vartheta }{s}_1=-c_1{s}_1+s_2+(z_2^c-{\alpha }_1)+{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)+{\tilde{\delta }}_1.\end{array}$$

(24)

To solve the explosion of the complexity problem resulting from the repeated differentiation of ${\alpha }_1$, a new variable $z_2^c$ is introduced. Let ${\alpha }_1$ adopt from a command filter with accelerating elements ${\omega }_1$ and ${\beta }_1$ to obtain $z_2^c$ as

$$\left\{\begin{array}{c}{D}_t^{\vartheta }{\varsigma }_{11}\left(t\right)={\omega }_1{\varsigma }_{12}\left(t\right),\hfill \\ D_t^{\vartheta }{\varsigma }_{12}\left(t\right)=-2{\omega }_1{\beta }_1{\varsigma }_{12}\left(t\right)-{\omega }_1\left({\varsigma }_{11}\left(t\right)-{\alpha }_1\right),\hfill \end{array}\right.$$

(25)

where $z_2^c={\varsigma }_{11}\left(t\right)$, ${\varsigma }_{11}\left(0\right)={\alpha }_1\left(0\right)$, and ${\varsigma }_{12}\left(0\right)=0$. The error compensation functions $v_1=s_1-{\varpi }_1$ and $v_2=s_2-{\varpi }_2$ are developed to remove filter errors, where ${\varpi }_1$ and ${\varpi }_2$ are middle variables to be designed. The error compensation signal ${\varpi }_1$ can be constructed as

$$D_t^{\vartheta }{\varpi }_1=-c_1{\varpi }_1+{\varpi }_2+(z_2^c-{\alpha }_1).$$

(26)

Considering (24) and (26), one has

$$D_t^{\vartheta }{v}_1=-c_1{v}_1+v_2+{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)+{\tilde{\delta }}_1.$$

(27)

Consider the following Lyapunov function as

$$V_1=\frac{1}{2}{v}_1^2+\frac{1}{2{\gamma }_{11}}{\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1+\frac{1}{2{\gamma }_{12}}{\tilde{\delta }}_1^2,$$

(28)

where ${\gamma }_{12}$ is a positive parameter. Invoking (21), (23), and (27), (28) can be computed as

$$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_1& \le v_1{D}_t^{\vartheta }{v}_1-\frac{1}{{\gamma }_{11}}{\tilde{\mathit{W}}}_1^T{D}_t^{\vartheta }{\mathit{W}}_1+\frac{1}{{\gamma }_{12}}{\tilde{\delta }}_1{D}_t^{\vartheta }{\tilde{\delta }}_1\hfill \\ \hfill & =-c_1{v}_1^2+v_1{v}_2+v_1{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)+v_1{\tilde{\delta }}_1-\frac{1}{{\gamma }_{11}}{\tilde{\mathit{W}}}_1^T{D}_t^{\vartheta }{\mathit{W}}_1\hfill \\ \hfill & +\frac{1}{{\gamma }_{12}}{\tilde{\delta }}_1\left(D_t^{\vartheta }{\delta }_1-l_1{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)-l_1{\tilde{\delta }}_1\right)\hfill \\ \hfill & =-c_1{v}_1^2+v_1{v}_2+v_1{\tilde{\delta }}_1+\frac{{\rho }_1}{{\gamma }_{11}}{\tilde{\mathit{W}}}_1^T{\mathit{W}}_1-\frac{l_1}{{\gamma }_{12}}{\tilde{\delta }}_1^2\hfill \\ \hfill & +\frac{1}{{\gamma }_{12}}{\tilde{\delta }}_1{D}_t^{\vartheta }{\delta }_1-\frac{l_1}{{\gamma }_{12}}{\tilde{\delta }}_1{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right).\hfill \end{array}$$

(29)

Utilizing Young’s inequality, one has

$$\left\{\begin{array}{c}{v}_1{\tilde{\delta }}_1\le \frac{a_{11}}{2}{v}_1^2+\frac{1}{2a_{11}}{\tilde{\delta }}_1^2,\hfill \\ {\tilde{\delta }}_1{D}_t^{\vartheta }{\delta }_1\le \frac{1}{2a_{11}}{\tilde{\delta }}_1^2+\frac{a_{11}}{2}{\overline{\delta }}_1^2,\hfill \\ {\tilde{\mathit{W}}}_1^T{\mathit{W}}_1\le -\frac{1}{2}{\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1+\frac{1}{2}{\mathit{W}}_1^{*T}{\mathit{W}}_1^{*},\hfill \\ -{\tilde{\delta }}_1{\tilde{\mathit{W}}}_1^T{\mathit{S}}_1\left(\mathbf{\eta }\right)\le \frac{1}{2a_{12}}\left|\right|{\mathit{S}}_1\left(\mathbf{\eta }\right){\left|\right|}^2{\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1+\frac{a_{12}}{2}{\tilde{\delta }}_1^2,\hfill \end{array}\right.$$

(30)

where $a_{11}$ and $a_{12}$ are positive constants.

By substituting (30) into (29), one can obtain

$$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_1& \le -(c_1-\frac{a_{11}}{2})v_1^2+v_1{v}_2-(\frac{{\rho }_1}{2{\gamma }_{11}}-\frac{l_1}{2a_{12}{\gamma }_{12}}\left|\right|{\mathit{S}}_1\left(\mathbf{\eta }\right){\left|\right|}^2){\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1\hfill \\ \hfill & -(\frac{l_1}{{\gamma }_{12}}-\frac{1}{a_{11}}-\frac{l_1{a}_{12}}{2{\gamma }_{12}}){\tilde{\delta }}_1^2+\frac{a_{11}}{2}{\overline{\delta }}_1^2+\frac{{\rho }_1}{2{\gamma }_{11}}{\mathit{W}}_1^{*T}{\mathit{W}}_1^{*}.\hfill \end{array}$$

(31)

Step i$(i=2,3,\dots ,n-1)$: Let $s_i=z_i-z_i^c$ be the dynamic surface error, one has

$$\begin{array}{cc}\hfill D_t^{\vartheta }{s}_i& =s_{i+1}+(z_{i+1}^c-{\alpha }_i)+{\alpha }_i+g_i\left(\mathbf{\eta }\right)-f_i\left(\mathbf{\xi }\right)\hfill \\ \hfill & +{\tilde{\mathit{W}}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)+{\mathit{W}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)+{\delta }_i-D_t^{\vartheta }{z}_i^c,\hfill \end{array}$$

(32)

where $s_{i+1}=z_{i+1}-z_{i+1}^c$, ${\alpha }_i$ and $z_{i+1}^c$ will be given later, and ${\tilde{\mathit{W}}}_i={\mathit{W}}_i^{*}-{\mathit{W}}_i$.

The i-th intermediate control function ${\alpha }_i$, the time derivative of ${\widehat{\delta }}_i$, and adaptive law $D_t^{\vartheta }{\mathit{W}}_i$ are designed as

$$\begin{array}{cc}\hfill {\alpha }_i& =-c_i{s}_i-s_{i-1}-g_i\left(\mathbf{\eta }\right)+f_i\left(\mathbf{\xi }\right)-{\mathit{W}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)-{\widehat{\delta }}_i+D_t^{\vartheta }{z}_i^c,\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill D_t^{\vartheta }{\widehat{\delta }}_i& =D_t^{\vartheta }{\widehat{\phi }}_i+l_i{D}_t^{\vartheta }{z}_i=l_i{\tilde{\mathit{W}}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)+l_i{\tilde{\delta }}_i,\hfill \end{array}$$

(34)

$$D_t^{\vartheta }{\mathit{W}}_i={\gamma }_{i1}{v}_i{\mathit{S}}_i\left(\mathbf{\eta }\right)-{\rho }_i{\mathit{W}}_i,$$

(35)

where $c_i$, ${\gamma }_{i1}$, and ${\rho }_i$ are positive design parameters. To extirpate the influence of the known error $z_{i+1}^c-{\alpha }_i$, a compensatory tracking error function is defined as $v_i=s_i-{\varpi }_i$, where ${\varpi }_i$ is constructed as

$$D_t^{\vartheta }{\varpi }_i=-c_i{\varpi }_i-{\varpi }_{i-1}+{\varpi }_{i+1}+(z_{i+1}^c-{\alpha }_i).$$

(36)

Construct the Lyapunov function as

$$V_i=V_{i-1}+\frac{1}{2}{v}_i^2+\frac{1}{2{\gamma }_{i1}}{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{1}{2{\gamma }_{i2}}{\tilde{\delta }}_i^2,$$

(37)

where ${\gamma }_{i2}$ is a positive constant.

Using Lemma 2, taking the derivative of $V_I$ along with (32)–(36) yields

$$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_i& \le D_t^{\vartheta }{V}_{i-1}-c_i{v}_i^2+v_i{v}_{i+1}-v_i{v}_{i-1}+v_i{\tilde{\mathit{W}}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)-\frac{1}{{\gamma }_{i1}}{\tilde{\mathit{W}}}_i^T{D}_t^{\vartheta }{\mathit{W}}_i\hfill \\ \hfill & +v_i{\tilde{\delta }}_i+\frac{1}{{\gamma }_{i2}}{\tilde{\delta }}_i\left(D_t^{\vartheta }{\delta }_i-l_i{\tilde{\mathit{W}}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)-l_i{\tilde{\delta }}_i\right)\hfill \\ \hfill & =D_t^{\vartheta }{V}_{i-1}-c_i{v}_i^2+v_i{v}_{i+1}-v_i{v}_{i-1}+v_i{\tilde{\delta }}_i\left(t\right)+\frac{{\rho }_i}{{\gamma }_{i1}}{\tilde{\mathit{W}}}_i^T{\mathit{W}}_i\hfill \\ \hfill & -\frac{l_i}{{\gamma }_{i2}}{\tilde{\delta }}_i^2+\frac{1}{{\gamma }_{i2}}{\tilde{\delta }}_i{D}_t^{\vartheta }{\delta }_i\left(t\right)-\frac{l_i}{{\gamma }_{i2}}{\tilde{\delta }}_i{\tilde{\mathit{W}}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right).\hfill \end{array}$$

(38)

Applying Young’s inequality, one obtains

$$\left\{\begin{array}{c}{v}_i{\tilde{\delta }}_i\le \frac{a_{i1}}{2}{v}_i^2+\frac{1}{2a_{i1}}{\tilde{\delta }}_i^2,\hfill \\ {\tilde{\delta }}_i{D}_t^{\vartheta }{\delta }_i\le \frac{1}{2a_{i1}}{\tilde{\delta }}_i^2+\frac{a_{i1}}{2}{\overline{\delta }}_i^2,\hfill \\ {\tilde{\mathit{W}}}_i^T{\mathit{W}}_i\le -\frac{1}{2}{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{1}{2}{\mathit{W}}_i^{*T}{\mathit{W}}_i^{*},\hfill \\ -{\tilde{\delta }}_i{\tilde{\mathit{W}}}_i^T{\mathit{S}}_i\left(\mathbf{\eta }\right)\le \frac{1}{2a_{i2}}\left|\right|{\mathit{S}}_i\left(\mathbf{\eta }\right){\left|\right|}^2{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{a_{i2}}{2}{\tilde{\delta }}_i^2,\hfill \end{array}\right.$$

(39)

where $a_{i1}$ and $a_{i2}$ are positive constants.

In light of (31) and (39), one obtains

$$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_i& \le -\sum _{k=1}^i(c_k-\frac{a_{k1}}{2})v_k^2+v_i{v}_{i+1}-\sum _{k=1}^i(\frac{{\rho }_k}{2{\gamma }_{k1}}-\frac{l_k}{2a_{k2}{\gamma }_{k2}}\left|\right|{\mathit{S}}_k\left(\mathbf{\eta }\right){\left|\right|}^2){\tilde{\mathit{W}}}_k^T{\tilde{\mathit{W}}}_k\hfill \\ \hfill & -\sum _{k=1}^i(\frac{l_k}{{\gamma }_{k2}}-\frac{1}{a_{k1}}-\frac{l_k{a}_{k2}}{2{\gamma }_{k2}}){\tilde{\delta }}_k^2+\sum _{k=1}^i\frac{a_{k1}}{2}{\overline{\delta }}_k^2+\sum _{k=1}^i\frac{{\rho }_k}{2{\gamma }_{k1}}{\mathit{W}}_k^{*T}{\mathit{W}}_k^{*}.\hfill \end{array}$$

(40)

Let ${\alpha }_i$ pass through the FO filter with two constants ${\omega }_i$ and ${\beta }_i$ to gain $z_{i+1}^c$ as

$$\left\{\begin{array}{c}{D}_t^{\vartheta }{\varsigma }_{i1}\left(t\right)={\omega }_i{\varsigma }_{i2}\left(t\right),\hfill \\ D_t^{\vartheta }{\varsigma }_{i2}\left(t\right)=-2{\omega }_i{\beta }_i{\varsigma }_{i2}\left(t\right)-{\omega }_i\left({\varsigma }_{i1}\left(t\right)-{\alpha }_i\right),\hfill \end{array}\right.$$

(41)

where $z_{i+1}^c={\varsigma }_{i1}\left(t\right)$, ${\varsigma }_{i1}\left(0\right)={\alpha }_i\left(0\right)$, and ${\varsigma }_{i2}\left(0\right)=0$.

Step n: Define the error variable as $s_n=z_n-z_n^c$ and the compensated tracking error signal as $v_n=s_n-{\varpi }_n$; $z_n^c$ denotes the filter signal output from the command filter, and the auxiliary variable ${\varpi }_n$ can be computed as $D_t^{\vartheta }{\varpi }_n=-c_n{\varpi }_n-{\varpi }_{n-1}$, where $c_n$ is a positive number to be ascertained. The derivative of $v_n$ can be obtained by (17)

$$\begin{array}{cc}\hfill D_t^{\vartheta }{v}_n& =g_n\left(\mathbf{\eta }\right)-f_n\left(\mathbf{\xi }\right)+{\mathit{W}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)+{\tilde{\mathit{W}}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)+{\delta }_n\hfill \\ \hfill & +u\left(t\right)-D_t^{\vartheta }{z}_n^c+c_n{\varpi }_n+{\varpi }_{n-1},\hfill \end{array}$$

(42)

where ${\tilde{\mathit{W}}}_n={\mathit{W}}_n^{*}-{\mathit{W}}_n$. Similar to (21) and (34), one has

$$D_t^{\vartheta }{\widehat{\delta }}_n=l_n{\tilde{\mathit{W}}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)+l_n{\tilde{\delta }}_n,$$

(43)

where ${\tilde{\delta }}_n={\delta }_n-{\widehat{\delta }}_n$. The Lyapunov function is $V_n=V_{n-1}+\frac{1}{2}{v}_n^2+\frac{1}{2{\gamma }_{n1}}{\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n+\frac{1}{2{\gamma }_{n2}}{\tilde{\delta }}_n^2$, where ${\gamma }_{n1}$ and ${\gamma }_{n2}$ are positive constants. By invoking (42) and (43), the time-fractional derivative of $V_n$ is given by

$$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_n& \le D_t^{\vartheta }{V}_{n-1}+v_n(u\left(t\right)+g_n\left(\mathbf{\eta }\right)-f_n\left(\mathbf{\xi }\right)+{\mathit{W}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)+{\delta }_n\hfill \\ \hfill & -D_t^{\vartheta }{z}_n^c+c_n{\varpi }_n+{\varpi }_{n-1})-{\tilde{\mathit{W}}}_n^T\left(\frac{1}{{\gamma }_{n1}}{D}_t^{\vartheta }{\mathit{W}}_n-v_n{\mathit{S}}_n\left(\mathbf{\eta }\right)\right)\hfill \\ \hfill & +\frac{1}{{\gamma }_{n2}}{\tilde{\delta }}_n{D}_t^{\vartheta }{\delta }_n-\frac{l_n}{{\gamma }_{n2}}{\tilde{\delta }}_n^2-\frac{l_n}{{\gamma }_{n2}}{\tilde{\delta }}_n{\tilde{\mathit{W}}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right).\hfill \end{array}$$

(44)

The adaptive event-triggering command filter controller $\psi \left(t\right)$ and the adaptive parameter $D_t^{\vartheta }{\mathit{W}}_n$ are designed as

$$\begin{array}{c}\hfill \psi \left(t\right)=-(1+\tau \left(t\right))\left({\alpha }_{n}tanh\left(\frac{v_n{\alpha }_n}{\mu }\right)+qtanh\left(\frac{q{v}_n}{\mu }\right)\right),\end{array}$$

(45)

$$\begin{array}{c}\hfill D_t^{\vartheta }{\mathit{W}}_n={\gamma }_{n1}{v}_n{\mathit{S}}_n\left(\mathbf{\eta }\right)-{\rho }_n{\mathit{W}}_n,\end{array}$$

(46)

where ${\alpha }_n=-c_n{s}_n-s_{n-1}-g_n\left(\mathbf{\eta }\right)+f_n\left(\mathbf{\xi }\right)-{\mathit{W}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)-{\widehat{\delta }}_n+D_t^{\vartheta }{z}_n^c$, ${\rho }_n$ is a positive parameter to be decided. The event-triggered mechanism is chosen as

$$u\left(t\right)=\psi \left(t_k\right),\forall t\in [t_k,t_{k+1}),$$

(47)

$$t_{k+1}=inf\{t\in R||\psi \left(t\right)-u\left(t\right)|\ge \tau \left(t\right)\left|u\left(t\right)\right|+\overline{q}\},$$

(48)

where $q>0$, $\overline{q}>0$, $q>\frac{\overline{q}}{1-\tau \left(t\right)}>0$, and $\mu >0$ are constants to be designed later and $t_k$$(k\in {\mathbb{Z}}^{+})$ indicates the update time of the controller. $D_t^{\vartheta }\tau \left(t\right)$ is given as $D_t^{\vartheta }\tau \left(t\right)=-k_{\tau }{\tau }^2\left(t\right)$, where $\tau \left(0\right)\in (0,1)$ and $k_{\tau }>0$ and it can be concluded that $\tau \left(t\right)\in (0,1)$.

Remark 3.

It is worth mentioning that the inequality in (53) holds when the condition $q>\frac{\overline{q}}{1-\tau \left(t\right)}>0$ is satisfied, that is, the design positive function meets $\tau \left(t\right)\in (0,1)$. In order to obtain a function that satisfies the above conditions, the equation $D_t^{\vartheta }\tau \left(t\right)=-k_{\tau }{\tau }^2\left(t\right)$ is selected. It can be calculated as $\tau \left(t\right)\le {\left[\tau \left(0\right)E_{\vartheta }(-k_{\tau }{t}^{\vartheta })\right]}^{\frac{1}{2}}$ by Theorem 5.1 and Example 7.1 in [36]. According to $0<E_{\vartheta }(-k_{\tau }{t}^{\vartheta })\le 1$ in Definition 3 and $\tau \left(0\right)\in (0,1)$, it is easy to obtain $\tau \left(t\right)\in (0,1)$. If the event-triggered condition in (48) is always not activated, the time $t_k$ remains the same. The constant time $t_k$ will be converted to $t_{k+1}$ for $t\in [t_k,t_{k+1})$ when the condition in (48) is activated so the update time $t_k$ of the controller in (47) is a monotonically increasing subsequence, which can be expressed as $t_0<t_1<\dots <t_k<\dots$. The actual controller $u\left(t\right)$ can be acquired by (45) during the time period $[t_k,t_{k+1})$, that is, the actual control input is a discontinuous signal that is activated by (48) for the error system in (17).

In light of (48), it can be concluded that $|\psi \left(t\right)-u\left(t\right)|\le \tau \left(t\right)\left|u\left(t\right)\right|+\overline{q}$ for $t\in [t_k,t_{k+1})$. Therefore, there exist two continuous time-varying functions ${\varphi }_1\left(t\right)$ and ${\varphi }_2\left(t\right)$ such that

$$\psi \left(t\right)=(1+\tau \left(t\right){\varphi }_1\left(t\right))u\left(t\right)+{\varphi }_2\left(t\right)\overline{q},$$

(49)

where ${\varphi }_1\left(t\right)$ and ${\varphi }_2\left(t\right)$ satisfy ${\varphi }_1\left(t\right)\in [-1,1]$ and ${\varphi }_2\left(t\right)\in [-1,1]$, respectively. It is easy to obtain

$$v_{n}u\left(t\right)=\frac{v_n\psi \left(t\right)}{1+\tau \left(t\right){\varphi }_1\left(t\right)}-\frac{\overline{q}{v}_n{\varphi }_2\left(t\right)}{1+\tau \left(t\right){\varphi }_1\left(t\right)}.$$

(50)

According to (45), one has

$$v_n\psi \left(t\right)=-(1+\tau \left(t\right))v_n{\alpha }_{n}tanh\left(\frac{v_n{\alpha }_n}{\mu }\right)-(1+\tau \left(t\right))q{v}_{n}tanh\left(\frac{q{v}_n}{\mu }\right),$$

(51)

where the relationship between q and $\overline{q}$ is defined above. Based on $-ϵtanh\left(\frac{ϵ}{\kappa }\right)\le 0$, $\forall ϵ\in R$ and $\kappa >0$, thus, $v_n\psi \left(t\right)<0$. Since $|{\varphi }_1\left(t\right)|\le 1$ and $|{\varphi }_2\left(t\right)|\le 1$, one has

$$\left\{\begin{array}{c}\frac{v_n\psi \left(t\right)}{1+\tau \left(t\right){\varphi }_1\left(t\right)}\le \frac{v_n\psi \left(t\right)}{1+\tau \left(t\right)},\hfill \\ -\frac{\overline{q}{v}_n{\varphi }_2\left(t\right)}{1+\tau \left(t\right){\varphi }_1\left(t\right)}\le \left|\frac{\overline{q}{v}_n}{1-\tau \left(t\right)}\right|.\hfill \end{array}\right.$$

(52)

Based on Lemma 3, substituting (45) into (52) yields

$$\begin{array}{cc}\hfill v_{n}u\left(t\right)& \le |\frac{\overline{q}{v}_n}{1-\tau \left(t\right)}|+|v_n{\alpha }_n|-v_n{\alpha }_{n}tanh\left(\frac{v_n{\alpha }_n\left(t\right)}{\mu }\right)\hfill \\ \hfill & +|q{v}_n|-q{v}_{n}tanh\left(\frac{q{v}_n}{\mu }\right)-|v_n{\alpha }_n\left(t\right)|-|q{v}_n|\hfill \\ \hfill & \le 0.557\mu +|\frac{\overline{q}{v}_n}{1-\tau \left(t\right)}|-|v_n{\alpha }_n\left(t\right)|-|q{v}_n|\hfill \\ \hfill & \le 0.557\mu +v_n{\alpha }_n,\hfill \end{array}$$

(53)

where $|\frac{\overline{q}{v}_n}{1-\tau \left(t\right)}|-|q{v}_n|<0$ and $-|v_n{\alpha }_n|\le v_n{\alpha }_n$.

The utilization of Young’s inequality is given as follows

$$\left\{\begin{array}{c}{v}_n{\tilde{\delta }}_n\le \frac{a_{n1}}{2}{v}_n^2+\frac{1}{2a_{n1}}{\tilde{\delta }}_n^2,\hfill \\ {\tilde{\delta }}_n{D}_t^{\vartheta }{\delta }_n\le \frac{1}{2a_{n1}}{\tilde{\delta }}_n^2+\frac{a_{n1}}{2}{\overline{\delta }}_n^2,\hfill \\ {\tilde{\mathit{W}}}_n^T{\mathit{W}}_n\le -\frac{1}{2}{\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n+\frac{1}{2}{\mathit{W}}_n^{*T}{\mathit{W}}_n^{*},\hfill \\ -{\tilde{\delta }}_n{\tilde{\mathit{W}}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)\le \frac{1}{2a_{n2}}\left|\right|{\mathit{S}}_n\left(\mathbf{\eta }\right){\left|\right|}^2{\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n+\frac{a_{n2}}{2}{\tilde{\delta }}_n^2,\hfill \end{array}\right.$$

(54)

where $a_{n1}$ and $a_{n2}$ are positive constants.

Then, (44) can be written as

$$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_n& \le D_t^{\vartheta }{V}_{n-1}-c_n{v}_n^2-v_n{v}_{n-1}+v_n{\tilde{\delta }}_n+0.557\mu +\frac{{\rho }_n}{{\gamma }_{n1}}{\tilde{\mathit{W}}}_n^T{\mathit{W}}_n\hfill \\ \hfill & +\frac{1}{{\gamma }_{n2}}{\tilde{\delta }}_n{D}_t^{\vartheta }{\delta }_n-\frac{l_n}{{\gamma }_{n2}}{\tilde{\delta }}_n^2-\frac{l_n}{{\gamma }_{n2}}{\tilde{\delta }}_n{\tilde{\mathit{W}}}_n^T{\mathit{S}}_n\left(\mathbf{\eta }\right)\hfill \\ \hfill & \le -\sum _{i=1}^n(c_i-\frac{a_{i1}}{2})v_i^2-\sum _{i=1}^n(\frac{{\rho }_i}{2{\gamma }_{i1}}-\frac{l_i}{2a_{i2}{\gamma }_{i2}}\left|\right|{\mathit{S}}_i\left(\mathbf{\eta }\right){\left|\right|}^2){\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+0.557\mu \hfill \\ \hfill & -\sum _{i=1}^n(\frac{l_i}{{\gamma }_{i2}}-\frac{1}{a_{i1}}-\frac{l_i{a}_{i2}}{2{\gamma }_{i2}}){\tilde{\delta }}_i^2+\sum _{i=1}^n\frac{a_{i1}}{2}{\overline{\delta }}_i^2+\sum _{i=1}^n\frac{{\rho }_i}{2{\gamma }_{i1}}{\mathit{W}}_i^{*T}{\mathit{W}}_i^{*}\hfill \\ \hfill & \le -\overline{c}{V}_n+\overline{r},\hfill \end{array}$$

(55)

where $\overline{c}=min\{2c_i-a_{i1},{\rho }_i-\frac{l_i{\gamma }_{i1}}{a_{i2}{\gamma }_{i2}}\left|\right|{\mathit{S}}_i{\left(\mathbf{\eta }\right)\left|\right|}^2,2l_i-\frac{{\gamma }_{i2}}{a_{i1}}-l_i{a}_{i2}\}$ and $\overline{r}={\sum }_{i=1}^n\frac{a_{i1}}{2}{\overline{\delta }}_i^2+{\sum }_{i=1}^n\frac{{\rho }_i}{2{\gamma }_{i1}}$${\mathit{W}}_i^{*T}{\mathit{W}}_i^{*}+0.557\mu$. The design parameter selection rules for the proposed control algorithm can be given as follows:

Step 1: Draw up the fuzzy rules and the membership functions, then, the FLSs can be obtained.

Step 2: Choose the approximate parameters $c_i$, ${\gamma }_{i1}$, ${\gamma }_{i2}$, ${\rho }_i$, $a_{i1}$, $a_{i2}$, and $l_i$ such that $c_i-\frac{a_{i1}}{2}>0$ and $\frac{{\rho }_i}{2{\gamma }_{i1}}-\frac{l_i}{2a_{i2}{\gamma }_{i2}}\left|\right|{\mathit{S}}_i\left(\mathbf{\eta }\right){\left|\right|}^2>0$, and determine the control signals ${\alpha }_i$ using (22), (33), and (45) together with the adaptation laws ${\mathit{W}}_i$ in (23), (35), and (46). In addition, the disturbance observer parameters in (20), (40), and (55) should meet the condition $\frac{l_i}{{\gamma }_{i2}}-\frac{1}{a_{i1}}-\frac{l_i{a}_{i2}}{2{\gamma }_{i2}}>0$, where $0<a_{i2}<2$.

Step 3: Select the suitable parameters satisfying $q>0$, $\overline{q}>0$, $\mu >0$, $k_{\tau }>0$, and $0<\tau \left(t\right)<1$, and ascertain the adaptive event-triggered controller (47).

Step 4: On the basis of Steps 1–3, by increasing the parameters $c_i$, $a_{i1}$, $a_{i2}$, ${\gamma }_{i2}$, ${\rho }_i$, and $l_i$ or decreasing $a_{i1}$, $a_{i2}$, ${\gamma }_{i1}$, ${\gamma }_{i2}$, and $l_i$, the synchronization tracking performance can be improved due to the synchronization errors being inversely proportional to the control resources. Therefore, one has to make a trade-off between the control energy and the tracking performance by choosing the design parameters appropriately.

3.2. Stability Analysis

In light of the above adaptive fuzzy control design scheme, Theorem 1 is summarized as follows.

Theorem 1.

For the error system in (17) with the dynamic event-triggered adaptive backstepping control method in (45), (47), and (48), the disturbance observer in (18) and (19), virtual control signals in (22) and (33), and the actual control signal in (47), together with the FO adaptation laws in (23), (35), and (46), one can determine that all signals remain bounded. Moreover, the Zeno phenomenon is avoided.

Proof. First, according to Lemma 2, it can be concluded that

$$\begin{array}{c}\hfill V_n\left(t\right)\le V_n\left(0\right)E_{\vartheta ,1}(-\overline{c}{t}^{\vartheta })+\frac{\overline{r}\chi }{\overline{c}}.\end{array}$$

(56)

Based on some properties of the $E_{\vartheta ,1}(-\overline{c}{t}^{\vartheta })$ in Definition 3 and Lemma 1, (56) can be computed as

$$\begin{array}{cc}\hfill V_n\left(t\right)& \le V_n\left(0\right)\frac{\sigma }{1+|\overline{c}{t}^{\vartheta }|}+\frac{\overline{r}\chi }{\overline{c}}\hfill \\ \hfill & \le \chi \left(\frac{V_n\left(0\right)}{1+|\overline{c}{t}^{\vartheta }|}+\frac{\overline{r}}{\overline{c}}\right),\hfill \end{array}$$

(57)

where $\chi =max\{1,\sigma \}$. Based on (57), one has ${lim}_{t\to \infty }{V}_n\left(t\right)\le \frac{\chi \overline{r}}{\overline{c}}$. Then, it can be seen that $v_i$, ${\tilde{\mathit{W}}}_i$, ${\tilde{\delta }}_i$, ${\mathit{W}}_i$, and ${\widehat{\delta }}_i$ are semiglobally ultimately bounded from ${\mathit{W}}_i^{*}={\tilde{\mathit{W}}}_i+{\mathit{W}}_i$ and ${\delta }_i={\tilde{\delta }}_i+{\widehat{\delta }}_i$. Next, error compensating signals are proved to be bounded. Define the Lyapunov function as $V_{\varpi }=\frac{1}{2}{\sum }_{i=1}^n{\varpi }_i^2$. Then,

$$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_{\varpi }& \le {\varpi }_1{D}_t^{\vartheta }{\varpi }_1+\dots +{\varpi }_i{D}_t^{\vartheta }{\varpi }_i+{\varpi }_n{D}_t^{\vartheta }{\varpi }_n\hfill \\ \hfill & =-\sum _{i=1}^n{c}_i{\varpi }_i^2+\sum _{i=1}^{n-1}{\varpi }_i(z_{i+1}^c-{\alpha }_i)\hfill \\ \hfill & \le -\sum _{i=1}^{n-1}(c_i-\frac{1}{2}){\varpi }_i^2-c_n{\varpi }_n^2+\frac{1}{2}\sum _{i=1}^{n-1}{\iota }_i^2\hfill \\ \hfill & \le -c_0{V}_{\varpi }+{\chi }_0,\hfill \end{array}$$

(58)

where $c_0=min\{2(c_i-\frac{1}{2}),2c_n\}$ and ${\chi }_0=\frac{1}{2}{\sum }_{i=1}^{n-1}{\iota }_i^2$. Similar to (56), one has ${lim}_{t\to \infty }{V}_{\varpi }\left(t\right)\le \frac{{\chi }_0{r}_0}{c_0}$, which indicates ${\varpi }_i$ is bounded. In view of $s_i=v_i+{\varpi }_i$, the boundedness of $s_i$ can be obtained. Because ${\alpha }_1$ is a continuous function containing $g_1\left(\mathbf{\eta }\right)$, $f_1\left(\mathbf{\xi }\right)$, ${\mathit{W}}_1$, ${\widehat{\delta }}_1$, and $s_1$, it is easy to see that ${\alpha }_1$ and $z_2^c$ are bounded based on Lemma 5. By $z_2=s_2+z_2^c$, it can be seen that $z_2$ is bounded. With these results, all signals involved in closed systems are bounded. In addition, from $s_i=v_i+{\varpi }_i$, it can be concluded that $s_i$ can converge to the compact set by selecting the appropriate parameters, and one has $|s_i|\le \sqrt{\frac{2\chi \overline{r}}{\overline{c}}}+\sqrt{\frac{2{\chi }_0{r}_0}{c_0}}$. In summary, the synchronized behavior of the two chaotic systems can be achieved. Finally, one can see that the Zeno behavior does not occur under the proposed control approach. The definition of the measurement error is $\Delta \left(t\right)=\psi \left(t\right)-u\left(t\right)$, where $u\left(t\right)=\psi \left(t_k\right)$ for ∀$t\in [t_k,t_{k+1})$, then, one has $D_t^{\vartheta }(\Delta \left(t\right))=D_t^{\vartheta }(\psi \left(t\right)-u\left(t\right))=D_t^{\vartheta }\left(\psi \left(t\right)\right)$. On the basis of Definition 2, one has

$$\begin{array}{cc}\hfill D_t^{\vartheta }|\Delta \left(t\right)|& =\frac{1}{\mathrm{\Gamma }(m-\vartheta )}{\int }_0^t\frac{{|\Delta \left(\tau \right)|}^{\left(m\right)}}{{(t-\tau )}^{1+\vartheta -m}}d\tau \hfill \\ \hfill & =\frac{1}{\mathrm{\Gamma }(m-\vartheta )}{\int }_0^t\frac{\mathrm{sgn}(\Delta \left(\tau \right))\Delta {\left(\tau \right)}^{\left(m\right)}}{{(t-\tau )}^{1+\vartheta -m}}d\tau \hfill \\ \hfill & =\frac{\mathrm{sgn}(\Delta (t\left)\right)}{\mathrm{\Gamma }(m-\vartheta )}{\int }_0^t\frac{\Delta {\left(\tau \right)}^{\left(m\right)}}{{(t-\tau )}^{1+\vartheta -m}}d\tau \hfill \\ \hfill & =\mathrm{sgn}(\Delta \left(t\right))D_t^{\vartheta }\Delta \left(t\right),\hfill \end{array}$$

(59)

where ∀$t\in [t_k,t_{k+1})$ ($m=1$ due to $\vartheta \in (0,1)$). Then, one has $D_t^{\vartheta }|\Delta \left(t\right)|=\mathrm{sgn}(\Delta \left(t\right))D_t^{\vartheta }\Delta \left(t\right)$$\le |D_t^{\vartheta }\psi \left(t\right)|$. Referring to the definition in (45), it can be concluded that $\psi \left(t\right)$ is the $\vartheta$-th differentiable and ${\mathcal{D}}_t^{\vartheta }\psi \left(t\right)$ is a function of the bounded variables $v_n$, ${\alpha }_n$, and $\tau \left(t\right)$ in the closed system. Therefore, it is clear that there exists a constant $\zeta >0$ such that $|{\mathcal{D}}_t^{\vartheta }\psi \left(t\right)|\le \zeta$ for ∀$t\in [t_k,t_{k+1})$. Furthermore, one has ${|}_{t_k}{I}_t^{\vartheta }\left[{}_{t_k}{D}_t^{\vartheta }\Delta \left(t\right)\right]|=|\Delta \left(t\right)-\Delta \left(t_k\right)|$ for $t\in [t_k,t_{k+1})$ in Definition 2. Thus, one can obtain

$$\begin{array}{cc}\hfill |\Delta \left(t\right)-\Delta \left(t_k\right)|& {=|}_{t_k}{I}_t^{\vartheta }{[}_{t_k}{D}_t^{\vartheta }\Delta \left(t\right)]|\hfill \\ \hfill & =|\frac{1}{\mathrm{\Gamma }\left(\vartheta \right)}{\int }_{t_k}^t{(t-\tau )}^{\vartheta -1}{}_{t_k}{D}_t^{\vartheta }\Delta \left(t\right)|\hfill \\ \hfill & \le |\frac{1}{\mathrm{\Gamma }\left(\vartheta \right)}{\int }_{t_k}^t{(t-\tau )}^{\vartheta -1}{}_{t_k}{D}_t^{\vartheta }|\psi \left(t\right)||\hfill \\ \hfill & \le \frac{\zeta {(t-t_k)}^{\vartheta }}{\mathrm{\Gamma }(\vartheta +1)}.\hfill \end{array}$$

(60)

According to the event-triggering rule in (48), the value of the controller does not change before the $t_{k+1}$ moment, which means $\Delta \left(t_k\right)=0$ and ${lim}_{t⟶t_{k+1}}\Delta \left(t\right)=\tau \left(t\right)\left|u\left(t\right)\right|+\overline{q}=q_1$. When $t=t_{k+1}$, one has $t_{k+1}-t_k\ge {\left(\frac{\mathrm{\Gamma }(\vartheta +1)q_1}{\zeta }\right)}^{\frac{1}{\vartheta }}$. Therefore, one has $t_{k+1}-t_k>0$ for any $t\in [t_k,t_{k+1})$, that is, the Zeno behavior is excluded. Theorem 1 is completely proved.

Remark 4.

If the master chao

$$\left\{\begin{array}{c}{\mathcal{D}}_t^{\vartheta }{\xi }_i=h_i\left(\mathbf{\xi }\right),\hfill \\ {\mathcal{D}}_t^{\vartheta }{\xi }_n=h_n\left(\mathbf{\xi }\right),\hfill \end{array}\right.$$

(61)

which can be written as

$$\left\{\begin{array}{c}{\mathcal{D}}_t^{\vartheta }{\xi }_i={\xi }_{i+1}+f_i\left(\mathbf{\xi }\right),\hfill \\ {\mathcal{D}}_t^{\vartheta }{\xi }_n=f_n\left(\mathbf{\xi }\right),\hfill \end{array}\right.$$

(62)

where $f_i\left(\mathbf{\xi }\right)=h_i\left(\mathbf{\xi }\right)-{\xi }_{i+1}$ and $f_n\left(\mathbf{\xi }\right)=h_n\left(\mathbf{\xi }\right)$. Therefore, the proposed method is also valid for (61). In addition, the nonlinear functions $f_i\left(\mathbf{\xi }\right)$ in (13) and $g_i\left(\mathbf{\eta }\right)$ in (14) are not required to be the same in this paper. Different types of FO chaotic systems can also be synchronized by utilizing the proposed control algorithm when the corresponding dimension is the same, such as the FO Chen system (master system) and the FO Rössler system (slave system).

Remark 5.

In [14,15,16,17], the synchronization of FO chaotic systems with external disturbances was studied using an adaptive tracking controller. However, the maximum boundary values of disturbances were provided to compensate for external disturbances, which increased the loss of energy. In [24,25], sampling controllers that were updated at fixed intervals were developed, in which similar or the same data packages were transmitted repeatedly in the case of insufficient control resources. Therefore, to save control resources and reduce task executions, some effective event-triggered strategies were designed in [28,29]. Unlike the above event-triggered control strategies, a dynamic event-triggered controller based on disturbance observers is constructed in this paper.

Remark 6.

It is well known that mechanical equipment can only send out a signal in a limited time interval $[t_k,t_{k+1})$ due to the fact that the time period of the actuator operation may be influenced by external conditions such as the working environment, combination of components within the system, system model parameters, and voltage. If the condition of (48) is triggered, the control input will be converted to $u\left(t_{k+1}\right)$; otherwise, the control signal $\psi \left(t_k\right)$ remains unchanged. The chief advantage of the event-triggered strategy is that it can reduce the triggered time of the control signal $u\left(t\right)$, which not only avoids continuous monitoring and testing but is also relatively easy to manipulate. Unlike the traditional event-triggered strategy, $\tau \left(t\right)$ is an adjustable dynamic variable rather than a constant, which is convenient for adjusting the time interval length. Because parameter $\overline{q}$ is fixed while the system is working, a dynamic parameter $\tau \left(t\right)$ is introduced to prevent the unnecessarily frequent transitions of the controller and it provides a reasonable strategy for the synchronization of chaotic systems.

4. Simulation

To verify and demonstrate the effectiveness of the control scheme proposed in the previous section, an FO chaotic system is given. Taking into account (63) as the master system, which represents the FO Chua-Hartley system,

$$\left\{\begin{array}{c}{D}_t^{\vartheta }{\xi }_1={\xi }_2+\frac{10}{7}({\xi }_1-{\xi }_1^3),\hfill \\ D_t^{\vartheta }{\xi }_2={\xi }_3+10{\xi }_1-{\xi }_2,\hfill \\ D_t^{\vartheta }{\xi }_3=-\frac{100}{7}{\xi }_2,\hfill \end{array}\right.$$

(63)

where $\vartheta =0.98$ and $\mathbf{\xi }\left(0\right)={[0.8,-2,1]}^T$. The slave system with model uncertainties and disturbances is rewritten as

$$\left\{\begin{array}{c}{D}_t^{\vartheta }{\eta }_1={\eta }_2+\frac{10}{7}({\eta }_1-{\eta }_1^3)+d_1\left(t\right)+\Delta g_1\left(\mathbf{\eta }\right),\hfill \\ D_t^{\vartheta }{\eta }_2={\eta }_3+10{\eta }_1-{\eta }_2+d_2\left(t\right)+\Delta g_2\left(\mathbf{\eta }\right),\hfill \\ D_t^{\vartheta }{\eta }_3=-\frac{100}{7}{\eta }_2+d_3\left(t\right)+\Delta g_3\left(\mathbf{\eta }\right)+u\left(t\right),\hfill \end{array}\right.$$

(64)

where $\Delta g_1\left(\mathbf{\eta }\right)=0$, $d_1\left(t\right)=0$, $\Delta g_2\left(\mathbf{\eta }\right)=0.5{\eta }_1{\eta }_2+sin\left({\eta }_3\right)$, $d_2\left(t\right)=1-0.4sint$, $\Delta g_3\left(\mathbf{\eta }\right)=0.8{(sin({\eta }_2+{\eta }_3))}^2$, $d_3\left(t\right)=0.6cost$, and the initial condition of (64) is $\mathbf{\eta }={[0.35,-1,0]}^T$. When the control input $u\left(t\right)$ in (64) is zero, the dynamics of the master system (63) and the slave system (64) are calculated, as shown in Figure 1.

The controller parameters are designed as $c_1=8$, $c_2=12$, $c_3=16$, $\mu =2$, $\tau \left(0\right)=0.4$, $q=0.1$, $\overline{q}=0.05$, $k_{\tau }=0.3$, ${\omega }_1={\omega }_2=5$, ${\beta }_1={\beta }_2=0.5$; the adaptive update parameters are chosen as ${\gamma }_{21}={\gamma }_{31}=1.2$, ${\gamma }_{22}={\gamma }_{32}=2$, ${\rho }_2={\rho }_3=0.5$; the disturbance observer parameters are selected as $l_2=l_3=1.1$; the tuning parameter is selected as $a_{21}=a_{31}=5$, $a_{22}=a_{32}=1.5$; and the other initial values are chosen as zero. ${\mathit{W}}_2^T{\mathit{S}}_2\left(\mathbf{\eta }\right)$ contains 225 fuzzy rules with centers evenly assigned in ${[-2,2]}_5\times {[-2,2]}_5\times {[-20,20]}_9$; ${\mathit{W}}_3^T{\mathit{S}}_3\left(\mathbf{\eta }\right)$ contains 45 fuzzy rules with centers evenly assigned in ${[-2,2]}_5\times {[-20,20]}_9$.

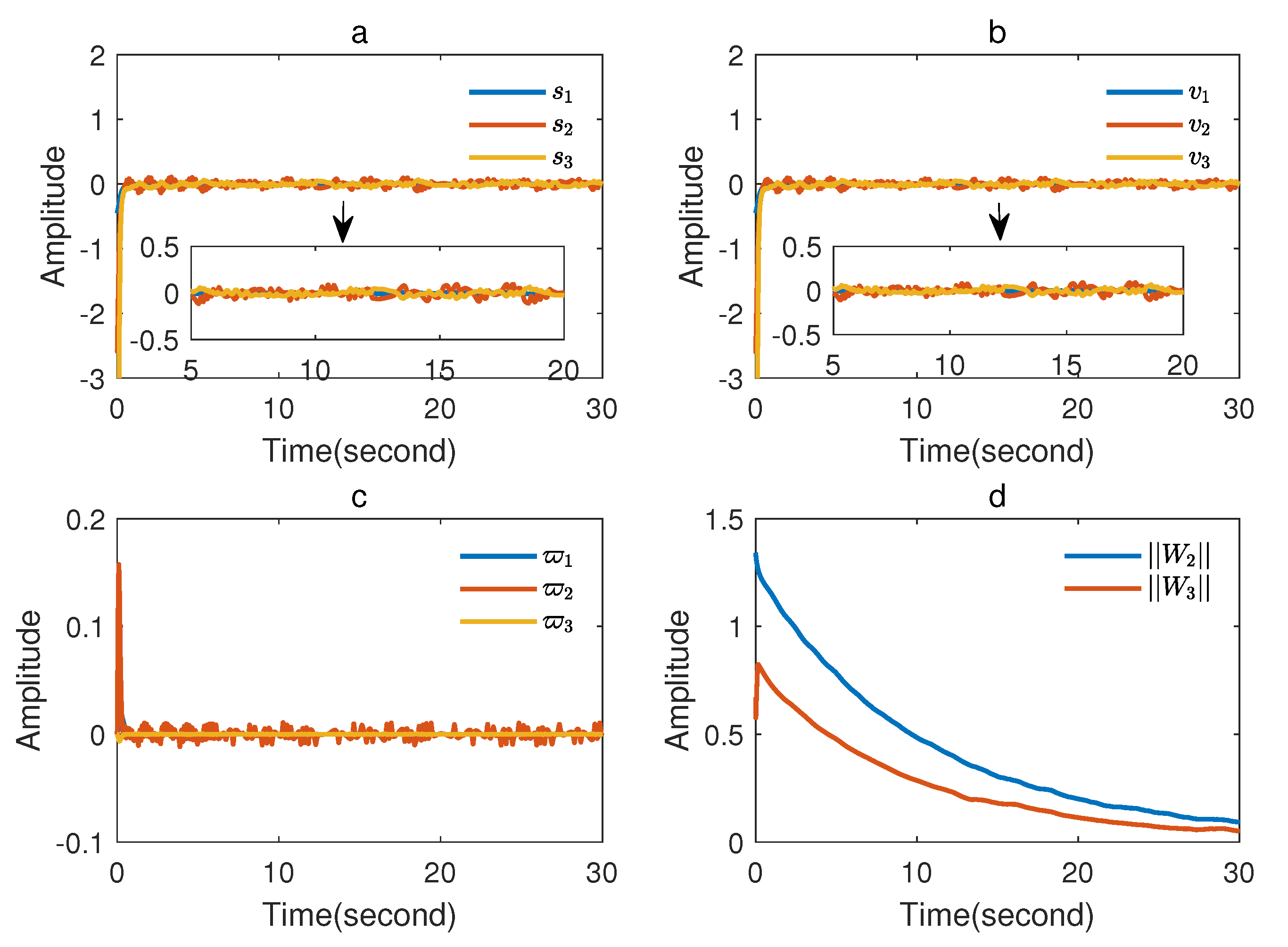
The simulation results are presented in Figure 2, Figure 3 and Figure 4. The state trajectories of the master and uncertain slave chaotic systems are displayed in Figure 2, which demonstrates the synchronization purpose of the master and slave systems. To make a comparison, the synchronization trajectories in [17] without the FO disturbance observer are also presented in Figure 2, where it can be seen that the control performance of the method this paper is better than that in [17]. Figure 3a–c display the trajectories of the tracking errors, compensated tracking errors, and error compensation signals, and the fuzzy parameters are shown in Figure 3d. 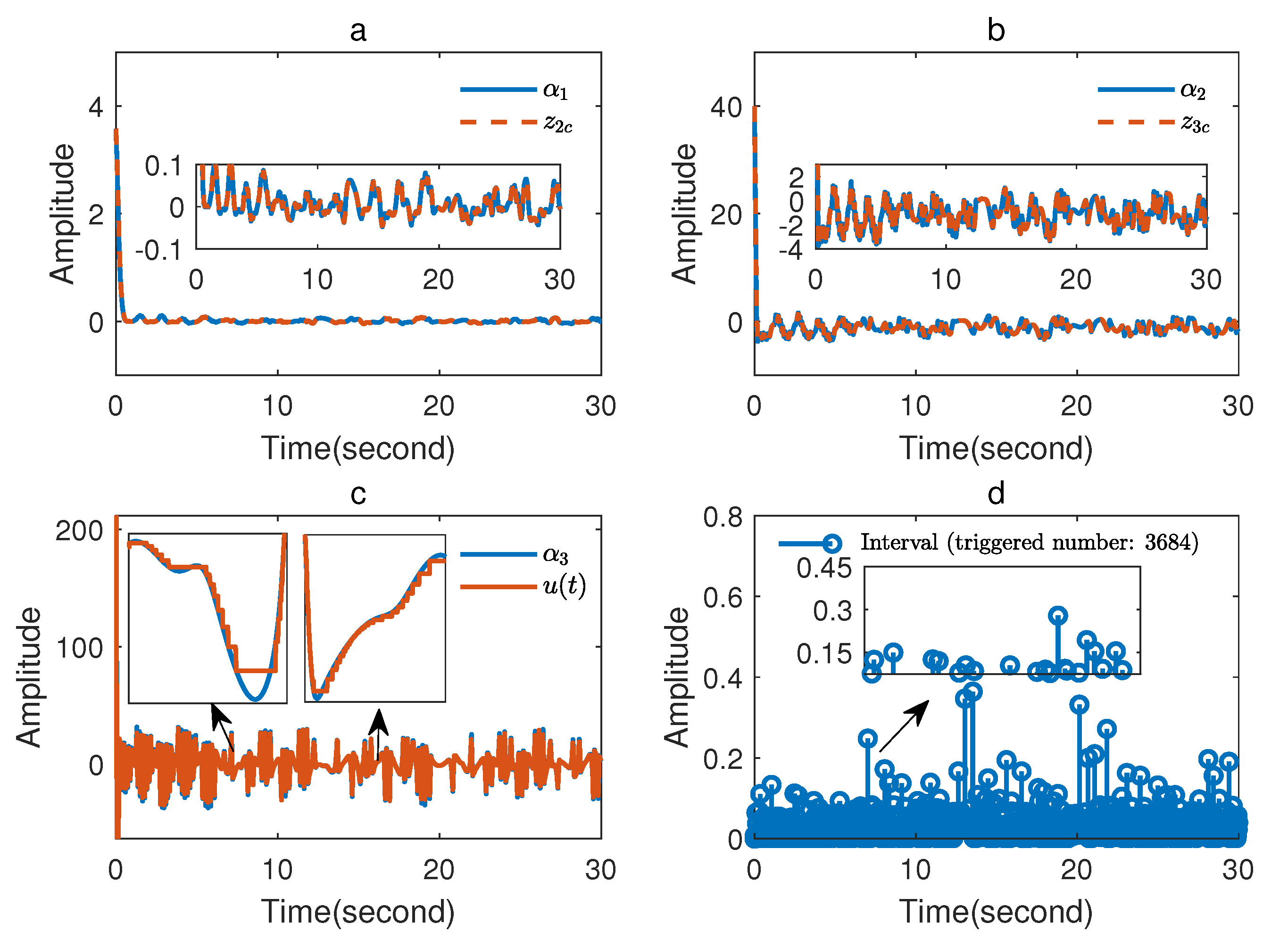In Figure 4, the trajectories of the virtual control signals ${\alpha }_1$, ${\alpha }_2$, the intermittently updated control input $u\left(t\right)$, and the number of triggering events are given simultaneously. It can be seen that the event-triggered strategy only required 3684 events to synchronize chaotic systems (sampling time is $0.001s$), whereas the number of times the traditional periodic sampling data controller in [19] executed was 30,000. Based on the above results, it can be inferred that the proposed event-triggered controller not only achieves the goal of synchronizing chaotic systems but also greatly reduces the number of controller executions and save a large amount of communication resources.

Remark 7.

An FLS is used to approximate any continuous functions on a compact operating space with a desired precision when enough fuzzy rules are provided. However, it should be emphasized that the structure of the FLS needs to be roughly determined in advance by the designer, that is, the number of membership functions, the membership function parameters, and other relevant inputs are required to be specified through analysis In this paper, the states of an FO Chua–Hartley chaotic system are known and measurable, that is, the value range of the system states have been determined, as seen in Figure 1. Therefore, the definition interval of the membership functions can be given, which is convenient for selecting the fuzzy approximation interval to improve approximation accuracy. In addition, increasing the number of fuzzy basis functions (fuzzy rules) can also improve the accuracy of FLSs but will increase the computational burden. Thus, based on computational resources, the appropriate number of fuzzy basis functions is chosen to deal with model uncertainties. In conclusion, since the fuzzy approximation is only ensured within a compact set, the stability results proposed are semiglobal when the initial values of the system are within the given compact set.

5. Conclusions

This paper investigated the chaos synchronization of FO chaotic systems using an adaptive fuzzy backstepping control scheme. By designing a dynamic event-triggered control method, the communication burden of control signals is reduced and the computational burden caused by the repeated differentiation of the virtual control signals is removed. To solve unknown model uncertainties and external disturbances, FLSs and a disturbance observer are introduced. It is proven that the mentioned control method is effective for solving the chaos synchronization problem. Although control performance is improved using the disturbance observer, it is difficult to obtain accurate estimation information of the time-varying external disturbance and function uncertainty because the estimation information between fuzzy systems and the disturbance observer is not shared. In the future, in order to obtain an accurate estimation, ways of sharing the estimation information between fuzzy systems and the disturbance observer will be studied.