An Extension on the Local Convergence for the Multi-Step Seventh Order Method with ψ-Continuity Condition in the Banach Spaces
Abstract
1. Introduction
2. Local Convergence Analysis
3. Numerical Example
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Behl, R.; Motsa, S.S. Geometric construction of eighth-order optimal families of Ostrowski’s method. Sci. World J. 2015, 2015, 614612. [Google Scholar] [CrossRef] [PubMed]
- Sharma, J.R.; Arora, H. A new family of optimal eighth order methods with dynamics for nonlinear equations. Appl. Math. Comput. 2016, 273, 924–933. [Google Scholar] [CrossRef]
- Rall, L.B. Computational Solution of Nonlinear Operator Equations; Robert, E., Ed.; Krieger Publishing Company: New York, NY, USA, 1979. [Google Scholar]
- Regmi, S.; Argyros, C.I.; Argyros, I.K.; George, S. Extended convergence of a sixth order scheme for solving equations under–continuity conditions. Moroc. J. Pure Appl. Anal. 2022, 8, 92–101. [Google Scholar] [CrossRef]
- Sharma, J.R.; Argyros, I.K. Local convergence of a Newton-Traub composition in Banach spaces. SeMA 2018, 75, 57–68. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Chelsea Publishing Company: New York, NY, USA, 1977. [Google Scholar]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Argyros, I.K.; George, S. Local convergence of two competing third order methods in Banach spaces. Appl. Math. 2016, 41, 341–350. [Google Scholar] [CrossRef]
- Argyros, I.K.; Khattri, S.K. Local convergence for a family of third order methods in Banach spaces, Punjab Univ. J. Math. 2016, 46, 52–63. [Google Scholar]
- Argyros, I.K.; Gonzalez, D.; Khattri, S.K. Local convergence of a one parameter fourth-order Jarratt-type method in Banach spaces. Comment. Math. Univ. Carol. 2016, 57, 289–300. [Google Scholar]
- Cordero, A.; Ezquerro, J.A.; Hernéz, M.A.; Torregrosa, J. On the local convergence of a fifth-order iterative method in Banach spaces. Appl. Math. Comput 2015, 251, 396–403. [Google Scholar] [CrossRef]
- Martínez, E.; Singh, S.; Hueso, J.L.; Gupta, D.K. Enlarging the convergence domain in local convergence studies for iterative methods in Banach spaces. Appl. Math. Comput. 2016, 281, 252–265. [Google Scholar] [CrossRef]
- Sharma, J.R.; Gupta, P. An efficient fifth order method for solving systems of nonlinear equations. Comput. Math. Appl. 2014, 67, 591–601. [Google Scholar] [CrossRef]
- Panday, B.; Jaiswal, J.P. On the local convergence of modified Homeier-like method in Banach spaces. Numer. Anal. Appl. 2018, 11, 332–345. [Google Scholar] [CrossRef]
- Xiao, X.; Yin, H. A new class of methods with higher order of convergence for solving systems of nonlinear equations. Appl. Math. Comput. 2015, 264, 300–309. [Google Scholar] [CrossRef]
- Saxena, A.; Jaiswal, J.P.; Pardasani, K.R. Broadening the convergence domain of Seventh-order method satisfying Lipschitz and Holder conditions. Results Nonlinear Anal. 2022, 5, 473–486. [Google Scholar] [CrossRef]
- Argyros, I.K.; Hilout, S. Computational Methods in Nonlinear Analysis; World Scientific Publishing Company: Singapore, 2013. [Google Scholar]
- Behl, R.; Argyros, I.K.; Mallawi, F.O. Some High-Order Convergent Iterative Procedures for Nonlinear Systems with Local Convergence. Mathematics 2021, 9, 1375. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Integral Equations; Chapman and Hall/CRC: Florida, NY, USA, 1998. [Google Scholar]
- Argyros, I.K.; George, S. Increasing the order of convergence for iterative methods in Banach space under weak conditions. Malaya J. Mat. 2018, 6, 396–401. [Google Scholar] [CrossRef] [PubMed][Green Version]
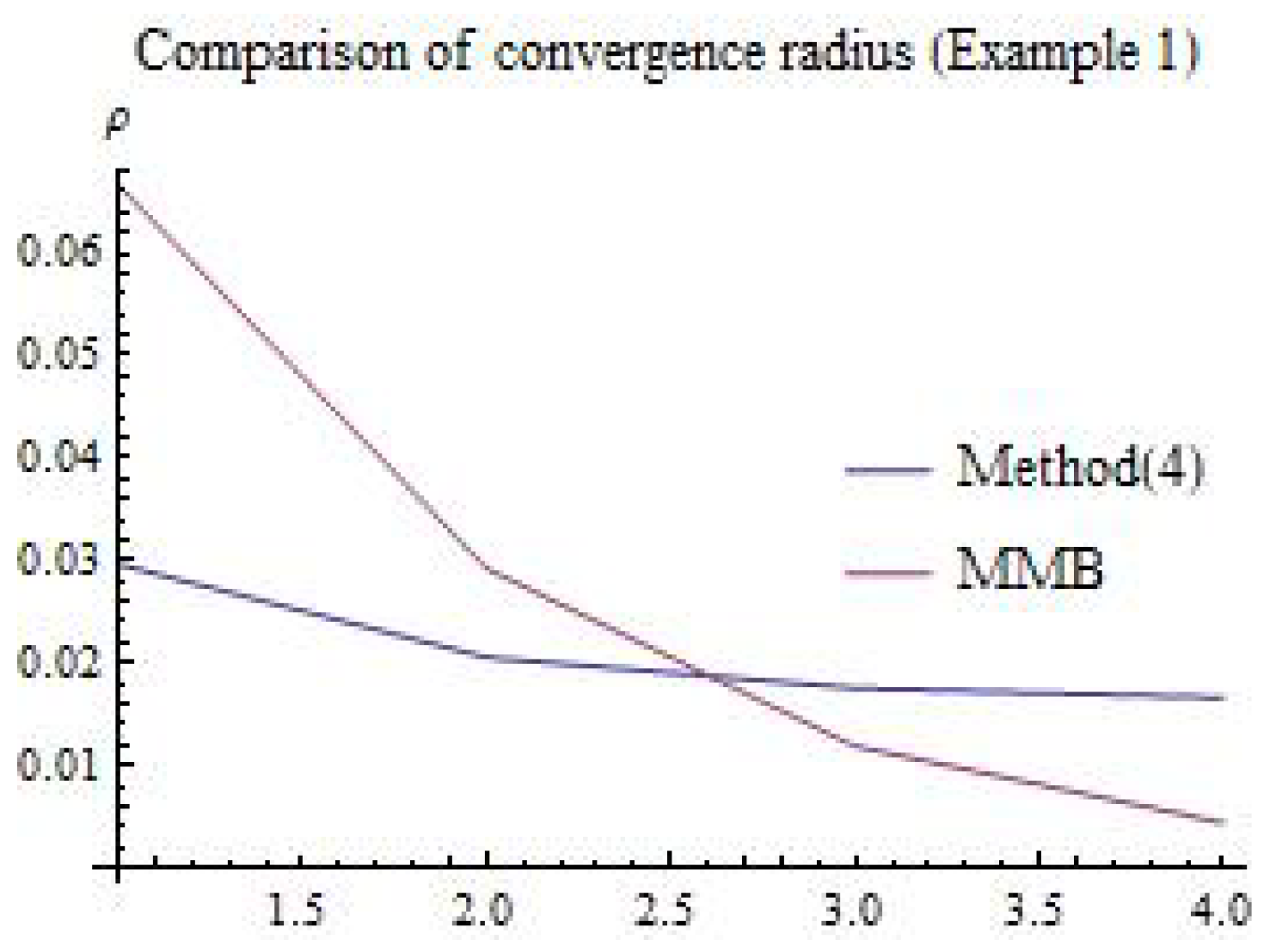



| Radius | |||||
|---|---|---|---|---|---|
| Method (4) | 0.0296296 | 0.0205601 | 0.0175449 | 0.0166341 | 0.0166341 |
| MMB | 0.0666667 | 0.0292298 | 0.0118907 | 0.00440901 | 0.00440901 |
| Radius | |||||
|---|---|---|---|---|---|
| Method (4) | 0.164331 | 0.135757 | 0.119283 | 0.114151 | 0.114151 |
| MMB | 0.382692 | 0.198328 | 0.0949498 | 0.040525 | 0.040525 |
| Radius | |||||
|---|---|---|---|---|---|
| Method (4) | 0.285714 | 0.238655 | 0.210099 | 0.201186 | 0.201186 |
| MMR | 0.44444 | 0.277466 | 0.15771 | - | 0.15771 |
| Radius | |||||
|---|---|---|---|---|---|
| Method (4) | 0.00295578 | 0.00246894 | 0.00217353 | 0.00208131 | 0.00208131 |
| MMB | 0.00689682 | 0.00344841 | 0.0015606 | 0.000621105 | 0.000621105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darvishi, M.T.; Al-Obaidi, R.H.; Saxena, A.; Prakash Jaiswal, J.; Raj Pardasani, K. An Extension on the Local Convergence for the Multi-Step Seventh Order Method with ψ-Continuity Condition in the Banach Spaces. Fractal Fract. 2022, 6, 713. https://doi.org/10.3390/fractalfract6120713
Darvishi MT, Al-Obaidi RH, Saxena A, Prakash Jaiswal J, Raj Pardasani K. An Extension on the Local Convergence for the Multi-Step Seventh Order Method with ψ-Continuity Condition in the Banach Spaces. Fractal and Fractional. 2022; 6(12):713. https://doi.org/10.3390/fractalfract6120713
Chicago/Turabian StyleDarvishi, Mohammad Taghi, R. H. Al-Obaidi, Akanksha Saxena, Jai Prakash Jaiswal, and Kamal Raj Pardasani. 2022. "An Extension on the Local Convergence for the Multi-Step Seventh Order Method with ψ-Continuity Condition in the Banach Spaces" Fractal and Fractional 6, no. 12: 713. https://doi.org/10.3390/fractalfract6120713
APA StyleDarvishi, M. T., Al-Obaidi, R. H., Saxena, A., Prakash Jaiswal, J., & Raj Pardasani, K. (2022). An Extension on the Local Convergence for the Multi-Step Seventh Order Method with ψ-Continuity Condition in the Banach Spaces. Fractal and Fractional, 6(12), 713. https://doi.org/10.3390/fractalfract6120713







