Triple-Positive Solutions for a Nonlinear Singular Fractional q-Difference Equation at Resonance

Abstract

Fractional q-calculus plays an extremely important role in mathematics and physics. In this paper, we aim to investigate the existence of triple-positive solutions for nonlinear singular fractional q-difference equation boundary value problems at resonance by means of the fixed-point index theorem and the q-Laplace transform, where the nonlinearity $f(t,u,v)$ permits singularities at $t=0,1$ and $u=v=0$. The obtained theorem is well illustrated with the aid of an example.

1. Introduction

Quantum calculus (or q-calculus) is calculus without limits, which was initially defined by Jackson [1], and has demonstrated applications in a variety of subjects such as quantum mechanics, hypergeometric series, particle physics and complex analysis (see [2,3,4]). In the development of q-calculus, fractional q-calculus was first proposed by Al-Salam and Agarwal in the 1960s (see [5,6]). Fractional q-calculus is widely used in physics, mathematics and other fields. It is well known that many practical problems can be reduced to fractional q-difference equations. In recent years, the solvability of boundary value problems (BVPs) for fractional q-difference equations has attracted much attention as a new research direction (see [7,8,9,10,11] and the references therein).

As is well known, fractional calculus has the characteristics of time memory and long distance spatial correlation. It is better than integer calculus at describing the properties of a polymer. It can also reflect the properties of viscoelastic materials with elastic solids and viscous fluids. In particular, it can describe the viscoelastic medium damping in the forced vibration equation well. To the best of our knowledge, the discussion of resonant problems is indispensable in the theoretical study of vibration equation, and many scholars have explored the resonant fractional BVPs by using various methods and techniques (see [12,13,14,15,16] and the references therein). Recently, in [17], Wang and Liu found the existence and uniqueness of positive solutions for a class of non-local fractional 3-point BVPs at resonance by means of the fixed-point index theory and iterative technique. In [18], Wang and Wang studied the existence of three positive solutions to a class of resonant fractional BVPs by using the fixed-point index theorem in a cone. In [19], Feng and Bai studied a class of nonlinear Caputo fractional differential equation BVPs at resonance in ${\mathbb{R}}^n$ and gave the sufficient conditions for the existence of solutions in different kernel spaces by using the Mawhin coincidence degree theorem.

It is worth noting that although there have been many rich results on the solution of the non-resonant fractional q-difference equation BVPs, limited work has been performed on the nonlinear q-difference equations at resonance. To fill this gap, we establish the existence of triple-positive solutions for a fractional q-difference equation BVP at resonance:

$$\left\{\begin{array}{c}{D}_q^{\beta }u\left(t\right)+f\left(t,u\left(t\right),D_q^{\alpha }u\left(t\right)\right)=0,t\in J,\hfill \\ {\displaystyle u\left(0\right)=D_{q}u\left(0\right)=0,D_q^{\alpha }u\left(1\right)=\sum _{i=1}^m{\sigma }_i{D}_q^{\alpha }u\left({\eta }_i\right),}\hfill \end{array}\right.$$

(1)

where $J:=(0,1)$, $q\in J$, $2\le \beta <3$, $0<\alpha <\beta -2$, ${\sigma }_i>0$, $0<{\eta }_1<\cdots <{\eta }_m<1$ and ${\sum }_{i=1}^m{\sigma }_i{\eta }_i^{\beta -\alpha -1}=1$, $D_q^{\beta }$ is the fractional q-derivative of the Riemann–Liouville type and of the order $\beta$. The nonlinearity $f(t,u,v)$ permits singularities at $t=0,1$ and $u=v=0$. It is clear that $\lambda =0$ and $c{t}^{\beta -1}$ solve the fractional q-difference equation $D_q^{\beta }u\left(t\right)+\lambda u\left(t\right)=0$ with the boundary conditions in Equation (1), and thus, the fractional q-difference equation BVP in Equation (1) is resonant.

Inspired by the work mentioned above, we are concerned in this paper with the existence of triple-positive solutions for the nonlinear singular fractional q-difference equation BVP at resonance in Equation (1) via the fixed-point index theorem and a q-Laplace transform. This paper is organized as follows. In Section 2, we give some definitions and lemmas which are used to prove the main theorem of this paper. In Section 3, the main theorem is established and proved. In Section 4, an example is given to demonstrate the validity of the results.

2. Preliminary Results

To begin with, we recall some necessary definitions and results of fractional q-calculus.

Definition 1

([20]). The Mittag-Leffler function is defined by

$$e_{\alpha ,\beta }(z;q)=\sum _{n=0}^{\infty }\frac{z^n}{{\Gamma }_q(n\alpha +\beta )}\left(\left|z{(1-q)}^{\alpha }\right|<1\right).$$

Definition 2

([6]). Let $\alpha \ge 0$ and f be a function defined on $[0,1]$. The fractional q-integral of the Riemann–Liouville type is $\left(I_q^{0}f\right)\left(x\right)=f\left(x\right)$, and

$$\left(I_q^{\alpha }f\right)\left(x\right)=\frac{1}{{\Gamma }_q\left(\alpha \right)}{\int }_0^x{(x-qt)}^{(\alpha -1)}f\left(t\right)d_{q}t,\alpha >0,x\in [0,1].$$

Definition 3

([6]). The fractional q-derivative of the Riemann–Liouville type of $\beta \ge 0$ is defined by

$$\left(D_q^{\beta }f\right)\left(s\right)=\left(D_q^l{I}_q^{l-\beta }f\right)\left(s\right),\beta >0,s\in [0,1],$$

where l is the smallest integer greater than or equal to β.

Next, we introduce the q-Laplace transform of the Riemann–Liouville fractional q-derivative and solve the fractional q-difference equation using the q-Laplace transform.

Lemma 1

([20]). If $n-1<\alpha \le n$ and $I_q^{n-\alpha }f\left(x\right)\in C_q^{\left(n\right)}[0,a]$, then the q-Laplace transform of the fractional q-derivative is given by

$${\displaystyle {}_q{L}_s{D}_q^{\alpha }f\left(x\right)=p^{\alpha }F\left(s\right)-\sum _{m=1}^n{D}_q^{\alpha -m}f\left(0^{+}\right)\frac{p^{m-1}}{1-q},}$$

where $p={\displaystyle \frac{s}{1-q}}$.

Lemma 2

([20]). Let $\alpha ,\beta ,a\in R^{+}$ and $k\in N$. Then, the identity

$${}_q{L}_s\left(t^{k\alpha +\beta -1}{e}_{\alpha ,\beta }^{\left(k\right)}(\pm a{t}^{\alpha };q)\right)=\frac{p^{\alpha -\beta }}{1-q}·\frac{k!}{{(p^{\alpha }\mp a)}^{k+1}},{\left|p\right|}^{\alpha }>a$$

is valid in the disk $\{t\in C:a|t(1-q){|}^{\alpha }<1\}.$

Lemma 3.

For $n-1<\alpha \le n$, the general solution to $D_q^{\alpha }f\left(t\right)-af\left(t\right)=h\left(t\right)$ is

$$f\left(t\right)={\int }_0^{t}G(t-q\tau ,\alpha ,\alpha )h\left(\tau \right)d_q\tau +\sum _{m=1}^n{D}_q^{\alpha -m}f\left(0^{+}\right)D_q^{m-1}G(t,\alpha ,\alpha ),$$

where

$$\begin{array}{c}\hfill G(t,\alpha ,\beta )=t^{\beta -1}{e}_{\alpha ,\beta }\left(a{t}^{\alpha };q\right),D_q^{m-1}G(t,\alpha ,\beta )=t^{\beta -m}{e}_{\alpha ,\beta -m+1}\left(a{t}^{\alpha };q\right).\end{array}$$

Proof. 

By combining Lemma 1 and the q-Laplace transform of both sides of this equation, we obtain

$${\displaystyle p^{\alpha }F\left(s\right)-\sum _{m=1}^n{D}_q^{\alpha -m}f\left(0^{+}\right)\frac{p^{m-1}}{1-q}-aF\left(s\right)=H\left(s\right).}$$

Thus, we have

$$F\left(s\right)=\frac{H\left(s\right)}{p^{\alpha }-a}+\frac{{\displaystyle {\sum }_{m=1}^n{D}_q^{\alpha -m}f\left(0^{+}\right)\frac{p^{m-1}}{1-q}}}{p^{\alpha }-a}.$$

Then, let

$$C\left(s\right)={}_q{L}_{s}c\left(t\right)=\frac{1}{p^{\alpha }-a},Z\left(s\right)={}_q{L}_{s}z\left(t\right)=\frac{{\displaystyle {\sum }_{m=1}^n{D}_q^{\alpha -m}y\left(0^{+}\right)\frac{p^{m-1}}{1-q}}}{p^{\alpha }-a}.$$

Hence, $F\left(s\right)=C\left(s\right)·H\left(s\right)+Z\left(s\right)$.

From Lemma 2, we can obtain

$${\displaystyle c\left(t\right)=(1-q)G(t,\alpha ,\alpha ),z\left(t\right)=\sum _{m=1}^n{D}_q^{\alpha -m}f\left(0^{+}\right)D_q^{m-1}G(t,\alpha ,\alpha ).}$$

According to the convolution theorem (see [20]) and the inverse of the q-Laplace transform, we obtain

$${}_q{L}_s^{-1}(C\left(s\right)·H\left(s\right))=c\left(t\right)\ast h\left(t\right)=\frac{1}{1-q}{\int }_0^{t}h\left(\tau \right)c(t-q\tau )d_q\tau .$$

Consequently, we obtain

$$\begin{array}{cc}\hfill f\left(t\right)& =\frac{1}{1-q}{\int }_0^{t}h\left(\tau \right)c(t-q\tau )d_q\tau +{\sum }_{m=1}^n{D}_q^{\alpha -m}f\left(0^{+}\right)D_q^{m-1}G(t,\alpha ,\alpha )\hfill \\ \hfill & ={\int }_0^{t}G(t-q\tau ,\alpha ,\alpha )h\left(\tau \right)d_q\tau +{\sum }_{m=1}^n{D}_q^{\alpha -m}f\left(0^{+}\right)D_q^{m-1}G(t,\alpha ,\alpha ).\hfill \end{array}$$

The proof is completed. □

Denote an increasing function

$${\displaystyle g\left(t\right)=\sum _{j=0}^{+\infty }\frac{t^j{[(j+1)(\beta -\alpha )-2]}_q{[(j+1)(\beta -\alpha )-3]}_q}{{\Gamma }_q\left((j+1)(\beta -\alpha )\right)},t>0.}$$

It is easy to know that $g\left(t\right)$ is well-defined and continuous on $[0,+\infty )$. By a simple calculation, we have $D_{q}g\left(t\right)>0$ on $(0,+\infty )$, and

$$g\left(0\right)=\frac{{[\alpha -\beta -2]}_q{[\alpha -\beta -3]}_q}{{\Gamma }_q(\alpha -\beta )}<0,\underset{t\to +\infty }{lim}g\left(t\right)=+\infty .$$

Therefore, there exists a unique positive root $a^{\ast }>0$; that is, $g\left(a^{\ast }\right)=0.$ Thus, we obtain the following lemma.

Lemma 4.

Let $u\left(t\right)=I_q^{\alpha }v\left(t\right)$. Then, the fractional q-BVP in Equation (1) is equivalent to

$$\left\{\begin{array}{c}-D_q^{\beta -\alpha }v\left(t\right)+av\left(t\right)=f(t,I_q^{\alpha }v\left(t\right),v\left(t\right))+av\left(t\right),t\in J,\hfill \\ {\displaystyle I_q^{\alpha }v\left(0\right)=D_q^{1-\alpha }v\left(0\right)=0,v\left(1\right)=\sum _{i=1}^m{\sigma }_{i}v\left({\eta }_i\right),}\hfill \end{array}\right.$$

(2)

where $2<\beta -\alpha <3$ and $a\in (0,a^{\ast })$ is a constant.

Proof. 

From Definition 3 and $u\left(t\right)=I_q^{\alpha }v\left(t\right)$, we obtain

$$D_q^{\beta }u\left(t\right)=D_q^{\beta -\alpha }v\left(t\right),D_{q}u\left(t\right)=D_q^{1-\alpha }v\left(t\right),D_q^{\alpha }u\left(t\right)=v\left(t\right).$$

Then, Equation (1) is equivalent to

$$\left\{\begin{array}{c}{D}_q^{\beta -\alpha }v\left(t\right)+f(t,I_q^{\alpha }v\left(t\right),v\left(t\right))=0,t\in J,\hfill \\ {\displaystyle I_q^{\alpha }v\left(0\right)=D_q^{1-\alpha }v\left(0\right)=0,v\left(1\right)=\sum _{i=1}^m{\sigma }_{i}v\left({\eta }_i\right).}\hfill \end{array}\right.$$

(3)

Obviously, Equation (3) is equivalent to Equation (2). Therefore, Equation (1) is equivalent to Equation (2). □

Lemma 5.

Let $h\in L_q^1[0,1].$ Then, the linear fractional q-BVP

$$\left\{\begin{array}{c}-D_q^{\beta -\alpha }v\left(t\right)+av\left(t\right)=h\left(t\right),t\in J,\hfill \\ {\displaystyle I_q^{\alpha }v\left(0\right)=D_q^{1-\alpha }v\left(0\right)=0,v\left(1\right)=\sum _{i=1}^m{\sigma }_{i}v\left({\eta }_i\right),}\hfill \end{array}\right.$$

(4)

has a unique solution

$$v\left(t\right)={\int }_0^{1}W(t,qs)h\left(s\right)d_{q}s,$$

where

$$\begin{array}{cc}\hfill & W(t,qs)=U(t,qs)+\frac{{\sum }_{i=1}^m{\sigma }_{i}U\left({\eta }_i,qs\right)G\left(t\right)}{G\left(1\right)-{\sum }_{i=1}^m{\sigma }_{i}G\left({\eta }_i\right)},\hfill \\ \hfill & G\left(t\right)=G(t,\beta -\alpha ,\beta -\alpha ),\hfill \\ \hfill & U(t,qs)=\frac{1}{G\left(1\right)}\left\{\begin{array}{c}G\left(t\right)G(1-qs),0\le t\le qs\le 1,\hfill \\ G\left(t\right)G(1-qs)-G\left(1\right)G(t-qs),0\le qs\le t\le 1.\hfill \end{array}\right.\hfill \end{array}$$

Proof. 

According to Lemma 3, we know that the solution to Equation (4) can be expressed by

$$v\left(t\right)=-{\int }_0^{t}G(t-qs)h\left(s\right)d_{q}s+c_{1}G\left(t\right)+c_2{D}_{q}G\left(t\right)+c_3{D}_q^{2}G\left(t\right),$$

where $c_1$, $c_2$ and $c_3$ are some constants to be determined. By $I_q^{\alpha }v\left(0\right)=D_q^{1-\alpha }v\left(0\right)=0$, there is $c_3=c_2=0$. Then, we obtain

$$v\left(t\right)=-{\int }_0^{t}G(t-qs)h\left(s\right)d_{q}s+c_{1}G\left(t\right).$$

By the boundary value condition ${\displaystyle v\left(1\right)=\sum _{i=1}^m{\sigma }_{i}v\left({\eta }_i\right)}$, we obtain

$$c_1=\frac{{\displaystyle {\int }_0^{1}G(1-qs)h\left(s\right)d_{q}s-{\sum }_{i=1}^m{\sigma }_i{\int }_0^{{\eta }_i}G({\eta }_i-qs)h\left(s\right)d_{q}s}}{{\displaystyle G\left(1\right)-{\sum }_{i=1}^m{\sigma }_{i}G\left({\eta }_i\right)}}.$$

Therefore, the solution to Equation (4) is

$$\begin{array}{cc}\hfill v\left(t\right)& =-{\int }_0^{t}G(t-qs)h\left(s\right)d_{q}s+\frac{{\displaystyle {\int }_0^{1}G(1-qs)h\left(s\right)d_{q}s-{\sum }_{i=1}^m{\sigma }_i{\int }_0^{{\eta }_i}G({\eta }_i-qs)h\left(s\right)d_{q}s}}{{\displaystyle G\left(1\right)-{\sum }_{i=1}^m{\sigma }_{i}G\left({\eta }_i\right)}}G\left(t\right)\hfill \\ \hfill & =\frac{{\int }_0^{1}G\left(t\right)G(1-qs)h\left(s\right)d_{q}s-{\int }_0^{t}G\left(1\right)G(t-qs)h\left(s\right)d_{q}s}{G\left(1\right)}-\frac{{\int }_0^{1}G(1-qs)h\left(s\right)d_{q}s}{G\left(1\right)}G\left(t\right)\hfill \\ \hfill & +\frac{{\displaystyle {\int }_0^{1}G(1-qs)h\left(s\right)d_{q}s-{\sum }_{i=1}^m{\sigma }_i{\int }_0^{{\eta }_i}G({\eta }_i-qs)h\left(s\right)d_{q}s}}{{\displaystyle G\left(1\right)-{\sum }_{i=1}^m{\sigma }_{i}G\left({\eta }_i\right)}}G\left(t\right)\hfill \\ \hfill & ={\int }_0^{1}U(t,qs)h\left(s\right)d_{q}s+\frac{{\displaystyle {\sum }_{i=1}^m{\sigma }_i{\int }_0^{1}U({\eta }_i,qs)h\left(s\right)d_{q}s}}{{\displaystyle G\left(1\right)-{\sum }_{i=1}^m{\sigma }_{i}G\left({\eta }_i\right)}}G\left(t\right)\hfill \\ \hfill & ={\int }_0^{1}W(t,qs)h\left(s\right)d_{q}s.\hfill \end{array}$$

The proof is completed. □

Lemma 6.

The function $U(t,qs)$ has the following properties:

(1) $U(t,qs)\ge {\tau }_1\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}(1-t)t^{\beta -\alpha -1},\forall t,qs\in \overline{J}=[0,1]$;

(2) $U(t,qs)\le {\tau }_2\left(qs\right){(1-qs)}^{(\beta -\alpha -1)},\forall t,qs\in \overline{J}$,

where

$${\tau }_1=\frac{1}{G\left(1\right){\left[{\Gamma }_q(\beta -\alpha )\right]}^2},{\tau }_2=\frac{{\left[D_{q}G\left(1\right)\right]}^2}{G\left(1\right)}.$$

Proof. 

The proof is similar to Theorem 3.1 in [21]. □

Lemma 7.

The function $W(t,qs)$ has the following properties:

(1) $W(t,qs)\ge {\rho }_1\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{t}^{\beta -\alpha -1},\forall t,qs\in \overline{J}$;

(2) $W(t,qs)\le {\rho }_2\left(qs\right){(1-qs)}^{(\beta -\alpha -1)},\forall t,qs\in \overline{J}$,

where

$${\rho }_1=\frac{{\displaystyle {\tau }_1(1-{\sum }_{i=1}^m{\sigma }_i{\eta }_i^{\beta -\alpha })}}{{\displaystyle {\Gamma }_q(\beta -\alpha )[G\left(1\right)-{\sum }_{i=1}^m{\sigma }_{i}G\left({\eta }_i\right)]}},{\rho }_2={\tau }_2[1+\frac{{\displaystyle G\left(1\right){\sum }_{i=1}^m{\sigma }_i}}{{\displaystyle G\left(1\right)-{\sum }_{i=1}^m{\sigma }_{i}G\left({\eta }_i\right)}}].$$

Proof. 

The proof is similar to Lemma 2.3 in [18]. □

Finally, we give the fixed-point index theorems, which are the key tools for our main results.

Lemma 8

([22]). Let P be a cone in a Banach space E, Ω be a bounded open set in E and θ be the zero element of Ω. $A:\overline{\mathsf{\Omega }}\cap P\to P$ is a completely continuous operator:

(1) If $\exists x_0\in P\setminus \left\{\theta \right\}$ such that $x-Ax\ne \lambda x_0,\forall \lambda \ge 0,x\in \partial \mathsf{\Omega }\cap P,$ then $i(A,\mathsf{\Omega }\cap P,P)=0$;

(2) If $Ax\ne \lambda x,\forall \lambda \ge 1,x\in \partial \mathsf{\Omega }\cap P,$ then $i(A,\mathsf{\Omega }\cap P,P)=1$.

Lemma 9

([23]). Let $A:\overline{P_{k_3}}\to P$ be a completely continuous operator. If there exist a concave positive functional ω with $\omega \left(x\right)\le \Vert x\Vert (x\in P)$ and numbers $k_3\ge k_2>k_1>0$ satisfying the following conditions:

(1) $\stackrel{\circ }{P}\left(\omega ,k_1,k_2\right)\ne \varnothing ,$ and $\omega \left(Ax\right)>k_1$ if $x\in P(\omega ,k_1,k_2);$

(2) $Ax\in \overline{P_{k_3}}$ if $x\in P(\omega ,k_1,k_3);$

(3) $\omega \left(Ax\right)>k_1$ for all $x\in P(\omega ,k_1,k_3)$ with $\Vert Ax\Vert >k_2$.

Then, $i(A,\stackrel{\circ }{P}\left(\omega ,k_1,k_3\right),\overline{P_{k_3}})=1$.

3. Existence Theorem of Positive Solutions

Let the Banach space $E=C\left(\overline{J}\right)$ with the norm $\Vert u\Vert ={max}_{0\le t\le 1}\left|u\left(t\right)\right|$. Define a cone

$$P=\left\{u\in E:u\left(t\right)\ge {\Lambda }_2\left(t\right)\Vert u\Vert ,t\in \overline{J}\right\}.$$

Set $b\in J$, denote ${\Lambda }^{\ast }={min}_{t\in [b,1]}{\Lambda }_2\left(t\right)$ and $\omega \left(u\right)={min}_{t\in [b,1]}u\left(t\right)$, $u\in P.$ $\forall k^{\ast }\ge k>0,$ and let $P(\omega ,k,k^{\ast })=\{u\in P:k\le \omega \left(u\right),\Vert u\Vert \le k^{\ast }\}$, $\stackrel{\circ }{P}\left(\omega ,k,k^{\ast }\right)=\{u\in P:k<\omega \left(u\right),\Vert u\Vert \le k^{\ast }\}$ and $P_k=\{u\in P:\Vert u\Vert <k\}$. Define the height functions such that

$$\begin{array}{cc}\hfill {\psi }_0(t,k,k^{\ast })& =max\left\{f(t,u,v)+av:k{\Lambda }_1\left(t\right)\le u\le \frac{k^{\ast }{t}^{\alpha }}{{\Gamma }_q(\alpha +1)},k{\Lambda }_2\left(t\right)\le v\le k^{\ast }\right\},\hfill \\ \hfill {\psi }_1(t,k)& =min\left\{f(t,u,v):k{\Lambda }_1\left(t\right)\le u\le \frac{k{t}^{\alpha }}{{\Gamma }_q(\alpha +1)},k{\Lambda }_2\left(t\right)\le v\le k\right\},\hfill \\ \hfill {\psi }_2(t,k,k^{\ast })& =min\left\{f(t,u,v)+av:\frac{k{t}^{\alpha }}{{\Gamma }_q(\alpha +1)}\le u\le \frac{k^{\ast }{t}^{\alpha }}{{\Gamma }_q(\alpha +1)},k\le v\le k^{\ast }\right\},\hfill \end{array}$$

where ${\Lambda }_1\left(t\right)=\frac{{\rho }_1{\Gamma }_q(\beta -\alpha )}{{\rho }_2{\Gamma }_q\left(\beta \right)}{t}^{\beta -1}$ and ${\Lambda }_2\left(t\right)=\frac{{\rho }_1}{{\rho }_2}{t}^{\beta -\alpha -1}.$

Theorem 1.

Suppose that there exist numbers $k_1$, $k_2$, $k_3$, $k_4$ and $k_5$ with $0<k_1<k_2<k_3<k_4\le k_5$ and $k_3\le k_4{\Lambda }^{\ast }$ such that the following are true:

$\left(H_1\right)$ f is continuous, and $(0,1)\times (0,\frac{k_5}{{\Gamma }_q(\alpha +1)})\times (0,k_5)$ with $f(t,u,v)+av\ge 0.$

$\left(H_2\right)$${\psi }_0\left(t,k_1,k_5\right)\in L_q^1[0,1].$

$\left(H_3\right)$${\psi }_1\left(t,k_1\right)\ge 0.$

$\left(H_4\right)$${\int }_0^1{\psi }_0\left(s,k_2,k_2\right)\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{d}_{q}s<k_2{\rho }_2^{-1}$.

$\left(H_5\right)$${\int }_b^1{\psi }_2\left(s,k_3,k_4\right)\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{d}_{q}s>k_3{\left[{\Lambda }^{\ast }{\rho }_2\right]}^{-1}$.

$\left(H_6\right)$${\int }_0^1{\psi }_0\left(s,k_3,k_5\right)\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{d}_{q}s\le k_5{\rho }_2^{-1}$.

Then, the resonant fractional q-difference equation BVP in Equation (1) has at least three positive solutions.

Proof. 

Set

$$Tv\left(t\right)={\int }_0^{1}W(t,qs)v\left(s\right)d_{q}s,Av\left(t\right)={\int }_0^{1}W(t,qs)\left[f\left(s,I_q^{\alpha }v\left(s\right),v\left(s\right)\right)+av\left(s\right)\right]d_{q}s.$$

Clearly, $T:P\to P$ is a completely continuous linear operator. By Lemma 2.3 in [24], we know the first eigenvalue of T is ${\lambda }_1=a$, and $\phi \left(t\right)=t^{\beta -\alpha -1}$ is a corresponding eigenfunction; that is, $aT\phi =\phi$. For any $v\in \overline{P_{k_5}}\setminus P_{k_1}$, we have $k_1{\Lambda }_2\left(t\right)\le v\left(t\right)\le k_5$ and $k_1{\Lambda }_1\left(t\right)\le I_q^{\alpha }v\left(t\right)\le \frac{k_5{t}^{\alpha }}{{\Gamma }_q(\alpha +1)}$. Combining $\left(H1\right)$ and $\left(H2\right)$, we have $A:\overline{P_{k_5}}\setminus P_{k_1}\to P$ being completely continuous. (The proof is similar to Lemma 2.6 in [25]). By applying the extension theorem of a completely continuous operator, A can be extended to a completely continuous operator $\tilde{A}:P\to P$. For simplicity, write $\tilde{A}$ as A.

Next, we will prove A has two fixed points on $\stackrel{\circ }{P}\left(\omega ,k_3,k_5\right)$ and $P_{k_5}\setminus (\stackrel{\circ }{P}\left(\omega ,k_3,k_5\right)\cup P_{k_2})$.

(1) It is easy to show that $\stackrel{\circ }{P}\left(\omega ,k_3,k_4\right)\ne \varnothing$. For any $v\in P(\omega ,k_3,k_4)$, we have $k_3\le v\left(t\right)\le k_4$ and $\frac{k_3{t}^{\alpha }}{{\Gamma }_q(\alpha +1)}\le I_q^{\alpha }v\left(t\right)\le \frac{k_4{t}^{\alpha }}{{\Gamma }_q(\alpha +1)}$ for $t\in [b,1]$. By Lemma 7 and $\left(H5\right)$, we have

$$\begin{array}{cc}\hfill \omega \left(Av\right)& =\underset{t\in [b,1]}{min}Av\left(t\right)\hfill \\ \hfill & \ge \underset{t\in [b,1]}{min}{\rho }_1{t}^{\beta -\alpha -1}{\int }_0^1\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}[f\left(s,I_q^{\alpha }v\left(s\right),v\left(s\right)\right)+av\left(s\right)]d_{q}s\hfill \\ \hfill & \ge {\Lambda }^{\ast }{\rho }_2{\int }_a^1\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{\psi }_2\left(s,k_3,k_4\right)d_{q}s>k_3.\hfill \end{array}$$

(2) For any $v\in P(\omega ,k_3,k_5)$, we have $k_3{\Lambda }_2\left(t\right)\le v\left(t\right)\le k_5$ and $k_3{\Lambda }_1\left(t\right)\le I_q^{\alpha }v\left(t\right)\le \frac{k_5{t}^{\alpha }}{{\Gamma }_q(\alpha +1)}$ for $t\in \overline{J}$. By Lemma 7 and $\left(H6\right)$, we have

$$Av\le {\rho }_2{\int }_0^1\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{\psi }_0\left(s,k_3,k_5\right)d_{q}s\le k_5.$$

Therefore, $Av\in \overline{P_{k_5}}$.

(3) For any $v\in P(\omega ,k_3,k_5)$ with $\Vert Av\Vert >k_4,$ we have

$$\omega \left(Av\right)=\underset{t\in [b,1]}{min}\left(Av\right)\left(t\right)\ge \underset{t\in [b,1]}{min}{\Lambda }_2\left(t\right)\Vert Av\Vert ={\Lambda }^{\ast }\Vert Av\Vert >{\Lambda }^{\ast }{k}_4\ge k_3.$$

It follows from Lemma 9 that

$$i(A,\stackrel{\circ }{P}\left(\omega ,k_3,k_5\right),\overline{P_{k_5}})=1.$$

(5)

For $v\in \partial P_{k_2}$, we have $k_2{\Lambda }_2\left(t\right)\le v\left(t\right)\le k_2$ and $k_2{\Lambda }_1\left(t\right)\le I_q^{\alpha }v\left(t\right)\le \frac{k_2{t}^{\alpha }}{{\Gamma }_q(\alpha +1)}$. By Lemma 7 and $\left(H_4\right)$, we have

$$Av\left(t\right)\le {\rho }_2{\int }_0^1\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{\psi }_0\left(s,k_2,k_2\right)d_{q}s<k_2,$$

which implies that $Av\ne \lambda v, \forall \lambda \ge 1$. Then, it follows from Lemma 8 that

$$i(A,P_{k_2},P)=1.$$

(6)

Similarly, for $v\in \partial P_{k_5}$, by Lemma 7 and $\left(H6\right)$, we obtain

$$Av\left(t\right)\le {\rho }_2{\int }_0^1\left(qs\right){(1-qs)}^{(\beta -\alpha -1)}{\psi }_0\left(s,k_3,k_5\right)d_{q}s<k_5.$$

Then, we obtain

$$i(A,P_{k_5},P)=1.$$

(7)

It follows from Equations (5)–(7) that

$$i(A,P_{k_5}\setminus (\stackrel{\circ }{P}\left(\omega ,k_3,k_5\right))\cup P_{k_2},\overline{P_{k_5}})=-1.$$

(8)

Equations (5) and (8) yield that A has two fixed points $v_1\in \stackrel{\circ }{P}\left(\omega ,k_3,k_5\right)$ and $v_2\in P_{k_5}\setminus (\stackrel{\circ }{P}\left(\omega ,k_3,k_5\right)\cup P_{k_2})$.

Finally, we need to show that A has another positive fixed point on $P_{k_2}\setminus P_{k_1}$.

Suppose there exist ${\lambda }_2>0$ and $v_1\in \partial P_{k_1}$ such that

$$v_1-A{v}_1={\lambda }_2\phi .$$

Then, $v_1\ge {\lambda }_2\phi .$ By having ${\lambda }^{\ast }=sup\{\lambda :v_1\ge \lambda \phi \}$, we can obtain $v_1\ge {\lambda }^{\ast }\phi .$ According to $\left(H3\right)$, we have

$$A{v}_1\left(t\right)={\int }_0^{1}W(t,qs)\left[f\left(s,I_q^{\alpha }{v}_1\left(s\right),v_1\left(s\right)\right)+a{v}_1\left(s\right)\right]d_{q}s\ge a{\int }_0^{1}W(t,qs)v_1\left(s\right)d_{q}s=aT{v}_1.$$

Therefore, we obtain

$$v_1=A{v}_1+{\lambda }_2\phi \ge aT{v}_1+{\lambda }_2\phi \ge aT\left({\lambda }^{\ast }\phi \right)+{\lambda }_2\phi =({\lambda }^{\ast }+{\lambda }_2)\phi .$$

This is a contradiction to the definition of ${\lambda }^{\ast }$. Therefore, condition (1) of Lemma 8 is satisfied, and we have

$$i(A,P_{k_1},P)=0.$$

(9)

Therefore, by Equations (6) and (9), we find that A has a fixed point $v_3\in P_{k_2}\setminus P_{k_1}.$ Clearly, $I_q^{\alpha }{v}_i\left(t\right),i=1,2,3$ are three positive solutions to Equation (1). The proof is completed. □

4. Application

Consider the resonant fractional q-difference equation BVP

$$\left\{\begin{array}{c}{D}_q^{2.6}u\left(t\right)+f(t,u\left(t\right),D_q^{0.1}u\left(t\right))=0,t\in J,\hfill \\ u\left(0\right)=D_{q}u\left(0\right)=0,D_q^{0.1}u\left(1\right)=0.8^{-1.5}{D}_q^{0.1}u\left(0.8\right),\hfill \end{array}\right.$$

(10)

where $q=0.5$, $\beta =2.6$, $\alpha =0.1$ and

$$f(t,u,v)=\left\{\begin{array}{c}{\displaystyle \frac{t^6{u}^{-0.5}}{300}}+{\displaystyle \frac{v^{-0.5}}{380}}+{\displaystyle \frac{{(1-t)}^6{v}^{-0.5}}{300}}-{\displaystyle \frac{v}{5}},(t,u,v)\in J\times (0,+\infty )\times (0,1],\hfill \\ {\displaystyle \frac{{(1-t)}^6}{300}}+{\displaystyle \frac{t^6{u}^{-0.5}}{300}}+{\displaystyle \frac{v^6}{380}}-{\displaystyle \frac{v}{5}},(t,u,v)\in J\times (0,+\infty )\times (1,5],\hfill \\ {\displaystyle \frac{{(1-t)}^6}{300}}+{\displaystyle \frac{t^6{u}^{-0.5}}{300}}+{\displaystyle \frac{v^{0.5}+5^6-\sqrt{5}}{380}}-{\displaystyle \frac{v}{5}},(t,u,v)\in J\times (0,+\infty )\times (5,+\infty ).\hfill \end{array}\right.$$

From

$${\displaystyle g\left(t\right)=\sum _{j=0}^{+\infty }\frac{t^j{[2.5(j+1)-2]}_q{[2.5(j+1)-3]}_q}{{\Gamma }_q\left(2.5(j+1)\right)},}$$

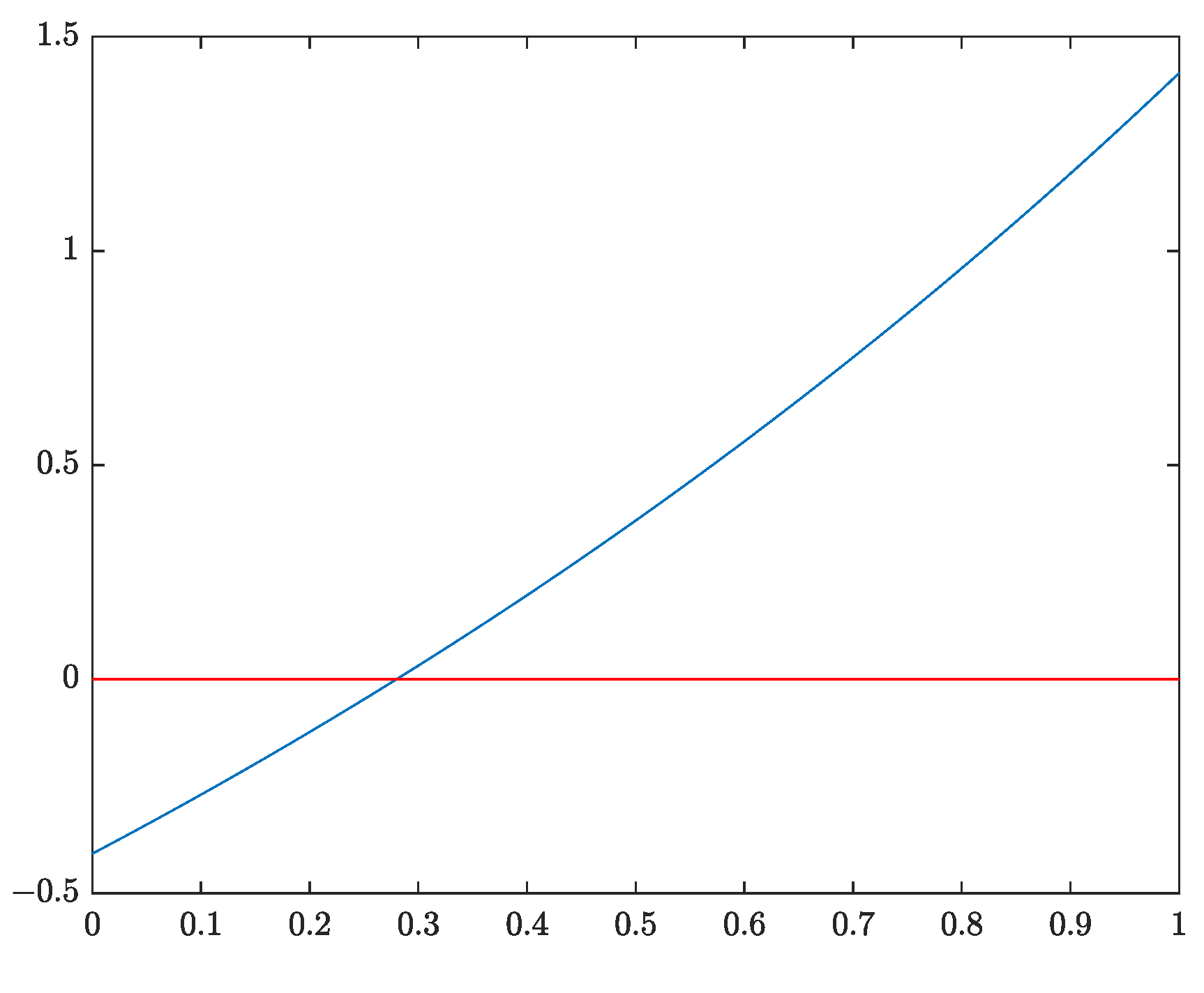
with the help of a MATLAB calculation, we find the function image of $g\left(t\right)$ (see Figure 1). As shown in Figure 1, we obtain $a^{\ast }\in (0.2,0.3)$. Let $a=0.2$ and $b=0.8.$

By simple calculations, we get $G\left(1\right)=0.8821$, $D_{q}G\left(1\right)=1.1652$, ${\tau }_1=0.7997$, ${\tau }_2=1.5392$, ${\rho }_1=7.2864$, ${\rho }_2=104.4550$, ${\Lambda }_1\left(t\right)=0.0669t^{1.6}$, ${\Lambda }_2\left(t\right)=0.0698t^{1.5}$, ${\Lambda }^{\ast }=0.05$ and ${\Lambda }^{\ast }{\rho }_2=5.2175.$

Choose $k_1=0.05$, $k_2=1$, $k_3=5$, $k_4=100$ and $k_5=717.$ It is easy to find that $\left(H1\right)$, $\left(H2\right)$ and $\left(H3\right)$ hold. By direct calculations, we have

$${\rho }_2{\int }_0^1{\psi }_0\left(s,k_2,k_2\right)\left(qs\right){(1-qs)}^{\left(1.5\right)}{d}_{q}s\approx 0.4322,$$

$${\Lambda }^{\ast }{\rho }_2{\int }_{0.8}^1{\psi }_2\left(s,k_3,k_4\right)\left(qs\right){(1-qs)}^{\left(1.5\right)}{d}_{q}s>{\Lambda }^{\ast }{\rho }_2{\int }_{0.8}^1\frac{k_3^6}{380}\left(qs\right){(1-qs)}^{\left(1.5\right)}{d}_{q}s\approx 8.7001,$$

and

$$\begin{array}{cc}\hfill & {\rho }_2{\int }_0^1{\psi }_0\left(s,k_3,k_5\right)\left(qs\right){(1-qs)}^{\left(1.5\right)}{d}_{q}s\hfill \\ \hfill <& {\rho }_2{\int }_0^1{\left[k_3{\Lambda }_2\left(s\right)\right]}^{-0.5}\left[\frac{1}{380}+\frac{{(1-s)}^6}{300\sqrt{s}}\right]\left(qs\right){(1-qs)}^{\left(1.5\right)}{d}_{q}s\hfill \\ \hfill & +{\rho }_2{\int }_0^1\left[\frac{s^6{\left(k_3{\Lambda }_1\left(s\right)\right)}^{-0.5}}{300}+\frac{{(1-s)}^6}{300\sqrt{s}}+\frac{k_5^{0.5}+5^6-\sqrt{5}}{380}\right]\left(qs\right){(1-qs)}^{\left(1.5\right)}{d}_{q}s\hfill \\ \hfill \approx & 716.7175.\hfill \end{array}$$

As shown above, $\left(H4\right)$, $\left(H5\right)$ and $\left(H6\right)$ hold. Therefore, according to Theorem 1, we have at least three positive solutions to the resonant fractional q-difference equation BVP in Equation (10).

5. Conclusions

Resonance problems play an important role in the study of vibration theory. However, there is little research on q-difference equation BVPs at resonance. In this article, we obtained the existence results of triple-positive solutions for a class of fractional q-difference equation BVPs at resonance by applying the fixed-point index theorem in a cone and a q-Laplace transform, which enriched the theories for q-difference equation resonance problems. Obviously, when the limit $q\to 1^{-}$, the equation in our paper reduced to the equation in the literature [18]. In the future, we will study the integral resonance problems and the impulse resonance problems on the infinite interval, develop the numerical simulation of the fractional q-difference equation resonance problems and explore the application of the fractional q-difference equation resonance problems.