A Stochastic Bayesian Neural Network for the Mosquito Dispersal Mathematical System
Abstract
1. Introduction
- A computational novel AI based BSR-NNs is presented to get the numerical solutions of the MDMS.
- The performance of the AI based BSR-NNs is observed to solve three different variations of the MDMS.
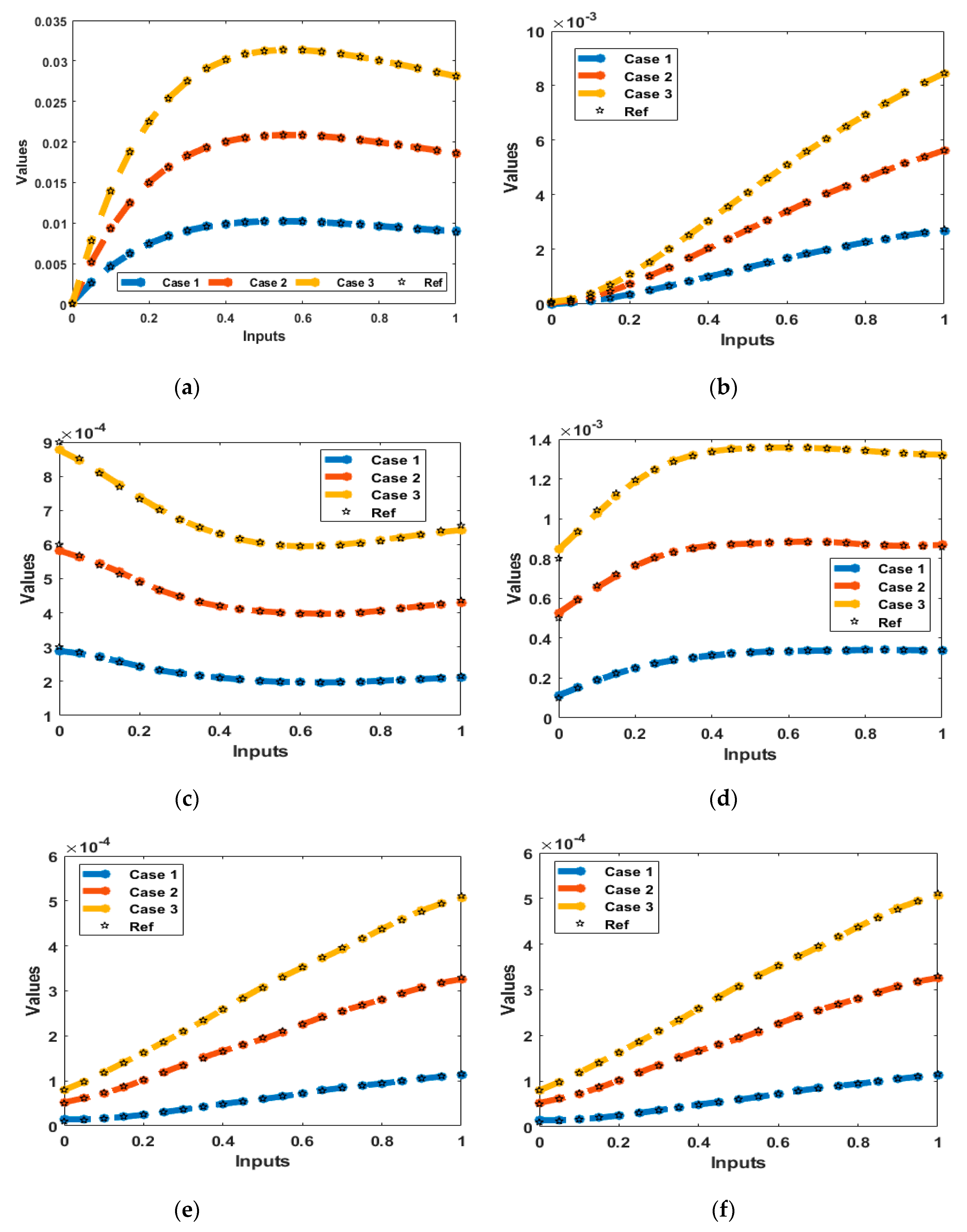
- For the correctness of the AI scheme portrayed by the BSR-NNs, the comparison performances using the obtained and reference solutions have been presented.
- Twelve number of hidden neurons have been taken to solve effectively the MDMS by applying the BSR-NNs.
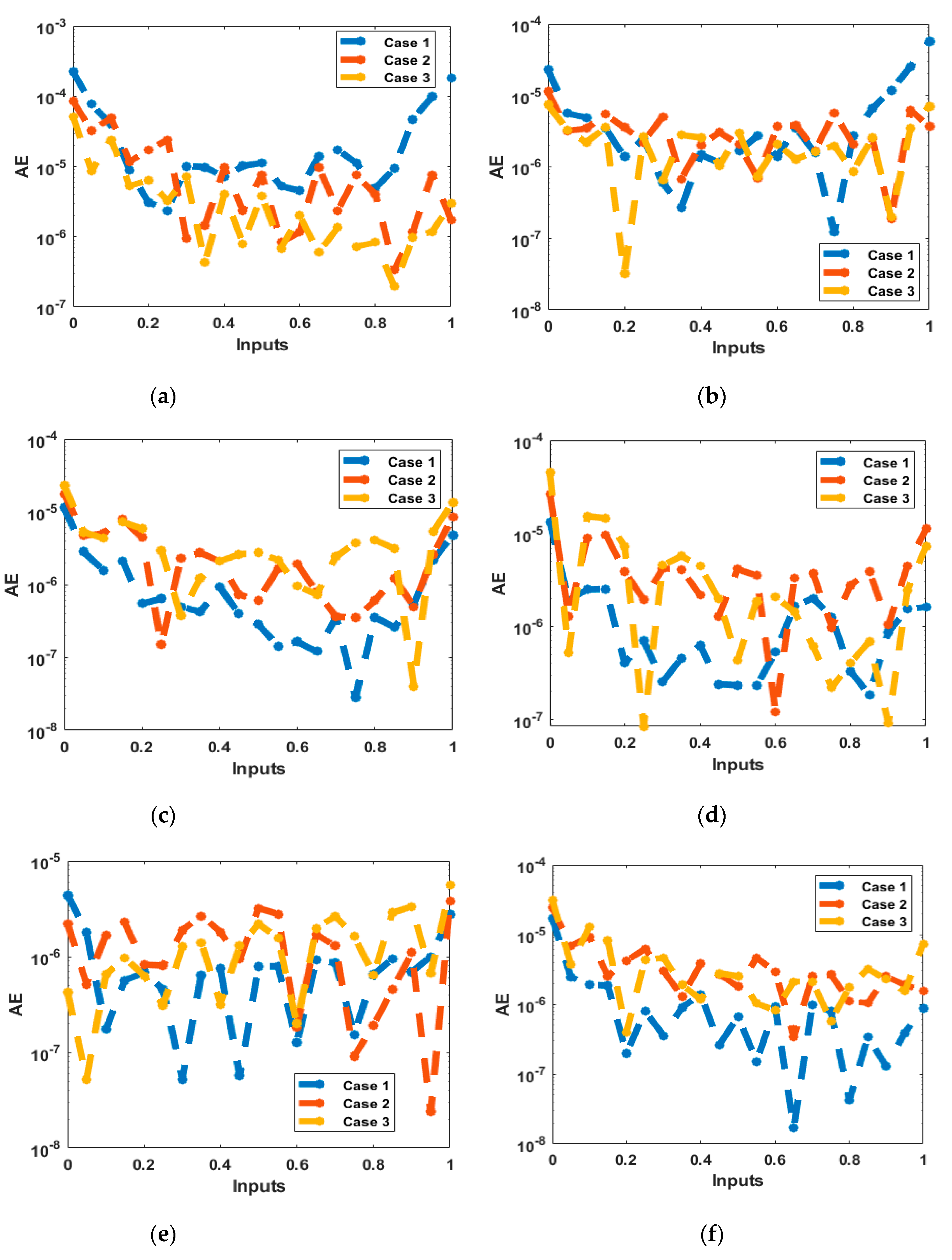
- The absolute error (AE) is achieved in exceptional performances that demonstrate the accuracy of the BSR-NNs.
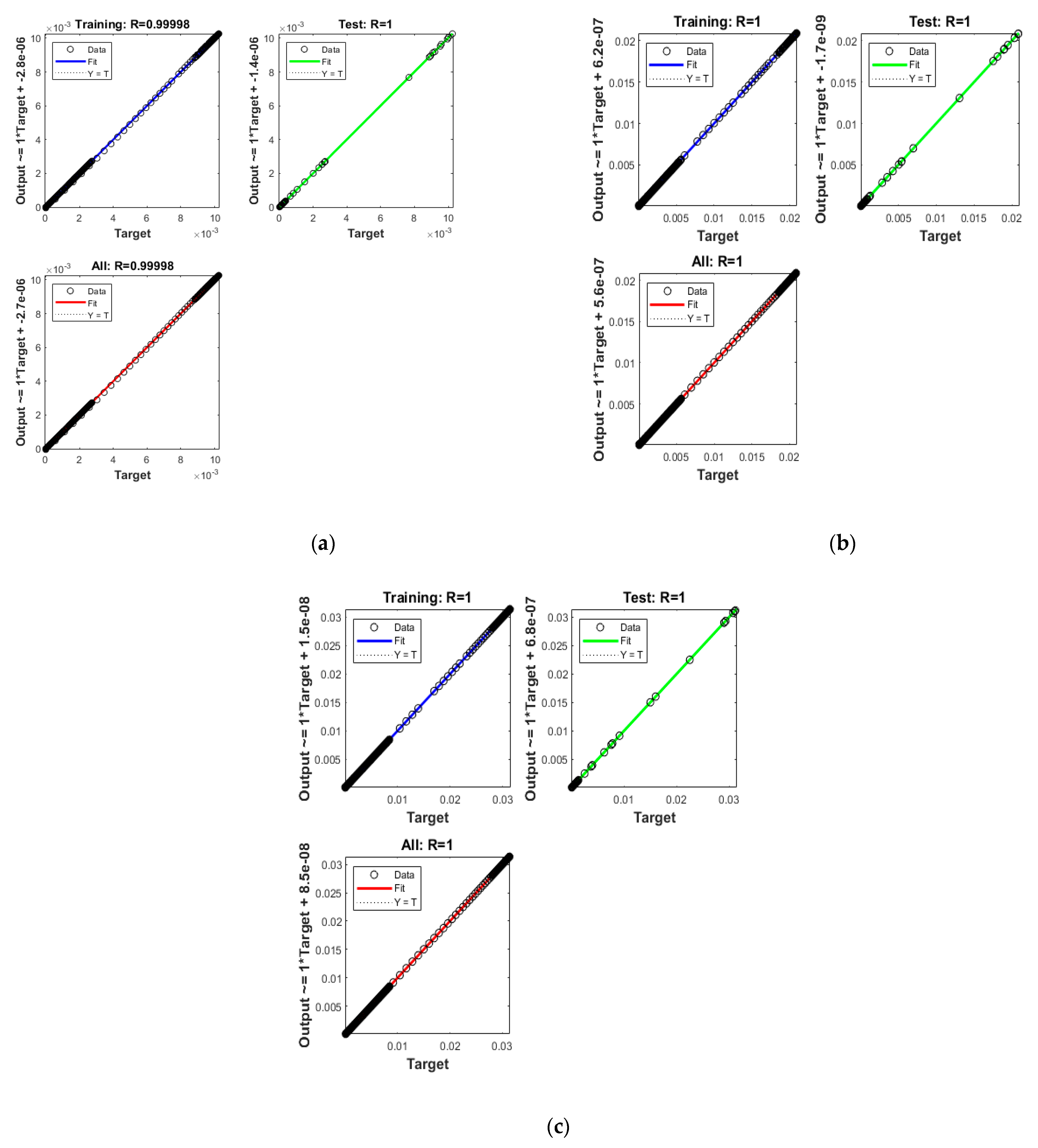
- For the solution of the dynamical MDMS, the correlation performances, error histograms, regression are also provided that endorsed the accuracy.
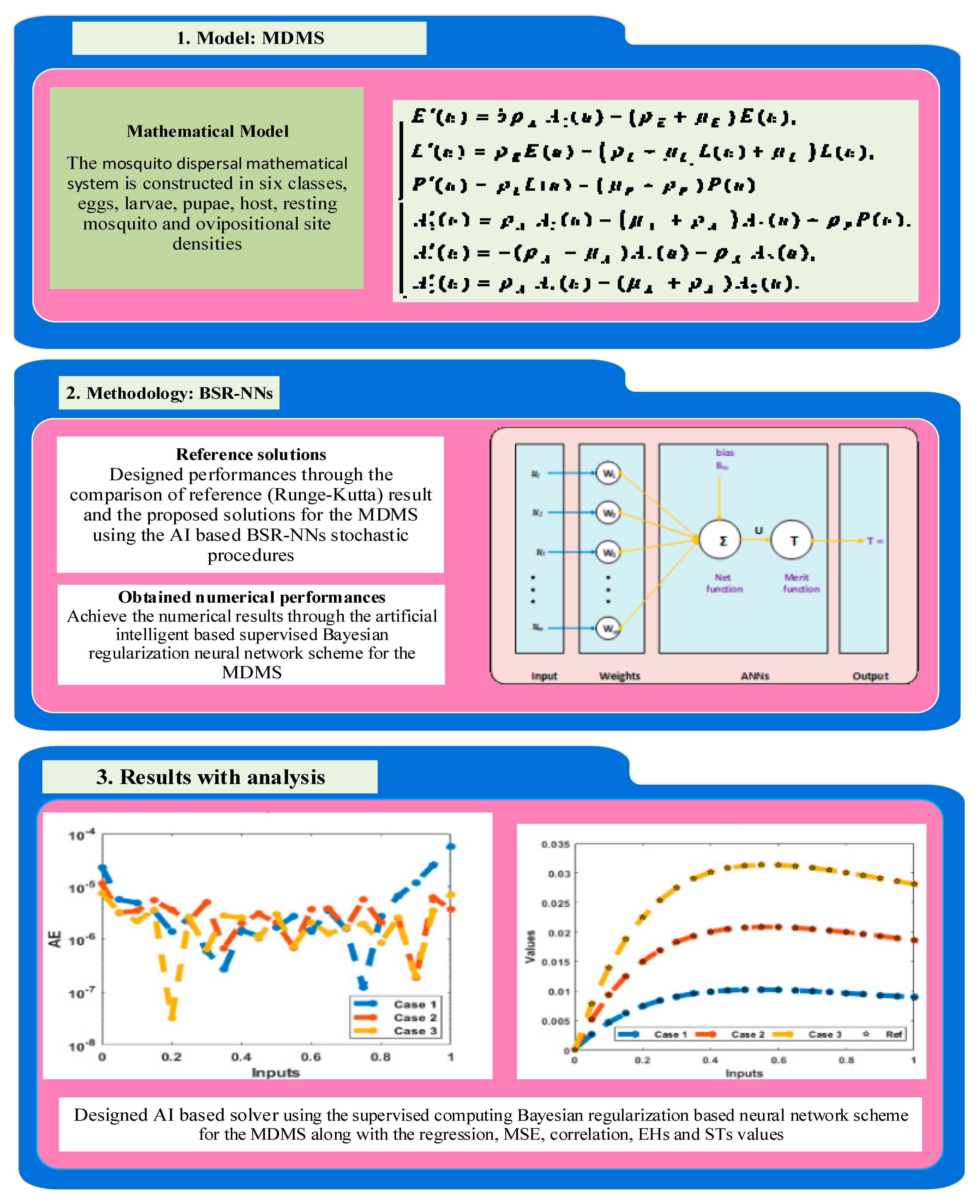
2. Methodology
3. Results and Discussion
4. Concluding Remarks
- The stochastic artificial intelligence based on Bayesian regularization neural network procedure has never been provided before for the numerical solutions of the MDMS.
- The computing BSR-NNs procedure is implemented to solve three different variations based on the data of training, testing and verification that is respectively given as 75%, 15%, 10%.
- Twelve hidden numbers of neurons have been applied to present the solutions of the nonlinear mathematical system.
- The correctness of the AI based BSR-NNs is observed by using the comparison procedures of the obtained and reference solutions.
- The AE performances in good measures enhance the precision and exactness of the scheme for solving the model.
- The achieved results have been presented to authenticate the efficiency of the artificial intelligence enhanced by the Bayesian regularization neural networks using the regression/correlation, state transitions and error histograms.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gething, P.W.; Patil, A.P.; Smith, D.L.; Guerra, C.A.; Elyazar, I.R.; Johnston, J.L.; Tatem, A.J.; Hay, S.I. A new world malaria map: Plasmodium falciparum endemicity in 2010. Malar. J. 2011, 10, 378. [Google Scholar] [CrossRef] [PubMed]
- Tatem, A.J.; Rogers, D.J.; Hay, I.S. Estimating the malaria risk of African mosquito movement by air travel. Malar. J. 2006, 5, 57. [Google Scholar] [CrossRef] [PubMed]
- Le Menach, A.; McKenzie, F.E.; Flahault, A.; Smith, D.L. The unexpected importance of mosquito oviposition behaviour for malaria: Non-productive larval habitats can be sources for malaria transmission. Malar. J. 2005, 4, 23. [Google Scholar] [CrossRef]
- Ross, R. An Address on the logical basis of the sanitary policy of mosquito reduction: Delivered at the Section of Preventive Medicine of the International Congress of Arts and Science, Universal Exposition, St. Louis, September, 1904. Br. Med. J. 1905, 1, 1025. [Google Scholar] [CrossRef]
- Manga, L.; Fondjo, E.; Carnevale, P.; Robert, V. Importance of low dispersion of Anopheles gambiae (Diptera: Culicidae) on malaria transmission in hilly towns in south Cameroon. J. Med. Entomol. 1993, 30, 936–938. [Google Scholar] [CrossRef]
- Gu, W.; Novak, R.J. Agent-based modelling of mosquito foraging behaviour for malaria control. Trans. R. Soc. Trop. Med. Hyg. 2009, 103, 1105–1112. [Google Scholar] [CrossRef] [PubMed]
- Cano, J.; Descalzo, M.; Moreno, M.; Chen, Z.; Nzambo, S.; Bobuakasi, L.; Buatiche, J.N.; Ondo, M.; Micha, F.; Benito, A. Spatial variability in the density, distribution and vectorial capacity of anopheline species in a high transmission village (Equatorial Guinea). Malar. J. 2006, 5, 21. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ghosh, A.; Chowdhury, N.; Chandra, G. Plant extracts as potential mosquito larvicides. Indian J. Med. Res. 2012, 135, 581. [Google Scholar]
- Gillies, M.T.; Wilkes, T.J. Field experiments with a wind tunnel on the flight speed of some West African mosquitoes (Diptera: Culicidae). Bull. Entomol. Res. 1981, 71, 65–70. [Google Scholar] [CrossRef]
- Midega, J.T.; Mbogo, C.M.; Mwambi, H.; Wilson, M.D.; Ojwang, G.; Mwangangi, J.M.; Nzovu, J.G.; Githure, J.I.; Yan, G.; Beier, J.C. Estimating dispersal and survival of Anopheles gambiae and Anopheles funestus along the Kenyan coast by using mark–release–recapture methods. J. Med. Entomol. 2007, 44, 923–929. [Google Scholar] [CrossRef] [PubMed]
- Ngwa, G.A. On the population dynamics of the malaria vector. Bull. Math. Biol. 2006, 68, 2161–2189. [Google Scholar] [CrossRef] [PubMed]
- White, M.T.; Griffin, J.T.; Churcher, T.S.; Ferguson, N.M.; Basáñez, M.-G.; Ghani, A.C. Modelling the impact of vector control interventions on Anopheles gambiae population dynamics. Parasites Vectors 2011, 4, 153. [Google Scholar] [CrossRef] [PubMed]
- Otero, M.; Solari, H.G.; Schweigmann, N. A stochastic population dynamics model for Aedes aegypti: Formulation and application to a city with temperate climate. Bull. Math. Biol. 2006, 68, 1945–1974. [Google Scholar] [CrossRef]
- Saul, A. Zooprophylaxis or zoopotentiation: The outcome of introducing animals on vector transmission is highly dependent on the mosquito mortality while searching. Malar. J. 2003, 2, 32. [Google Scholar] [CrossRef]
- Raffy, M.; Tran, A. On the dynamics of flying insects populations controlled by large scale information. Theor. Popul. Biol. 2005, 68, 91–104. [Google Scholar] [CrossRef] [PubMed]
- Tran, A.; Raffy, M. On the dynamics of dengue epidemics from large-scale information. Theor. Popul. Biol. 2006, 69, 3–12. [Google Scholar] [CrossRef]
- Dumont, Y. Modeling mosquito distribution. Impact of the landscape. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2011; Volume 1389, pp. 1244–1247. [Google Scholar]
- Dumont, Y.; Dufourd, C. November. Spatio-temporal Modeling of Mosquito Distribution. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2011; Volume 1404, pp. 162–167. [Google Scholar]
- Umar, M.; Raja, M.A.Z.; Sabir, Z.; Alwabli, A.S.; Shoaib, M. A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment. Eur. Phys. J. Plus 2020, 135, 565. [Google Scholar] [CrossRef]
- Nisar, K.; Sabir, Z.; Raja, M.Z.; Ibrahim, A.A.; Rodrigues, J.; Khan, A.S.; Gupta, M.; Kamal, A.; Rawat, D. Evolutionary Integrated Heuristic with Gudermannian Neural Networks for second Kind of Lane–Emden Nonlinear Singular Models. Appl. Sci. 2021, 11, 4725. [Google Scholar] [CrossRef]
- Ammar, M.K.; Amin, M.R.; Hassan, M. Calculation of line of site periods between two artificial satellites under the action air drag. Appl. Math. Nonlinear Sci. 2018, 3, 339–352. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Khalique, C.M.; Unlu, C. Neuro-evolution computing for nonlinear multi-singular system of third order Emden–Fowler equation. Math. Comput. Simul. 2021, 185, 799–812. [Google Scholar] [CrossRef]
- Boykov, I.; Roudnev, V.; Boykova, A. Stability of Solutions to Systems of Nonlinear Differential Equations with Discontinuous Right-Hand Sides: Applications to Hopfield Artificial Neural Networks. Mathematics 2022, 10, 1524. [Google Scholar] [CrossRef]
- Ammar, M.K.; Amin, M.R.; Hassan, M. Visibility intervals between two artificial satellites under the action of Earth oblateness. Appl. Math. Nonlinear Sci. 2018, 3, 353–374. [Google Scholar] [CrossRef]
- Khodadadian, A.; Parvizi, M.; Teshnehlab, M.; Heitzinger, C. Rational Design of Field-Effect Sensors Using Partial Differential Equations, Bayesian Inversion, and Artificial Neural Networks. Sensors 2022, 22, 4785. [Google Scholar] [CrossRef]
- Dai, P.; Yu, X. An Artificial Neural Network Approach for Solving Space Fractional Differential Equations. Symmetry 2022, 14, 535. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X.; Liu, B.; Gao, M. Solving partial differential equations using deep learning and physical constraints. Appl. Sci. 2020, 10, 5917. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.; Shoaib, M.; Gupta, M.; Sánchez, Y. A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics. Symmetry 2020, 12, 1628. [Google Scholar] [CrossRef]
- Sabir, Z.; Umar, M.; Guirao, J.L.G.; Shoaib, M.; Raja, M.A.Z. Integrated intelligent computing paradigm for nonlinear multi-singular third-order Emden–Fowler equation. Neural Comput. Appl. 2021, 33, 3417–3436. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M.; Shoaib, M. Design of neuro-swarming-based heuristics to solve the third-order nonlinear multi-singular Emden–Fowler equation. Eur. Phys. J. Plus 2020, 135, 410. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Ying, S. DWNN: Deep Wavelet Neural Network for Solving Partial Differential Equations. Mathematics 2022, 10, 1976. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Global Mittag—Leffler Synchronization for Neural Networks Modeled by Impulsive Caputo Fractional Differential Equations with Distributed Delays. Symmetry 2018, 10, 473. [Google Scholar] [CrossRef]
- Akhmet, M.; Aruğaslan Çinçin, D.; Tleubergenova, M.; Nugayeva, Z. Unpredictable oscillations for Hopfield-type neural networks with delayed and advanced arguments. Mathematics 2021, 9, 571. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Tavera Romero, C.A.; Alarfaj, F.K. Theoretical analysis on absorption of carbon dioxide (CO2) into solutions of phenyl glycidyl ether (PGE) using nonlinear autoregressive exogenous neural networks. Molecules 2021, 26, 6041. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Zhang, G.T. Deep learning method based on physics informed neural network with resnet block for solving fluid flow problems. Water 2021, 13, 423. [Google Scholar] [CrossRef]
- Ilhan, E.; Kıymaz, I.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method. Appl. Math. Nonlinear Sci. 2019, 4, 141–150. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sreenadh, S.; Saravana, R. Influence of velocity slip and temperature jump conditions on the peristaltic flow of a Jeffrey fluid in contact with a Newtonian fluid. Appl. Math. Nonlinear Sci. 2017, 2, 429–442. [Google Scholar] [CrossRef]
- Pérez-García, V.M.; Fitzpatrick, S.; Pérez-Romasanta, L.A.; Pesic, M.; Schucht, P.; Arana, E.; Sánchez-Gómez, P. Applied mathematics and nonlinear sciences in the war on cancer. Appl. Math. Nonlinear Sci. 2016, 1, 423–436. [Google Scholar]
- Selvi, M.S.M.; Rajendran, L. Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems. Appl. Math. Nonlinear Sci. 2019, 4, 351–364. [Google Scholar]
- Aghili, A. Complete solution for the time fractional diffusion problem with mixed boundary conditions by operational method. Appl. Math. Nonlinear Sci. 2021, 6, 9–20. [Google Scholar] [CrossRef]
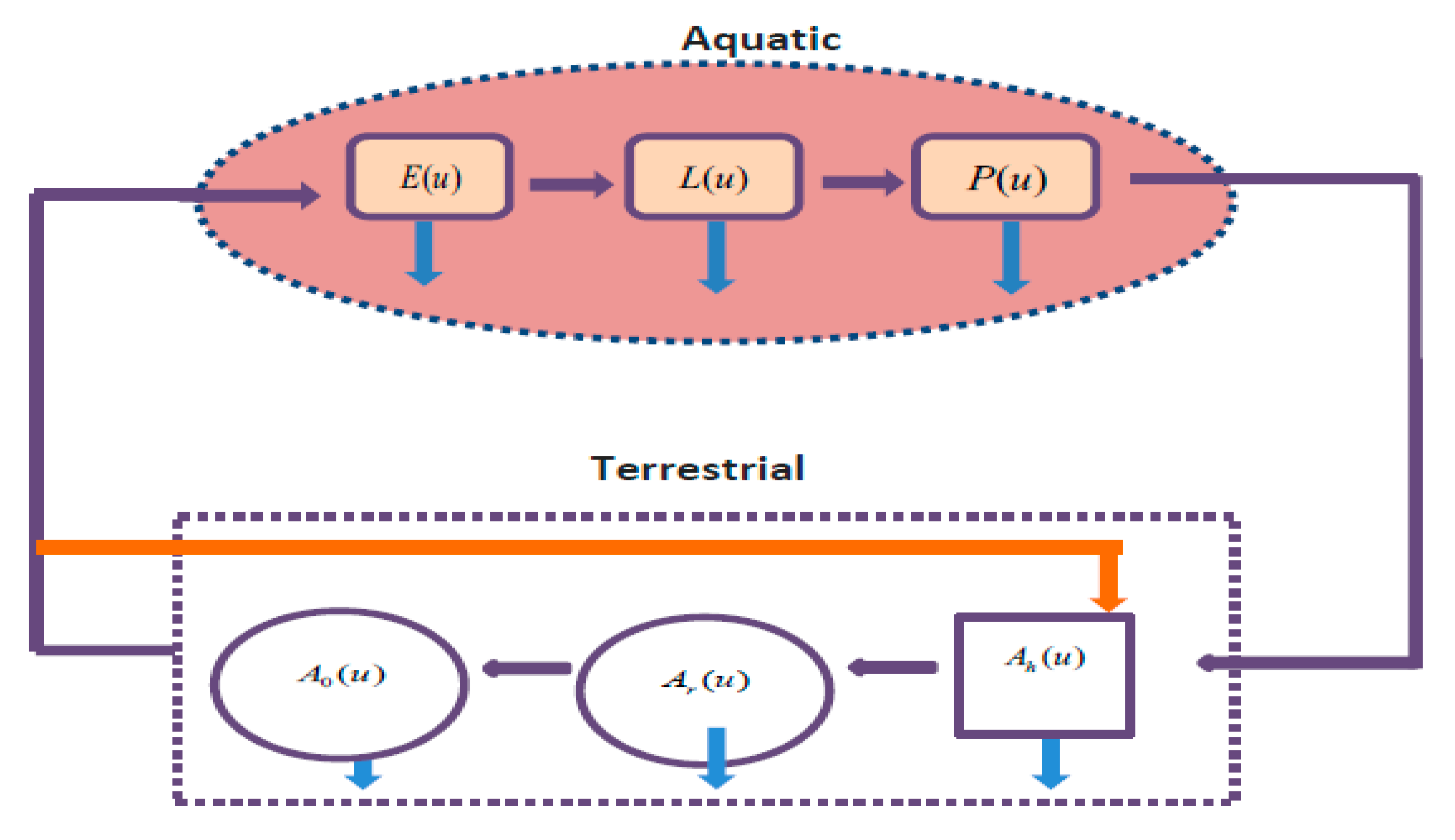




| Index | Particulars | Values | Range |
|---|---|---|---|
| Resting mortality rate (MR) to go in ovipositional places | 0.5 | 0.30–0.56 | |
| Pupae MR | 0.4 | 0.22–0.52 | |
| MR of eggs | 0.5 | 0.32–0.8 | |
| Mature larvae rate into pupae | 0.12 | 0.08–0.17 | |
| Resting MR mosquitoes | 0.0043 | 0.03–0.01 | |
| Host mosquitos using the latent conditions | 0.46 | 0.322–0.6 | |
| Dependent density rate-based larvae mortality | 0.02 | 0–1 | |
| Female eggs located per ovipositional | 60 | 50–300 | |
| Density-independent based larvae MR | 0.4 | 0.30–0.58 | |
| MR Mosquito using the ovipositional sites | 0.41 | 0.41–0.56 | |
| Rate of pupae growth into mature | 0.7 | 0.33–1 | |
| Ovipositional rate | 3.2 | 3–4 | |
| Mosquitoes MR using the hosts penetrating | 0.18 | 0.12–0.23 | |
| Eggs rate into larvae | 0.4 | 0.33–1 |
| Parameter | Settings |
|---|---|
| Maximum epochs | 200 |
| Fitness | 0 |
| Hidden neurons | 12 |
| Setting up Mu | 0.25 |
| Increasing performances of Mu | 14 |
| Adaptive Mu performances | 6 × 10−2 |
| Validation fail amount | 8 |
| Highest mu values | 109 |
| Minimum values of gradient | 10−8 |
| Train data | 75% |
| Verification statics | 10% |
| Test performances | 15% |
| Sample selection | Random |
| Output/input/hidden values | Single |
| Dataset generation | Runge-Kutta |
| Other | Default |
| Case | MSE | Epoch | Gradient | Performance | Mu | Time | |
|---|---|---|---|---|---|---|---|
| Test | Train | ||||||
| 1 | 5.504 × 10−10 | 4.942 × 10−10 | 3 | 5.74 × 10−8 | 4.94 × 10−10 | 0.0500 | 4 |
| 2 | 6.064 × 10−11 | 7.220 × 10−11 | 5 | 8.98 × 10−8 | 7.22 × 10−11 | 5 | 3 |
| 3 | 3.775 × 10−11 | 3.544 × 10−11 | 6 | 2.23 × 10−8 | 3.54 × 10−11 | 50 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suantai, S.; Sabir, Z.; Raja, M.A.Z.; Cholamjiak, W. A Stochastic Bayesian Neural Network for the Mosquito Dispersal Mathematical System. Fractal Fract. 2022, 6, 604. https://doi.org/10.3390/fractalfract6100604
Suantai S, Sabir Z, Raja MAZ, Cholamjiak W. A Stochastic Bayesian Neural Network for the Mosquito Dispersal Mathematical System. Fractal and Fractional. 2022; 6(10):604. https://doi.org/10.3390/fractalfract6100604
Chicago/Turabian StyleSuantai, Suthep, Zulqurnain Sabir, Muhammad Asif Zahoor Raja, and Watcharaporn Cholamjiak. 2022. "A Stochastic Bayesian Neural Network for the Mosquito Dispersal Mathematical System" Fractal and Fractional 6, no. 10: 604. https://doi.org/10.3390/fractalfract6100604
APA StyleSuantai, S., Sabir, Z., Raja, M. A. Z., & Cholamjiak, W. (2022). A Stochastic Bayesian Neural Network for the Mosquito Dispersal Mathematical System. Fractal and Fractional, 6(10), 604. https://doi.org/10.3390/fractalfract6100604








