Fractals Flow Simulation for Groundwater Flow with Varying Apertures by Using Analytic Element Method

Abstract

The work presented in this article is composed of 2-dimensional groundwater flow simulations for fractured porous media with different aperture of fractures by using the Analytic Element Method. In order to investigate the flow behavior and its effect on fractures, we considered different systems of fractures with varying apertures, hydraulic conductivities and orientations in the presence of uniform flow field and a well. We also introduced the matrix method to solve the problems for which the unknown coefficients are obtained from the discharge potential of all the elements present in the systems. The numerical solution of the prescribed problem is based on a series expansion, while the influence of each fracture is expressed in a series that satisfy Laplace’s equation.

1. Introduction

Groundwater is one of the most important source of water. In recent decades, several groundwater models have been developed to study the effects of intervention into the underground environment [1]. Groundwater is the study of occurrence, movement and distribution of water with different geological features beneath the earth surface. The flow direction of groundwater in an aquifer is measured by the static groundwater elevation at various points throughout the aquifer. It flows from higher static elevations to the lower ones. The most common methodology to understand the flow behavior on large scale is drawing contours lines inferred to equipotential hydraulic head, which is used to determine its flow direction. The contour lines for such methodology are perpendicular to the flow direction [2].

The problem of fractures is one of the most important and major challenge that overcome in groundwater flow. Over the last few decades, there has been significant increase in research into flows in fractured porous media. The presence of fractures that affect the flow and transport are features of various types of fractures ranging from millimeters to hundreds of kilometers [3]. In geophysical applications, the presence of fractures can have significant impact on flow in porous media. Fractures in fractured rocks have a wide range of scales from small joints to the larger faults. In particular, they can act as barriers or preferential flow paths due to their varying permeability. The problems of fractured porous media are complex and experimental data for such kind of problems is difficult to obtain [4]. The study of fractured porous media is necessary due to numerous reasons, for example, aquifers that have been fractured are significant resources of fresh water [5]. In view of recent advances in the context of geologic repository, simulation of groundwater flow in fractured porous media is a significant subject. Fractures, both natural and engineered provide major conduits and barriers for the fluid flows in different types of media. Fractures are classified in various sets each with it’s own geological history, direction and features. Various fracture sets consist of more or less interconnected networks. The hydraulic conductivity of an individual fracture is not the only factor that influence the flow, some other factors including fracture’s orientation, size, density and degree of connection also influence the flow in the system [6]. It is mostly observed in all geologic formations that spreading of groundwater is much faster than the porous media and act as a contamination vector. A fracture’s geometry is an important aspect in its formation and the process that occurs in it. It should have an elliptical form with no flow at the ends according to one of its basic principles. Fractures are typically thin and saturated with water. The fracture’s walls are symmetrical in relation to the planes passing through its centers [7,8]. The most prevalent conceptual model is that the fracture is generated by smooth and flat parallel plates as shown in many studies in various laboratories, see Refs. [8,9,10]. In literature, there are two types of flow models for fracture networks: continuous and discrete.

1.1. Continuous Models

Two or more continuous interacting fractures make up a continuous model. Such models are used when fractures are well-connected with one another but the porous medium is overlooked due to its directional dependency as well as influence of different scales on the features of fractures for transport. In general, in most circumstances its very difficult to suppose a continuous model for fractured system because of its complex nature [11].

1.2. Discrete Models

One of the most popular and widely used methodology for fractures is discrete network modeling, which describe fractured rocks as a population of individual fracture whose parameters (size, shape, orientation, aperture, and position) are derived from statistical probability distributions derived from the observations. Such models are used to describe phenomena as they explicitly include the attributes of each individual fracture. These models shows each fracture independently explaining it’s geometric features as well as the relationship between them [7]. Some uni, bi, tri-dimensional elements and parallel plate models are used in previous works to represent discrete-shaped fractured networks, for detail see Refs. [7,10,11,12,13,14].

In the literature, several conceptual flow models for fractured porous media have been proposed. Commonly groundwater simulations are made by employing finite difference, finite volume as well as finite element methods. Such methods are capable for simulating fractured flow phenomena but have drawbacks in terms of mesh generation, difficulties with scale differences, solution approximations and reliance on domain discretization etc. [7,15]. The required processing time for discrete model of network’s simplification and its simulation with such methods is large. Due to the given facts, the analytic element method (AEM) has a significant addition to groundwater modeling approaches and its computational cost.

1.3. Analytic Element Method

Otto D. L STRACK at University of Minnesota introduced the analytic element method over 30 years ago to solve the partial differential equations that model groundwater flow problems [16]. This method is computational, based on superposition principle of analytical expressions and is applied to both finite and infinite domains, which is commonly used to solve problems with intern boundaries [9]. It employ analytical elements, which are the exact solutions to the governing equations for basic aquifer characteristics such as rivers, wells, impermeable barriers and sinks to approximate solutions of considerably more complex issues. The governing equations generated by using the AEM are precise, while the boundary conditions only be approximated [7,12,15,16,17,18]. The proposed method is used for solving the groundwater flow systems that involve the combination of elementary analytic solutions. The analytical elements which are actually mathematical functions are chosen in this method to be represented as specific hydrogeologic features. Each solution represents hydrogeologic feature with free coefficients on the said function. The free coefficients may be calculated by specifying the boundary conditions for the elements coordinate points. This method has gained popularity in recent years due to its applications to harmonically heterogeneous aquifers among other advances. From the literature, several approaches have been introduced and solved the problems of groundwater flow to improve the numerical accuracy and reduce the processing time for the resulting system of equations [19,20]. Besides that, this method has advantage due to the lack of a model grid for a trade-off between model resolution and area size, as a result, the analytic element method is scale-insensitive. The prescribed method is much more efficient for solving problems in large aquifers. It solves regional flow problems by providing a composite analytic solution that satisfies the governing equations everywhere and guarantees flow continuity.

In this work, we introduced discrete models of fractured porous media by using the analytic element method as well as the matrix method by using the intern boundary conditions for simulation of groundwater flow. In order to investigate the flow behavior and its effects, different systems of fractures with varying apertures, orientations and hydraulic conductivities in the presence of uniform flow field and a well have been considered in this paper. To solve the system of linear equations deriving from analytical elements, we apply the concept of AEM and get the desired results for fractured networks with varying apertures. The remaining work in this paper is organized as follows: Section 2 consists of complex potential for fractured networks, Section 3 recalls description of boundary conditions with different hydraulic conductivities in comparison with background hydraulic conductivity, Section 4 and Section 5 describe equations of unknown coefficients for solution algorithm, whereas Section 6 and Section 7 composed of results and its detailed description as well as conclusion part of the desired work.

2. Complex Potential

The complex potential $\Omega \left(z\right)$ is described as follows:

$$\Omega \left(z\right)=\Phi \left(z\right)+i\Psi \left(z\right),$$

(1)

where $z=x+iy$ represent the location in complex plane, $\Phi \left(z\right)$ represent the discharge potential and $\Psi \left(z\right)$ represent the related stream function. The complex potential is represented as the sum of multiple components of the complex potential in the analytic element method utilizing the superposition principle [16,17,18]. The discharge potential is the real part of complex potential, which is denoted by $\Phi$ and specified for confined as well as unconfined aquifers. The discharge potential for confined aquifer using hydraulic conductivity K and thickness H take the form:

$$\Phi \left(z\right)=KH\varphi -\frac{K{H}^2}{2}$$

(2)

and for an unconfined aquifer:

$$\Phi \left(z\right)=\frac{K{\varphi }^2}{2}.$$

(3)

Similarly, the uniform flow depict the domain’s streamlining behavior. Its formulation for global coordinate system with intensity Q forming an angle $\beta$ with x-axis specified in [7], is given by:

$${\Omega }_{uf}\left(z\right)=-Q_{x_0}z{e}^{-i\beta }+C.$$

(4)

The reference point constant C for the said methodology must be computed based on the hydraulic head at a reference point. Let us consider $z=x+iy$ represent the location in the complex plane, then the transformation of z to a dimensionless variable Z in local coordinate system give:

$$Z=X+iY=\frac{z-\frac{1}{2}(z_1-z_2)}{\frac{1}{2}(z_2-z_1)},$$

(5)

where $z_1$ and $z_2$ are the fracture’s initial and final points and the length is $L=|z_2-z_1|$, as shown in Figure 1.

According to [8,16], the uniform flow in local coordinate system is expressed as:

$${\Omega }_{uf}\left(Z\right)=-\frac{Q_{x_0}L{e}^{-i(\alpha -\beta )}}{2}+C,$$

(6)

whereas the complex potential for a single fracture is:

$$\Omega \left(Z\right)=A(Z-\sqrt{(Z-1)(Z+1)})$$

(7)

and constant A for the above equation is given by:

$$A=\frac{\frac{1}{2}{K}^{+}{b}^{\ast }}{K^{+}{b}^{\ast }+KL}\left(Q_{x_0}Lcos(\alpha -\beta )\right),$$

(8)

where $\alpha$ and $K^{+}$ are the fracture’s angle w.r.t. the x-axis and hydraulic conductivity inside the fracture, L represent the length of the fracture and $b^{\ast }$ represent the maximum aperture of the fracture respectively. According to [7,15], the combined form of Equation (6) with Equation (7) provide the exact solution, which is defined by:

$${\Omega }_e\left(Z\right)=AZ-\frac{Q_{x_0}L{e}^{i(\alpha -\beta )}Z}{2}-A\sqrt{(Z-1)(Z+1)}+C.$$

(9)

In this work, we considered the complex potential given by Equation (7) as a series and truncate it’s expansion as a numerical approximation. Hence the complex potential become:

$$\Omega \left(Z\right)=\sum _{n=1}^N{a}_n{(Z-\sqrt{Z-1}\sqrt{Z+1})}^n.$$

(10)

The real coefficients of the elements and dimensionless variable described in Equation (5) are represented by $a_n$ and Z, whereas n represent the series expansion order. In case of many fractures, one may write the complex potential as:

$$\Omega \left(Z\right)=\sum _{j=1}^M\sum _{n=1}^N{a}_n{(Z-\sqrt{Z-1}\sqrt{Z+1})}^n,$$

(11)

where M is used for number of fractures.

3. Boundary Conditions

According to [7,13], the approximate solution for a single fracture in terms of local cartesian coordinate system is obtained by considering the laminar flow in an elliptical fracture for which ‘n’ and ‘s’ are normal and parallel to the fracture’s axis. Let the fracture’s center is at the origin and it’s width b varies, whereas it’s length is given by L, as shown in Figure 2.

The fracture’s boundary conditions by using cubic law is described in the literature [7,16] and is given by:

$$Q_s={\psi }^{+}-{\psi }^{-}=\frac{\beta b^3}{K}\frac{\partial \Phi }{\partial s},$$

(12)

where b represent the fracture’s aperture, $\beta =\frac{\rho g}{12\mu }$, $\rho$ represent the water density and $\mu$ represent the viscosity. The intern boundary conditions throughout the fracture’s length after transformation of Equation (12) to the linear law give:

$$Q_s={\psi }^{+}-{\psi }^{-}=\frac{K^{+}b}{K}\frac{\partial \Phi }{\partial s},$$

(13)

where the external and internal hydraulic conductivities are represented by K and $K^{+}$. Similarly,

$$b=b^{\ast }\sqrt{1-x^2}=b^{\ast }\sqrt{1-\Re {\left(Z\right)}^2}=b^{\ast }sin\theta ,$$

(14)

where the fracture’s maximum aperture at center is represented by $b^{\ast }$. The derivative of the complex potential may provide the discharge vector for an analytical element, which may take the form:

$$W\left(z\right)=-\frac{d\Omega \left(z\right)}{dz}=Q_x\left(z\right)-i{Q}_y\left(z\right),$$

(15)

where the discharge vectors in Z-plane are represented by $Q_x\left(z\right)$ and $Q_y\left(z\right)$. By using chain rule, Equation (15) may be written as:

$$W\left(z\right)=-\frac{2}{z_2-z_1}\frac{d\Omega \left(z\right)}{dZ}.$$

(16)

The real part of the derived discharge potential rotated to direction of fracture provide the fracture’s discharge vector, which may be written as:

$$Q_s=\frac{d\Omega \left(z\right)}{ds}=\Re \left(W\left(z\right)e^{i\alpha }\right),$$

(17)

and finally Equation (13) become:

$$Q_s={\psi }^{+}-{\psi }^{-}=\frac{K^{+}b}{K}\Re \left(W\left(z\right)e^{i\alpha }\right).$$

(18)

Now by putting the value of b from Equation (14), Equation (18) become:

$$Q_s=\frac{K^{+}{b}^{\ast }}{K}\Re \left(W\left(z\right)e^{i\alpha }\right)sin\left(\theta \right).$$

(19)

4. Unknown Coefficients

The orthogonality of the Fourier series can be used to compute the unknown coefficients of potential expansion for a single fracture. The discharge vector $Q_s$ has the form of Equation (20) because of discontinuity occurs in the imaginary part of the complex potential, that is:

$$Q_s=\sum _{n=0}^N{a}_n(e^{-in\theta }-e^{in\theta }),$$

(20)

which implies

$$Q_s=-2\sum _{n=0}^N{a}_n\frac{(e^{in\theta }-e^{-in\theta })}{2}$$

(21)

and

$$Q_s=-2\sum _{n=0}^N{a}_{n}sin\left(n\theta \right).$$

(22)

Multiplying both sides by $sin\left(m\theta \right)$ of Equation (22) and integrating in interval $[0,\pi ]$ provide:

$${\int }_0^{\pi }{Q}_{s}sin\left(m\theta \right)d\theta =-2\sum _{n=0}^N{a}_n{\int }_0^{\pi }sin\left(m\theta \right)sin\left(n\theta \right)d\theta ,$$

(23)

By using orthogonal property of Fourier series and letting $m=n$, after simplification we have:

$${\int }_0^{\pi }{Q}_{s}sin\left(n\theta \right)d\theta =-\pi a_n.$$

(24)

Therefore,

$$a_n=-\frac{1}{\pi }{\int }_0^{\pi }{Q}_{s}sin\left(n\theta \right)d\theta .$$

(25)

Furthermore, by using value of $Q_s$ into Equation (25), we may get:

$$a_n=-\frac{K^{+}{b}^{\ast }}{\pi K}{\int }_0^{\pi }\Re \left(W\left(z\right)e^{i\alpha }\right)sin\left(\theta \right)sin\left(n\theta \right)d\theta .$$

(26)

The derived equation need to be used for calculating the unknown coefficients in the prescribed work.

5. Solution Algorithm

In the literature, it is presented that Barnes and Janković used the iterative method for solving problems of circular inhomogeneities and high-order line elements [17,18]. Marin adopted the same procedure for solving problems of fractured inhomogeneities but failed to converge [8]. Therefore, in our work we introduced the matrix method as a direct solver instead of iterative one and get the desired results. To calculate the unknown coefficients for the fractures, Equation (26) may be used in the form of:

$$a_{i,n}=P_{i,n}{\int }_0^{\pi }\Re \left({\Omega }_T\left({\theta }_i\right)\right)sin\left(n{\theta }_i\right)d{\theta }_i,$$

(27)

where

$$P_{i,n}=-\frac{K^{+}{b}^{\ast }}{\pi K},$$

(28)

that determine the n-th unknown coefficient for fracture i, whereas ${\Omega }_T$ represent the sum of all presented elements with its complex potentials including uniform regional flow, defined by Equation (4).

Equation (27) generate a set of linear equations that is used to be solved the system by using the matrix method as a direct solver. Now the general form of the coefficients matrix ‘A’ for linear system of equations is [21]:

$$Ax=b.$$

(29)

The matrix ‘A’ is built by expanding the fractures’ complex potential by using power series and the known vector ‘b’ of Equation (29) is the integral result of the uniform flow. Moreover, after substitution and simplification, we may express Equation (27) by:

$$\begin{array}{c}\hfill \frac{a_{i,n}}{P_{i,n}}-\sum _{j\ne i}^M\sum _{m=1}^N{\int }_0^{\pi }\Re \left(\left(\frac{m{a}_{j,m}(Z_j-\sqrt{Z_j-1\sqrt{Z_j+1}{)}^m}}{\sqrt{Z_j-1}\sqrt{Z_j+1}}\right)\frac{2e^{i{\alpha }_i}}{z_2-z_1}\right)sin\left({\theta }_i\right)sin\left(n{\theta }_i\right)d{\theta }_i\\ \hfill ={\int }_0^{\pi }\Re (-Q_{uf}{e}^{i({\alpha }_i-{\beta }_{uf})})sin\left({\theta }_i\right)sin\left(n{\theta }_i\right)d{\theta }_i.\end{array}$$

(30)

6. Results and Discussion

This section intend to analyze the findings and discuss the overall scenario of 2-dimensional groundwater flow simulations for fractured porous media with varying aperture of fractures, hydraulic conductivities and orientations in the presence of uniform flow field by using the analytic element method (AEM). In order to analyze the flow behavior and its effect on fractures, we will begin by introducing some parameters that define the problem of fractured inhomogeneities in a porous media. The length parameters are specified in meters (m), while the simulations for all the cases are made by the use of matrix method as a direct solver with the following data:

• Reference point: $z_0=(x,y)=(0,0)$
• Hydraulic head position: ${\varphi }_0=100$ m
• Well position: $z_w=(x,y)=(88,88)$
• Hydraulic conductivity at background: $K=1$ m/day.

6.1. Numerical Solution for a Single Fracture

We will begin by simulating the impact of a fracture parallel to the uniform flow field. The uniform flow rate for the said case is assumed to be 0.5 m/day, the aquifer’s background hydraulic conductivity is 1 m/day, while the hydraulic conductivity of an elliptical fracture with aperture of 0.5 m is 500 m/day. The numerical solution after simulation for a single fracture centered at origin, parallel to horizontal direction is illustrated in Figure 3. The dotted lines represent the hydraulic head contours, whereas the solid lines represent the streamlines. By comparing the exact solution defined in Equation (9) with the numerical solution, almost identical results was obtained with maximal relative error $6.9\times {10}^{-4}$.

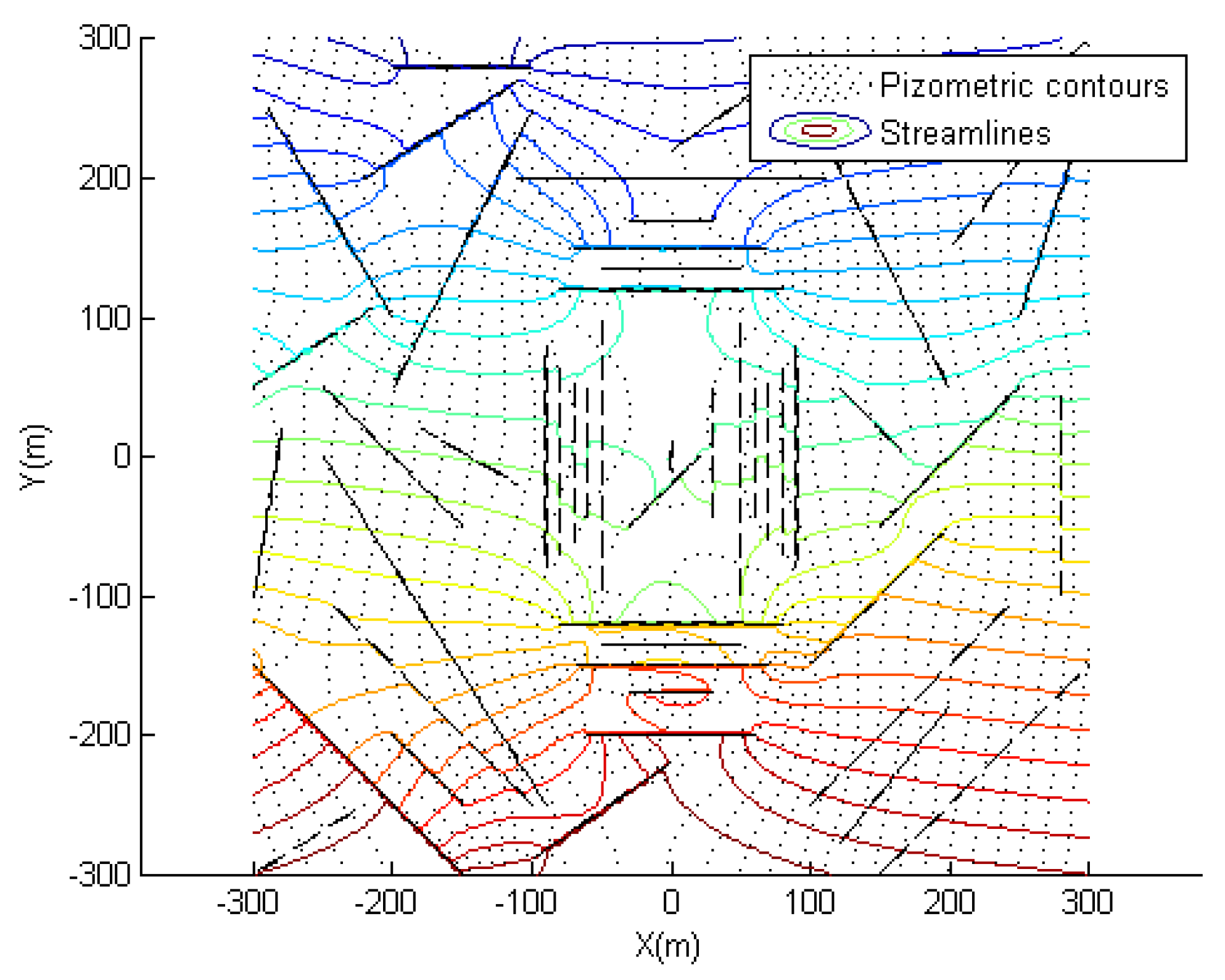
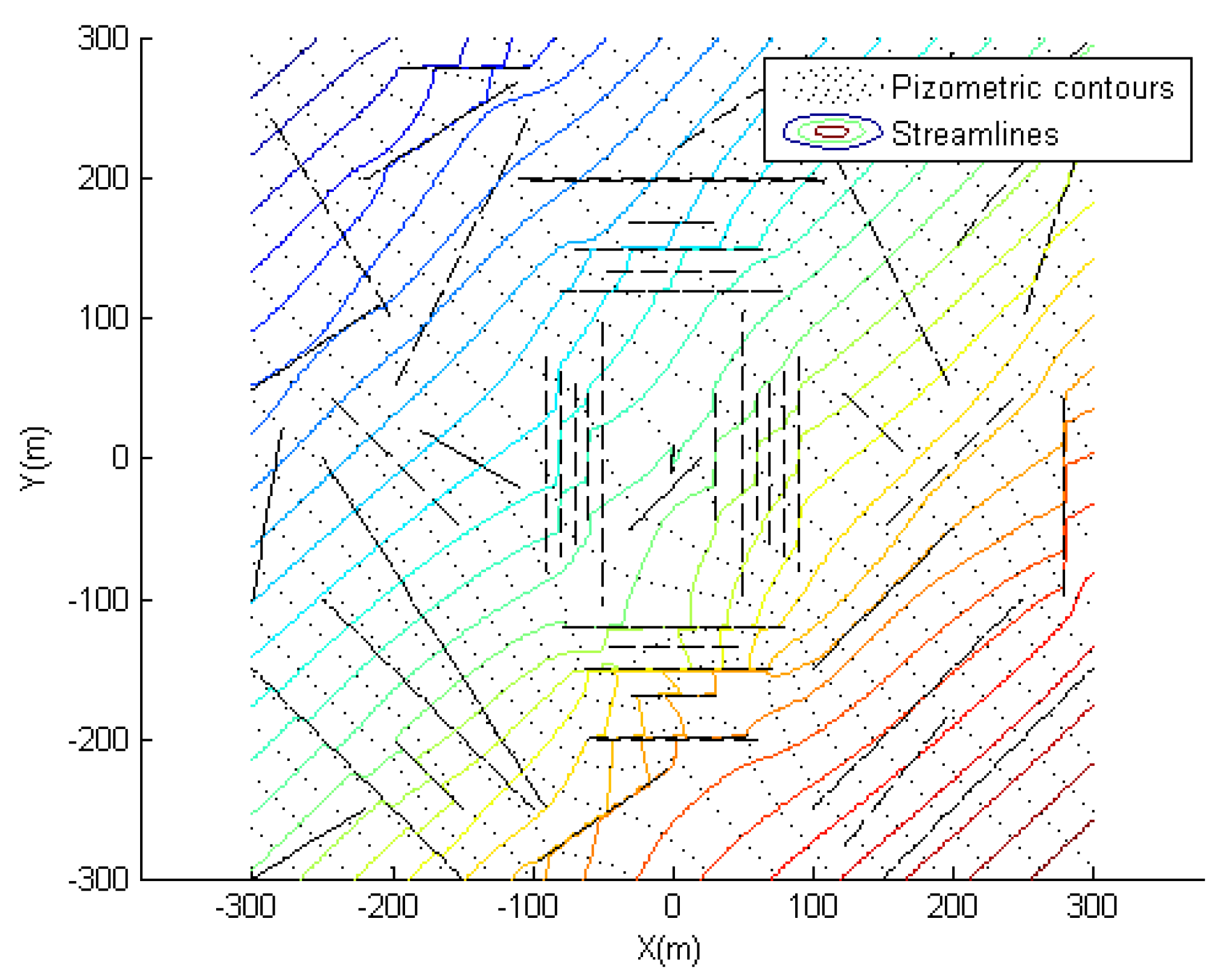
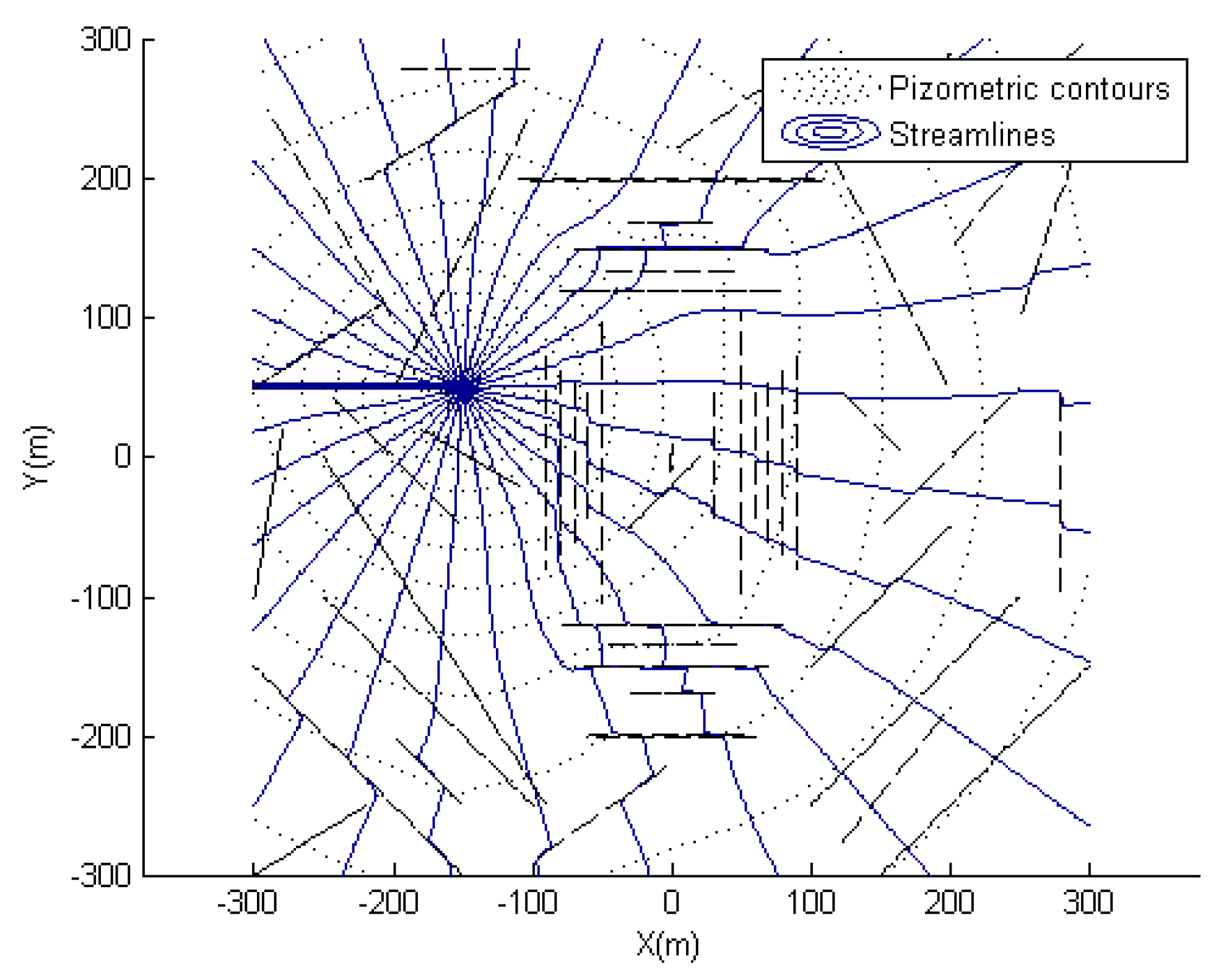
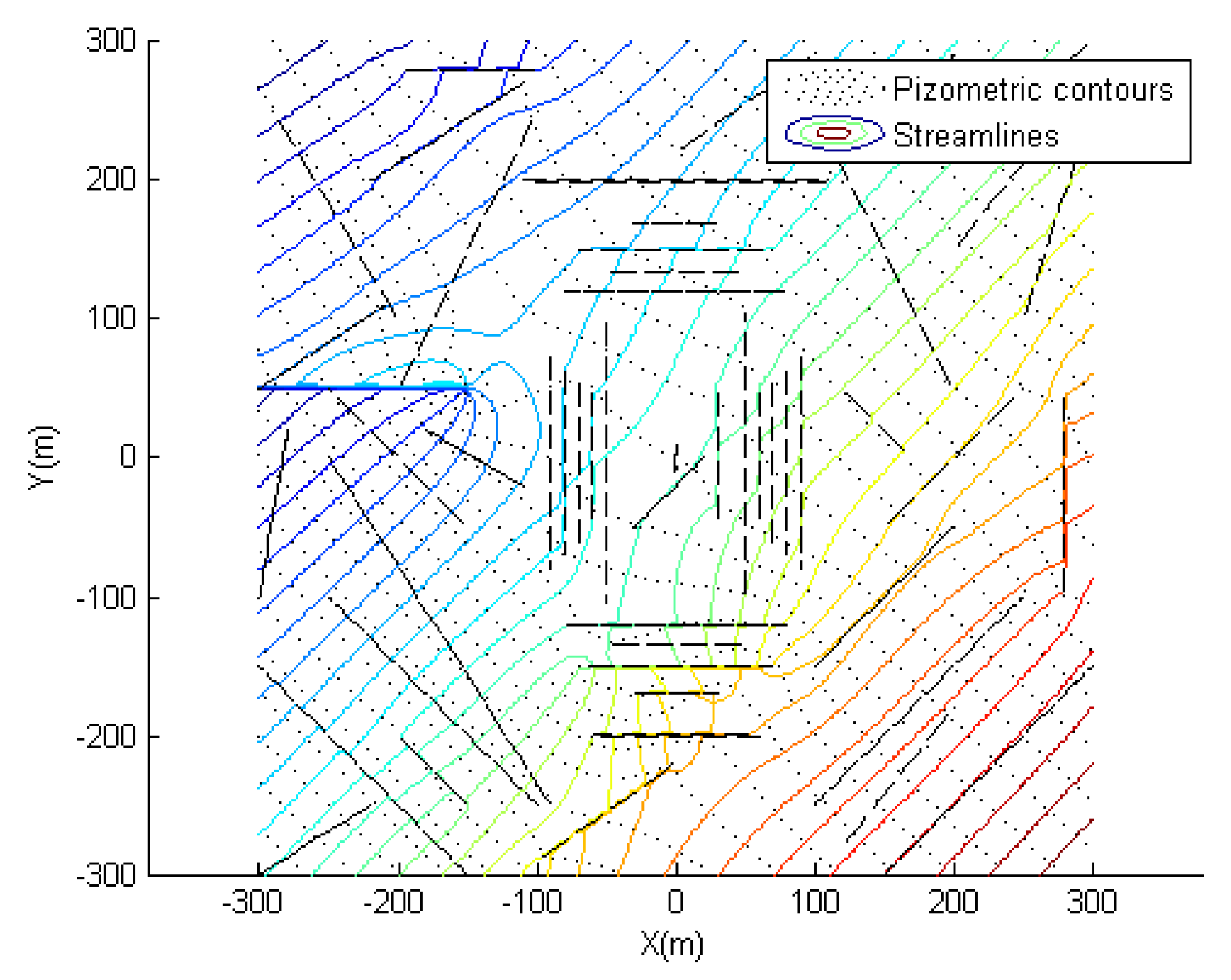
6.2. Simulation for a Bunch of Fractures

In this subsection we are going to divide our results in two cases: Case-1 consists of fractured inhomogeneities with different hydraulic conductivities, lengths and apertures, whereas Case-2 consists of fractured inhomogeneities with same hydraulic conductivities but different lengths and apertures. The following cases are given below:

6.2.1. Case-1

In this test case, different configurations of fractured models subject to the uniform flow field are presented to examine the flow behavior of the numerical solutions. The simulated systems consists of different number of fractures with different apertures, lengths and hydraulic conductivities. For cluster of fractures shown in Figure 4, the impact of three fractures parallel to each other directed at an angle of 45${}^{\circ }$ to the uniform flow have been observed.

Table 1. Described parameters for Figure 4.

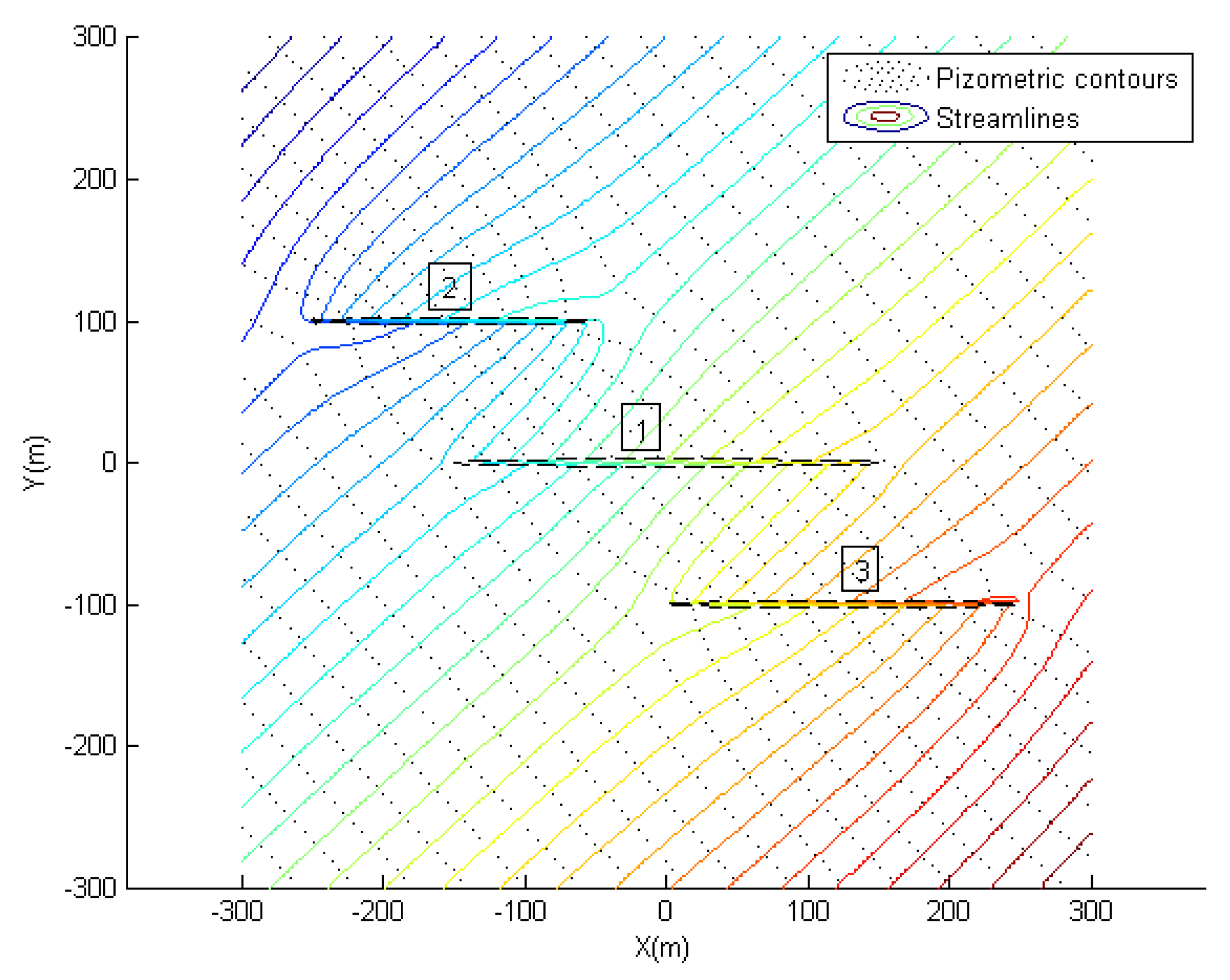
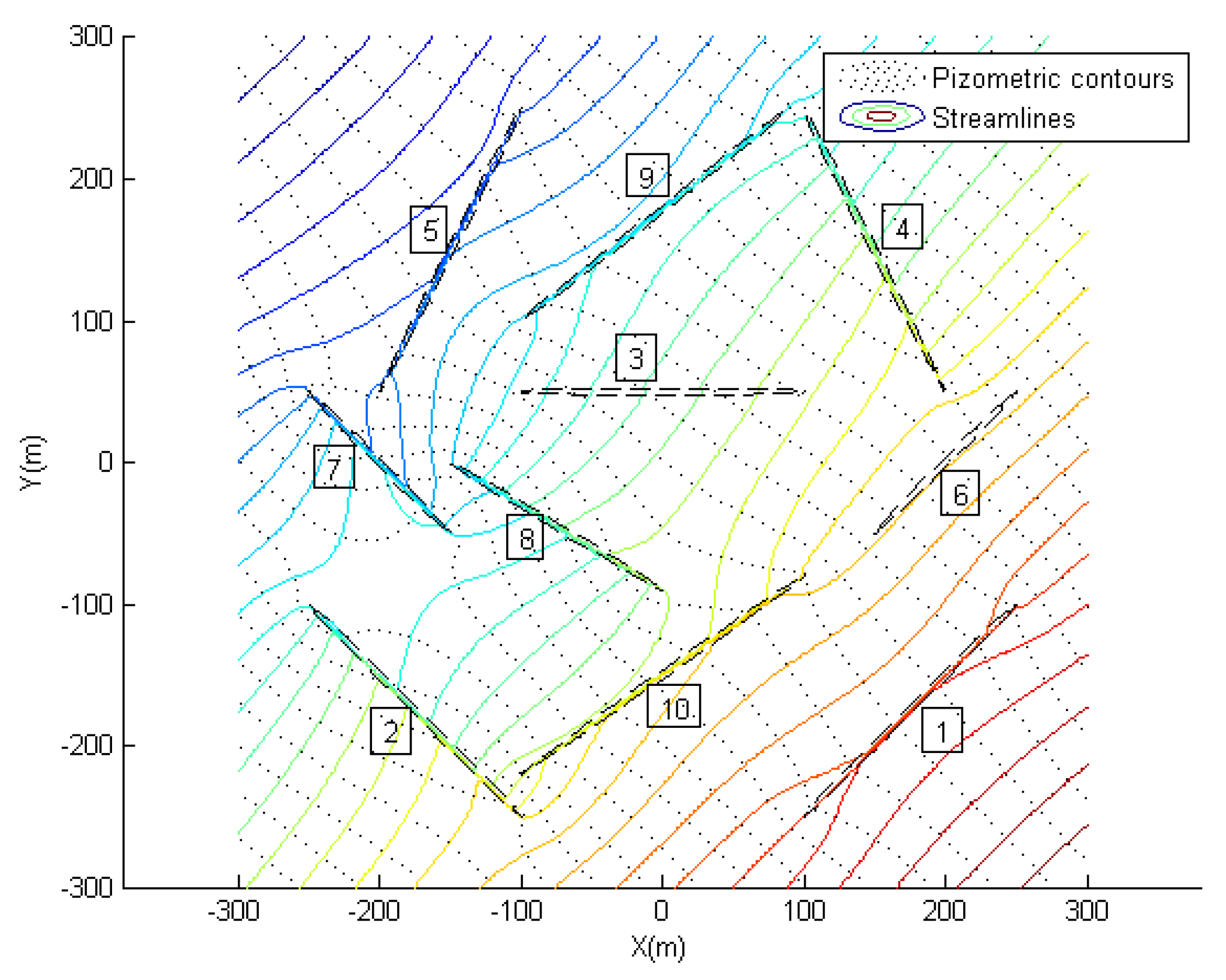
Fracture	${\mathit{K}}^{+}$ m/d	Width (m)	Length (m)
1	0.000007	5.0	300
2	5000	0.5	200
3	2500	10.5	250

lists the fracture parameters for the said problem. The resulting flow field illustrate the expected behavior of the flow in which the high conductivity of the fractures lead the flow through it’s limited widths and controls the uniform flow field.

Figure 5 depicts simulation of 10 fractures randomly placed in a domain with different hydraulic conductivities, lengths and apertures, given in

Table 2. Hydraulic conductivities, widths and lengths for Figure 5.

Fracture	${\mathit{K}}^{+}$ m/d	Width (m)	Length (m)
1	0.000007	5.0	150
2	50,000	0.5	150
3	2500	10.5	200
4	0.00006	20.5	200
5	2600	1.02	200
6	200	0.003	100
7	80,000	25.8	100
8	1300	0.7	150
9	0.000001	30	190
10	40,000	0.9	200

. The system include a regional uniform flow field with 45${}^{\circ }$ orientation along horizontal direction. Similarly, in Figure 6 and Figure 7 we assume the systems consists of 50 fractures each with varying apertures and hydraulic conductivities in order to make the problem more complex. The lengths, hydraulic conductivities and widths of the fractures are arbitrary selected for the given test cases by using parameters in

Table 3. Parameters defined for Figure 6 and Figure 7.

Fracture	${\mathit{K}}^{+}$ m/d	Width (m)	Length (m)	Fracture	${\mathit{K}}^{+}$ m/d	Width (m)	Length (m)
1	1000	0.01	20	26	10,000	0.6	100
2	5000	0.005	100	27	7100	0.003	100
3	2500	0.5	100	28	0.001	0.005	200
4	2000	0.1	100	29	5100	0.0006	100
5	2600	0.02	100	30	0.0006	0.9	150
6	200	0.003	100	31	8000	0.1	150
7	300	0.8	100	32	2500	0.6	150
8	1300	0.7	100	33	250	0.8	150
9	9900	1	100	34	0.005	0.4	250
10	4000	0.9	100	35	0.1	1	100
11	100	0.05	100	36	4500	2	100
12	0.7	7	150	37	40,000	4	150
13	50	0.06	150	38	6600	0.8	100
14	150	0.6	100	39	0.0006	0.1	80
15	0.02	0.7	200	40	33,300	0.01	100
16	200	2	200	41	30	0.6	100
17	1100	0.09	100	42	90	0.7	100
18	0.7	0.8	100	43	6900	0.8	110
19	0.003	0.05	100	44	5400	0.9	90
20	1000	0.7	100	45	0.008	0.6	120
21	5500	0.03	100	46	1100	0.7	50
22	50,000	0.05	100	47	0.0006	0.8	70
23	60,000	0.06	100	48	800	0.4	50
24	0.0008	0.8	100	49	10	0.5	100
25	0.007	0.8	100	50	0.0045	1	60

. The fractures have substantial impact on the uniform flow for which the generated streamlines are continuous and appropriately depict the influence of the fractures on expected behavior of the flow.

Furthermore, we simulate the test cases by letting 50 fractures with same parameters and orientations as shown in Table 3, and Figure 6 and Figure 7. In one case, we introduced a well with discharge $Q_w=100$ m${}^3$/day, located at point $z_w=-150+50i$, whereas in the second case we considered the well, as well as the uniform flow field in the domain. The complex potential for the well as described in [7,18] is:

$${\Omega }_w=\frac{Q_w}{2\pi }ln(z-z_w).$$

(31)

The results presented in Figure 8 illustrate that the well draws all of it’s water from everywhere for which the streamlines depicts the flow direction towards the well, whereas Figure 9 illustrate that a part of the uniform flow move towards the well while the remaining is distributed in the domain as per influence of the hydraulic conductivities in the uniform flow field.

6.2.2. Case-2

In this subsection, we assume some examples of fractured inhomogeneities having the same hydraulic conductivities (equals 1000 m/d) with varying apertures and lengths. First of all in Figure 10, we consider 3 parallel fractures oriented at an angle ${45}^{\circ }$ to the uniform flow field along horizontal direction with prescribed parameters of

Table 4. Parameters given for Figure 10.

Fracture	b (m)	Length (m)
1	5.0	300
2	0.5	200
3	10.5	250

.

To highlight the capability of our proposed method, further simulations were carried out for the systems consists of 10 and 50 fractures randomly oriented in the uniform flow fields as shown in Figure 11 and Figure 12 with prescribed parameters of

Table 5. Described parameters for Figure 11.

Fracture	b (m)	Length (m)
1	5.0	150
2	0.5	150
3	10.5	200
4	20.5	200
5	1.02	200
6	0.003	100
7	25.8	100
8	0.7	150
9	30	200
10	0.9	200

and

Table 6. Parameters given for Figure 12.

Fracture	Width (m)	Length (m)	Fracture	Width (m)	Length (m)
1	0.01	20	26	0.6	100
2	0.05	100	27	0.003	100
3	0.5	100	28	0.005	200
4	0.1	100	29	0.0006	100
5	0.02	100	30	0.9	150
6	0.003	100	31	0.1	150
7	0.8	100	32	0.6	150
8	0.7	100	33	0.8	150
9	1	100	34	0.4	250
10	0.9	100	35	1	100
11	0.05	100	36	2	100
12	7	150	37	0.8	150
13	0.06	150	38	0.8	100
14	0.6	100	39	0.1	80
15	0.7	200	40	0.01	100
16	2	200	41	0.6	100
17	0.09	100	42	0.7	100
18	0.8	100	43	0.8	110
19	0.05	100	44	0.9	90
20	0.7	100	45	0.6	120
21	0.03	100	46	0.7	50
22	0.05	100	47	0.8	70
23	0.06	100	48	0.4	50
24	0.8	100	49	0.5	100
25	0.8	100	50	1	60

.

The results obtained for all the test cases in this subsection demonstrate the expected flow behavior of the streamlines and piezometric contours in the uniform flow fields as described in literature, see [7,16].

7. Conclusions

The work presented in this article is composed of 2-dimensional groundwater flow for fractured porous media with different aperture of fractures by using the Analytic Element Method. In order to investigate the flow behavior and its effect on fractures, we simulate different systems of fractures with varying widths, hydraulic conductivities and orientations in the presence of uniform flow field and a well with an appropriate technique of matrix method as a direct solver. The prescribed work indicates that the high conductivity of the fractures lead the flow through it’s limited widths, which controls the uniform flow field and summarize that if the hydraulic conductivity inside the fractures is high than the background, the streamlines enters whereas the piezometric contours avoid to enter or vice versa. This yields that the fractures widths and orientations have substantial impact on the uniform flow field for which the generated streamlines are continuous and appropriately depict the expected flow behavior in the desired region.