Abstract
The universal fractality of river networks is very well known, however understanding of their underlying mechanisms is still lacking from a stochastic point of view. In this study, we have described the fractal natures of river networks by introducing a stochastic model where the direction of river flow at a site is determined by the dynamical replication probability which depends on the drainage area at the site rather than at random. We found that the probability induces dynamical persistency in river flows resulting in the self-affine properties shown in real river basins.
1. Introduction
The fractal properties shown in a variety of patterns of nature have attracted attention in many fields for several decades [1]. One of the fields where these fractal properties is well exhibited is hydrology. Extensive measurements of real river basins support these characteristics well [2,3]. The structures of river networks are characterized by unified scaling laws, regardless of size, vegetation, geological features, climate, orientation of the basin, etc. [4,5]. The Hack’s law [6] is the representative law describing the fractal geology in river networks describing the relation between the main stream length l and the river basin A giving as , where h is the Hack’s exponent having the values in the range 0.56–6.0 for real river basins. The drainage area a is defined as the number of sites connected to the actual site through drainage direction, and the distribution of drainage areas obeys a scaling form with the following scaling function [2,4],
where the scaling function behaves as
and the characteristic area satisfies the relation,
with of which relation is drawn from a river basin with a longitudinal length L and a perpendicular length following the power-law behavior between them as . The exponent H is called the Hurst exponent and for the cases where the main stream length l is linearly proportional to the longitudinal length L, the scaling relations relate the exponents h and in terms of H as and , respectively [7]. It means that we may concentrate on the Hurst exponent in studying the fractal properties of river basins. Also the Hurst exponent for real basins is in the range of 0.75–0.80. The fact that the Hurst exponent is greater than 0.5 indicates that there is persistency in the river flows.
It is necessary to theoretically understand the formation mechanism of river networks whose fractal properties are well known through actual measurements. And thus several models have been suggested with quite different origins to do so. First of all, the optimal channel network (OCN) [8,9,10,11,12] developed river networks based on the integrating principle of minimizing the total energy dissipation defined as in the system. Second, river networks developed on the landforms sculpted mostly by local erosion [13,14,15,16,17,18,19] or formed by avalanches evoking a long-range slope-slope correlation [20], have been introduced. Third, the evolution of the river network has been considered by the framework of the self-organized criticality [21,22], which describes threshold dynamics resulting in the fractal natures in a process [7,23]. Finally, in the Scheidegger model [24] where the drainage direction of water-flows is determined only probabilistically without taking account of any detailed contexts of the basin, water flows are regarded as a stochastic process. In the models based on OCN, evolution of landforms, and self-organized criticality, the exponent values such as those measured in real river basins have been obtained, however, the Scheidegger model is mapped into the well-known random walk model with and thus does not explain the pattern of river basins showing the persistency in flows well. For stochastic diffusive phenomena [25,26] several representative models such as the fractional Brownian motion (fBM) [27], the continuous time random walks (CTRW) [28,29,30], and Lévy walk model [31,32,33,34,35,36,37] have well described the persistent property, however, they do not directly explain how persistent water-flows are in river basins.
Recently, the memory effects of previous history of a process have been introduced as the main origin inducing the persistency in a stochastic process [38,39,40,41,42,43,44,45,46,47,48]. Also we have introduced the nonstationary Markovian replication process (NMRP) that can induce persistency by taking into consideration only the shortest-term memory [49,50]. In NMRP, the direction of a next step is determined by replicating that of the previous step with a replication probability which changes each time. For the constant replication probability, it becomes the persistent random-walk model [51] and in continuum limit, the telegrapher equation [52,53,54,55,56,57] which initially introduces the wave equation property and is related to the ballistic motion of diffusive particles, but it reduces asymptotically to normal diffusive behavior. Unlike the persistent random-walk model, the time-varying replication probability of NMRP controls the tendency to move in the same direction over time, which reflects adaptations to act in response to changes of environment and give rise to the persistency (or antipersistency) despite Markovianity of a process. Likewise, for water flows in river basins, the direction of water flowing into a site can influence the next direction of outflow from the site at each moment differently. Therefore we can consider the origin of the persistency of river flows from the viewpoint of NMRP. Furthermore, for the real complex contexts it may be more plausible for the probability to depend on dynamical quantities mainly characterizing a system rather than explicitly on time. In this study, we have attempted to generalize the NMRP to the problem of river networks. As the drainage area at each site is a key dynamical quantity characterizing river networks, we have taken it into consideration as surrogating time and have developed the river basin that shows the fractal natures of real river basins.
2. Nonstationary Markovian Replication Process
It is known that short-term memory eventually leads to normal diffusion [51,52], whereas long-term memory may be the origin to explain the non-Markovian processes deviating from the normal random walk [38,39,48]. However, it is known that even in short-term memory, if the memory effect changes with time, it can generate stochastic processes with long-term memory. This model is a NMRP model [49] and it has short-term memory in the sense that it remembers only the immediately preceding step, but it is a nonstationary process in which the degree of memorizing of the previous step changes at every time. In one dimension, the NMRP model is defined as a stochastic process of which dynamics are controlled by the time-varying probability (we call it the replication probability) as follows,
where is a step at time t and is the time interval in which a walker moves to one of the two neighboring sites. The relation between the walker’s position at time t, , and the step a walker takes, , is defined as . The first step () is randomly chosen between the two possibilities with equal probabilities where l is the uniform spacing between neighboring sites in one dimensional lattice. Successive steps at are determined by the rule (4). As a result, the degree to which the previous steps are memorized and followed at every moment varies according to the replication probability . By changing this replication probability , various types of non-Markovian and nonstationary processes different from normal processes can be generated. Unlike the diffusion equation, the equation that the probability distribution of this NMRP follows is given in the form including the second derivative with respect to time as follows [49].
where
and
with being the diffusion coefficient for the normal diffusion. When is constant, and become constant and the Equation (5) is reduced to the telegrapher equation. The relation between the coefficients and and the replication probability are given by the Equations (6) and (7), respectively, which indicates that the larger , the larger coefficients. Note that when approaches 1, two coefficients and diverge, whereas the coefficient of the first term on the left hand side of Equation (5) remains constant. Therefore, if the divergence is fast enough, a contribution from the first term on the left hand side of Equation (5) becomes negligible. In this case, Equation (5) evolves into the wave equation with the speed , which implies the occurrence of the ballistic motion of the walker. In the telegraph process, initial ballistic motion is transient; however, in the NMRP, ballistic motion appears whenever the replication is more dominant than the anti-replication, namely, becomes close to 1. In more usual cases where does not tend to 1 so fast, because of the relatively small value of the in the continuum limit and the asymptotically small nature of the second order derivative of the PDF in t compared to the first order one, the second term on the left hand side of Equation (5) can be neglected. In this case, Equation (5) is reduced to the diffusion equation with the time dependent diffusion coefficient [39,58,59,60,61],
and the solution is given by the Gaussian distribution provided zero mean of displacement,
As such, the nonstationary stochastic processes that are different from the normal stochastic processes can be applied much more appropriately to actual complex systems.
3. Stochastic Model with Dynamic Replications for River Networks
In order to describe the fractal nature of river basins we have introduced the generalized NMRP model. The rule of the generalized NMRP model is as follows: Consider a lattice of size in which the position of a site is denoted as with and . Initially, a water drop is allocated at each site, that is, reflecting uniform rainfall and is a random variable that determines the direction of water flows at site . When , water at site flows down into the right site and when , the water flows into the left site . Here, flow from a site into is not allowed for simplicity, which does not affect the results. For the value of is assigned with 1 or −1 at random, for , is determined by the probability as follows,
where if water flows into a site from only a neighboring site, is the same as of the previous step of the neighboring site, while if water flows from both of the two neighboring sites into that site, takes the value of of the previous step of the neighboring site with a larger drainage area.
The probability is given as follows,
Here and where if water flows from a left site (a right site ) into the site , then , and if not, . This probability makes it flow in the same direction as the previous flow with the probability that becomes larger as is larger. can be regarded as the momentum of water at that site if it is regarded as its velocity is uniform and thus the larger the momentum is over time, the stronger the tendency to maintain the direction of the flow becomes. In other words, it brings about the dynamical persistency in the sense that the persistency is determined by the drainage area changing dynamically at each moment. Also the probability is not explicitly dependent on time and thus not predetermined unlike NMRP. Rather, it is dynamically generated according to the drainage area every time, and we refer to the probability as the dynamical replication probability. Figure 1 shows the schematic pictures for all cases where water can flow from a site into downward sites according to previous movements.

Figure 1.
All possible water-flow cases being able to appear by this stochastic model. The bolder line indicates that the drainage area at that site is larger than that of the other site represented with normal lines. When the position of a center is , the dynamical replication probabilities for several cases are as follows: for a, , for e, , and for from i to l, .
4. Methods
We have introduced the generalized NMRP model for which rules are detailed in the previous section. To find out whether this stochastic model works well, we have simulated the model by computers with 1000 independent realizations. For , the distribution of drainage areas for several longitudinal lengths L from which the exponents and can be obtained, is measured. Also to independently measure the exponent , we use an alternative definition of the characteristic area
of which the scaling relation is able to be obtained from the Equation (1).
To further clarify the properties of river networks from the viewpoint of random walks in one dimension, we consider that is a position of water starting from a site x initially, at time t that surrogates a position y. Its evolution is given as
where and is a x position of water starting from site at y. The deviation from the staring point of a stochastic process over time is usually measured by the mean-squared displacement (MSD) which is related to the time as
The MSD is measured and the value of the Hurst exponent obtained from it is compared to those obtained from the distribution of drainage areas.
Meanwhile, if the parameter is adjusted, the degree of flow to move in the same direction as the previous step can change, which makes it possible to get different values of the exponents. By changing values of the parameter we obtain the different values of the exponents.
5. Results
The distribution of drainage areas have been measured for several longitudinal lengths L with . The inset (a) of the Figure 2 shows with for various L and the main panel shows the data collapse of with and .
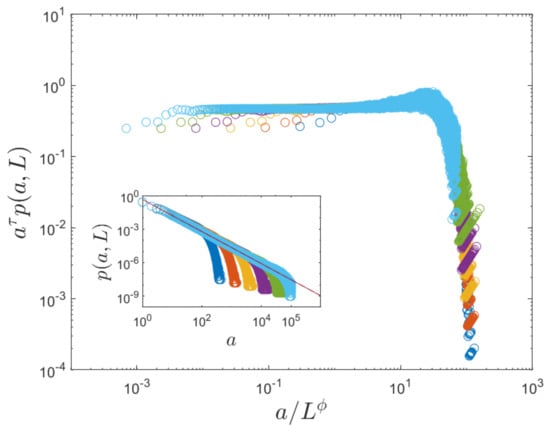
Figure 2.
The plot of the scaling function of for various values of , and 1024 with . The data are very well collapsed with and . The inset shows the plot of for the same L as in the main panel and the straight guide line represents .
The Figure 3 shows the plot of the characteristic area versus longitudinal length L and that which is in excellent agreement with that obtained from the data collapse of the distribution of drainage areas. Thus the values of the exponents are in excellent agreement with those observed in real river basins, which indicates that this stochastic model very well represents real river basins. And the probability itself being a dynamical variable plays a key role in explaining the universal properties of river networks.
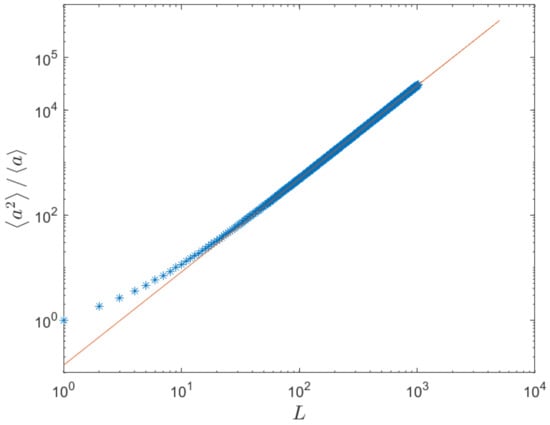
Figure 3.
The value of the exponent has been obtained as from the relation, .
Figure 4 shows a pattern of a river network drawn by this model. In the background, all paths of flowing water from each site into sinks have been drawn in green in the bottom line and the purple lines in the background pattern represent the paths connecting to the largest sink among them, which looks like a real river network with a single sink. Meanwhile, the red line is a sample line representing a flow path of site (x, 1) from a top site to the bottom site and it can be treated as a one dimensional stochastic process. The value of the Hurst exponent H measured by averaging paths of is for as shown in the Figure 5, which is in excellent agreement with that which was obtained from the relation of . This means that the deviation of the stochastic process composed by these one dimensional paths represents the width of the river basin.
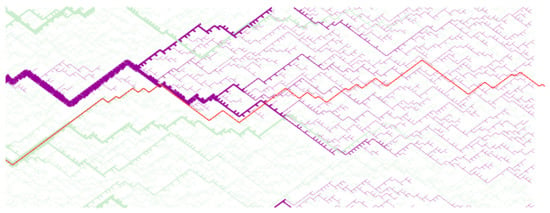
Figure 4.
The river network drawn by this stochastic model. In the background, all paths of flowing water from at each site into sinks have been drawn in green. The links sharing a single largest sink are depicted as purple lines. The red line is a sample of the entire path of water flow starting from an initial site.
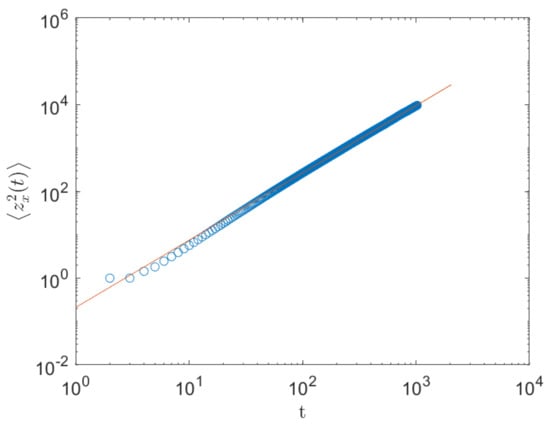
Figure 5.
The MSD averaged by the stochastic processes formed by water flows from the initial sites is shown and the slope of the straight guide line represents .
Meanwhile, by changing values of the parameter we have obtained the different values of the exponents. Figure 6a shows the plot of the distribution of the drainage area versus the drainage area a for various L with . The straight guide line represents that the value of the exponent is and in the Figure 6b it is shown that the data of are well collapsed with the values of the exponents, and . Figure 6c shows the plot of versus the length L and the straight guide line represents that the value of the exponent becomes 1.87. In the Figure 6d–f, we have measured the values of the exponents for and have obtained and . Although the values of exponents for real basins span a small range rather than a specific value, these exponent values for and are slightly larger than the measured values in real basins. It means that a certain range of the parameter in the model can be suitable for describing the fractal natures of river basins. We have measured the Hurst exponents for various values of by two independent methods. One is obtained from the MSD of (star symbols in the Figure 7) and the other is obtained by measuring the characteristic drainage area (circle symbols in the Figure 7). It can be seen that both values are the same overall. The slight difference between two values of H for small can be originated from the initial behaviors that could be affected differently according to the development of the drainage area. As a result we have found that the Hurst exponent H is almost linearly increased as increases as shown in the Figure 7 and especially, for , it matches the values measured in real basins well.
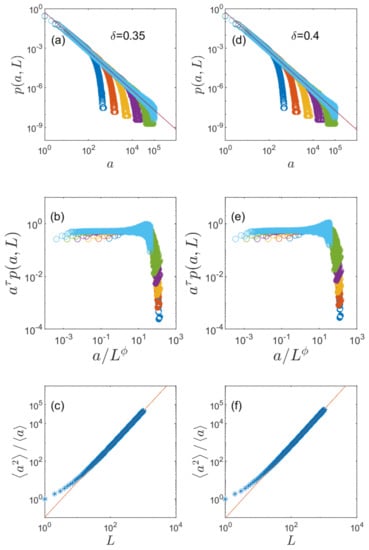
Figure 6.
(a) The plot of the scaling function of for various values of , and 1024 from the left to the right for . The straight guide line represents . In the figure (b), the data are very well collapsed with and . The figure (c) shows the value of the exponent which has been obtained as from the relation, . The figure (d) shows the plot of for various values of , and 1024 for . The straight guide line represents . The data are very well collapsed with and as shown in the figure (e) and in the figure (f) the value of the exponent was obtained as 0.91 by measuring the characteristic drainage areas.
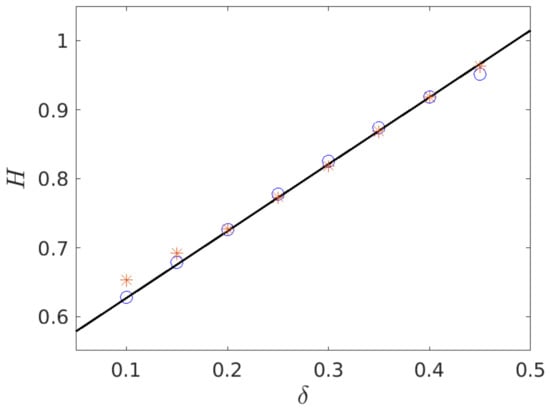
Figure 7.
The plot of the Hurst exponent versus the parameter . The data marked by a circle and star are obtained from the MSD of stochastic processes and the characteristic area, respectively. The straight guide line has been obtained by a linear regression on the data of the characteristic area and represents that .
6. Discussion
We have introduced a stochastic model that describes very well the fractal characteristics of real river basins. It suggests that river networks can be understood with only the viewpoint of stochastic processes of water flow, which have good points to describe the unified scaling laws of real river basins in respect to a simple rule without consideration of the details of the contexts that makes it be possible. The key point in explaining the persistency in river flows is the idea of the dynamical replication probability by which the greater the momentum of the flow, the greater the tendency to follow the previous direction of water flow. The momentum of flow at a site is related to its drainage area which is a key dynamical quantity of characterizing the river basin. That is, drainage areas determine the probability constructing a river network and in turn the dynamical probability determines the fractal nature of river basins.
Thus the dynamical replication probability yields fractal characteristics of real river networks, however, further attempts to test more properties of the model using other known properties of river basins are required. These properties include main stream length distributions and Horton’s law [62,63,64,65] which states that the relationship between the stream numbers, stream lengths, stream areas and stream order can be meaningful to understand the topological randomness of networks [63]. Also the dynamical probability could be an important origin for construction of other complex systems which can be developed by nonstationary or non-Markovian stochastic processes. Therefore, applying the dynamical probability to construct various complex systems where stochastic natures are used in an abnormal fashion can be helpful to understand the systems.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1983. [Google Scholar]
- Rodríguez-Iturbe, I.; Rinaldo, A. Fractal River Basins: Chance and Self-Organization; Cambridge Univ Press: Cambridge, UK, 1997. [Google Scholar]
- Rinaldo, A.; Rigon, R.; Banavar, J.R.; Maritan, A.; Rodriguez-Iturbe, I. Evolution and selection of river networks: Statics, dynamics, and complexity. Proc. Natl. Acad. Sci. USA 2014, 111, 2417–2424. [Google Scholar] [CrossRef] [PubMed]
- Maritan, A.; Rinaldo, A.; Rigon, R.; Giacometti, A.; Rodriguez-Iturbe, I. Scaling laws for river networks. Phys. Rev. E 1996, 53, 1510. [Google Scholar] [CrossRef] [PubMed]
- Dodds, P.S.; Rothman, D.H. Unified view of scaling laws for river networks. Phys. Rev. E 1999, 59, 4865. [Google Scholar] [CrossRef] [PubMed]
- Hack, J.T. Studies of Longitudinal Stream-Profiles in Virginia and Maryland. U.S. Geol. Surv. Prof. Paper 1957, 294, 45–97. [Google Scholar]
- Caldarelli, G. Cellular models for river networks. Phys. Rev. E 2001, 63, 021118. [Google Scholar] [CrossRef]
- Rinaldo, A.; Rodriguez-Iturbe, I.; Rigon, R.; Ijjasz-Vasquez, E.; Bras, R.L. Self-organized fractal river networks. Phys. Rev. Lett. 1993, 70, 822. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Rinaldo, A.; Rigon, R.; Bras, R.L.; Marani, A.; Ijjász-Vásquez, E. Energy dissipation, runoff production, and the three-dimensional structure of river basins. Water Resour. Res. 1992, 28, 1095–1103. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Rinaldo, A.; Rigon, R.; Bras, R.L.; Ijjasz-Vasquez, E.; Marani, A. Fractal structures as least energy patterns: The case of river networks. Geophys. Res. Lett. 1992, 19, 889–892. [Google Scholar] [CrossRef]
- Rinaldo, A.; Rodriguez-Iturbe, I.; Rigon, I.R.; Bras, R.L.; Ijjasz-Vasquez, E.; Marani, A. Minimum energy and fractal structures of drainage networks. Water Resour. Res. 1992, 28, 2183–2195. [Google Scholar] [CrossRef]
- Briggs, L.A.; Krishnamoorthy, M. Exploring network scaling through variations on optimal channel networks. Proc. Natl. Acad. Sci. USA 2013, 110, 19295. [Google Scholar] [CrossRef]
- Takayasu, H.; Inaoka, H. New type of self-organized criticality in a model of erosion. Phys. Rev. Lett. 1992, 68, 966. [Google Scholar] [CrossRef]
- Inaoka, H.; Takayasu, H. Water erosion as a fractal growth process. Phys. Rev. E 1993, 47, 899. [Google Scholar] [CrossRef]
- Kramer, S.; Marder, M. Evolution of river networks. Phys. Rev. Lett. 1992, 68, 205. [Google Scholar] [CrossRef]
- Leheny, R.L.; Nagel, S.R. Model for the evolution of river networks. Phys. Rev. Lett. 1993, 71, 1470. [Google Scholar] [CrossRef]
- Giacometti, A.; Maritan, A.; Banavar, J.R. Continuum model for river networks. Phys. Rev. Lett. 1995, 577, 577. [Google Scholar] [CrossRef]
- Banavar, J.R.; Colaiori, F.; Flammini, A.; Giacometti, A.; Maritan, A.; Rinaldo, A. Sculpting of a Fractal River Basin. Phys. Rev. Lett. 1997, 78, 4522. [Google Scholar]
- Somfai, E.; Sander, L.M. Scaling and river networks: A Landau theory for erosion. Phys. Rev. E 1997, 56, R5. [Google Scholar] [CrossRef]
- Kim, H.-J.; Kim, I.-M.; Kim, J.M. River networks on the slope-correlated landscape. Phys. Rev. E 2000, 62, 3121. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality. Phys. Rev. A 1988, 38, 364. [Google Scholar] [CrossRef]
- Hergarten, S.; Neugebauer, H.J. Self-organized critical drainage networks. Phys. Rev. Lett. 2001, 86, 2689. [Google Scholar] [CrossRef] [PubMed]
- Scheidegger, A.E. Horton’s laws of stream lengths and drainage areas. Water Resour. Res. 1968, 4, 1015. [Google Scholar] [CrossRef]
- Abouagwa, M.; Aljoufi, L.S.; Bantan, R.A.R.; Khalaf, A.D.; Elgarhy, M. Mixed Neutral Caputo Fractional Stochastic Evolution Equations with Infinite Delay: Existence, Uniqueness and Averaging Principle. Fractal Fract. 2022, 6, 105. [Google Scholar] [CrossRef]
- Khalaf, A.D.; Saeed, T.; Abu-Shanab, R.; Almutiry, W.; Abouagwa, M. Estimating Drift Parameters in a Sub–Fractional Vasicek–Type Process. Entropy 2022, 24, 594. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B.; van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 39, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. Phys. A: Math. Gen. 2004, 37, R161. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks, 1st ed.; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Barkai, E.; Dubkov, A.A. Lévy flights versus Lévy walks in bounded domains. Phys. Rev. E 2017, 95, 052102. [Google Scholar] [CrossRef]
- Fedotov, S.; Korab, N. Emergence of Lévy walks in systems of interacting individuals. Phys. Rev. E 2017, 95, 030107. [Google Scholar] [CrossRef]
- Zaburdaev, V.; Fouxon, I.; Denisov, S.; Barkai, E. Superdiffusive Dispersals Impart the Geometry of Underlying Random Walks. Phys. Rev. Lett. 2016, 117, 270601. [Google Scholar] [CrossRef]
- Boyer, D.; Pineda, I. Slow Lévy flights. Phys. Rev. E 2016, 93, 022103. [Google Scholar] [CrossRef]
- Rebenshtok, A.; Denisov, S.; Hänggi, P.; Barkai, E. Infinite densities for Lévy walks. Phys. Rev. E 2014, 90, 062135. [Google Scholar] [CrossRef]
- Godec, A.; Metzler, R. Linear response, fluctuation-dissipation, and finite-system-size effects in superdiffusion. Phys. Rev. E 2013, 88, 012116. [Google Scholar] [CrossRef]
- Schutz, G.M.; Trimper, S. Elephants can always remember: Exact long-range memory effects in a non-Markovian random walk. Phys. Rev. E 2004, 70, 045101. [Google Scholar] [CrossRef]
- Boyer, D.; Solis-Salas, C. Random Walks with Preferential Relocations to Places Visited in the Past and their Application to Biology. Phys. Rev. Lett. 2014, 112, 240601. [Google Scholar] [CrossRef]
- Boyer, D.; Romo-Cruz, J.C.R. Solvable random-walk model with memory and its relations with Markovian models of anomalous diffusion. Phys. Rev. E 2014, 90, 042136. [Google Scholar] [CrossRef]
- Cressoni, J.C.; da Silva, M.A.A.; Viswanathan, G.M. Amnestically induced persistence in random walks. Phys. Rev. Lett. 2007, 98, 070603. [Google Scholar] [CrossRef]
- Liemert, A.; Sandev, T.; Kantz, H. Generalized Langevin equation with tempered memory kernel. Physica A 2017, 466, 356–369. [Google Scholar] [CrossRef]
- Budini, A.A. Memory-induced diffusive-superdiffusive transition: Ensemble and time-averaged observables. Phys. Rev. E 2017, 95, 052110. [Google Scholar] [CrossRef]
- Budini, A.A. Inhomogeneous diffusion and ergodicity breaking induced by global memory effects. Phys. Rev. E 2016, 94, 052142. [Google Scholar] [CrossRef]
- Budini, A.A. Weak ergodicity breaking induced by global memory effects. Phys. Rev. E 2016, 94, 022108. [Google Scholar] [CrossRef] [PubMed]
- Kürsten, R. Random recursive trees and the elephant random walk. Phys. Rev. E 2016, 93, 032111. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Harbola, U.; Lindenberg, K. Memory-induced anomalous dynamics: Emergence of diffusion, subdiffusion, and superdiffusion from a single random walk model. Phys. Rev. E 2010, 82, 021101. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-J. Anomalous diffusion induced by enhancement of memory. Phys. Rev. E 2014, 90, 012103. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, H.-J. Nonstationary Markovian replication process causing diverse diffusions. Phys. Rev. E 2017, 96, 042144. [Google Scholar] [CrossRef]
- Kim, D.; Kim, H.-J. Transition phenomena in diffusive motions due to the change of memory effects. Mod. Phys. Lett. B 2019, 96, 2050013. [Google Scholar] [CrossRef]
- Goldstein, S. On diffusion by discontinuous movements, and on the telegraph equation. Q. J. Mech. Appl. Math. 1951, 4, 129–156. [Google Scholar] [CrossRef]
- Kac, M. A stochastic model related to the telegrapher’s equation. Rocky Mt. J. Math. 1974, 4, 497–509. [Google Scholar] [CrossRef]
- Masoliver, J.; Lindenberg, K.; Weiss, G.H. A continuous-time generalization of the persistent random walk. Physica A 1989, 157, 891–898. [Google Scholar] [CrossRef]
- Masoliver, J.; Weiss, G.H. Finite-velocity diffusion. Eur. J. Phys. 1996, 190, 17. [Google Scholar] [CrossRef]
- Masoliver, J.; Weiss, G.H. Telegrapher’s equations with variable propagation speeds. Phys. Rev. E 1994, 49, 3852. [Google Scholar] [CrossRef]
- Weiss, G.H. Some applications of persistent random walks and the telegrapher’s equation. Physica A 2002, 311, 381–410; [Google Scholar] [CrossRef]
- Masoliver, J. Fractional telegrapher’s equation from fractional persistent random walks. Phys. Rev. E 2016, 93, 052107. [Google Scholar] [CrossRef]
- Wang, K.G. Long-time-correlation effects and biased anomalous diffusion. Phys. Rev. E 1992, 45, 833. [Google Scholar] [CrossRef]
- Wang, K.G.; Lung, C.W. Long-time correlation effects and fractal Brownian motion. Phys. Lett. A 1990, 151, 119–121. [Google Scholar] [CrossRef]
- Lim, S.C.; Muniandy, S.V. Self-similar Gaussian processes for modeling anomalous diffusion. Phys. Rev. E 2002, 66, 021114. [Google Scholar] [CrossRef]
- Thiel, F.; Sokolov, I.M. Scaled Brownian motion as a mean-field model for continuous-time random walks. Phys. Rev. E 2014, 89, 012115. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Kirchner, J.W. Statistical inevitability of Horton’s laws and the apparent randomness of stream channel networks. Geology 1993, 21, 591. [Google Scholar] [CrossRef]
- Beer, T.; Borgas, M. Horton’s laws and the fractal nature of streams. Water Resour. Res. 1993, 29, 1475. [Google Scholar] [CrossRef]
- Rosso, R.; Bacchi, B.; La Barbera, P. Fractal relation of mainstream length to catchment area in river networks. Water Resour. Res. 1991, 27, 381–387. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).