Solvability of a New q-Differential Equation Related to q-Differential Inequality of a Special Type of Analytic Functions
Abstract
1. Introduction
2. Methods
2.1. Quantum Calculus
2.2. Meromorphiclly Multivalent Functions (MMF)
2.3. Q-Symmetric Differential Operator (q-SDO)
2.4. Lemmas
3. Results
3.1. q-Differential Inequalities
3.2. q-Differential Equations
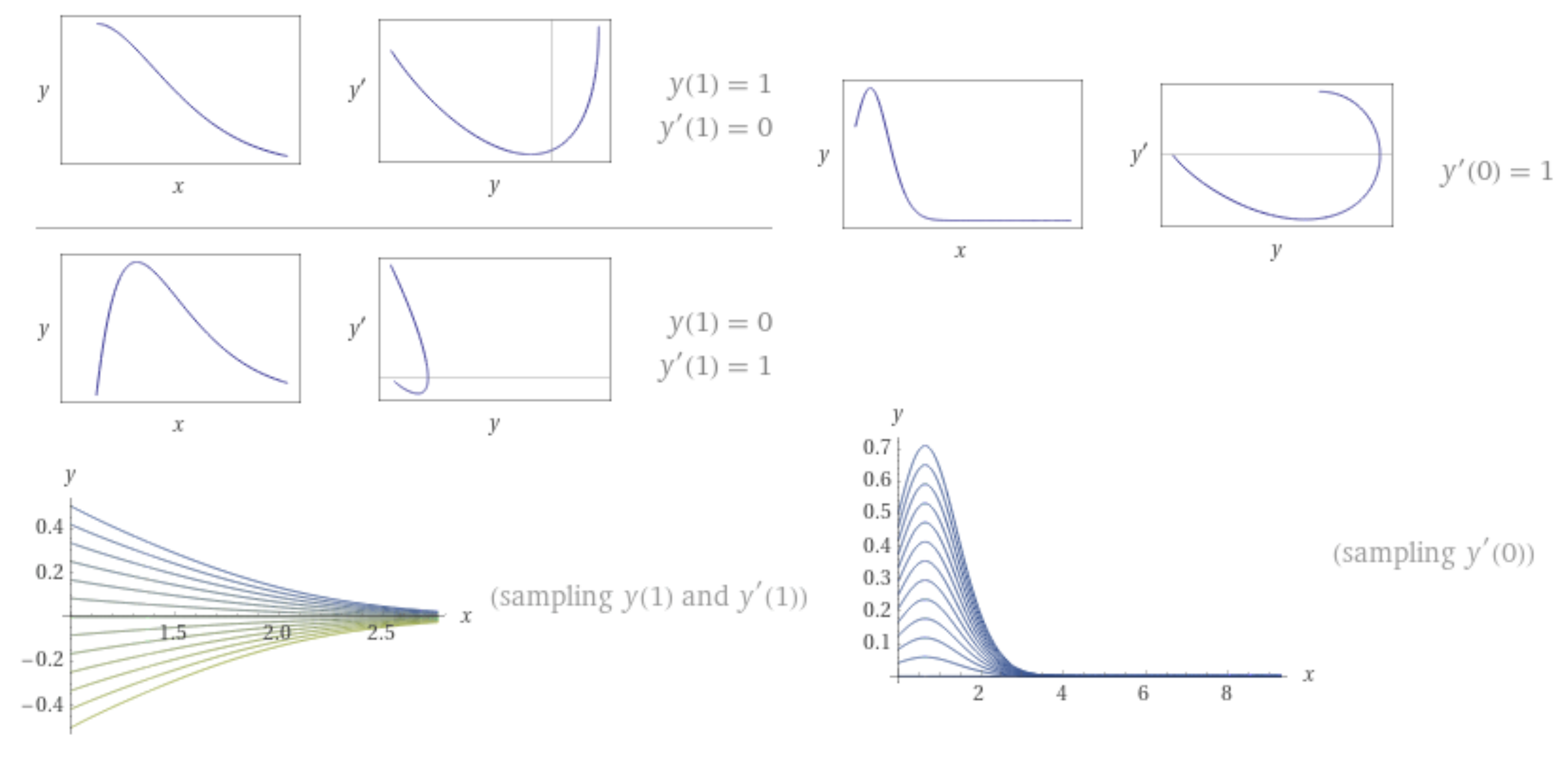
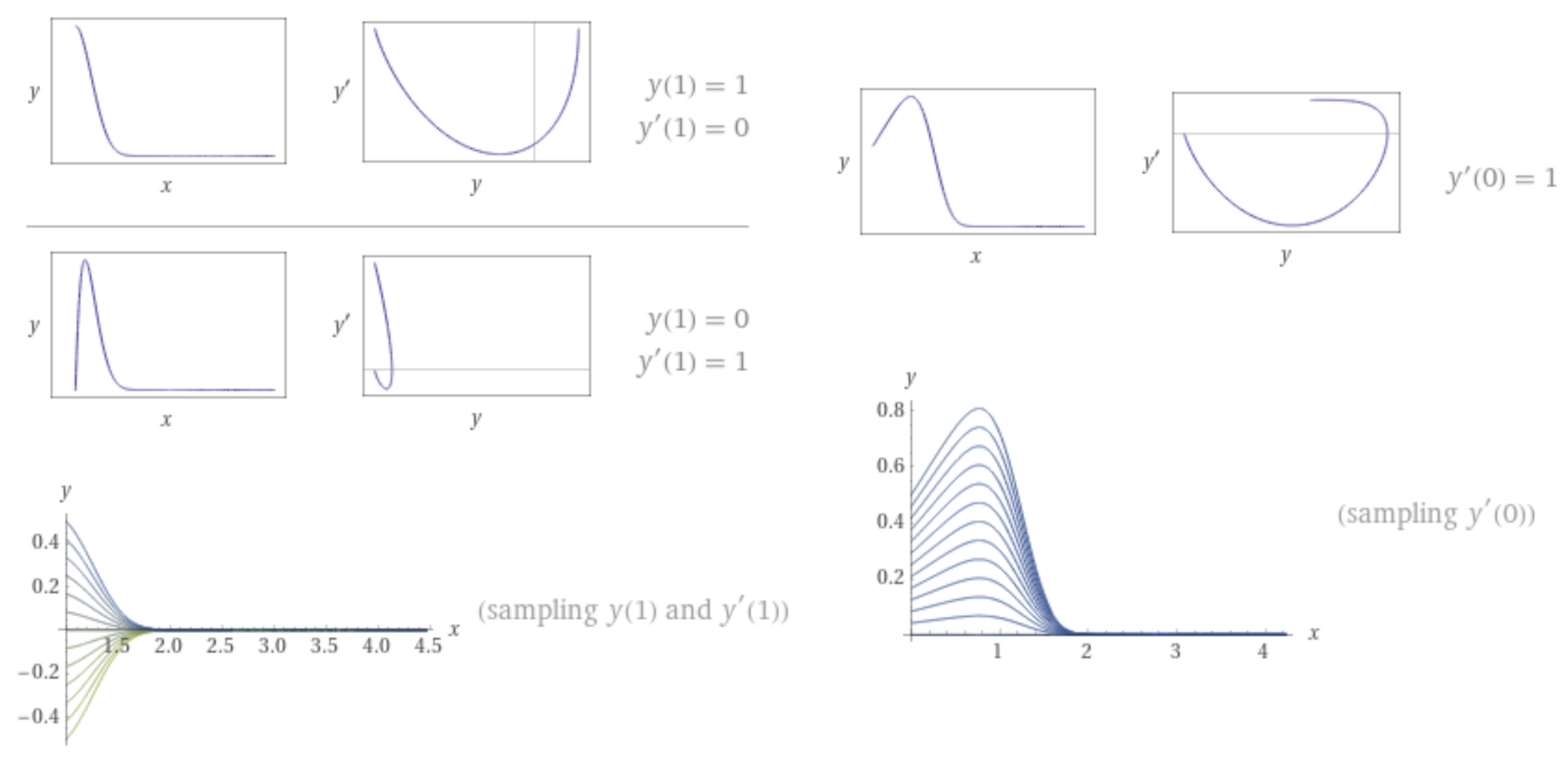
3.3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jackson, F.H. q-form of Taylor’s theorem. Messenger Math. 1909, 38, 62–64. [Google Scholar]
- Ismail, M.E.H.; Merkes, E.; Styer, D. A generalization of starlike functions. Complex Var. Theory Appl. Int. J. 1990, 14, 77–84. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Darus, M. New symmetric differential and integral operators defined in the complex domain. Symmetry 2019, 11, 906. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Elobaid, R.M.; Obaiys, S.J. Symmetric conformable fractional derivative of complex variables. Mathematics 2020, 8, 363. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Elobaid, R.M.; Obaiys, S.J. On subclasses of analytic functions based on a quantum symmetric conformable differential operator with application. Adv. Differ. Equ. 2020, 2020, 325. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Elobaid, R.M.; Obaiys, S.J. Geometric inequalities via a symmetric differential operator Defined by quantum calculus in the open unit disk. J. Funct. Spaces 2020, 2020, 6932739. [Google Scholar] [CrossRef]
- Carroll, R. Quantum Theory, Deformation and Integrability; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Shklyarov, D.; Sinel’shchikov, S.; Vaksman, L. On function theory in quantum disc: Integral representations. arXiv 1998, arXiv:math/9808015. [Google Scholar]
- Shklyarov, D.; Sinel’shchikov, S.; Vaksman, L. On Function Theory in Quantum Disc: A q-Analogue of Berezin Transform. arXiv 1998, arXiv:math/9809018. [Google Scholar]
- Ortigueira, M.D.; Machado, J.A.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Ortigueira, M.; Machado, J. Which derivative? Fractal Fract. 2017, 1, 3. [Google Scholar] [CrossRef]
- Miller, D.A.B. Quantum Mechanics for Scientists and Engineers; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.; et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef]
- Douglas, J.F. Some applications of fractional calculus to polymer science. Adv. Chem. Phys. 1997, 102, 121–192. [Google Scholar]
- Sumelka, W.; Blaszczyk, T.; Liebold, C. Fractional Euler—Bernoulli beams: Theory, numerical study and experimental validation. Eur. J. Mech.-A/Solids 2015, 54, 243–251. [Google Scholar] [CrossRef]
- Sumelka, W.; Blaszczyk, T. Fractional continua for linear elasticity. Arch. Mech. 2014, 66, 147–172. [Google Scholar]
- Patnaik, S.; Semperlotti, F. A generalized fractional-order elastodynamic theory for non-local attenuating media. Proc. R. Soc. A 2020, 476, 20200200. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Variable-order particle dynamics: Formulation and application to the simulation of edge dislocations. Philos. Trans. R. Soc. A 2020, 378, 20190290. [Google Scholar] [CrossRef] [PubMed]
- Magin, R. Fractional Calculus in Bioengineering; Begell House Inc.: Danbury, CT, USA, 2006. [Google Scholar]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Floreanini, R.; Vinet, L. A Quantum Algebraic Interpretation of the Basic Hypergeometric Series rΦs. In Symmetries in Science VI; Springer: Boston, MA, USA, 1993; pp. 235–245. [Google Scholar]
- Govindaraj, M.; Sivasubramanian, S. On a class of analytic functions related to conic domains involving q-calculus. Anal. Math. 2017, 43, 475–487. [Google Scholar] [CrossRef]
- Yalcin, S.; Vijaya, K.; Murugusundaramoorthy, G. Certain class of analytic functions involving Salagean type q-difference operator. Konuralp J. Math. 2018, 6, 264–271. [Google Scholar]
- Hussain, S.; Khan, S.; Zaighum, M.A.; Darus, M. Applications of a q-Salagean type operator on multivalent functions. J. Inequal. Appl. 2018, 2018, 301. [Google Scholar] [CrossRef]
- El-Qadeem, A.H.; Mamon, M.A. Comprehensive subclasses of multivalent functions with negative coefficients defined by using a q-difference operator. Trans. A Razmadze Math. Inst. 2018, 172, 510–526. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Darus, M. On a class of analytic functions associated to a complex domain concerning q-differential-difference operator. Adv. Differ. Equ. 2019, 2019, 515. [Google Scholar] [CrossRef]
- Komatu, Y. Note on the theory of conformal representation by meromorphic functions II. Proc. Jpn. Acad. 1945, 21, 278–284. [Google Scholar] [CrossRef]
- Rogosinski, W. On subordination functions. Proc. Camb. Philos. Soc. 1939, 35, 1–26. [Google Scholar] [CrossRef]
- Hayman, W.K. Meromorphic Functions; Oxford Mathematical Monographs: Oxford, UK, 1964. [Google Scholar]
- Ruscheweyh, S. Convolutions in Geometric Function Theory; Les Presses De L’Universite De Montreal: Montreal, QC, Canada, 1982. [Google Scholar]
- Ibrahim, R.W.; Aldawish, I. Difference formula defined by a new differential symmetric operator for a class of meromorphically multivalent functions. Adv. Differ. Equ. 2021, 2021, 281. [Google Scholar] [CrossRef]
- Miller, S.S.; Mocanu, P.T. Differential Subordinations: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Janowski, W. Some extremal problems for certain families of analytic functions I. Ann. Polon. Math. 1973, 28, 298–326. [Google Scholar] [CrossRef]
- Jahangiri, J.M.; Silverman, H.; Silvia, E.M. Inclusion relations between classes of functions defined by subordination. J. Math. Anal. Appl. 1990, 151, 318–329. [Google Scholar] [CrossRef][Green Version]
- Ahuja, O.; Anand, S.; Jain, N.K. Bohr radius problems for some classes of analytic functions using quantum calculus approach. Mathematics 2020, 8, 623. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Elobaid, R.M.; Obaiys, S.J. A class of quantum Briot-Bouquet differential equations with complex coefficients. Mathematics 2020, 8, 794. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ahmad, Q.Z.; Khan, N.; Khan, N.; Khan, B. Hankel and Toeplitz determinants for a subclass of q-starlike functions associated with a general conic domain. Mathematics 2019, 7, 181. [Google Scholar] [CrossRef]
- Srivastava, H.M.; El-Deeb, S.M. A certain class of analytic functions of complex order connected with a q-analogue of integral operators. Miskolc Math. Notes 2020, 21, 417–433. [Google Scholar] [CrossRef]
- Srivastava, H.M. Operators of basic (or q-) calculus and fractional q-calculus and their applications in geometric function theory of complex analysis. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 327–344. [Google Scholar] [CrossRef]
- Shanmugam, T.N.; Sivasubramanian, S.; Srivastava, H.M. Differential sandwich theorems for certain subclasses of analytic functions involving multiplier transformations. Integral Transform. Spec. Funct. 2006, 17, 889–899. [Google Scholar] [CrossRef]
- Miller, S.S.; Mocanu, P.T. Subordinants of differential superordinations. Complex Var. 2003, 48, 815–826. [Google Scholar] [CrossRef]
- Duren, P.L. Univalent Functions, Grundlehren der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1983; Volume 259, ISBN 0-387-90795-5. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldawish, I.; Ibrahim, R.W. Solvability of a New q-Differential Equation Related to q-Differential Inequality of a Special Type of Analytic Functions. Fractal Fract. 2021, 5, 228. https://doi.org/10.3390/fractalfract5040228
Aldawish I, Ibrahim RW. Solvability of a New q-Differential Equation Related to q-Differential Inequality of a Special Type of Analytic Functions. Fractal and Fractional. 2021; 5(4):228. https://doi.org/10.3390/fractalfract5040228
Chicago/Turabian StyleAldawish, Ibtisam, and Rabha W. Ibrahim. 2021. "Solvability of a New q-Differential Equation Related to q-Differential Inequality of a Special Type of Analytic Functions" Fractal and Fractional 5, no. 4: 228. https://doi.org/10.3390/fractalfract5040228
APA StyleAldawish, I., & Ibrahim, R. W. (2021). Solvability of a New q-Differential Equation Related to q-Differential Inequality of a Special Type of Analytic Functions. Fractal and Fractional, 5(4), 228. https://doi.org/10.3390/fractalfract5040228






