Extreme Multistability of a Fractional-Order Discrete-Time Neural Network
Abstract
:1. Introduction
- It provides a new way to describe fractional order systems resulting by replacing the Caputo fractional derivative with Caputo difference operator, without any loss in the memory effects, which leads to better results.
- It is the first fractional-order discrete-time neural network to exhibit extreme multistability, or the coexistence of several attractors given the same variety of system parameters and initial conditions.
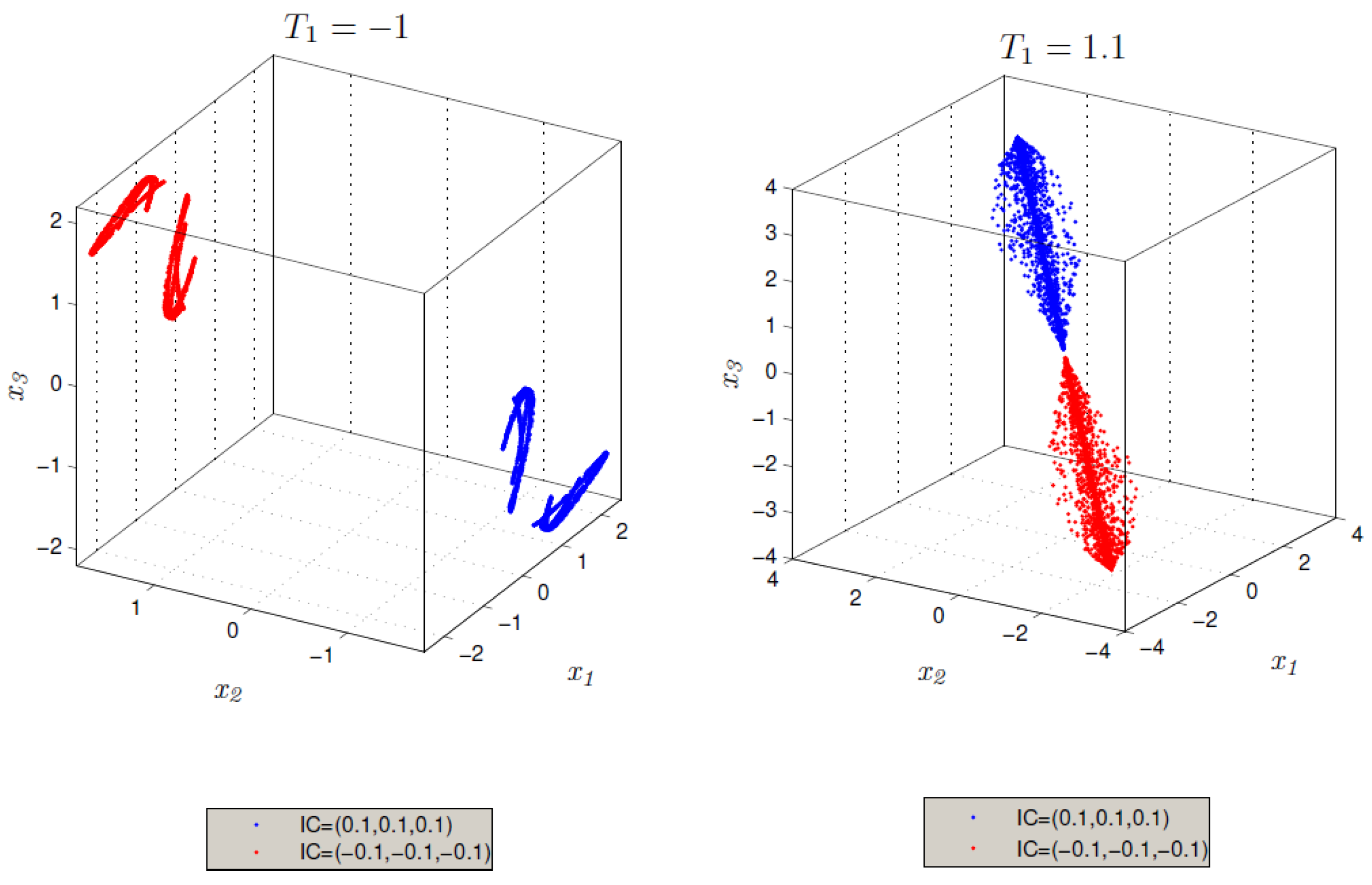
- For different fractional order values, different coexisting behaviors of asymmetric attractors emerged under different initial conditions.
- Extreme multistability behaviors of symmetric attractors have been discovered and thoroughly explored.
2. Preliminaries
3. A Fractional Order Discrete-Time Neural Network
3.1. The Mathematical Model
3.2. Dynamical Analysis and Numerical Simulations
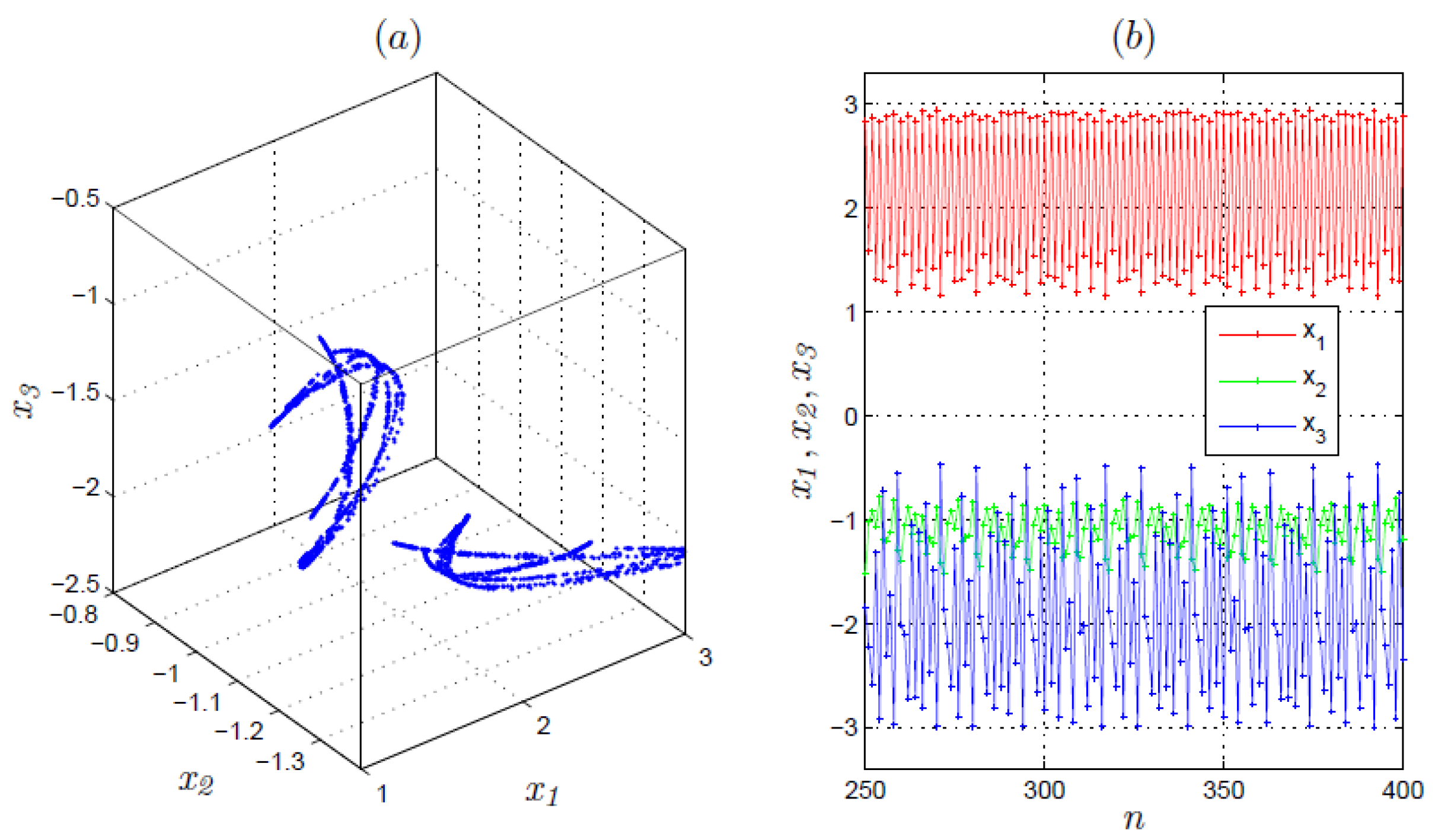
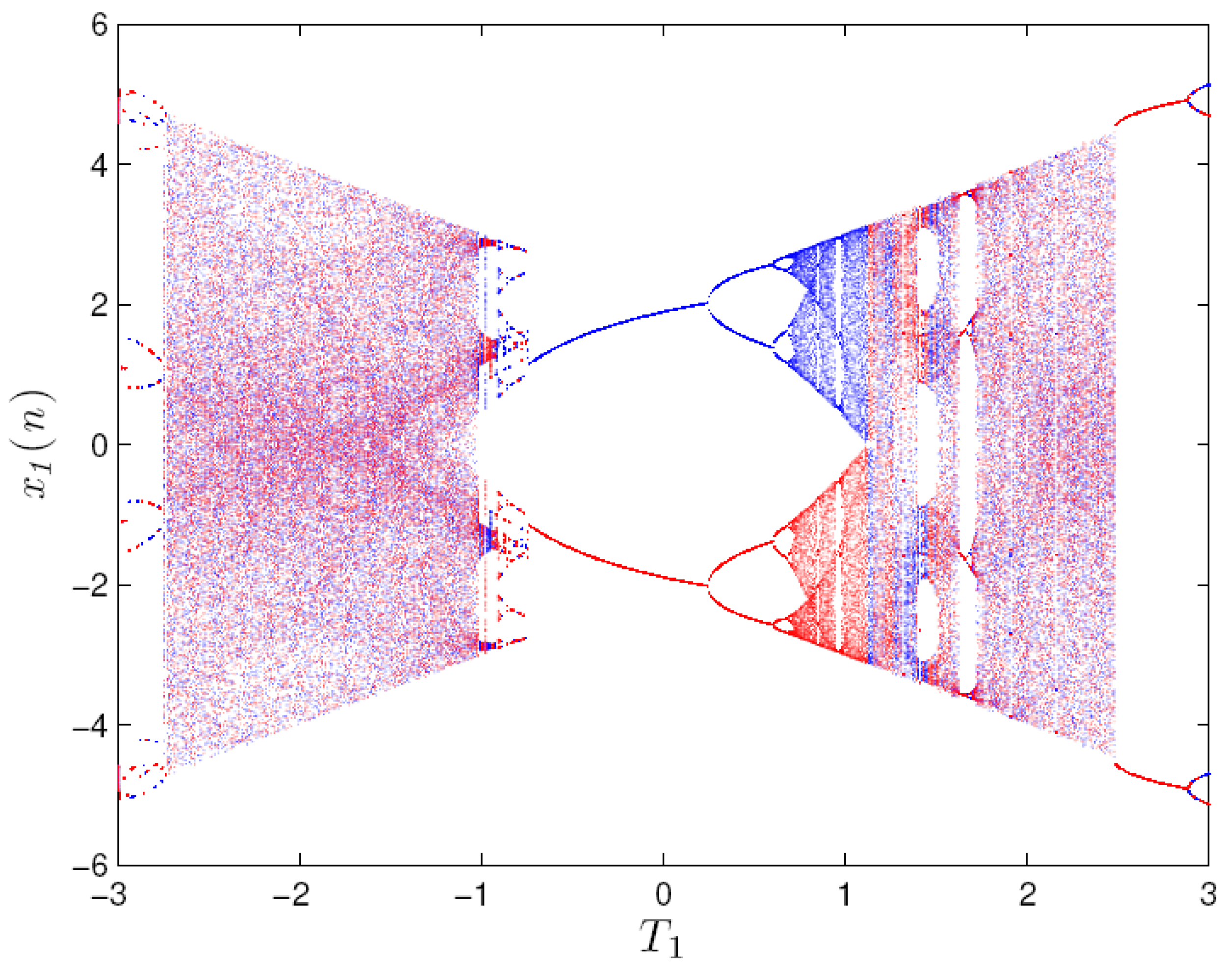
3.2.1. Coexisting of Symmetric Attractors Depending on System Parameter
3.2.2. Coexisting Symmetric Attractors Depending on the Fractional Order ℑ
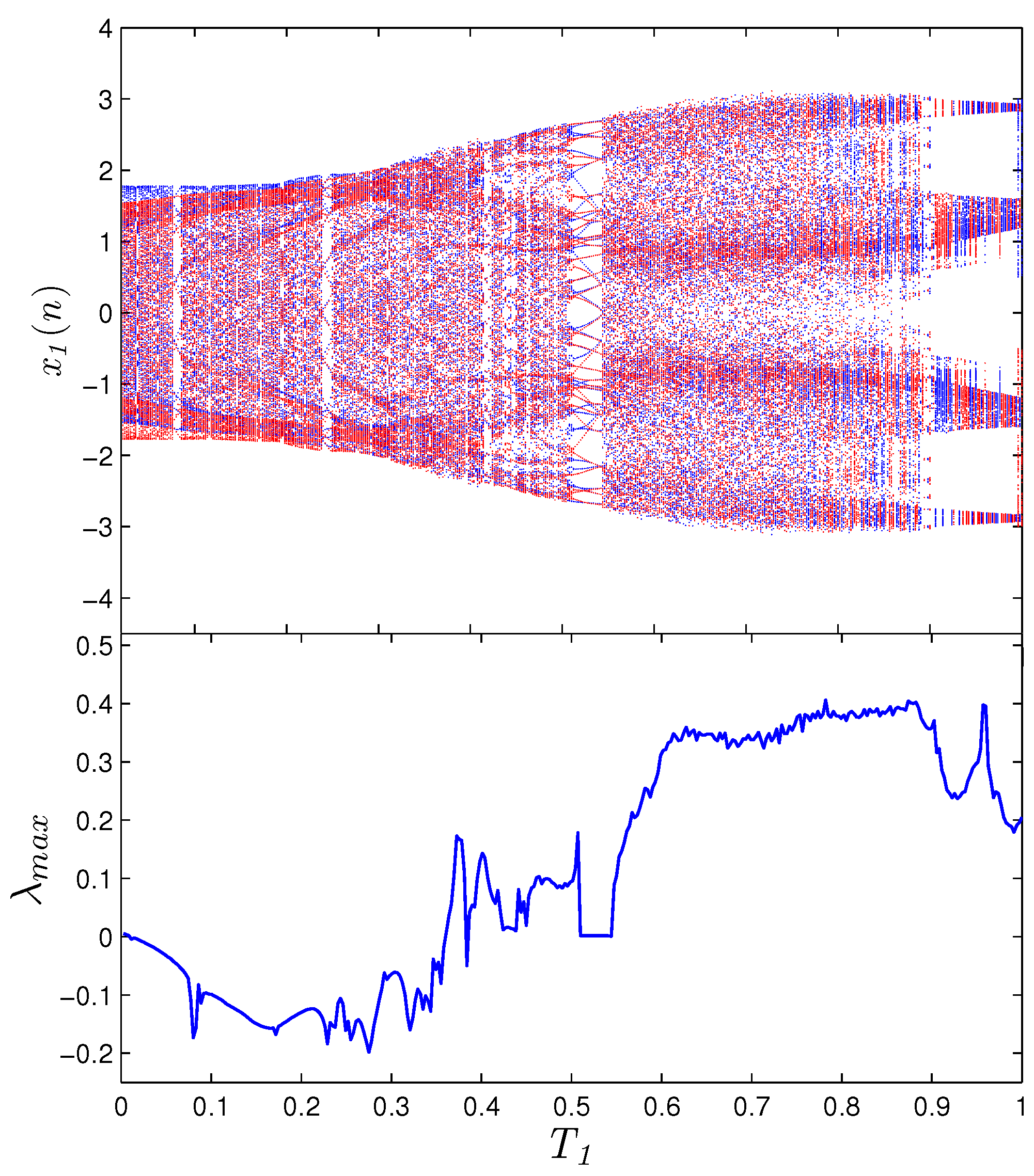
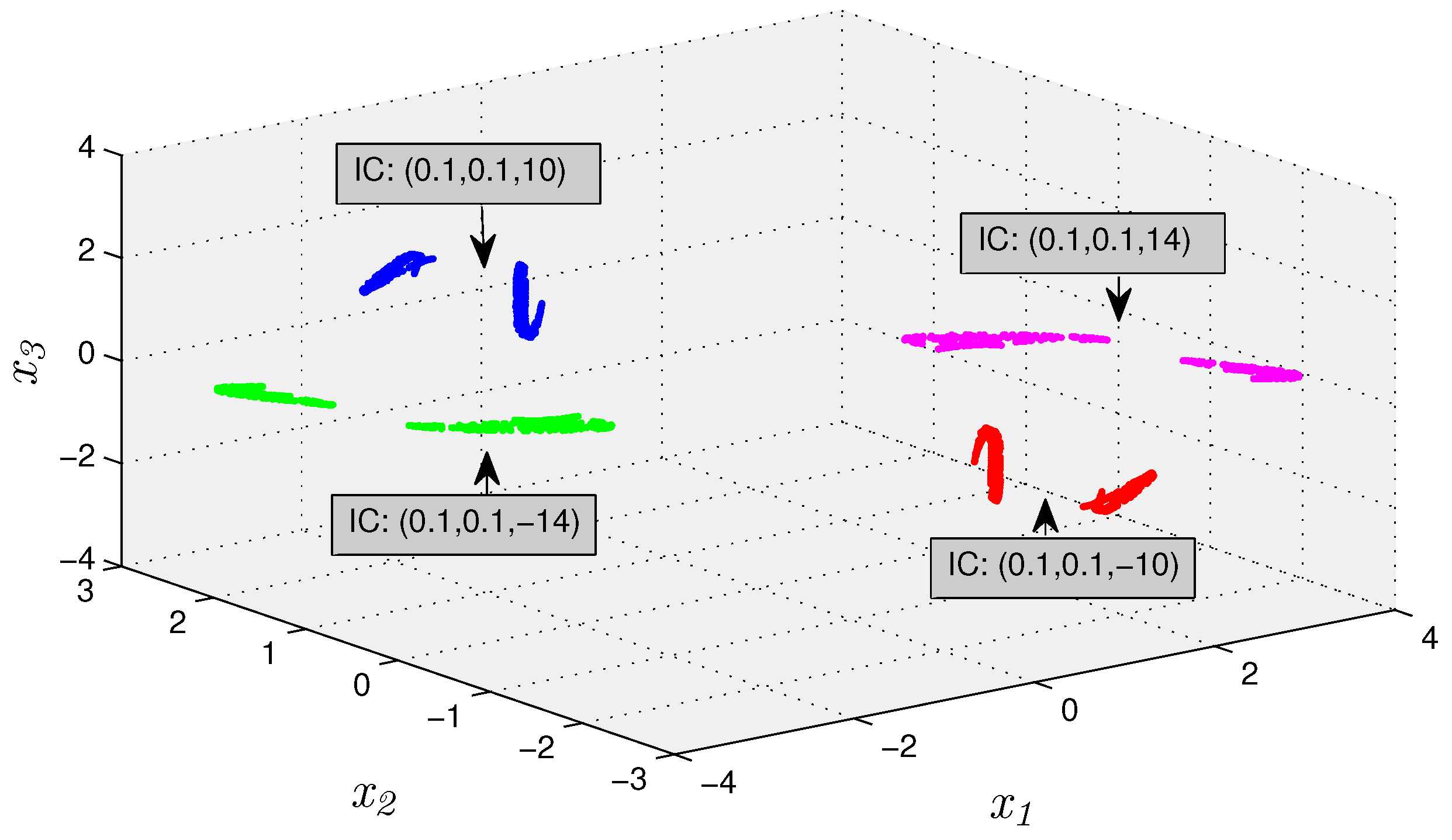
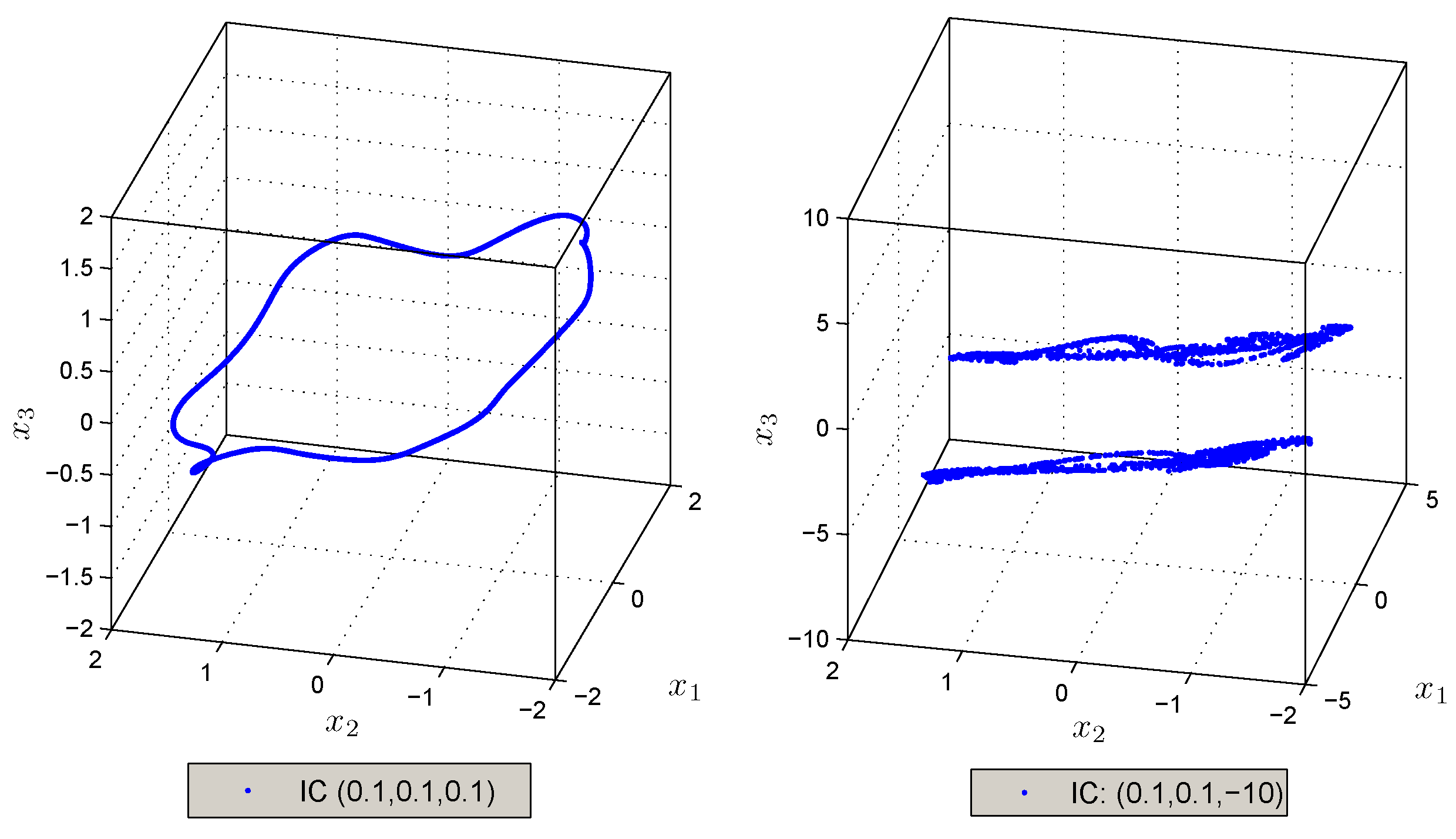
3.2.3. Extreme Multistability Analysis
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N.; Lorenz, F.N. The Nature and Theory of the General Circulation of the Atmosphere; World Meteorological Organization: Geneva, Switzerland, 1967. [Google Scholar]
- Lazaros, M.; Eleftherios, P.; Christos, V.; Hector, N.; Ioannis, S. A chaotic path planning generator based on logistic map and modulo tactics. Robot. Auton. Syst. 2020, 124, 103377. [Google Scholar]
- Guangyi, W.; Chuanbao, S.; Xiaowei, W.; Fang, Y. Coexisting oscillation and extreme multistability for a memcapacitor-based circuit. Math. Probl. Eng. 2017, 2017, 6504969. [Google Scholar]
- Kaslik, E.; Sivasundaram, S. Dynamics of Fractional-Order Neural Networs. In Proceedings of the International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific: Singapore, 2015. [Google Scholar]
- Atici, F.M.; Eloe, P. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 3, 1–12. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Principles of delta fractional calculus on time scales and inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Diaz, J.B.; Osler, T.J. Differences of fractional order. Math. Comput. 1974, 125, 185–202. [Google Scholar] [CrossRef] [Green Version]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.C.; Dumitru, B. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Odibat, Z.; Pham, V.T.; Grassi, G. On the dynamics, control and synchronization of fractional-order Ikeda map. Chaos Solitons Fractals 2019, 123, 108–115. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Lozi, R.P.; Pham, V.T. On Fractional Order Discrete Time Systems: Chaos, Stabilization and Synchronization. Chaos Solitons Fractals 2019, 119, 150–162. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Wang, X.; Pham, V.T.; Alsaadi, F.E. Chaos, control, and synchronization in some fractional-order difference equations. Adv. Differ. Equ. 2019, 1, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Hopfield, J.J. Neuron with graded response have computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [Green Version]
- Kaslik, E.; Radulescu, I.R. Dynamics of complex-valued fractional-order neural networks. Neural Netw. 2017, 89, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Arena, P.; Caponetto, R.; Fortuna, L.; Porto, D. Bifurcation and chaos in noninteger order cellular neural networks. Int. J. Bifurc. Chaos 1998, 8, 1527–1539. [Google Scholar] [CrossRef]
- Allehiany, F.M.; Mahmoud, E.E.; Jahanzaib, L.S.; Trikha, P.; Alotaibi, H. Chaos control and analysis of fractional order neural network under electromagnetic radiation. Results Phys. 2021, 21, 103786. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Global Mittag-Leffler stability and synchronization of discrete-time fractional-order complex-valued neural networks with time delay. Neural Netw. 2020, 122, 382–394. [Google Scholar] [CrossRef]
- Chen, L.; Hao, Y.; Huang, T.; Yuan, L.; Zheng, S.; Yin, L. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020, 125, 177–184. [Google Scholar] [CrossRef]
- Wu, G.C.; Luo, M.; Huang, L.L.; Banerjee, S. Short memory fractional differential equations for new memristor and neural network design. Nonlinear Dyn. 2020, 100, 3611–3623. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yao, W.; Tan, Y. Chaotic dynamics in a neural network with different types of external stimuli. Commun. Nonlinear Sci. Numer. Simulat. 2020, 90, 105390. [Google Scholar] [CrossRef]
- Wu, G.C.; Deng, Z.G.; Baleanu, D.; Zneg, D.Q. New variable-order fractional chaotic systems for fast image encryption. Chaos 2019, 29, 083103. [Google Scholar] [CrossRef] [PubMed]
- Khennaoui, A.A.; Almatroud, A.O.; Ouannas, A.; Al-sawalha, M.M.; Grassi, G.; Pham, V.T.; Batiha, I.M. An Unprecedented 2-Dimensional Discrete-Time Fractional-Order System and Its Hidden Chaotic Attractors. Math. Probl. Eng. 2021, 2021, 6768215. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, J.; Wang, X.; Zeng, Z. A novel no-equilibruim HR neuron model with hidden homogeneous extreme multistability. Chaos Solitons Frractals 2021, 145, 110761. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almatroud, A.O. Extreme Multistability of a Fractional-Order Discrete-Time Neural Network. Fractal Fract. 2021, 5, 202. https://doi.org/10.3390/fractalfract5040202
Almatroud AO. Extreme Multistability of a Fractional-Order Discrete-Time Neural Network. Fractal and Fractional. 2021; 5(4):202. https://doi.org/10.3390/fractalfract5040202
Chicago/Turabian StyleAlmatroud, A. Othman. 2021. "Extreme Multistability of a Fractional-Order Discrete-Time Neural Network" Fractal and Fractional 5, no. 4: 202. https://doi.org/10.3390/fractalfract5040202
APA StyleAlmatroud, A. O. (2021). Extreme Multistability of a Fractional-Order Discrete-Time Neural Network. Fractal and Fractional, 5(4), 202. https://doi.org/10.3390/fractalfract5040202




