An Approximate Solution of the Time-Fractional Two-Mode Coupled Burgers Equation

Abstract

In this paper, we consider the time-fractional two-mode coupled Burgers equation with the Caputo fractional derivative. A modified homotopy perturbation method coupled with Laplace transform (He-Laplace method) is applied to find its approximate analytical solution. The method is to decompose the equation into a series of linear equations, which can be effectively and easily solved by the Laplace transform. The solution process is illustrated step by step, and the results show that the present method is extremely powerful for fractional differential equations.

1. Introduction

The classical Burgers equation, introduced by Bateman [1], is a fundamental model in viscous fluid mechanics. In fact, it is widely used to express different physical phenomenon like shock waves, dispersion in porous media, modelling of gas dynamics, traffic flow and so on [2,3,4,5,6]. The partial differential equations that are first-order in time model the right-moving unidirectional waves in the positive x-direction. A new nonlinear PDE of second-order in time which model both left- and right- going waves are called two-mode equations. Korunsky [7] was the first one to introduce two-mode KdV equation in the scaled form as

$$u_{tt}-{\alpha }^2{u}_{xx}+(\frac{\partial }{\partial t}-\mu \alpha \frac{\partial }{\partial x})u_{xxx}+(\frac{\partial }{\partial t}-\lambda \alpha \frac{\partial }{\partial x})u{u}_x=0,$$

where $x,t\in \mathbb{R},\alpha >0,|\lambda |\le 1,|\mu |\le 1,u(x,t)$ is a field function and represents the height of the water’s free surface above a flat bottom. $\lambda ,\mu$ and $\alpha$ are the parameters of nonlinearity, dispersion and phase velocities respectively. This two-mode KdV equation describes the propagation of two different wave modes in the same direction simultaneously, with the same dispersion relation but different parameters of phase velocities, nonlinearity and dispersion. In 2016, Wazwaz [8] used the sense of Korunsky to introduce a new two-mode Burgers equation (TMBE) in the scaled for as

$$u_{tt}-{\alpha }^2{u}_{xx}+(\frac{\partial }{\partial t}-\mu \alpha \frac{\partial }{\partial x})u_{xx}+(\frac{\partial }{\partial t}-\lambda \alpha \frac{\partial }{\partial x})u{u}_x=0$$

where $\lambda , \mu , \alpha$ are as defined earlier.

However, it is very rare that a real life model can be represented by a single partial differential equation, therefore, a couple of partial differential equations are required to provide a complete model. This idea of Korunsky and Wazwaz was further generalized by Jaradat [9], where he introduced a new two-mode coupled Burgers equation (TMCBE) which has the form

$$\begin{array}{c}\hfill u_{tt}-{\alpha }^2{u}_{xx}-a_1(\frac{\partial }{\partial t}-\mu \alpha \frac{\partial }{\partial x})u_{xx}-b_1(\frac{\partial }{\partial t}-\lambda \alpha \frac{\partial }{\partial x})u{u}_x\\ \hfill & +c_1(\frac{\partial }{\partial t}-\mu \alpha \frac{\partial }{\partial x}){\left(uv\right)}_x=0,\hfill \\ \hfill v_{tt}-{\alpha }^2{v}_{xx}-a_2(\frac{\partial }{\partial t}-\mu \alpha \frac{\partial }{\partial x})v_{xx}-b_2(\frac{\partial }{\partial t}-\lambda \alpha \frac{\partial }{\partial x})v{v}_x\\ \hfill & +c_2(\frac{\partial }{\partial t}-\mu \alpha \frac{\partial }{\partial x}){\left(uv\right)}_x=0.\hfill \end{array}$$

(1)

It can be observed that if we put $\alpha =0$ in Equation (1) and integrate with respect to the variable t once, we obtain the standard coupled Burgers equation (see [10]).

The study of coupled Burgers equations is very important in the sense that it describes the sedimentation of polydispersive suspension under the effect of gravity [11].

Fractional differential equations involve real or complex order derivatives. They provide more accurate models of the real world problems than the integer order differential equations (for detail [12,13,14,15]). Due to the vast applications of fractional calculus in various disciplines of Science and Engineering, there has been significant growth in its literature in the last few decades. In this paper, we extend the time-derivative in Equation (1) with the fractional derivative. Thus, for $1/2<\xi \le 1$, the modified fractional version of Equation (1) obtained is given by the following.

$$\begin{array}{cc}\hfill & D_t^{2\xi }u-{\alpha }^2{u}_{xx}-a_1({\mathcal{D}}_t^{\xi }-\mu \alpha \frac{\partial }{\partial x})u_{xx}-b_1({\mathcal{D}}_t^{\xi }-\lambda \alpha \frac{\partial }{\partial x})u{u}_x\hfill \\ \hfill & +c_1({\mathcal{D}}_t^{\xi }-\mu \alpha \frac{\partial }{\partial x}){\left(uv\right)}_x=0,\hfill \\ \hfill & D_t^{2\xi }v-{\alpha }^2{v}_{xx}-a_2({\mathcal{D}}_t^{\xi }-\mu \alpha \frac{\partial }{\partial x})v_{xx}-b_2({\mathcal{D}}_t^{\xi }-\lambda \alpha \frac{\partial }{\partial x})v{v}_x\hfill \\ \hfill & +c_2({\mathcal{D}}_t^{\xi }-\mu \alpha \frac{\partial }{\partial x}){\left(uv\right)}_x=0.\hfill \end{array}$$

(2)

where the fractional derivative ${\mathcal{D}}_t^{\xi }$ may be considered as Caputo fractional derivative as defined in Definition 2 in Section 2. The Equation (2) can be rewritten as

$$\begin{array}{cc}\hfill D_t^{2\xi }u& ={\mathcal{D}}_t^{\xi }(a_1{u}_{xx}+b_{1}u{u}_x-c_1{\left(uv\right)}_x)+{\alpha }^2{u}_{xx}-a_1\mu \alpha u_{xxx}-b_1\lambda \alpha {\left(u{u}_x\right)}_x\hfill \\ \hfill & +c_1\mu \alpha {\left(uv\right)}_{xx},\hfill \\ \hfill D_t^{2\xi }v& ={\mathcal{D}}_t^{\xi }(a_2{v}_{xx}+b_{2}v{v}_x-c_2{\left(uv\right)}_x)+{\alpha }^2{v}_{xx}-a_2\mu \alpha v_{xxx}-b_2\lambda \alpha {\left(v{v}_x\right)}_x\hfill \\ \hfill & +c_2\mu \alpha {\left(uv\right)}_{xx}.\hfill \end{array}$$

(3)

Explicit solutions to the fractional problems involving Burgers equation are rare and possibly non-existent in the literature. Therefore, it is more desirable to look for new techniques to get solutions of fractional differential equations. Methods like Adomian Decomposition Method, Iteration Method, Homotopy Analysis Method, Homotopy Perturbation Method, and Laplace Transform Methods are some of very powerful and useful techniques [16,17,18,19,20,21]. The combination of Laplace Transform and Homotopy Perturbation Method is a new tool which is being used to solve linear and nonlinear fractional differential equations [22].

The paper is organised as follows: Section 2 consists of the definitions and theory required for rest of the paper. In Section 3, we apply Laplace homotopy perturbation method to the considered nonlinear time-fractional model. In Section 4, we discuss a concrete example of main equation and demonstrate the solution graphically. The last section concludes this paper.

2. Definitions and Mathematical Preliminaries

There are various versions of fractional derivatives given by different authors and new definitions have been proposed in recent decades. Here we give the Caputo definition of fractional derivative. Please refer to the books [23,24,25] for the detailed theory of fractional calculus.

Definition 1.

The Riemann-Liouville fractional integral of order ξ for a locally integerable function f of two variables is defined by

$${\mathcal{J}}_t^{\xi }f(x,t)=\frac{1}{\Gamma \left(\xi \right)}{\int }_0^t{(t-s)}^{\xi -1}f(x,s)ds,\xi >0,$$

and

$${\mathcal{J}}_t^{0}f(x,t)=f(x,t),$$

where Γ denotes the Gamma function.

Definition 2.

The Caputo fractional derivative of order ξ of a m-times continuously differentiable function which is locally integerable function f is defined by

$${\mathcal{D}}_t^{\xi }f(x,t)=\frac{1}{\Gamma (m-\xi )}{\int }_0^t{(t-k)}^{m-\xi -1}{f}^{\left(m\right)}(x,k)dk,$$

where $m-1<\xi \le m$.

In particular, for $0<\xi \le 1$, we have

$${\mathcal{D}}_t^{\xi }f(x,t)=\frac{1}{\Gamma (1-\xi )}{\int }_0^t{(t-k)}^{-\xi }{f}^{\prime }(x,k)dk.$$

Definition 3.

The Laplace transform of the Caputo fractional derivative is given by

$$\mathcal{L}\left\{{\mathcal{D}}_t^{\xi }g(x,t)\right\}\left(p\right)=\frac{1}{p^{m-\xi }}[p^m\mathcal{L}\left\{g(x,t)\right\}\left(p\right)-p^{m-1}g(x,0)-\dots -g^{(m-1)}(x,0)],$$

In particular, for $0<\xi \le 1$, we have

$$\mathcal{L}\left\{{\mathcal{D}}_t^{\xi }g(x,t)\right\}\left(p\right)=p^{\xi }\mathcal{L}\left\{g(x,t)\right\}\left(p\right)-p^{\xi -1}g(x,0).$$

3. Existence and Uniqueness

Let $\Omega$ be a bounded interval of real numbers and T be a constant such that $0<T<\infty$. We establish the existence and uniqueness of the solution of the system (3) in this section. Consider the Banach space of real-valued continuous functions defined on $\overline{\Omega }\times [0,T]$ (that is, $C(\overline{\Omega }\times [0,T])$) with norm given by

$$\parallel u\parallel =\underset{(x,t)\in \overline{\Omega }\times [0,T]}{max}|u(x,t)|.$$

Apply the integral operator ${\mathcal{J}}_t^{2\xi }$ on both sides of each equation in system (3), to have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill u(x,t)-u(x,0)& ={\mathcal{J}}_t^{\xi }{\tau }_1(x,t,u)+{\mathcal{J}}_t^{2\xi }{\tau }_2(x,t,u),\hfill \\ \hfill v(x,t)-v(x,0)& ={\mathcal{J}}_t^{\xi }{\tau }_3(x,t,v)+{\mathcal{J}}_t^{2\xi }{\tau }_4(x,t,v),\hfill \end{array}\end{array}$$

(4)

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tau }_1(x,t,u)& =a_1{u}_{xx}+b_{1}u{u}_x-c_1{\left(uv\right)}_x,\hfill \\ \hfill {\tau }_2(x,t,u)& ={\alpha }^2{u}_{xx}-a_1\mu \alpha u_{xxx}-b_1\lambda \alpha {\left(u{u}_x\right)}_x+c_1\mu \alpha {\left(uv\right)}_{xx},\hfill \\ \hfill {\tau }_3(x,t,v)& =a_2{v}_{xx}+b_{2}v{v}_x-c_2{\left(uv\right)}_x,\hfill \\ \hfill {\tau }_4(x,t,v)& ={\alpha }^2{v}_{xx}-a_2\mu \alpha v_{xxx}-b_2\lambda \alpha {\left(v{v}_x\right)}_x+c_2\mu \alpha {\left(uv\right)}_{xx}.\hfill \end{array}\end{array}$$

(5)

If we assume that $\parallel u\parallel \le m_1, \parallel w\parallel \le m_2, \parallel v\parallel \le m_3$, $\parallel v_x\parallel \le m_4, {\parallel (u-w)}_{xx}\parallel \le {\delta }_1\parallel u-w\parallel , \parallel {(u^2-w^2)}_x\parallel \le {\delta }_2\parallel u^2-w^2\parallel \le {\delta }_2(m_1+m_2)\parallel u-w\parallel , \parallel {(u-w)}_x\parallel \le {\delta }_3\parallel u-w\parallel$, for $m_1,m_2,m_3,m_4,{\delta }_1,{\delta }_2,{\delta }_3\ge 0$, then ${\tau }_1(x,t,u)$ satisfy the Lipschitz condition. For, let $u(x,t)$ and $w(x,t)$ be any two arbitrary functions bounded above, then we have

$$\begin{array}{c}\parallel {\tau }_1(x,t,u)-{\tau }_1(x,t,w)\parallel \hfill \\ =\parallel a_1(u_{xx}-w_{xx})+\frac{b_1}{2}{(u^2-w^2)}_x-c_1(u_{x}v+u{v}_x)+c_1(w_{x}v+w{v}_x)\parallel \hfill \\ \le \parallel a_1{(u-w)}_{xx}\parallel +\parallel \frac{b_1}{2}{\left((u+w)(u-w)\right)}_x\parallel +\parallel c_1{(u-w)}_{x}v\parallel +\parallel c_1(u-w)v_x\parallel \hfill \\ \le {\delta }_1|a_1|\parallel u-w\parallel +{\delta }_2(m_1+m_2)\frac{|b_1|}{2}\parallel u-w\parallel +(m_3{\delta }_3+m_4)|c_1|\parallel u-w\parallel \hfill \\ =L_1\parallel u-w\parallel ,\hfill \end{array}$$

where $L_1=|a_1|{\delta }_1+|\frac{b_1}{2}|{\delta }_2(m_1+m_2)+|c_1|(m_3{\delta }_3+m_4)$ is the Lipschitz constant. Similarly, it can be shown that there exist Lipschitz constants $L_2,L_3$ and $L_4$ for ${\tau }_2(x,t,u),{\tau }_3(x,t,v)$ and ${\tau }_4(x,t,v)$ respectively. Thus, we note that if $u(x,t)$ and $v(x,t)$ are bounded above, then

$$\begin{array}{cc}\hfill \parallel {\tau }_1(x,t,u)-{\tau }_1(x,t,w)\parallel & \le L_1\parallel u-w\parallel ,\hfill \\ \hfill \parallel {\tau }_2(x,t,u)-{\tau }_2(x,t,w)\parallel & \le L_2\parallel u-w\parallel ,\hfill \\ \hfill \parallel {\tau }_3(x,t,v)-{\tau }_3(x,t,y)\parallel & \le L_3\parallel v-y\parallel ,\hfill \\ \hfill \parallel {\tau }_4(x,t,v)-{\tau }_4(x,t,y)\parallel & \le L_4\parallel v-y\parallel .\hfill \end{array}$$

where $L_i\ge 0,i=1,2,3,4,$ are Lipschitz constants.

3.1. Existence of the Solution

Using the definition of integral operator (1), we construct the following iterative formula for the system (4)

$$\begin{array}{cc}\hfill u_{n+1}(x,t)& =\frac{1}{\Gamma \left(\xi \right)}{\int }_0^t{(t-k)}^{\xi -1}{\tau }_1(x,k,u_n)dk,\hfill \\ \hfill & +\frac{1}{\Gamma \left(2\xi \right)}{\int }_0^t{(t-k)}^{2\xi -1}{\tau }_2(x,k,u_n)dk,\hfill \\ \hfill v_{n+1}(x,t)& =\frac{1}{\Gamma \left(\xi \right)}{\int }_0^t{(t-k)}^{\xi -1}{\tau }_3(x,k,v_n)dk,\hfill \\ \hfill & +\frac{1}{\Gamma \left(2\xi \right)}{\int }_0^t{(t-k)}^{2\xi -1}{\tau }_4(x,k,v_n)dk.\hfill \end{array}$$

Let the differences between successive terms be given by ${\mathsf{\Xi }}_n(x,t)=u_n(x,t)-u_{n-1}(x,t)$ and ${\Theta }_n(x,t)=v_n(x,t)-v_{n-1}(x,t)$, then we have

$$u_n(x,t)=\sum _{j=0}^n{\mathsf{\Xi }}_j(x,t),$$

$$v_n(x,t)=\sum _{j=0}^n{\Theta }_j(x,t).$$

Now, we consider

$$\begin{array}{cc}\hfill \parallel {\mathsf{\Xi }}_n(x,t)\parallel & =\parallel u_n(x,t)-u_{n-1}(x,t)\parallel \hfill \\ \hfill & =\parallel \frac{1}{\Gamma \left(\xi \right)}{\int }_0^t{(t-k)}^{\xi -1}[{\tau }_1(x,k,u_{n-1})-{\tau }_1(x,k,u_{n-2})]dk,\hfill \\ \hfill & +\frac{1}{\Gamma \left(2\xi \right)}{\int }_0^t{(t-k)}^{2\xi -1}[{\tau }_2(x,k,u_n)-{\tau }_2(x,k,u_{n-2})]dk,\parallel \hfill \\ \hfill & \le \frac{L_1}{\Gamma \left(\xi \right)}\parallel u_{n-1}-u_{n-2}\parallel \frac{t^{\xi }}{\xi }+\frac{L_2}{\Gamma \left(2\xi \right)}\parallel u_{n-1}-u_{n-2}\parallel \frac{t^{2\xi }}{2\xi }\hfill \\ \hfill & \le [\frac{L_1{T}^{\xi }}{\Gamma (\xi +1)}+\frac{L_2{T}^{2\xi }}{\Gamma (2\xi +1)}]\parallel u_{n-1}-u_{n-2}\parallel .\hfill \end{array}$$

Let $\gamma :=\frac{L_1{T}^{\xi }}{\Gamma (\xi +1)}+\frac{L_2{T}^{2\xi }}{\Gamma (2\xi +1)}<1$, then

$$\begin{array}{cc}\hfill \parallel {\mathsf{\Xi }}_n(x,t)\parallel & <\gamma \parallel u_{n-1}-u_{n-2}\parallel \hfill \\ \hfill & <{\gamma }^2\parallel u_{n-2}-u_{n-3}\parallel \hfill \\ \hfill ·\\ \hfill ·\\ \hfill ·\\ \hfill & <{\gamma }^n\parallel u_0\parallel .\hfill \end{array}$$

Therefore, $u_n(x,t)={\sum }_{j=0}^n{\mathsf{\Xi }}_j(x,t)$ exists and is smooth. Similarly, it can be shown that $v_n(x,t)={\sum }_{j=0}^n{\Theta }_j(x,t)$ exists and is smooth.

3.2. Uniqueness

Let $u(x,t)$ and $r(x,t)$ are two solutions, then

$$\begin{array}{cc}\hfill u(x,t)-r(x,t)& =\frac{1}{\Gamma \left(\xi \right)}{\int }_0^t{(t-k)}^{\xi -1}[{\tau }_1(x,k,u)-{\tau }_1(x,k,r)]dk\hfill \\ \hfill & +\frac{1}{\Gamma \left(2\xi \right)}{\int }_0^t{(t-k)}^{2\xi -1}[{\tau }_2(x,k,u)-{\tau }_2(x,k,r)]dk\parallel .\hfill \end{array}$$

$$\Rightarrow \parallel u(x,t)-r(x,t)\parallel \le [\frac{L_1{T}^{\xi }}{\Gamma (\xi +1)}+\frac{L_2{T}^{2\xi }}{\Gamma (2\xi +1)}]\parallel u(x,t)-r(x,t)\parallel ,$$

that is

$$(1-\frac{L_1{T}^{\xi }}{\Gamma (\xi +1)}-\frac{L_2{T}^{2\xi }}{\Gamma (2\xi +1)})\parallel u(x,t)-r(x,t)\parallel \le 0.$$

If we assume that $1-\frac{L_1{T}^{\xi }}{\Gamma (\xi +1)}-\frac{L_2{T}^{2\xi }}{\Gamma (2\xi +1)}>0$, then

$$\begin{array}{c}\hfill \parallel u(x,t)-r(x,t)\parallel =0\Rightarrow u(x,t)=r(x,t).\end{array}$$

Similarly, we can prove the uniqueness of $v(x,t)$.

Hence, system (3) has a unique solution.

4. Solution of Two Mode Coupled Burgers Equations

We consider the nonlinear coupled fractional partial differential Equation (3) and apply Laplace Homotopy Perturbation Method [19,26,27,28]. Now, applying Laplace transform in Equation (3) with respect to the variable t and using the Laplace transform of Caputo fractional derivative, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{u}_{xx}-a_1\mu \alpha u_{xxx}-b_1\lambda \alpha {\left(u{u}_x\right)}_x+c_1\mu \alpha {\left(uv\right)}_{xx}\right\},\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_1{u}_{xx}+b_{1}u{u}_x-c_1{\left(uv\right)}_x\right\}\hfill \\ \hfill & -\frac{1}{p^{\xi +1}}[a_1{u}_{xx}+b_{1}u{u}_x-c_1{\left(uv\right)}_x](x,0)+\frac{u(x,0)}{p}+\frac{u_t(x,0)}{p^2}.\hfill \\ \hfill V(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{v}_{xx}-a_2\mu \alpha v_{xxx}-b_2\lambda \alpha {\left(v{v}_x\right)}_x+c_2\mu \alpha {\left(uv\right)}_{xx}\right\}\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_2{v}_{xx}+b_{2}v{v}_x-c_2{\left(uv\right)}_x\right\}\hfill \\ \hfill & -\frac{1}{p^{\xi +1}}[a_2{v}_{xx}+b_{2}v{v}_x-c_2{\left(uv\right)}_x](x,0)+\frac{v(x,0)}{p}+\frac{v_t(x,0)}{p^2},\hfill \end{array}\end{array}$$

(6)

where $\mathcal{L}u(x,t)=U(x,p)$, $\mathcal{L}v(x,t)=V(x,p)$. We construct the homotopy for the Equation (6) as follows.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U(x,p)& =\frac{h}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{u}_{xx}-a_1\mu \alpha u_{xxx}-b_1\lambda \alpha {\left(u{u}_x\right)}_x+c_1\mu \alpha {\left(uv\right)}_{xx}\right\}\hfill \\ \hfill & +\frac{h}{p^{\xi }}\mathcal{L}\left\{a_1{u}_{xx}+b_{1}u{u}_x-c_1{\left(uv\right)}_x\right\}\hfill \\ \hfill & -\frac{1}{p^{\xi +1}}[a_1{u}_{xx}+b_{1}u{u}_x-c_1{\left(uv\right)}_x](x,0)\hfill \\ \hfill & +\frac{u(x,0)}{p}+\frac{u_t(x,0)}{p^2}.\hfill \\ \hfill V(x,p)& =\frac{h}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{v}_{xx}-a_2\mu \alpha v_{xxx}-b_2\lambda \alpha {\left(v{v}_x\right)}_x+c_2\mu \alpha {\left(uv\right)}_{xx}\right\}\hfill \\ \hfill & +\frac{h}{p^{\xi }}\mathcal{L}\left\{a_2{v}_{xx}+b_{2}v{v}_x-c_2{\left(uv\right)}_x\right\}\hfill \\ \hfill & -\frac{1}{p^{\xi +1}}[a_2{v}_{xx}+b_{2}v{v}_x-c_2{\left(uv\right)}_x](x,0)\hfill \\ \hfill & +\frac{v(x,0)}{p}+\frac{v_t(x,0)}{p^2}.\hfill \end{array}\end{array}$$

(7)

Let

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U(x,p)=& \sum _{m=0}^{\infty }{h}^m{U}_m(x,p),\hfill \\ \hfill V(x,p)=& \sum _{m=0}^{\infty }{h}^m{V}_m(x,p),\hfill \end{array}\end{array}$$

(8)

or

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill u(x,t)& =\sum _{m=0}^{\infty }{h}^m{u}_m(x,t),\hfill \\ \hfill v(x,t)& =\sum _{m=0}^{\infty }{h}^m{v}_m(x,t),\hfill \end{array}\end{array}$$

(9)

where $\mathcal{L}{u}_m(x,t)=U_m(x,p),\mathcal{L}{v}_m(x,t)=V_m(x,p)$. Substituting Equation (8) into Equation (7), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{m=0}^{\infty }{h}^m{U}_m(x,p)& =\frac{h}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2\sum _{m=0}^{\infty }{h}^m{u}_{m_{xx}}-a_1\mu \alpha \sum _{m=0}^{\infty }{h}^m{u}_{m_{xxx}}\right.\hfill \\ \hfill & \left.-b_1\lambda \alpha \sum _{m=0}^{\infty }{h}^m{(\sum _{k=0}^m{u}_k{u}_{{(m-k)}_x})}_x+c_1\mu \alpha \sum _{m=0}^{\infty }{h}^m{(\sum _{k=0}^m{u}_k{v}_{m-k})}_{xx}\right\}\hfill \\ \hfill & +\frac{h}{p^{\xi }}\mathcal{L}\left\{a_1\sum _{m=0}^{\infty }{h}^m{u}_{m_{xx}}+b_1\sum _{m=0}^{\infty }{h}^m\sum _{k=0}^m{u}_k{u}_{{(m-k)}_x}\right.\hfill \\ \hfill & \left.-c_1\sum _{m=0}^{\infty }{h}^m{(\sum _{k=0}^m{u}_k{v}_{m-k})}_x\right\}-\frac{[a_1{u}_{xx}+b_{1}u{u}_x-c_1{(uv)}_x](x,0)}{p^{\xi +1}}\hfill \\ \hfill & +\frac{u(x,0)}{p}+\frac{u_t(x,0)}{p^2}.\hfill \\ \hfill \sum _{m=0}^{\infty }{h}^m{V}_m(x,p)& =\frac{h}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2\sum _{m=0}^{\infty }{h}^m{v}_{m_{xx}}-a_2\mu \alpha \sum _{m=0}^{\infty }{h}^m{v}_{m_{xxx}}\right.\hfill \\ \hfill & \left.-b_2\lambda \alpha \sum _{m=0}^{\infty }{h}^m{(\sum _{k=0}^m{v}_k{v}_{{(m-k)}_x})}_x+c_2\mu \alpha \sum _{m=0}^{\infty }{h}^m{(\sum _{k=0}^m{u}_k{v}_{m-k})}_{xx}\right\}\hfill \\ \hfill & +\frac{h}{p^{\xi }}\mathcal{L}\left\{a_2\sum _{m=0}^{\infty }{h}^m{v}_{m_{xx}}+b_2\sum _{m=0}^{\infty }{h}^m\sum _{k=0}^m{v}_k{v}_{{(m-k)}_x}\right.\hfill \\ \hfill & \left.-c_2\sum _{m=0}^{\infty }{h}^m{(\sum _{k=0}^m{u}_k{v}_{m-k})}_x\right\}-\frac{[a_2{v}_{xx}+b_{2}v{v}_x-c_2{(uv)}_x](x,0)}{p^{\xi +1}}\hfill \\ \hfill & +\frac{v(x,0)}{p}+\frac{v_t(x,0)}{p^2}.\hfill \end{array}\end{array}$$

(10)

Now comparing the corresponding powers of h in (10), we get the following homotopies.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill h^0:U_0(x,p)& =\frac{u(x,0)}{p}+\frac{u_t(x,0)}{p^2}-\frac{1}{p^{\xi +1}}[a_1{u}_{xx}(x,0)+b_{1}u(x,0)u_x(x,0)\hfill \\ \hfill & -c_1{(u(x,0)v(x,0))}_x]\hfill \\ \hfill V_0(x,p)& =\frac{v(x,0)}{p}+\frac{v_t(x,0)}{p^2}-\frac{1}{p^{\xi +1}}[a_2{v}_{xx}(x,0)+b_{2}v(x,0)v_x(x,0)\hfill \\ \hfill & -c_2{(u(x,0)v(x,0))}_x],\hfill \\ \hfill h^1:U_1(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{u}_{0_{xx}}-a_1\mu \alpha u_{0_{xxx}}-b_1\lambda \alpha {(u_0{u}_{0_x})}_x+c_1\mu \alpha {(u_0{v}_0)}_{xx}\right\}\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_1{u}_{0_{xx}}+b_1{u}_0{u}_{0_x}-c_1{(u_0{v}_0)}_x\right\},\hfill \\ \hfill V_1(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{v}_{0_{xx}}-a_2\mu \alpha v_{0_{xxx}}-b_2\lambda \alpha {(v_0{v}_{0_x})}_x+c_2\mu \alpha {(u_0{v}_0)}_{xx}\right\},\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_2{v}_{0_{xx}}+b_2{v}_0{v}_{0_x}-c_2{(u_0{v}_0)}_x\right\},\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill h^2:U_2(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{u}_{1_{xx}}-a_1\mu \alpha u_{1_{xxx}}-b_1\lambda \alpha {(u_0{u}_{1_x}+u_1{u}_{0_x})}_x\right.\hfill \\ \hfill & \left.+c_1\mu \alpha {(u_0{v}_1+u_1{v}_0)}_{xx}\right\}\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_1{u}_{1_{xx}}+b_1(u_0{u}_{1_x}+u_1{u}_{0_x})-c_1{(u_{0v_1}+u_{1v_0})}_x\right\},\hfill \\ \hfill V_2(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{v}_{1_{xx}}-a_2\mu \alpha v_{1_{xxx}}-b_2\lambda \alpha {(v_0{v}_{1_x}+v_1{v}_{0_x})}_x\right.\hfill \\ \hfill & \left.+c_2\mu \alpha {(u_0{v}_1+u_1{v}_0)}_{xx}\right\}\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_2{v}_1{}_{xx}+b_2(v_0{v}_{1_x}+v_1{v}_{0_x})-c_2{(u_0{v}_1+u_1{v}_0)}_x,\right\}\hfill \end{array}\end{array}$$

and so on. In fact, we can rewrite the above system of equations as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U_0(x,p)& =\frac{u(x,0)}{p}+\frac{u_t(x,0)}{p^2}-\frac{1}{p^{\xi +1}}[a_1{u}_{xx}(x,0)+b_{1}u(x,0)u_x(x,0)\hfill \\ \hfill & -c_1{(u(x,0)v(x,0))}_x]\hfill \\ \hfill V_0(x,p)& =\frac{v(x,0)}{p}+\frac{v_t(x,0)}{p^2}-\frac{1}{p^{\xi +1}}[a_2{v}_{xx}(x,0)+b_{2}v(x,0)v_x(x,0)\hfill \\ \hfill & -c_2{(u(x,0)v(x,0))}_x],\hfill \end{array}\end{array}$$

(11)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U_{k+1}(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{u}_{k_{xx}}-a_1\mu \alpha u_{k_{xxx}}-b_1\lambda \alpha {(\sum _{j=0}^k{u}_j{u}_{{k-j}_x})}_x\right.\hfill \\ \hfill & \left.+c_1\mu \alpha {(\sum _{j=0}^k{u}_j{v}_{k-j})}_{xx}\right\}\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_1{u}_{k_{xx}}+b_1\sum _{j=0}^k{u}_j{u}_{{k-j}_x}-c_1{(\sum _{j=0}^k{u}_j{v}_{k-j})}_x\right\}\hfill \\ \hfill V_{k+1}(x,p)& =\frac{1}{p^{2\xi }}\mathcal{L}\left\{{\alpha }^2{v}_{k_{xx}}-a_2\mu \alpha v_{k_{xxx}}-b_2\lambda \alpha {(\sum _{j=0}^k{v}_j{v}_{{k-j}_x})}_x\right.\hfill \\ \hfill & \left.+c_2\mu \alpha {(\sum _{j=0}^k{u}_j{v}_{k-j})}_{xx}\right\}\hfill \\ \hfill & +\frac{1}{p^{\xi }}\mathcal{L}\left\{a_2{v}_{k_{xx}}+b_2\sum _{j=0}^k{v}_j{v}_{{k-j}_x}-c_2{(\sum _{j=0}^k{u}_j{v}_{k-j})}_x\right\}\hfill \end{array}\end{array}$$

(12)

for $k=0,1,2,\cdots$

Now applying the inverse laplace transform in each of the above equations, we obtain $u_0,v_0,u_1,v_1,u_2,v_2\dots$ and so on.

Hence, we get an approximate solution of Equation (2) as

$$u(x,t)=u_0(x,t)+u_1(x,t)+u_2(x,t)+\cdots$$

and

$$v(x,t)=v_0(x,t)+v_1(x,t)+v_2(x,t)+\cdots$$

5. Convergence Analysis

We discuss the convergence of the solution of given problem in the following theorem.

Theorem 1.

Let $u_n(x,t),v_n(x,t),u(x,t)$ and $v(x,t)$ be in the Banach space $C(\overline{\Omega }\times [0,T])$ as defined by Equation (9). If there exist constants $0<{\beta }_u<1,0<{\beta }_v<1$ such that $u_n(x,t)\le {\beta }_u{u}_{n-1}(x,t)$, $v_n(x,t)\le {\beta }_v{v}_{n-1}(x,t)$ for all $n\in \mathbb{N}$, then the infinite series ${\sum }_{k=0}^{\infty }{u}_k(x,t)$ and ${\sum }_{k=0}^{\infty }{v}_k(x,t)$ converge to the solution $u(x,t)$ and $v(x,t)$ of the problem (2).

Proof. 

Let ${\mathcal{S}}_n$ and ${\mathcal{R}}_n$ be the sequence of partial sums of the series ${\sum }_{k=0}^{\infty }{u}_k(x,t)$ and ${\sum }_{k=0}^{\infty }{v}_k(x,t)$ respectively. For all $n\in \mathbb{N}$, we have

$$\begin{array}{c}\hfill {\mathcal{S}}_n(x,t)-{\mathcal{S}}_{n-1}(x,t)=u_n(x,t)\le {\beta }_u{u}_{n-1}(x,t)\le {\beta }_u^2{u}_{n-2}(x,t)\le \dots \le {\beta }_u^n{u}_0(x,t),\end{array}$$

So that

$$\begin{array}{cc}\hfill {\mathcal{S}}_n(x,t)-{\mathcal{S}}_m(x,t)& =({\mathcal{S}}_n(x,t)-{\mathcal{S}}_{n-1}(x,t))+({\mathcal{S}}_{n-1}(x,t)-{\mathcal{S}}_{n-2}(x,t))\hfill \\ \hfill & +\dots +({\mathcal{S}}_{m+1}(x,t)-{\mathcal{S}}_m(x,t))\hfill \\ \hfill & =u_n(x,t)+u_{n-1}(x,t)+\dots +u_{m+1}(x,t)\hfill \\ \hfill & \le {\beta }_u^{m+1}(1+{\beta }_u+{\beta }_u^2+\dots +{\beta }_u^{n-m-1})u_0(x,t),\hfill \end{array}$$

which implies

$$\begin{array}{c}\hfill |{\mathcal{S}}_n(x,t)-{\mathcal{S}}_m(x,t)|\le {\beta }_u^{m+1}{\displaystyle \frac{(1-{\beta }_u^{n-m})}{(1-{\beta }_u)}}\underset{(x,t)\in \overline{\Omega }\times [0,T]}{max}|u_0(x,t)|.\end{array}$$

(13)

Now, $0<{\beta }_u<1$ implies that $1-{\beta }_u^{n-m}<1$, then

$$\parallel {\mathcal{S}}_n-{\mathcal{S}}_m\parallel \le {\displaystyle \frac{{\beta }_u^{m+1}}{(1-{\beta }_u)}}\underset{(x,t)\in \overline{\Omega }\times [0,T]}{max}|v_0(x,t)|.$$

Since, $v_0$ is bounded, we get

$$\underset{n,m\to \infty }{lim}\parallel {\mathcal{S}}_n-{\mathcal{S}}_m\parallel =0.$$

Thus the sequence $({\mathcal{S}}_n)$ is Cauchy in the Banach space $C(\overline{\Omega }\times [0,T])$ and hence convergent. Similarly, we can show that the sequence $({\mathcal{R}}_n)$ is convergent. Hence, that the infinite series ${\sum }_{k=0}^{\infty }{u}_k(x,t)$ and ${\sum }_{k=0}^{\infty }{v}_k(x,t)$ converge to $u(x,t)$ and $v(x,t)$ respectively. □

6. An Illustrative Example

We consider the nonlinear coupled fractional partial differential Equation (3) along with the initial conditions given as

$$u(x,0)=v(x,0)=sinx,u_x(x,0)=v_x(x,0)=cosx,$$

$$u_{xx}(x,0)=v_{xx}(x,0)=-sinx,u_t(x,0)=v_t(x,0)=-sinx.$$

Now solving the system (3) by Laplace Homotopy Perturbation Method, we have

$$\begin{array}{cc}\hfill U_0(x,p)& =\frac{sinx}{p}-\frac{sinx}{p^2}-\frac{-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x}{p^{\xi +1}}\hfill \\ \hfill V_0(x,p)& =\frac{sinx}{p}-\frac{sinx}{p^2}-\frac{-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x}{p^{\xi +1}}\hfill \end{array}$$

Taking inverse Laplace transform of above equations, we get

$$\begin{array}{cc}\hfill u_0(x,t)& =sinx-tsinx-\frac{t^{\xi }}{\Gamma (\xi +1)}(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)\hfill \\ \hfill v_0(x,t)& =sinx-tsinx-\frac{t^{\xi }}{\Gamma (\xi +1)}(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \end{array}$$

Next, we have

$$\begin{array}{cc}\hfill U{}_1& (x,p)={\alpha }^2\left\{\frac{-sinx}{p^{2\xi +1}}+\frac{sinx}{p^{2\xi +2}}-\frac{a_{1}sinx+(4c_1-2b_1)sin2x}{p^{3\xi +1}}\right\}\hfill \\ \hfill & -a_1\mu \alpha \left\{\frac{-cosx}{p^{2\xi +1}}+\frac{cosx}{p^{2\xi +2}}-\frac{a_{1}cosx+2(4c_1-2b_1)cos2x}{p^{3\xi +1}}\right\}\hfill \\ \hfill & -b_1\lambda \alpha \left\{cos2x(\frac{1}{p^{2\xi +1}}-\frac{2}{p^{2\xi +2}}+\frac{2}{p^{2\xi +3}})+(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-a_{1}cos2x\right.\hfill \\ \hfill & +b_1({cos}^{3}x-2{sin}^{2}xcosx)-c_1(2cos2xcosx-sin2xsinx))\hfill \\ \hfill & +(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-a_{1}cos2x+(b_1-2c_1)(cos2xcosx-2sin2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{4\xi +1}}[{(-a_{1}cosx+b_{1}cos2x-2c_{1}cos2x)}^2\hfill \\ \hfill & +\left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)(a_{1}sinx-2b_{1}sin2x+4c_{1}sin2x)]\right\}\hfill \\ \hfill & +c_1\mu \alpha \left\{2cos2x(\frac{1}{p^{2\xi +1}}-\frac{2}{p^{2\xi +2}}+\frac{2}{p^{2\xi +3}})+(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-2a_{1}cos2x\right.\hfill \\ \hfill & +b_1(2{cos}^{3}x-7{sin}^{2}xcosx)-c_1(4cos2xcosx-5sin2xsinx))\hfill \\ \hfill & +(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-2a_{2}cos2x+b_2(2{cos}^{3}x-7{sin}^{2}xcosx)\hfill \\ \hfill & -c_2(4cos2xcosx-5sin2xsinx))+\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{4\xi +1}}\hfill \\ \hfill & [2(-a_{1}cosx+(b_1-2c_1)cos2x)(-a_{2}cosx+(b_2-2c_2)cos2x)\hfill \\ \hfill & +(-a_{1}sinx-2(b_1-2c_1)sin2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & +\left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)(a_{2}sinx-2(b_2-2c_2)sin2x)]\right\}\hfill \\ \hfill & +a_1\left\{\frac{-sinx}{p^{\xi +1}}+\frac{sinx}{p^{\xi +2}}-\frac{a_{1}sinx+(4c_1-2b_1)sin2x}{p^{2\xi +1}}\right\}\hfill \\ \hfill & +b_1\left\{cosxsinx(\frac{1}{p^{\xi +1}}-\frac{2}{p^{\xi +2}}+\frac{2}{p^{\xi +3}})+(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})(-a_{1}sinxcosx\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +b_{1}sinx{cos}^{2}x-c_{1}sin2xcosx)\hfill \\ \hfill & +(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})(-a_{1}sinxcosx+(b_1-2c_1)(cos2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{3\xi +1}}[(-a_{1}cosx+b_{1}cos2x-2c_{1}cos2x)\hfill \\ \hfill & \left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)]\right\}\hfill \\ \hfill & -c_1\left\{sin2x(\frac{1}{p^{\xi +1}}-\frac{2}{p^{\xi +2}}+\frac{2}{p^{\xi +3}})+(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})(-a_{1}sin2x\right.\hfill \\ \hfill & +b_1(2sinx{cos}^{2}x-{sin}^{3}x)-c_1(2cos2xsinx+sin2xcosx))\hfill \\ \hfill & +(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})(-a_{2}sin2x+b_2(2sinx{cos}^{2}x-{sin}^{3}x)\hfill \\ \hfill & -c_2(2cos2xsinx+sin2xcosx))+\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{3\xi +1}}\hfill \\ \hfill & [(-a_{1}cosx+(b_1-2c_1)cos2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & \left.(-a_{2}cosx+(b_2-2c_2)cos2x)(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)]\right\}\hfill \end{array}$$

$$\begin{array}{cc}\hfill V{}_1& (x,p)={\alpha }^2\left\{\frac{-sinx}{p^{2\xi +1}}+\frac{sinx}{p^{2\xi +2}}-\frac{a_{2}sinx+(4c_2-2b_2)sin2x}{p^{3\xi +1}}\right\}\hfill \\ \hfill & -a_2\mu \alpha \left\{\frac{-cosx}{p^{2\xi +1}}+\frac{cosx}{p^{2\xi +2}}-\frac{a_{2}cosx+2(4c_2-2b_2)cos2x}{p^{3\xi +1}}\right\}\hfill \\ \hfill & -b_2\lambda \alpha \left\{cos2x(\frac{1}{p^{2\xi +1}}-\frac{2}{p^{2\xi +2}}+\frac{2}{p^{2\xi +3}})+(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-a_{2}cos2x\right.\hfill \\ \hfill & +b_2({cos}^{3}x-2{sin}^{2}xcosx)-c_2(2cos2xcosx-sin2xsinx))\hfill \\ \hfill & +(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-a_{2}cos2x+(b_2-2c_2)(cos2xcosx-2sin2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{4\xi +1}}[{(-a_{2}cosx+b_{2}cos2x-2c_{2}cos2x)}^2\hfill \\ \hfill & +\left.(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)(a_{2}sinx-2b_{2}sin2x+4c_{2}sin2x)]\right\}\hfill \\ \hfill & +c_2\mu \alpha \left\{2cos2x(\frac{1}{p^{2\xi +1}}-\frac{2}{p^{2\xi +2}}+\frac{2}{p^{2\xi +3}})+(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-2a_{1}cos2x\right.\hfill \\ \hfill & +b_1(2{cos}^{3}x-7{sin}^{2}xcosx)-c_1(4cos2xcosx-5sin2xsinx))\hfill \\ \hfill & +(\frac{\xi +1}{p^{3\xi +2}}-\frac{1}{p^{3\xi +1}})(-2a_{2}cos2x+b_2(2{cos}^{3}x-7{sin}^{2}xcosx)\hfill \\ \hfill & -c_2(4cos2xcosx-5sin2xsinx))+\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{4\xi +1}}\hfill \\ \hfill & [2(-a_{1}cosx+(b_1-2c_1)cos2x)(-a_{2}cosx+(b_2-2c_2)cos2x)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +(-a_{1}sinx-2(b_1-2c_1)sin2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & +\left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)(a_{2}sinx-2(b_2-2c_2)sin2x)]\right\}\hfill \\ \hfill & +a_2\left\{\frac{-sinx}{p^{\xi +1}}+\frac{sinx}{p^{\xi +2}}-\frac{a_{2}sinx+(4c_2-2b_2)sin2x}{p^{2\xi +1}}\right\}\hfill \\ \hfill & +b_2\left\{cosxsinx(\frac{1}{p^{\xi +1}}-\frac{2}{p^{\xi +2}}+\frac{2}{p^{\xi +3}})+(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})\right.\hfill \\ \hfill & (-a_{2}sinxcosx+b_{2}sinx{cos}^{2}x-c_{2}sin2xcosx)\hfill \\ \hfill & +(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})(-a_{2}sinxcosx+(b_2-2c_2)(cos2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{3\xi +1}}[(-a_{2}cosx+b_{2}cos2x-2c_{2}cos2x)\hfill \\ \hfill & \left.(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)]\right\}\hfill \\ \hfill & -c_1\left\{sin2x(\frac{1}{p^{\xi +1}}-\frac{2}{p^{\xi +2}}+\frac{2}{p^{\xi +3}})+(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})(-a_{1}sin2x\right.\hfill \\ \hfill & +b_1(2sinx{cos}^{2}x-{sin}^{3}x)-c_1(2cos2xsinx+sin2xcosx))\hfill \\ \hfill & +(\frac{\xi +1}{p^{2\xi +2}}-\frac{1}{p^{2\xi +1}})(-a_{2}sin2x+b_2(2sinx{cos}^{2}x-{sin}^{3}x)\hfill \\ \hfill & -c_2(2cos2xsinx+sin2xcosx))+\frac{\Gamma (2\xi +1)}{\Gamma {(\xi +1)}^2{p}^{3\xi +1}}\hfill \\ \hfill & [(-a_{1}cosx+(b_1-2c_1)cos2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & \left.(-a_{2}cosx+(b_2-2c_2)cos2x)(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)]\right\}\hfill \end{array}$$

Taking inverse Laplace transform, we get

$$\begin{array}{cc}\hfill & u_1(x,t)\hfill \\ \hfill & ={\alpha }^2\left\{\frac{-t^{2\xi }sinx}{\Gamma (2\xi +1)}+\frac{t^{2\xi +1}sinx}{\Gamma 2\xi +2}-(a_{1}sinx+(4c_1-2b_1)sin2x)\frac{t^{3\xi }}{\Gamma (3\xi +1)}\right\}\hfill \\ \hfill & -a_1\mu \alpha \left\{\frac{-t^{2\xi }cosx}{\Gamma (2\xi +1)}+\frac{t^{2\xi +1}cosx}{\Gamma 2\xi +2}-(a_{1}cosx+(4c_1-2b_1)cos2x)\right.\hfill \\ \hfill & \left.\frac{t^{3\xi }}{\Gamma (3\xi +1)}\right\}\hfill \\ \hfill & -b_1\lambda \alpha \left\{cos2x(\frac{t^{2\xi }}{\Gamma (2\xi +1)}-\frac{2t^{2\xi +1}}{\Gamma (2\xi +2)}+\frac{2t^{2\xi +2}}{\Gamma (2\xi +3)})\right.\hfill \\ \hfill & +(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})(-a_{1}cos2x+b_1({cos}^{3}x-2{sin}^{2}xcosx)\hfill \\ \hfill & -c_1(2cos2xcosx-sin2xsinx))+(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})\hfill \end{array}$$

$$\begin{array}{cc}\hfill & (-a_{1}cos2x+(b_1-2c_1)(cos2xcosx-2sin2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)t^{4\xi }}{\Gamma {(\xi +1)}^2\Gamma (4\xi +1)}[{(-a_{1}cosx+b_{1}cos2x-2c_{1}cos2x)}^2\hfill \\ \hfill & +\left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)(a_{1}sinx-2b_{1}sin2x+4c_{1}sin2x)]\right\}\hfill \\ \hfill & +c_1\mu \alpha \left\{2cos2x(\frac{t^{2\xi }}{\Gamma (2\xi +1)}-\frac{2t^{2\xi +1}}{\Gamma (2\xi +2)}+\frac{2t^{2\xi +2}}{\Gamma (2\xi +3)})\right.\hfill \\ \hfill & +(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})(-2a_{1}cos2x+b_1(2{cos}^{3}x-7{sin}^{2}xcosx)\hfill \\ \hfill & -c_1(4cos2xcosx-5sin2xsinx))\hfill \\ \hfill & +(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})(-2a_{2}cos2x+b_2(2{cos}^{3}x-7{sin}^{2}xcosx)\hfill \\ \hfill & -c_2(4cos2xcosx-5sin2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)t^{4\xi }}{\Gamma {(\xi +1)}^2\Gamma (4\xi +1)}[2(-a_{1}cosx+(b_1-2c_1)cos2x)\hfill \\ \hfill & (-a_{2}cosx+(b_2-2c_2)cos2x)\hfill \\ \hfill & +(-a_{1}sinx-2(b_1-2c_1)sin2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & +\left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)(a_{2}sinx-2(b_2-2c_2)sin2x)]\right\}\hfill \\ \hfill & +a_1\left\{\frac{-t^{\xi }sinx}{\Gamma (\xi +1)}+\frac{t^{\xi +1}sinx}{\Gamma (\xi +2)}-\frac{t^{2\xi }}{\Gamma (2\xi +1)}(a_{1}sinx+(4c_1-2b_1)sin2x)\right\}\hfill \\ \hfill & +b_1\left\{cosxsinx(\frac{t^{\xi }}{\Gamma (\xi +1)}-\frac{2t^{\xi +1}}{\Gamma (\xi +2)}+\frac{2p^{\xi +2}}{\Gamma (\xi +3)})+\right.\hfill \\ \hfill & (\frac{(\xi +1)t^{2\xi +1}}{\Gamma (2\xi +2)}-\frac{t^{2\xi }}{\Gamma (2\xi +1)})(-a_{1}sinxcosx+b_{1}sinx{cos}^{2}x-c_{1}sin2xcosx)\hfill \\ \hfill & +(\frac{(\xi +1)t^{2\xi +1}}{\Gamma (2\xi +2)}-\frac{t^{2\xi }}{\Gamma (2\xi +1)})(-a_{1}sinxcosx+(b_1-2c_1)(cos2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)t^{3\xi }}{\Gamma {(\xi +1)}^2\Gamma (3\xi +1)}[(-a_{1}cosx+b_{1}cos2x-2c_{1}cos2x)\hfill \\ \hfill & \left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)]\right\}\hfill \\ \hfill & -c_1\left\{sin2x(\frac{t^{\xi }}{\Gamma (\xi +1)}-\frac{2t^{\xi +1}}{\Gamma (\xi +2)}+\frac{2p^{\xi +2}}{\Gamma (\xi +3)})(-a_{1}sin2x\right.\hfill \\ \hfill & +b_1(2sinx{cos}^{2}x-{sin}^{3}x)-c_1(2cos2xsinx+sin2xcosx))\hfill \\ \hfill & +(\frac{(\xi +1)t^{2\xi +1}}{\Gamma (2\xi +2)}-\frac{t^{2\xi }}{\Gamma (2\xi +1)})(-a_{2}sin2x+b_2(2sinx{cos}^{2}x-{sin}^{3}x)\hfill \\ \hfill & -c_2(2cos2xsinx+sin2xcosx))+\frac{\Gamma (2\xi +1)t^{3\xi }}{\Gamma {(\xi +1)}^2\Gamma (3\xi +1)}\hfill \\ \hfill & [(-a_{1}cosx+(b_1-2c_1)cos2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & \left.(-a_{2}cosx+(b_2-2c_2)cos2x)(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)]\right\}\hfill \end{array}$$

$$\begin{array}{cc}\hfill v_1& (x,t)\hfill \\ \hfill =& {\alpha }^2\left\{\frac{-t^{2\xi }sinx}{\Gamma (2\xi +1)}+\frac{t^{2\xi +1}sinx}{\Gamma 2\xi +2}-\frac{(a_{2}sinx+(4c_2-2b_2)sin2x)t^{3\xi }}{\Gamma (3\xi +1)}\right\}\hfill \\ \hfill & -a_2\mu \alpha \left\{\frac{-t^{2\xi }cosx}{\Gamma (2\xi +1)}+\frac{t^{2\xi +1}cosx}{\Gamma 2\xi +2}-\frac{(a_{2}cosx+(4c_2-2b_2)cos2x)t^{3\xi }}{\Gamma (3\xi +1)}\right\}\hfill \\ \hfill & -b_2\lambda \alpha \left\{cos2x(\frac{t^{2\xi }}{\Gamma (2\xi +1)}-\frac{2t^{2\xi +1}}{\Gamma (2\xi +2)}+\frac{2t^{2\xi +2}}{\Gamma (2\xi +3)})\right.\hfill \\ \hfill & +(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})(-a_{2}cos2x+b_2({cos}^{3}x-2{sin}^{2}xcosx)\hfill \\ \hfill & -c_2(2cos2xcosx-sin2xsinx))+(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})\hfill \\ \hfill & (-a_{2}cos2x+(b_2-2c_2)(cos2xcosx-2sin2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)t^{4\xi }}{\Gamma {(\xi +1)}^2\Gamma (4\xi +1)}[{(-a_{2}cosx+b_{2}cos2x-2c_{2}cos2x)}^2\hfill \\ \hfill +& \left.(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)(a_{2}sinx-2b_{2}sin2x+4c_{2}sin2x)]\right\}\hfill \\ \hfill & +c_2\mu \alpha \left\{2cos2x(\frac{t^{2\xi }}{\Gamma (2\xi +1)}-\frac{2t^{2\xi +1}}{\Gamma (2\xi +2)}+\frac{2t^{2\xi +2}}{\Gamma (2\xi +3)})\right.\hfill \\ \hfill & +(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})(-2a_{1}cos2x+b_1(2{cos}^{3}x-7{sin}^{2}xcosx)\hfill \\ \hfill & -c_1(4cos2xcosx-5sin2xsinx))\hfill \\ \hfill & +(\frac{(\xi +1)t^{3\xi +1}}{\Gamma (3\xi +2)}-\frac{t^{3\xi }}{\Gamma (3\xi +1)})(-2a_{2}cos2x+b_2(2{cos}^{3}x-7{sin}^{2}xcosx)\hfill \\ \hfill & -c_2(4cos2xcosx-5sin2xsinx))+\frac{\Gamma (2\xi +1)t^{4\xi }}{\Gamma {(\xi +1)}^2\Gamma (4\xi +1)}\hfill \\ \hfill & [2(-a_{1}cosx+(b_1-2c_1)cos2x)(-a_{2}cosx+(b_2-2c_2)cos2x)\hfill \\ \hfill & +(-a_{1}sinx-2(b_1-2c_1)sin2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & +\left.(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)(a_{2}sinx-2(b_2-2c_2)sin2x)]\right\}\hfill \\ \hfill & +a_2\left\{\frac{-t^{\xi }sinx}{\Gamma (\xi +1)}+\frac{t^{\xi +1}sinx}{\Gamma (\xi +2)}-\frac{t^{2\xi }}{\Gamma (2\xi +1)}(a_{2}sinx+(4c_2-2b_2)sin2x)\right\}\hfill \\ \hfill & +b_2\left\{cosxsinx(\frac{t^{\xi }}{\Gamma (\xi +1)}-\frac{2t^{\xi +1}}{\Gamma (\xi +2)}+\frac{2t^{\xi +2}}{\Gamma (\xi +3)})+(\frac{(\xi +1)t^{2\xi +1}}{\Gamma (2\xi +2)}\right.\hfill \\ \hfill & -\frac{t^{2\xi }}{\Gamma (2\xi +1)})(-a_{2}sinxcosx+b_{2}sinx{cos}^{2}x-c_{2}sin2xcosx)\hfill \\ \hfill & +(\frac{(\xi +1)t^{2\xi +1}}{\Gamma (2\xi +2)}-\frac{t^{2\xi }}{\Gamma (2\xi +1)})(-a_{2}sinxcosx+(b_2-2c_2)(cos2xsinx))\hfill \\ \hfill & +\frac{\Gamma (2\xi +1)t^{3\xi }}{\Gamma {(\xi +1)}^2\Gamma (3\xi +1)}[(-a_{2}cosx+b_{2}cos2x-2c_{2}cos2x)\hfill \\ \hfill & \left.(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)]\right\}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & -c_2\left\{sin2x(\frac{t^{\xi }}{\Gamma (\xi +1)}-\frac{2t^{\xi +1}}{\Gamma (\xi +2)}+\frac{2p^{\xi +2}}{\Gamma (\xi +3)})(-a_{1}sin2x\right.\hfill \\ \hfill & +b_1(2sinx{cos}^{2}x-{sin}^{3}x)-c_1(2cos2xsinx+sin2xcosx))\hfill \\ \hfill & +(\frac{(\xi +1)t^{2\xi +1}}{\Gamma (2\xi +2)}-\frac{t^{2\xi }}{\Gamma (2\xi +1)})(-a_{2}sin2x+b_2(2sinx{cos}^{2}x-{sin}^{3}x)\hfill \\ \hfill & -c_2(2cos2xsinx+sin2xcosx))+\frac{\Gamma (2\xi +1)t^{3\xi }}{\Gamma {(\xi +1)}^2\Gamma (3\xi +1)}\hfill \\ \hfill & [(-a_{1}cosx+(b_1-2c_1)cos2x)(-a_{2}sinx+b_{2}sinxcosx-c_{2}sin2x)\hfill \\ \hfill & \left.(-a_{2}cosx+(b_2-2c_2)cos2x)(-a_{1}sinx+b_{1}sinxcosx-c_{1}sin2x)]\right\}\hfill \end{array}$$

Thus, we can find the rest of the terms in a similar manner.

Hence, the approximate solution is given by $u(x,t)=u_0(x,t)+u_1(x,t)+\dots$ and $v(x,t)=v_0(x,t)+v_1(x,t)+\dots$.

As we can see that the evaluation of the terms $u_1,v_1,u_2,v_2,\dots$ becomes cumbersome, we further simplify the fractional two-mode coupled burgers equations by taking $\alpha =0, a_1=a_2=1, b_1=b_2=2, c_1=c_2=1$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_t^{2\xi }u& ={\mathcal{D}}_t^{\xi }(u_{xx}+2u{u}_x-{(uv)}_x)\hfill \\ \hfill D_t^{2\xi }v& ={\mathcal{D}}_t^{\xi }(v_{xx}+2v{v}_x-{(uv)}_x)\hfill \end{array}\end{array}$$

(14)

with initial conditions

$$u(x,0)=v(x,0)=sinx,u_x(x,0)=v_x(x,0)=cosx,$$

$$u_{xx}(x,0)=v_{xx}(x,0)=-sinx,u_t(x,0)=v_t(x,0)=-sinx.$$

Applying LHPM, we have

$$\begin{array}{cc}\hfill h^0:U_0(x,p)& =\frac{sinx}{p}-\frac{sinx}{p^2}-\frac{-sinx}{p^{\xi +1}}\hfill \\ \hfill & =\frac{sinx}{p}-\frac{sinx}{p^2}+\frac{sinx}{p^{\xi +1}}\hfill \\ \hfill h^1:U_1(x,p)& =\frac{1}{p^{\xi }}\mathcal{L}\left\{u_{0_{xx}}+2u_0{u}_{0_x}-{(u_0{v}_0)}_x\right\}\hfill \\ \hfill & =\frac{1}{p^{\xi }}\mathcal{L}\left\{-sinx+tsinx-\frac{t^{\xi }sinx}{\Gamma (\xi +1)}\right\}\hfill \\ \hfill & =-\frac{sinx}{p^{\xi +1}}+\frac{sinx}{p^{\xi +2}}-\frac{sinx}{p^{2\xi +1}}\hfill \\ \hfill h^2:U_2(x,p)& =\frac{1}{p^{\xi }}\mathcal{L}\left\{u_{1_{xx}}+2{(u_0{u}_1)}_x-{(u_0{v}_1+u_1{v}_0)}_x\right\}\hfill \\ \hfill & =\frac{1}{p^{\xi }}\mathcal{L}\left\{\frac{t^{\xi }sinx}{\Gamma (\xi +1)}-\frac{t^{\xi +1}sinx}{\Gamma (\xi +2)}+\frac{t^{2\xi }sinx}{\Gamma (2\xi +1)}\right\}\hfill \\ \hfill & =\frac{sinx}{p^{2\xi +1}}-\frac{cosx}{p^{2\xi +2}}+\frac{sinx}{p^{3\xi +1}}\hfill \end{array}$$

and so on. Now we apply inverse Laplace transform in each of the above equations to get the $u_0,u_1,u_2,\cdots$ as follows,

$$\begin{array}{cc}\hfill u_0(x,t)& =sinx-tsinx+\frac{t^{\xi }sinx}{\Gamma (\xi +1)}\hfill \\ \hfill u_1(x,t)& ={\mathcal{L}}^{-1}\left\{-\frac{sinx}{p^{\xi +1}}+\frac{sinx}{p^{\xi +2}}-\frac{sinx}{p^{2\xi +1}}\right\}\hfill \\ \hfill & =-\frac{t^{\xi }sinx}{\Gamma (\xi +1)}+\frac{t^{\xi +1}sinx}{\Gamma (\xi +2)}-\frac{t^{2\xi }sinx}{\Gamma (2\xi +1)}\hfill \\ \hfill u_2(x,t)& ={\mathcal{L}}^{-1}\left\{\frac{sinx}{p^{2\xi +1}}-\frac{sinx}{p^{2\xi +2}}+\frac{sinx}{p^{3\xi +1}}\right\}\hfill \\ \hfill & =\frac{t^{2\xi }sinx}{\Gamma (2\xi +1)}-\frac{t^{2\xi +1}sinx}{\Gamma (2\xi +2)}+\frac{t^{3\xi }sinx}{\Gamma (3\xi +1)}\hfill \end{array}$$

and so on. Thus, the approximate solution is given by

$$\begin{array}{cc}\hfill u_0(x,t)+u_1(x,t)+u_2(x,t)+\dots & =sinx-tsinx+\frac{t^{\xi }sinx}{\Gamma (\xi +1)}\hfill \\ \hfill & -\frac{t^{\xi }sinx}{\Gamma (\xi +1)}+\frac{t^{\xi +1}sinx}{\Gamma (\xi +2)}-\frac{t^{2\xi }sinx}{\Gamma (2\xi +1)}\hfill \\ \hfill & +\frac{t^{2\xi }sinx}{\Gamma (2\xi +1)}-\frac{t^{2\xi +1}sinx}{\Gamma (2\xi +2)}+\frac{t^{3\xi }sinx}{\Gamma (3\xi +1)}\hfill \\ \hfill & +\dots \hfill \end{array}$$

Following the similar arguments give us

$$\begin{array}{cc}\hfill v_0(x,t)+v_1(x,t)+v_2(x,t)+\dots & =sinx-tsinx+\frac{t^{\xi }sinx}{\Gamma (\xi +1)}\hfill \\ \hfill & -\frac{t^{\xi }sinx}{\Gamma (\xi +1)}+\frac{t^{\xi +1}sinx}{\Gamma (\xi +2)}-\frac{t^{2\xi }sinx}{\Gamma (2\xi +1)}\hfill \\ \hfill & +\frac{t^{2\xi }sinx}{\Gamma (2\xi +1)}-\frac{t^{2\xi +1}sinx}{\Gamma (2\xi +2)}+\frac{t^{3\xi }sinx}{\Gamma (3\xi +1)}\hfill \\ \hfill & +\dots \hfill \end{array}$$

We note that the approximate solutions $u(x,t)$ and $v(x,t)$ both tend to $sinx{e}^{-t}$ as $\xi \to 1$ which is the exact solution of the standard coupled burgers equation.

The graphical representation of an approximate solutions for different values of $\xi$ are given in Figure 1. Furthermore, the comparison of Figure 1 and Figure 2 shows that the approximate solutions calculated by LHPM is very close to the exact solution as $\xi$ is very close to 1 because both graphs are similar.

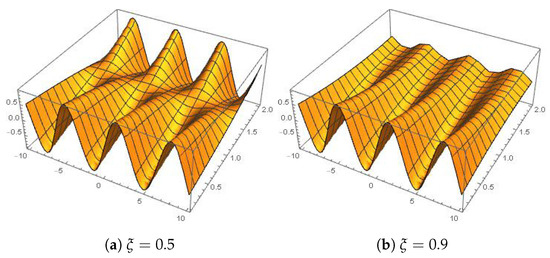
Figure 1. Approximate solutions for $\xi =0.5$ and $\xi =0.9$.

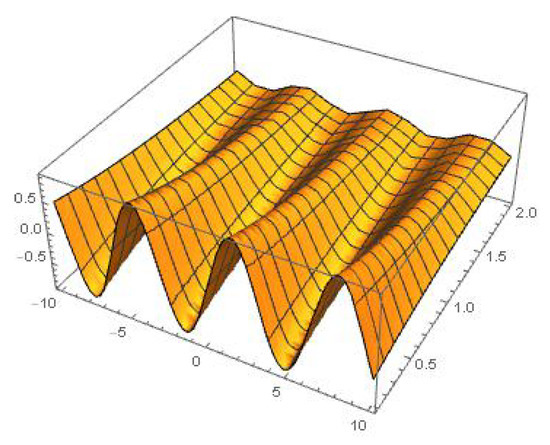
Figure 2. Exact solution.

7. Conclusions

In this paper, we have solved time-fractional two-mode coupled Burgers equations using Laplace homotopy perturbation method. An illustrative example has been solved with initial conditions. It has been shown by a well-known example that the given method is very efficient and reliable.