Monotone Iterative and Upper–Lower Solution Techniques for Solving the Nonlinear ψ−Caputo Fractional Boundary Value Problem
Abstract
:1. Introduction
2. Preliminaries
3. Main Results
- (H1)
- , such that and are the l-solution and u-solution of problem (3), respectively, with ;
- (H2)
- ∃ a function such that , for ;
- (H3)
- and .
4. Some Relevant Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Supporting Informations
| Algorithm A1 MATLAB lines for the calculation of in Equation (4). |
| 1: LSfractionalintegral
Require: 2: syms ; 3: E = ; 4: mathbbI = ; 5: return mathbbI |
| Algorithm A2 MATLAB lines for the calculation of in Equation (5). |
| 1: LSfractionalderivative |
| Require |
| 2: syms ; |
| 3: ; |
| 4: ; |
| 5: ; |
| 6: ; |
| 7: ; |
| 8: mathbbD = F; |
| 9: return mathbbD |
| Algorithm A3 MATLAB lines for the calculation of in Equation (6). |
| 1: LSCaputofractionalderivative |
| Require: |
| 2: syms ; |
| 3: ; |
| 4: if then |
| 5: ; |
| 6: ; |
| 7: else |
| 8: ; |
| 9: ; |
| 10: end if |
| 11: mathbbD = E; |
| 12: return mathbbD |
| Algorithm A4 MATLAB lines for the calculation of and in Example 1. |
| Require: |
| 1: syms ; |
| 2: clear; |
| 3: format long; |
| 4: syms ; |
| 5: ; ; ; ; ; |
| 6: ; ; |
| 7: ; ; |
| 8: ; |
| 9: |
| 10: ; ; |
| 11: ; |
| 12: ; ; |
| 13: for i = 1 to 3 do |
| 14: ; |
| 15: ; |
| 16: ; |
| 17: ; |
| 18: ; |
| 19: ; |
| 20: ; |
| 21: ; |
| 22: ; |
| 23: ; |
| 24: ; |
| 25: ; |
| 26: ; |
| 27: while do |
| 28: ; |
| 29: ; |
| 30: ; |
| 31: ; |
| 32: ; |
| 33: ; |
| 34: ; |
| 35: ; |
| 36: ; |
| 37: ; |
| 38: ; |
| 39: end while |
| 40: ; |
| 41: end for |
| 42: return |
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Oldham, K.B. Fractional differential equations in electrochemistry. Adv. Eng. Softw. 2010, 41, 9–12. [Google Scholar] [CrossRef]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus-Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Application of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volune 204. [Google Scholar]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef] [Green Version]
- Alzabut, J.; Selvam, A.G.M.; El-Nabulsi, R.A.; Dhakshinamoorthy, V.; Samei, M.E. Asymptotic Stability of Nonlinear Discrete Fractional Pantograph Equations with Non-Local Initial Conditions. Symmetry 2021, 13, 473. [Google Scholar] [CrossRef]
- Almeida, R.; Malinowska, A.B.; Monteiro, M.T.T. Fractional differential equations with a Caputo derivative with respect to a kernel function and their applications. Math. Meth. Appl. Sci. 2018, 41, 336–352. [Google Scholar] [CrossRef] [Green Version]
- Almeida, R.; Jleli, M.; Samet, B. A numerical study of fractional relaxation-oscillation equations involving ψ-Caputo fractional derivative. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 2019, 113, 1873–1891. [Google Scholar] [CrossRef]
- Baitiche, Z.; Derbazi, C.; Alzabut, J.; Samei, M.E.; Kaabar, M.K.A.; Siri, Z. Monotone Iterative Method for Langevin Equation in Terms of ψ-Caputo Fractional Derivative and Nonlinear Boundary Conditions. Fractal Fract. 2021, 5, 81. [Google Scholar] [CrossRef]
- Samei, M.; Hedayati, V.; Rezapour, S. Existence results for a fraction hybrid differential inclusion with Caputo-Hadamard type fractional derivative. Adv. Differ. Equations 2019, 2019, 163. [Google Scholar] [CrossRef]
- Adjabi, Y.; Samei, M.E.; Matar, M.M.; Alzabut, J. Langevin differential equation in frame of ordinary and Hadamard fractional derivatives under three point boundary conditions. AIMS Math. 2021, 6, 2796–2843. [Google Scholar] [CrossRef]
- Samet, B.; Aydi, H. Lyapunov-type inequalities for an anti-periodic fractional boundary value problem involving ψ-Caputo fractional derivative. J. Inequal. Appl. 2018, 2018, 286. [Google Scholar] [CrossRef] [Green Version]
- Abdo, M.S.; Panchal, S.K.; Saeed, A.M. Fractional boundary value problem with ψ-Caputo fractional derivative. Proc. Math. Sci. 2019, 129, 14. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M.; N’Guŕékata, G.M. Topics in Fractional Differential Equations; Springer: New York, NY, USA, 2015. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Academic Press: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2014. [Google Scholar]
- Agarwal, R.P.; Benchohra, M.; Hamani, S. A survey onexistence results for boundary value problems of nonlinear fractional differential equations and inclusions. Acta Appl. Math. 2010, 109, 973–1033. [Google Scholar] [CrossRef]
- Benchohra, M.; Graef, J.R.; Hamani, S. Existence results for boundary value problems with non-linear fractional differential equations. Appl. Anal. 2008, 87, 851–863. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M.; Hamidi, N.; Henderson, J. Caputo–Hadamard fractional differential equations in Banach spaces. Fract. Calc. Appl. Anal. 2018, 21, 1027–1045. [Google Scholar] [CrossRef]
- Boutiara, A.; Guerbati, K.; Benbachir, M. Caputo-Hadamard fractional differential equation with three-point boundary conditions in Banach spaces. AIMS Math. 2020, 5, 259–272. [Google Scholar]
- Aghajani, A.; Pourhadi, E.; Trujillo, J.J. Application of measure of noncompactness to a Cauchy problem for fractional differential equations in Banach spaces. Fract. Calc. Appl. Anal. 2013, 16, 962–977. [Google Scholar] [CrossRef]
- Kucche, K.D.; Mali, A.D.; Sousa, J.V.C. On the nonlinear Ψ-Hilfer fractional differential equations. Comput. Appl. Math. 2019, 38, 25. [Google Scholar] [CrossRef]
- Zhang, L.; Ahmad, B.; Wang, G. Explicit iterations and extremal solutions for fractional differential equations with nonlinear integral boundary conditions. Appl. Math. Comput. 2015, 268, 388–392. [Google Scholar] [CrossRef]
- Derbazi, C.; Baitiche, Z.; Benchohra, M.; Cabada, A. Initial Value Problem For Nonlinear Fractional Differential Equations With ψ-Caputo Derivative Via Monotone Iterative Technique. Axioms 2020, 9, 57. [Google Scholar] [CrossRef]
- Ali, S.; Shah, K.; Jarad, F. On stable iterative solutions for a class of boundary value problem of nonlinear fractional order differential equations. Math. Methods Appl. Sci. 2019, 42, 969–981. [Google Scholar] [CrossRef]
- Al-Refai, M.; Hajji, M.A. Monotone iterative sequences for nonlinear boundary value problems of fractional order. Nonlinear Anal. 2011, 74, 3531–3539. [Google Scholar] [CrossRef]
- Alsaedi, A.; Ahmad, B.; Alghanmi, M. Extremal solutions for generalized Caputo fractional differential equations with Steiltjes-type fractional integro-initial conditions. Appl. Math. Lett. 2019, 91, 113–120. [Google Scholar] [CrossRef]
- Chen, C.; Bohner, M.; Jia, B. Method of upper and lower solutions for nonlinear Caputo fractional difference equations and its applications. Fract. Calc. Appl. Anal. 2019, 22, 1307–1320. [Google Scholar] [CrossRef]
- Dhaigude, D.; Rizqan, B. Existence and uniqueness of solutions of fractional differential equations with deviating arguments under integral boundary conditions. Kyungpook Math. J. 2019, 59, 191–202. [Google Scholar]
- Fazli, H.; Sun, H.; Aghchi, S. Existence of extremal solutions of fractional Langevin equation involving nonlinear boundary conditions. Int. J. Comput. Math. 2020, 2020, 1720662. [Google Scholar] [CrossRef]
- Lin, X.; Zhao, Z. Iterative technique for a third-order differential equation with three-point nonlinear boundary value conditions. Electron. J. Qual. Theory Differ. Equ. 2016, 12, 10. [Google Scholar] [CrossRef]
- Mao, J.; Zhao, Z.; Wang, C. The unique iterative positive solution of fractional boundary value problem with q-difference. Appl. Math. Lett. 2020, 100, 106002. [Google Scholar] [CrossRef]
- Meng, S.; Cui, Y. The extremal solution to conformable fractional differential equations involving integral boundary condition. Mathematics 2019, 7, 186. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Sudsutad, W.; Zhang, L.; Tariboon, J. Monotone iterative technique for a nonlinear fractional q-difference equation of Caputo type. Adv. Diff. Equ. 2016, 2016, 211. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S. Monotone iterative method for initial value problem involving Riemann-Liouville fractional derivatives. Nonlinear Anal. 2009, 71, 2087–2093. [Google Scholar] [CrossRef]
- Eswari, R.; Alzabut, J.; Samei, M.E.; Zhou, H. On periodic solutions of a discrete Nicholson’s dual system with density-dependent mortality and harvesting terms. Adv. Differ. Equations 2021, 2021, 360. [Google Scholar] [CrossRef]
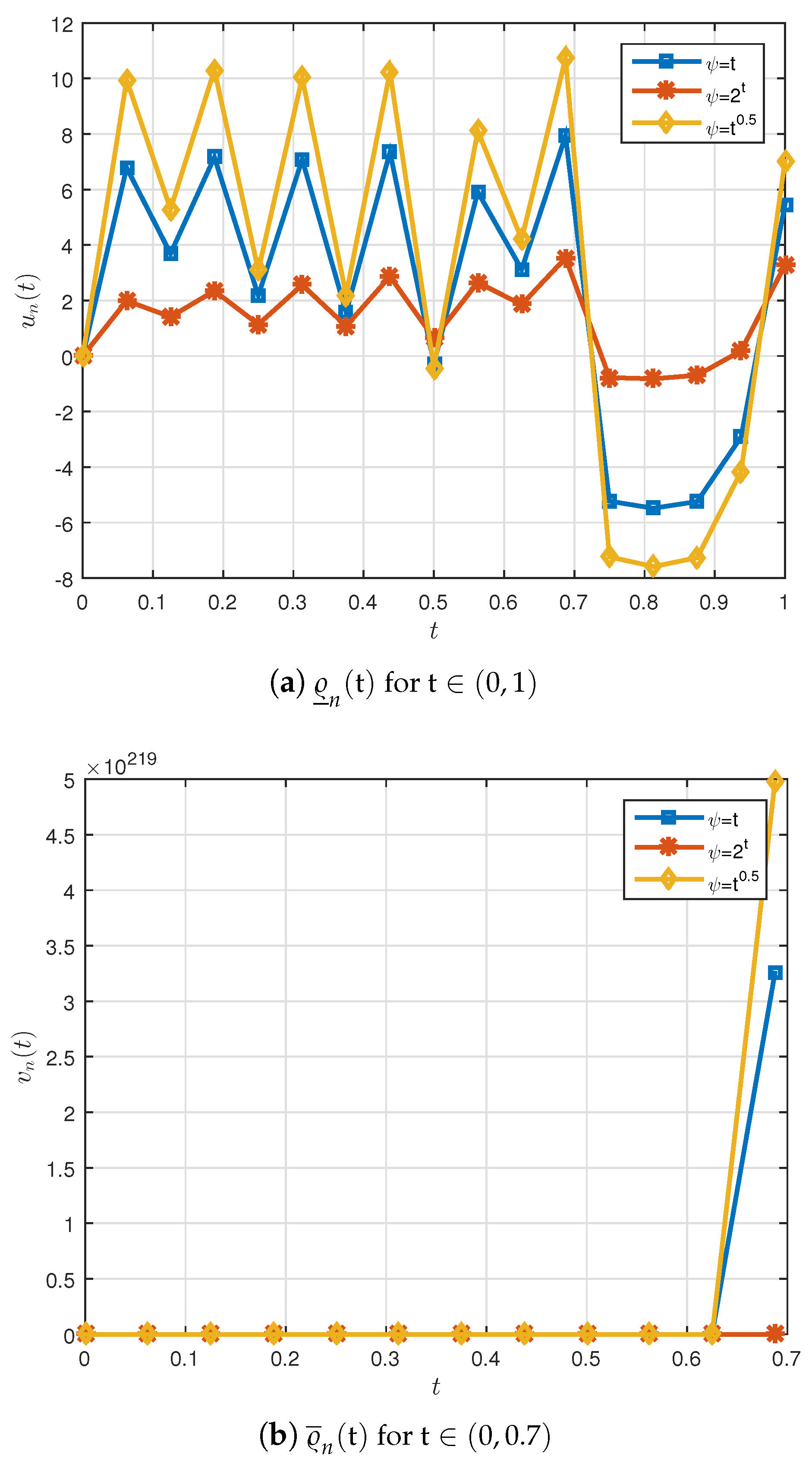
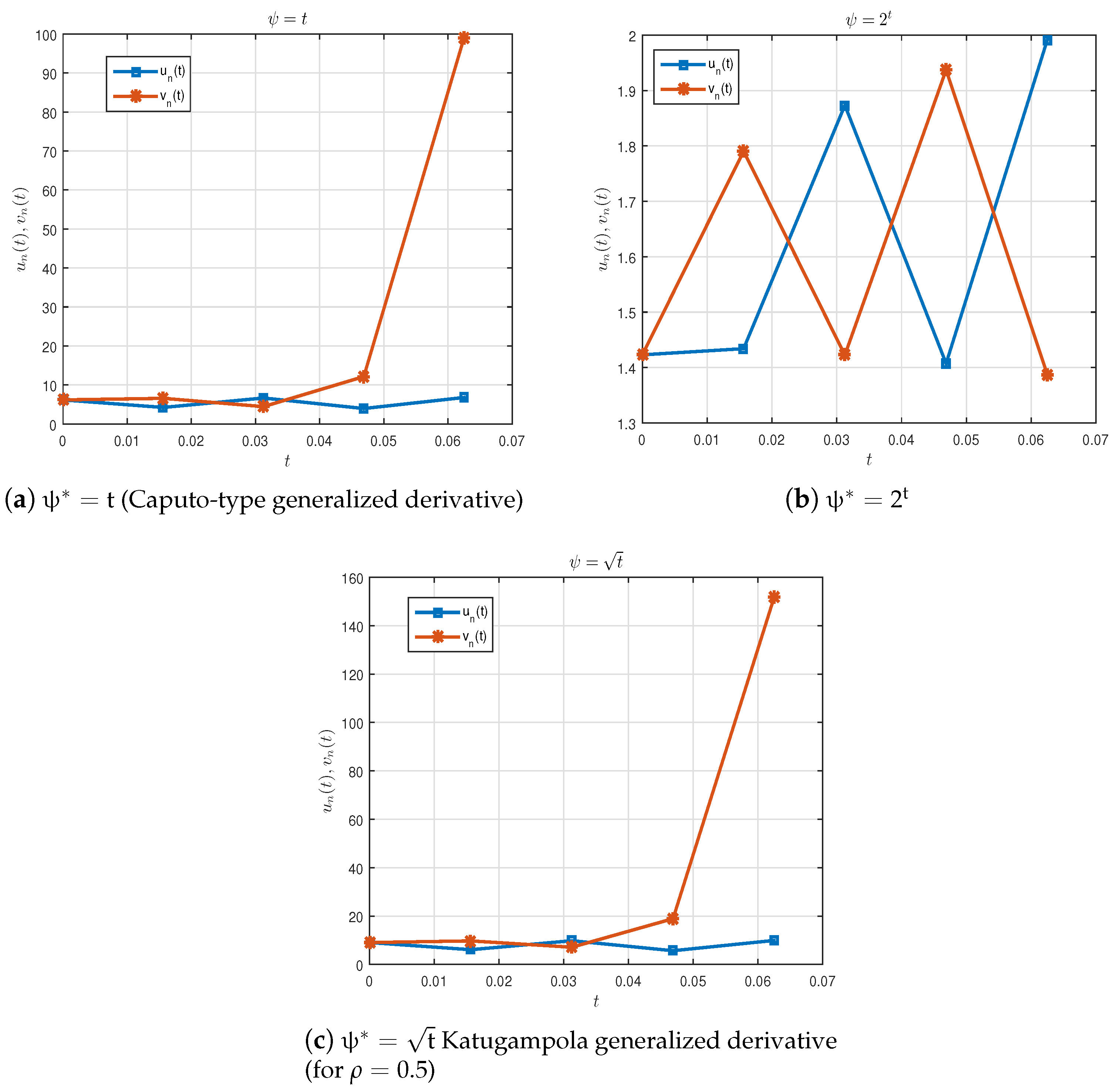

| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 16 | ||||
| 17 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 16 | ||||
| 17 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boutiara, A.; Benbachir, M.; Alzabut, J.; Samei, M.E. Monotone Iterative and Upper–Lower Solution Techniques for Solving the Nonlinear ψ−Caputo Fractional Boundary Value Problem. Fractal Fract. 2021, 5, 194. https://doi.org/10.3390/fractalfract5040194
Boutiara A, Benbachir M, Alzabut J, Samei ME. Monotone Iterative and Upper–Lower Solution Techniques for Solving the Nonlinear ψ−Caputo Fractional Boundary Value Problem. Fractal and Fractional. 2021; 5(4):194. https://doi.org/10.3390/fractalfract5040194
Chicago/Turabian StyleBoutiara, Abdelatif, Maamar Benbachir, Jehad Alzabut, and Mohammad Esmael Samei. 2021. "Monotone Iterative and Upper–Lower Solution Techniques for Solving the Nonlinear ψ−Caputo Fractional Boundary Value Problem" Fractal and Fractional 5, no. 4: 194. https://doi.org/10.3390/fractalfract5040194
APA StyleBoutiara, A., Benbachir, M., Alzabut, J., & Samei, M. E. (2021). Monotone Iterative and Upper–Lower Solution Techniques for Solving the Nonlinear ψ−Caputo Fractional Boundary Value Problem. Fractal and Fractional, 5(4), 194. https://doi.org/10.3390/fractalfract5040194








