Approximating Real-Life BVPs via Chebyshev Polynomials’ First Derivative Pseudo-Galerkin Method
Abstract
1. Introduction
2. Preliminaries
3. Chebyshev Polynomials’ First Derivatives
3.1. Chebyshev Polynomials’ First Derivatives Operational Matrix
3.2. Chebyshev’s Derivative Pseudo-Galerkin Method
| Algorithm 1: Algorithm steps for solving ODE via FDCHPs pseudo-Galerkin |
| Step 1: Input: ;
Step 2: Select the (collocation or the equidistant points); Step 3: Build the base function matrix using Equation (9); Step 4: Construct the derivative’s matrices using Equation (19); Step 5: Expand the ODE as shown in Equation (25) using steps and ; Step 6: Solve the previous system to obtain the ; Step 7: Substitute from step into Equation (23) to obtain the approximate solution. |
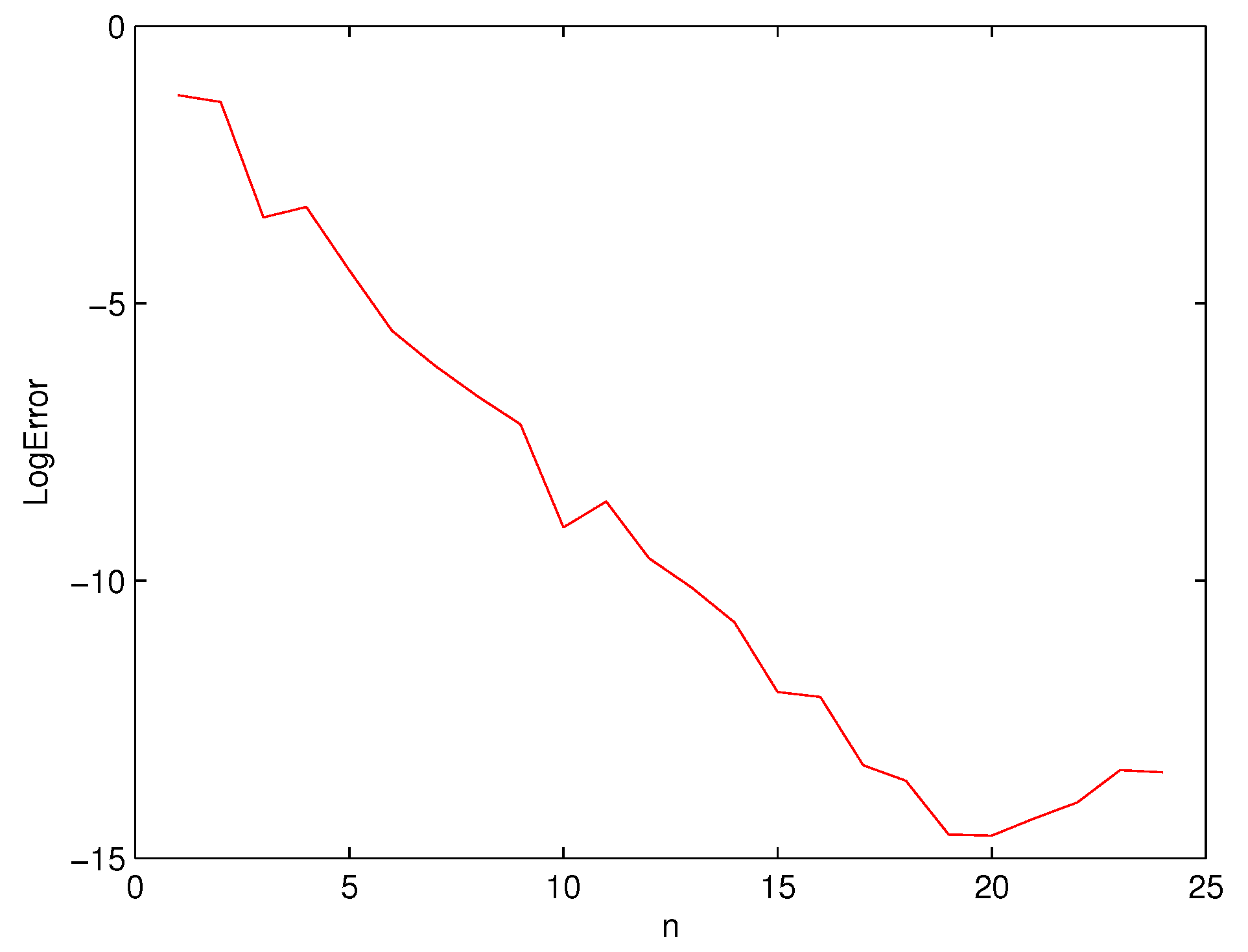
4. Error Analysis
5. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Danish, G.A.; Imran, M.; Tahir, M.; Waqas, H.; Asjad, M.I.; Akgül, A.; Baleanu, D. Effects of non-linear thermal radiation and chemical reaction on time dependent flow of Williamson nanofluid with combine electrical MHD and activation energy. J. Appl. Comput. Mech. 2021, 7, 546–558. [Google Scholar]
- Farman, M.; Ahmad, A.; Akgül, A.; Saleem, M.U.; Naeem, M.; Baleanu, D. Epidemiological Analysis of the Coronavirus Disease Outbreak with Random Effects. Comput. Mater. Contin. 2021, 67, 3215–3227. [Google Scholar] [CrossRef]
- Nan, A.; Khan, U.; Ahmed, N.; Mohyud-Din, S.T.; Khan, I.; Baleanu, D.; Nisar, K.S. Al2O3 and gamma Al2O3 nanomaterials based nanofluid models with Surface Diffusion: Applications for thermal performance in multiple engineering systems and industries. CMC 2021, 66, 1563–1576. [Google Scholar]
- Çelik, E.; Bayram, M. The numerical solution of physical problems modeled as a systems of differential algebraic equations (DAEs). J. Frankl. Inst. 2005, 342, 1–6. [Google Scholar] [CrossRef]
- Çelik, E. On the numerical solution of chemical differential-algebraic equations by Pade series. Appl. Math. Comput. 2004, 153, 13–17. [Google Scholar] [CrossRef]
- He, W.; Chen, N.; Dassios, I.; Shah, N.A.; Chung, J.D. Fractional system of Korteweg-De Vries equations via Elzaki transform. Mathematics 2021, 9, 673. [Google Scholar] [CrossRef]
- Kumar, S.; Shaw, P.K.; Abdel-Aty, A.H.; Mahmoud, E.E. A numerical study on fractional differential equation with population growth model. Numer. Methods Part. Differ. Eq. 2020, 1–2. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Hafez, R.M. Chebyshev collocation treatment of Volterra–Fredholm integral equation with error analysis. Arab. J. Math. 2020, 9, 471–480. [Google Scholar] [CrossRef]
- Lu, Y.; Yin, Q.; Li, H. The LS-SVM algorithms for boundary value problems of high-order ordinary differential equations. Adv. Differ. Equ. 2019, 2019, 195. [Google Scholar] [CrossRef]
- Akram, G.; Beck, C. Hierarchical cascade model leading to 7-th order initial value problem. Appl. Numer. Math. 2015, 91, 89–97. [Google Scholar] [CrossRef]
- Alsaedi, A.; Hayat, T.; Qayyum, S.; Yaqoob, R. Eyring-Powell nanofluid flow with nonlinear mixed convection: Entropy generation minimization. Comput. Methods Programs Biomed. 2020, 186, 105183. [Google Scholar] [CrossRef] [PubMed]
- Bhrawy, A.H. A new spectral algorithm for time-space fractional partial differential equations with subdiffusion and superdiffusion. Proc. Rom. Acad. Ser. A 2016, 17, 39–47. [Google Scholar]
- Abdelkawy, M.A.; Ezz-Eldien, S.S.; Amin, A.Z.M. Jacobi spectral collocation scheme for solving Abel’s integral equations. Prog. Fract. Differ. 2015, 1, 187–200. [Google Scholar]
- Youssri, Y.H.; Abd-Elhameed, W.M.; Abdelhakem, M. A robust spectral treatment of a class of initial value problems using modified Chebyshev polynomials. Math. Meth. Appl. Sci. 2021, 44, 9224–9236. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Doha, M.R.; Saadallah, A.F.; El-Kady, M. Monic Gegenbauer approximations for solving differential equations. J. Sci. Eng. Res. 2018, 5, 317–321. [Google Scholar]
- Abdelhakem, M.; Ahmed, A.; El-kady, M. Spectral monic Chebyshev approximation for higher order differential equations. Math. Sci. Lett. 2019, 8, 11–17. [Google Scholar]
- Sweilam, N.H.; Nagy, A.M.; Youssef, I.K.; Mokhtar, M.M. New spectral second kind Chebyshev wavelets scheme for solving systems of integro-differential equations. Int. J. Appl. Comput. Math. 2017, 3, 333–345. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. Fifth-kind orthonormal Chebyshev Polynomial solutions for fractional differential equations. Comp. Appl. Math. 2018, 37, 2897–2921. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. Sixth-Kind Chebyshev spectral approach for solving fractional differential equations. Int. J. Nonlin. Sci. Num. 2019, 20, 191–203. [Google Scholar] [CrossRef]
- De Florio, M.; Schiassi, E.; D’Ambrosio, A.; Mortari, D.; Furfaro, R. Theory of Functional Connections Applied to Linear ODEs Subject to Integral Constraints and Linear Ordinary Integro-Differential Equations. Math. Comput. Appl. 2021, 26, 65. [Google Scholar] [CrossRef]
- Guan, X.; Zhong, R.; Qin, B.; Wang, Q.; Shao, W. Vibro-acoustic analysis of combined elliptical–cylindrical–elliptical shells immersed in acoustic medium. J. Fluids Struct. 2021, 106, 103391. [Google Scholar] [CrossRef]
- Shen, J. Efficient spectral-Galerkin Method I. direct solvers of second- and fourth-order equations. SIAM J. Sci. Comput. 1995, 15, 1489–1505. [Google Scholar] [CrossRef]
- Issa, K.; Adeniyi, R.B. Extension of generalized recursive Tau method to non-linear ordinary differential equations. J. Niger. Math. Soc. 2016, 35, 18–24. [Google Scholar] [CrossRef][Green Version]
- Shahni, J.; Singh, R. Bernstein and Gegenbauer-wavelet collocation methods for Bratu-like equations arising in electrospinning process. J. Math. Chem. 2021, 1–17. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşı, Ş.; Baleanu, D. A Taylor–Chebyshev approximation technique to solve the 1D and 2D nonlinear Burgers equations. Math. Sci. 2021, 1–13. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Biomy, M.; Kandil, S.A.; Baleanu, D. A numerical method based on Legendre differentiation matrices for higher order ODEs. Inf. Sci. Lett. 2020, 9, 175–180. [Google Scholar]
- Napoli, A.; Abd-Elhameed, W.M. An innovative harmonic numbers operational matrix method for solving initial value problems. Calcolo 2017, 54, 57–76. [Google Scholar] [CrossRef]
- Youssri, Y.H. Two Fibonacci operational matrix pseudo-spectral schemes for nonlinear fractional Klein-Gordon equation. Int. J. Mod. Phys. C 2021. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Mahmoud, D.; Baleanu, D. Shifted ultraspherical pseudo-Galerkin method for approximating the solutions of some types of ordinary fractional problems. Adv. Differ. Equ. 2021, 2021, 110. [Google Scholar] [CrossRef]
- Elbarbary, E.M.E. Efficient Chebyshev–Petrov–Galerkin method for solving second-order equations. J. Sci. Comput. 2008, 34, 113–126. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Youssri, Y.H. Two Spectral Legendre’s Derivative Algorithms for Lane-Emden, Bratu Equations, and Singular Perturbed Problems. Appl. Numer. Math. 2021, 169, 243–255. [Google Scholar] [CrossRef]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials, 1st ed.; Chapman, Hall/CRC: New York, NY, USA, 2002; p. 360. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analyses and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011; p. 472. [Google Scholar]
- Darvishi, M.; Darvishi, N. SOR- Steffensen–Newton method to solve systems of nonlinear equations. J. Appl. Math. 2012, 2, 21–27. [Google Scholar] [CrossRef][Green Version]
- Abd-Elhameed, W.; Youssri, Y.H. Numerical solutions for Volterra-Fredholm-Hammerstein integral equations via second kind Chebyshev quadrature collocation algorithm. Adv. Math. Sci. Appl. 2014, 24, 129–141. [Google Scholar]
- Tomar, S. A Rapid-Converging Analytical Iterative Scheme for Solving Singular Initial Value Problems of Lane–Emden Type. Int. J. Appl. Comput. Math. 2021, 7, 1–17. [Google Scholar] [CrossRef]
- Hadian-Rasanan, A.H.; Rahmatic, D.; Gorgind, S.; Paranda, K. A single layer fractional orthogonal neural network for solving various types of Lane–Emden equation. New Astron. 2020, 75, 101307. [Google Scholar] [CrossRef]
- Aydinlik, S. A high-order numerical method for solving nonlinear. Astrophys. Space Sci. 2018, 363, 264. [Google Scholar] [CrossRef]
- Zhu, H.; Niu, J.; Zhang, R.; Lin, Y. A new approach for solving nonlinear singular boundary value problems. Math. Model. Anal. 2018, 23, 33–43. [Google Scholar] [CrossRef]
- Mohsenyzadeh, M.; Maleknejad, K.; Ezzati, R. A numerical approach for the solution of a class of singular boundary value problems arising in physiology. Adv. Differ. Equ. 2015, 2015, 231. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, X. Numerical solutions for the linear and nonlinear singular boundary value problems using Laguerre wavelets. Adv. Diff. Equ. 2016, 2016, 17. [Google Scholar] [CrossRef]
- Alam, M.P.; Begum, T.; Khan, A. A high-order numerical algorithm for solving Lane–Emden equations with various types of boundary conditions. Comp. Appl. Math. 2021, 40. [Google Scholar] [CrossRef]
- Yüzbas, S. Improved Bessel collocation method for linear Volterra integro-differential equations with piecewise intervals and application of a Volterra population model. Appl. Math. Model. 2016, 40, 5349–5363. [Google Scholar] [CrossRef]
- Yüzbas, S.; Sezer, M.; Kemancı, B. Numerical solutions of integro-differential equations and application of a population model with an improved Legendre method. Appl. Math. Model. 2016, 37, 2086–2101. [Google Scholar] [CrossRef]
- Kudenatti, R.B. A new exact solution for boundary layer flow over a stretching plate. Int. J. Non-Linear Mech. 2012, 47, 727–733. [Google Scholar] [CrossRef]
- Kudenatti, R.B.; Awati, V.B.; Bujurke, N. Approximate analytical solutions of a class of boundary layer equations over nonlinear stretching surface. Appl. Math. Comput. 2011, 218, 2952–2959. [Google Scholar] [CrossRef]
- Sachdev, P.L.; Bujurke, N.M.; Awati, V.B. Boundary value problems for third-order nonlinear ordinary differential equations. Stud. Appl. Math. 2015, 115, 303–318. [Google Scholar] [CrossRef]
- Afzal, N. Momentum transfer on power law stretching plate with free stream pressure gradient. Int. J. Eng. Sci. 2003, 41, 1197–1207. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Karkera, H.; Katagi, N.N.; Kudenatti, R.B. Analysis of general unified MHD boundary-layer flow of a viscous fluid—A novel numerical approach through wavelets. Math. Comput. Simul. 2020, 168, 135–154. [Google Scholar] [CrossRef]

| s | FDCHPs Pseudo-Galerkin | [38] |
|---|---|---|
| 0.0 | - | |
| 0.1 | 0 | |
| 0.2 | - | |
| 0.3 | - | |
| 0.4 | 0 | - |
| 0.5 | ||
| 0.6 | 0 | - |
| 0.7 | 0 | - |
| 0.8 | 0 | - |
| 0.9 | 0 | - |
| s | FDCHPs Pseudo-Galerkin | [38] |
|---|---|---|
| 0.0 | 0 | |
| 0.1 | ||
| 0.2 | ||
| 0.3 | ||
| 0.4 | ||
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 | ||
| 1.0 | ||
| 1.5 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 | ||
| 3.1 |
| s | FDCHPs Pseudo-Galerkin | [40] | [41] | [41] | ||
|---|---|---|---|---|---|---|
| 0.0 | - | - | ||||
| 0.1 | ||||||
| 0.2 | ||||||
| 0.3 | ||||||
| 0.4 | ||||||
| 0.5 | ||||||
| 0.6 | ||||||
| 0.7 | ||||||
| 0.8 | ||||||
| 0.9 | ||||||
| 1.0 | - | - | ||||
| Method | Best MAE |
|---|---|
| [39] “” | |
| [40] “” | |
| [41] “” | |
| [42] “” | |
| FDCHPs Pseudo-Galerkin“” |
| s | FDCHPs Pseudo-Galerkin | [8] | |
|---|---|---|---|
| −1 | 0 | ||
| −0.6 | |||
| −0.2 | |||
| 0.2 | |||
| 0.6 | |||
| 1 | 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelhakem, M.; Alaa-Eldeen, T.; Baleanu, D.; Alshehri, M.G.; El-Kady, M. Approximating Real-Life BVPs via Chebyshev Polynomials’ First Derivative Pseudo-Galerkin Method. Fractal Fract. 2021, 5, 165. https://doi.org/10.3390/fractalfract5040165
Abdelhakem M, Alaa-Eldeen T, Baleanu D, Alshehri MG, El-Kady M. Approximating Real-Life BVPs via Chebyshev Polynomials’ First Derivative Pseudo-Galerkin Method. Fractal and Fractional. 2021; 5(4):165. https://doi.org/10.3390/fractalfract5040165
Chicago/Turabian StyleAbdelhakem, Mohamed, Toqa Alaa-Eldeen, Dumitru Baleanu, Maryam G. Alshehri, and Mamdouh El-Kady. 2021. "Approximating Real-Life BVPs via Chebyshev Polynomials’ First Derivative Pseudo-Galerkin Method" Fractal and Fractional 5, no. 4: 165. https://doi.org/10.3390/fractalfract5040165
APA StyleAbdelhakem, M., Alaa-Eldeen, T., Baleanu, D., Alshehri, M. G., & El-Kady, M. (2021). Approximating Real-Life BVPs via Chebyshev Polynomials’ First Derivative Pseudo-Galerkin Method. Fractal and Fractional, 5(4), 165. https://doi.org/10.3390/fractalfract5040165







