Fractal Calculus on Fractal Interpolation Functions
Abstract
:1. Introduction
2. Fractal Calculus
2.1. Fractal Calculus of the Weierstrass Function
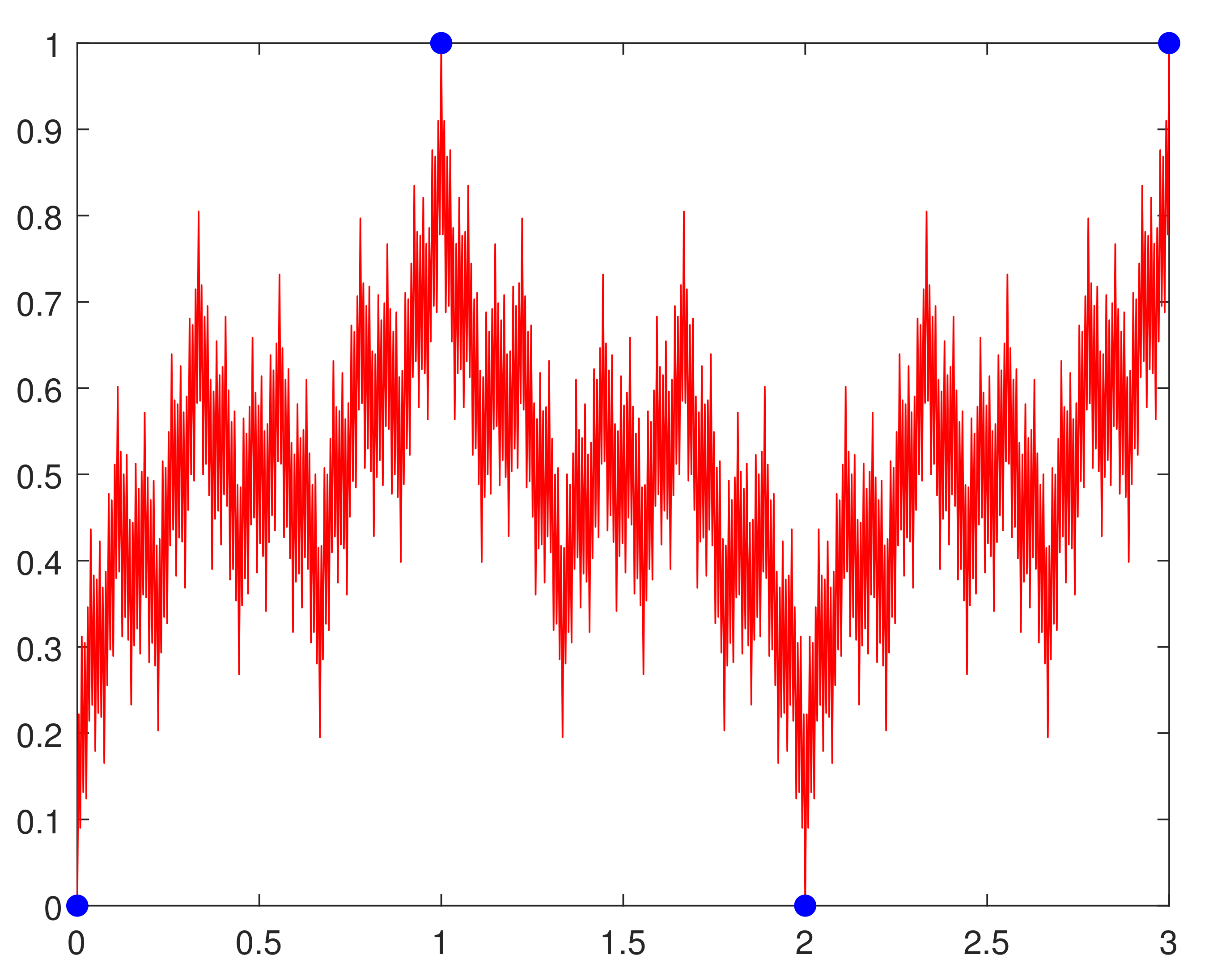
3. Fractal Interpolation Functions
3.1. The Original Formulation
3.2. System of Iterative Functional Equations
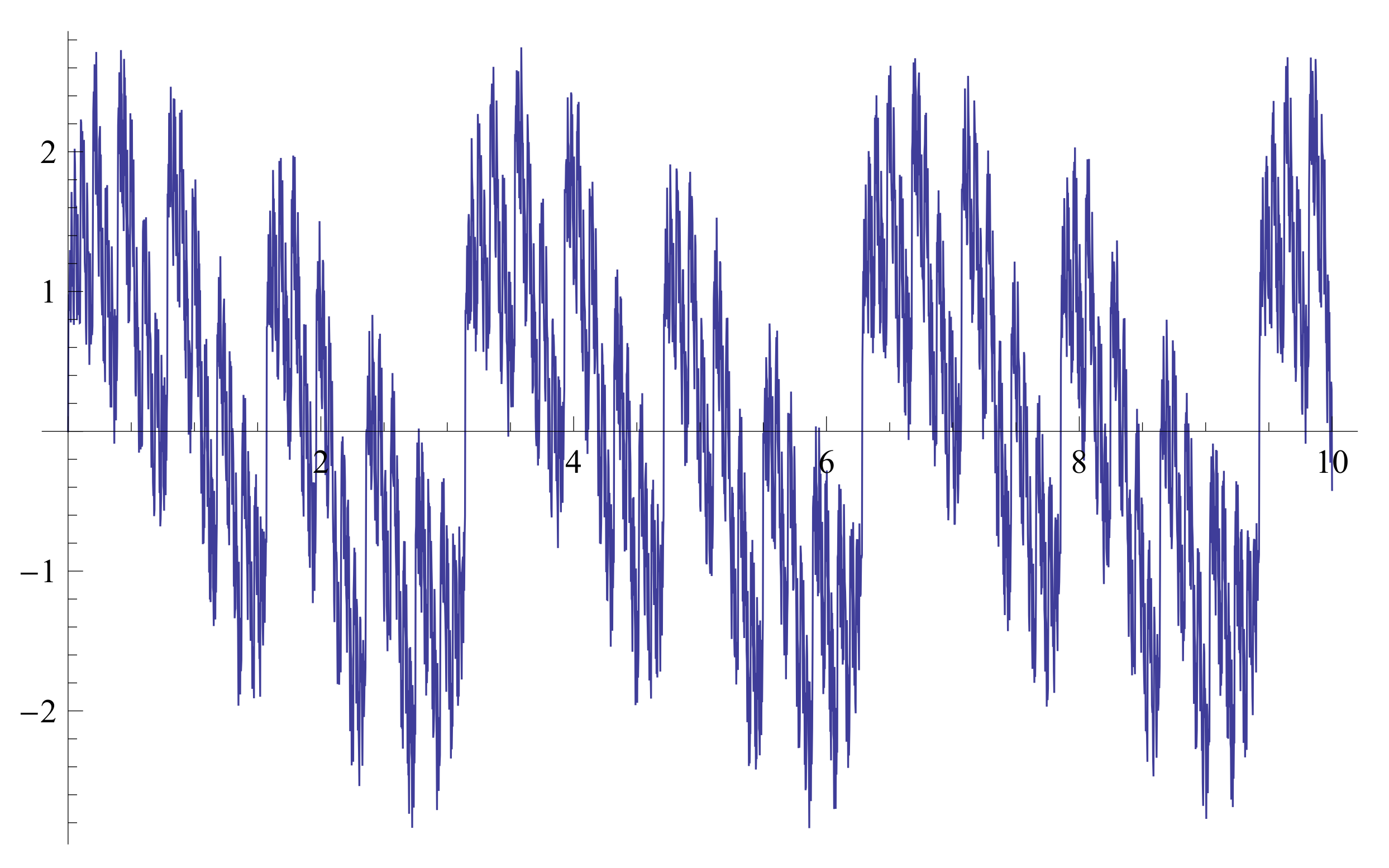
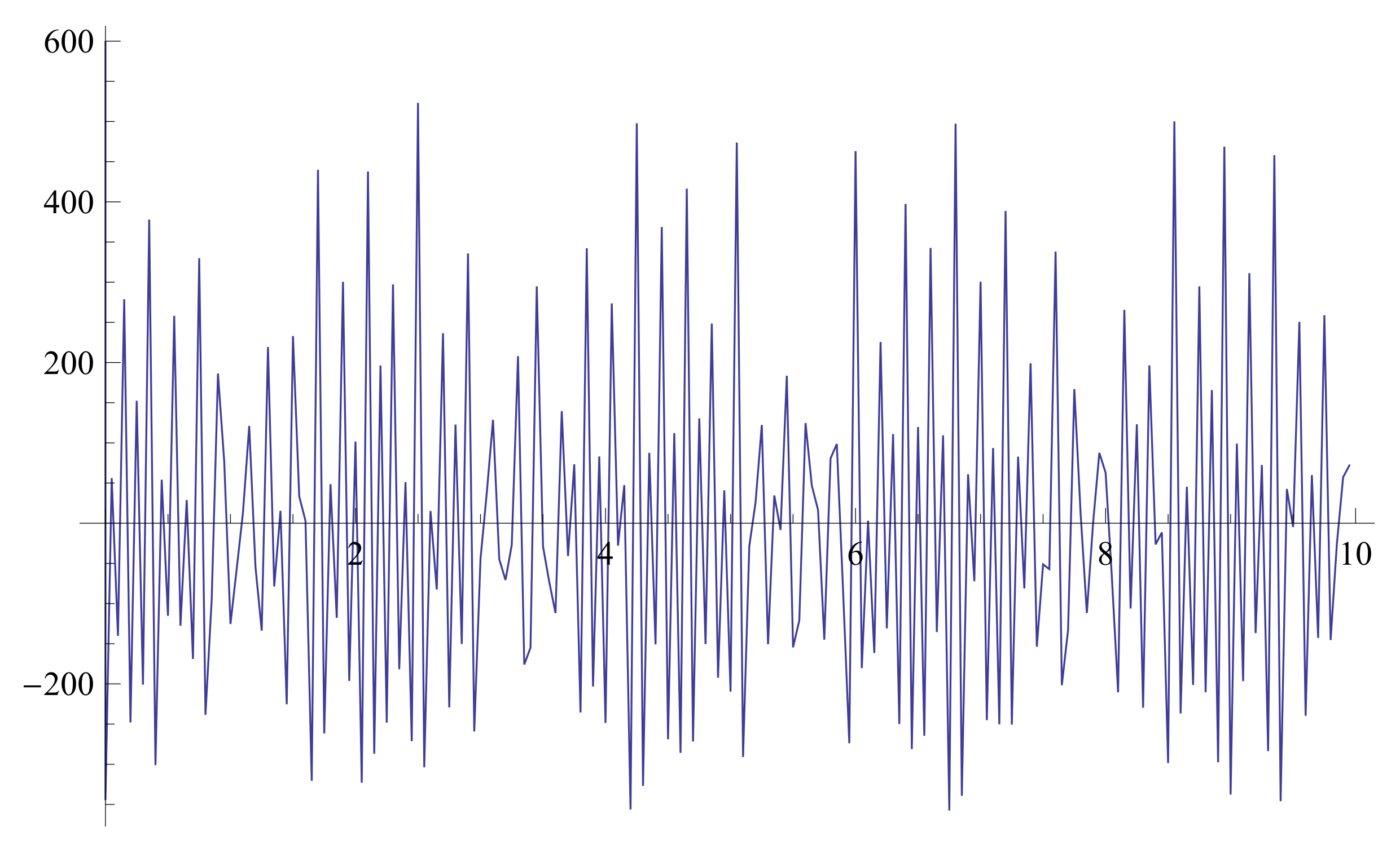
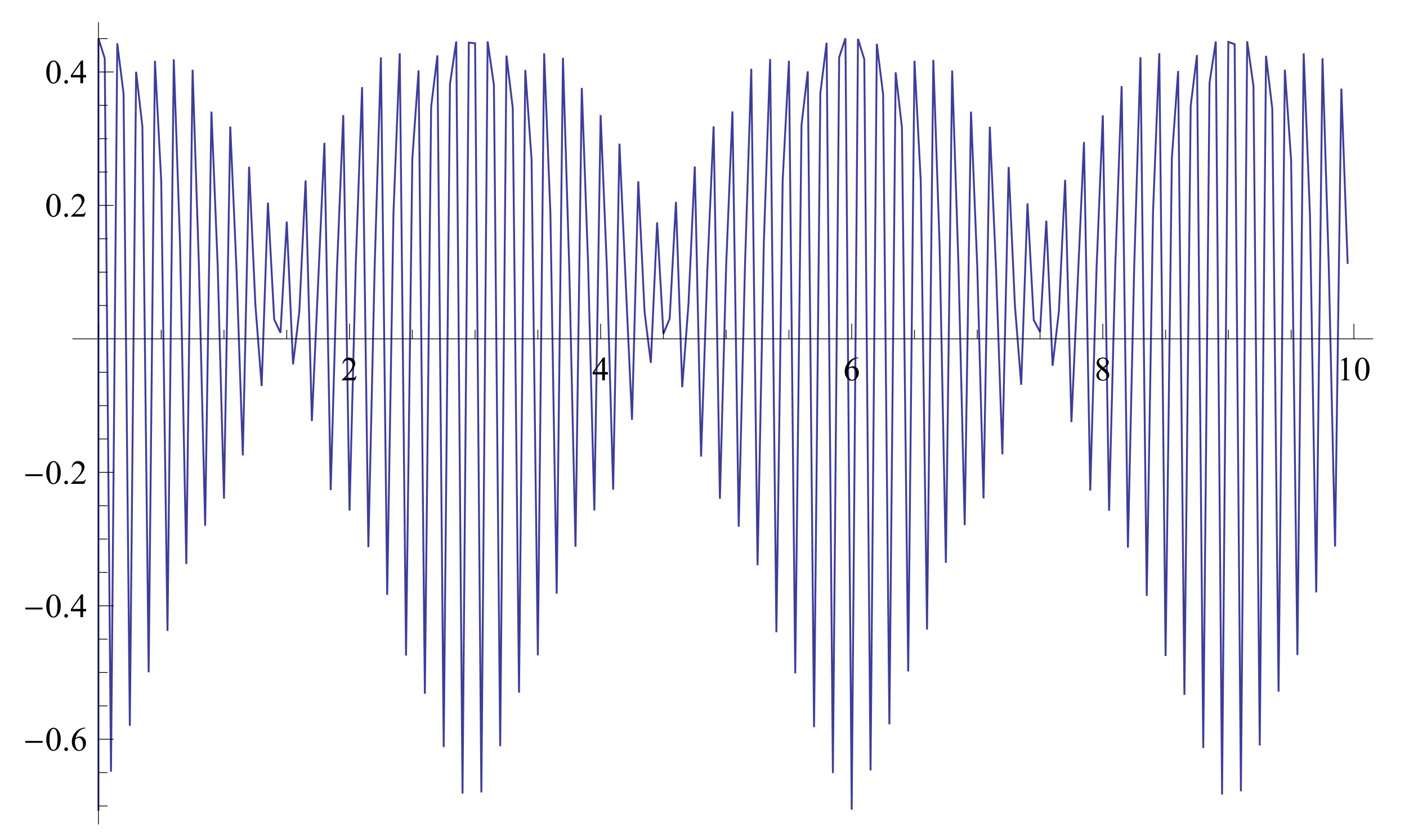
4. Fractal Calculus on Fractal Interpolation Function
4.1. With Cantor like Sets Domains
4.2. The -Integral
4.3. The -Integral as a FIF
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blackledge, J.M.; Evans, A.K.; Turner, M.J. Fractal Geometry: Mathematical Methods, Algorithms, Applications; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Pesin, Y.B. Dimension Theory in Dynamical Systems: Contemporary Views and Applications; University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar]
- Edgar, G. Measure, Topology, and Fractal Geometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Pietronero, L.; Tosatti, E. Fractals in Physics; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Massopust, P.R. Fractal Functions, Fractal Surfaces, and Wavelets; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Losa, G.A.; Merlini, D.; Nonnenmacher, T.F.; Weibel, E.R. Fractals in Biology and Medicine; Birkhäuser: Basel, Switzerland, 2005. [Google Scholar]
- Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise; Courier Corporation: North Chelmsford, MA, USA, 2009. [Google Scholar]
- Sandev, T.; Iomin, A.; Kantz, H. Anomalous diffusion on a fractal mesh. Phys. Rev. E 2017, 95, 052107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1983; Volume 173. [Google Scholar]
- Barnsley, M.F. Fractal functions and interpolation. Constr. Approx. 1989, 2, 303–329. [Google Scholar] [CrossRef]
- Serpa, C.; Buescu, J. Fractal and Hausdorff dimensions for systems of iterative functional equations. J. Math. Anal. Appl. 2019, 480, 123429. [Google Scholar]
- Serpa, C.; Buescu, J. Constructive solutions for systems of iterative functional equations. Constr. Approx. 2017, 45, 273–299. [Google Scholar] [CrossRef]
- Serpa, C.; Buescu, J. Explicitly defined fractal interpolation functions with variable parameters. Chaos Solitons Fractals 2015, 75, 76–83. [Google Scholar] [CrossRef]
- Banerjee, S.; Easwaramoorthy, D.; Gowrisankar, A. Fractal Functions, Dimensions and Signal Analysis; Springer: Cham, Switerland, 2021. [Google Scholar]
- Navascués, M.A. Fractal polynomial interpolation. Z. Anal. Anwend. 2005, 25, 401–418. [Google Scholar] [CrossRef]
- Navascués, M.A. Non-Smooth polynomial. Int. J. Math. Anal. 2007, 1, 159–174. [Google Scholar]
- Katiyar, S.K.; Chand, A.K.B.; Saravana, K.G. A new class of rational cubic spline fractal interpolation function and its constrained aspects. Appl. Math. Comput. 2019, 346, 319–335. [Google Scholar] [CrossRef]
- Banerjee, S.; Hassan, M.K.; Mukherjee, S.; Gowrisankar, A. Fractal Patterns in Nonlinear Dynamics and Applications; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Tatom, F.B. The relationship between fractional calculus and fracta. Fractals 1995, 3, 217–229. [Google Scholar] [CrossRef]
- Satin, S.; Gangal, A.D. Random walk and broad distributions on fractal curves. Chaos Solitons Fractals 2019, 127, 17–23. [Google Scholar] [CrossRef] [Green Version]
- Satin, S.; Gangal, A.D. Langevin equation on fractal curves. Fractals 2016, 24, 1650028. [Google Scholar] [CrossRef] [Green Version]
- Kolwankar, K.M.; Gangal, A.D. Fractional differentiability of nowhere differentiable functions and dimensions. Chaos 1996, 6, 505–513. [Google Scholar] [CrossRef] [Green Version]
- Yao, K.; Su, W.Y.; Zhou, S.P. On the connection between the order of fractional calculus and the dimensions of a fractal function. Chaos Solitons Fractals 2005, 23, 621–629. [Google Scholar] [CrossRef]
- Ruan, H.J.; Su, W.Y.; Yao, K. Box dimension and fractional integral of linear fractal interpolation functions. J. Approx. Theory 2009, 161, 187–197. [Google Scholar] [CrossRef] [Green Version]
- Gowrisankar, A.; Uthayakumar, R. Fractional calculus on fractal interpolation function for a sequence of data with countable iterated function system. Mediterr. J. Math. 2016, 13, 3887–3906. [Google Scholar] [CrossRef]
- Liang, Y.S.; Zhang, Q. A type of fractal interpolation functions and their fractional calculus. Fractals 2016, 24, 1650026. [Google Scholar] [CrossRef]
- Xiao, E.W.; Jun, H.D. Box dimension of Hadamard fractional integral of continuous functions of bounded and unbounded variation. Fractals 2017, 25, 1750035. [Google Scholar]
- Gowrisankar, A.; Prasad, M.G.P. Riemann-Liouville Calculus on Quadratic Fractal Interpolation Function with Variable Scaling Factors. J. Anal. 2019, 27, 347–363. [Google Scholar] [CrossRef]
- Liang, Y.S. Progress on estimation of fractal dimensions of fractional calculus of continuous functions. Fractals 2019, 27, 1950084. [Google Scholar] [CrossRef]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [Green Version]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483. [Google Scholar] [CrossRef] [Green Version]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [Green Version]
- Lapidus, M.L.; Frankenhuijsen, M.V. Fractal Geometry, Complex Dimensions and Zeta Functions: Geometry and Spectra of Fractal Strings; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Barlow, M.T.; Perkins, E.A. Brownian motion on the Sierpinski gasket. Probab. Theory Relat. Fields 1988, 79, 543–623. [Google Scholar] [CrossRef]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Freiberg, U.; Zahle, M. Harmonic calculus on fractals-a measure geometric approach I. Potential Anal. 2002, 16, 265–277. [Google Scholar] [CrossRef]
- Falconer, K. Techniques in Fractal Geometry; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Zubair, M.; Mughal, M.J.; Naqvi, Q.A. Electromagnetic Fields and Waves in Fractional Dimensional Space; Springer: New York, NY, USA, 2012. [Google Scholar]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimension. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Balankin, A.S. A continuum framework for mechanics of fractal materials I: From fractional space to continuum with fractal metric. Eur. Phys. J. B 2015, 88, 1–13. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2014. [Google Scholar]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line—I: Formulation. Fractals 2009, 17, 53–81. [Google Scholar] [CrossRef]
- Parvate, A.; Satin, S.; Gangal, A.D. Calculus on fractal curves in Rn. Fractals 2011, 19, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line—II: Conjugacy with ordinary calculus. Fractals 2011, 19, 271–290. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K. On the calculus of parameterized fractal curves. Turk. J. Phys. 2017, 41, 418–425. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Tunç, C. Stochastic differential equations on fractal sets. Stochastics 2019, 92, 1244–1260. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Tunç, C. Sumudu transform in fractal calculus. Appl. Math. Comput. 2019, 350, 386–401. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Fernandez, A. Fractal calculus of functions on cantor tartan spaces. Fractal Fract. 2018, 2, 30. [Google Scholar] [CrossRef] [Green Version]
- Buescu, J.; Serpa, C. Compatibility Conditions for Systems of Iterative Functional Equations with Non-trivial Contact Sets. Results Math. 2021, 76, 68. [Google Scholar] [CrossRef]
- Serpa, C. A note on fractal interpolation vs. fractal regression. Acad. Lett. 2021, 808. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gowrisankar, A.; Khalili Golmankhaneh, A.; Serpa, C. Fractal Calculus on Fractal Interpolation Functions. Fractal Fract. 2021, 5, 157. https://doi.org/10.3390/fractalfract5040157
Gowrisankar A, Khalili Golmankhaneh A, Serpa C. Fractal Calculus on Fractal Interpolation Functions. Fractal and Fractional. 2021; 5(4):157. https://doi.org/10.3390/fractalfract5040157
Chicago/Turabian StyleGowrisankar, Arulprakash, Alireza Khalili Golmankhaneh, and Cristina Serpa. 2021. "Fractal Calculus on Fractal Interpolation Functions" Fractal and Fractional 5, no. 4: 157. https://doi.org/10.3390/fractalfract5040157
APA StyleGowrisankar, A., Khalili Golmankhaneh, A., & Serpa, C. (2021). Fractal Calculus on Fractal Interpolation Functions. Fractal and Fractional, 5(4), 157. https://doi.org/10.3390/fractalfract5040157






