Abstract
Fractional derivative models involving generalized Mittag-Leffler kernels and opposing models are investigated. We first replace the classical derivative with the GMLK in order to obtain the new fractional-order models (GMLK) with the three parameters that are investigated. We utilize a spectral collocation method based on Legendre’s polynomials for evaluating the numerical solutions of the pr. We then construct a scheme for the fractional-order models by using the spectral method involving the Legendre polynomials. In the first model, we directly obtain a set of nonlinear algebraic equations, which can be approximated by the Newton-Raphson method. For the second model, we also need to use the finite differences method to obtain the set of nonlinear algebraic equations, which are also approximated as in the first model. The accuracy of the results is verified in the first model by comparing it with our analytical solution. In the second and third models, the residual error functions are calculated. In all cases, the results are found to be in agreement. The method is a powerful hybrid technique of numerical and analytical approach that is applicable for partial differential equations with multi-order of fractional derivatives involving GMLK with three parameters.
Keywords:
fractional derivative; generalized Mittag-Leffler kernel (GMLK); Legendre polynomials; Legendre spectral collocation method MSC:
26A33; 41A30; 65N12; 33C45; 33E12; 65N22
1. Introduction
During the past three decades, the science of fractional calculus has attracted the interest of many scientists and researchers (see, for example, [1,2,3,4,5,6]; see also [7] for some recent developments on the subject of fractional calculus). The main motive for presenting and researching numerical and approximate methods for solving fractional-order differential equations is the scarcity and difficulty of finding analytical solutions to these equations. Therefore, many researchers resorted to deriving and presenting various numerical methods for this purpose (see [8,9,10]).
In order to learn more about the definitions and properties of fractional integrals and fractional derivatives, the reader can refer to (for example) [2,3]. Many researchers have drawn attention to the fractional-order modeling of a considerably wide variety of problems in mathematical, physical, chemical, biological and engineering sciences. In particular, in fluid mechanics, viscoelasticity and other applications, use has been made of fractional integrals and fractional derivatives involving non-singular kernels (see, for details, [11,12]). Such kernels as those with one parameter were considered in [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]). Abdeljawad (see [38,39]), Abdeljawad and Baleanu [40] considered fractional derivatives and fractional integrals with Mittag-Leffler kernels involving three parameters. For the existence of the solution to fractional-order differential equations, one of the most important advantages is in using the GMLK. This can be illustrated by noticing that the solution of the following problem:
where a and are constants, does not exist for . However, via the new definition, the solution exists (see [39]).
Our contribution in this work is to utilize the above-mentioned new definition of a fractional derivative in investigating new fractional-order models according to the associated fractional derivative operator. We also use several important and potentially useful properties of such special functions as the Legendre polynomials with a view of obtaining a special scheme through means of which we can derive the numerical solutions of the fractional-order models presented in this paper.
The format of this paper is structured as follows: In Section 2, we give some preliminaries and introduce the basic definitions and associated properties that will be used in this paper. In Section 3, the Legendre polynomials are presented together with their properties, including their fractional derivatives. In the fourth section (Section 4), the scheme and the algorithm for numerical solutions of the fractional-order models presented in this paper are constructed. In the fifth section (Section 5), the numerical results for the solutions to the presented models are discussed. Finally, in Section 6, we present our conclusions.
2. Preliminaries
In this section, we present the definition of the fractional derivative with generalized Mittag-Leffler kernels. This definition and its properties were studied by Abdeljawad and Baleanu [40] and Abdeljawad [39]. Abdeljawad [38] also undertook further study of the fundamentals and properties of these operators as well as their discrete versions.
Definition 1.
The left-sided fractional derivative with generalized Mittag-Leffler kernel is defined, for
by
where is a normalization function such that
and that is, the fractional part of the parameter α.
Remark 1.
We note that, if we obtain the ordinary derivative of of order n.
Remark 2.
Henceforth, in this paper, we assume that the parameter μ is real and positive .
Theorem 1.
The fractional derivative with generalized Mittag-Leffler kernel of of order is given, for and , by
Proof.
Using Definition 1 of the fractional derivative with generalized Mittag-Leffler kernel and the series of given by (2), we have
which evidently proves Theorem 1. □
Definition 2
(see [40]). Let f be a continuous function defined on the closed interval and assume that and . Then the left-sided fractional integral involving the two parameters α and μ is defined by
where
is the Riemann-Liouville fractional integral of the function of order β.
The following remarks can be found in [39].
Remark 3.
For the left-sided AB fractional integral of order is given, for by
Remark 4.
For and it is easily seen that
3. The Shifted Legendre Polynomials and the Fractional Derivatives with Generalized Mittag-Leffler Kernel
In order to obtain the shifted Legendre polynomials on the interval , we introduce the new variable . The so-shifted Legendre polynomials are defined as follows:
where the set
forms a family of orthogonal Legendre polynomials on the interval .
The shifted Legendre polynomial of degree s has the expansion given by (see [41])
so that, clearly, , , and so on.
For deriving approximate solutions, we can approximate the function as a linear combination of the following terms of given by (6):
where the coefficients are given by
Now, in Theorem 2 below, we construct the approximation formula for .
Theorem 2.
Given the approximation (7), it is asserted for that
where
and
with
being the greatest integer less than or equal to .
Proof.
We apply the linearization property of the fractional derivative with generalized Mittag-Leffler kernel in (1) and Equation (7). We thus find that
The connection between Equations (1), (6) and (11) leads us to
and
The desired result (8) follows when we combine the Equations (11)–(13). The proof of Theorem 2 is thus completed. □
4. Construction of the Schemes of the Proposed Models
In this section, we construct the schemes of the three models presented below, which are based on the spectral method and the properties of the Legendre polynomials as described in the preceding section.
Model 1
Consider the following fractional differential equation:
where is the fractional derivative based on the generalized Mittag-Leffler kernel in the Liouville-Caputo sense.
The exact solution of the initial value problem (14) can be found by applying the operator on both sides of the first Equation (14) with the help of Remark 4. We thus get
For this model, we now transform Equation (14) into a system of algebraic equations. Indeed, by using a linear combination of the first terms of , we can approximate and expand the function as follows:
In view of Formulas (8) and (16), and upon substituting them into Equation (14), we find that
Thus, in order to obtain the system of algebraic equations, we collocate Equation (17) at points as given below:
If we now substitute Equation (16) into (14), we obtain the following initial condition:
Since the set of Equations (18) to (19) is linear, we can solve it by using known methods and we obtain .
Finally, we substitute these into (16) and obtain the approximate solution of the initial-value problem (14).
Model 2
In this second model, we consider the following fractional-order Fisher equation (FFE) with the generalized Mittag-Leffler kernel:
The exact solution of the Fisher Equation (20) for is given by (see [42])
subject to the following initial and boundary conditions:
with
Based on the following the steps, we can obtain the numerical solution of Model 2 as follows.
- We write where .
- We can approximate and expand the function by using a linear combination of the first terms of as given below:
- In view of the Formulas (8) and (24), and upon substituting them into Equation (20), we obtain
- We collocate Equation (25) at points in order to get the following system of first-order ODEs:
- Substituting from Equation (24) into (20), we can obtain the following boundary conditions of the system (26):
- To obtain systems of nonlinear algebraic equations, we apply the FDM to the ODE (26) and (27), whereare unknown. We thus obtainandwith
- We can explain more fully for the case when . By using the NIM, we obtain the following system given by (28) and (30) in the matrix form:whereis the inverse of the Jacobian matrix and is the vector that represents the nonlinear equations. The initial solution can be obtained by setting in the initial condition (23) as detailed below.
- (a)
- After substituting Equation (24) into the initial condition (23), we obtain
- (b)
- Solving the following system of linear equations, we obtain the components of the initial solution :where the points are the roots of .
Model 3
Now, with the third model we consider the fractional Korteweg–de Vries equation (FKdVE) with generalized Mittag-Leffler kernel
where and .
The exact solution for the classical integer-form is given by
subject to the following initial and boundary conditions:
and
Following the same steps as we used in the cases of Model 1 and Model 2, together with
and , we can obtain the following set of algebraic equations solving Model 3:
5. Numerical Results, Graphical Illustrations and Discussions
In this section, we discuss the numerical results for the approximate solutions presented in Section 4. These results will be illustrated in a number of figures.
For Model 1, the accuracy and efficiency of the numerical approximate solution are verified by comparison with the analytical solution that we computed. For Model 2 and Model 3, the accuracy of the numerical solutions can be satisfied by using the residual error function. This will also be illustrated in various figures.
Figure 1 shows the behavior of the analytical solution (15) of Model 1 for different values of and . In this figure, we set and
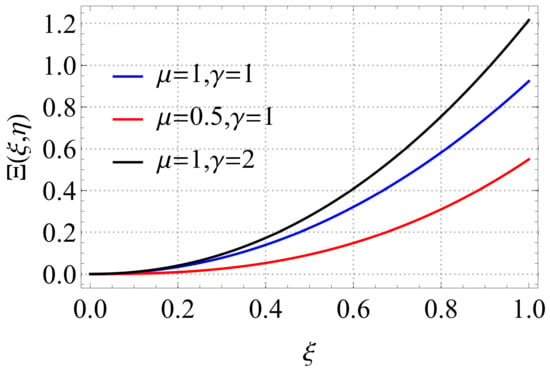
Figure 1.
Graph of the exact solutions of Model 1, with and and for different values of and .
Figure 2 shows the absolute error between the approximate and the exact solutions of Model 1 with and and for different values of and It is clear from Figure 2 that the absolute error is very small and of the order of the error is . This gives a good impression of the accuracy and efficiency of the solutions, since the comparison is made with the analytical solution. This impression is useful when numerical solutions are found for fractional-order systems that do not have an analytical solution.
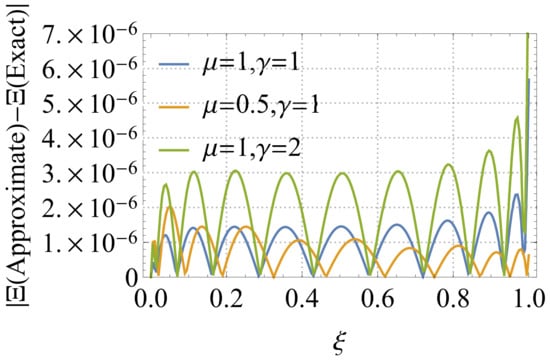
Figure 2.
Graph of the absolute error between the exact and the approximate solutions of Model 1 when and and for different values of and .
In Figure 3, we show the approximate solution of the FFE for different values of . In Model 2, we set , and . In Model 2, the analytical solution is unknown; thus, in order to verify the accuracy of the approximate solution, we define the residual error function (REF) as follows:
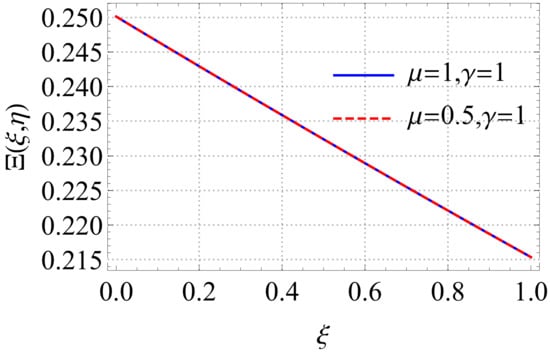
Figure 3.
Graph of the solutions of Model 2, with and and for different values of and .
We illustrate the REF in Figure 4 for different values of and , and for and We note from this illustration in Figure 4 that the order of the REF is .
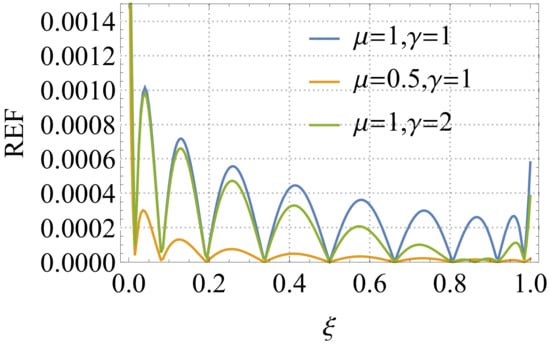
Figure 4.
Graph of the residual error function (REF) of the approximate solution of Model 2, with and and for different values of and .
In the case of Model 3 for the FKdVE, we follow the same procedures and treatments that were applied for Model 2. In Model 3, we set and The numerical results of Model 3 are illustrated in Figure 5 and Figure 6.
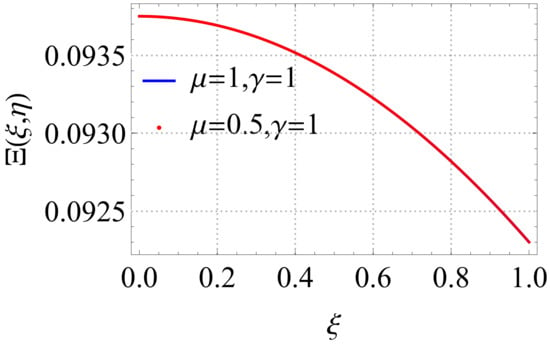
Figure 5.
Graph of the solution of Model 3, with and and for different values of and .
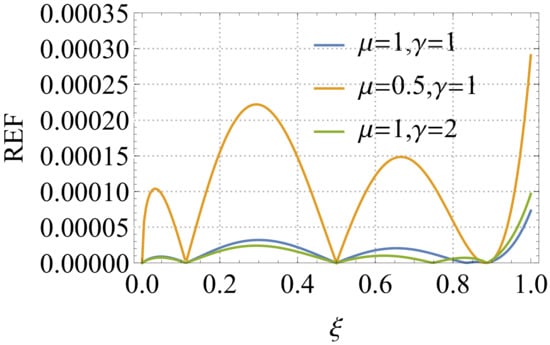
Figure 6.
Graph of the of the residual error function (REF) of the approximate solution of Model 3, with and and for different values of and .
Remarkably, it is presumably the first time that the numerical results, which are presented in this paper, are based upon the use of the fractional derivatives and also upon the properties of the Legendre polynomials as well as GMLK.
6. Conclusions
In this paper, classical (integer-order) derivatives have been replaced by some fractional-order derivatives, which are based upon generalized Mittag-Leffler type kernels. Three fractional-order models have been presented: The first model belongs to fractional ordinary differential equations, and the other two models involve fractional partial differential equations. In the first case, the treatment was achieved by directly converting the fractional-order model with the help of the Legendre polynomials to a system of algebraic equations and then finding approximate solutions by using the Newton-Raphson method, in addition to finding the solution analytically. In the second and the third fractional-order models, they were converted into differential equations, and by using the finite-difference method (FDM) to approximate the derivative with respect to time, we were led to algebraic equations. We then obtained approximate solutions as in the first model.
The accuracy of the solution was verified in the first model in comparison with the exact solution. For the second and the third models, the accuracy of the approximate solutions was verified by calculating the residual error function (REF). In all cases, the order of the error is small, and its value ranges between and In all of the calculations in this paper, the Mathematica software package was used. Finally, we suggest that the researchers test the algorithm’s efficiency using several special functions, such as Bernstein, Chebyshev, and others.
Author Contributions
H.M.S. suggested and initiated this work, performed its validation, as well as reviewed and edited the paper. A.-K.N.A. performed the formal analysis of the investigation, the methodology, the software, and wrote the first draft of the paper. K.M.S. performed the formal analysis of the investigation, the methodology, the software, and wrote the first draft of the paper. W.M.H. performed the methodology, the software, and reviewed and edited the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that there are no conflict of interest regarding the publication of this paper.
References
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Reading, UK; Tokyo, Japan; Paris, France; Berlin, Germany; Langhorne, PA, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK; Sydney, NSW, Australia; Tokyo, Japan; Toronto, ON, Canada, 1999; Volume 198. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications, 2nd ed.; Springer: New York, NY, USA, 2020. [Google Scholar]
- Srivastava, H.M. Some parametric and argument variations of the operators of fractional calculus and related special functions and integral transformations. J. Nonlinear Convex Anal. 2021, 22, 1501–1520. [Google Scholar]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
- Diethelm, K. An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. (ETNA) 1997, 5, 1–6. [Google Scholar]
- Khader, M.M.; Saad, K.M. A numerical approach for solving the problem of biological invasion (fractional Fisher equation) using Chebyshev spectral collocation method. Chaos Solitons Fractals 2018, 110, 169–177. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K.M. On the numerical evaluation for studying the fractional KdV, KdV-Burgers’, and Burgers’ equations. Eur. Phys. J. Plus 2018, 133, 1–13. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Saad, K.M.; Khader, M.M.; Gómez-Aguilar, J.F.; Baleanu, D. Numerical solutions of the fractional Fisher’s type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023116. [Google Scholar] [CrossRef]
- Fernandez, A.; Abdeljawad, T.; Baleanu, D. Relations between fractional models with three-parameter Mittag-Leffler kernels. Adv. Differ. Equ. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Abdeljawad, T. A Lyapunov type inequality for fractional operators with nonsingular Mittag-Leffler kernel. J. Inequalities Appl. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Hammouch, Z. On a class of ordinary differential equations in the frame of Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 16–20. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. Numerical approximations to the nonlinear fractional-order logistic population model with fractional-order Bessel and Legendre bases. Chaos Solitons Fractals 2021, 145, 110779. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Saad, K.M.; Khan, M.A.; Agarwal, P. Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: A fractional calculus approach. Physica A Stat. Mech. Its Appl. 2019, 523, 48–65. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ahmad, H.; Ahmad, I.; Thounthong, P.; Khan, M.N. Numerical simulation of 3-D fractional-order convection-diffusion PDE by a local meshless method. Therm. Sci. 2021, 25, 347–358. [Google Scholar] [CrossRef]
- Saad, K.M. A reliable analytical algorithm for space-time fractional cubic isothermal autocatalytic chemical system. Pramana J. Phys. 2018, 91, 1–15. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M. Numerical investigation of the fractional-order Liénard and Duffing equation arising in oscillating circuit theory. Front. Phys. 2020, 8, 120. [Google Scholar] [CrossRef]
- Alomari, A.K. Homotopy-Sumudu transforms for solving system of fractional partial differential equations. Adv. Differ. Equ. 2020, 2020, 222. [Google Scholar] [CrossRef]
- Kumar, S.; Pandey, R.K.; Srivastava, H.M.; Singh, G.N. A convergent collocation approach for generalized fractional integro-differential equations using Jacobi poly-fractonomials. Mathematics 2021, 9, 979. [Google Scholar] [CrossRef]
- Alomari, A.K.; Syam, M.I.; Anakira, N.R.; Jameel, A.F. Homotopy Sumudu transform method for solving applications in physics. Results Phys. 2020, 18, 103265. [Google Scholar] [CrossRef]
- Aljhani, S.; Noorani, M.S.; Alomari, A.K. Numerical solution of fractional-order HIV Model using homotopy method. Discret. Dyn. Nat. Soc. 2020, 2020, 2149037. [Google Scholar] [CrossRef] [Green Version]
- Saad, K.M.; Al-Sharif, E.H.F. Comparative study of a cubic autocatalytic reaction via different analysis methods. Discret. Contin. Dyn.-Syst.-S 2019, 12, 665–684. [Google Scholar]
- Saad, K.M.; Gómez-Aguilar, J.F. Coupled reaction-diffusion waves in a chemical system via fractional derivatives in Liouville-Caputo sense. Rev. Mex. Física 2018, 64, 539–547. [Google Scholar]
- Saad, K.M.; Gómez-Aguilar, J.F. Analysis of reaction-diffusion system via a new fractional derivative with non-singular kernel. Physica A Stat. Mech. Its Appl. 2018, 509, 703–716. [Google Scholar] [CrossRef]
- Saad, K.M.; Baleanu, D.; Atangana, A. New Fractional derivatives applied to the Korteweg-de Vries and Korteweg-de Vries-Burgers equations. Comput. Appl. Math. 2018, 37, 5203–5216. [Google Scholar] [CrossRef]
- Saad, K.M.; Deniz, S.; Baleanu, D. On a new modified fractional analysis of Nagumo equation. Int. J. Biomath. 2019, 12, 1950034. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M. Some new and modified fractional analysis of the time-fractional Drinfeld-Sokolov-Wilson system. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 113104. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Deniz, S.; Saad, K.M. An efficient semi-analytical method for solving the generalized regularized long wave equations with a new fractional derivative operator. J. King Saud Univ. Sci. 2021, 33, 101345. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M. A comparative Study of the fractional-order clock chemical model. Mathematics 2020, 8, 1436. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Gómez-Aguilar, J.F.; Almadiy, A.A. Some new mathematical models of the fractional-order system of human immune against IAV infection. Math. Biosci. Eng. 2020, 17, 4942–4969. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Khader, M.M. An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals 2020, 140, 110174. [Google Scholar]
- Saad, K.M. Comparative study on fractional isothermal chemical model. Alex. Eng. J. 2021, 60, 3265–3274. [Google Scholar] [CrossRef]
- Saad, K.M. Comparing the Caputo, Caputo-Fabrizio and Atangana-Baleanu derivative with fractional order: Fractional cubic isothermal auto-catalytic chemical system. Eur. Phys. J. Plus 2018, 133, 94. [Google Scholar] [CrossRef]
- Abdeljawad, T. Fractional difference operators with discrete generalized Mittag-Leffler kernels. Chaos Solitons Fractals 2019, 126, 315–324. [Google Scholar] [CrossRef]
- Abdeljawad, T. Fractional operators with generalized Mittag-Leffler kernels and their iterated differintegrals. Chaos Interdiscip. Nonlinear Sci. 2019, 29, 023102. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D. On fractional derivatives with generalized Mittag-Leffler kernels. Adv. Differ. Equ. 2018, 2018, 468. [Google Scholar] [CrossRef]
- Hesthaven, J.; Gottlieb, S.; Gottlieb, D. Spectral Methods for Time-Dependent Problems; Cambridge University Press: Cambridge, UK; London, UK; New York, NY, USA, 2007. [Google Scholar]
- Feng, Z. Travelling wave solutions and proper solutions to the two-dimensional Burgers-Korteweg-de Vries. J. Phys. A Math. Gen. 2003, 36, 8817–8827. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).