Jacobi Spectral Collocation Technique for Time-Fractional Inverse Heat Equations
Abstract
:1. Introduction
2. Preliminaries and Notations
3. Fully Spectral Collocation Treatment
3.1. Initial-Boundary Conditions
3.2. Nonlocal Conditions
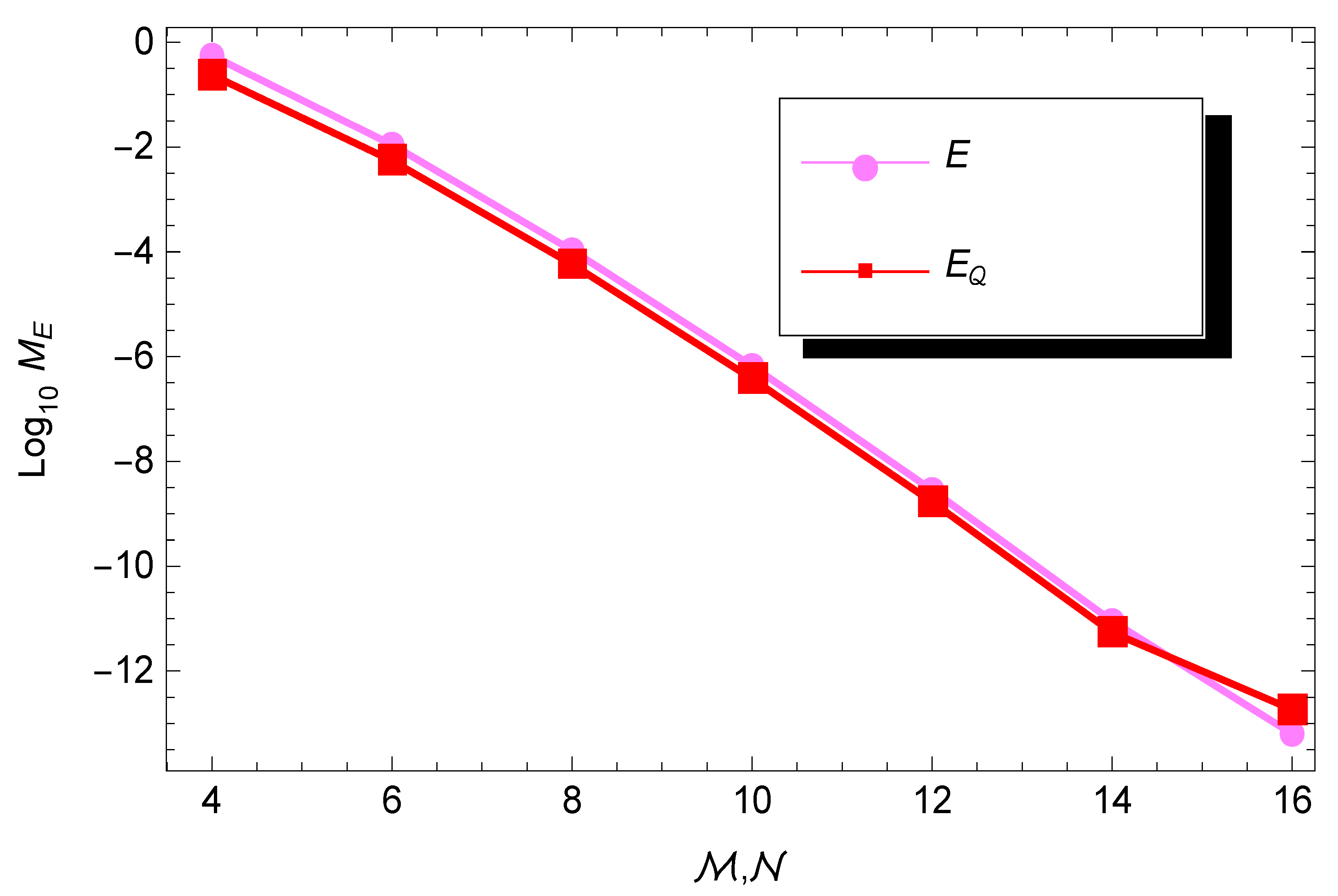
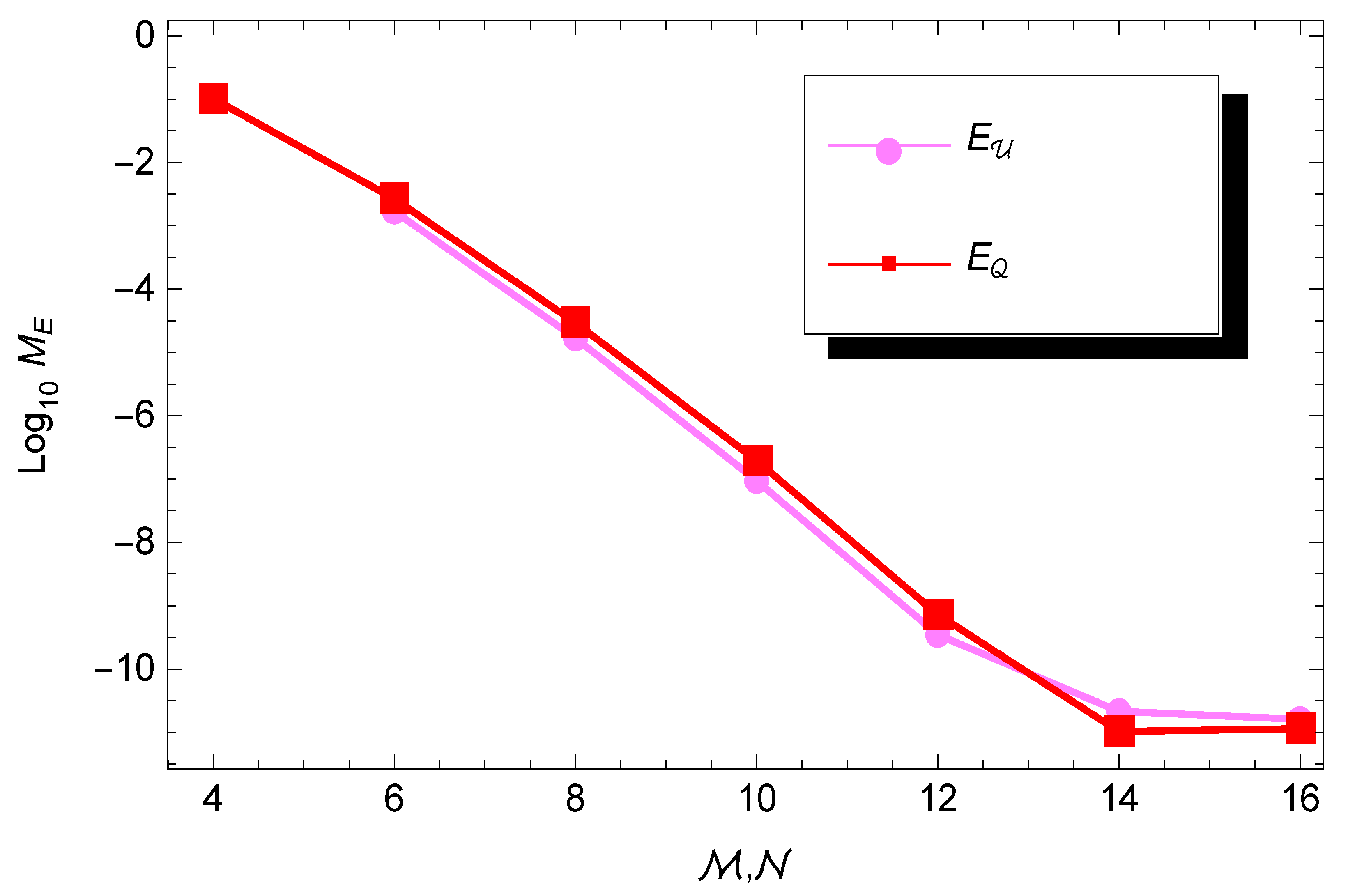
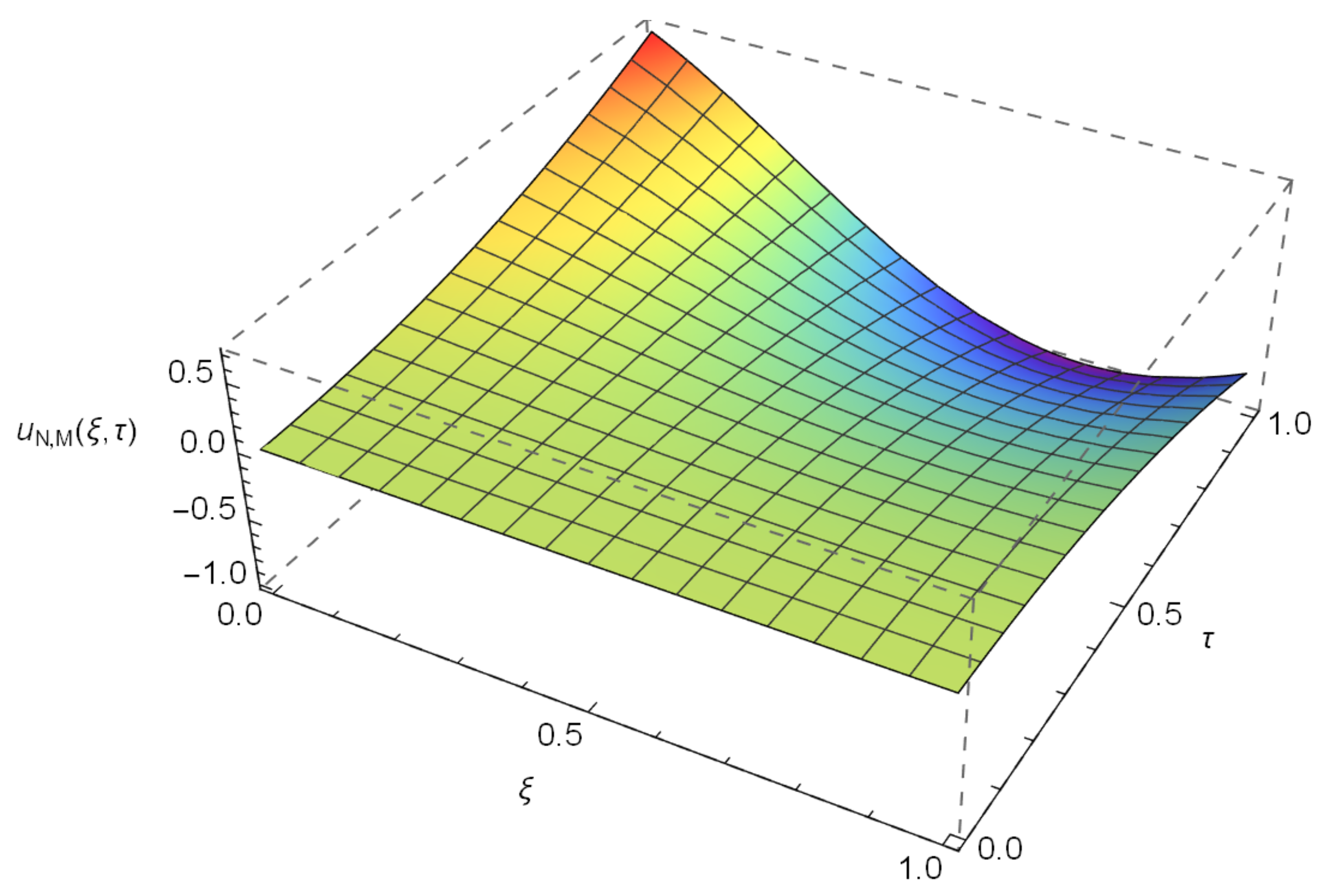
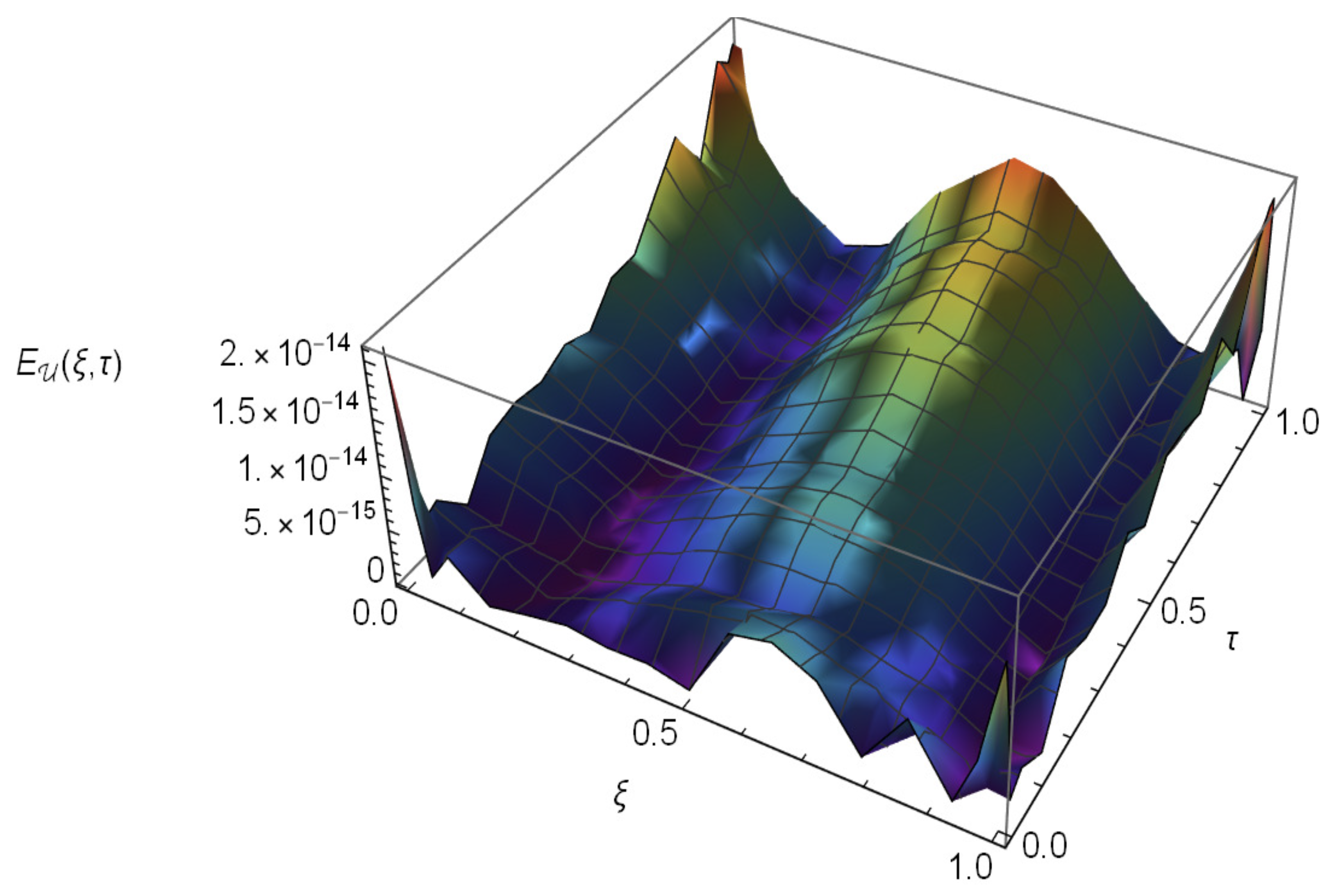
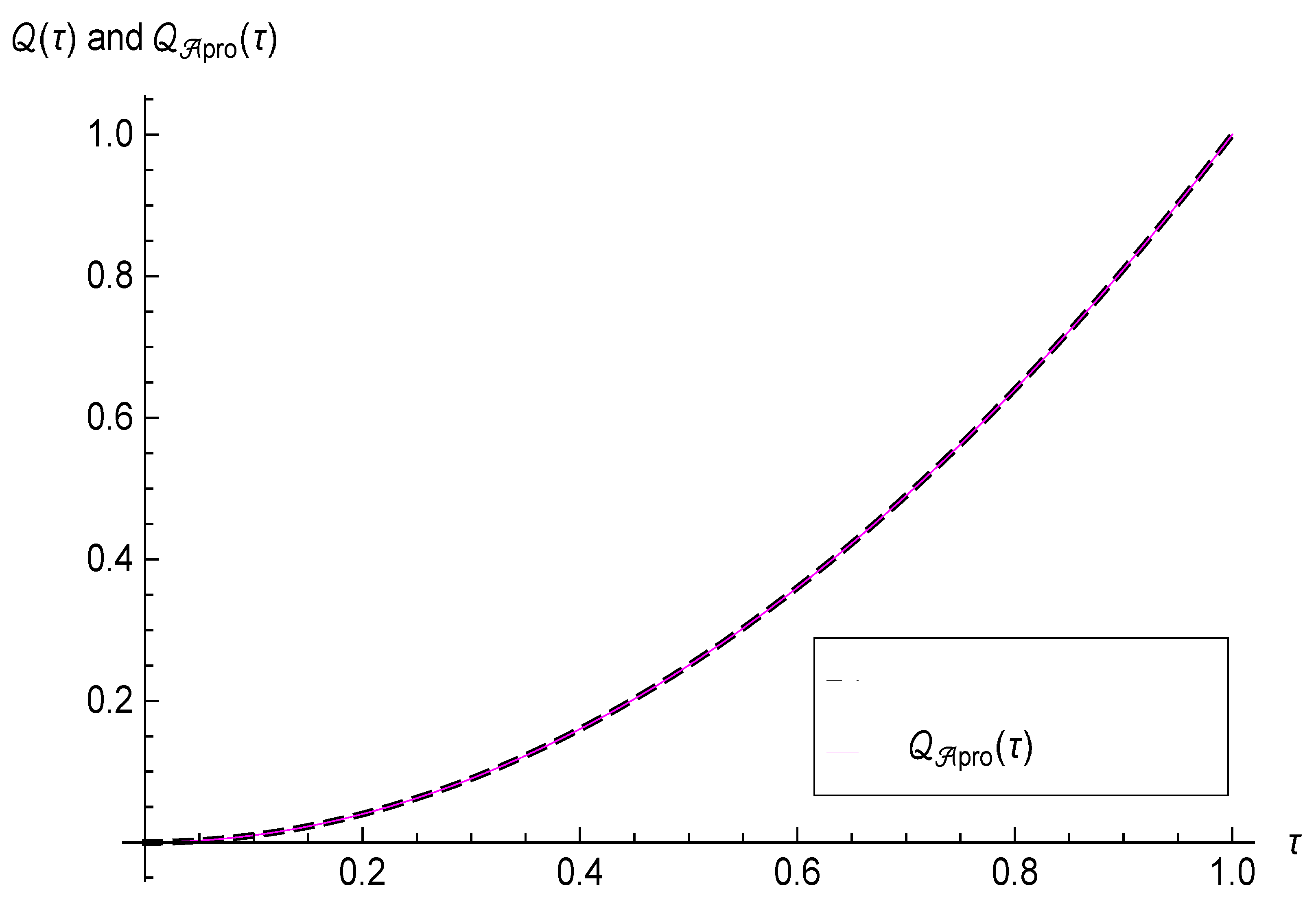
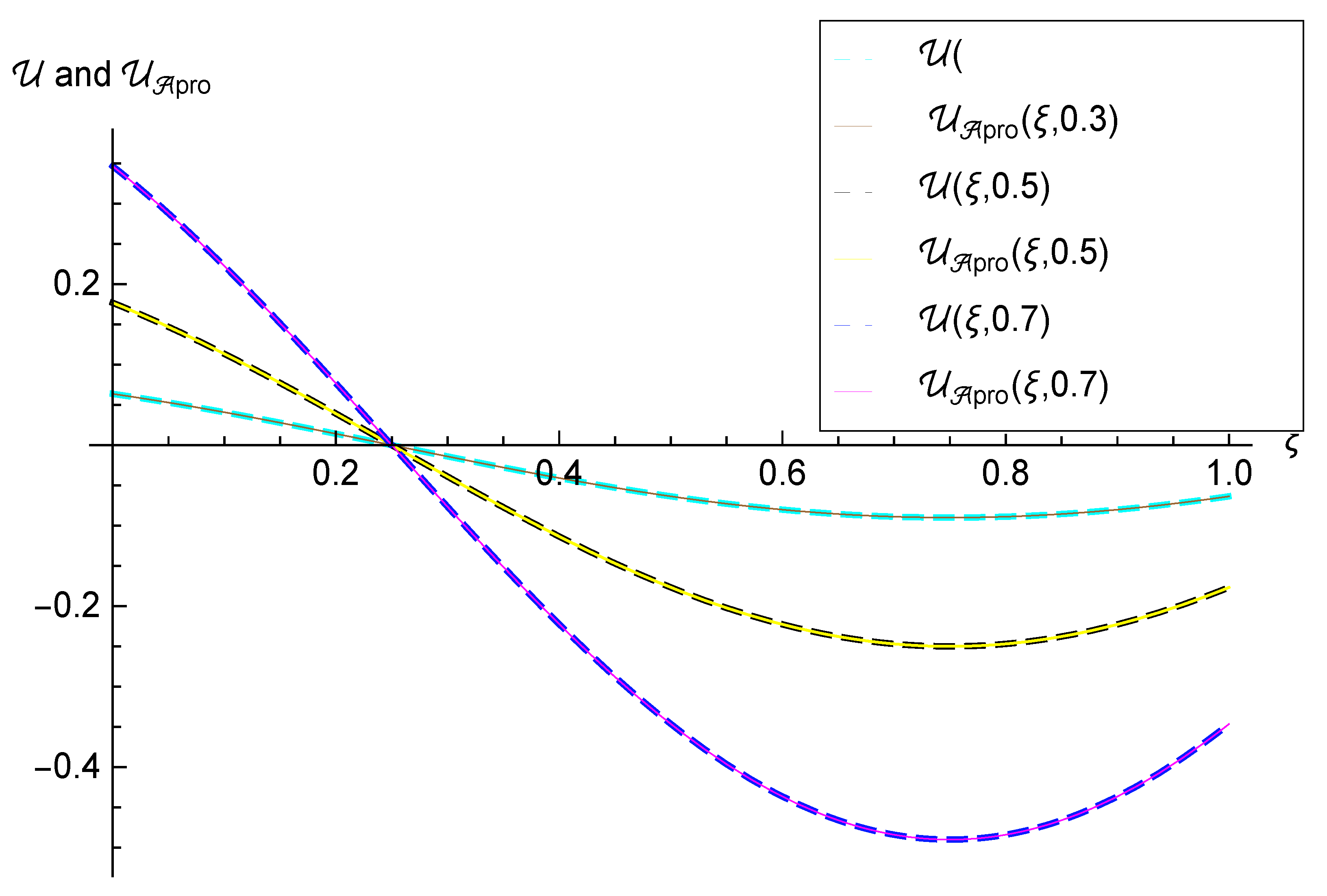
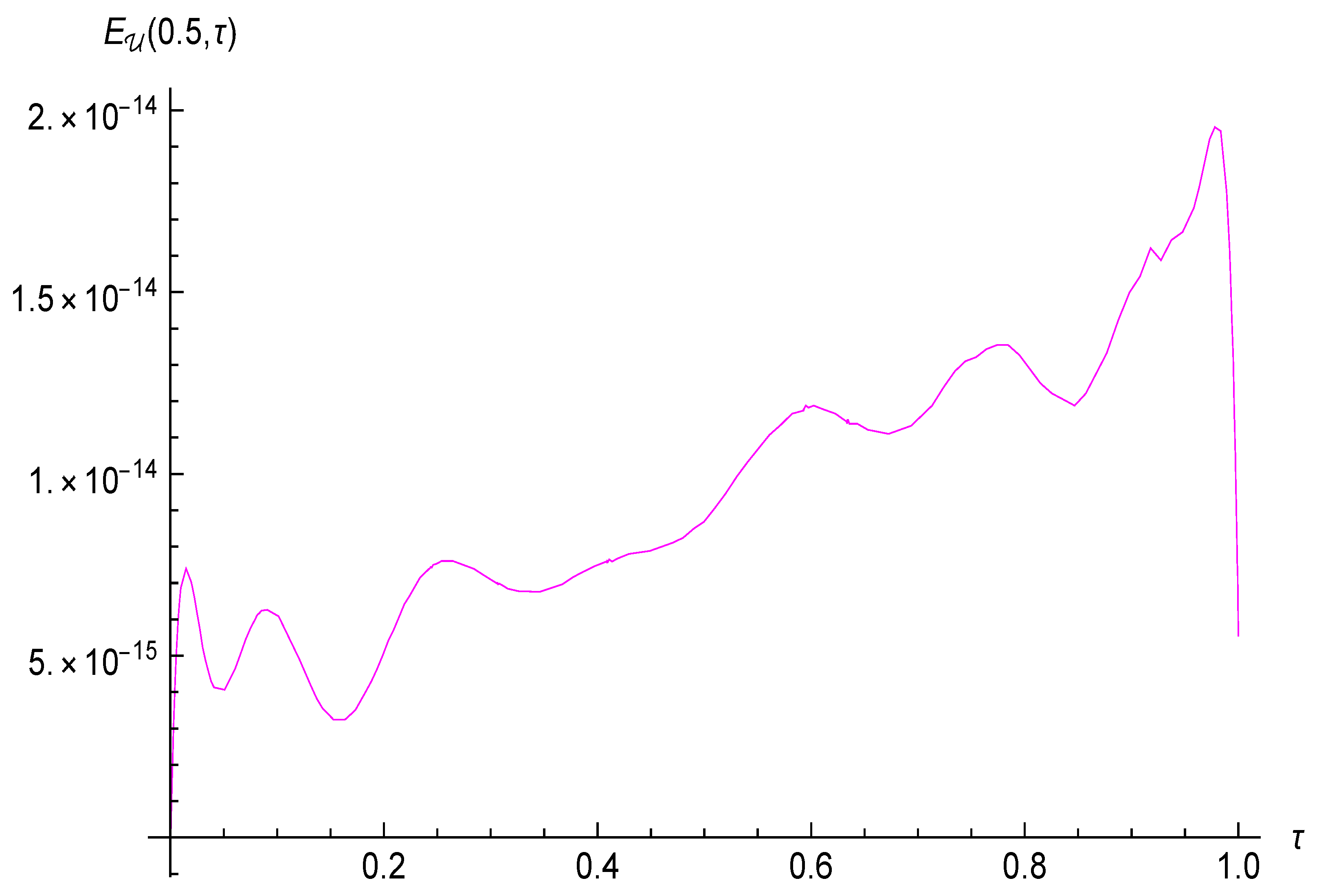
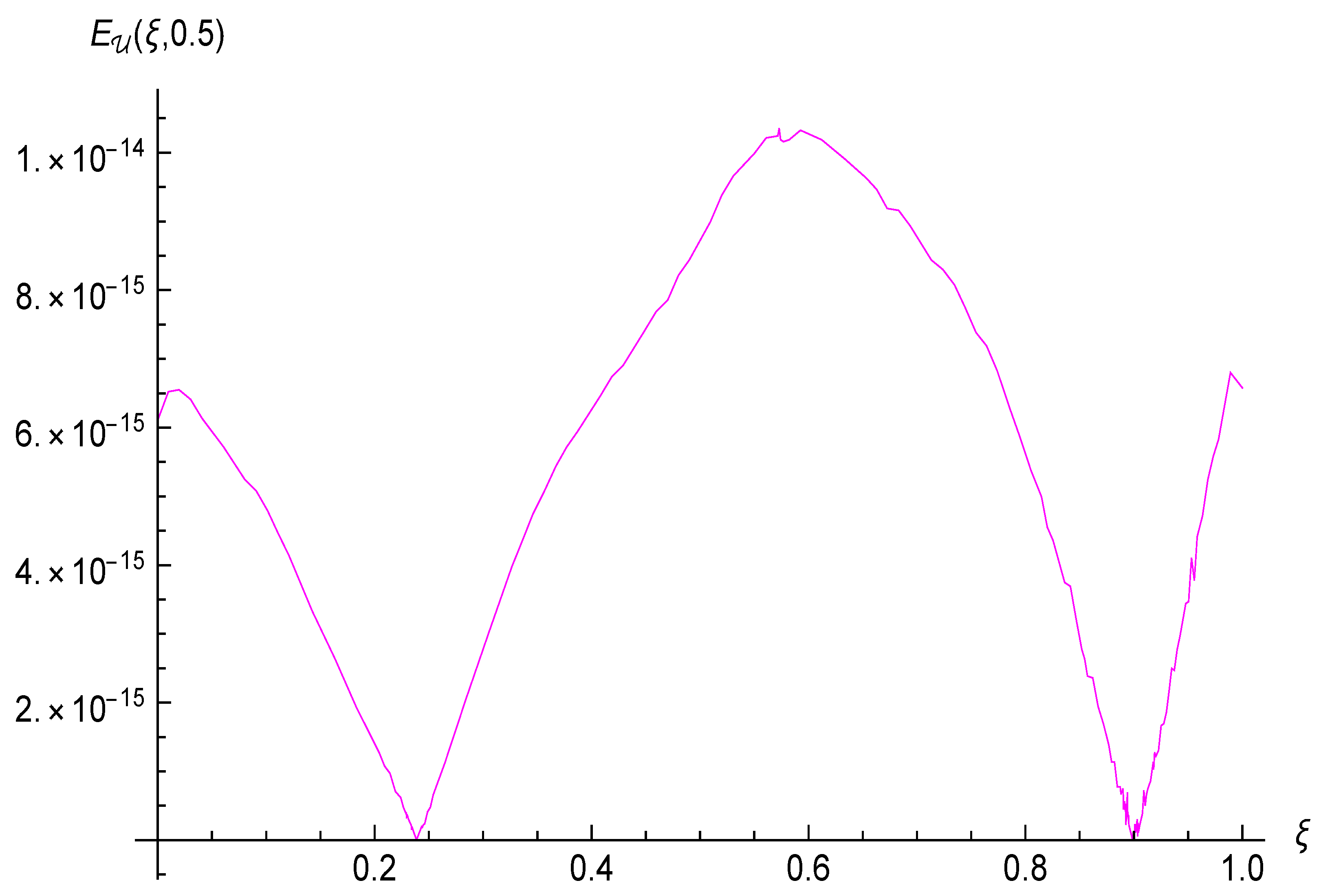
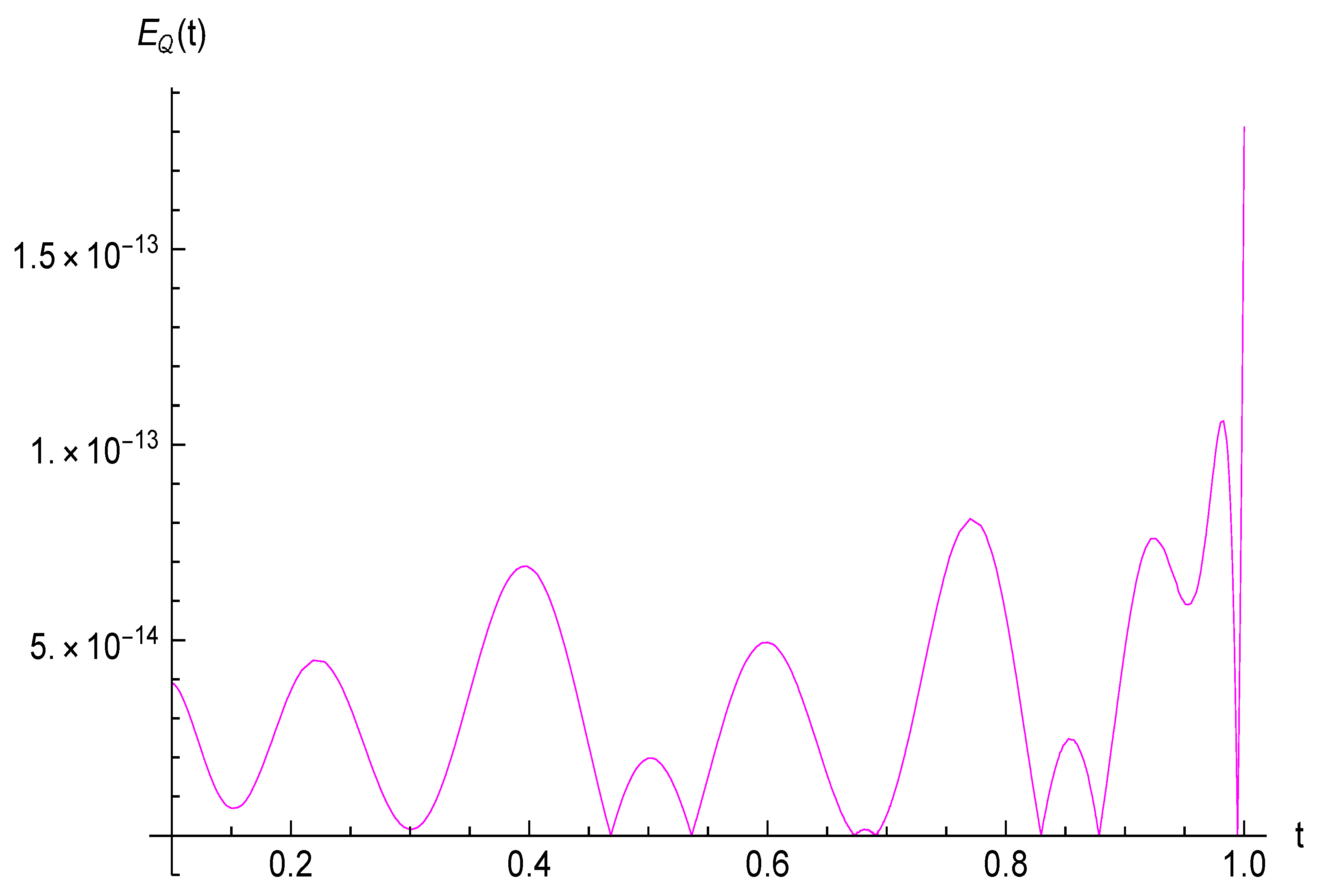
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- West, B.J. Fractional Calculus View of Complexity: Tomorrow’s Science; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- West, B.J. Nature’s Patterns and the Fractional Calculus; De Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Seki, K.; Wojcik, M.; Tachiya, M. Fractional reaction-diffusion equation. J. Chem. Phys. 2003, 119, 2165–2170. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Magin, R.L.; Bhalekar, S.; Daftardar-Gejji, V. Chaos in the fractional order nonlinear Bloch equation with delay. Commun. Nonlinear Sci. Numer. Simul. 2015, 25, 41–49. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Liu, Q.; Anh, V. Numerical simulation of anomalous infiltration in porous media. Numer. Algorithms 2015, 68, 443–454. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Sumelka, W.; Łuczak, B.; Gajewski, T.; Voyiadjis, G. Modelling of AAA in the framework of time-fractional damage hyperelasticity. Int. J. Solids Struct. 2020, 206, 30–42. [Google Scholar] [CrossRef]
- Podlubnv, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA; Boston, MA, USA, 1999. [Google Scholar]
- Zhou, Y.; Zhang, Y. Noether symmetries for fractional generalized Birkhoffian systems in terms of classical and combined Caputo derivatives. Acta Mech. 2020, 231, 3017–3029. [Google Scholar] [CrossRef]
- Eidelman, S.D.; Kochubei, A.N. Cauchy problem for fractional diffusion equations. J. Differ. Equ. 2004, 199, 211–255. [Google Scholar] [CrossRef] [Green Version]
- Luchko, Y. Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation. Comput. Math. Appl. 2010, 59, 1766–1772. [Google Scholar] [CrossRef] [Green Version]
- Metzler, R.; Klafter, J. Boundary value problems for fractional diffusion equations. Phys. A Stat. Mech. Appl. 2000, 278, 107–125. [Google Scholar] [CrossRef]
- Yuste, S.; Acedo, L.; Lindenberg, K. Reaction front in an A + B → C reaction-subdiffusion process. Phys. Rev. E 2004, 69, 036126. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Burrage, K. Novel techniques in parameter estimation for fractional dynamical models arising from biological systems. Comput. Math. Appl. 2011, 62, 822–833. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Jiang, X.; Wang, C. Numerical algorithms to estimate relaxation parameters and Caputo fractional derivative for a fractional thermal wave model in spherical composite medium. Appl. Math. Comput. 2016, 274, 106–118. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.; Turner, I. Numerical solution of the space fractional Fokker–Planck equation. J. Comput. Appl. Math. 2004, 166, 209–219. [Google Scholar] [CrossRef] [Green Version]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Fan, W.; Jiang, X.; Qi, H. Parameter estimation for the generalized fractional element network Zener model based on the Bayesian method. Phys. A Stat. Mech. Appl. 2015, 427, 40–49. [Google Scholar] [CrossRef]
- Cannon, J.R.; van der Hoek, J. Diffusion subject to the specification of mass. J. Math. Anal. Appl. 1986, 115, 517–529. [Google Scholar] [CrossRef] [Green Version]
- Cannon, J.R.; Esteva, S.P.; Van Der Hoek, J. A Galerkin procedure for the diffusion equation subject to the specification of mass. SIAM J. Numer. Anal. 1987, 24, 499–515. [Google Scholar] [CrossRef]
- Huang, C.H.; Lin, C.Y. Inverse hyperbolic conduction problem in estimating two unknown surface heat fluxes simultaneously. J. Thermophys. Heat Transf. 2008, 22, 766–774. [Google Scholar] [CrossRef]
- Yang, C.y. Direct and inverse solutions of the two-dimensional hyperbolic heat conduction problems. Appl. Math. Model. 2009, 33, 2907–2918. [Google Scholar] [CrossRef]
- Tang, D.; Araki, N. An Inverse Analysis to Estimate Relaxation Parameters and Thermal Diffusivity with a Universal Heat Conduction Equation 1. Int. J. Thermophys. 2000, 21, 553–561. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J. Total variation regularization for a backward time-fractional diffusion problem. Inverse Probl. 2013, 29, 115013. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X. Inverse source problem for a fractional diffusion equation. Inverse Probl. 2011, 27, 035010. [Google Scholar] [CrossRef]
- Bhrawy, A.H. An efficient Jacobi pseudospectral approximation for nonlinear complex generalized Zakharov system. Appl. Math. Comput. 2014, 247, 30–46. [Google Scholar] [CrossRef]
- Bhrawy, A.H. A Jacobi spectral collocation method for solving multi-dimensional nonlinear fractional sub-diffusion equations. Numer. Algorithms 2016, 73, 91–113. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A.; Baleanu, D.; Amin, A.Z. A spectral technique for solving two-dimensional fractional integral equations with weakly singular kernel. Hacet. J. Math. Stat. 2018, 47, 553–566. [Google Scholar] [CrossRef] [Green Version]
- Abdelkawy, M.A.; Doha, E.H.; Bhrawy, A.H.; Amin, A.Z. Efficient pseudospectral scheme for 3D integral equations. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci 2017, 18, 199–206. [Google Scholar]
- Ameen, I.G.; Zaky, M.A.; Doha, E.H. Singularity preserving spectral collocation method for nonlinear systems of fractional differential equations with the right-sided Caputo fractional derivative. J. Comput. Appl. Math. 2021, 392, 113468. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Amin, A.Z.; Bhrawy, A.H.; Machado, J.A.T.; Lopes, A.M. Jacobi collocation approximation for solving multi-dimensional Volterra integral equations. Int. J. Nonlinear Sci. Numer. Simul. 2017, 18, 411–425. [Google Scholar] [CrossRef]
- Doha, E.; Abdelkawy, M.; Amin, A.; Baleanu, D. Spectral technique for solving variable-order fractional Volterra integro-differential equations. Numer. Methods Partial. Differ. Equ. 2018, 34, 1659–1677. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Abdelkawy, M.A.; Van Gorder, R.A. Jacobi–Gauss–Lobatto collocation method for the numerical solution of 1+ 1 nonlinear Schrödinger equations. J. Comput. Phys. 2014, 261, 244–255. [Google Scholar] [CrossRef]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.Z.; Baleanu, D. Approximate solutions for solving nonlinear variable-order fractional Riccati differential equations. Nonlinear Anal. Model. Control. 2019, 24, 176–188. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A.; Baleanu, D. New numerical approximations for space-time fractional Burgers’ equations via a Legendre spectral-collocation method. Rom. Rep. Phys. 2015, 67, 340–349. [Google Scholar]
- Bhrawy, A.H.; Zaky, M.A. Highly accurate numerical schemes for multi-dimensional space variable-order fractional Schrödinger equations. Comput. Math. Appl. 2017, 73, 1100–1117. [Google Scholar] [CrossRef]
- Bhrawy, A.; Zaky, M. An improved collocation method for multi-dimensional space–time variable-order fractional Schrödinger equations. Appl. Numer. Math. 2017, 111, 197–218. [Google Scholar] [CrossRef]
- Bhrawy, A.; Doha, E.; Baleanu, D.; Ezz-Eldien, S.; Abdelkawy, M. An accurate numerical technique for solving fractional optimal control problems. Differ. Equ. 2015, 15, 23. [Google Scholar]
- Bhrawy, A.H.; Abdelkawy, M.A. A fully spectral collocation approximation for multi-dimensional fractional Schrödinger equations. J. Comput. Phys. 2015, 294, 462–483. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Zaky, M.A.; Bhrawy, A.H.; Baleanu, D. Numerical simulation of time variable fractional order mobile-immobile advection-dispersion model. Rom. Rep. Phys. 2015, 67, 773–791. [Google Scholar]
- Hendy, A.S.; Zaky, M.A.; Hafez, R.M.; De Staelen, R.H. The impact of memory effect on space fractional strong quantum couplers with tunable decay behavior and its numerical simulation. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef] [Green Version]
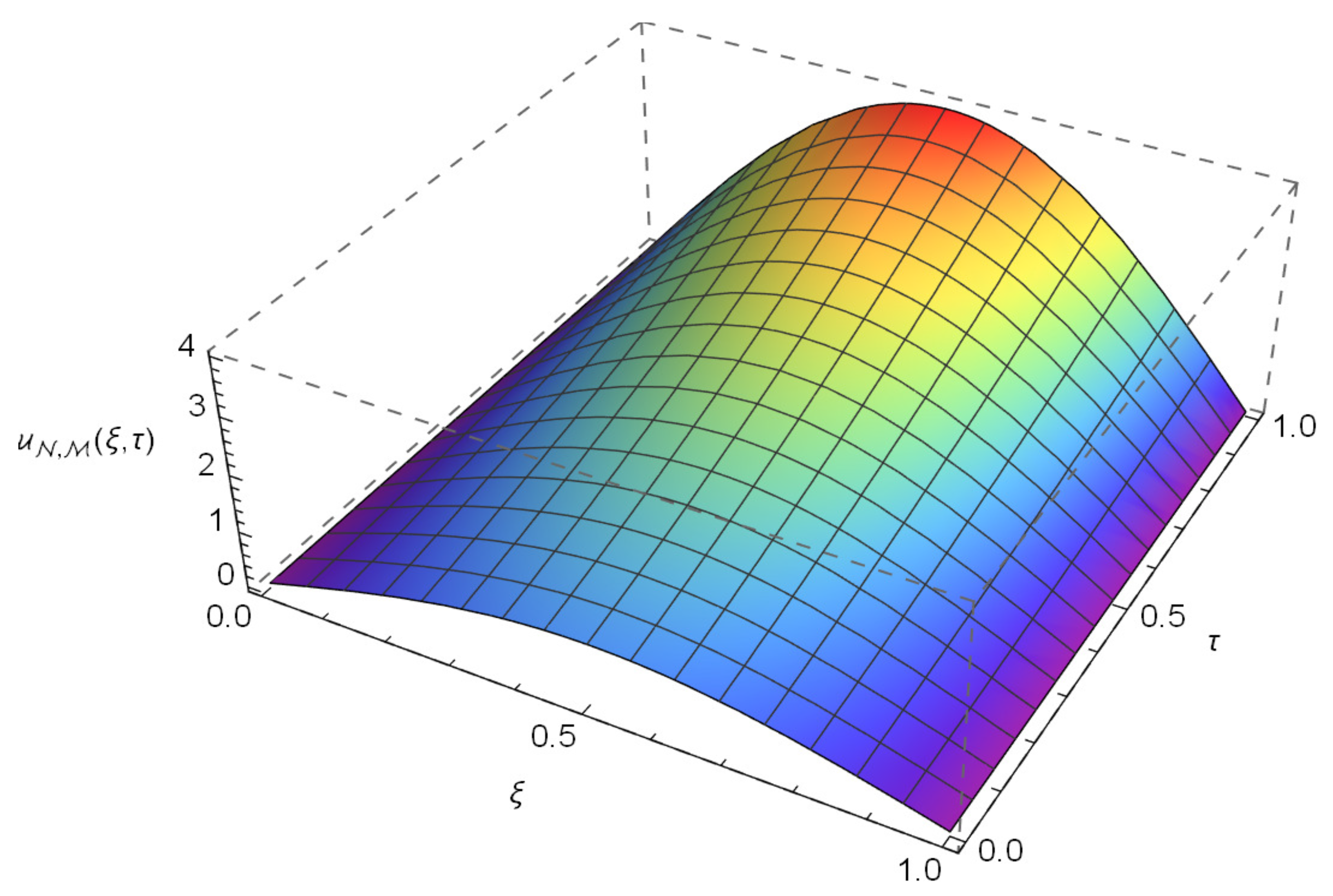

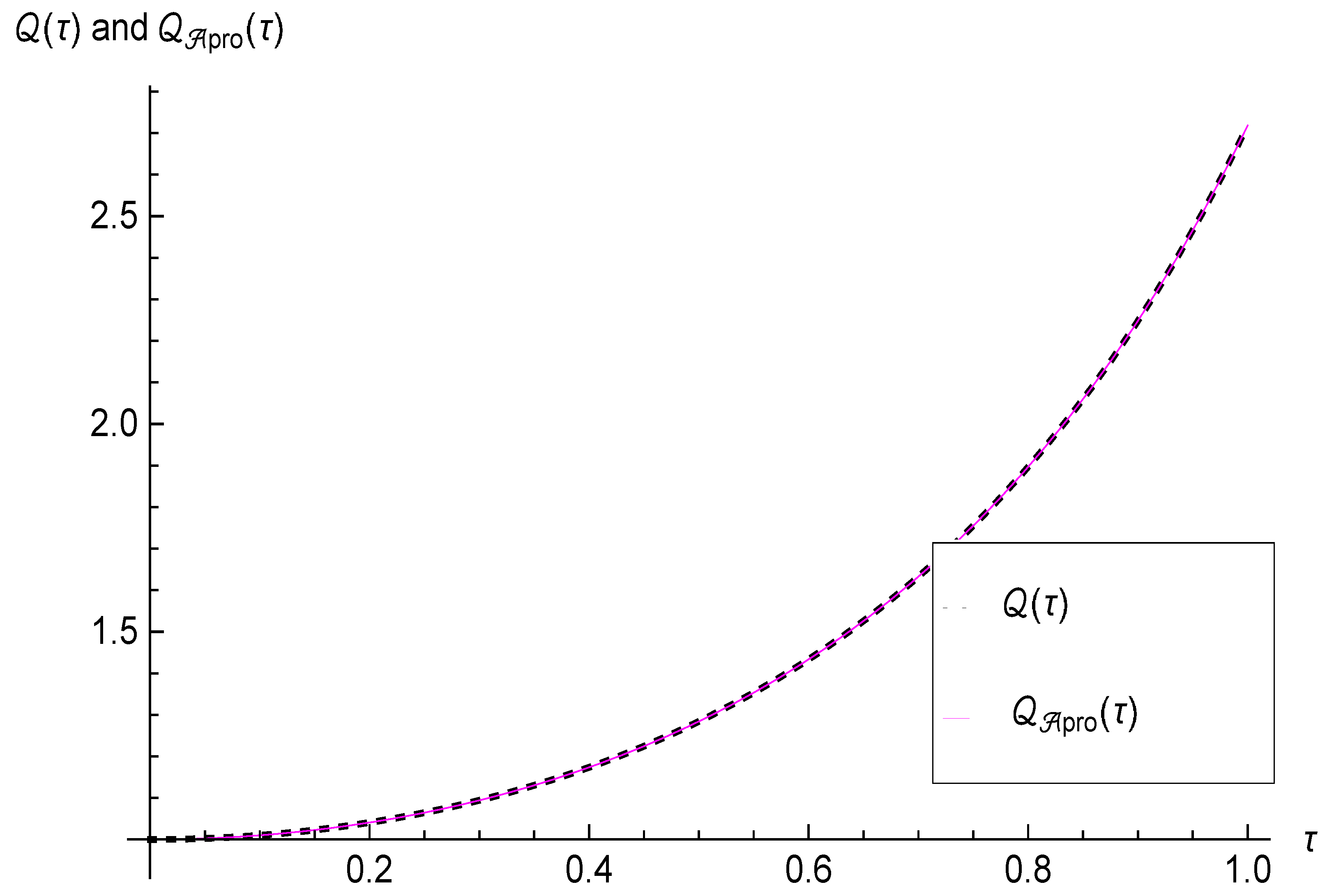


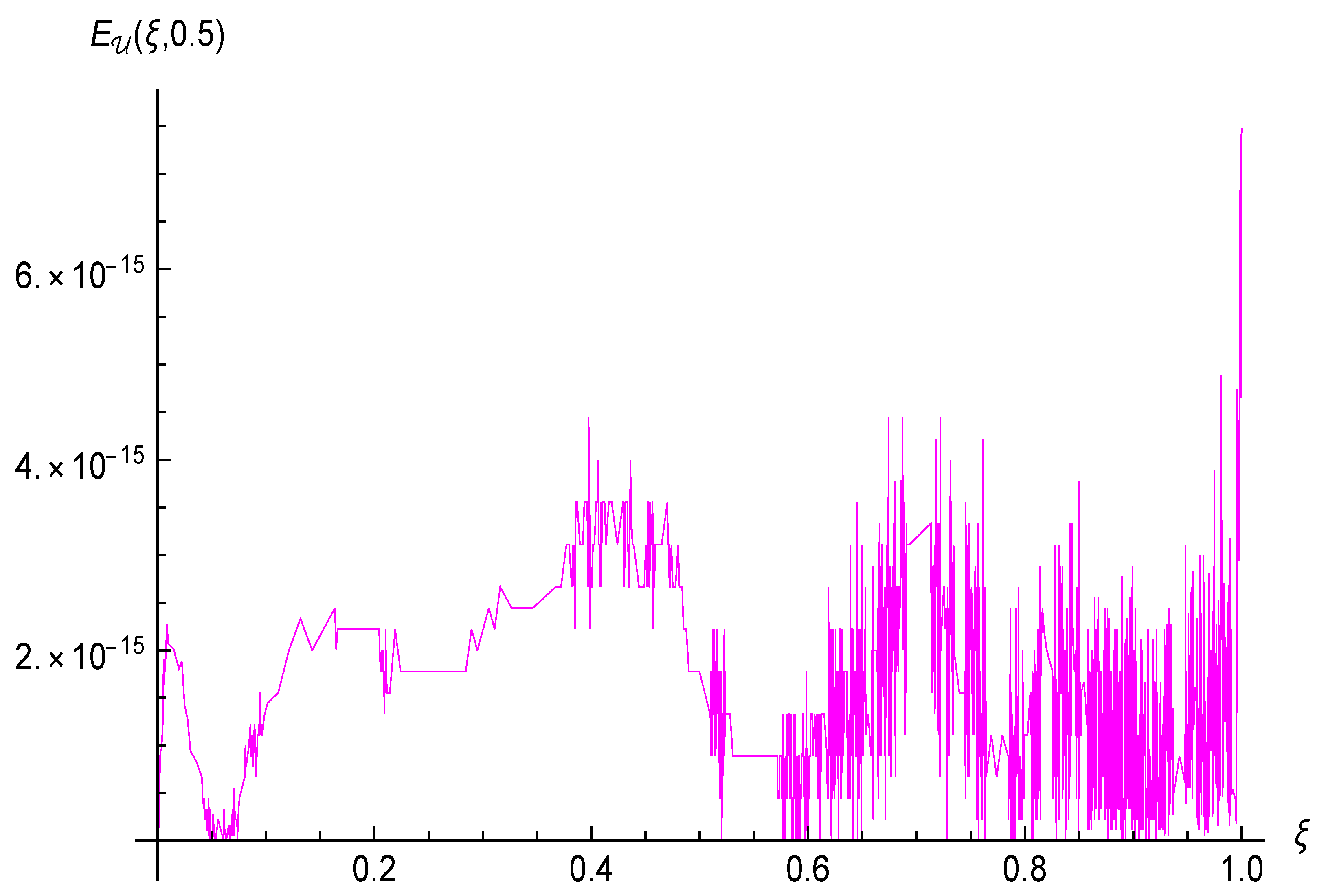
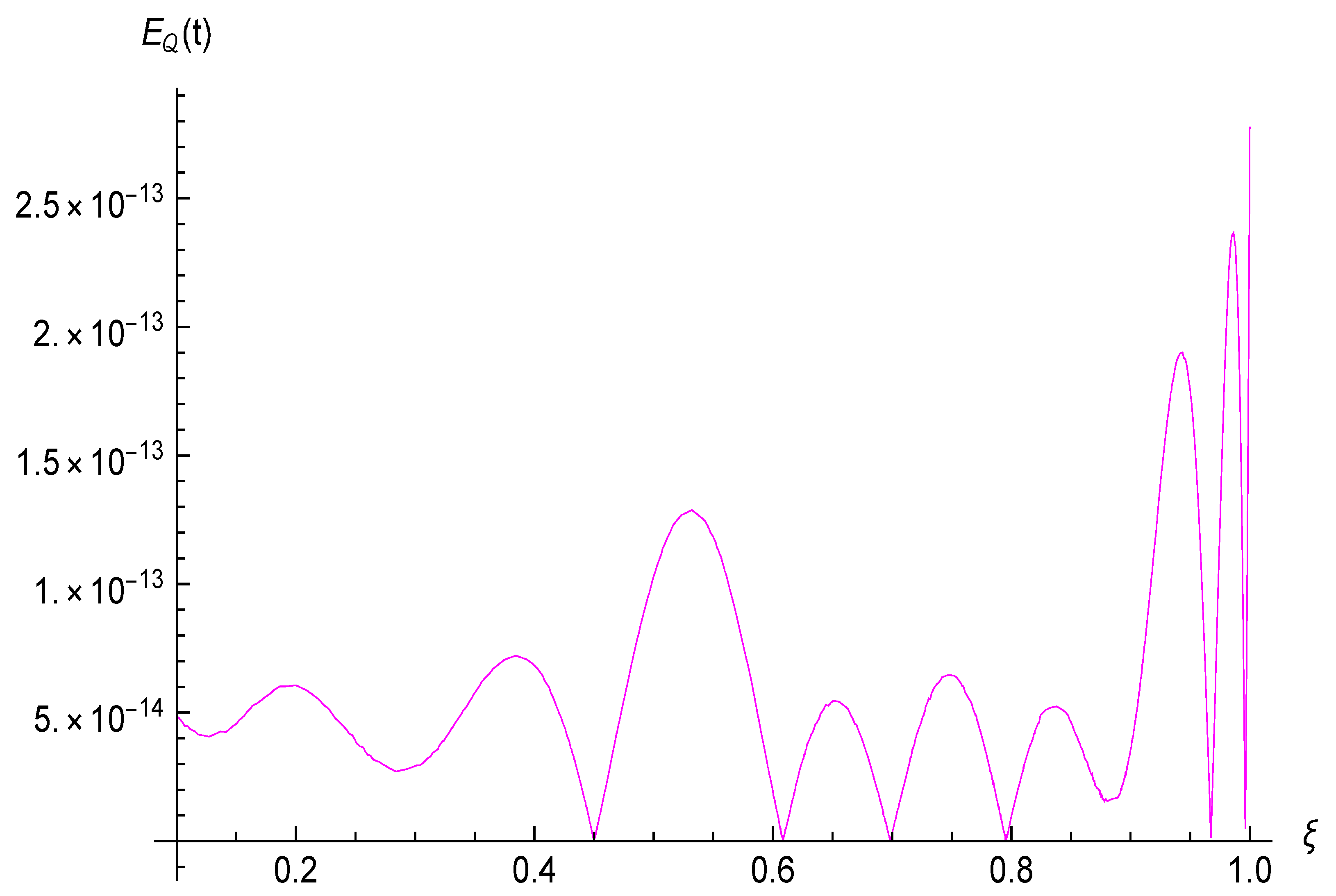
| CPU Time | (0, 0, 0, 0) | (0, −0.5, 0, 0.5) | (−0.5, −0.5, 0, 0) | (−0.5, −0.5, 0.5, 0.5) | ||
|---|---|---|---|---|---|---|
| 0.5 | (4,4) | 3.874 | ||||
| (8,8) | 10.937 | |||||
| (12,12) | 55.062 | |||||
| (16,16) | 232.329 | |||||
| 0.9 | (4,4) | 5.751 | ||||
| (8,8) | 12.657 | |||||
| (12,12) | 61.278 | |||||
| (16,16) | 239.312 | |||||
| 1.0 | (4,4) | |||||
| (8,8) | ||||||
| (12,12) | 1.39463 | |||||
| (16,16) |
| (0, 0, 0, 0) | (0, −0.5, 0, 0.5) | (−0.5, −0.5, 0, 0) | (−0.5, −0.5, 0.5, 0.5) | ||
|---|---|---|---|---|---|
| 0.5 | (4,4) | ||||
| (8,8) | |||||
| (12,12) | |||||
| (16,16) | |||||
| 0.9 | (4,4) | ||||
| (8,8) | |||||
| (12,12) | |||||
| (16,16) | |||||
| 1.0 | (4,4) | ||||
| (8,8) | |||||
| (12,12) | |||||
| (16,16) |
| (0, 0, 0, 0) | (0, −0.5, 0, 0.5) | (−0.5, −0.5, 0, 0) | (−0.5, −0.5, 0.5, 0.5) | ||
|---|---|---|---|---|---|
| 0.5 | (4,4) | ||||
| (8,8) | |||||
| (12,12) | |||||
| (16,16) | |||||
| 0.9 | (4,4) | ||||
| (8,8) | |||||
| (12,12) | |||||
| (16,16) |
| (0, 0, 0, 0) | (0, −0.5, 0, 0.5) | (−0.5, −0.5, 0, 0) | (−0.5, −0.5, 0.5, 0.5) | ||
|---|---|---|---|---|---|
| 0.5 | (4,4) | ||||
| (8,8) | |||||
| (12,12) | |||||
| (16,16) | |||||
| 0.9 | (4,4) | ||||
| (8,8) | |||||
| (12,12) | |||||
| (16,16) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkawy, M.A.; Amin, A.Z.M.; Babatin, M.M.; Alnahdi, A.S.; Zaky, M.A.; Hafez, R.M. Jacobi Spectral Collocation Technique for Time-Fractional Inverse Heat Equations. Fractal Fract. 2021, 5, 115. https://doi.org/10.3390/fractalfract5030115
Abdelkawy MA, Amin AZM, Babatin MM, Alnahdi AS, Zaky MA, Hafez RM. Jacobi Spectral Collocation Technique for Time-Fractional Inverse Heat Equations. Fractal and Fractional. 2021; 5(3):115. https://doi.org/10.3390/fractalfract5030115
Chicago/Turabian StyleAbdelkawy, Mohamed A., Ahmed Z. M. Amin, Mohammed M. Babatin, Abeer S. Alnahdi, Mahmoud A. Zaky, and Ramy M. Hafez. 2021. "Jacobi Spectral Collocation Technique for Time-Fractional Inverse Heat Equations" Fractal and Fractional 5, no. 3: 115. https://doi.org/10.3390/fractalfract5030115
APA StyleAbdelkawy, M. A., Amin, A. Z. M., Babatin, M. M., Alnahdi, A. S., Zaky, M. A., & Hafez, R. M. (2021). Jacobi Spectral Collocation Technique for Time-Fractional Inverse Heat Equations. Fractal and Fractional, 5(3), 115. https://doi.org/10.3390/fractalfract5030115







