Influence of Fin Length on Magneto-Combined Convection Heat Transfer Performance in a Lid-Driven Wavy Cavity
Abstract
:1. Introduction
2. Mathematical Formulation
2.1. Boundary Conditions
2.2. Dimensionless Analysis
2.3. Dimensionless Boundary Conditions
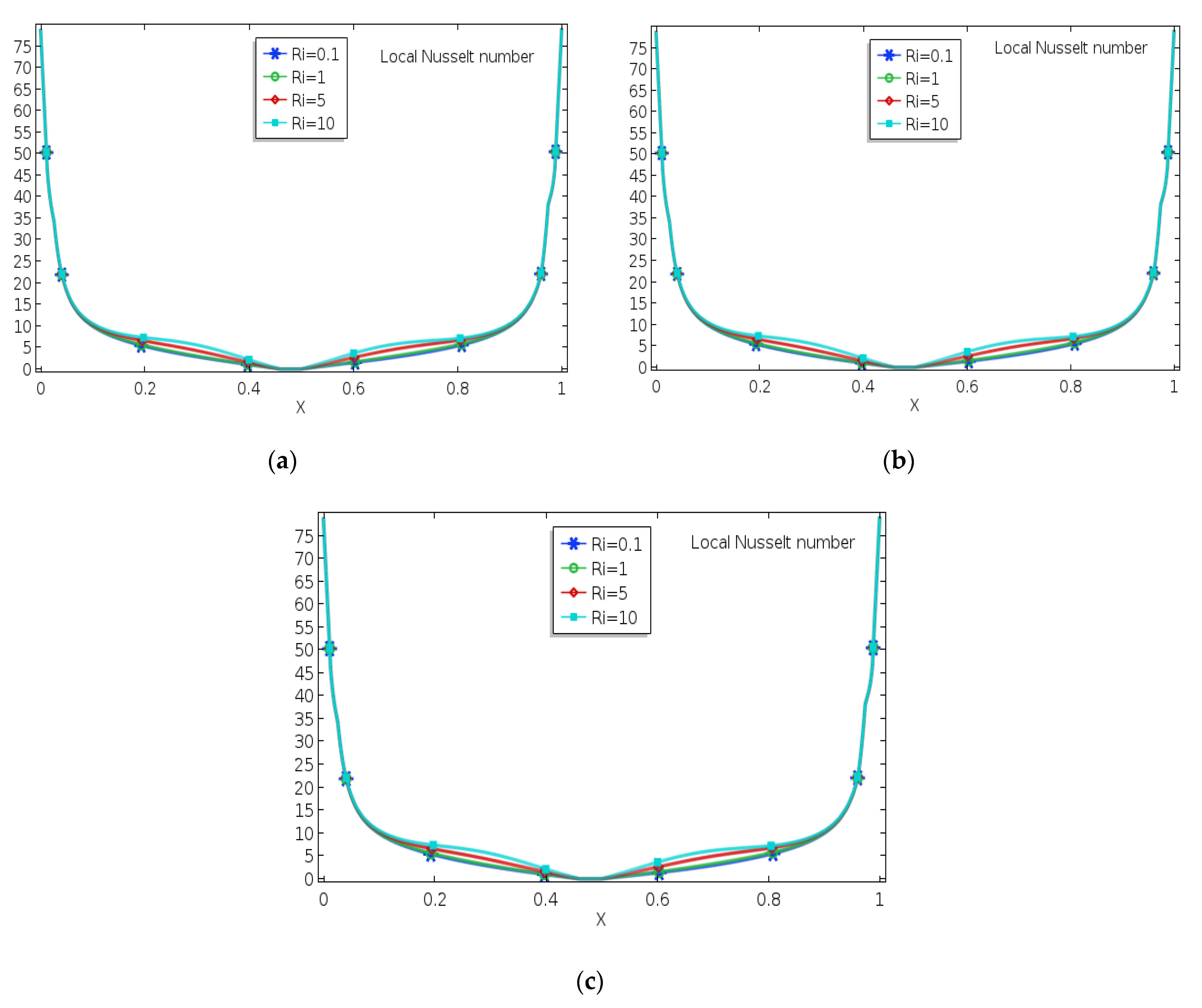
2.4. Nusselt Number
3. Fin Effectiveness
4. Computational Outline
5. Grid Refinement Test
6. Code Validation
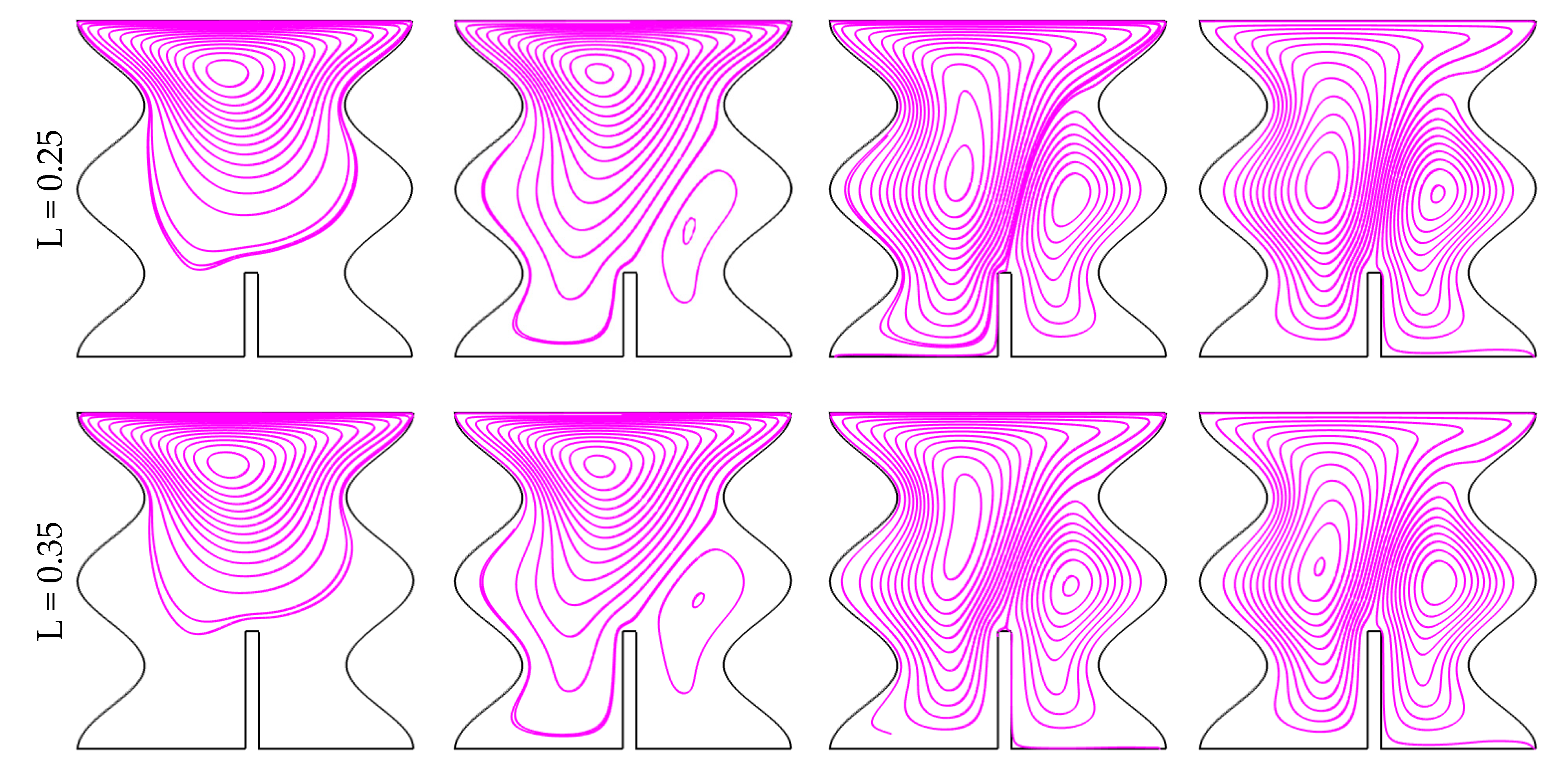
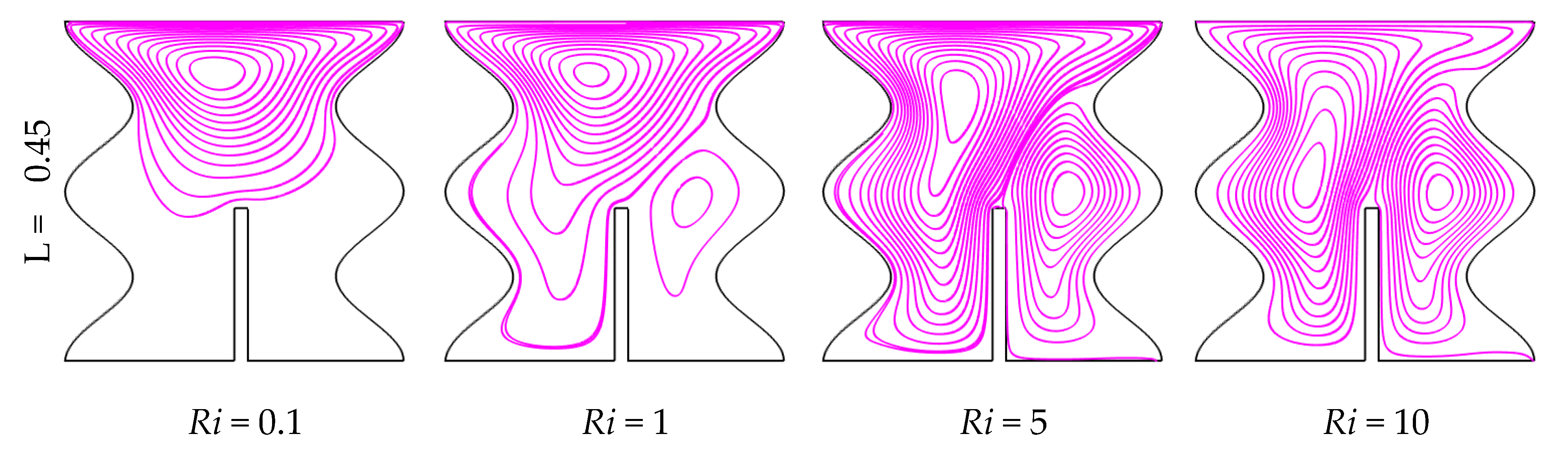
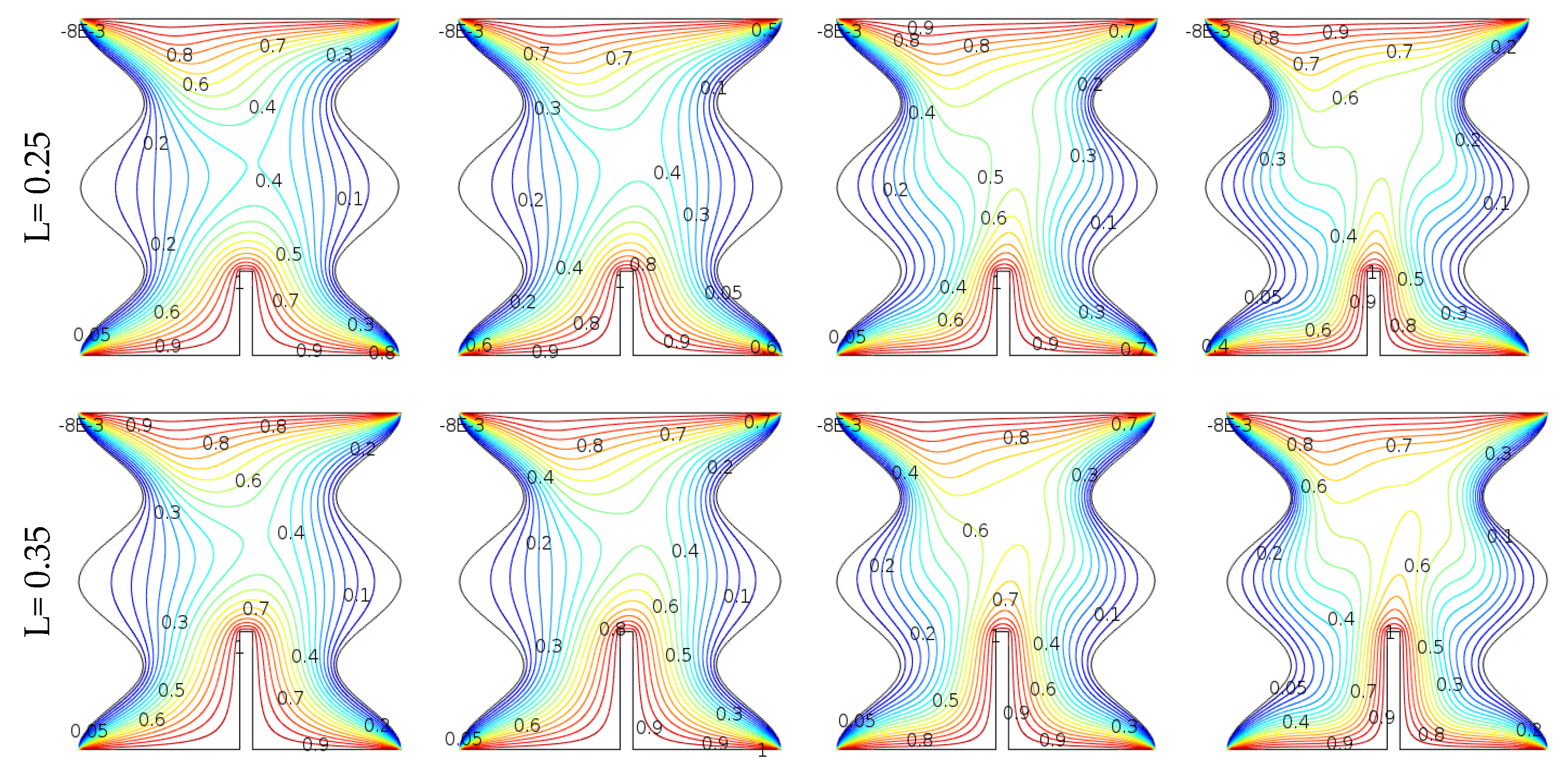
7. Discussion on Results
8. Conclusions
- ▪
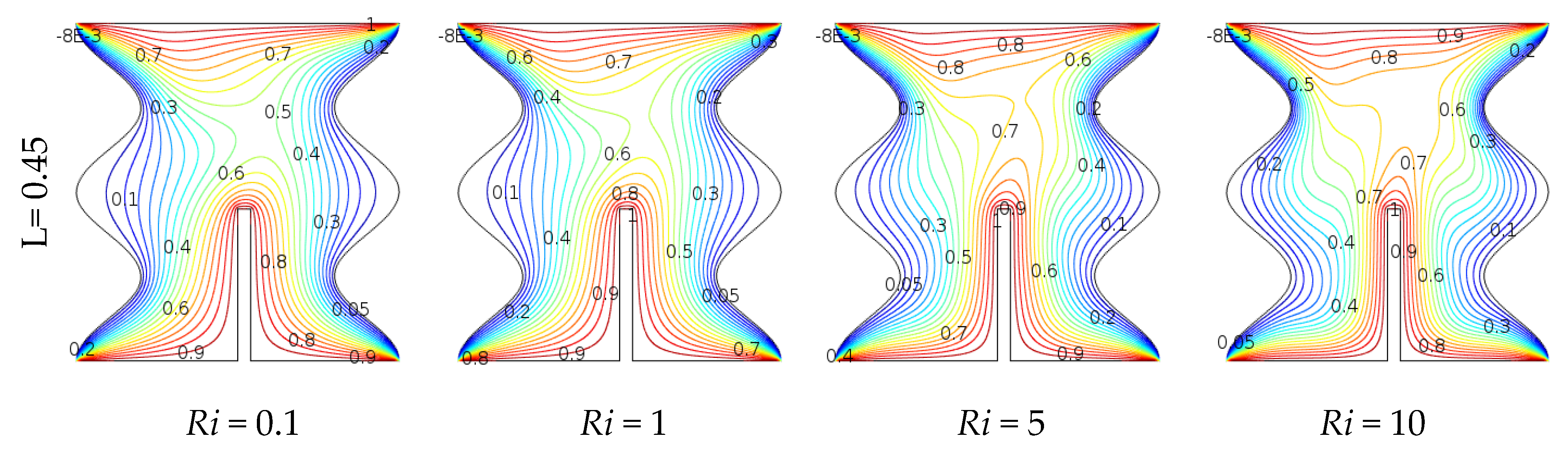
- The mixed convection variable Ri had significant impacts on flow field and isotherm contours. Flow field and heat transfer increased with increasing Richardson number for all fin lengths. The best result was seen at L= 0.45 for the greatest number of Ri;
- ▪
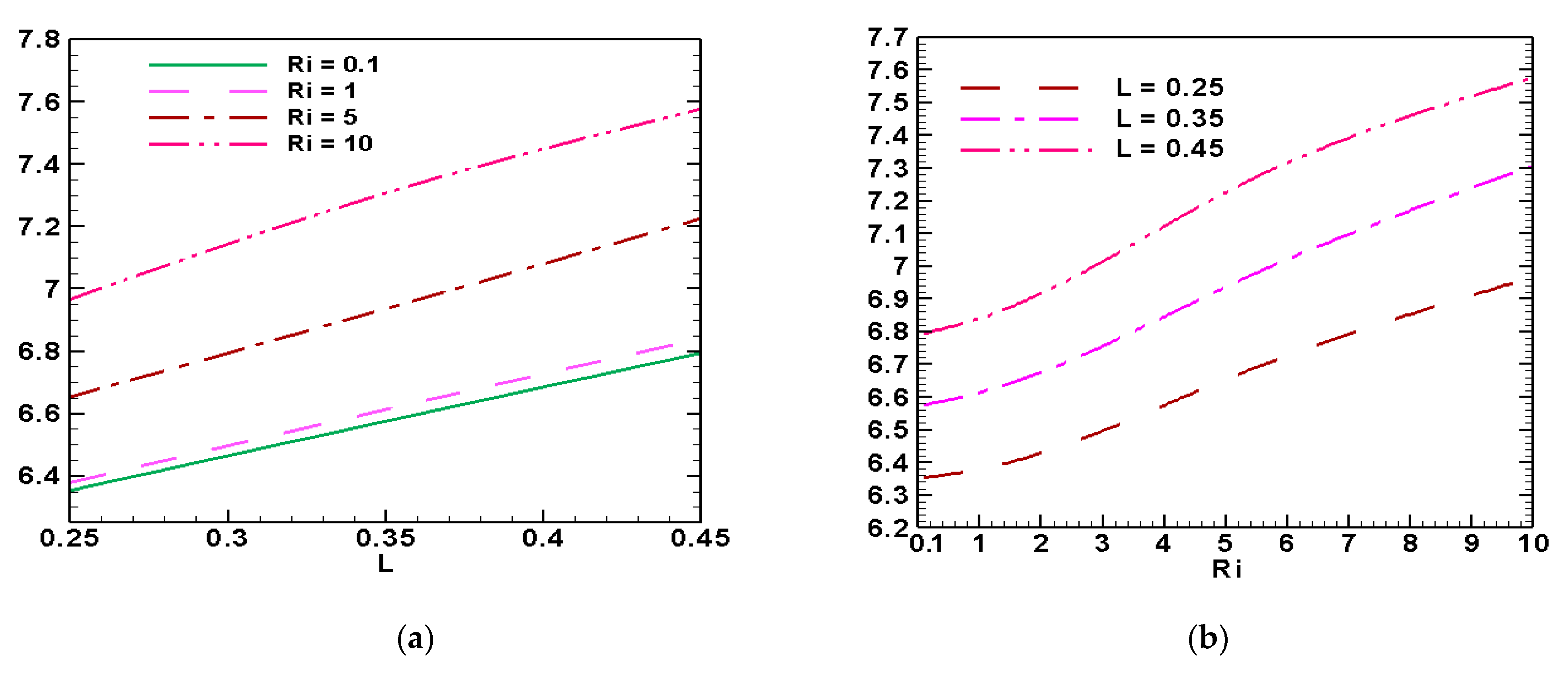
- The impacts of fin length on flow field and temperature characteristics were exposed to be noticeable in all fin lengths. Moreover, the fin length extended the heat transfer rate and the global Nusselt number and mean fluid temperature changes. The best result was found at L = 0.45;
- ▪
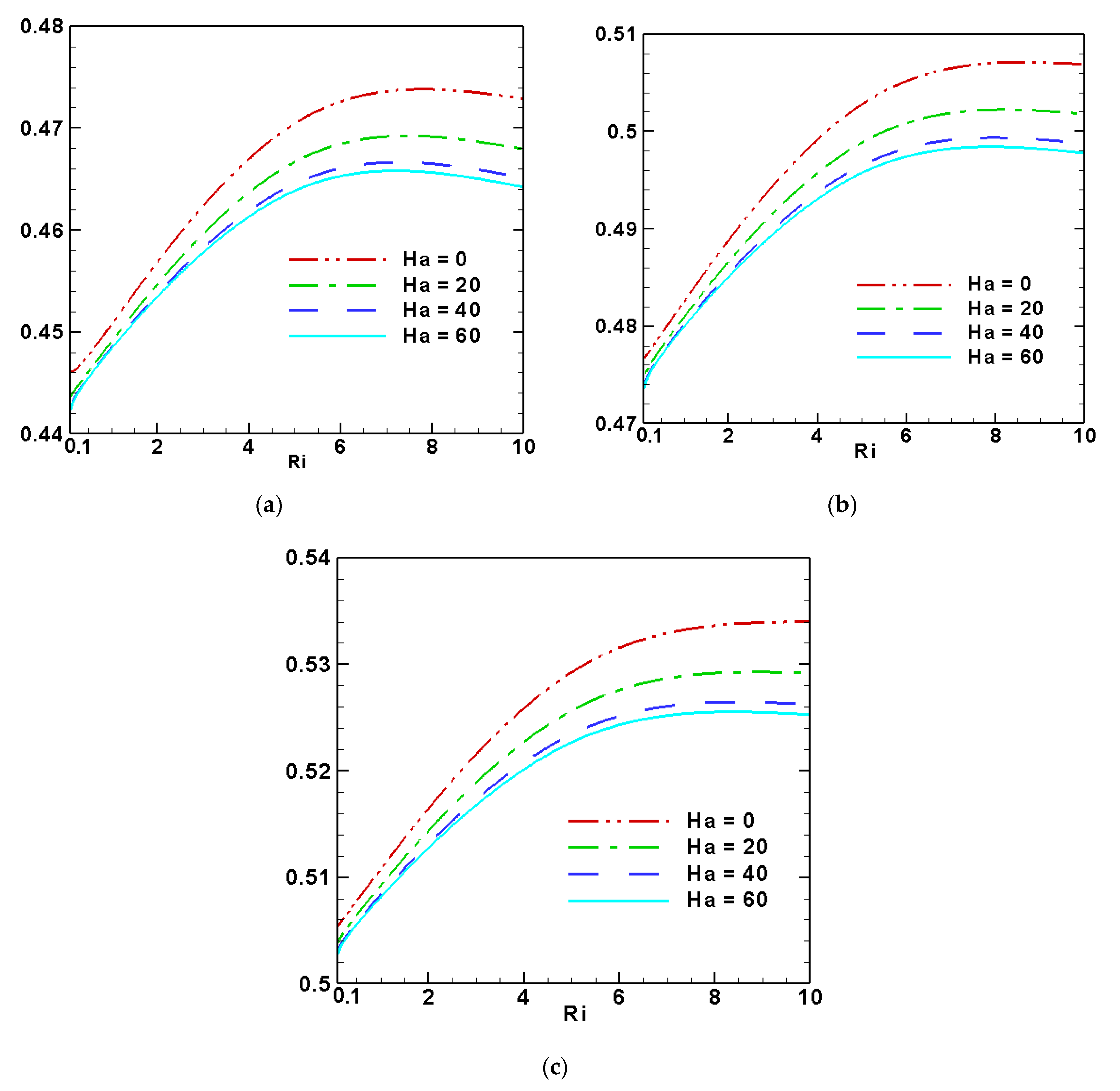
- The maximum rate of heat transfer was achieved for the highest Ri with the lowest Ha at the fin length L = 0.45;
- ▪
- Fin effectiveness was improved by raising Ri for distinct fin length. Moreover, the most remarkable fin effectiveness concerning fin length (L = 0.45) and Richardson number (Ri = 10) was found at Hartmann number (Ha = 20).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclatures
| A | amplitude |
| B | dimensionless fin thickness |
| g | gravitational acceleration |
| h* | heat transfer coefficient |
| h | fin position |
| H | dimensionless fin position |
| L | dimensionless fin length |
| N | dimensionless distance normal to surface coordinates |
| Nuav | average Nusselt number |
| NuL | local Nusselt number |
| Ha | Hartmann number |
| Pr | Prandlt number |
| Re | Reynold number |
| Ri | Richardson number |
| S | dimensionless special coordinate along enclosure surface |
| ψ, φ | dimensionless velocity in X and Y axis respectively |
| W | Enclosure height and width |
| Greek symbols | |
| α | thermal diffusivity |
| ρ | local density |
| β | a coefficient of thermal expansion |
| μ | dynamic viscosity |
| υ | kinematic viscosity |
| θ | dimensionless temperature |
| ε | effectiveness |
| λ | number of oscillations |
| Subscripts | |
| c | cool |
| f | fin |
| h | hot |
References
- Azizul, F.M.; Alsabery, A.I.; Hashim, I.; Chamkha, A.J. Impact of heat source on mixed convection flow inside wavy-walled cavity filled with nanofluids via heatline concept. Appl. Math. Comput. 2021, 393, 125754. [Google Scholar]
- Das, P.K.; Mahmud, S. Numerical investigation of natural convection inside a wavy enclosure. Int. J. Therm. Sci. 2003, 42, 397–406. [Google Scholar] [CrossRef]
- Misirlioglu, A.; Baytas, A.C.; Pop, I. Natural convection inside an inclined wavy enclosure filled with a porous medium. Transp. Porous Media 2006, 64, 229–246. [Google Scholar] [CrossRef]
- Al-Amiri, A.; Khanafer, K.; Bull, J.; Pop, I. Effect of sinusoidal wavy bottom surface on mixed convection heat transfer in a lid-driven cavity. Int. J. Heat Mass Transf. 2007, 50, 1771–1780. [Google Scholar] [CrossRef]
- Rostami, J. Unsteady natural convection in an enclosure with vertical wavy walls. Heat Mass Transf. 2008, 44, 1079–1087. [Google Scholar] [CrossRef]
- Mansour, M.; El-Aziz, M.A.; Mohamed, R.; Ahmed, S.E. Numerical simulation of natural convection in wavy porous cavities under the influence of thermal radiation using a thermal non-equilibrium model. Transp. Porous Media 2011, 86, 585–600. [Google Scholar] [CrossRef]
- Mushate, K.S. CFD prediction of natural convection in a wavy cavity filled with porous medium. Glob. J. Res. Eng. 2011, 11, 29–45. [Google Scholar]
- Nada, E.A.; Chamkha, A.J. Mixed convection flow of a nanofluid in a lid-driven cavity with a wavy wall. Int. Commun. Heat Mass Transf. 2014, 57, 36–47. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I. Natural convection in a wavy porous cavity with sinusoidal temperature distributions on both side walls filled with a nanofluid: Buongiorno’s mathematical model. J. Heat Transf. 2015, 137, 072601. [Google Scholar] [CrossRef]
- Sheremet, M.; Cimpean, D.; Pop, I. Free convection in a partially heated wavy porous cavity filled with a nanofluid under the effects of Brownian diffusion and thermophoresis. Appl. Therm. Eng. 2017, 113, 413–418. [Google Scholar] [CrossRef]
- Cheong, H.T.; Sivasankaran, S.; Sivasankaran, S.; Bhuvaneswari, M.; Bhuvaneswari, M. Natural convection in a wavy porous cavity with sinusoidal heating and internal heat generation. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 287–309. [Google Scholar] [CrossRef]
- Asad, M.F.A.; Alam, M.N.; Tunç, C.; Sarker, M.M.A. Heat Transport Exploration of Free Convection Flow inside Enclosure Having Vertical Wavy Walls. J. Appl. Comput. Mech. 2021, 7, 520–527. [Google Scholar]
- Fayz-Al-Asad, M.; Alam, M.N.; Ahmad, H.; Sarker, M.M.A.; Alsulami, M.D.; Gepreel, K.A. Impact of a closed space rectangular heat source on natural convective flow through triangular cavity. Results Phys. 2021, 23, 104011. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Tayebi, T.; Chamkha, A.J.; Hashim, I. Effect of rotating solid cylinder on entropy generation and convective heat transfer in a wavy porous cavity heated from below. Int. Commun. Heat Mass Transf. 2018, 95, 197–209. [Google Scholar] [CrossRef]
- Rahman, M.M.; Alim, M.A.; Sarker, M.M.A. Numerical study on the conjugate effect of joule heating and magnato-hydrodynamics mixed convection in an obstructed lid-driven square cavity. Int. Commun. Heat Mass Transf. 2010, 37, 524–534. [Google Scholar] [CrossRef]
- Öztop, H.F.; Sakhrieh, A.; Abu-Nada, E.; Al-Salem, K. Mixed convection of MHD flow in nanofluid filled and partially heated wavy walled lid-driven enclosure. Int. Commun. Heat Mass Transf. 2017, 86, 42–51. [Google Scholar] [CrossRef]
- Ashorynejad, H.R.; Shahriari, A. MHD natural convection of hybrid nanofluid in an open wavy cavity. Results Phys. 2018, 9, 440–455. [Google Scholar] [CrossRef]
- Öztop, H.F.; Salem, K.A.; Pop, I. MHD mixed convection in a lid-driven cavity with corner heater. Int. J. Heat Mass Transf. 2011, 54, 3494–3504. [Google Scholar] [CrossRef]
- Cho, C. Mixed convection heat transfer and entropy generation of Cu-water nanofluid in wavy-wall lid-driven cavity in presence of magnetic field. Int. J. Mech. Sci. 2019, 151, 703–714. [Google Scholar] [CrossRef]
- Mansour, M.A.; Rashad, A.M.; Morsy, Z. MHD free convection and sinusoidal heating in a wavy cavity filled with a heat generation porous medium using Cu-water nanofluids. Comput. Therm. Sci. Int. J. 2020, 12, 217–232. [Google Scholar]
- Alsabery, A.I.; Tayebi, T.; Kadhim, H.T.; Ghalambaz, M.; Hashim, I.; Chamkha, A.J. Impact of two-phase hybrid nanofluid approach on mixed convection inside wavy lid-driven cavity having localized solid block. J. Adv. Res. 2020, 30, 63–74. [Google Scholar] [CrossRef]
- Gupta, A.; Garu, A. Analysis heat transfer phenomenon from different fin geometries using CFD simulation in ANSYS. Int. J. Eng. Sci. Comput. 2019, 9, 23722–23729. [Google Scholar]
- Nag, A.; Sarkar, A.; Sastri, V.M.K. Natural convection in a differentially heated square cavity with horizontal partition plate on the hot wall. Comput. Methods Appl. Mech. Eng. 1993, 110, 143–156. [Google Scholar] [CrossRef]
- Tasnim, S.H.; Collins, M.R. Numerical analysis of heat transfer in a square cavity with a baffle on the hot wall. Int. Commun. Heat Mass Transf. 2004, 31, 639–650. [Google Scholar] [CrossRef]
- Sun, C.; Yu, B.; Öztop, H.F.; Wang, Y.; Wei, J. Control of mixed convection in lid-driven enclosures using conductive triangular fins. Int. J. Heat Mass Transf. 2011, 54, 894–909. [Google Scholar] [CrossRef]
- Xu, F.; Saha, S.C. Transition to an unsteady flow induced by a fin on the sidewall of a differentially heated air-filled square cavity and heat transfer. Int. J. Heat Mass Transf. 2014, 71, 236–244. [Google Scholar] [CrossRef]
- Elatar, A.; Teamah, M.A.; Hassab, M.A. Numerical study of laminar natural convection inside square enclosure with single horizontal fin. Int. J. Therm. Sci. 2016, 99, 41–51. [Google Scholar] [CrossRef]
- Palaniappan, G.; Murugan, M.; Mdalla, Q.M.A.; Doh, B.A.D.H. Numerical investigation of open cavities with parallel insulated baffles. Int. J. Heat Technol. 2020, 38, 611–621. [Google Scholar] [CrossRef]
- Siddiqui, M.A.; Riaz, A.; Khan, I.; Nisar, K.S. Augmentation of mixed convection heat transfer in a lid-assisted square enclosure utilizing micropolar fluid under magnetic environment: A numerical approach. Results Phys. 2020, 18, 103245. [Google Scholar] [CrossRef]
- Kouz, W.A.; Muhtady, A.A.; Owhaib, W.; Dahidi, S.A.; Hader, M.; Alghanam, R.A. Entropy generation optimization for rarified nanofluid flows in a square cavity with two fins at the hot wall. Entropy 2019, 21, 103. [Google Scholar] [CrossRef] [Green Version]
- Shulepova, E.V.; Sheremet, M.A.; Öztop, H.F.; Hamdeh, N.A. Mixed convection of Al2O3-H2O nanoliquid in a square chamber with complicated fin. Int. J. Mech. Sci. 2020, 165, 105192. [Google Scholar] [CrossRef]
- Hussain, S.; Jamal, M.; Geridonmez, B.P. Impact of fins and inclined magnetic field in double lid-driven cavity with Cu-water nanofluid. Int. J. Therm. Sci. 2021, 161, 106707. [Google Scholar] [CrossRef]
- Asad, M.F.A.; Sarker, M.M.A.; Hossain, M.A. Numerical investigation of MHD mixed convection heat transfer having vertical fin in a lid-driven square cavity. AIP Conf. Proc. 2019, 2121, 030023-6. [Google Scholar]
- Asad, M.F.A.; Sarker, M.M.A.; Munshi, M.J.H. Numerical investigation of natural convection flow in a hexagonal enclosure having vertical fin. J.Sci. Res. 2019, 11, 173–183. [Google Scholar] [CrossRef] [Green Version]
- Asad, M.F.A.; Munshi, M.J.H.; Sarker, M.M.A. Effect of fin length and location on natural convection heat transfer in a wavy cavity. Int. J. Thermofluid Sci. Tech. 2020, 7, 070303. [Google Scholar]
- Yavuz, M.; Sene, N. Approximate Solutions of the Model Describing Fluid Flow Using Generalized ρ-Laplace Transform Method and Heat Balance Integral Method. Axioms 2020, 9, 123. [Google Scholar] [CrossRef]
- Althobati, S.; Bazighifan, O.; Yavuz, M. Some Important Criteria for Oscillation of Non-Linear Differential Equations with Middle Term. Mathematics 2021, 9, 346. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Bazighifan, O.; Ragusa, M.A. Nonlinear Neutral Delay Differential Equations of Fourth-Order: Oscillation of Solutions. Entropy 2021, 23, 129. [Google Scholar] [CrossRef]
- Taylor, C.; Hood, P. A numerical solution of the Navier–Stokes equations using finite element technique. Comput. Fluids 1973, 1, 73–89. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]

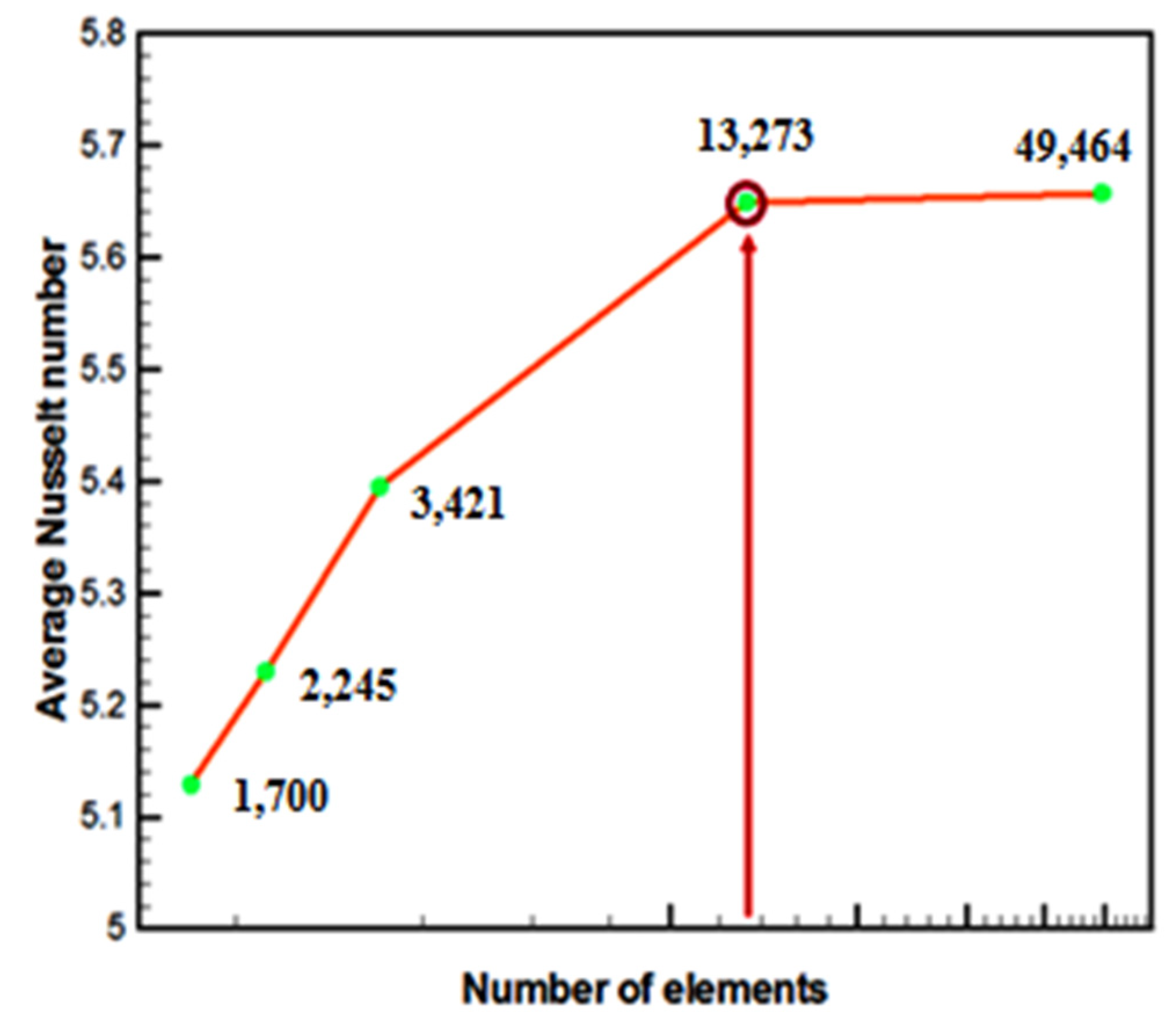



| Nodes (Elements) | 931 (1700) | 1213 (2245) | 1823 (3421) | 6844 (13,273) | 25,133 (49,464) |
| 5.1290 | 5.2303 | 5.3952 | 5.6491 | 5.6617 | |
| Time (s) | 7 | 10 | 13 | 21 | 38 |
| B | 0.1 | 0.02 | 0.04 |
|---|---|---|---|
| Nag et al. [22] | 9.033 | 8.861 | 8.888 |
| Elatar et al. [26] | 8.947 | 8.672 | 8.710 |
| Present result | 8.985 | 8.783 | 8.838 |
| Fin Effectiveness | ||||
|---|---|---|---|---|
| L | Ri = 0.1 | Ri = 1 | Ri = 5 | Ri = 10 |
| 0.25 | 1.081425 | 1.087349 | 1.103860 | 1.118086 |
| 0.35 | 1.132538 | 1.138264 | 1.153317 | 1.169180 |
| 0.45 | 1.183970 | 1.187686 | 1.197163 | 1.211730 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fayz-Al-Asad, M.; Yavuz, M.; Alam, M.N.; Sarker, M.M.A.; Bazighifan, O. Influence of Fin Length on Magneto-Combined Convection Heat Transfer Performance in a Lid-Driven Wavy Cavity. Fractal Fract. 2021, 5, 107. https://doi.org/10.3390/fractalfract5030107
Fayz-Al-Asad M, Yavuz M, Alam MN, Sarker MMA, Bazighifan O. Influence of Fin Length on Magneto-Combined Convection Heat Transfer Performance in a Lid-Driven Wavy Cavity. Fractal and Fractional. 2021; 5(3):107. https://doi.org/10.3390/fractalfract5030107
Chicago/Turabian StyleFayz-Al-Asad, Md., Mehmet Yavuz, Md. Nur Alam, Md. Manirul Alam Sarker, and Omar Bazighifan. 2021. "Influence of Fin Length on Magneto-Combined Convection Heat Transfer Performance in a Lid-Driven Wavy Cavity" Fractal and Fractional 5, no. 3: 107. https://doi.org/10.3390/fractalfract5030107
APA StyleFayz-Al-Asad, M., Yavuz, M., Alam, M. N., Sarker, M. M. A., & Bazighifan, O. (2021). Influence of Fin Length on Magneto-Combined Convection Heat Transfer Performance in a Lid-Driven Wavy Cavity. Fractal and Fractional, 5(3), 107. https://doi.org/10.3390/fractalfract5030107










